Abstract
The insatiable appetite for energy to support human brain function is mainly supplied by glucose oxidation (CMRglc(ox)). But how much energy is consumed for signaling and nonsignaling processes in gray/white matter is highly debated. We examined this issue by combining metabolic measurements of gray/white matter and a theoretical calculation of bottom-up energy budget using biophysical properties of neuronal/glial cells in conjunction with species-exclusive electrophysiological and morphological data. We calculated a CMRglc(ox)-derived budget and confirmed it with experimental results measured by PET, autoradiography, 13C-MRS, and electrophysiology. Several conserved principles were observed regarding the energy costs for brain’s signaling and nonsignaling components in both human and rat. The awake resting cortical signaling processes and mass-dependent nonsignaling processes, respectively, demand ∼70% and ∼30% of CMRglc(ox). Inhibitory neurons and glia need 15–20% of CMRglc(ox), with the rest demanded by excitatory neurons. Nonsignaling demands dominate in white matter, in near opposite contrast to gray matter demands. Comparison between 13C-MRS data and calculations suggests ∼1.2 Hz glutamatergic signaling rate in the awake human cortex, which is ∼4 times lower than signaling in the rat cortex. Top-down validated bottom-up budgets could allow computation of anatomy-based CMRglc(ox) maps and accurate cellular level interpretation of brain metabolic imaging.
Keywords: Aerobic glycolysis, spiking rate, astrocyte, glutamate, electroencephalography, lactate
Introduction
The human brain is extremely energy demanding compared to other organs in the body1 to support the conscious state.2 The human brain is estimated to require 10–20 watts, while a few million watts is needed to power supercomputers.3 A highly energy efficient mammalian brain implies optimal organization of cortical circuits for cognitive functions.4 Recent experimental and theoretical research suggest that multiple factors such as optimized ion-channel kinetics, axon myelination, and warmer body temperature play key roles in minimizing the energy cost for action potential generation and propagation.5–11 It is also suggested that brain circuitries are organized in an energy-optimized way.4
These and other recent results highlight the importance of a more accurate brain energy budget calculation12–14 to promote a better understanding of the energetic basis of brain computation. Furthermore, understanding the relationship between energetics and function of the brain is crucial to the interpretation of functional magnetic resonance imaging (fMRI) studies of the human brain. The understanding of fMRI studies is based on experimental observations that brain energy metabolism from glucose oxidation (CMRglc(ox)) changes in a correlated manner with signaling processes,15–18 which include action potential, synaptic transmission, glutamate or GABA recycling, calcium activities, and hemodynamics through neurovascular coupling.19 Nonsignaling processes are generally assigned to housekeeping needs (e.g. biosynthesis or proton leaks) and maintenance of resting cell membrane potentials, which generally do not change significantly with brain activity. At physiological temperatures, action potentials generally take around 2 ms duration. For low firing rates (<10 Hz), neuronal membranes spend less than 2% of the spiking duty cycle at the action potential level and are at the resting potential level for over 98% of the time. Therefore, for the range of firing rates modeled in this paper, we approximate the membrane potential during inter-signaling periods as being a constant at the resting potential value. However, there is still uncertainty regarding the cost for signaling and nonsignaling components in mammalian brain, especially in humans.20 This uncertainty in nonsignaling processes also inherently implies ambiguity for signaling components, and thus makes quantitative interpretation of brain fMRI signals difficult.
Here, we construct a comprehensive bottom-up CMRglc(ox)-derived energy budget for human gray and white matter based on biophysical properties of neuronal and glial cells, together in conjunction with electrophysiological and morphological data from human and rat brain. While similar bottom-up approaches have been used previously,12,14,20–22 our approach differs in that we use extensive top-down validation, and associated our bottom-up calculations with a range of behavioral or metabolic states (e.g. anesthetized, awake, sleep, etc.) measured by various experimental techniques. Furthermore, we update the biophysical and physiological parameters previously used in bottom-up budgets for both rat and human brain. We compare CMRglc(ox) computed from the budget with CMRglc(ox) from experimental measurements (by [18F]-fluorodeoxyglucose (FDG) positron emission tomography (PET), 13C magnetic resonance spectroscopy (13C-MRS), [14C]-2-deoxyglucose (2DG) autoradiography). We also compare the neuronal activity computed from the budget with neuronal activity from experimental measurements (by firing rates from extracellular recordings in rats and bispectral index (BIS) from electroencephalography (EEG) recordings in humans), allowing investigations of both signaling processes associated with ion flux and mass-dependent nonsignaling processes. This top-down validation of bottom-up energy budgets for gray and white matter may help provide solutions for several open issues, e.g. how the signaling and nonsignaling components interact with each other to underlie the metabolic data collected by methods like fMRI, PET, and 13C-MRS in the human brain.
Materials and methods
The budget details are in SI Text, Sections (a) to (f), where the important parameters are shown in Table 1. Note that all these parameters are based on more recent experimental reports and computational estimations, where we also did calculations to confirm some of these parameters. For example, recent in vivo 13C-MRS studies in rat and human brain suggest that 70–75% of the energy in the awake state supports cortical signaling functions, whereas the remaining 25–30% fraction is attributed to nonsignaling functions.13 Previous bottom-up budget estimates range from 20% to 50% of the ATP derived from CMRglc(ox) supporting rat cerebral cortex nonsignaling functions.20 This large uncertainty in nonsignaling functions is mainly due to the lack of experimental evidence of specific cellular physiologic and metabolic processes. We used the allometry theory of metabolism for individual cells to estimate the housekeeping cost by computing averaged mass value of individual cells and mass-dependent metabolic rate23–25 (see SI Text, Section A.1).
Table 1.
Comparison of energy budget “input” parameters, which include morphological (e.g. cell number, cell mass, cell size, etc.) and biophysical (e.g. membrane resistance and capacitance, etc.) components of individual cell types.
| Parameters | Budget parameters |
SI text | ||
|---|---|---|---|---|
| Current | Previous | |||
| Number cells (, units of billions of cells) for human brain | ||||
| 13.64 (ref.25) | Section D | |||
| 19.15 (ref.25) | Section D | |||
| 41.69 (ref.25) | Section D | |||
| unmyelinated axon | 2.71 (ref.25) | Section B | ||
| myelinated axon | 9.43 (ref.21) | Section B | ||
| 1.48 (ref.21) | Section B | |||
| 4.28 (ref.21) | Section B | |||
| 35.9 (ref.21) | Section B | |||
| Mass of tissues (Mx) in units of g and cells (mx) in units of ng for human brain | ||||
| Mgm | 638.37 g (ref.25) | 475 g (ref.22) | Section E | |
| Mwm | 593.89 g (ref.25) | Section E | ||
| mn | 29.5 ng (ref.25) | Section F | ||
| mg | 12.3 ng (ref.25) | Section F | ||
| Cellular anatomy by length (Lx) and diameter (Dx) in units of cm, mm, or μm | ||||
| Laxon human neuron | 7.56 cm (ref.28) | 10 cm (ref.22) | Section A.3 | |
| Ldendrite human neuron | 0.84 cm (ref.28) | 1.1 cm (ref.22) | Section A.3 | |
| Laxon rat neuron | 4 cm (ref.14) | 4 cm (ref.14) | Section A.3 | |
| Ldendrite rat neuron | 0.44 cm (ref.14) | 0.44 cm (ref.14) | Section A.3 | |
| Daxon human/rat neuron | 0.3 mm (ref.14,22) | 0.3 mm (ref.14,22) | Section A.3 | |
| Ddendrite human/rat neuron | 0.9 μm (ref.14,22) | 0.9 μm (ref.14,22) | Section A.3 | |
| Cellular density (ρ) for gray matter (GM) in units of millions of cells/g | ||||
| Human GM neuronal ρ | 21.4 (ref.25) | 40 (ref.22) | 18.3 (ref.13) | Section A.3 |
| Rat GM neuronal ρ | 40.3 (ref.56) | 92 (ref.21) | 47.5 (ref.13,2) | Section A.3 |
| Human GM glial ρ | 30.0 (ref.25) | 38 (ref.22) | 18.3 (ref.13) | Section A.3 |
| Rat GM glial ρ | 59.4 (ref.56) | 92 (ref.21) | 47.5 (ref.13,32) | Section A.3 |
| Membrane resistance (Rm, MΩ) and capacitance (Cm, μF/cm) in gray (GM) and white (WM) matter | ||||
| Rm pyramidal cell | 100 (ref.57) | 74 (ref.13) | 200 (ref. 14) | Section B |
| Rm interneuron | 200 (ref.58,59) | 74 (ref.13) | Section B | |
| Rm glial cell | 200 (ref.60) | 74 (ref.13) | 10,500 (ref. 61) | Section B |
| Rm astrocyte in WM | 560 (ref. 21) | 560 (ref.21) | Section B | |
| Rm OPC in WM | 800 (ref.21) | 800 (ref.21) | Section B | |
| Rm oligodendrocyte in WM | 200 (ref.21) | 200 (ref.21) | Section B | |
| Rm myelinated axon in WM | 0.55 × 103 (ref.21) | 0.55 × 103 (ref.21) | Section B | |
| Cm for axon | 1 (ref.12,21) | 1 (ref.12,21) | Section B | |
| Cm for myelinated axon | 0.08 (ref.12,21) | 0.08 (ref.12,21) | Section B | |
| Na+ entry ratio (ɛ) and oxygen-to-glucose (OGI) index; both without units | ||||
| ɛ pyramidal | 1.5 (ref.8) | 1.3 (ref.12,21) | Section A.3 | |
| ɛ interneuron | 2.3 (ref.6) | 2.3 (ref.12,21) | Section A.3 | |
| OGI | 5.3 (ref.13) | 5.3 (ref.13) | Section A.1 | |
In addition, to our knowledge, all the previous bottom-up budgets did not include glial activity.12,14,21,22 However, as reported in recent studies,26,27 astrocytes in gray matter as well as oligodendrocyte precursor cells (OPCs) and oligodendrocytes in white matter have active calcium responses related to spiking process through at least two different mechanisms, i.e. (i) transmembrane calcium influx via voltage-operated calcium channels, and (ii) calcium release from IP3-sensitive internal calcium stores. Hence, it is necessary to calculate energy cost for the calcium-related activities of glia. Furthermore, we accounted for billions of glial cells and unmyelinated axons in white matter25 (see SI Text, Section B for details). Considering that the large number of glial cells may contribute to a non-negligible portion of the brain budget, we carefully considered glial cells in our bottom-up budget calculation for both gray and white matter (see SI Text, Sections A and B for details).
Moreover, the total axonal length of a human neuron – 7.56 cm – was calculated based on a more recently established relation of cross-species neuroanatomical data.25,28,29 Indeed, with this value (see Results), the calculated energy budget matches the PET data better than axon length of 10 cm, as reported by a previous study.30 In addition, a new cell counting method25,31 estimated that human gray matter neuronal density is 21.4 million/g and glial cell density is 30 million/g, which are both lower than 40 and 38 million/g, respectively, in previous rough estimations which are based on extrapolation of cell counts from localized measurements.30 These new methods were also able to estimate that rat cortical neuronal and glial cell densities are 40.3 and 59.4 million/g, which are slightly different from earlier reports.32
The energy budgets for neuronal and glial cells in gray matter (SI Text, Section A) and white matter (SI Text, Section B) of the human brain were calculated separately, using cellular biophysical properties with electrophysiological and morphological data of human brain. The same principles, but scaled according to species differences, were then applied for energy budgets for neurons and glial cells in gray matter and white matter of the rat brain (SI Text, Section C). All the “output” parameters of the energy budget, both for rat and human, are listed in Table 2. Specifically for the human cerebrum, we estimated the number of neuronal and glial cells in gray and white matter (SI Text, Section D), masses of gray and white matter (SI Text, Section E), and masses of individual neuron and glial cells in gray and white matter (SI Text, Section F). We found that that gray matter and white matter weigh roughly the same, but there is a significantly larger number of glial cells (19.2 and 41.7 billion, respectively, in gray and white matter) than neurons (13.6 and 2.7 billion, respectively, in gray and white matter) and an individual neuron weighs more than twice the mass of a glial cell (SI Text, Sections D to F). The cerebellum was excluded in our budget.
Table 2.
Comparison of energy budget “output” parameters, which include energies of individual cell types (e.g. neuronal and glial cells), energies of all cells (e.g. in gray and white matter), and neuronal firing rate.
| Parameters | Budget parameters |
SI Text | ||
|---|---|---|---|---|
| Current | Previous | |||
| Energy of individual cells (, units of ATP/s) for gray (GM) and white (WM) matter; fe = 1 Hz and fi = 2 Hz | ||||
| Human GM | 2.1 × 109 | 4.81 × 109 (ref.13) | 6.1 × 109 (ref.22) | Section A |
| Human GM | 1.22 × 109 | 0.92 × 109 (ref.13) | 0.86 × 109 (ref.22) | Section A |
| Human GM | 2.87 × 109 | Section A | ||
| Human GM | 0.88 × 109 | Section A | ||
| Human GM | 5.38 × 108 | Section A.1 | ||
| Human GM | 3.55 × 108 | Section A.1 | ||
| Human GM | 1.37 × 108 | Section A.1 | ||
| Human GM | 6.82 × 108 | 3.42 × 108 (ref.14) | 8.6 × 108 (ref.22) | Section A.2 |
| Human GM | 3.41 × 108 | Section A.2 | ||
| Human GM | 2.54 × 108 | 1.02 × 108 (ref.14) | 3.1 × 108 (ref.22) | Section A.2 |
| Human GM | 2.65 × 108 | 2.4 × 109 (ref.22) | Section A.3 | |
| Human GM | 3.09 × 108 | Section A.3 | ||
| Human GM | 15.8 × 108 | 3.18 × 109 (ref.22) | Section A.4 | |
| Human GM | 20.5 × 108 | Section A.4 | ||
| Human GM | 1.41 × 108 | 2.4 × 108 (ref.22) | Section A.5 | |
| Human GM | 1.82 × 108 | Section A.5 | ||
| Human GM | 1.16 × 108 | 3.05 × 108 (ref.22) | Section A.6 | |
| Human GM | 2.31 × 108 | Section A.6 | ||
| Human GM | 0.924 × 108 | Section A.6 | ||
| Ee Human GM | 3.32 × 109 | 5.73 × 109 (ref.13) | 6.96 × 109 (ref.22) | Section A |
| Ei Human GM | 3.75 × 109 | Section A | ||
| Eg Human GM | 5.69 × 108 | Section A | ||
| Human WM | 2.23 × 108 | Section B | ||
| Human WM | 2.23 × 108 | Section B | ||
| Human WM | 2.23 × 108 | Section B | ||
| Human WM | 9.05 × 108 | Section B | ||
| Human WM | 8.51 × 108 | Section B | ||
| Human WM | 3.4 × 108 | Section B | ||
| Human WM | 0.92 × 108 | Section B | ||
| Human WM | 0.92 × 108 | Section B | ||
| Rat GM | 1.58 × 109 | 4.81 × 109 (ref.13) | 0.71 × 109 (ref.14) | Section A, C |
| Rat GM | 1.17 × 109 | 0.92 × 109 (ref.13) | 0.34 × 109 (ref.14) | Section A, C |
| Ee Rat GM | 2.75 × 109 | 5.73 × 109 (ref.13) | 1.05 × 109 (ref.14) | Section A, C |
| Ei Rat GM | 2.78 × 109 | Section A, C | ||
| Eg Rat GM | 0.924 × 108 | Section A, C | ||
| Energy of all cells (, units of ATP/s) in whole cerebrum with awake resting firing rate. | ||||
| 2.65 × 1019 | Section B | |||
| 1.36 × 1019 | Section B | |||
| 2.4 × 1019 | 5.18 × 1019 (ref.21) | Section A | ||
| 4.6 × 1019 | 7.77 × 1019 (ref.21) | Section A | ||
| Ewm | 4.01 × 1019 | Section B | ||
| Egm | 7.0 × 1019 | 12.95 × 019 (ref.21) | Section A | |
| Cortical firing rate of excitatory neurons in awake resting state (fe, units of Hz) | ||||
| fe Human | 1.15 Hz | 0.024 (ref.22) | 0.5-2 (ref.42,43) | Section A |
| fe Rat | 4.3 Hz | 4 Hz (ref.12) | Section C | |
Results
We first validated energy budgets for gray matter of rat and human brain to identify unifying principles of neuronal and glial cells. We then applied these validated components for estimating white matter energetics in rat and human brain.
Gray matter budget validation from in vivo PET, 2DG, and electrophysiology measurements
The total ATP consumption rate in human gray matter (Egm; SI Text, Section A; equations S1 to S12) contains nonsignaling () and signaling () processes. includes energy demands for housekeeping mechanisms () and resting potential maintenance () of all cell types, whereas depends on rate of neural firing (f) and includes energy demands for action potential conduction (), synaptic transmission (), glutamate or GABA recycling (, ), and calcium activity () of all the neuronal and glial cells, respectively. Based on the available metabolic and neurophysiologic data in rat (Table S1) and human (Table S2) brain, we calculated and of 1.1 × 1019 ATP/s and 1.3 × 1019 ATP/s, respectively (using equations S2 to S6), which together make = 2.4 × 1019 ATP/s (Table 2). We assumed a fixed relationship for firing rates of excitatory (fe; see equation S2(a)) and inhibitory (fi; see equation S2(b)) neurons based on limited in vivo data of somatosensory cortex33 (see SI Text, Section A), but this can be amended based on future fe and fi values measured across brain regions. Likewise, for f = 1 Hz, we calculated , , , and (using equations S3 to S6) of 0.37 × 1019 ATP/s, 2.28 × 1019 ATP/s, 0.2 × 1019 ATP/s, and 0.34 × 1019 ATP/s, respectively (Table 2). These terms together contribute to (4.6 × 1019 ATP/s for f = 1.15 Hz). So the total gray matter cost (Egm) for f = 1 Hz, which is given by sum of and , is 7.0 × 1019 ATP/s. Comparison of these terms show that is by far the largest contributor to Egm, where the vesicle transmitter releases probability also contributes to (ρves in equations S10 and S11). Given that ρves is dependent on ambient temperature, we used more physiologically relevant ρves values than used in previous studies14 (see SI Text, Section A.4). However, exocytic release of neurotransmitters from synaptic vesicles at the nerve terminal and subsequent retrieval of membranes that make up synaptic vesicles is likely to be energy free as lipids are completely recycled in this process.34 Moreover, it is noted that is solely dependent on number of cells (i.e. mass of brain tissue), whereas relies on both brain tissue mass and neuronal firing rate. We converted Egm (units of ATP/s) to total glucose oxidation (calcCMRglc(ox),T; units of μmol/g/min) by
| (1a) |
where h depends on the glucose-to-ATP transduction rate (GTR) which is given by 38 × (OGI/6) and OGI is the measured oxygen-to-glucose index that is determined by the ratio of cerebral metabolic rates of oxygen (CMRO2) and glucose (CMRglc) consumption (i.e. OGI = CMRO2/CMRglc). Experimental measures indicate that glucose is not fully oxidized, resulting in GTR = 33.6 with OGI = 5.3.35,36 Thus, h is given by 6 × 107/(GTR Mgm Avo), where Mgm is the total mass of gray matter (Mgm = 638 g is used here,25 Table 1) and Avo is the Avogadro constant (6.023 × 1023/mol). Because Egm is the sum of and , then
| (1b) |
| (1c) |
where the total glucose oxidation is (calcCMRglc(ox),T) given by the sums of signaling (calcCMRglc(ox),signaling) and nonsignaling (calcCMRglc(ox),nonsignaling) components
| (1d) |
and neuronal (calcCMRglc(ox),N) and astrocytic (calcCMRglc(ox),A) components
| (1e) |
We compared calcCMRglc(ox),T with experimental measurements of CMRglc in the rat (Table S1, by 2DG autoradiography) and human (Table S2, by FDG PET) brain. These were converted to total glucose oxidation rate (measCMRglc(ox),T) by
| (2a) |
| (2b) |
where OGI was assumed to be 5.3 (see above) and the measCMRglc(ox),T is the sum of neuronal (measCMRglc(ox),N) and astrocytic (measCMRglc(ox),A) components, both of which can be measured by 13C-MRS. Figure 1(a) compares values of calcCMRglc(ox),T and measCMRglc(ox),T for different behavioral states in both rat and human brain. The goodness of fit between calcCMRglc(ox),T and measCMRglc(ox),T is indicated by the line with an R2 value of 0.99 for 10 behavioral states in rat and 6 behavioral states in human. We obtained the calculated firing rate (calcRate, unit of Hz) based on the relationship between and its components (using equation S4(c); SI Text, Section A)
| (3) |
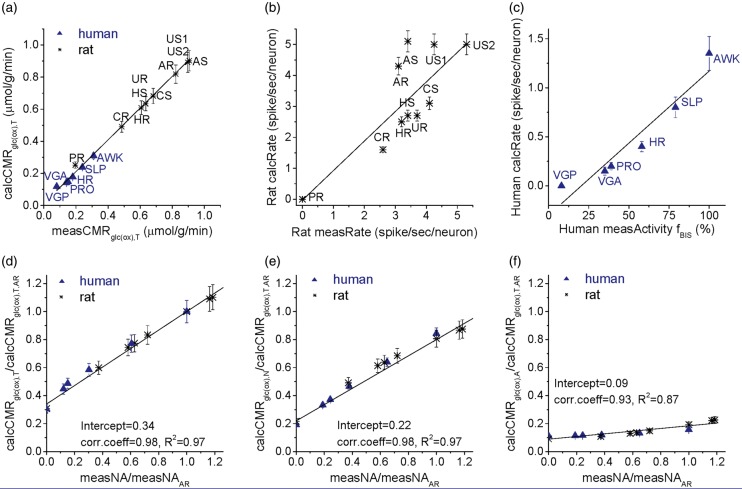
where the denominator terms were estimated for f = 1 Hz (Table 2) so that we could compare with measured neural activity rates (measRate for rat, measActivity for human). Recordings of neural activity were available for the rat (Table S1) and human (Table S2) brain under the same behavioral states as the metabolic measurements (see above). In the rat and human brain, respectively, the measRate for rat (f in units of Hz in Table S1) was represented by neuronal firing rates (f in units of Hz) and BIS-measured EEG recordings (fBIS in units of BIS for human in Table S2), Figure 1(b) shows good agreement between calcRate and measRate for 10 different behavioral states in rats (i.e. Pearson’s correlation coefficient of 0.79 and R2 = 0.62 with fit slope equal to 0.955). Human brain EEG, which measures summed activity of post-synaptic currents,37 indicates that brain activity changes with different behavioral states. Figure 1(c) shows excellent agreement between calcRate with measActivity for six human behavioral states (i.e. Pearson’s correlation coefficient of 0.98 and R2 = 0.96). Overall, both in rat and human gray matter, Figures 1(a) to (c) emphasize the need for ATP yielded from glucose oxidation to support higher signaling activity in cerebral cortex.
Figure 1.
Relationship between CMRglc(ox) and neuronal activity. (a) Comparison between cortical values of calculated total CMRglc(ox) (calcCMRglc(ox),T) and measured total CMRglc(ox) (measCMRglc(ox),T), where CMRglc(ox),T is defined as the sum neuronal (CMRglc(ox),N) and glial (CMRglc(ox),A) components. Values of measCMRglc(ox),T for rat (asterisk) and human (blue triangles) brain were derived from 2-deoxyglucose (2DG) autoradiography and fluoro-2-deoxyglucose (FDG) PET, respectively, in rat (Table S1) and human (Table S2) brain. The abbreviated labels are: PR: pentobarbital; US: urethane stimulation; AR: awake rest; AS: awake stimulation; UR: urethane rest; US2: urethane stimulation; CR: α-chloralose rest; CS: α-chloralose stimulation; HR: halothane rest; HS: halothane stimulation; for human data, VGP: persistent vegetative; VGA: acute vegetative; PRO: propofol; SEV: sevoflurane; HR: halothane rest; SLP: non-REM sleep; AWK: awake. The relationship between calcCMRglc(ox),T and measCMRglc(ox),T is fitted by y = −0.013 + 0.99 x, with an R2 value of 0.99. (b) In rat somatosensory cortex, comparison between calculated and measured neuronal activity for the rat (asterisk), where the calculated cortical mean firing rates per neuron (calcRate) for each value of calcCMRglc(ox),T in Figure 1(a) is plotted versus measured average neuronal firing rate per neuron (measRate). Experimental conditions and values for measRate in the rat are listed in Table S1. The relationship between calcRate and measRate is fitted by y = −0.03 + 0.955 x, with an R2 value of 0.62 Note that the calcRate, similar to measRate, range is from 0 to 5 Hz for all conditions shown in the rat. (c) In human visual cortex, comparison between calculated (calcRate) and measured (measActivity) neuronal activity (triangles), where the values of calcRate for each value of calcCMRglc(ox),T in Figure 1(a) is plotted versus measActivity given by EEG-derived bispectral index (BIS, fBIS). Experimental conditions and values for human measActivity fBIS are listed in Table S2. The relationship between calcRate and measActivity is fitted by y = −0.297 + 0.0198 x, with an R2 value of 0.96. Note that the calcRate in human, different from to calcRate in rat, range is 0–2 Hz for all conditions shown. (d) Values of calcCMRglc(ox),T for both rat (asterisk) and human (triangles) as a function of measured neuronal activity (measNA), which is fitted by a linear function y = 0.34 + 0.66 x, with an R2 value of 0.97. Values of measNA for rat and human brain are from Tables S1 to S2, respectively. The horizontal and vertical axes are normalized to the awake resting state values of measNA and calcCMRglc(ox),T, respectively (i.e. measNAAR and calcCMRglc(ox),T,AR). (e) Values of calculated neuronal CMRglc(ox) (calcCMRglc(ox),N) in both rat (asterisk) and human (triangles) brain as a function of measNA, which is fitted by a function 0.22 + 0.58 x, with an R2 value of 0.97. The horizontal and vertical axes are normalized to the awake resting state values of measNA and calcCMRglc(ox),T, respectively (i.e. measNAAR and calcCMRglc(ox),T,AR). (f) Values of calculated astrocytic CMRglc(ox) (calcCMRglc(ox),A) in both rat (asterisk) and human (triangles) brains as a function of measNA, which is fitted by a function y = 0.09 + 0.096 x, with an R2 value of 0.87. The horizontal and vertical axes are normalized to the awake resting state values of measNA and calcCMRglc(ox),T, respectively (i.e. measNAAR and calcCMRglc(ox),T,AR). See Figure S2(a) and (b) for separation of the signaling and nonsignaling components of calcCMRglc(ox),T for all of the behavioral states in both species.
Figures 1(d) to (f) are quite similar in the sense that the values of calcCMRglc(ox),T, calcCMRglc(ox),N, and calcCMRglc(ox),A (but each normalized to the value of the awake resting state calcCMRglc(ox),T) of different behavioral states for both rat and human are plotted against measured neuronal activity rates (normalized to the awake resting state activity). The intercepts in Figure 1(d) to (f) are all nonzero as activity approached zero (i.e. absence of signaling): around 34% of awake resting state calcCMRglc(ox),T for total cellular nonsignaling cost (Figure 1(d); Pearson’s correlation coefficient 0.98 and R2 = 0.97); 22% of awake resting state calcCMRglc(ox),T for neuronal nonsignaling cost (Figure 1(e); Pearson’s correlation coefficient 0.98 and R2 = 0.97), and 9% of awake resting state calcCMRglc(ox),T for astrocytic nonsignaling cost (Figure 1(f); Pearson’s correlation coefficient 0.93 and R2 = 0.87). The slopes in Figure 1(d) and (e) were significantly greater than the slope in Figure 1(f), suggesting that energy demand of neuronal activity is about 6 times greater than cost of glial activity.
Gray matter budget validation from in vivo 13C-MRS measurements
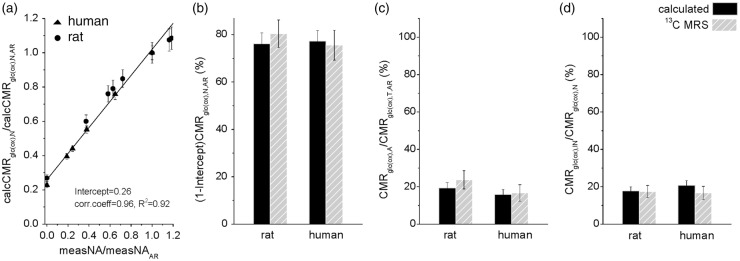
13C-MRS provides independent measures of neuronal (CMRglc(ox),N) and astrocytic (CMRglc(ox),A) components of glucose oxidation, but also independent measures of neuronal activity of glutamatergic (excitatory) and GABAergic (inhibitory) synaptic activity and their independent energy demands.36 Thus, the gray matter energetics calculated for rat and human brain can also be validated by comparison with prior 13C-MRS data acquired in rat and human brain (Tables S3 to S5).
Figure 2(a) is similar to Figure 1(e) except that the normalizing factor of the y-axis differs (i.e. divided by calcCMRglc(ox),N and calcCMRglc(ox),T, respectively, in Figures 2(a) and 1(e)). The intercept on the vertical axis is ∼25% of awake resting state calcCMRglc(ox),N for both species (Figure 2(a); Pearson’s correlation coefficient = 0.96 and R2 = 0.92). This indicates that the total energy for signaling related demands is 75–78% of neuronal metabolism and nonsignaling neuronal components (including resting potential and housekeeping) occupy 22–25% of total neuronal metabolism (Figure 2(b), black). These results from non-MRS based methods match extremely well with results from 13C-MRS (Table S3; Figure S1), where the signaling neuronal demands occupy 75–80% of total neuronal metabolism and the nonsignaling neuronal components demand about 20–25% of total neuronal metabolism (Figure 2(b), gray).
Figure 2.
Comparison of CMRglc(ox) calculated from energy budget with experimentally measured CMRglc(ox) by 13C-MRS. (a) Calculated neuronal CMRglc(ox) (calcCMRglc(ox),N) in both rat (asterisk) and human (triangles) brain as a function of measured neuronal activity (measNA), which is fitted by a function 0.26 + 0.76 x, with an R2 value of 0.92. The horizontal and vertical axes are normalized to the awake resting state values of measNA and calcCMRglc(ox),N, respectively (i.e. measNAAR and calcCMRglc(ox),T,AR). Since values above the intercept reflect signaling (i.e. measNA > 0), this plot suggests that nonsignaling-dependent energy demand of neurons is ∼ 26% of CMRglc(ox),N,AR. This intercept derived from 2DG autoradiography, FDG PET, and electrophysiology data (Tables S1 and S2) is very similar to prior observations with 13C-MRS in rat and human brain (Figure S1 and Table S3). (b) The signaling-dependent CMRglc(ox) of neuron populations (i.e. (1-intercept) × CMRglc(ox),N,AR from Figure 2(a)) for rat and human cortex calculated (black bars) and measured by 13C-MRS (gray bars) shows that the signaling-dependent energy demand of neurons is 75–80% of CMRglc(ox),N,AR. The CMRglc(ox) experimental values for 13C-MRS in the rat and human are shown in Figure S1 and Table S3. (c) The fraction of astrocytic CMRglc(ox) (CMRglc(ox),A) in relation to CMRglc(ox),T,AR (i.e. CMRglc(ox),A/CMRglc(ox),T,AR) for calculated (black bars) and measured by 13C-MRS (gray bars) shows that the glial energy demand is ∼20% of CMRglc(ox),T,AR. The glial experimental values for 13C-MRS in the rat and human are shown in Table S4. (d) The fraction of inhibitory (GABAergic) neuronal CMRglc(ox) (CMRglc(ox),IN) in relation to CMRglc(ox),N (i.e. CMRglc(ox),IN/CMRglc(ox),N) calculated (black bars) and measured by 13C-MRS (gray bars) shows that the inhibitory (GABAergic) neuronal energy demand is ∼20% of CMRglc(ox),N. The GABAergic experimental values for 13C-MRS in the rat and human are shown in Table S5.
Similarly, the in vivo 13C-MRS experimental results of CMRglc(ox),A/CMRglc(ox),T ratio in the awake state for both species (Table S4), showed that cortical glial cells in the awake state demand about 17–22% of total oxidative ATP (Figure 2(c), gray). The calculations provided matching results, where astrocytes in cortex demand 16–19% of total oxidative ATP (Figure 2(c), black). Finally, energy demand of GABAergic synapses (CMRglc(ox),IN) in relation to CMRglc(ox),N has been measured in both rat and human brain (Table S5). The 13C-MRS measured CMRglc(ox),IN/CMRglc(ox),N ratio in the awake state for both species is 17–18% of oxidative ATP in neuronal populations (Figure 2(d), gray), while the theoretical calculations provide comparative results that interneurons demand 18–21% of neuronal oxidative metabolism (Figure 2(d), black).
Energy demands of specific cellular components across species
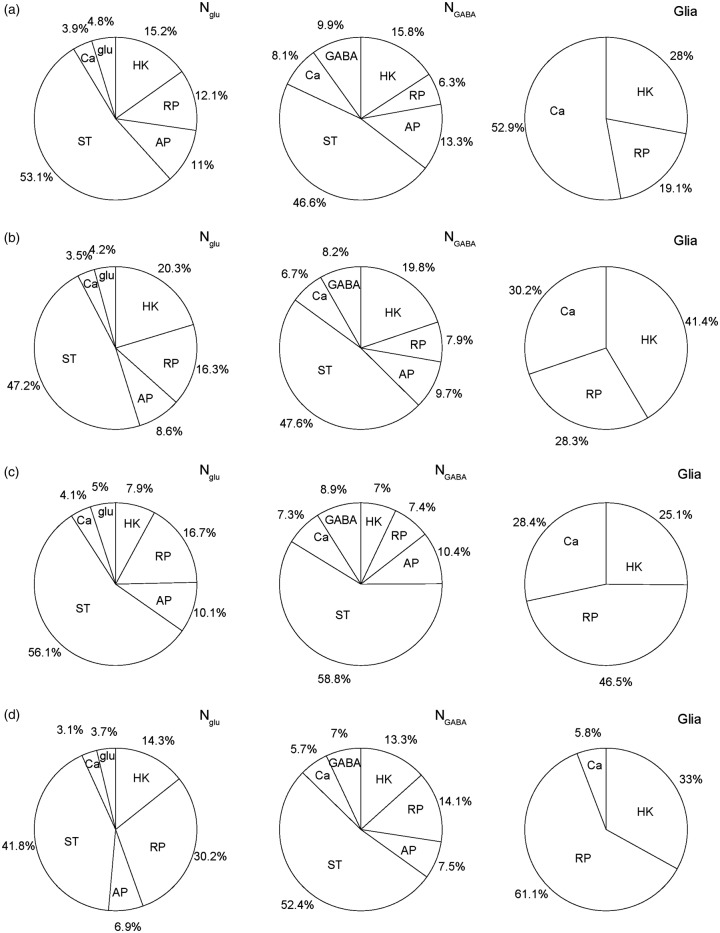
In resting awake rat (Figure 3(a)), with an average neuronal firing rate of 4.3 Hz, nonsignaling processes (including housekeeping and resting potential) demand ∼27% in excitatory neurons, ∼22% in inhibitory neurons, and ∼47% in glial cells. Synaptic transmission processes cost almost half of metabolism for both glutamatergic (∼53%) and GABAergic (∼47%) neurons. Action potential processes cost 10–15% of neuronal metabolism, while other signaling-related processes including calcium responses and glutamate/GABA recycling cost about 9% to 18% of neuronal metabolism. In halothane-anesthetized rat (Figure 3(b)), with an averaged neuronal firing rate of 2.5 Hz, nonsignaling processes demand a greater fraction of metabolism (i.e. ∼36% in excitatory neurons, ∼28% in inhibitory neurons, and ∼70% in glial cells) and costs of other signaling-related processes are lower than in the awake state, but interestingly the fraction of energetics for GABAergic synaptic transmission is negligibly affected by halothane.
Figure 3.
Distributions of ATP usage for different cellular mechanisms in excitatory glutamatergic neurons (NGlu), inhibitory GABAergic interneurons (NGABA), and glial cells (Glia) for the cerebral cortex of rat and human. The different cellular components represent housekeeping (HK), resting potential (RP), action potentials (APs), glutamate or GABA recycling (glu or GABA), presynaptic calcium (Ca), and synaptic transmission (ST). Distributions of energy budget for NGlu, NGABA, and Glia in rat cortex for (a) awake resting state and (b) halothane anesthesia compared to similar cellular components in human cortex for (c) awake resting state and (d) halothane anesthesia. Overall, in the cerebral cortex of rat and human, the HK and RP needs are greatest, while Ca need is quite small for Glia, and ST needs are nearly half of the total for NGlu and NGABA. From halothane anesthesia to awake resting states, the HK needs in NGlu, NGABA, and Glia are increased, whereas the APs, Ca, and glu needs in NGlu and NGABA are decreased relatively. See Figures S2 for further details of NGlu, NGABA, and Glia under awake resting and halothane anesthesia states for each species.
The calculated average neuronal firing rate in the resting awake human is about 1.15 Hz, much lower than that of rat. Nonsignaling processes in awake human demand ∼1/4 of excitatory neuronal metabolism (i.e. similar to rat), ∼1/8 of inhibitory neuronal metabolism (i.e., lower than rat), and ∼3/4 of glial cell metabolism (i.e. higher than rat). Synaptic transmission processes in the awake human cost slightly more than half of neuronal metabolism (i.e. ∼56% for glutamatergic and ∼59% GABAergic activities). The similarities between rat and human are found for action potential processes (i.e. ∼10% of neuronal metabolism) and signaling-related processes (i.e. 9% to 16% of neuronal metabolism for calcium responses and glutamate/GABA recycling). Upon induction with halothane anesthesia, as in the rat, a much lower average neuronal firing rate of 0.4 Hz is observed in human brain (Figure 3(d)), where demands of nonsignaling processes comprise a much greater fraction (i.e. ∼45% in excitatory, ∼27% in inhibitory neurons, and ∼94% in glial cells) and costs of other signaling-related processes are dropped relatively because of weaker activity.
Recent experimental evidence indicates that astrocytes have very high calcium activity.26,27 As Figures 1(f) and 2(c) indicate, if glial calcium cost was ignored, there will be a relatively large mismatch between calculated energy budget and measured glial metabolic cost measured by 13C-MRS. As the right panels in Figure 3(a) to (d) demonstrate, calcium activities may cost significant fractions of glial metabolism, especially during non-anesthetized conditions when nearly half of glial metabolism is attributed to glial calcium signals.
Energy demands of specific cellular components in gray and white matter
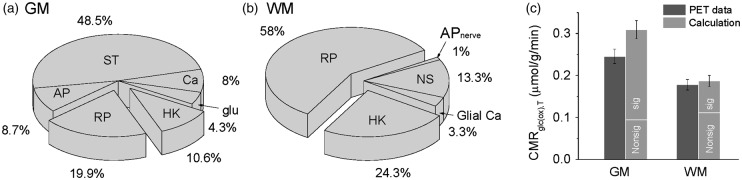
There are some anatomical experimental data which show that white matter may contain a significant portion of unmyelinated axons and neurons even in adult human brain (see Figure 4 in Azevedo et al.25), although most axons in nerves observed are myelinated in adult white matter.21 Hence, in our calculation for white matter, in addition to the 9.43 billion myelinated axons in white matter, we included 2.7 billion unmyelinated axons mainly from sparsely distributed neurons in white matter as reported by Azevedo et al.25 These 2.7 billion neurons with unmyelinated axons may be actively signaling and will consume a significant portion of energy for adult white matter (Table 1; SI Text, Section B). These accounts in conjunction with nearly identical gray matter bottom-up descriptions for white matter (Ewm; using equations S13(a) to (d); SI Text, Section B) led us to compare distributions of cellular components in gray and white matter of human brain (Figure 4).
Figure 4.
Distributions of ATP usage of different cellular mechanisms in gray matter (GM) and white matter (WM) of the human brain. The cellular components in GM represent housekeeping (HK), resting potential (RP), action potentials (AP), glutamate (and GABA) recycling (glu), presynaptic calcium (Ca), and synaptic transmission (ST). The cellular mechanisms in WM represent housekeeping (HK), resting potential (RP), neuron signaling (NS), action potentials in nerves (APnerve), and astrocyte calcium (glial Ca). Distributions of energy budget for (a) GM and (b) WM are shown in pie chart format where 100% represent the awake resting values of CMRglc(ox) in each tissue type. Nonsignaling costs (i.e. RP and HK) account for 30.5% and 82.3% of GM and WM demands respectively, suggesting that the total signaling costs in GM and WM are the remaining 69.5% and 17.7% portions, respectively. While the signaling costs in GM are assigned to energy needs of synaptic activity (i.e. ST, AP, Ca, glu), the signaling costs in WM are assigned to energy needs of 2.7 billion unmyelinated axons and 41.7 billion glial cells (i.e. NS, APnerve, Glial Ca). (see SI Text, Section B for details). (c) Bar plots of CMRglc(ox) for human brain PET data (dark gray38,55) and calculated budget results (gray). For calculation, signaling (“sig” in the bar plot) and nonsignaling (“Nonsig” in the bar plot) components in GM and WM are shown in absolute value, and the nonsignaling component in GM is double the energy demand in WM. See Figure S3 for further details of GM and WM behavior at different levels of neuronal activity.
In gray matter, the nonsignaling and signaling processes respectively cost ∼30% and ∼70% (Figure 4(a)), whereas in white matter, the nonsignaling and signaling processes respectively cost ∼80% and ∼20% (Figure 4(b)). Nonsignaling costs, which primarily comprise of resting potential and housekeeping, account for 30.5% and 82.3% of gray and white matter demands, respectively. This suggests that signaling costs in gray matter (69.5% of total) are assigned to synaptic activity, whereas signaling costs in white matter (17.7% of total) meet the needs of billions of unmyelinated axons and glial cells. The calcCMRglc(ox),T values in gray and white matter of 0.31 and 0.19 μmol/g/min, respectively, in the awake state (Figure 4(c)) agree well with prior observations.38
Both FDG PET and 2DG autoradiographic measures of metabolism only detect the usage of glucose molecules, whereas brain cells may also metabolize other substrates (e.g. lactate, ketone bodies) to provide the ATP they require.39 In our calculations all ATP, which includes both aerobic and glycolytic pathways, are assumed to be generated through glucose. Thus, some of the deviations of our predictions from the experimental data could be explained by contributions from these alternate substrates. It should also be noted that the measured PET values for CMRglc(ox),T were averaged for gray and white matter, respectively, from the entire cerebrum. While absolute levels of metabolism differ significantly between gray and white matter, the absolute amount of energy attributed to nonsignaling in both tissues is roughly similar (Figure 4(c)).
Discussion
Although bottom-up gray matter energy budgets have existed since the early 2000 s,12–14,21,22,40 experimental validation across behavioral states and/or species has been limited to largely comparison with a single experimental measurement from either 2DG autoradiography or FDG PET, usually just the awake resting value. We pooled a range of metabolic and physiologic measurements, using different methods, both in the rat and the human brain across several behavioral states (i.e. from awake to different anesthetized levels; Tables S1 to S5), to validate a comprehensive CMRglc(ox)-derived cellular level energy budget for gray and white matter (Figures 1 to 4). Based on our calculations, the higher metabolism in rat brain compared to human brain is primarily due to the higher firing rate and secondarily due to differences in synaptic density. Indeed, this issue was carefully formulated in a previous theoretical study,41 where energy consumption was reported to depend on many parameters, but most of them were species independent neurophysiological and structural invariants, except firing rate. The excellent fit we found to neuroenergetic measurements across a wide range of brain activity strongly supports this previous theoretical conclusion and extends it to glia and GABAergic neurons.
While the majority of the morphological data were for rat brain (Table 1), upon scaling to human brain, the biophysical parameters were essentially unchanged (Table 2). This suggests that basic properties of action potential generation and synaptic transmission processes are conserved across mammalian species, consistent with the conclusion made from a pure top-down analysis.13 However, this current work differs from our previous work, which calculated microscopic parameters based on a top-down fit of the model to experimental data13 by demonstrating that excellent agreement with experimental data is obtained using an ab initio bottom-up approach incorporating current best experimental values of these parameters.
In cases where the microscopic experimental values were not well determined, the validation of theoretical budget calculations with experimental measurements provided a valuable way to predict some uncertain parameters. For example, although most of the human experimental data suggest that the averaged firing rate of awake human neurons is in the range of 0.5 to 2 Hz,42,43 an accurate estimation has been missing from both experimental and theoretical approaches. Lennie22 predicted the average neuronal firing rate to be ∼0.024 Hz, whereas Karbowski41,44 predicted values closer to 1 Hz. By comparing our budget calculation with human brain 13C-MRS and PET metabolic data from different behavioral states, we predict that the resting average neuronal firing rate in resting awake human brain is ∼1.15 Hz, which is in good agreement with the mean of the range reported in the human brain in vivo42,43 and theoretical estimation from Karbowski.41,44 Updated accounts of cerebellar budget12 with cerebellar morphology45 will be crucial to extending this budget.
Principles of neuronal and glial energetics in gray matter
The agreement between the measured and calculated values (of metabolism and firing rate) provided good validation of biophysical properties of neuronal and glial cells (Figure 1). As shown in Figure 1(a), varying the firing rate alone without changing the costs of different components can explain the majority of the change in energy consumption with state. However, the data leaves open the possibility that the variations seen from perfect agreement (Figure 1(b) and (c)) could be explained by small changes in membrane resistance, synaptic transmission per spike, and/or housekeeping activities with each behavioral state. However, these changes cannot be large, indicating that the system maintains these factors close to constancy, which in turn may be important for maintaining fidelity of neuronal communication. The possibility of these factors having a dependence on the firing rate could be explored using the model presented by assessing if they provide a better fit to the experimental data. Despite differences in absolute metabolism and neuronal activity for rat (Table S1) and human (Table S2) brain, upon normalization to the awake state for each species, the energy demands for the total, neuronal, and astrocytic activities were nearly identical for both the species (Figures 1 to 3; Table 2).
The universal principles for gray matter are: (i) Up to 30% of total ATP in the awake state is attributed to nonsignaling processes like maintenance of resting potential and housekeeping metabolism in neurons and astrocytes; (ii) ATP demand of neuronal activity during signaling processes dominates in comparison to energy demand of astrocytic activity; (iii) ATP demand increases almost linearly with increasing neuronal activity; however, glial activity demands increase in a non-linear manner beyond the awake state.
The finding that signaling and nonsignaling costs, respectively, occupy ∼80% and ∼20% of neuronal energy in the awake state (Figure 2(a)) was independently verified by comparison with 13C-MRS measurements (Figure S1). In Figure 2(a), we plotted neuronal glucose oxidation vs. neuronal firing rate, as measured by PET, 2DG, and electrophysiology methods, whereas in Figure S1, we plotted neuronal glucose oxidation vs. neurotransmitter recycling, as measured by 13C-MRS. The agreement between the non-MRS and 13C-MRS results provides good validation of biophysical properties used in the calculations for neuronal and glial cells (Figure 2).
The agreement between these two plots reveals that synaptic transmission is indeed proportional to firing rate (electrical activity) or neurotransmitter recycling (chemical activity).46 Additionally, we find that the amount of neurotransmitter being recycled at 1 Hz is effectively identical between species. For the awake rat, a value of 0.55 μmol/g/min has been measured by 13C-MRS for neurotransmitter cycling (Table S3) at a neuronal firing rate of 4.3 Hz (Table 2). This corresponds to about 0.13 μmol/g/min recycling of neurotransmitter at 1 Hz firing. For the human cortex, where the neuronal density is exactly half that in the rat cortex (Table 1), we calculate nearly an identical value of neurotransmitter recycling at 1 Hz firing in the awake state (i.e. 0.34/1.15/2) (Tables 2 and S3). This suggests that the amount of neurotransmitter packaged, released by vesicles, and then recycled through glial cells is nearly proportional across species as a function of cortical firing rate, despite the different neuronal sizes across species. Given the similar slopes of Figures 2(a) and S1, incremental rise in firing by 1 Hz will increase glucose oxidation by ∼0.1 μmol/g/min (i.e. 0.13 × 0.8 = 0.1). In other words, in 1 g of cortical tissue ∼1 quadrillion glutamate molecules are recycled through the synapse per firing event per second, and this is independent of species. The agreement between model predictions and experimental data (Figure 2(a)), which include 13C-MRS where energy contributions of glutamatergic and GABAergic neurons were measured (Figure S1), suggests that our morphological estimates of different cell types are reasonable.
While signaling-associated functions of pyramidal cells dominate, energy demands of glial cells and inhibitory neurons are not negligible (Figure 3). The nonsignaling costs of glial cells are three times higher than that of neurons, and nearly half of glial metabolism is due to glial calcium signaling (Figure 3). We predict that glial energy possibly can increase quite significantly at very high activity levels (Figure 1(f)). Recent in vivo measurements indicate activity-dependent increase in glial function.27,47,48
Principles of neuronal and glial energetics in white matter
In human gray matter, there are 32.8 billion total cells with glial cell to neuron ratio of about 3:2, whereas of the 44.4 billion total cells in human white matter an overwhelming majority are glial cells (Table 1). Despite these immense differences in number of glial cells between gray and white matter in the human brain, there is a two to three times difference in CMRglc(ox) between these tissues and the nonsignaling energy demands in gray and white matter are roughly of the same magnitude (Figure 4(c)). This indicates that the main difference between gray and white matter arises from the higher energy costs associated with neuronal signaling in the cerebral cortex (Figure 4(a)).
We estimated the cost for human white matter based on the same method used for rat data in a recent report,21 but here we included a small amount of non-glial cells in white matter (2.7 billion unmyelinated and 9.4 billion myelinated axons, Table 1).25 Treating these non-glial cells as neurons would provide an upper limit of white matter energy demand. Since neurons fire spikes to induce synaptic transmission, these relatively few neurons in white matter may add non-ignorable costs to the white matter budget. This factor was not considered fully in the earlier report.21 Both glial calcium activity and activity of non-glial cells make energy cost in white matter increase slowly with rising cortical activity (e.g. switching from anesthesia to awake state, Figure S3). In support of this possibility, studies show small but significant state-dependent changes in white matter metabolism,49 an issue perhaps more relevant in specific disease conditions.50 Furthermore, experimental evidence directly suggests that individual astrocytes27,48,49,51 or oligodendrocytes26,51,52 may also have large demands for maintenance of resting potentials (Figure 3).
Significant nonsignaling energetic demands
Recent in vivo 13C-MRS studies in rat and human brain suggest that majority of the energy in the awake state, as much as 70–75% of the total ATP derived from CMRglc(ox), support cortical signaling functions, whereas the remaining 25–30% fraction is attributed to nonsignaling functions.13 However, theoretical bottom-up budget estimates have varied from 20% to 50% of the ATP derived from CMRglc(ox) supporting rat cerebral cortex nonsignaling functions.20 This uncertainty is mainly due to the lack of modeling and measurements of specific cellular physiologic and metabolic processes that occur in the nonsignaling state. Here, we take a new way to calculate the nonsignaling costs by computing the averaged mass value of individual neurons and glia, and mass-dependent basal metabolic rate23–25 (see SI Text Section A1 for details). This makes the calculated budget match the 13C-MRS results well. Moreover, budget results show that nonsignaling needs of white matter are more than double of that in the gray matter, presumably due to higher biosynthesis turnover demands (Figure 3). Together, the nonsignaling demands of white matter could be very large (Figure 4), as discussed below. Overall, our calculations show that in white matter, the energetic cost of the nonsignaling processes is 4 times higher than signaling processes, whereas in gray matter, the energetic cost of the signaling processes is 2.5 times higher than nonsignaling processes in the awake state.
Validation of CMRglc(ox) and neuronal activity in the gray matter budget (Figures 1 to 2) strengthened the synergy between “input” (Table 1) and “output” (Table 2) parameters for both rat and human brain to help narrow the recent debate on the magnitude of the nonsignaling cost20 and provided evidence that signaling-dependent energy is a dominant part of the brain budget.13,53,54 In fact, we estimate that the signaling costs may increase up to 85% in awake and physiological stimulated conditions. However, significant fraction of CMRglc(ox) can now be assigned for housekeeping needs (i.e. ∼11% in gray matter and ∼24% in white matter, Figure 4) and maintaining resting potential (i.e. ∼20% in gray matter and ∼58% in white matter, Figure 4). These two factors together are assigned to nonsignaling costs, which were highest for glial cells and lowest for interneurons (Figure 3). While our budget has not detailed different types of biosynthetic processes (e.g. protein, lipid, or myelin) or proton leaks for housekeeping needs, we have assigned a significant part of nonsignaling costs to maintaining resting potential.
In summary, this type of top-down validated bottom-up energy budget of the normal human brain provides exciting prospects to test the impact of microscopic variations or compartmentalized cellular perturbations on macroscopic CMRglc(ox), as measured in vivo by PET and 13C-MRS. The key to this top-down validated bottom-up energy budget was the rat data, which included independent measurements of electrical firing rate and 13C-MRS measurements of energy signaling and nonsignaling components. From the standpoint of using this model to interpret PET results, we believe the model allows us, within a linear approximation, to distinguish whether a change in regional activity is signaling or nonsignaling dependent, and whether it reflects changes in glutamatergic neurons, GABAergic neurons, or glial cells. In the near future, it may be possible to create both hemodynamic-based energy budgets of brain function, which could provide the basis for brain networks that are revealed by methods like fMRI and PET.
Supplementary Material
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: YY thanks for the support from China 863 program (2015AA020508), the National Natural Science Foundation of China (81761128011, 31571070), Shanghai Science and Technology Committee support (16410722600), the program for the Professor of Special Appointment (Eastern Scholar SHH1140004) at Shanghai Institutions of Higher Learning. FH thanks for the support from NIH grants (R01 MH-067528, P30 NS-052519, R01 NS-100106, R21 MH110862). DLR acknowledges support from the NIH grant (R01 NS-087568, R01 NS-100106, R01 MH-109159). YY thanks Omics-based precision medicine of epilepsy being entrusted by Key Research Project of the Ministry of Science and Technology of China (Grant No. 2016YFC0904400) for the support.
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Authors’ contributions
YY, PH, FH designed and performed research. YY, PH, DLR, DA, FH analyzed data and wrote paper.
Supplementary material
Supplementary material for this paper can be found at the journal website: http://journals.sagepub.com/home/jcb
References
- 1.Aiello LC, Wheeler P. The expensive-tissue hypothesis: the brain and the digestive system in human and primate evolution. Curr Anthropol 1995; 36: 199–221. [Google Scholar]
- 2.Shulman RG, Hyder F, Rothman DL. Baseline brain energy supports the state of consciousness. Proc Natl Acad Sci U S A 2009; 106: 11096–11101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fox D. IBM reveals the biggest artificial brain of all time. Popular Mechanics, 17 December 2009. Available at: www.popularmechanics.com/technology/a4948/4337190.
- 4.Laughlin SB, Sejnowski TJ. Communication in neuronal networks. Science 2003; 301: 1870–1874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Alle H, Roth A, Geiger JR. Energy-efficient action potentials in hippocampal mossy fibers. Science 2009; 325: 1405–1408. [DOI] [PubMed] [Google Scholar]
- 6.Carter BC, Bean BP. Sodium entry during action potentials of mammalian neurons: incomplete inactivation and reduced metabolic efficiency in fast-spiking neurons. Neuron 2009; 64: 898–909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yu Y, Hill AP, McCormick DA. Warm body temperature facilitates energy efficient cortical action potentials. PLoS Comput Biol 2012; 8: e1002456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hallermann S, de, Kock CP, Stuart GJ, et al. State and location dependence of action potential metabolic cost in cortical pyramidal neurons. Nat Neurosci 2012; 15: 1007–1014. [DOI] [PubMed] [Google Scholar]
- 9.Sengupta B, Stemmler M, Laughlin SB, et al. Action potential energy efficiency varies among neuron types in vertebrates and invertebrates. PLoS Comput Biol 2010; 6: e1000840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schmidt-Hieber C, Bischofberger J. Fast sodium channel gating supports localized and efficient axonal action potential initiation. J Neurosci 2010; 30: 10233–10242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hasenstaub A, Otte S, Callaway E, et al. Metabolic cost as a unifying principle governing neuronal biophysics. Proc Natl Acad Sci U S A 2010; 107: 12329–12334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Howarth C, Gleeson P, Attwell D. Updated energy budgets for neural computation in the neocortex and cerebellum. J Cereb Blood Flow Metab 2012; 32: 1222–1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hyder F, Rothman DL, Bennett MR. Cortical energy demands of signaling and nonsignaling components in brain are conserved across mammalian species and activity levels. Proc Natl Acad Sci U S A 2013; 110: 3549–3554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Attwell D, Laughlin SB. An energy budget for signaling in the grey matter of the brain. J Cereb Blood Flow Metab 2001; 21: 1133–1145. [DOI] [PubMed] [Google Scholar]
- 15.Sanganahalli BG, Herman P, Rothman DL, et al. Metabolic demands of neural-hemodynamic associated and disassociated areas in brain. J Cereb Blood Flow Metab 2016; 36: 1695–1707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Herman P, Sanganahalli BG, Blumenfeld H, et al. Quantitative basis for neuroimaging of cortical laminae with calibrated functional MRI. Proc Natl Acad Sci U S A 2013; 110: 15115–15120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Herman P, Sanganahalli BG, Blumenfeld H, et al. Cerebral oxygen demand for short-lived and steady-state events. J Neurochem 2009; 109(Suppl 1): 73–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sanganahalli BG, Herman P, Blumenfeld H, et al. Oxidative neuroenergetics in event-related paradigms. J Neurosci 2009; 29: 1707–1718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shulman RG, Hyder F, Rothman DL. Insights from neuroenergetics into the interpretation of functional neuroimaging: an alternative empirical model for studying the brain’s support of behavior. J Cereb Blood Flow Metab 2014; 34: 1721–1735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Engl E, Attwell D. Non-signalling energy use in the brain. J Physiol 2015; 593: 3417–3429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Harris JJ, Attwell D. The energetics of CNS white matter. J Neurosci 2012; 32: 356–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lennie P. The cost of cortical computation. Curr Biol 2003; 13: 493–497. [DOI] [PubMed] [Google Scholar]
- 23.Henry CJ. Basal metabolic rate studies in humans: measurement and development of new equations. Pub Health Nutr 2005; 8: 1133–1152. [DOI] [PubMed] [Google Scholar]
- 24.Baddeley H. Physics and the human body: Stories of who discovered what, Bloomington, IN: AuthorHouse, 2008. [Google Scholar]
- 25.Azevedo FA, Carvalho LR, Grinberg LT, et al. Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J Comp Neurol 2009; 513: 532–541. [DOI] [PubMed] [Google Scholar]
- 26.Kettenmann H, Kirishchuk S, Verkhratskii A. Calcium signalling in oligodendrocytes. Neurophysiology 1994; 26: 21–25. [Google Scholar]
- 27.Matute C. Calcium dyshomeostasis in white matter pathology. Cell Cal 2010; 47: 150–157. [DOI] [PubMed] [Google Scholar]
- 28.Herculano-Houzel S, Manger PR, Kaas JH. Brain scaling in mammalian evolution as a consequence of concerted and mosaic changes in numbers of neurons and average neuronal cell size. Front Neuroanat 2014; 8: 77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mota B, Herculano-Houzel S. All brains are made of this: a fundamental building block of brain matter with matching neuronal and glial masses. Front Neuroanat 2014; 8: 127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mukamel R, Gelbard H, Arieli A, et al. Coupling between neuronal firing, field potentials, and FMRI in human auditory cortex. Science 2005; 309: 951–954. [DOI] [PubMed] [Google Scholar]
- 31.Herculano-Houzel S, Lent R. Isotropic fractionator: a simple, rapid method for the quantification of total cell and neuron numbers in the brain. J Neurosci 2005; 25: 2518–2521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Beaulieu C. Numerical data on neocortical neurons in adult rat, with special reference to the GABA population. Brain Res 1993; 609: 284–292. [DOI] [PubMed] [Google Scholar]
- 33.McCormick DA, Connors BW, Lighthall JW, et al. Comparative electrophysiology of pyramidal and sparsely spiny stellate neurons of the neocortex. J Neurophysiol 1985; 54: 782–806. [DOI] [PubMed] [Google Scholar]
- 34.Puchkov D, Haucke V. Greasing the synaptic vesicle cycle by membrane lipids. Trends Cell Biol 2013; 23: 493–503. [DOI] [PubMed] [Google Scholar]
- 35.Gibson GE, Dienel GA. Handbook of neurochemistry and molecular neurobiology, New York: Springer, 2007. [Google Scholar]
- 36.Hyder F, Patel AB, Gjedde A, et al. Neuronal-glial glucose oxidation and glutamatergic-GABAergic function. J Cereb Blood Flow Metab 2006; 26: 865–877. [DOI] [PubMed] [Google Scholar]
- 37.Buzsaki G, Anastassiou CA, Koch C. The origin of extracellular fields and currents – EEG, ECoG, LFP and spikes. Nat Rev Neurosci 2012; 13: 407–420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hyder F, Fulbright RK, Shulman RG, et al. Glutamatergic function in the resting awake human brain is supported by uniformly high oxidative energy. J Cereb Blood Flow Metab 2013; 33: 339–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Siesjo BK. Brain energy metabolism, New York: Wiley and Sons, 1978. [Google Scholar]
- 40.Buzsáki G, Kaila K, Raichle M. Inhibition and brain work. Neuron 2007; 56: 771–783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Karbowski J. Thermodynamic constraints on neural dimensions, firing rates, brain temperature and size. J Comput Neurosci 2009; 27: 415–436. [DOI] [PubMed] [Google Scholar]
- 42.Peyrache A, Dehghani N, Eskandar EN, et al. Spatiotemporal dynamics of neocortical excitation and inhibition during human sleep. Proc Natl Acad Sci U S A 2012; 109: 1731–1736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Goldstein S, Bak M, Oakley J, et al. An instrument for stable single cell recording from pulsating human cerebral cortex. Electroencephalograph Clin Neurophysiol 1975; 39: 667–670. [DOI] [PubMed] [Google Scholar]
- 44.Karbowski J. Approximate invariance of metabolic energy per synapse during development in mammalian brains. PloS One 2012; 7: e33425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Herculano-Houzel S. Coordinated scaling of cortical and cerebellar numbers of neurons. Front Neuroanat 2010; 4: 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pereda AE. Electrical synapses and their functional interactions with chemical synapses. Nat Rev Neurosci 2014; 15: 250–263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zonta M, Angulo MC, Gobbo S, et al. Neuron-to-astrocyte signaling is central to the dynamic control of brain microcirculation. Nat Neurosci 2003; 6: 43–50. [DOI] [PubMed] [Google Scholar]
- 48.Metea MR, Newman EA. Glial cells dilate and constrict blood vessels: a mechanism of neurovascular coupling. J Neurosci 2006; 26: 2862–2870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Weber B, Fouad K, Burger C, et al. White matter glucose metabolism during intracortical electrostimulation: a quantitative [(18)F]Fluorodeoxyglucose autoradiography study in the rat. Neuroimage 2002; 16: 993–998. [DOI] [PubMed] [Google Scholar]
- 50.Buchsbaum MS, Buchsbaum BR, Hazlett EA, et al. Relative glucose metabolic rate higher in white matter in patients with schizophrenia. Am J Psychiatr 2007; 164: 1072–1081. [DOI] [PubMed] [Google Scholar]
- 51.Parys B, Cote A, Gallo V, et al. Intercellular calcium signaling between astrocytes and oligodendrocytes via gap junctions in culture. Neuroscience 2010; 167: 1032–1043. [DOI] [PubMed] [Google Scholar]
- 52.Takeda M, Nelson DJ, Soliven B. Calcium signaling in cultured rat oligodendrocytes. Glia 1995; 14: 225–236. [DOI] [PubMed] [Google Scholar]
- 53.Astrup J, Sorensen PM, Sorensen HR. Oxygen and glucose consumption related to Na+-K+ transport in canine brain. Stroke 1981; 12: 726–730. [DOI] [PubMed] [Google Scholar]
- 54.Sibson NR, Dhankhar A, Mason GF, et al. Stoichiometric coupling of brain glucose metabolism and glutamatergic neuronal activity. Proc Natl Acad Sci U S A 1998; 95: 316–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hyder F, Rothman DL. Quantitative fMRI and oxidative neuroenergetics. Neuroimage 2012; 62: 985–994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Herculano-Houzel S, Mota B, Lent R. Cellular scaling rules for rodent brains. Proc Natl Acad Sci U S A 2006; 103: 12138–12143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Anderson TR, Huguenard JR, Prince DA. Differential effects of Na+-K+ ATPase blockade on cortical layer V neurons. J Physiol 2010; 588(Pt 22): 4401–4414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Gittis AH, Nelson AB, Thwin MT, et al. Distinct roles of GABAergic interneurons in the regulation of striatal output pathways. J Neurosci 2010; 30: 2223–2234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Fino E, Deniau JM, Venance L. Cell-specific spike-timing-dependent plasticity in GABAergic and cholinergic interneurons in corticostriatal rat brain slices. J Physiol 2008; 586: 265–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Schools GP, Zhou M, Kimelberg HK. Development of gap junctions in hippocampal astrocytes: evidence that whole cell electrophysiological phenotype is an intrinsic property of the individual cell. J Neurophysiol 2006; 96: 1383–1392. [DOI] [PubMed] [Google Scholar]
- 61.Bergles DE, Jahr CE. Synaptic activation of glutamate transporters in hippocampal astrocytes. Neuron 1997; 19: 1297–1308. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.