Many-body effect determines the selectivity for Ca²⁺ and Mg²⁺ in proteins

Significance

Metal ions have important biological functions and are associated with diseases including cancer and neurodegenerative disorders. The fundamental question of metal ion selectivity in proteins has received continued interest over the past decades. Compared with Na⁺/K⁺, the selectivity for Mg²⁺/Ca²⁺ is less well understood. Although Mg²⁺ is a better charge acceptor, calcium-binding proteins with highly charged binding pockets can selectively bind Ca²⁺ against a much higher concentration of Mg²⁺. Here we show that this selectivity is dictated by the many-body polarization effect, which is a cost arising from the dense packing of multiple residues around the metal ion. By combining geometric constraint and the many-body effect, it is possible to fine-tune the selectivity for metal ions of different sizes.

Abstract

Calcium ion is a versatile messenger in many cell-signaling processes. To achieve their functions, calcium-binding proteins selectively bind Ca²⁺ against a background of competing ions such as Mg²⁺. The high specificity of calcium-binding proteins has been intriguing since Mg²⁺ has a higher charge density than Ca²⁺ and is expected to bind more tightly to the carboxylate groups in calcium-binding pockets. Here, we showed that the specificity for Ca²⁺ is dictated by the many-body polarization effect, which is an energetic cost arising from the dense packing of multiple residues around the metal ion. Since polarization has stronger distance dependence compared with permanent electrostatics, the cost associated with the smaller Mg²⁺ is much higher than that with Ca²⁺ and outweighs the electrostatic attraction favorable for Mg²⁺. With the AMOEBA (atomic multipole optimized energetics for biomolecular simulation) polarizable force field, our simulations captured the relative binding free energy between Ca²⁺ and Mg²⁺ for proteins with various types of binding pockets and explained the nonmonotonic size dependence of the binding free energy in EF-hand proteins. Without electronic polarization, the smaller ions are always favored over larger ions and the relative binding free energy is roughly proportional to the net charge of the pocket. The many-body effect depends on both the number and the arrangement of charged residues. Fine-tuning of the ion selectivity could be achieved by combining the many-body effect and geometric constraint.

Metal ions are essential for a variety of biological functions such as homeostasis, muscle contraction, and enzyme catalysis (1–3). For example, Ca²⁺ acts as a second messenger that controls many cellular processes by inducing conformational changes of the receptor proteins. Ca²⁺ signaling is used throughout the life cycle of an organism, including proliferation, metabolism, and cell death (4, 5). Under certain conditions, elevated Ca²⁺ levels are cytotoxic. Thus, Ca²⁺ concentration must be strictly maintained within spatial and temporal boundaries (4, 5). Mg²⁺ is crucial in energy-requiring metabolic reactions since ATP must be bound to Mg²⁺ to be biologically active (2, 6). Mg²⁺ also forms a component of RNA and DNA tertiary structures, and is necessary for the proper structure and activity of RNA and DNA polymerases (2).

The ability of proteins to select a specific metal ion over similar ones is critical to these cellular processes. Many efforts have been made to understand the selectivity of proteins for metal ions (7–12). One well-studied case over the past decades is potassium channel. The selectivity of potassium channels for K⁺ over Na⁺ has been attributed to the intrinsic electrostatic properties of the pores, geometric flexibility in the structural aspects, and kinetic effects (7, 11–13).

Another puzzling pair of metal ions is Ca²⁺ and Mg²⁺. Mg²⁺ is a better charge acceptor due to its smaller size and higher charge density, so it would be expected to bind more tightly to carboxylate groups commonly found in calcium-binding motifs (7, 14), if the energy cost of ion dehydration is omitted. Counterintuitively, EF hands (named after the E and F helices of parvalbumin) typically have 10²- to 10⁴-fold higher affinity for Ca²⁺ (15). Two popular explanations for the EF-hand selectivity are (i) the pentagonal bipyramidal geometry and relatively large size preferable for Ca²⁺ and (ii) the larger solvation penalty of Mg²⁺ (7, 16). The geometric explanation is closely related to the snug-fit mechanism for ion channels and classical concepts in host-guest chemistry (13, 17). However, mutants of EF-hand protein with octagonal geometry also favor Ca²⁺ (albeit with weaker selectivity) (18), which indicates that the bipyramidal geometry is not essential. On the other hand, the solvation penalty argument is more of a phenomenological explanation; the question remains as to why the strong interaction of Mg²⁺ with charged carboxylate groups in the binding pocket cannot overcome the relatively weak interaction with water. In addition, EF-hand proteins have high specificity for Ca²⁺ over Mg²⁺, Sr²⁺, and Ba²⁺ (19), while the CheY protein, also with multiple carboxylate groups in the binding pocket, has very weak size selectivity (20). These different patterns of size selectivity cannot be attributed to the solvation penalty. In other words, fine-tuning of selectivity of Ca²⁺ vs. Mg²⁺ has to come from the interaction with the binding pockets rather than solvation.

There have been insightful studies on the determinants of calcium selectivity. The effect of the number of negatively charged residues has been studied both experimentally and computationally, and mechanisms based on the electrostatic repulsion have been proposed (21–23). The geometric constraint or deformation (24–26) is a frequently discussed factor for size selectivity. Lim and coworkers (7, 9, 27, 28) showed that the second shell and the protein environment either stabilize or enhance the properties of the inner shell. The roles of polarization (29–34) and quantum effects (26, 35, 36) have also been pointed out. Nevertheless, the preference for Ca²⁺ can be found in many families of proteins (7, 19, 37–41), including an Mg-dependent enzyme ribonuclease H1 (42), while Mg-specific proteins are less common. A general understanding of the higher affinity for Ca²⁺ in different proteins is still lacking.

In this work, we first used ab initio calculations on model compounds of the binding pockets to illustrate the importance of the many-body effect on Ca²⁺ selectivity. Then, through free energy calculations with a polarizable force field for six calcium- and magnesium-binding proteins, we demonstrated that the many-body effect depends on both the composition and the geometry of the binding pocket. Further, we showed how proteins can precisely control the selectivity by utilizing many-body effect and geometric constraint, leading to nonmonotonic size dependence of ion selectivity.

Results and Discussion

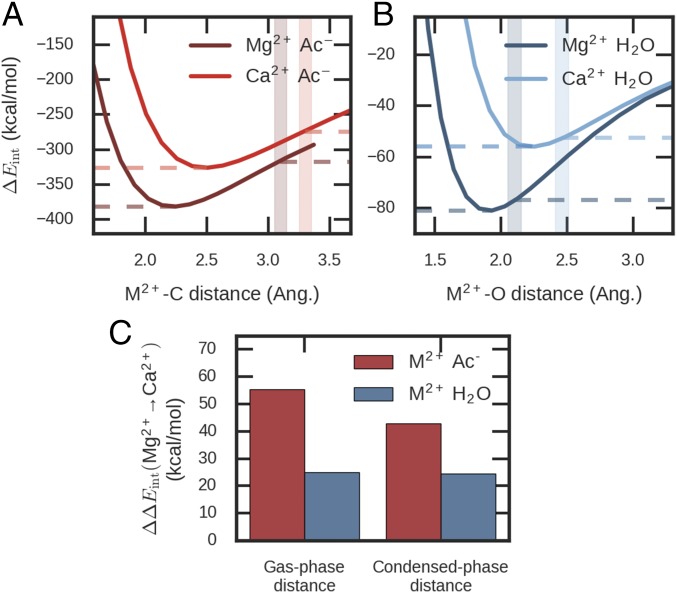
Due to its smaller size, Mg²⁺ interacts much more strongly with acetate in gas phase than Ca²⁺ does compared with the corresponding ion–water interactions (Fig. 1). At typical separation distances in crystal structures, the difference between the Mg²⁺-acetate and Ca²⁺-acetate dimer interaction energies is ∼40 kcal/mol, significantly larger than the difference of ∼25 kcal/mol for the ion–water dimer. EF-hand binding pockets have three to four carboxylate groups (Asp/Glu) (16) together with carbonyl and hydroxyl groups, and the coordination numbers for Mg²⁺ and Ca²⁺ are generally the same as those in water (6 for Mg²⁺ and 7 for Ca²⁺). If all these interactions between metal ions and individual functional groups are additive, EF-hand binding pockets would favorably bind Mg²⁺ by a large margin.

Fig. 1.

Comparison of ion–acetate and ion–water dimer interaction energies. (A) Mg²⁺/Ca²⁺ and acetate; (B) Mg²⁺/Ca²⁺ and water; (C) difference between the interaction energies of Mg²⁺ and Ca²⁺. The ions were placed on the bisector of the O-C-O or H-O-H angle. The interaction energies were calculated by RI-MP2/def2-QZVPPD. The shaded areas in A and B indicate typical distances in PDB or aqueous solution. ΔE_int, interaction energy; Ac, acetate; Ang., angstrom.

In solution, Mg²⁺ and Ca²⁺ have comparable binding free energies with acetate (−1.7 vs. −1.6 kcal/mol) (43). In fact, chemical concepts from solution-phase experiments indicate that Mg²⁺ and Ca²⁺ are similar in binding abilities. The hard-ligand scale of Mg²⁺ is barely larger than that of Ca²⁺ (i.e., the two metal ions have similar binding affinities for hard ligands) (44). In Hofmeister series, Mg²⁺ and Ca²⁺ are close to each other while their order varies depending on the solute (41, 45–47). The similarity between Mg²⁺ and Ca²⁺ binding affinities may be explained by the dielectric screening of the solvent (48). However, multivalent ligands such as EDTA (49) and many proteins (7, 19, 37–42) tend to have higher affinities for Ca²⁺. These strong preferences for Ca²⁺ must be due to the cooperative or many-body effect of the ligands around the ions (50).

To illustrate the many-body effect in ion binding, we calculated the quantum-mechanical (QM) interaction energies for model compounds of protein–ion complexes and conducted many-body energy decomposition analysis (Table 1). Three EF-hand proteins with both Ca²⁺- and Mg²⁺-bound structures available in the Protein Data Bank (PDB) were chosen. The model systems were constructed by taking the first shell chemical groups (including water) around the ion out of the PDB structures. By definition, the total interaction energy is the sum of two-body and many-body energies, where the two-body energy is the sum of interaction energies of all pairs of molecular fragments in the system. Similar to the dimer interaction energies in Fig. 1, the two-body energies for Ca²⁺ are much weaker than those for Mg²⁺, as evidenced by the large positive numbers of ΔΔE_2B(Mg²⁺ → Ca²⁺). However, the large difference in the repulsive many-body interactions favors Ca²⁺, which compensates for its unfavorable two-body interactions. After incorporating the contribution of many-body interactions, the gaps between Mg²⁺ and Ca²⁺ interaction energies, ΔΔE_int(Mg²⁺ → Ca²⁺), are brought down to ∼70 kcal/mol, which approaches the difference in experimental hydration free energy (∼78 kcal/mol). It is noteworthy that the two-body interactions here include both ion–ligand attraction and ligand–ligand repulsion, so the two-body repulsive interaction between ligands is not a decisive factor for the observed selectivity. We estimated the relative free energies using the total interaction energies of the model systems and the experimental hydration free energies (Table 1). The calculated ΔΔG_bind(Mg²⁺ → Ca²⁺) values of all of the three EF-hand systems are lower than or close to 0, meaning that the binding pockets would prefer Ca²⁺. Without the many-body interactions, the predicted free energies would strongly favor Mg²⁺, which conflicts with experiments. Alternative analyses using the same binding pocket geometry for Mg²⁺ and Ca²⁺ or using different reference hydration free energies also show that many-body interactions strongly favor Ca²⁺. (See SI Appendix for details.) The calculations with the simple model systems suggest that the many-body interactions in the first shell are crucial for explaining Ca²⁺ selectivity.

Table 1.

Comparison of relative binding free energies from QM calculation and experiment

PDB	Model compounds	ΔΔE2B,M-L	ΔΔE2B,l-L	ΔΔE2B	ΔΔEMB	ΔΔEint	Calc. ΔΔGbind	Expt. ΔΔGbind
1IG5/4ICB	Ac3B2W2	251.9	−19.3	232.6	−165.6	67.0	−10.8	−6.2
2LVJ/K	Ac4B1W1	160.9	−16.6	144.3	−73.1	71.1	−6.7	−2.4
1B8L/C	Ac4B1W1	217.8	−37.5	180.3	−103.4	77.0	−0.8	−1.6

Reported values are the differences (in kcal/mol) between Mg complexes and Ca complexes, ΔΔE = ΔE (Ca²⁺) − ΔE (Mg²⁺). ΔΔG_bind is approximately calculated by ΔΔG_bind = ΔΔE_int − ΔΔG_solv^Expt = ΔΔE_int − 77.8 kcal/mol. The total interaction energy is calculated by ΔE_{int =} E_total − Σ_i E_i, where E_i is the energy of isolated monomer i. The two-body interaction energy is calculated by ΔE_2B = Σ_{i, j} (E_ij − E_i − E_j), where E_ij is the energy of isolated dimer. ΔΔE_2B,M-L and ΔΔE_2B,L-L are the two-body interaction energies between the metal ion and ligands and between ligands and ligands, respectively. The many-body interaction energy is ΔE_MB = ΔE_int − ΔE_2B. Ac, B, and W represent acetate, acetamide, and water, respectively. Calc., calculated; Expt., experiment; int, interaction; solv, solvation.

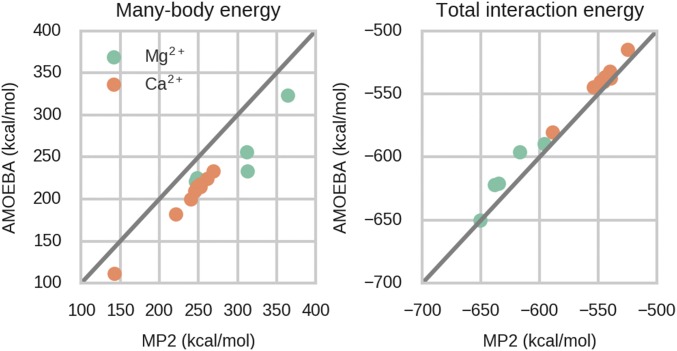
It should be emphasized that because of the approximations made in the above calculations (e.g., simplified model compounds, use of static structures, lack of entropy contribution, the choices of solvation free energies, and errors of QM methods; see SI Appendix for detailed discussion), the apparently good agreement between calculated and experimental free energies seems fortuitous. Therefore, the results can perhaps only be used to demonstrate the qualitative effect of the many-body interactions. To calculate the free energies rigorously, the effect of protein environment and conformational sampling at finite temperature should be considered [e.g., through molecular dynamics (MD) simulations]. Due to their computation cost, MD simulations are usually performed with empirical force fields. The large, repulsive many-body energy in Table 1 is not explicitly modeled in additive force fields, while it is included in polarizable force fields since a large portion of the many-body energy comes from polarization (51, 52). A comparison between many-body energies from MP2 and the AMOEBA (atomic multipole optimized energetics for biomolecular simulation) force field for several model compounds of protein–metal ion complexes (see SI Appendix, Fig. S2 for structures), including both EF hand and non-EF hand, is shown in Fig. 2 and SI Appendix, Table S3. The many-body energy increases with the number of carboxylate groups, and Mg²⁺ complexes have larger many-body energies than Ca²⁺ systems. Although, compared with MP2, AMOEBA systematically underestimates the many-body energies by ∼30 kcal/mol for both Mg²⁺ and Ca²⁺, a strong correlation is observed. The systematic error of AMOEBA should not have a significant impact on the calculation of relative affinity. The AMOEBA total interaction energies for Mg²⁺ complexes are noticeably weaker than MP2 energies.

Fig. 2.

Comparison between MP2 and AMOEBA many-body energies and total interaction energies of the model compounds. Data are tabulated in SI Appendix, Table S3.

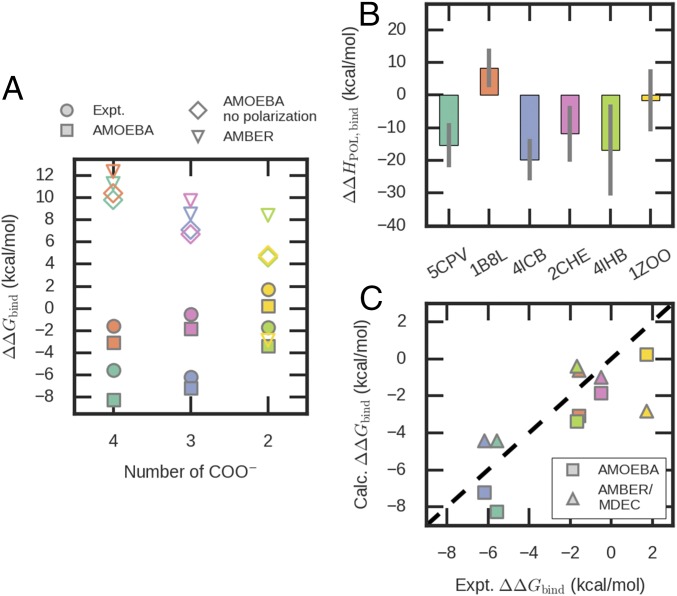
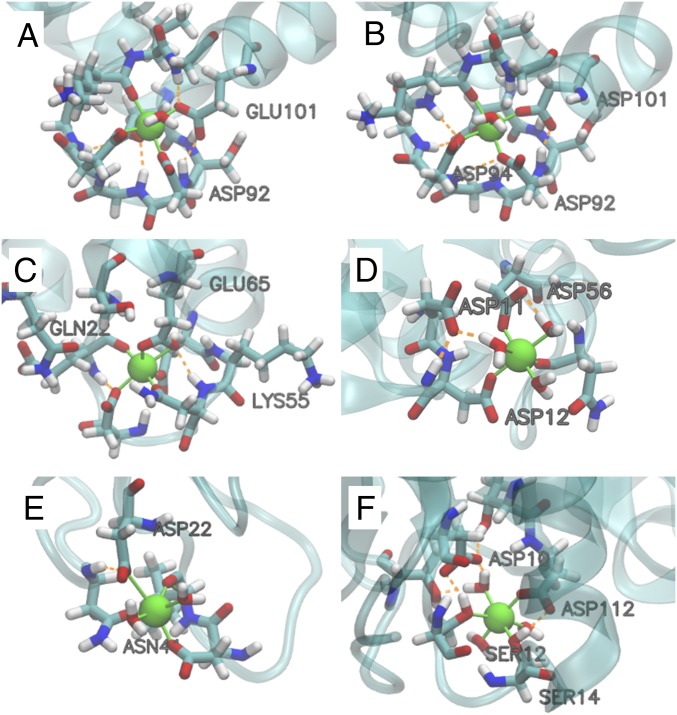
The importance of the many-body interactions motivated us to investigate the binding between different proteins and Mg²⁺/Ca²⁺ ions through MD simulations. Fig. 3A shows the calculated and experimental relative binding free energy ΔΔG_bind(Mg²⁺ → Ca²⁺). Since the many-body effect is modeled by polarization in the force field, we also performed nonpolarizable simulations for comparison (Fig. 3A). The nonpolarizable simulations used either AMOEBA with polarization turned off or the fixed-charge AMBER (assisted model building with energy refinement) force field. Six proteins were studied: namely, EF-hand proteins parvalbumin (5CPV and 1B8L) (18) and calbindin D9k (4ICB) (39), a carboxylate cluster Mg-binding protein CheY (20), the C2 domain of dysferlin (4IHB) (38), and an inserted (I) domain of integrin (1ZOO) (53). A description of these proteins and the structures of the binding pockets are provided in Fig. 4 and Table 2. While ΔΔG_bind(Mg²⁺ → Ca²⁺) values are systematically underestimated by ∼2 kcal/mol by AMOEBA (Fig. 3A), which is likely because the Mg²⁺ interaction is not strong enough (Fig. 2), the trend across all six proteins is reproduced. The binding pockets with more Asp/Glu tend to prefer Ca²⁺, while the selectivity is not solely determined by the net charge of the pocket. For example, 1B8L and 2CHE are highly charged but have relatively weak selectivity. Both trends can be explained by the many-body effect. When there are more charged residues, the repulsive many-body effect is more significant and outweighs the favorable pairwise interactions with individual side chains. 1B8L and 2CHE have a relatively weaker many-body effect due to their pocket geometries: 1B8L is a triple mutant of 5CPV in which the last residue Glu101 of the EF-hand motif is replaced by Asp, which creates a larger binding pocket and reduces the many-body effect. In 2CHE, the charged residues are clustered in one hemisphere so that they cannot all tightly bind to the metal ion (Fig. 4), which also reduces the many-body response of the binding pocket. This explanation is confirmed by the relative binding enthalpies in Fig. 3B. Among the four proteins with three or more charged residues, 5CPV and 4ICB have favorable polarization enthalpies for Ca²⁺ binding, while 1B8L and 2CHE have relatively unfavorable polarization enthalpies. In the AMOEBA nonpolarizable simulations, all ΔΔG_bind(Mg²⁺ → Ca²⁺) values become positive and roughly proportional to the number of Asp/Glu. This coincides with the naive intuition that proteins with more negative charges should bind more strongly to Mg²⁺ but is contrary to the results of polarizable MD simulations and experiments. For pockets with the same number of Asp/Glu, the relative binding free energies are similar in AMOEBA nonpolarizable simulations but variable in polarizable simulations. Clearly, polarization is more sensitive to the pocket geometry than permanent electrostatic interaction. In AMBER simulations, the correlation between ΔΔG_bind(Mg²⁺ → Ca²⁺) and the number of Asp/Glu is weaker, possibly due to the partial incorporation of polarization in atomic charge parameters (54, 55).

Fig. 3.

Comparison between experimental and calculated relative binding free energies. (A) Experimental and calculated free energies as a function of the number of carboxylate groups. The SDs of all calculated free energies are 0.2 kcal/mol. The color codes represent different proteins and are the same as used in B. (B) Polarization contribution to relative binding enthalpy in AMOEBA results. For most of the binding pockets, the relative binding enthalpy and the polarization contribution are negative. (C) Correlation between experimental binding free energies and calculated values using AMOEBA or AMBER/MDEC. The Pearson correlation coefficients are 0.97 and 0.63 for AMOEBA and AMBER/MDEC, respectively. Data are tabulated in SI Appendix, Tables S4 and S5. Calc., calculated; Expt., experiment; POL, polarization.

Fig. 4.

Structures of the binding pockets from MD simulations. (A–F) 5CPV, 1B8L, 4ICB, 2CHE, 4IHB, and 1ZOO bound with Mg²⁺, respectively. A–C are EF-hand proteins.

Table 2.

Description of proteins studied in this work

PDB	Protein	Function	Ion	Expt. ΔGbind (kcal/mol)		No. of COO− in first/second shell
				Mg2+	Ca2+
5CPV	Carp parvalbumin	Muscle contraction	Ca2+	−5.4	−11.0	4/0
1B8L	D51A/E101D/F102W mutant of 5CPV		Ca2+	−6.7	−8.3	4/0
4ICB	Bovine calbindin D9k	Calcium transport	Ca2+	−3.0	−9.2	3/0
2CHE	Response regulator protein CheY	Bacterial chemotaxis	Mg2+	−4.0	−4.5	2/1
4IHB	C2A domain from human dysferlin	Membrane repair	Ca2+	−5.7	−7.4	2/0
1ZOO	I domain from the CD11a integrin	Leukocyte adhesion	Mg2+	−6.4	−4.7	1/1

Expt., experiment.

We also explored whether the polarization effect can be modeled by a dielectric continuum, as proposed by Leontyev and Stuchebrukhov (56). In their MD in electric continuum (MDEC) method, the atomic charges of ionized groups are scaled by 0.7, corresponding to a uniform effective dielectric constant of ∼2. The calculated binding free energies (Fig. 3C) indeed show a significant improvement over the results of unscaled AMBER force field (Fig. 3A). However, MDEC gives a weaker correlation with experimental relative binding free energy (R² = 0.63) than the fully polarizable AMOEBA force field does (R² = 0.97) across the six proteins. MDEC also predicts the inconsistent ranking of selectivity for Mg²⁺-binding proteins 1ZOO and 2CHE and the EF-hand mutant 1B8L. These results are not surprising as the local polarization depends on the detailed chemical composition and geometry while MDEC assumes a universal dielectric constant.

The striking difference between polarizable and nonpolarizable simulations reveals the effect of polarization on Ca²⁺ selectivity. Polarization energy can also be decomposed into two-body and many-body contributions. In the classical AMOEBA model, the many-body effect arises solely from polarization, so the many-body energy is the same as many-body polarization energy. Since Mg²⁺ has higher charge density and shorter coordination distances, the two-body polarization strongly favors Mg²⁺ binding over Ca²⁺ binding (see SI Appendix, Table S2 for energy decomposition analysis of model compounds). Therefore, we may also argue that it is the many-body (polarization) effect, rather than two-body polarization, that dictates the Ca²⁺ selectivity.

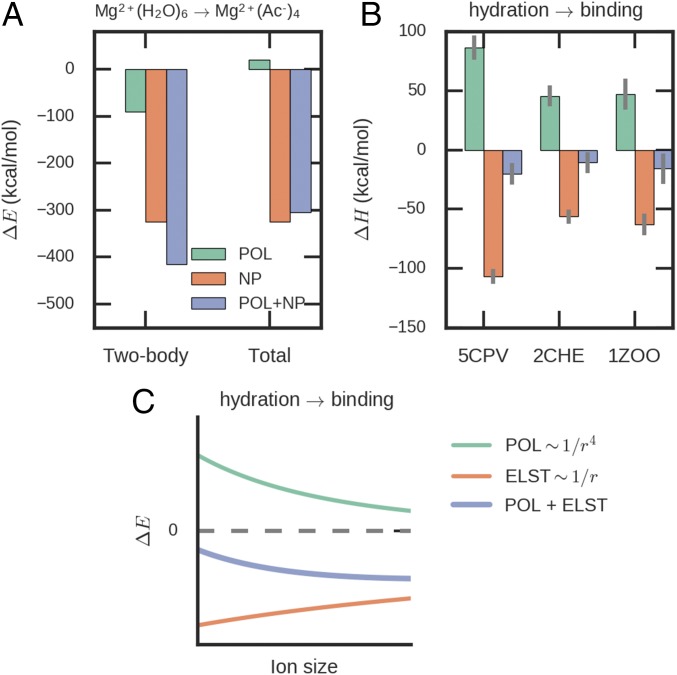
To understand the polarization effect, we can write the polarization energy as the sum of dielectric screening energy and self-energy or Born energy, E_POL = E_screen + E_Born (56). The Born energy reflects the relaxation of the electronic degrees of freedom in the environment, which is always negative. The screening energy reduces the magnitude of electrostatic interaction, and is thus positive in most cases. The total polarization energy is always negative. If only two-body interaction is considered (i.e., the interaction between a pair of molecular fragments is independent of the polarization of others), there will be no screening of electrostatic interaction and the Born energy will dominate. Consequently, the two-body polarization in the highly charged binding pocket is stronger than in ion hydration (Fig. 5A). After including the many-body polarization, there will be a large screening energy in the binding pocket because of the strong electrostatic interactions. Therefore, the total polarization energy in the binding pocket becomes less favorable than that in ion hydration, which can be seen in the results of both gas-phase cluster calculation and condensed-phase MD simulations (Fig. 5 A and B). In general, the binding pockets with more carboxylate groups (e.g., 5CPV) have more unfavorable polarization enthalpy than pockets with fewer carboxylate groups (e.g., 2CHE and 1ZOO). The ion selectivity for Ca²⁺ vs. Mg²⁺ is mainly caused by the different distance dependence of electrostatic and polarization energies. As the ion size increases and ion-residue distances increase accordingly, the magnitudes of the favorable permanent electrostatic interaction and the many-body polarization penalty both decrease, while the latter decreases much faster (Fig. 5C and SI Appendix, Fig. S3). Thus, the overall binding energy becomes more favorable with increasing ion size. For large ions, the short-ranged polarization contribution gradually disappears and the change in total binding energy would slow down or even reverse direction.

Fig. 5.

Role of polarization in ion selectivity. (A) Energy changes between Mg²⁺(H₂O)₆ cluster and Mg²⁺(Ac⁻)₄ cluster. POL and NP are the polarization and nonpolarization contributions. NP is defined as the sum of all energy terms in AMOEBA except polarization, including intramolecular bonded energy, van der Waals, and permanent electrostatics energies. In ionic interactions, the NP term is dominated by electrostatics. The Mg²⁺(H₂O)₆ cluster has more favorable two-body polarization energy but less favorable total polarization energy. (B) Polarization and nonpolarization enthalpy changes ΔH for Mg²⁺–protein binding. The same as in A, Mg–protein binding has favorable ΔH compared with hydration but less favorable polarization enthalpy. (C) Illustration of energy changes due to polarization and permanent electrostatics (ELST) for transferring aqueous metal ion to protein. Protein–ion binding is driven by electrostatics and must overcome the polarization penalty. As the ion size increases, both permanent electrostatic interaction and polarization penalty become weaker, while the polarization penalty decreases much faster. As a result, larger ions will be favored. Ac, acetate.

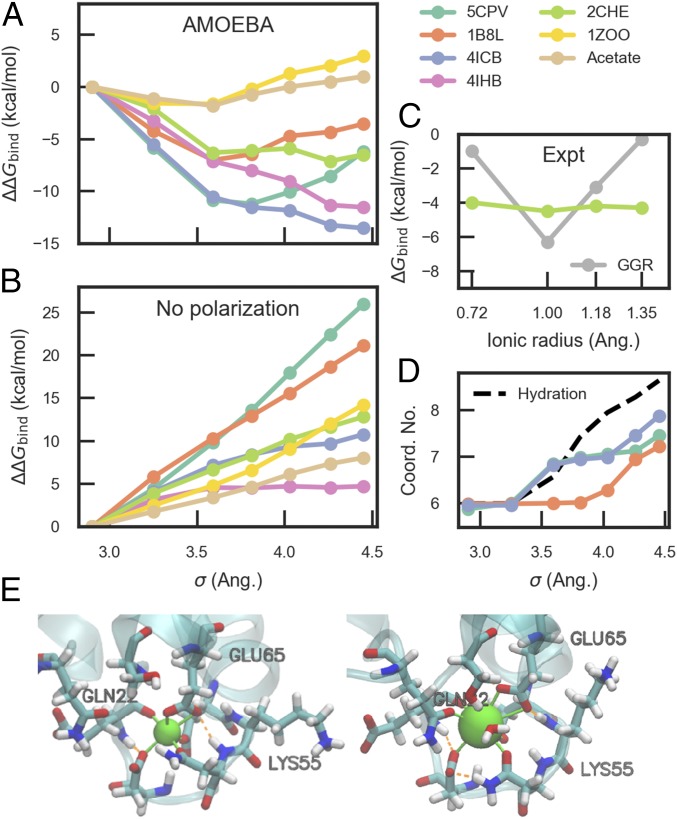
To examine whether the simple rule of ion selectivity stated above applies to divalent ions beyond Mg²⁺ and Ca²⁺, we conducted an alchemical experiment in which the size of the metal ion was varied from that of Mg²⁺ to roughly that of Ba²⁺. It is known that Mg²⁺ has stronger polarizing ability than Ca²⁺ at the same separation distance, while polarizabilities of the metal ions are negligible (57). To focus on the effect of ion size, the polarization parameter of Mg²⁺ in our model was used for all ions in this series (see SI Appendix, Table S7 for force-field parameters). Relative binding free energies for these ions are plotted in Fig. 6. The six proteins show different patterns of dependence on the ion size. Among the three EF-hand proteins, 4ICB favors the largest ion, while 5CPV and 1B8L have an optimal ion size around vdW (van der Waals) diameter σ = 3.6 Å. These trends are related to competition between electrostatic and polarization discussed above as well as the flexibility of the binding pockets. 4ICB has a more flexible binding pocket: the carbonyl group from Gln22 is available for coordinating large ions, allowing the coordination number to increase to 8 for the largest ion (Fig. 6D), close to the coordination number of 9 in water. Similarly, the binding free energy of the C2 domain 4IHB decreases monotonically with ion size, since the binding pocket is formed by flexible loops and there is no constraint on the pocket geometry. The other two EF hands, 5CPV and 1B8L, have extensive hydrogen-bond networks and rigid binding pockets (Fig. 4), which restrict the coordination number to ∼7 (SI Appendix, Fig. S4). This causes both strain energy and a loss in electrostatic interaction for large ions compared with the binding with flexible pockets, and consequently an upward trend of the binding free energy. As discussed earlier, the relatively small many-body effect in 2CHE binding pocket leads to a weaker selectivity for large ions. 1ZOO is the only protein with positive relative binding free energy for the largest ion, which results from a combination of its small many-body effect and rigid binding pocket.

Fig. 6.

Relative binding free energy as a function of vdW size. (A) Calculated relative binding free energies using AMOEBA; (B) calculated relative binding free energies without polarization; (C) experimental binding free energies for the d-galactose and d-glucose receptor (GGR) and the CheY protein 2CHE (19, 20); (D) ion coordination number in AMOEBA simulations; (E) structures of 4ICB bound to Mg²⁺ (Left) and the largest hypothetical ion (Right). 5CPV, 1B8L, and 4ICB in A and GGR in C have EF-hand motifs. The ions in the simulations all have +2 charges and the same polarization parameters as Mg²⁺. All of the calculated binding free energies are relative to that of Mg²⁺, which has a vdW size of 2.90 Å. σ = 3.59, 4.03, and 4.45 Å roughly correspond to Ca²⁺, Sr²⁺, and Ba²⁺, respectively. The SDs of all calculated results are ∼0.2 kcal/mol. Ang., angstrom; Coord. No., coordination number; Expt, experiment.

The presence of an optimal ion size for the EF-hand proteins 5CPV and 1B8L and the weak selectivity of 2CHE for large-sized ions agree qualitatively with experimental data for an EF-handlike protein, d-galactose and d-glucose receptor (GGR), and the CheY protein (Fig. 6C) (19, 20). It should be noted that since the simulated ions have stronger polarization compared with their real-world counterparts, the binding free energies relative to that of Mg²⁺ would be more negative than those of real ions. Although there is no direct experimental data to compare with the simulation results of the bovine calbindin D9k (4ICB), it has been shown that neutral substitution at the gateway position of an EF hand retains the selectivity for Ca²⁺ over Mg²⁺ but leads to a partial loss of selectivity over larger ions (22). This is consistent with our results—that is, when the geometry of the binding pockets is less well constrained, the binding affinities for larger ions will be enhanced.

The contribution of polarization can be clearly seen by comparing the results of polarizable and nonpolarizable simulations (Fig. 6B). In nonpolarizable simulations, the binding free energies of all proteins increase with the ion size. 5CPV and 1B8L have the steepest slopes due to their strong geometric restraint and high number of negative charges. Without polarization, the diversity of ion selectivity in proteins would be greatly reduced.

Conclusion

We have shown that the selectivity of proteins for Ca²⁺ over Mg²⁺ originates from the energetic cost due to many-body interactions, which can be captured with a classical polarization model based on self-consistent atomic dipole induction. The binding of the larger ion Ca²⁺ is associated with lower cost than the smaller Mg²⁺, and thus has higher binding affinities. Our simulations with a polarizable force field could reproduce the relative binding energies between Mg²⁺ and Ca²⁺ across various types of binding pockets. Without polarization, Mg²⁺ will be favored by all highly charged binding pockets. The many-body polarization depends on the number of charged residues surrounding the ion and is sensitive to their spatial arrangement, which can be used to fine-tune the selectivity. We also demonstrated that the nonmonotonic ion size dependence of binding free energies for different proteins arises from the competitions among permanent electrostatic, many-body polarization and geometric restraints. In particular, the precise control of ion size selectivity in EF hands is achieved by combining geometric constraint and the many-body effect.

As general principles, Mg-binding proteins should have more polar and fewer charged groups (to reduce the polarizability and electrostatic interaction) or suboptimal geometries that weaken the electrostatic interaction. Ca-binding proteins should have multiple charged residues and rigid geometry; highly charged and flexible binding pockets would favor large divalent ions.

Materials and Methods

Model compounds for QM calculations were extracted from three proteins with both Mg-bound and Ca-bound structures in PDB (i.e., 1IG5/4ICB, 2LVJ/2LVK, and 1B8L/C). The first-shell carboxylate, carbonyl, and hydroxyl groups were represented by acetate, acetamide, and ethanol, respectively. The first shell is defined as functional groups that directly coordinate the metal ion, and the second shell interacts with the first shell but not in contact with the metal ion. Second-shell Asp or water in 2LVJ, 1IG5, and 4ICB was also included to ensure the same number of molecules in Mg²⁺ and Ca²⁺ complexes. The positions of all of the nonhydrogen atoms were fixed at their respective PDB coordinates, while the hydrogen positions were optimized at the B3LYP/6–31G(d) level of theory. The many-body energy decomposition for these model compounds was calculated at the RI-MP2/def2-QZVPPD level. Considering the large size of the basis set, no correction for basis-set superposition error was applied. The Gaussian 09 (58) and the Psi4 package (59) were used for the geometry optimization and energy calculations, respectively.

The AMOEBA free energy simulations were performed using the TINKER-OpenMM package (60). The latest AMOEBA parameter was used (51, 61, 62), which includes modifications detailed in SI Appendix. The parameter file in TINKER format is also included in Dataset S1. The absolute binding free energies of acetate computed by AMOEBA were −2.7 ± 0.2 and −2.5 ± 0.2 kcal/mol for Mg²⁺ and Ca²⁺, respectively; for comparison, the corresponding experimental values are −1.7 and −1.6 kcal/mol (43). For the artificial ions, the vdW parameters were obtained by linear interpolation using Mg²⁺ and Ca²⁺ parameters and experimental ionic radii (63). The Bennet acceptance ratio method was employed to analyze the free energy differences. The system set-up was as follows. The hydrogen of each protein was assigned at pH 7 by using PDB2PQR 2.0.0. Then, the protein was solvated in a periodic cubic box with the edge length ≥30 Å larger than the longest dimension of the protein. Sodium and chloride ions were added to neutralize the charge and to give a salt concentration of 150 mM. The systems were minimized, equilibrated at 100 K for 100 ps with protein position fixed, and gradually heated from 100 to 300 K in 1.6 ns. Then, the box volumes were determined by a 1-ns NPT (isothermal–isobaric ensemble) simulation at 300 K and 1 bar. In free energy perturbation, Mg²⁺ was gradually changed to Ca²⁺ in five steps, with all force-field parameters linearly interpolated. A 6-ns NVT (canonical ensemble) simulation at 300 K for each alchemical state was carried out with a 3-fs integration time step and coordinates were saved every 3 ps for analysis. Hydrogen-mass repartitioning was applied to allow the large time step. Additional simulation parameters, including the vdW cutoff, the polarization PME parameters, and thermostat, are same as in our previous work (60) (Dataset S2). The AMBER and AMBER/MDEC simulations were performed using the PMEMD CUDA program in Amber 16 package (64, 65), with the ff14SB protein force field (66) and the HFE set of ion parameters from Li et al. (67). All of the bonds involving hydrogen were constrained by the SHAKE algorithm. The integration time step was 2 fs and temperature was controlled by the Langevin thermostat. For each alchemical state, a 10-ns NVT trajectory was collected with an interval of 5 ps. The system setup and analysis were identical to those of the AMOEBA simulations.