Computational discovery of chemically patterned surfaces that effect unique hydration water dynamics

Significance

By combining molecular dynamics simulation with genetic algorithm optimization, we show how nanoscale surface chemical patterning provides a broad strategy to engineer materials with designed hydration water dynamics. Moreover, we find a striking, general relationship between interfacial water’s dynamics and thermodynamic properties that spans many different surface types, suggesting the potential for a unified understanding of the interplay between water structure and mobility as well as a thermodynamic basis for practical surface engineering to control dynamics. These findings may translate to powerful materials design principles for the development of industrially relevant separations and catalytic processes, where precise control of water dynamics at interfaces strongly influences performance.

Abstract

The interactions of water with solid surfaces govern their apparent hydrophobicity/hydrophilicity, influenced at the molecular scale by surface coverage of chemical groups of varied nonpolar/polar character. Recently, it has become clear that the precise patterning of surface groups, and not simply average surface coverage, has a significant impact on the structure and thermodynamics of hydration layer water, and, in turn, on macroscopic interfacial properties. Here we show that patterning also controls the dynamics of hydration water, a behavior frequently thought to be leveraged by biomolecules to influence functional dynamics, but yet to be generalized. To uncover the role of surface heterogeneities, we couple a genetic algorithm to iterative molecular dynamics simulations to design the patterning of surface functional groups, at fixed coverage, to either minimize or maximize proximal water diffusivity. Optimized surface configurations reveal that clustering of hydrophilic groups increases hydration water mobility, while dispersing them decreases it, but only if hydrophilic moieties interact with water through directional, hydrogen-bonding interactions. Remarkably, we find that, across different surfaces, coverages, and patterns, both the chemical potential for inserting a methane-sized hydrophobe near the interface and, in particular, the hydration water orientational entropy serve as strong predictors for hydration water diffusivity, suggesting that these simple thermodynamic quantities encode the way surfaces control water dynamics. These results suggest a deep and intriguing connection between hydration water thermodynamics and dynamics, demonstrating that subnanometer chemical surface patterning is an important design parameter for engineering solid−water interfaces with applications spanning separations to catalysis.

Water dynamics near solid interfaces play a critical role in numerous technologies, including water purification, filtration and adsorption, chromatography, and catalysis. Modifying surface hydrophobicity and chemistry, by altering the average coverage or surface density of functional groups, is well known to influence the dynamics of hydrating water (1–5). Beyond this macroscopic view, however, there also potentially exists a rich design space for tuning dynamics related to the nanoscale patterning of functional groups at fixed coverage. Indeed, efforts have exploited patterning at nanoscopic to microscopic length scales to develop biomimetic surfaces with superhydrophobic (6) and other anomalous, even time-dependent, wetting behaviors (7). Even though a fundamental understanding of the effect of surface chemical heterogeneity on water dynamics is incomplete, there is good reason to expect marked behaviors. Recent theoretical work has shown that surface heterogeneity impacts interfacial thermodynamic properties (including hydrophobicity), in particular, highlighting nonadditive, pattern-specific effects upon arranging hydrophobic and hydrophilic groups on surfaces (8–11). Other work has also emphasized nonadditivities through the failure of macroscopic theories, like the Cassie−Baxter contact angle equation, applied to heterogeneous surfaces (12).

Nature is ripe with examples of biological interfaces that capitalize on chemical heterogeneity, using precise functional group patterns to produce unique hydration dynamics (13–15). In particular, proteins arrange surface amino acids to cooperatively adjust hydration shell water in ways that impact the mechanism and timescale of protein folding and association (14–17). For example, large hydrophobic patches at protein surfaces can induce large fluctuations in nearby water density (18), strengthening and accelerating protein−protein association (19). More generally, spatial heterogeneity in hydration shell dynamics, influenced by local geometry and chemical patterning, is a hallmark of proteins of all sizes and functions (20, 21). Recent experimental measurements have also shown that such heterogeneity is unique to the folded, structured protein and does not appear in corresponding peptide fragments or intrinsically disordered proteins, suggesting the importance of spatially organized heterogeneity in the well-defined folded structure (5).

Are there design principles for biologically inspired interfacial patterning that can be translated to arbitrary synthetic systems to control hydration water dynamics? We use simulations of model surfaces and inverse design algorithms to uncover how functional group patterning alone can influence hydration dynamics in unique and significant ways. While several case studies on specific systems have established how average surface properties such as functional group density (2, 3, 22) and surface−water energetics (23, 24) influence hydration dynamics, our study provides a systematic and general framework for the effect of heterogeneities on dynamics. Here we focus only on the chemical patterning of a surface without the additional effect of confinement, which is also known to induce unusual water dynamics (15, 25), both alone (26) and in conjunction with surface patterning (8, 27).

We examine three distinct model systems that provide complementary perspectives for the influence of surface heterogeneity: (i) Silica is a model material in many catalytic and separation processes, and the $10\overline{1}$ interface of $\alpha$-cristobalite allows variations in silanol (Si−OH) densities that span a spectrum of moderately to highly hydrophilic [contact angles of θ ≈ 42° to 0° (28)]. (ii) Mixed methyl- and hydroxyl-terminated self-assembled monolayers (SAMs) represent a softer interface with a wider range of hydropathy, spanning highly hydrophobic (θ ≈ 121°) to hydrophilic (θ≈ 0°) surfaces. (iii) As a control, we also examine toy Lennard-Jones (LJ) surfaces containing two uncharged particle types with hydrophobic/weak (θ ≈ 127°) and hydrophilic/strong (θ ≈ 91°) van der Waals interactions with water molecules. In some cases, we have also considered LJ surfaces in which the hydrophilic particles are “superattractive” (θ ≈ 49°), with a water−particle interaction energy double the original hydrophilic case. Importantly, all LJ particles interact only isotropically with water, whereas the hydroxyl groups in both the silica and SAM surfaces produce directional hydrogen bonding. All three systems allow distinct coverages and patterning of hydrophilic groups through the spatial arrangement of silanol groups on cristobalite, hydroxyl-terminated SAM chains, or strongly attractive LJ particles.

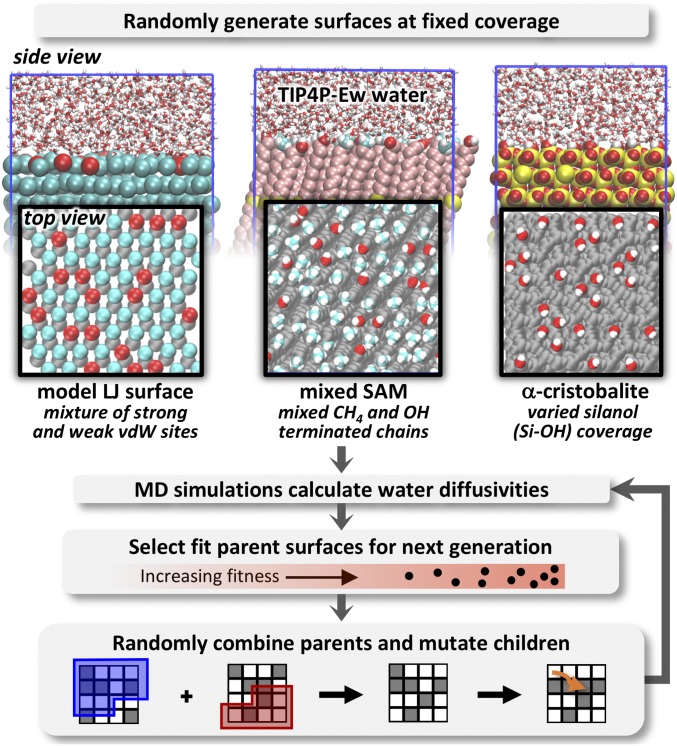
Rather than exhaustively explore all surface configurations for a fixed number of hydrophilic groups, we develop a genetic algorithm for discovering surface configurations that either maximize or minimize the dynamics of hydration layer water, as shown in Fig. 1. In effect, this approach identifies extremal surfaces that provide bounds for realizable water dynamics due to patterning and, in doing so, magnifies surface characteristics that impact and control mobility. The genetic algorithm rearranges surface chemical groups at fixed coverage, and, for each new surface pattern, it uses molecular dynamics (MD) simulations to assess the hydration water dynamics, quantified by the parallel diffusivity for waters within 8 Å of the surface. The algorithm evolves surface patterns toward extremal water dynamics through creation and evaluation of subsequent “generations” of surfaces. Further details are provided in Methods.

Fig. 1.

A schematic of the workflow for the genetic algorithm to optimize (minimize or maximize) hydration water dynamics via repatterning of surfaces at various fixed coverages of hydrophilic groups. Surfaces studied include the $10\overline{1}$ face of $\alpha$-cristobalite with varied silanol coverage, SAM surfaces with mixed methyl- and hydroxyl-terminated chains, and idealized surfaces of mixed binary LJ particles with either strong or weak LJ−water van der Waals (vdW) interactions.

Results and Discussion

Patterning of Surfaces Produces a Wide Range of Diffusivities at Fixed Surface Coverage.

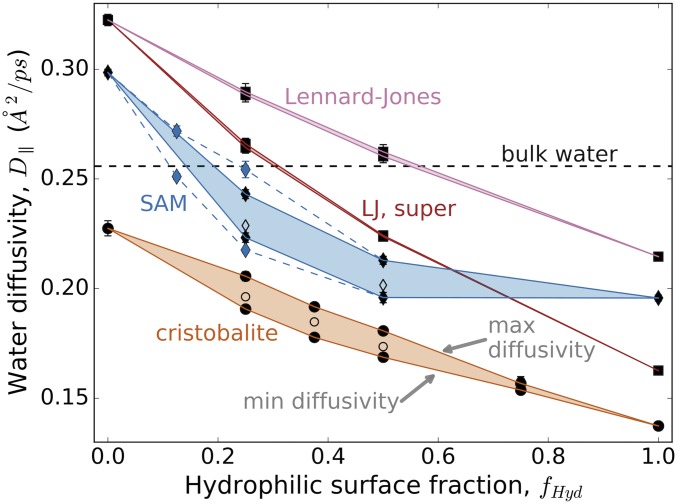
For all surface types studied, the diffusivity monotonically decreases as the number of hydrophilic groups (Si−OH, OH head groups, or more attractive LJ particles) increases, traversing a range of at least 0.1 Ų/ps in diffusivity between 0% and 100% hydrophilic surface fraction (Fig. 2). Diffusivities generally correlate with surface hydrophobicity as given by the simulation contact angle, increasing in the order of the cristobalite, SAM, and LJ surfaces. Similar to the way that hydration water thermodynamic properties vary with hydrophilic coverage (29), we observe an asymmetry in the response of water dynamics to addition of hydrophilic sites: At low hydrophilic fractions, the reduction in mobility is more pronounced than for higher coverages, giving rise to an overall convex relationship in Fig. 2. This effect is most apparent on surfaces with a wide range of effective hydrophilicity/phobicity, including the SAM surfaces and LJ surfaces composed of hydrophobic and superattractive bead types. While the asymmetry is less apparent for the cristobalite and standard LJ cases, the overall relationships still show a discernable convex character.

Fig. 2.

Regions of accessible hydration water diffusivities due to surface repatterning for the model surfaces. The hydrophilic surface fraction is defined for cristobalite as the percentage of the maximum possible silanol (Si−OH) density, for the SAMs as the fraction of hydroxyl-terminated chains, and for the LJ surfaces as the fraction of strongly attractive van der Waals sites. Filled symbols show the minimum and maximum diffusivity found by the genetic algorithm, while open symbols show the average diffusivity for randomly generated surfaces. Red curves show diffusivities for superattractive LJ surfaces, using patterns optimized from the original LJ case. The blue dashed lines and blue diamonds show the expanded diffusivity range for SAM surfaces at surface fractions of 0.125 and 0.25 with regularly spaced and circularly clustered hydroxyl groups (SI Appendix, Fig. S18). The black dashed line gives the average lateral diffusivity of simulation bulk water. Error bars, which are typically smaller than the symbol size, give 1% confidence intervals assuming Student’s t distribution from repeated simulation runs of the same surface.

Importantly, for both the cristobalite and SAM surfaces, the genetic algorithm identifies a wide range of diffusivities resulting from chemical patterning at partial surface coverages, where the number of possible patterns is combinatorically large. At intermediate hydrophilic fractions, patterning of these surfaces can produce a ∼10% change in absolute diffusivity. It is interesting to note, however, that the patterning-induced variation in diffusivity is a substantial fraction of the overall diffusivity range achievable by a given chemistry (i.e., of the range defined between zero and full hydrophilic surface fraction); this relative variation is 16% for cristobalite and 20% for SAM surfaces. Interestingly, for both surface types, the largest spread between minimum and maximum diffusivity occurs at coverages skewed toward smaller hydrophilic fractions. As shown in Dataset S1, the differences in diffusivities due to these surface reconfigurations are statistically significant and reproducible: In nearly all cases, the probability for erroneously predicting that the simulation-calculated minimum surface diffusivity is greater than the maximum is negligible. In contrast, no statistically significant range of diffusivities (for a 5% confidence interval) is obtained from genetic algorithm optimizations of the LJ surface at any coverage, implying that, unlike the other two cases, surface patterning for this system has no measurable effect on water dynamics. This is despite the fact that both LJ cases in Fig. 2 show some nonlinear character. While this nonlinearity is expected due to the higher probability of finding waters near more attractive sites (SI Appendix, section 1), the lack of pattern dependence is unexpected.

The ability of patterning to modulate hydration water dynamics is surprising from a macroscopic perspective. Purely continuum arguments would suggest that heterogeneous surfaces consisting of distinct macroscopic regions differing in hydration water diffusivity should see no patterning effect. Instead, the long-time interfacial dynamics on such surfaces should only depend on the fraction of each region type, unless molecular-scale effects are introduced in the form of barrier-crossing dynamics at region boundaries (SI Appendix, section 1). Indeed, our results show that molecular-scale (<1 nm) patterning is essential to produce pronounced changes in water mobility as surface patterns are adjusted, even without confinement or nontrivial variations in surface geometry.

The significant diffusivity ranges in Fig. 2 hold important implications for experimental measurements of surface hydration water dynamics, direct or inferred. For both the cristobalite and SAM systems, surfaces of intermediate hydrophilicity can have similar water diffusivities to those with nearly half the hydrophilic coverage, if the former are patterned so as to maximize water diffusivity and the latter are similar to randomly generated surfaces. Such results call into question hydropathy scales that paint an additive picture for the effect of surface chemical groups on water. Moreover, these results suggest that surface preparation techniques may critically influence interfacial properties through surface functional group organization. In particular, significant jumps in diffusivity with surface coverage may signal changes to the spatial clustering and distribution of groups, as recently observed for amorphous silica of varied hydroxylation (4). More broadly, measurements to assess the impacts of surface composition on water dynamics may be misleading if surface spatial organization is not also characterized. This further highlights the role of chemical heterogeneity as a significant design parameter in controlling water mobility near interfaces.

The Genetic Algorithm Reveals That Dispersion of Hydrophilic Groups Reduces Water Mobility.

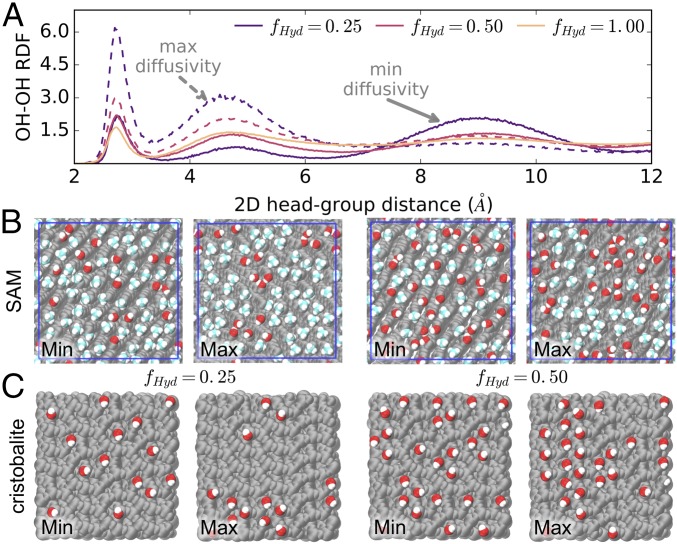
Fig. 3 demonstrates that water mobility is higher near surfaces with large clusters of hydrophilic groups and low on surfaces that evenly distribute such groups, as is clear from images and 2D surface OH radial distribution functions. These results for water dynamics now suggest a deep relationship to underlying thermodynamic and structural properties of hydration water. Ongoing efforts have sought to understand how surface chemistry and heterogeneities impact interfacial water density fluctuations that predict surface hydrophobicity (8, 9, 29–31), and affect dewetting transitions for water confined between plates or in the cavities of proteins (8, 10, 18, 32). Of particular note, Garde and coworkers found that surface groups impact water in a highly nonadditive manner for small length scale features; namely, patches of hydrophobic groups on hydrophilic surfaces must become larger than ∼1 nm before impacting water density fluctuations, while even single hydrophilic groups significantly alter the apparent local hydrophilicity of hydrophobic surfaces (8–11). Our results are consistent, in that dispersion of hydroxyl groups produces an overall more-hydrophilic surface with low water mobility, while hydrophilic clustering permits the exposure of locally more hydrophobic regions that exceed the critical ∼1-nm size necessary to impact local water diffusivity.

Fig. 3.

(A) The 2D radial distribution functions for SAM hydrophilic groups show that maximum diffusivity cases strengthen spatial correlations at short distances. Solid lines for RDFs indicate minimum diffusivity surfaces, while dashed lines give maximum diffusivity cases. (B and C) Simulation snapshots of the minimum and maximum diffusivity patterns for (B) SAM and (C) cristobalite surfaces at hydroxyl fractions of 0.25 and 0.50. Clustering of hydroxyl groups (shown in red) on maximum diffusivity surfaces is clear from visualization of surface structures.

It is possible that more extremal patterns exist such that the true diffusivity ranges are even broader, since the genetic algorithm finds only minimal bounds, due to its finite sampling of the surface landscape. To test the algorithm’s convergence, we simulated SAM surfaces that represent the extremes of discovered patterns, namely regularly dispersed and circularly clustered hydroxyl-terminated chains for hydrophilic chain fractions of 0.125 and 0.25. As seen from Fig. 2, such patterns do slightly increase the range of diffusivities (dashed blue lines), showing that, while the algorithm helps to objectively define the key features of optimal surfaces, it does not find the global optima. As an interesting contrast, we also simulated a more exotic pattern involving a single stripe of hydroxyls along the center of a SAM surface, again at 25% coverage. This pattern exhibits a diffusivity of 0.252 Ų/ps, almost as large as the circularly clustered configuration, and notably exhibits an anisotropy of 0.003 Ų/ps between the directions parallel and perpendicular to the stripe (significant on the 5% confidence interval). Compared with the overall effect of patterning, this anisotropy is small; however, in principle, the algorithm could be configured to locate patterns that maximize the anisotropy, resulting in potentially unintuitive arrangements.

In assessing the algorithm, it is also important to ensure that water diffusivity is optimized through functional group patterning and not by other means. SI Appendix, Figs. S3–S11 demonstrate that variations in simulation conditions other than patterning, like temperature, pressure, or even the rigidity and structure of SAM chains, are not significantly modified by the algorithm. Dataset S1 also characterizes the algorithm’s performance by estimating the probability of randomly observing at least one occurrence of an extremal diffusivity surface beyond the minimum and maximum currently found at each coverage. Overall, minimum diffusivity surfaces are more likely to be observed among random surfaces than are maximum diffusivity ones, but the low probabilities for the latter show that the algorithm is helpful, particularly at intermediate coverages. This occurs because higher water mobility surface patterns spatially cluster hydroxyl groups, and such cases are smaller in number and more difficult for the algorithm to locate than randomly dispersed ones. The same behavior is also highlighted by the fact that randomly generated surfaces have diffusivities more similar to minimum diffusivity ones (Fig. 2).

Orientation-Specific Surface−Water Interactions Drive Mobility Reductions.

We find that molecular measures of hydrophobicity for a given heterogeneous surface also reflect surface patterning in a manner consistent with variations in hydration water diffusivity. Spatially resolved density fluctuations within probes placed near interfaces reveal overall more-hydrophilic surfaces (lower density fluctuations) for those with lower water mobilities (SI Appendix, Fig. S12). More hydrophobic surfaces are also expected to exhibit increased fluctuations in the location of the surface−water interface itself (31). To define an instantaneous interface, we follow the water density isosurface definition of Willard and Chandler (33), and indeed see heightened fluctuations near regions of higher hydrophobicity and lower ones for hydrophilic locations (SI Appendix, Fig. S13). Although not pursued here, we expect that other estimates of local surface hydrophilicity (34, 35) will provide qualitatively similar results.

To quantify and compare the average hydrophobicity of a surface to average water mobility, we consider the excess chemical potential of hard-sphere insertion, given by

$${\mu }_{ex}^{HS}=-k_{B}T\ln {\wp }_V$$ [1]

where ${\wp }_V$ gives the probability for successful insertion of a hard sphere of volume $V$ randomly placed within a region of interest. Such excess chemical potentials can probe local hydrophobicity as an effective hydropathy map of heterogeneous, molecular-scale surfaces (9, 36). They are also intimately tied to the magnitude of molecular-scale fluctuations in water density, as a successful hard-sphere insertion only occurs when the probe volume density fluctuates to zero (37).

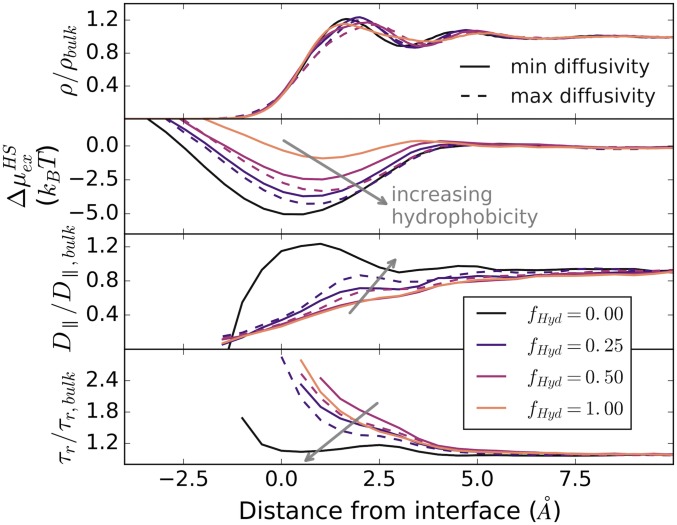
Fig. 4A shows that ${\mu }_{ex}^{HS}$ for methane-sized (3.3 Å) spheres within 8 Å of the surface correlates remarkably well with hydration water diffusivity, even across a wide range of surface types, coverages, and patterning. Comparable relationships are observed when instantaneous interface location fluctuations are taken into account (although the correlation weakens for the SAM surfaces due to their compressibility; see SI Appendix, Fig. S14). The notion of a relationship between mobility and ${\mu }_{ex}^{HS}$ is not new; Mittal et al. (38) found a strong correlation in the hard-sphere fluid. However, the persistence of this behavior here is surprising given water’s very different density fluctuations and liquid structure, which depart from simple liquids like hard spheres and influence many water-unique features of hydrophobic solvation (39). To illustrate the distinction, Fig. 5 shows water density, excess hard-sphere chemical potential, water parallel diffusivity, and reorientation times as a function of distance from the interface. While mobility is spatially correlated with density for confined hard-sphere fluids (38), here the average water density only weakly predicts diffusivity, and it fails to correctly rank surfaces in terms of either hydrophobicity or hydration water mobility. Instead, because ${\mu }_{ex}^{HS}$ is predictive, it is clear that water density fluctuations are strongly and locally correlated with both translational and orientational water mobility, a trend that was noted previously for the singular case of a hydrophobic SAM (40).

Fig. 4.

(A) Hydration water diffusivity correlates with the excess chemical potential for hard-sphere insertion near the interface across all surface types and patterning. Hatched points represent surfaces at hydrophilic fractions of zero or one, filled points represent minimum diffusivity surfaces, and open points represent maximum diffusivity ones. (B) The logarithm of water diffusivity correlates with the orientational contribution to the one-body intensive entropy. In both A and B, abscissa values report differences from bulk water.

Fig. 5.

Spatial variations as a function of distance from the mean interface (water density at 0.3 of its bulk value) are shown relative to bulk for water density, hard-sphere excess chemical potential, water diffusivity, and water reorientation times.

While ${\mu }_{ex}^{HS}$ seems to do an excellent overall job of predicting surface dynamics, it does not capture the entire picture. Specifically, binary patterning of the LJ surfaces produces small variations in ${\mu }_{ex}^{HS}$ but fails to impact water diffusivity (Fig. 4A). Indeed, earlier efforts for similar LJ surfaces have shown that particle arrangements do affect interfacial thermodynamic properties and alter surface hydrophobicity (10). It may then seem surprising that the genetic algorithm cannot uncover discernible diffusivity differences due to surface patterning in these systems (Fig. 2). Even if we transpose the minimum and maximum patterns from the SAM results to the LJ surface (the two systems share the same 2D lattice), we still do not find statistically significant variations in diffusivity (SI Appendix, Fig. S16). This behavior is also independent of the specific LJ interaction parameters: Doubling the van der Waals strength of the already sixfold more attractive hydrophilic particles reduces the contact angle of the pure surface from 91° to 49°, but still does not produce a diffusivity difference for dispersed and clustered particle arrangements (Fig. 2). However, pattern-induced variations in ${\mu }_{ex}^{HS}$ are still apparent and grow larger with the superattractive particles. This clearly disrupts the overall trend in Fig. 4A, suggesting that, while water dynamics and local density fluctuations (probed by ${\mu }_{ex}^{HS}$) are correlated, the nature of the surface−water interaction also plays a role.

The toy LJ surfaces highlight the important role of directional interactions in manipulating water dynamics and nuance the predictive capability of ${\mu }_{ex}^{HS}$. This observation agrees with models of water mobility based on hydrogen bond dynamics (16), and with studies showing that interfacial mobility depends on surface affinity, water−surface hydrogen bond strength, and water orientation with respect to the surface (41, 42). To further this idea, we consider entropic measures that quantify water orientational structure at the interface, since close relationships between fluid entropy and diffusivity are well established for both simple fluids (43) and bulk water (44). For small observation volumes, water degrees of freedom may be approximately decoupled (45), allowing a separation of entropy into translational and orientational terms. As a first approximation, we use the program GIST (Grid Inhomogeneous Solvation Theory) (46) to calculate such contributions to the entropy change from bulk for waters within 8 Å of the surface. This analysis ignores entropy contributions from intermolecular coupling, focusing only on changes related to single-molecule degrees of freedom.

Fig. 4B shows that hydration water orientation entropy strongly correlates with diffusivity. In contrast, the translational contribution to the entropy, which, at the single-molecule level, is only based on water density, is less predictive (SI Appendix, Fig. S17). Interestingly, the correlation of diffusivity with entropy improves if SAM chains are frozen, highlighting complexities induced by a flexible, fluctuating interface. Importantly, the LJ surfaces that demonstrate no dynamic effect of surface patterning are also invariant with respect to orientational entropy, showing a consistent and strong diffusivity−entropy correlation over the full range of coverages. Thus, while patterning can effect variations in density fluctuations and ${\mu }_{ex}^{HS}$, ultimately, a perspective that addresses the orientational structure of water is essential to understanding surface-induced dynamics. These findings reveal a close coupling of surface water diffusivity with orientational water entropy and suggest a future opportunity to probe the differential roles of translational and orientational entropies, the impact of surface flexibility, and the relationship between entropic measures and ${\mu }_{ex}^{HS}$.

Conclusions

This work illustrates that functional group patterning on heterogeneous surfaces can produce significant variations in hydration water dynamics, even if the surface coverage remains constant. A genetic algorithm treats surface patterning as an adjustable design parameter and can precisely delineate and magnify the effect of surface heterogeneity by locating surfaces that extremize the hydration water diffusion constant. Such an optimization approach seems broadly useful and could be adapted to also discover patterned surface flexibility (stiffness) and local geometry (roughness) that optimize a variety of thermodynamic and kinetic solvent properties across many distinct kinds of surface modalities and solvents. Recent experiments have also shown that careful design of chemical heterogeneity is crucial to controlling both thermodynamic and dynamic interfacial properties in silica materials (4), which are ubiquitous in catalytic reaction processes. This suggests exciting opportunities for computational design of novel materials in even more diverse applications, from antifouling membrane surfaces for water purification to the regulation of interfacial heat transfer (47).

The patterns that emerge from our optimization procedure exhibit dispersed/clumped hydrophilic groups for high-/low-mobility surfaces, a result reminiscent of patterning effects known to make surfaces less/more hydrophobic. Indeed, the correlation that we observe between mobility and excess hard-sphere chemical potentials suggests a deep, albeit not fully general, connection between water dynamics and density fluctuations. We also find that surfaces composed of LJ particles, without directional or electrostatic interactions, cannot manipulate water diffusivity via their patterning, which is surprising given results here and in previous studies (10, 31, 32) that demonstrate distinct, pattern-dependent changes in thermodynamic properties. While more investigation is necessary, this result highlights a key difference between the thermodynamic (water density fluctuations) and dynamic behavior of water at interfaces: Interactions that make use of the anisotropy of the water molecule (e.g., multipole electrostatics) may play a more fundamental role in determining dynamics than water density fluctuations. In turn, theoretical efforts seeking to connect water thermodynamics and mobility should explicitly consider effects associated with both translational and orientational degrees of freedom. The strong correlations between orientational hydration water entropies and diffusivities found here lend further support to this idea, and also reemphasize entropy-dynamic relationships that have been well studied in bulk fluids (43, 44). Thus, this work not only represents a step in the discovery of materials with surface patterns that modify water dynamics but also exposes fundamental connections between local mobility, structure, and entropy of liquid water. In particular, the inhomogeneous yet highly tunable model surfaces presented here, which exhibit pronounced spatial dependence of kinetic, thermodynamic, and structural water properties, provide an excellent testing ground for such theoretical developments.

Methods

Model Systems.

We model all surfaces using MD simulations of 3D periodic systems with slab geometries (Fig. 1). Surfaces are solvated on each side by TIP4P-Ew water (48), although we found no qualitative differences using other water models. Fully hydroxylated crystalline slabs of the $10\overline{1}$ face of $\alpha$-cristobalite were derived from the fully silonated library provided by Emami et al. (28). To reach lower densities for these models, we perform in silico “condensations” of two nearest-neighbor silanol groups, using ParmEd (49) to remove both hydrogens and one oxygen from the topology, then creating all necessary bonds, angles, and dihedrals surrounding the newly bridging oxygen. Force field functional forms and parameters come from the silica portion of the INTERFACE force-field parameterization (28).

We model methyl- and hydroxyl-terminated SAM chains similarly to the efforts of Garde and coworkers (29, 50), Levine et al. (51), and Zerze et al. (52). In brief, united atoms represent subsurface groups, while atomic detail is used for head groups. Further details are provided in SI Appendix, section 2, including modifications that were necessary to correct for discovered problems in the force field. Additionally, parameter and representative structure files, which include explicit values for all force field terms, are provided in Datasets S1–S11.

We generate surfaces of LJ particles on a 2D lattice identical to that of the SAM systems. This includes five lattice layers, which makes slabs for all systems (including SAM and cristobalite surfaces) at least ∼20 Å thick. “Hydrophobic” LJ particles use parameters for united-atom methane ($\mathit{ϵ}=1.2301$ kJ/mol and $\sigma =3.730\hspace{0.17em}\AA$) (53), while “hydrophilic” ones have a six times greater $\mathit{ϵ}$ for interactions with water. All intersurface interactions for LJ particles follow the purely hydrophobic case so that surface-surface energetics are not influenced by patterning. “Super-attractive” LJ particles are also employed in some simulations, with an epsilon that is 12 times greater than that for hydrophobic LJ particles.

MD Details.

We use the 2016.1 release of the GROMACS software suite (54) for all MD simulations. In all cases, the time step is 0.002 ps and we constrain all bonds involving hydrogens. Short-range, nonbonded interactions are truncated and shifted to zero at a 12-Å cutoff, with default GROMACS treatment for long-range electrostatics. All runs consist of ∼8,000 atoms and utilize graphical processing unit (GPU)-accelerated code on NVIDIA GTX 1080 Pascal GPUs provided by Exxact. SI Appendix, section 3 details equilibration procedures performed before each 10-ns production run. Additional simulation information, as well as details of analysis methods such as calculation of parallel diffusivity and hard-sphere insertion probabilities, are also provided in SI Appendix, section 3.

Genetic Algorithm Implementation.

The genetic algorithm workflow of Fig. 1 is coded in python 2.7, making extensive use of the ParmEd (49) and pytraj (55) packages. “Individuals” refers to specific realizations of surface patterns, and “parents” refers to a subset of fit individuals selected to produce “children” of the next generation. Boolean arrays store surface configurations with True values indicating that a surface site (i.e., silanol, SAM chain, or LJ particle) is hydrophilic. Initially, a pool of randomly generated surfaces/individuals is created. Tournament selection of parents collects high-fitness candidates (either high or low parallel diffusivity, depending on the optimization direction) for generating children. To combine two randomly paired parents, a random fraction of the first’s True values is combined with the conjugate fraction of the second’s, and a second child stems from the flipped version. While this strategy generally preserves surface coverage, in cases where it does not, we randomly mutate child sites until the desired surface density is reached. Once produced, children undergo a fixed number of random mutations proportional to the surface coverage via swapping of True and False Boolean array values; we skip this procedure if the surfaces have already reached the target number of mutations during the process of ensuring fixed surface density. We also explored an advanced algorithm approach involving clustering of surfaces, called “nicheing” in the genetic algorithm literature, but found only marginal gains in efficiency and results that were not distinct from the more basic procedure.

We have tuned the algorithm to efficiently utilize eight available GPU processors. Each “generation” consists of eight individuals (surfaces), and the first 11 generations (or 88 surfaces from generation 0 to 10) use random patterns to build a library of potential parents. Subsequently, the genetic optimization produces 20 generations. A second 20-generation optimization starting from the same random 88-surface pool but using a distinct random number seed follows. Finally, we perform another 20 generations of optimization after combining the full surface libraries from the random generations and both independent optimization runs. Each generation requires ∼2 h for all surface types, with the majority of time in MD simulations. Since each surface is identical on its upper and lower faces, 10-ns MD simulations produce effectively 20 ns of data used to evaluate diffusivities. In total, for each particular surface and coverage, the genetic algorithm preforms 1,048 MD simulations requiring 10.5 μs of simulation time.