How adaptive immunity constrains the composition and fate of large bacterial populations

Significance

Complex communities of microorganisms are important ecological forces and phages are integral components of microbial populations. Among the many bacterial defense mechanisms against phages, CRISPR-Cas is unique in its ability to learn from past infections by storing pieces of phage DNA (called spacers) in its own genome to neutralize future infections. Our work shows that the rank abundance distribution of spacers across the whole bacterial population, which is readily accessed using genomic sequencing, may provide a phenomenological observable that reflects important structural aspects of bacterial populations. This study lays out a path toward a phenomenological framework for understanding microbial dynamics and may provide insights into complex and diverse natural populations where microscopic modeling is plagued by overparameterization and overfitting.

Abstract

Features of the CRISPR-Cas system, in which bacteria integrate small segments of phage genome (spacers) into their DNA to neutralize future attacks, suggest that its effect is not limited to individual bacteria but may control the fate and structure of whole populations. Emphasizing the population-level impact of the CRISPR-Cas system, recent experiments show that some bacteria regulate CRISPR-associated genes via the quorum sensing (QS) pathway. Here we present a model that shows that from the highly stochastic dynamics of individual spacers under QS control emerges a rank-abundance distribution of spacers that is time invariant, a surprising prediction that we test with dynamic spacer-tracking data from literature. This distribution depends on the state of the competing phage–bacteria population, which due to QS-based regulation may coexist in multiple stable states that vary significantly in their phage-to-bacterium ratio, a widely used ecological measure to characterize microbial systems.

Complex communities of microorganisms are important ecological forces in almost every environment from hot springs (1) to humans (2–6). Phages, viruses which infect bacteria, are integral components of microbial populations: Phage predation has been shown to strongly influence bacterial evolution, diversity, and numbers (7, 8). To counter phages, bacteria have evolved many and complex immune mechanisms (9). CRISPR-Cas is one such defense mechanism which is both adaptive and heritable; i.e., it not only learns from past infections but also passes this knowledge to future generations. Many models have addressed the effects of CRISPR-Cas on microbial populations, but a conceptual vacuum remains: What experimental features of natural populations should be measured to compare with model predictions?

CRISPR-Cas machinery for adaptive immunity allows bacteria to acquire unique genetic elements (called spacers) from prior phage encounters to specifically target and evade recurrent attacks. The spacers are tens of nucleotides long and at each encounter may be acquired from any of the hundreds of possible locations on the infecting phage genome (called protospacers). Since individual spacers are distinguishable and because they are integrated in the genome, the result is a lineage of cells that can be identified by its spacer(s). The fate of an individual lineage, however, is subject to large fluctuations due to the stochastic dynamics of individual bacteria in a large rapidly evolving population. Experiments show that the abundance of individual spacers in a bacterial population under phage attack is indeed highly dynamic and varies over several orders of magnitude from one spacer to the next (7, 10–13). This leads to a natural question: What controls spacer diversity and abundance? In other words, how does recurrent phage attack alter the structure and composition of interacting spacer-marked lineages in a bacterial population?

Several previous models have addressed the role and dynamics of observed diversity of spacer types (14–21) in a qualitative way: (i) They have shown how system parameters such as phage adsorption rate (21), spacer acquisition rate (16, 21), and phage mutation and recombination (18) affect spacer diversity; (ii) they have shown how increasing diversity promotes population stability (16, 19); and (iii) they have reproduced the observed asymmetry in diversity along the locus in natural populations (14, 15, 18) by modeling biased acquisition at the leader end of the CRISPR locus. Most recently, Bradde et al. (20) showed a connection between spacer acquisition rates and spacer effectiveness to spacer diversity. To make a direct connection with data, we analyzed sequencing data from Paez-Espino et al. (12), a coevolution experiment with phage and bacteria which tracked spacer dynamics. Our analysis shows that despite rapid turnover of individual spacer types, the spacer rank-abundance distribution quickly stabilizes, which is a striking observation that previous models have not addressed.

Recently, similar questions about diversity in the adaptive immune system have gained traction in the context of vertebrates which generate and maintain a large population of specialized immune cells that, as a group, contain an extremely diverse set of binding sites that individually recognize different viruses. Like spacer abundance, the abundance of individual binding sites is highly variable (22–24). This observation has led to the suggestion that a broad abundance distribution of binding sites may strike a balance between generating a rapid response against likely invaders and capturing new invaders (24). Although this is hard to test in vertebrates, laboratory experiments that alter bacterial population composition synthetically show that bacteria are more successful at fending off phages as their population-level spacer diversity increases (25). How the dynamics of individual bacterial lineages shape spacer diversity and how diversity in spacer sequences or types relates to diversity in spacer abundances remain unanswered.

Beyond the role of individual spacer lineages in shaping population structure, recent experiments have shown that bacterial populations exert top–down control on the CRISPR system: Two species of bacteria have been observed to regulate their CRISPR-Cas systems in response to cell density (26, 27). Interestingly, this control acts via the quorum sensing pathway, a pathway which also controls population-level responses such as virulence. This suggests a different paradigm where the effects of CRISPR-Cas need to be considered at the collective population level, rather than at the level of individual cells. Previous population-level models have not addressed this effect (20, 21, 28–38), and modeling efforts addressing CRISPR-Cas regulation have focused on the relevant gene circuits and production of transcribed spacers called CRISPR RNAs (crRNAs), not on the population-level effects of regulation (39–41).

We build a model that addresses the two aforementioned fundamental and unaddressed aspects of the CRISPR-Cas system: (i) Our model shows how stable rank-abundance distributions may arise despite rapid turnover of individual spacer types that are identical in their ability to provide immunity, and (ii) our model shows that density-dependent regulation of CRISPR-Cas admits a bistable state at the population level where the phage–bacterial population can be stable with two different configurations under the same external conditions. We further argue how having the knowledge of spacer diversity along with bistable states may shed light on the fate of natural microbial populations.

Model

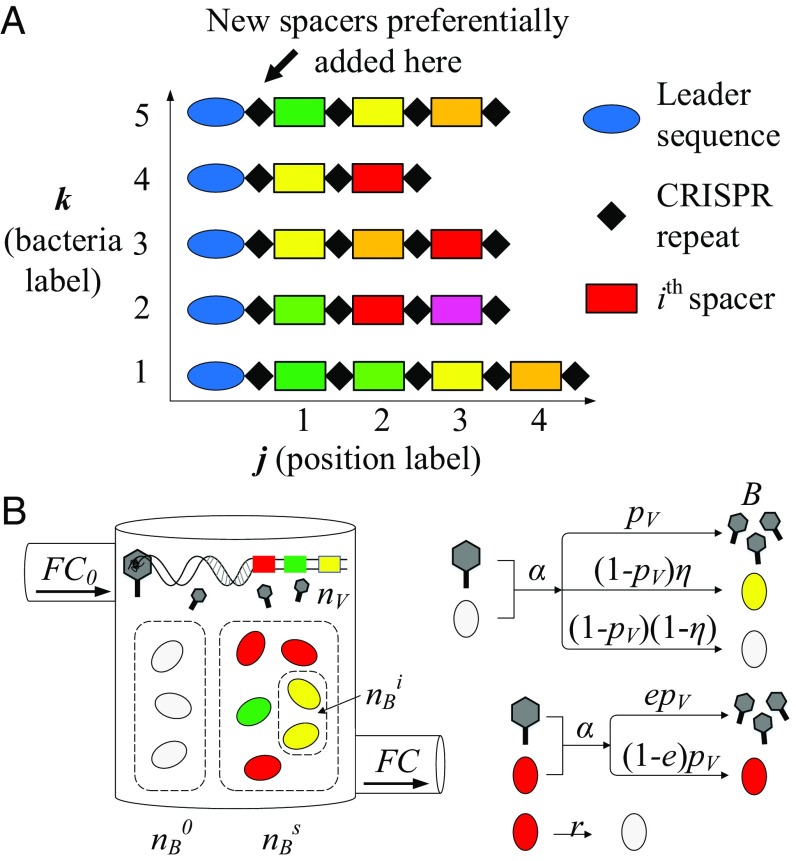
Adaptive immunity in bacteria is controlled by a set of Cas proteins, which in a nutshell accomplish two different tasks: (i) When an invading phage inserts its genome into a bacterial cell but is not successful in killing the bacterium, Cas proteins take a small piece of phage genome and insert it into the bacterial genome at a specific site called the CRISPR locus. (ii) During a subsequent phage attack, the bacterium can use the information stored in the CRISPR locus to recognize the invading phage and neutralize it. Multiple spacers can be stored at a CRISPR locus, providing a genetic record of immunization that is inherited during DNA replication. The immunization record in principle can be read via next-generation sequencing and provides a rich presence/absence observable: the binary variable $s_{ijk}$ indicating whether spacer type $i$ is in locus position $j$ in host bacterium $k$ (Fig. 1A and Eq. S1).

Fig. 1.

(A) CRISPR locus. Small ($\sim$30 nt) samples of invasive phage DNA called spacers (colored rectangles) are incorporated into the CRISPR genetic locus. Spacers are separated by short ($\sim$30 nt) sequences called repeats (black diamonds). Multiple spacers can be stored at a CRISPR locus, resulting in a genetic record of immunization (42). In our analysis of the experimental data shown in Fig. 3 A–C, we identify spacers with a type $i$, a locus position $j$, and a bacterium $k$. (B) In our model, bacteria and phages interact in a chemostat (flow cell) with a constant inflow and outflow rate $F$. Nutrients flow into the chemostat at a fixed concentration $C_0$. Phages are assumed to be identical with a large, fixed number of possible protospacers. Phages adsorb to bacteria with rate $\alpha$ and successfully infect and kill naive bacteria with probability $p_V$. Each bacterium can acquire a single spacer ($j=1$). Spacers are tracked in the population as the number of bacteria containing a spacer of type $i$, $n_B^i$. If a naive bacterium survives an infection, it can acquire a spacer with probability $\eta$. All spacers are assumed to be equally effective: The probability of phage success in an infection is reduced by $e$ if a bacterium has a spacer. Bacteria with spacers revert to naive bacteria by losing a spacer with rate $r$.

We model the abundance of the $i\mathrm{t}\mathrm{h}$ spacer, $n_B^i\left(t\right)$, which is obtained by summing over all bacteria and locus positions; i.e., $n_B^i\left(t\right)={\sum }_{j,k}{s}_{ijk}\left(t\right)$. An important simplifying assumption of our model is that each locus has at most one spacer; i.e., $j=1$; this assumption is borne out of analysis of a laboratory experiment that shows that spacer dynamics stabilize rapidly within tens of generations with each bacterium predominantly having one new spacer (see SI Appendix, section 1.2 for details of data analysis) (12). Additionally, a model that allowed more than one spacer also found that only the most recently acquired spacers dominate the dynamics (16). With this assumption, the abundance of individual spacer types can be mapped to the number of bacteria with a particular spacer, $n_B^i$. In addition, we assume each spacer to have equal effectiveness; this both is a simplifying assumption and also acknowledges our lack of experimental knowledge about differences among spacers and their effectiveness.

To capture the inherent stochastic nature of spacer dynamics, we model the probability distribution $P\left(n_B^0,\left\{n_B^i\right\},n_V,C,t\right)$, which is the probability at time $t$ of observing $n_B^0$ bacteria without spacers and $\left\{n_B^i\right\}$ bacteria with spacer type $i$, $n_V$ phages, and a nutrient concentration of $C$. Interactions included in the model are illustrated in Fig. 1B and described in detail in SI Appendix, section 2. This construction highlights another important simplifying assumption which is also valid for short timescales: lack of phage diversity; i.e., all phages are assumed to be identical. In addition, we model the phage–bacteria population in a flow cell or chemostat, a well-stirred vessel in which nutrients flow in at a constant rate and concentration and the mixture flows out with the same rate. A chemostat is not only comparable to periodic dilution experiments in the laboratory, it is also a reasonable approximation of real-world microbial populations from a gutter to a gut. In many of these natural environments, nutrients and waste flow in and out—the environment is not static like a Petri dish. Additionally, the chemostat flow rate $F$ is an experimental “knob” that can be used to tune a population-level bifurcation we describe later.

Our stochastic model has a corresponding mean-field or population-level description for average values of the different random variables, each represented by the same symbol as their corresponding random variable. At the mean-field level, all of the spacer-containing bacteria can be pooled into a single variable $n_B^s={\sum }_i{n}_B^i$, and the number of bacteria without spacers is $n_B^0$. The mean-field equations are given below. Parameter descriptions can be found in Fig. 1 and SI Appendix, Table S1. We assume that the bacterial growth rate is linear with the concentration of nutrients $C$; relaxing this assumption does not qualitatively change our results (SI Appendix, section 3.2):

$$\begin{array}{ll}\hfill \frac{dC}{dt}=& \underset{\text{flow in}}{\underbrace{F{C}_0}}-\underset{\text{bacterial growth}}{\underbrace{gC\left(n_B^s+n_B^0\right)}}-\underset{\text{flow out}}{\underbrace{FC}}\hfill \\ \hfill \frac{d{n}_V}{dt}=& \underset{\text{phage adsorption}}{\underbrace{-\alpha n_V\left(n_B^s+n_B^0\right)}}+\underset{\text{phage burst and bacterial lysis}}{\underbrace{\alpha B{p}_V{n}_V\left(n_B^s\left(1-e\right)+n_B^0\right)}}-F{n}_V\hfill \\ \hfill \frac{d{n}_B^0}{dt}=& gC{n}_B^0-\alpha p_V{n}_V{n}_B^0-\underset{\text{spacer acquisition}}{\underbrace{\alpha \left(1-p_V\right)\eta n_V{n}_B^0}}+\underset{\text{spacer loss}}{\underbrace{r{n}_B^s}}-F{n}_B^0\hfill \\ \hfill \frac{d{n}_B^s}{dt}=& gC{n}_B^s-\alpha p_V\left(1-e\right)n_V{n}_B^s+\alpha \left(1-p_V\right)\eta n_V{n}_B^0\hfill \\ \hfill & -r{n}_B^s-F{n}_B^s.\hfill \end{array}$$ [1]

Results

Mean-Field Steady States.

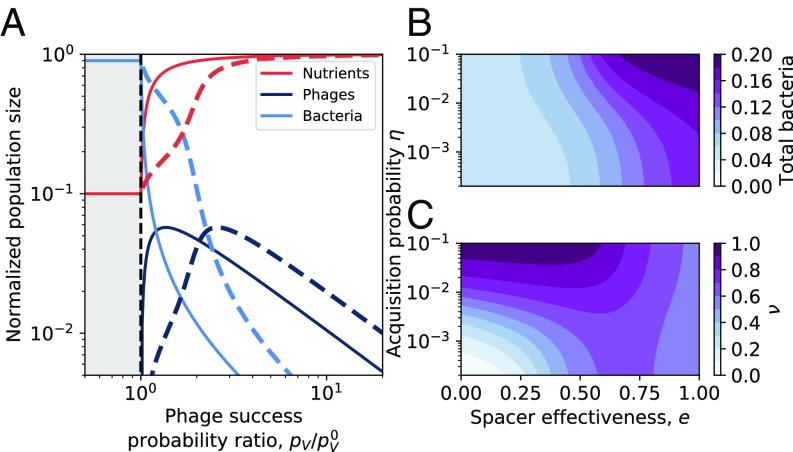
For phages to invade a bacterial population that is stable in a chemostat, their probability of successfully infecting bacteria without the benefits of adaptive immunity, $p_V$, needs to be above a certain minimum value given by $p_V^0=\frac{1}{B}\left(\frac{gf}{\left(1-f\right)\alpha }+1\right)$, where $f=F/\left(g{C}_0\right)$. For $\frac{gf}{\left(1-f\right)\alpha }<<1$ (satisfied at the parameters we use for low flow rates), $p_V^0$ is approximately $1/B$: Phages must succeed approximately every $1/B$ interactions to persist in the population. $p_V^0$ is surprisingly small for realistic values of the burst size $B$; for example, if $B=100$, then $p_V^0\approx 0.01$. As $p_V$ rises above the threshold value, the steady-state phage population, $n_V$, first rises while the bacterial population decreases as they get killed by phages. Interestingly, the steady-state bacterial population keeps decreasing with increasing $p_V$, but the phage population exhibits a nonmonotonic behavior with a maximum population size at an intermediate value of $p_V^{\star }=p_V^0+\sqrt{\frac{p_V^0}{f}\left(p_V^0-\frac{1}{B}\right)}$. This steady-state behavior is qualitatively the same for bacteria with adaptive immunity ($e>0$) as for bacteria without adaptive immunity ($e=0$). Quantitatively, however, bacteria always fare better in the presence of adaptive immunity (Fig. 2A). One surprising observation is that the minimum success probability required for phages to invade a bacterial culture is independent of adaptive immunity. This is because there are no bacteria with spacers at steady state below $p_V=p_V^0$, and, as a result, phage invasion occurs independently of the CRISPR system (SI Appendix, Fig. S12).

Fig. 2.

(A) Bacteria, phage, and nutrients at steady state as a function of the probability of phage success $p_V$ for a model without CRISPR (spacer effectiveness $e=0$, solid lines) and for a model where bacteria have CRISPR systems and are able to acquire spacers ($e=0.5$, dashed lines). Population sizes are normalized by the inflow nutrient concentration $C_0$, and phages are additionally scaled by the burst size $B$. As the probability of phage success $p_V$ increases, bacteria decrease in number. Below $p_V=p_V^0$, phages cannot persist and the fraction of bacteria with spacers is 0. Phages increase with increasing $p_V$ and then decrease at high $p_V$ because the bacterial population is too small to support more phages. (B) Normalized total bacteria as a function of spacer acquisition probability $\eta$ and spacer effectiveness (equal for all spacers). (C) Fraction of bacteria with spacers ($\nu$) as a function of $\eta$ and $e$.

Much like increasing $p_V$, an increasing spacer effectiveness $e$ causes the total number of bacteria at steady state to increase monotonically (Fig. 2B), since a bacterium with a spacer is less likely to be killed by phages as $e$ increases. However, even for $e>0$, not all bacterial cells in a population have a spacer, and the steady-state fraction of the bacterial population with spacers, $\nu$, is governed by a balance of spacer acquisition $\eta$, spacer loss $r$, and the effect of $e$ on the bacterial population. As a result, the steady-state level of bacteria can increase by either increased spacer acquisition or improved spacer effectiveness; contours in Fig. 2B show the tradeoff between $\eta$ and $e$ that maintains bacterial population size.

In contrast to the total bacterial population, $\nu$ first increases as $e$ increases but reaches a maximum at an intermediate value of $e$ (Fig. 2C). This can be understood as $\nu$ qualitatively tracking the phage population size, which shows a peak at intermediate spacer effectiveness (SI Appendix, Fig. S14). Qualitatively, this behavior is similar to the total phage population having a nonmonotonic behavior with increasing $p_V$.

Spacer Rank-Abundance Distributions.

Even at steady state with stable populations of phage and bacteria, the individual spacer abundances in the bacterial population are highly dynamic and vary significantly over time. This has been seen most directly in laboratory experiments (12, 13) but has also been observed in natural samples such as a hypersaline lake (43), human saliva (44), and acid mine drainage (10, 15). This continual spacer turnover is influenced by bacterial reproduction and death, spacer acquisition, and spacer loss, all of which have been observed in natural and laboratory populations.

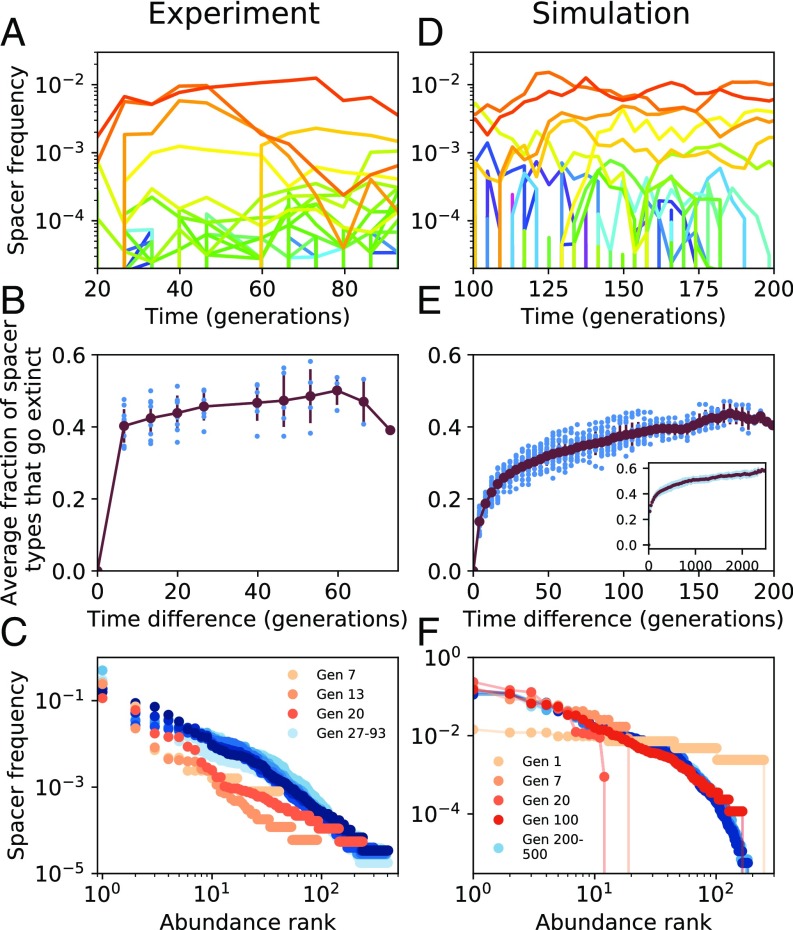
In our stochastic model, we keep track of individual spacer acquisition and loss events. Not surprisingly, we find that spacer abundances fluctuate over time (Fig. 3 D and E and SI Appendix, section 4.1). However, we also find that the spacer rank-abundance distribution reaches a stationary state from an initial state with no spacers, shown in Fig. 3F and SI Appendix, section 2.5. Not only does the spacer distribution in our simple model reach a stationary state while individual spacers turn over rapidly, it also shows 1,000-fold variation in spacer abundances despite the fact that all spacers are functionally identical in our model and provide resistance to the same phage. The exact shape of the distribution depends on various parameters (SI Appendix, section 2.5) and is well approximated by a gamma distribution which has been used to describe species abundance distributions in ecology (45–48) (SI Appendix, section 2.6).

Fig. 3.

Comparison of spacer distributions between simulations (D–F) and experimental data from ref. 12 (A–C). (A and D) Subset of spacer-type trajectories over time in generations for experimental data (A) and simulated data with $\eta =10^{-5}$ and $e=0.387$ (D). Qualitative simulation results are insensitive to the choice of $e$ and $\eta$. Individual spacer abundances fluctuate throughout the experiment and simulation. (B) As a function of time difference at steady state (day 4/generation 26 onward), we calculated the fraction of spacer types that have gone extinct (blue circles), averaged over all times (red line). Error bars are SD. (E) Same as B but for simulated data from generation 300 to 500. A large fraction of spacer types go extinct during the course of the experiment and simulation. (E, Inset) Fraction of spacer types that go extinct for a long simulation from generation 500 to 3,000. The fraction that go extinct continues to increase with time. (C) The rank-abundance distribution of spacer clone sizes reaches a steady state in the experiment after about 20 generations (day 3 of the experiment). Darker blue indicates later times. (F) The distribution of spacer clone sizes reaches a steady state in the simulation after about 100 generations. Plotted is the same quantity as in C. Even after the distribution of clone sizes has reached steady state, individual spacer types experience continual turnover.

To test predictions with data, we analyzed experimental data reported by Paez-Espino et al. (12) from a bacterial population under constant phage attack. We summarized their raw sequencing data into the presence/absence tensor $s_{ijk}$ as shown in Fig. 1A, and we tracked dynamics of individual spacers $n_B^i\left(t\right)={\sum }_{j,k}{s}_{ijk}\left(t\right)$. Our analysis showed that the abundance of individual spacer types fluctuated throughout the 15 d ($\sim 80$ generations) of the experiment (Fig. 3A), with more than $40\%$ of spacers going extinct within a time difference of a few generations from any starting time (Fig. 3B). In contrast, we find that the spacer rank-abundance distribution reaches a stationary state, as shown in Fig. 3C. Notably, the rank-abundance distribution is broad with some spacers having a roughly 1,000-fold higher abundance than others. However, in contrast to the intuition that highly abundant spacers may be more effective, these high-abundance spacers also experience continual turnover, shown in SI Appendix, Fig. S16 (SI Appendix, section 4). Both the simulated and experimental data show similar mean times to extinction as a function of spacer abundance (SI Appendix, section 4.1), another indication of continual spacer turnover at steady state.

In general our analysis highlights that individual spacer identity and abundance may not themselves be important but collectively may provide a time-invariant observable in the form of steady-state rank-abundance distributions. And somewhat counterintuitively, spacers need not be functionally different in their effectiveness or acquisition probability to get large variability in spacer abundances.

Regulation of cas Expression.

Merely having an effective spacer, however, is not enough: To effectively neutralize phage, bacteria need to express cas genes when under attack. Experimental work has shown that bacteria can regulate their CRISPR-Cas systems in response to cell density, controlled under the quorum sensing pathway (26, 27). A cell increases its expression of Cas proteins at high cell density in response to a high concentration of quorum sensing molecules and down-regulates its expression of Cas proteins at low cell density. To understand the role of cell density-dependent regulation of the CRISPR-Cas system, we made spacer effectiveness $e$ to be a function of cell density, $e\left(x\right)=e_{min}+\left(e_{max}-e_{min}\right)\left(\frac{x^n}{x^n+x_0^n}\right)$, where $x$ is the normalized bacterial population size. This function is characterized by three numbers: minimum effectiveness $e_{min}$, maximum effectiveness $e_{max}$, and typical population size where the behavior changes from low to high effectiveness (SI Appendix, section 5). Regulation of cas genes may also alter other parameters of the model such as acquisition, spacer loss, and growth rates, but we show in SI Appendix, section 5.3 that adding regulation to other possible parameters independent of effectiveness has little effect and that in conjunction with density-dependent effectiveness they do not change the qualitative features we describe below.

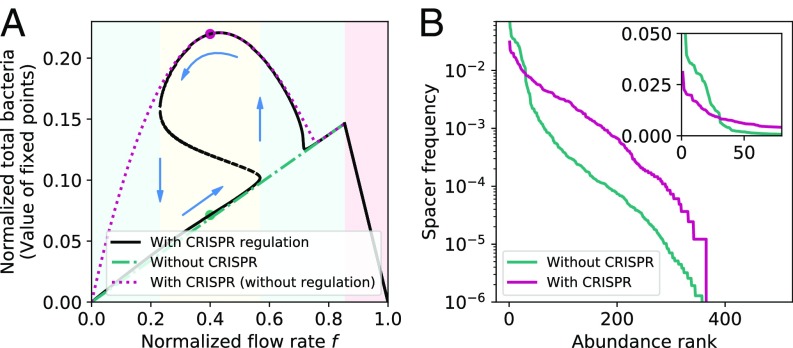
Notably, the dependence of spacer effectiveness on population size changes both the number and value of the steady-state fixed points. We find that the whole bacteria–phage–nutrient system undergoes a saddle-node bifurcation and is bistable for a range of parameters. The bistability results from a positive feedback that is established under quorum sensing (QS) control of the CRISPR-Cas system but is absent otherwise: The total bacterial population size increases with increasing spacer effectiveness, and in turn effectiveness increases as CRISPR-Cas is up-regulated by higher bacterial density (SI Appendix, Fig. S20). There are various parameters that can be used as the bifurcation parameter, but one that can be easily controlled in experimental systems and perhaps plays a role in natural systems is the normalized chemostat flow rate $f=F/\left(g{C}_0\right)$, which can also be thought of as the inverse of nutrient availability. Fig. 4 shows how bacterial and phage abundance varies as flow rate is changed in the presence of density-dependent regulation of the CRISPR-Cas system. At the two extremes, for low flow rate the system behaves with no adaptive immunity and bacterial (and phage) population size is low, while at high flow rate adaptive immunity kicks in and bacteria can maintain a higher population size. The phage population remains low at high flow rate both because bacteria are more resistant and because phages are removed from the system at a higher rate. At very high flow rate, phages go extinct and the bacterial population starts decreasing linearly with flow rate. For intermediate flow rate, the low and high states are both stable, allowing the system to be in either state. In principle these two population-level states could coexist and interact.

Fig. 4.

Bacterial upregulation of cas gene expression at high density can induce bistability (A, yellow shaded area) as a function of the normalized chemostat flow rate $f=F/\left(g{C}_0\right)$, a parameter that is easy to tune experimentally. The blue shaded region in A is monostable, and in the pink shaded region in A phages cannot persist. (A) The bacterial population size (solid black lines) exhibits hysteresis (blue arrows) between a low-expression, low-density state and a high-expression, high-density state. (B) The spacer rank-abundance distribution shape depends on the ecological state of the population. Plotted are two rank-abundance distributions from simulations of the high- and low-expression states, respectively; population sizes for each distribution are indicated by dots in A. B, Inset shows linear frequency scale.

This bistable system may also exhibit hysteresis, which may have important ecological consequences, possibly functioning as a memory of past phage pressure or providing a switch-like behavior between “on” and “off” states of the CRISPR system. Not only can the phage-to-bacterium ratio [called virus-to-prokaryote ratio (VPR)] be significantly different between the two states but also spacer composition and diversity can be quite different (Fig. 4B and SI Appendix, section 2.5).

Our model exhibits bistability quite generically for large parameter ranges but requires choosing an appropriately steep function for effectiveness (discussion in SI Appendix, section 5).

Discussion

CRISPR-Cas is a unique system in that adaptive immunity is both hereditary and acquired. Its impacts on population dynamics are thus unlike any other immune system, and experimental observations must be interpreted with theory specific to the CRISPR-Cas system. Our analysis of experimental data yielded a striking result: Rank-abundance spacer distributions are stable over time, paralleling population-level stability, despite what looks like ongoing turnover in the abundances of individual spacer types. This overall stability suggests a need for a population-level approach in which questions about spacer diversity are addressed alongside questions about CRISPR-Cas regulation. In this framework, communities of bacteria function collectively more like a single organism capable of complex signaling and behavior than like a collection of individual bacteria undergoing selective dynamics.

In this work, we propose and analyze a simplified model of interacting bacteria and phage in which bacteria regulate the CRISPR-Cas system in a density-dependent way, which in turn controls the spacer-marked clonal composition of the bacterial population under phage attack. We find that the bacteria–phage population exhibits bistability with the possibility of coexistence between two ecologically different states. These two stable states may differ by orders of magnitude in the phage-to-bacterium ratio as well as differing in the spacer diversity and composition of the population. Our model also provides a framework where large variability in spacer abundance may arise due to population dynamics rather than due to individual parameters of spacers, since our model is neutral with no selective advantage for particular spacers. And finally, our model shows how a stable spacer rank-abundance distribution may emerge while individual spacer types turn over rapidly.

Sequencing provides an easy way to track spacers, which in turn provide a direct record of past interactions between a bacterium and its phages. Although there has not been much effort toward spacer tracking in individual bacteria, population-level spacer dynamics are becoming readily accessible both from laboratory experiments (12, 13, 38) and from natural populations (7, 10). In the laboratory, both large variability and rapid turnover of individual spacer types have been observed. Understanding these dynamics is certainly interesting but requires a much higher level of sampling and resolution than what is currently available (49). Also, acquiring such data, especially time resolved, for natural systems such as microbial mats and acid mine drainage may not be practical. Here we show that the spacer rank-abundance distribution may provide a more useful time-invariant observable for understanding the underlying dynamics in both natural and laboratory systems; our work predicts that measuring spacer abundances in natural populations may reveal abundance distributions that are stable in time and potentially indicative of the environmental conditions despite differences in the level of spacer sequences between populations and over time.

Even without phage diversity and phage mutations in our model, we reproduce important features of the spacer dynamics observed in recent laboratory experiments (12). In the presence of mutant phages, the net effectiveness of different spacers in providing immunity against phages may vary from one spacer to the next. We expect that a spacer’s effectiveness will depend on the fraction of the phage population with a matching protospacer. This fitness difference between spacers will have consequences for the population dynamics, and some aspects have been addressed in experiments (13, 50, 51) and models (16, 19, 31–33, 38, 52) and reviewed in ref. 53.

Multistability at the level of cellular states, where a fraction of the population switches to an alternate state, has been explored at length with implications from bet hedging to lytic–lysogenic switching to antibiotic resistance and persistence (54–58). Similarly structured populations are now being explored in contexts from healthy regenerating tissues to pathologies such as cancer (59). While recent models for large interacting microbial populations using a statistical mechanical approach (60–63) show that ecological multistability akin to what is seen in a spin glass may be present in such populations, they remain experimentally inaccessible. A notable exception is Gore et al. (54), who observed population-level bistability and coexistence between two cooperating yeast strains in a mixed culture. Here we provide an example of multistable, multispecies ecological states that may be readily accessible in experiments. We show that for a population of bacteria and phages the flow rate of a chemostat or dilution rate of a serially diluted population can serve as a bifurcation parameter. Since both nutrient concentration (which controls population density) and dilution rate are easy to control experimentally, ecological states in our phage–bacteria population should be readily accessible (SI Appendix, section 5.4).

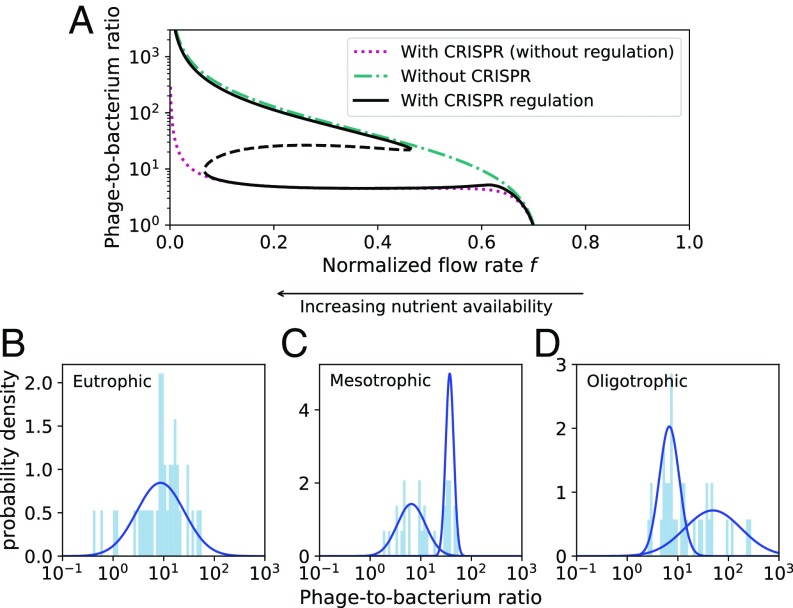
In natural populations where phages and bacteria coexist, the phage-to-bacterium ratio, also called VPR, has been measured and reported for a wide range of conditions. While viruses are generally assumed to outnumber bacteria by a factor of 10 (8, 34, 66, 67), the measured ratio can vary between samples by as much as a factor of $10^6$ (64). The underlying factors and ecological significance of observed VPR values are not well understood. Our model predicts a variable phage-to-bacterium ratio for different parameters. Notably, the VPR for the low-expression branch of the bistable system is approximately 10 times higher than that for the high-expression branch (Fig. 5A). These values reflect the two underlying ecological states: VPR is low when bacteria are at high density and up-regulate CRISPR-Cas expression, and VPR is high when bacteria are at low density and have turned down CRISPR-Cas expression. This suggests that low observed VPR values may be indicative of an active bacterial defense system, while high VPR may correspond to a bacterial population strongly controlled by phages. With deep metagenomic sequencing it will be possible to measure VPR in natural environments for phage–bacteria species pairs that are known to interact, shedding more light on the significance of phage pressure in natural microbial communities.

Fig. 5.

(A) The phage-to-bacterium ratio (virus-to-prokaryote ratio, VPR) can differ by more than 10-fold between the two bistable states in the model (solid black lines). These values reflect the two underlying ecological states: VPR is low when bacteria are at high density and up-regulate CRISPR-Cas expression, and VPR is high at low bacterial density and low CRISPR-Cas expression. (B–D) VPR histogram and fitted log-normal distributions for organisms from eutrophic (high nutrient), mesotrophic (moderate nutrient), and oligotrophic (low nutrient) environments [data from Parikka et al. (64)]. We fit 1D Gaussian mixture models with one and two Gaussian distributions, respectively, to the data and chose the best-fitting model (blue line), using the Akaike information criterion (AIC). The data were fitted better by a single Gaussian distribution for the eutrophic data ($\mathrm{\Delta }$ AIC $=45.7$) and two Gaussian distributions for the mesotrophic ($\mathrm{\Delta }$ AIC $=10.2$) and oligotrophic ($\mathrm{\Delta }$ AIC $=8.1$) data. For each fit, we calculated the likelihood that the not-chosen model was a better fit: $e^{-\mathrm{\Delta }\text{AIC}/2}$ (65). This likelihood is $1.2\times 10^{-10}$, 0.006, and 0.017 for the eutrophic, mesotrophic, and oligotrophic data, respectively.

In our model, the normalized chemostat flow rate $f$ is inversely proportional to the inflow nutrient concentration $C_0$, which suggests that the model’s VPR predictions and the ecological conditions under which CRISPR-Cas is advantageous may be impacted by nutrient availability. A study by Payet and Suttle (68) found that phage production and phage-induced mortality of bacteria were both highest in marine samples when the water was most productive and nutrient rich, while lysogens were more common when the water was oligotrophic. This is also consistent with the finding that phage infection risk is higher at high bacterial density (26, 69, 70).

To connect this qualitative feature of our model to natural populations, we analyzed VPR data from Parikka et al. (64) and found that the distribution of measured VPR values appears bimodal in low and moderate nutrient environments. It may be the case that at high nutrient levels where bacteria live in dense communities and are at high risk of lytic phage predation, most or all bacteria use a highly expressed CRISPR-Cas system and VPR is peaked at a single low value in that environment (Fig. 5B). Conversely, at low to moderate nutrient levels, different bacteria may use different immune strategies and so VPR values may span a wider range (Fig. 5 C and D). Note that at very low $f$ and high nutrient availability, our model predicts monostability in the low-density, low-expression stable state corresponding to high VPR, yet we observe a unimodal low VPR in high-nutrient environments (Fig. 5B). In these conditions when phages are a large threat, bacteria may use another signal besides density to up-regulate the CRISPR-Cas system. In this work we provide an intuitive connection between an observed quantity such as VPR and a nontrivial insight into the ecological state of interacting bacteria and phages.

Materials and Methods

Data Analysis.

We analyzed data from an experiment in which Streptococcus thermophilus bacteria were mixed with phages and sequenced to track the expanding portion of the CRISPR locus over 15 d (12) by labeling spacers with a type $i$ corresponding to a unique spacer sequence, a locus position $j$, and a bacteria label $k$. All spacers within an edit distance of 2 from each other were grouped into the same type. See SI Appendix, section 1 for details.

We compared data reported by Parikka et al. (64) with our model. When plotting VPR values, we combined average VPR measurements and individual VPR measurements (“VPR av” and “VPR” columns) to create a combined dataset of VPR values.

Our processed data can be found on GitHub at https://github.com/mbonsma/CRISPR-immunity.

Model Analysis.

The mean-field model was solved exactly at steady state in Mathematica. Steady-state values with regulation added were calculated numerically. See SI Appendix, section 3 for stability analysis.

Simulations.

Simulations were written in ${\text{C}}^{++}$ and performed using the tau leaping method (71). See SI Appendix, section 2.3 for details. Simulation code can be found on GitHub at https://github.com/mbonsma/CRISPR-immunity.