Abstract
Protein phase diagrams have a unique potential to identify the presence of additional thermodynamic states even when non–two–state character is not readily apparent from the experimental observables used to follow protein unfolding transitions. Two–state analysis of the von Willebrand factor A3 domain has previously revealed a discrepancy in the calorimetric enthalpy obtained from thermal unfolding transitions as compared to Gibbs–Helmholtz analysis of free energies obtained from the Linear Extrapolation Method (Tischer & Auton, Prot Sci 2013; 22(9):1147–60). We resolve this thermodynamic conundrum using a Clausius–Clapeyron analysis of the urea-temperature phase diagram that defines how ΔH and the urea m–value interconvert through the slope of cm versus T, (∂cm/∂T) = ΔH/(mT). This relationship permits the calculation of ΔH at low temperature from m–values obtained through iso–thermal urea denaturation and high temperature m–values from ΔH obtained through iso–urea thermal denaturation. Application of this equation uncovers sigmoid transitions in both cooperativity parameters as temperature is increased. Such residual thermal cooperativity of ΔH and the m–value confirms the presence of an additional state which is verified to result from a cooperative phase transition between urea-expanded and thermally-compact denatured states. Comparison of the equilibria between expanded and compact denatured ensembles of disulfide-intact and carboxyamidated A3 domains reveals that introducing a single disulfide crosslink does not affect the presence of the additional denatured state. It does, however, make a small thermodynamically favorable free energy (~−13 ± 1 kJ/mol) contribution to the cooperative denatured state collapse transition as temperature is raised and urea concentration is lowered. The thermodynamics of this “cooperative collapse” of the denatured state retain significant compensations between the enthalpy and entropy contributions to the overall free energy.
Keywords: denatured state collapse, Clausius-Clapeyron equation, disulfide bond, urea-temperature phase diagram, von Willebrand factor
Graphical abstract
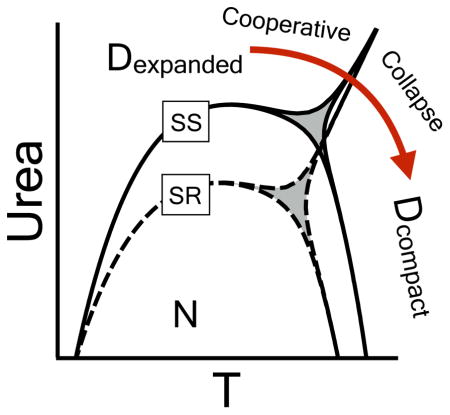
2 Introduction
The Clausius–Clapeyron relation, more often seen in physical chemistry textbooks in its approximate form, enables the prediction of vapor pressures at various temperatures when given the enthalpy of vaporization [1, 2]. It has its roots in pressure–temperature phase diagrams between liquid and gaseous states of matter and has found geophysical applications in atmospheric thermodynamics [3], climatology [4], and biophysical applications in protein unfolding [5, 6, 7, 8]. Importantly, the mathematical relationship which describes the tangent of phase boundaries is general, has no implications about the size of the system, and thus is applicable to any thermodynamic system of interest regardless of whether the system involves macroscopic states of matter or mesoscopic conformational states of proteins or other macromolecules.
A product of the works of Rudolf Julius Emanuel Clausius, who developed the mechanical theory of heat and introduced the concept of entropy [9], and Benoît Paul Émile Clapeyron, who developed concepts of reversibility in the Carnot cycle [10], the partial differential equation describes how the shape of a phase boundary changes with two intensive thermodynamic properties (λ1 and λ2 such as temperature, pressure and concentration) and yields changes in the conjugated extensive properties (A1 and A2 such as internal energy, enthalpy, particle number and volume). Eq. 1 evaluates to ΔH/(TΔV) for pressure–temperature phase diagrams [11].
| (1) |
Q, the partition function ratio of one phase relative to another, is constant and equal to unity on the phase boundary where two phases are equally populated at equilibrium. The beauty of Eq. 1 is that it makes no assumptions about how to define the relative partition function, Q. Any number of thermodynamic states or groups of states can be implemented. The practical importance is that when the slope of the phase diagram is known, Eq. 1 enables the determination of an unknown or experimentally inaccessible extensive property when the other is known [11]. Additionally, if both extensive properties are known, they can be used to predict the phase behavior of a system [12].
The phase diagram slope is essential for understanding protein interactions involving folding, unfolding, binding, and allostery because it quantifies the statistical correlation between linked conformational transitions [13, 11, 12, 14]. For the purpose of this study, the formulation of Eq. 1 into the context of urea and thermal denaturation of proteins defines the relationship between the respective unfolding cooperativity parameters, the m–value and ΔH, Eq. 2.
| (2) |
where β = 1/RT and ∂(1/RT)/∂T = −1/RT2. In practice, identification of the denaturation transition midpoints, cm and Tm, is straightforward, but the enthalpy of unfolding is not experimentally accessible at low temperature, nor is the m–value of urea denaturation accessible at high temperature. Thus, Eq. 2 permits the calculation of ΔH at low temperature from experimental m–values obtained through iso–thermal urea denaturation and m–values at high temperature from ΔH obtained via iso–urea thermal denaturation.
Traditional methods for verifying two–state unfolding have compared either 1) calorimetric enthalpies (ΔHcal) with van’t Hoff enthalpies (ΔHVH) that assume two–state thermal unfolding [15] or 2) free energies of thermal unfolding with free energies of urea denaturation using a combination of the Gibbs–Helmholtz equation and the Linear Extrapolation Method [16, 17, 18]. While both comparisons are acceptable, the first limits two–state verification to high temperature and the second compares only the free energy change, a quantity derived from the primary data using a two–state assumption provided that ΔHcal = ΔHVH. The advantage of the Clausius–Clapeyron relation is that it enables verification directly from the primary experimental observables, the transition midpoints and the cooperativities associated with protein unfolding in a two–coordinate plane or multi–coordinate surface [11], as follows.
Eq. 2 establishes criteria that can be used to assure thermodynamically consistent interpretations of urea and temperature denaturation data in face of potential non–two–state behavior. The classical criterion, 0) is to watch for sudden changes in the slope of phase diagrams as indicators for the appearance of more states [11, 19]. While the unfolding cooperativity parameters can be temperature dependent, 1) sigmoidicity in the temperature dependence of ΔH or the m–value immediately suggests additional thermodynamic states. Identifying additional states in ligand binding systems from changes in the slope of experimental phase boundaries (e.g. pH dependence of ligand binding, −ΔNH/ΔNL) is comparably straightforward [11], but since ΔH and m are not quantized, the slope is not a simple ratio of integers [12]. The sigmoidicity criterion, therefore, simplifies interpretation of the slope of protein denaturation phase diagrams. 2) While one is free to define the partition function in any way, the thermodynamic model for denaturation should reproduce the shape of the experimentally observed phase diagram to substantiate its validity. Finally, 3) the location of all phase boundaries predicted by the model must be experimentally verifiable.
These criteria are used in this study to resolve an apparent thermodynamic conundrum previously observed in the urea and thermal denaturation of the von Willebrand factor (VWF) A3 domain [20]. Even though the two–state criterion that ΔHcal = ΔHVH put forth by Privalov [15] is valid at high temperature, a discrepancy was revealed between the thermal unfolding enthalpies and those obtained from Gibbs–Helmholtz analysis of urea denaturation free energies obtained using the Linear Extrapolation Method of Pace [16, 17]. Here, we compare urea–temperature phase diagrams of the disulfide–intact and disulfide–free proteins to assess the contributions of a single disulfide bond to the thermodynamics of unfolding.
Through application of Eq. 2 and the sigmoidicity criterion, we identify an intrinsic property of both variants to unfold to distinct urea–expanded and thermally–compact denatured state ensembles. Thus, we derive a 3–state model to predict the location of the phase boundary between these denatured states in the urea–temperature plane and use circular dichroism and size–exclusion chromatography to directly measure the transition. This process of experimental validation of the phase diagram reveals the typical contraction of the urea–denatured state as temperature increases. It also observes a “cooperative collapse” from the urea–expanded to the thermally–compact denatured state, thermodynamically favored by the disulfide bond, as urea concentration decreases at high temperature under conditions where the native state population is minimized.
These studies provide new evidence of thermodynamically cooperative phase transitions in the denatured state amidst the more gradual denatured state contraction/expansion [21, 22, 23]. They also demonstrate that proper application of the phase diagram method provides a simple means to observe cooperativity in denatured state ensembles and to decipher the energetics of their interconversion. An added fringe benefit of the current analysis is that with all three phase transitions defined, thermodynamic contributions of the disulfide bond confirm entropic predictions of a crosslinked polymer theory proposed half a century ago [24, 25, 26, 27] true to the original context of denatured ensembles.
3 Materials and Methods
3.1 Spectroscopy
Protein concentrations were determined on a Shimadzu UV1201PC spectrophotometer using the Edelhoch method as modified by Pace from the absorption at 280 nm minus twice the absorption at 333 nm to correct for light scattering [28]. The extinction coefficient used for both A3 and RCAM A3 was ε = 10490 L/mol/cm calculated from 1 Trp and 4 Tyr residues. The concentration of ANS–solutions was measured at 350nm using an extinction coefficient of ε = 4950 L/mol/cm [29].
All fluorescence measurements were performed on a Horiba Jobin–Yvon Fluorolog 3 equipped with a Wavelength electronics Model LF1–3751 thermal controller. Intrinsic fluorescence spectra were recorded at 20°C between 310–440nm using 280nm or 295nm excitation wavelengths. ANS fluorescence was recorded between 360–660nm. All spectra were performed with 1nm step width and 1s integration time, averaged three times and corrected by the signal of the corresponding buffer. For iso–thermal urea unfolding, the fluorescence emission at 359nm was averaged for 20s after excitation at 280nm. Iso–urea thermal unfolding was monitored at 359nm after excitation at 280nm using a scan rate of 2°C/min with slight stirring. The protein concentration was 1μM. Acrylamide quenching of Trp–residues was performed using a 295nm excitation wavelength. After the addition of buffered acrylamide solution, the sample was equilibrated for ~5min and then the fluorescence emission intensity at 359nm was recorded for 20s and averaged. Fluorescence intensity was analyzed as a function of the molar concentration ([Q]) of acrylamide by Eq. 3 to obtain the Stern–Volmer constant, KQ. F0 the initial fluorescence intensity in absence of acrylamide and F the fluorescence in presence of acrylamide [30].
| (3) |
CD–spectra were measured on an Aviv Biomedical 420SF CD spectrometer. Far UV– (190–260nm) and Near UV CD– (260–360nm) spectra were measured at 20°C using a 0.1mm and a 5cm quartz cell, respectively, with a 1nm bandwidth and 60s integration time. For iso–thermal urea induced unfolding, the signal was averaged for 5–10min at 222nm using a 1mm or 2mm cell with protein concentrations between 5–10μM and a 1s integration time. Iso–urea thermal scans were performed with 1μM protein at 222nm under slight stirring using a scan rate of 2°C/min and a 20s integration time. At high urea concentrations a 1mm cell was used with protein concentrations between 5–10μM.
3.2 Limited proteolysis Mass Spectrometry
The concentration of A3 and RCAM A3 was adjusted to 5.7μM via dilution with buffer. 2mL of both protein solutions were mixed with 5μL of 1mg/mL Trypsin solution to yield a Protein to Trypsin ratio of 1:50. Both mixtures were incubated at 37°C and at certain time points (0–20h), 100μL aliquots were taken from each solution and the proteolysis was quenched by a drop in pH via addition of 5μL of 4%(v/v) Trifluoroacetic acid. Quenched reactions were immediately frozen on dry ice and stored at −80°C.
Proteolysis samples were analyzed in the Mayo Clinic Medical Genome Facility Proteomics Core using an Agilent 1200 HPLC System coupled to an Agilent 6224 TOF mass spectrometer. Water with 0.1% formic acid was used as solvent A and acetonitrile with 0.1% formic acid was used as solvent B. The flow rate on the system was 300μL/min and the injection volume was 5μL. Samples were separated on a Agilent Zorbax 300SB C18 column prior to positive mode ESI mass spectrometry analysis. The obtained data were correlated to the A3 domain amino acid sequence based on molecular mass with an accuracy of 10ppm using Agilent Mass Hunter Qualitative Analysis/BioConfirm Software.
3.3 Size–Exclusion Chromatography
Analytical size–exclusion chromatography was performed at 20°C and a flow rate of 1mL/min using a Phenomenex SEC–s3000 column on a Beckman Gold Analytical HPLC System. RCAM A3 and A3 were dialyzed overnight at 4°C against PGA–buffer with urea concentrations ranging from 0–8.5M. Prior to the injection of 100μL protein sample with a concentration of ~10μM, the dialysis buffers and samples were brought to a temperature of 20°C and the column was equilibrated with the buffer for at least 1hr.
Size–exclusion chromatography as a function of temperature at various urea concentrations on the 1% native boundary of the phase diagram for A3 was performed at 0.5mL/min and the column was immersed completely in water in a Neslab RTE–210 water bath. A 2mL superloop prior to the column was used for temperature equilibration of the protein sample. The water bath was sealed to prevent excessive evaporation and the temperature was precisely adjusted based on the readouts of two thermal sensors placed near the inlet and the outlet of the column. The system was equilibrated for 2h at a given urea concentration and temperature prior to injecting the protein.
Blue Dextran and sodium azide were used as markers for void volume (Vo) and included volume (Vi) at each urea concentration or temperature. The retention coefficient, Kd was calculated from the retention time of the protein (Ve) using Eq. 4.
| (4) |
3.4 Analysis of individual unfolding transitions
Isothermal–urea denaturation was performed at defined temperatures by incubating individual protein-urea mixtures overnight in an aluminum block placed into a circulating refrigerated water bath. At −5°C and 0°C temperatures, a water/antifreeze mixture (purchased at the local auto parts store) was used as the circulating coolant. Experiments at or below the freezing point of water were possible due to the freezing point depression caused by the presence of urea, buffers, salts, and the protein itself. Protein-urea mixtures were quickly transferred to a cuvette incubated in an Aviv CD spectrometer or Horiba Jobin–Yvon Fluorolog 3 Peltier temperature controlled sample chamber purged with N2 gas to prevent condensation of water in the air on the cuvette. Isourea–thermal denaturation samples were incubated at 10°C prior to thermal unfolding at 2°C/min. Thermodynamic reversibility was verified by thermal scan rate independence and % fluorescence recovery experiments described in the Supporting Information and in reference [20].
Unfolding transitions monitored by CD and fluorescence spectroscopy were analyzed using Eq. 5 where S is the spectroscopic observable, SN and SD are linear baselines for the native and denatured state spectroscopic observables and K is an apparent two–state unfolding equilibrium constant.
| (5) |
For the analysis of individual unfolding transitions, the urea concentration and temperature dependence of the equilibrium constant were expressed as linear functions of the natural logarithm of K with respect to Δc = (c − cm) and Δβ = (1/RT − 1/RTm). lnK is equal to zero at the midpoints of the iso–thermal urea and iso–urea thermal transitions (cm and Tm).
| (6) |
| (7) |
is representative of the m–value of iso–thermal urea denaturation at the cm. is the enthalpy of iso–urea thermal denaturation at the Tm.
3.5 Phase diagram analysis
Phase diagrams obtained from the iso–thermal urea and iso–urea thermal unfolding were fit using a fifth–order Taylor expansion of cm as a function of T, Eq. 8, where Tr = 298.15K.
| (8) |
m–values and enthalpies were determined from the first derivative of this Taylor expansion via the following relationship derived from the Clausius–Clapeyron Eq. 2.
| (9) |
| (10) |
Assuming two–state unfolding, apparent free energies of unfolding were calculated from the experimentally observed cm, m–values, and m–values calculated from Clausius–Clapeyron analysis of the experimental enthalpies (Eq. 9).
| (11) |
4 Results
In the following, we first investigate the native and denatured states individually. Then we use the phase diagram method to assess the thermodynamic relations between the different states, and uncover the existence of two distinct denatured states. Subsequently, we show that the alternative denatured state is produced by a “cooperative collapse”. Finally, we decipher the contributions of the disulfide bond to both native and denatured state energetics.
4.1 Loss of the disulfide results in minor spectroscopic and no functional changes of the native state
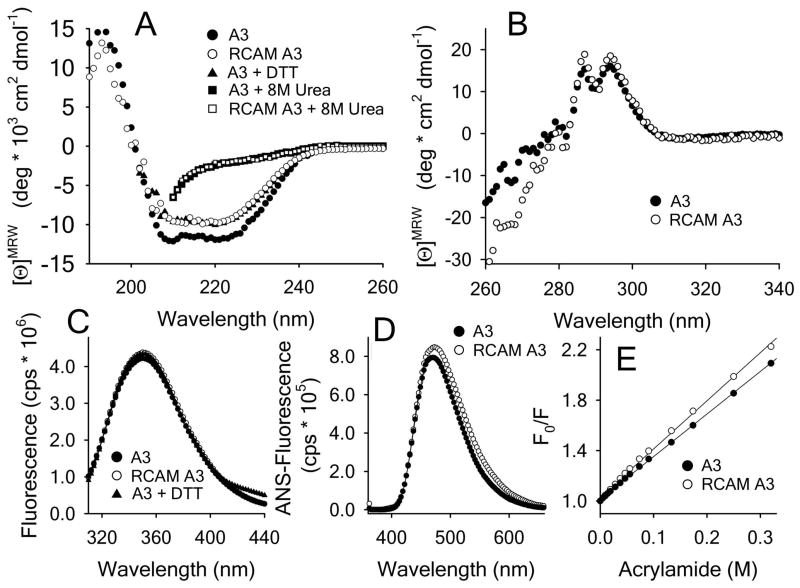
The A3 domain (MW = 23kDa) has an α/β-Rossmann fold that is cross-linked by a single disulfide bond at the N and C termini forming a loop of 187 residues. Reduction and carboxyamidation of this disulfide bond (disulfide–free RCAM A3) results in a far–UV CD spectrum (Fig. 1A) with a marginally decreased mean molar ellipticity between 208–222nm (~−10*103) relative to the disulfide–intact A3 (~−12*103 deg cm2 dmol−1). A far UV CD spectrum of A3 under reducing conditions in presence of 5mM DTT confirms the slight loss in ellipticity and that carboxyamidation was complete. Although slightly different in their overall native state spectra, both proteins have identical spectra when denatured in 8M urea.
Figure 1.
Spectroscopic properties of A3 and RCAM A3. A) Far UV CD (190–260nm) spectra in presence/absence of 5mM DTT and 8M urea at 20°C. B Near UV CD (260–360nm) spectra at 20°C. C) Intrinsic fluorescence spectra (1μM concentration) in the presence/absence of 5mM DTT using a 280nm excitation wavelength. D) ANS spectra after 1h incubation of 1μM protein with 100μM ANS using a 350nm excitation wavelength. E) Acrylamide quenching of Trp fluorescence in buffer with 295nm excitation and 359nm emission wavelengths. Stern–Volmer constants are 3.45 ± 0.03 M−1 for A3 and 4.0 ± 0.06 M−1 for RCAM A3.
The near UV CD spectra in Fig. 1B demonstrate that both A3 and RCAM A3 have well–defined spectral banding patterns with maxima at ~295nm and 280nm corresponding to 1 Trp and 4 Tyr residues present in asymmetric structural environments. Between 260–280nm small deviations between the spectra of both proteins become evident indicating a slight loosening of RCAM A3 tertiary structure combined with a loss of disulfide bond absorption compared to the disulfide–intact A3 [31].
The fluorescence emission spectra of A3, RCAM A3 and A3 in presence of 5 mM DTT in Fig. 1C have intensities that are identical within error over the full emission wavelength range with a λmax ≃ 350nm at 280nm excitation. The ANS–fluorescence emission spectrum in Fig. 1D is slightly increased for RCAM A3 relative to A3 (λmax ≃ 470nm), indicating a marginally increased solvent accessibility of hydrophobic residues in RCAM A3. Acrylamide quenching of Trp–fluorescence in Fig. 1E also results in slightly increased quenching constants from 3.45M−1 for A3 to 4.0M−1 for RCAM A3 indicating a slight increase of Trp solvent accessibility in RCAM A3 relative to A3.
The normal function of the VWF A3 domain is to bind collagen. SI Fig. 1 illustrates the binding of A3 to amine coupled collagen III observed by SPR where the saturated sensorgram response (inset) at the end of the association phase is plotted as a function of A3 concentration. Both A3 and RCAM A3 have similar collagen binding affinities, 4.1μM versus 4.8μM respectively with overlapping error margins, indicating that the slight structural changes in the native state caused by carboxyamidation of the disulfide bond observed in Fig. 1 do not alter the function of A3.
4.2 Loss of the disulfide increases native state flexibility
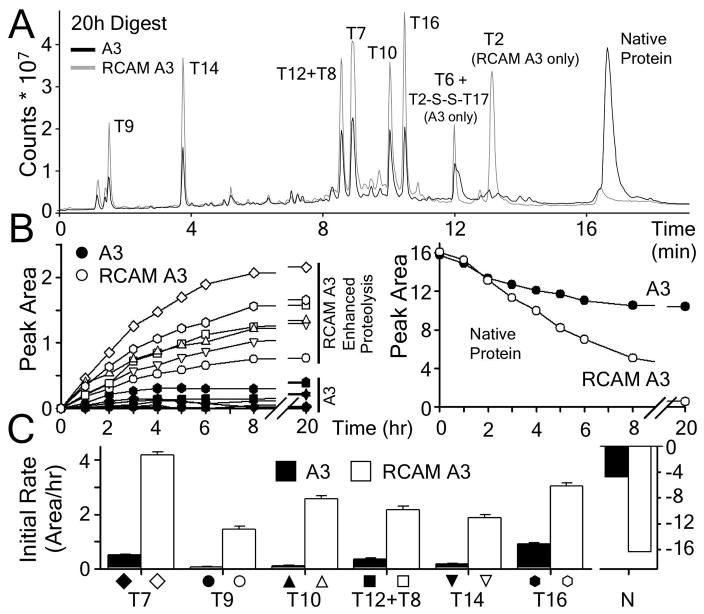
The flexibility of the native state of A3 and RCAM A3 was examined by limited proteolysis utilizing trypsin. Both proteins were incubated with trypsin at 37°C for defined time periods and the extent of proteolysis was monitored by mass spectrometry. In total, 17 of the theoretical trypsinolysis fragments (Supporting Information Table 1) were identified for A3 and RCAM A3 and the rate of appearance of 6 proteolytic fragments was followed in Fig. 2 as a function of time. In Fig. 2A, the proteolytic fragments T7, T9, T10, T12+T8, T14 and T16 are assigned to their corresponding peaks in the chromatograms of A3 and RCAM A3 after 20hrs of incubation. RCAM A3 has an additional fragment due to the reduction of the disulfide bond, T2, which is linked to T17 through the intact disulfide bond in A3. While RCAM A3 was completely digested, a major portion of A3 remained intact and uncleaved by trypsin (Fig. 2A & B, right panel). The accumulation of these 6 fragments (left panel of Fig. 2B) was faster for RCAM A3 than for A3 as evident by the cleavage rates obtained from the initial slope of the trypsinolysis (Fig. 2C). In agreement with the slight loss of secondary and tertiary structure in RCAM A3 relative to disufide–intact A3, these results demonstrate that the trypsinolysis of RCAM A3 is more efficient than A3, indicating an increased native state flexibility of RCAM A3 relative to A3.
Figure 2.
Limited proteolysis of A3 and of RCAM A3. A) Chromatograms of both proteins after 20h of incubation at 37°C. Peaks are labeled with tryptic fragments that were identified by mass spectrometry. B) Time dependent accumulation of tryptic fragments of A3 (filled symbols) and RCAM A3 (open symbols). The right panel shows the decrease of native protein over time. C) Rates of tryptic cleavage obtained from the initial slopes of the time courses.
4.3 Loss of the disulfide expands the urea–denatured state
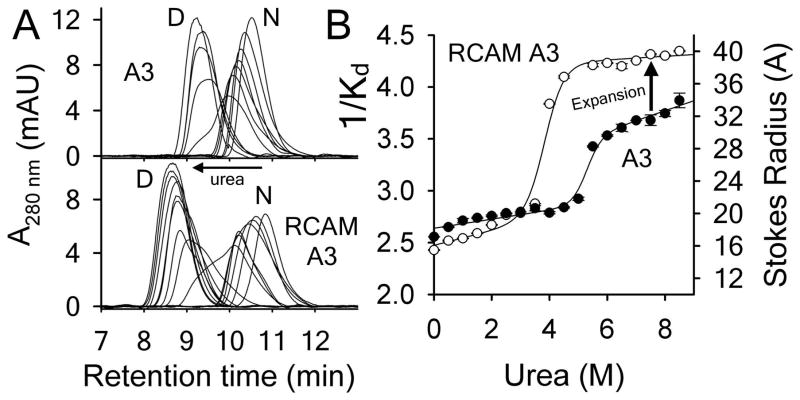
Analytical size–exclusion chromatography as a function of urea concentration was used to assess the different extents of urea–denatured state macromolecular dimensions. Chromatograms shown in Fig. 3A illustrate that both proteins elute as two global populations of native and urea–denatured states. Both native and urea–denatured states have increasing retention times as a function of urea concentration indicating that each state is thermodynamically variable [32, 33, 34]. This pre- and post–transition variability of the native and urea–denatured states is also evident in their hydrodynamic radii in Fig. 3B. While the hydrodynamic radii of A3 and RCAM A3 are similar under native conditions, the urea–denatured state of RCAM A3 is significantly larger (~6–10Å) than that of A3. A significant positive slope of the denatured state baseline indicates that the Stokes radius of urea–denatured A3 continues to expand, but the Stokes radius of urea–denatured RCAM A3 is fairly constant. Fitting the transitions using Eqs.5–6 yields urea cm values of 5.5M for A3 and 4.1M for RCAM A3 in agreement with spectroscopic determinations in Fig. 4.
Figure 3.
Analytical size–exclusion chromatography of A3 and RCAM A3 as a function of urea concentration at 20°C. A) Representative chromatograms of A3 (top) and RCAM A3 (bottom). B) Dependence of 1/Kd and Stokes Radius on urea molarity. Error bars are standard deviation of 3 measurements.
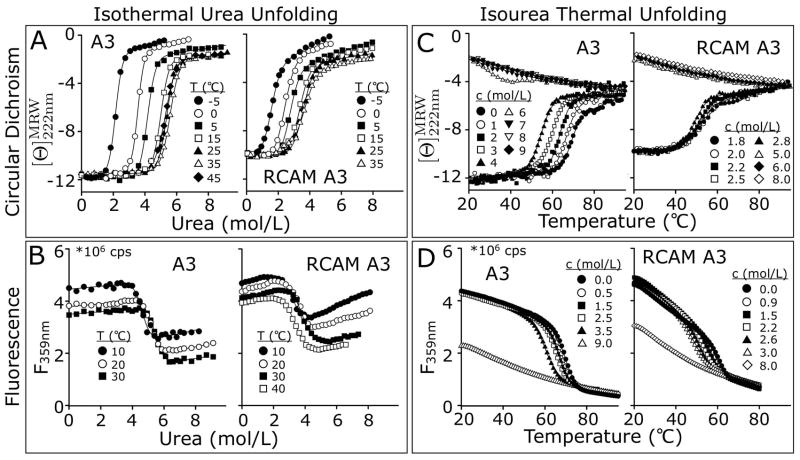
Figure 4.
One–dimensional analysis of A3 and RCAM A3 unfolding to obtain transition midpoints and unfolding cooperativity. Iso–thermal urea unfolding monitored A) by CD at 222 nm and B) by fluorescence (λEx = 280nm, λEm = 359nm). Iso–urea thermal unfolding at a scan rate of 2°C/min monitored C) by CD at 222 nm and D) by fluorescence (λEx = 280nm, λEm = 359nm).
4.4 Iso–thermal urea and iso–urea thermal unfolding
Urea denaturations at defined temperatures and thermal denaturations at defined urea concentrations were performed. Iso–thermal urea–induced unfolding was monitored via CD at 222nm between −5 & 45°C (Fig. 4A) and via intrinsic fluorescence emission at 359nm between 10 & 40°C (Fig. 4B). Iso–urea thermal unfolding in presence of increasing amounts of fixed urea concentrations was monitored via CD at 222nm (Fig. 4C) and fluorescence (Fig. 4D).
Unfolding of both A3 and RCAM A3 by temperature or urea causes a loss of secondary structure content and the solvent exposure of the Trp and Tyr residues upon unfolding decreases the fluorescence intensity. Due to RCAM A3’s enhanced propensity for aggregation at high temperature and concentrations required for CD, thermal unfolding traces monitored via CD at urea concentrations less than 1.8M resulted in denatured state baselines compromised by protein precipitation out of the solution. Consequently, CD was used to obtain thermal unfolding transitions at ≥1.8M urea and fluorescence at low concentrations of RCAM A3 was used to obtain unfolding transitions over the full range of urea concentrations extending down to 0M. Thermal denaturation in the presence of increasing concentrations of urea yields a consistent decrease in Tm for both applied spectroscopic methods.
CD demonstrates that although the native state baselines are well behaved as a function of temperature, the denatured state baselines have a strong urea and temperature dependence (Fig. 4A & C). This is evident from the temperature dependent negative CD slope of the urea–denatured states and the positive CD slope of the thermally–denatured states. Both proteins gain circular dichroic ellipticity with increasing temperature when denatured in urea and lose ellipticity with increasing urea when thermally denatured, even though the urea–denatured state macromolecular dimensions of A3 and RCAM A3 are different at 20°C (Fig. 3B). The spectroscopic behavior of the denatured state indicates a cooperative transition between urea–denatured and thermally–denatured states to be the probable cause for the non–two–state character revealed by the Clausius-Clapeyron analysis described next.
4.5 Clausius–Clapeyron analysis of the urea–temperature phase diagram reveals non–two–state character
Individual unfolding transitions in Fig. 4 are fit with the assumption of two–state character using Eqs.6–7 to obtain the denaturation midpoints and thermodynamic cooperativities. A cm and an m–value is obtained for iso–thermal urea unfolding at defined temperatures and a Tm and an enthalpy (ΔH) is obtained for iso–urea thermal unfolding at defined urea concentrations. The midpoints determine the shape of the urea–temperature phase diagram (Fig. 5A) where the native states of A3 and RCAM A3 are 50% populated relative to their denatured states. These phase diagrams were fit with a fifth–order Taylor expansion of cm[T] (Eq. 8). Fig. 5A illustrates that RCAM A3 is less stable than A3 because it unfolds at lower temperatures and urea concentrations over the entire range of thermodynamic stability. While the cold denaturation temperature of both proteins is TC ≃260K within error, the heat denaturation temperature (Tm) of RCAM A3 is 7.7±0.14°C lower than A3. The asymmetric shape of the phase diagrams deviates from the parabolic temperature dependence expected from two–state unfolding described by Becktel and Schellmann [35]. Classical two–state behavior, given a constant ΔCP and m–value, would yield the parabolic function cm(T) = −ΔG(T)/m and a linear temperature dependence of ∂cm/∂T. The nonlinearity of ∂cm/∂T (inset of Fig. 5A) is at least in part due to the variable thermodynamic character of the native and urea–denatured states at low temperature (Fig. 3), but the slight kink, occurring around ~320K for A3 and less visibly so for RCAM A3 (double arrow in Fig. 5A) indicates a high probability of an additional state [11]. Such non–two–state behavior is indeed confirmed in the following.
Figure 5.
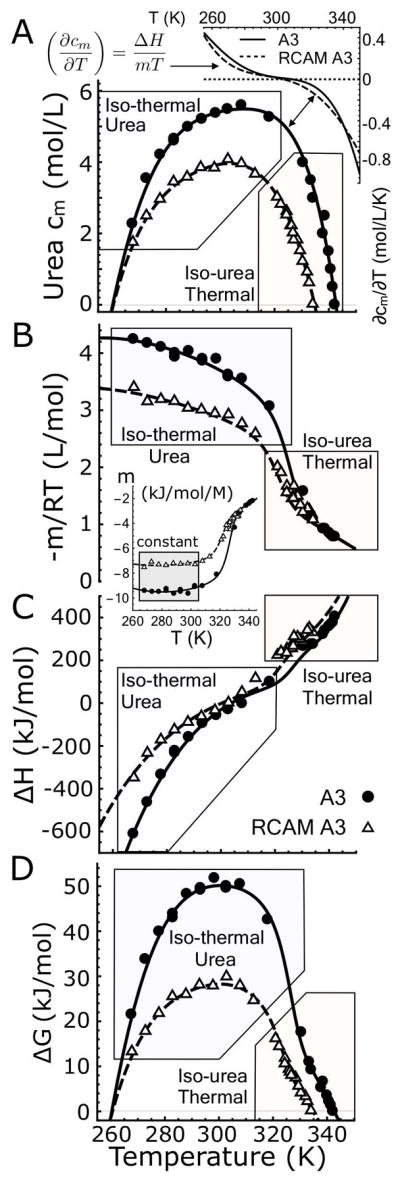
A) Urea–temperature phase diagrams of A3 and RCAM A3 fit with a fifth–order Taylor expansion according to Eq. 8. Inset: First derivative of the phase diagrams, ∂cm/∂T. B) Experimental −m/RT–values determined from isothermal–urea unfolding and −m/RT–values calculated from the experimental enthalpies from iso–urea thermal unfolding using Eq. 9. Inset: Traditional m–values expressed in (kJ/mol/M). Note they are constant at low temperature (gray box). C) Experimental enthalpies determined from iso–urea thermal unfolding and enthalpies calculated from the experimental m–values from iso–thermal urea unfolding using Eq. 10. D) Free energies of unfolding for A3 and RCAM A3 obtained from the Linear Extrapolation Method, Eq. 11. Fits in panels B and C are 2–dimensional projections of (−m/RT)[T, c] and ΔH[T, c] in which the urea concentration axis is replaced with the Taylor expansion of the phase diagram, cm[T], Eq. 8. Fits in panel B, C and D result from the global analysis of the CD data shown in Fig. 4A & C and Fig. 1 of the Supporting Information.
The Clausius–Clapeyron equation (Eq. 2) is used to derive high temperature m–values from the iso–urea thermal unfolding enthalpies and low temperature enthalpies from the iso–thermal urea unfolding m–values via the first derivative, ∂cm/∂T, (Fig. 5B & C). Fig. 5B illustrates that −m/RT (L/mol) transitions sigmoidally from a region of high unfolding cooperativity (high -m/RT) at low temperature to low cooperativity (low -m/RT) at high temperature for both A3 and RCAM A3. This transition is also evident in the traditional m–value = ∂ΔG/∂c in (kJ/mol/M), but in the low temperature range between 270–305K, m is constant indicating unfolding is two–state in this range (inset of Fig. 5B) [36]. A sigmoid transition in the enthalpies is also evident in Fig. 5C with significant contributions of the temperature and urea concentration derivatives of the enthalpy, ∂TΔH (heat capacity) and/or ∂cΔH, that give rise to the nonlinear pre– and post–transition behavior of ΔH. Finally, the free energy of unfolding in the absence of urea calculated by multiplying the m–value by the cm (Eq. 11) also produces a sigmoid transition between low and high temperature unfolding data (Fig. 5D). The stability curve looks like a transition between two regular parabolic two–state protein stability curves [35]. Notably, all the indicators for non–two–state behavior (kink in phase separation line and the sigmoid transitions in m, ΔH and ΔG) are centered at the same temperature, viz. ~325K for A3 and ~320K for RCAM A3.
In principle, this non–two–state behavior could arise from an additional state under the phase separation line, such as an intermediate state in the native region (e.g. an N1 ⇌ N2 transition with a common denatured state), or above it in the denatured region (e.g. a D1 ⇌ D2 transition with a common native state). The experimental CD unfolding transitions in Fig. 4A & C support the later interpretation of two denatured states since substantial spectroscopic variability is observed in the denatured state baselines, in contrast to that of the native state.
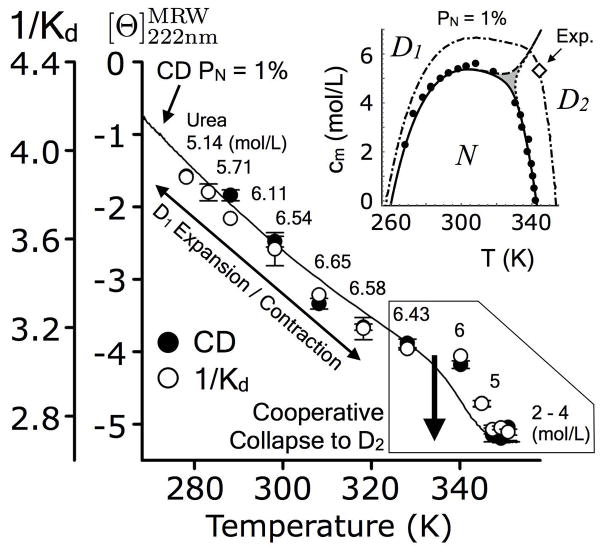
4.6 Experimental verification of a cooperative denatured state phase transition
To experimentally verify the presence of the D1 ⇌ D2 phase transition and identify its location in the urea–temperature phase space, size-exclusion chromatography of A3 was performed at temperatures and urea concentrations where the native state is 1% populated, as calculated from the fits of the individual unfolding transitions in Fig. 4. CD ellipticity was also used as a comparative measure. Fig. 6 demonstrates that both the ellipticity and 1/Kd initially decrease indicating a contraction of the urea–denatured state (D1) as temperature is raised and then rapidly transition to a compact thermal–denatured state (D2). Occurring between 340–350K, this transition has a small but detectable amplitude in which the ellipticity change is ~1*103 deg cm2 dmol−1 and 1/Kd changes ~0.3 units equivalent to a ~4Å change in Stokes radius. This change is approximately 1/3 of the change in Stokes radius upon urea denaturation of A3 at 20°C (Fig. 3B). In Fig. 6, ellipticity and 1/Kd are correlated with an R2 = 0.992, similar to the observations of Uversky [37].
Figure 6.
Analytical size–exclusion chromatography (1/Kd) and circular dichroism of A3 as a function of temperature at the indicated urea concentrations corresponding to the 1% native state phase boundary (inset). Transition is ~342K and 5.3M urea. Solid line represents the CD signal at a native population of 1% according to the global fitting in Fig. 2 of the Supporting Information. Diamond (inset) represents the approximate midpoint of the D1 ⇌ D2 transition observed experimentally.
The experimental sigmoid transition at ~ 5.3M and 342K is close to the expected T and c coordinate of ~ 6.1M and 340K derived from a three-state model described next (inset of Fig. 6). These experimental observations verify that the D1 ⇌ D2 transition is cooperative and, therefore, representative of a thermodynamic shift between two distinct populations of denatured states. As the temperature is lowered, the urea–denatured state, D1, expands concomitantly with a loss of ellipticity from −4 to −1*103 deg cm2 dmol−1 as is typical of urea–denatured states [38].
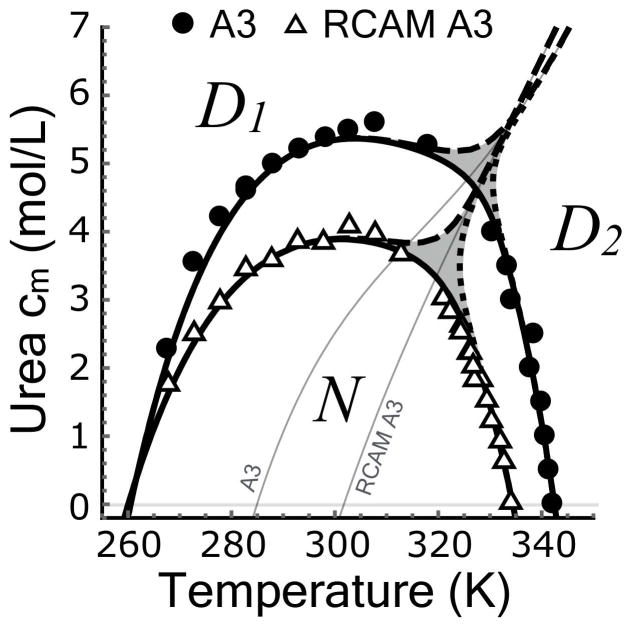
Supporting Information Fig. 2 demonstrates that a 3-state model (Supporting Information Section 1.4) involving unfolding to two distinct denatured states as a function of temperature and urea concentration sufficiently describes the experimental ellipticity data for both A3 and RCAM A3. Two-dimensional baseplanes were defined by the temperature and urea dependent circular dichroic ellipticities of the native, iso–urea thermal–denatured, and iso–thermal urea–denatured states (insets of SI Fig. 2) and the experimental ellipticities were globally fit to the 3-state model. The resulting phase space populations of each state (lower panels of SI Fig. 2) predict a phase boundary between a high urea concentration/low temperature denatured state (D1) and a low urea concentration/high temperature denatured state (D2).
The intersection of each state population predicts phase boundaries that can be compared with experiment. Fig. 7 demonstrates that the contour of the 50% populated phase boundaries obtained from the 3-state model coincides with the experimental cm’s and Tm’s. The gray triple area designates the phase space where all three states have a population less than 50%. Substitution of the Taylor expansion of cm versus T (Eq. 8) into the 3-state model equations for the overall m–value and enthalpy (SI Eqns. 4 & 6) yields temperature dependent functions that also coincide with the experimental and Clausius–Clapeyron derived m–values and enthalpies (ΔH) shown in Fig. 5B & C.
Figure 7.
Urea–temperature phase diagram in which the experimental transition midpoints are compared with the resulting phase boundaries of the three–state model involving an expanded urea–denatured state at low temperature/high urea (D1) and a compact thermally–denatured states at high temperature/low urea (D2). Phase boundaries for N (solid line), D1 (dashed line) and D2 (dotted line). Gray areas represent regions in which all three states are less than 50%. Thin gray lines represent the extrapolation of the D1 ⇌ D2 transition to the absence of urea.
4.7 Contribution of the disulfide bond to native and denatured state energetics
4.7.1 Stability of the native state
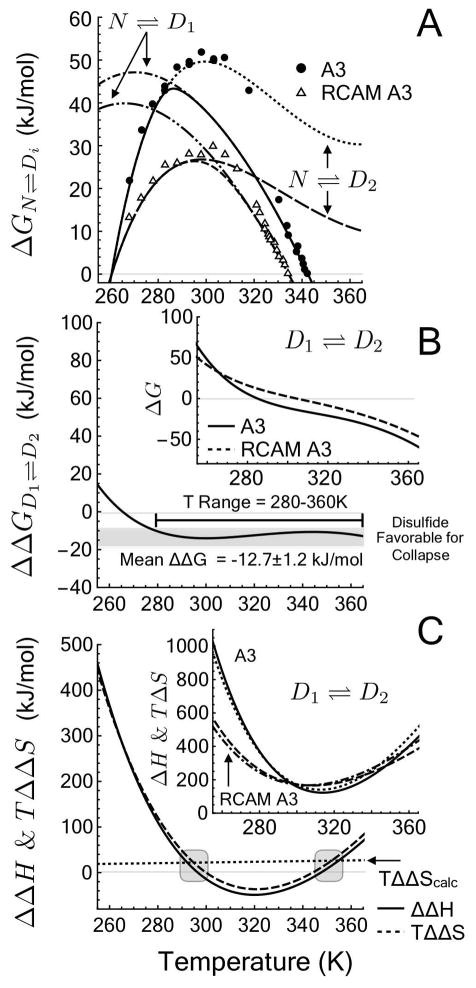
Supporting Information Table 2 lists the resulting N ⇌ D1 and N ⇌ D2 fit parameters used in the following quantitative analysis of the unfolding transitions. This 3-state model demonstrates that the N ⇌ D1 unfolding free energy coincides with apparent free energies of the iso–thermal urea denaturation, while the N ⇌ D2 unfolding free energy coincides with apparent free energies derived from iso–urea thermal denaturation (Fig. 8A) derived from the linear extrapolation to zero urea concentration. Within the experimental range of data, the presence of the disulfide bond stabilizes the native state. Both ΔGN⇌D1 and ΔGN⇌D2 are greater for A3 than for RCAM A3 and, therefore, the overall stability of the native state, ΔGN⇌D = −RT ln(([D1] + [D2])/[N]) = −RT ln(K1 + K2) (see Methods), is enhanced by the disulfide bond.
Figure 8.
Thermodynamic contribution of a disulfide bond in the absence of urea. A) ΔG. Unfolding free energy calculated from Linear Extrapolation Method (data points) and derived from the 3–state model of denaturation from N ⇌ D1 and N ⇌ D2. B) ΔΔGD1⇌D2. Free energy of a crosslinking the denatured state with a disulfide bond. Inset: ΔGD1⇌D2. Free energy of denatured state collapse from D1 to D2. C) ΔΔHD1⇌D2 and TΔΔSD1⇌D2. Enthalpic and entropic contributions to the free energy of crosslinking the denatured state and TΔΔScalc calculated from polymer theory, Eq. 16 (Gray area represents the predicted temperature range where ΔΔH = 0) [27]. Inset: ΔHD1⇌D2 and TΔSD1⇌D2. Enthalpic and entropic contributions to the free energy of denatured state collapse from D1 to D2.
4.7.2 “Cooperative collapse” of the denatured state
The difference between the two unfolding free energies in the absence of urea, ΔGN⇌D2 − ΔGN⇌D1, effectively removes the contribution of the native state to the energetics (Eq. 12) and enables the calculation of the ΔGD1⇌D2 for interconversion between expanded urea-denatured (D1) and compact thermal-denatured (D2) ensembles (inset of Fig. 8B).
| (12) |
Defined in this manner, ΔGD1⇌D2 in the limit of zero molar urea, is the free energy of collapsing the denatured ensemble from D1 to D2 in plain buffer. This free energy difference is favorable above 285K for A3 and above 303K for RCAM A3 (inset of Fig. 8B). A favorable ΔG < 0 indicates that the compact thermal–denatured state (D2) has a lower free energy than the expanded urea–denatured state (D1) at high temperature. Conversely, the compact D2 becomes energetically disfavored (ΔG > 0) relative to the expanded D1 at low temperature.
The enthalpic and entropic contributions of the denatured state collapse transition (Eq. 13), have similar magnitudes, but are positive for both proteins over the full temperature range (inset of Fig. 8C).
| (13) |
Both ΔH and TΔS increase upon collapse of the denatured ensemble from D1 to D2. Thus, for both A3 and RCAM A3, the expanded D1 is enthalpically favored over the more compact D2 denatured state and, counterintuitively, the entropy of the expanded D1 is actually lower than the more compact D2 denatured state. An increase in TΔS upon denatured state collapse can only arise in the presence of a compensating unfavorable enthalpy [39]. The favorable ΔG of denatured state collapse is entropically driven (TΔS > ΔH) at high temperature, but the compensation switches ΔH >TΔS, in favor of enthalpy driven collapse of the denatured state at low temperature where ΔG is unfavorable.
4.7.3 Disulfide bond contribution to denatured state collapse
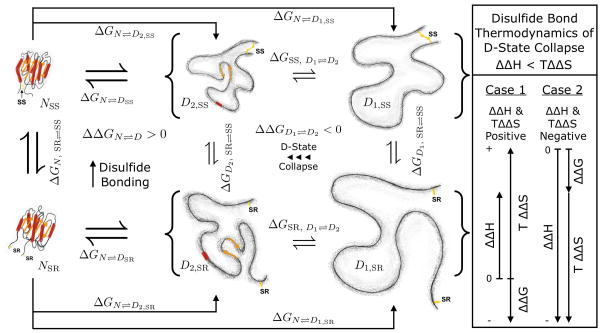
Taking yet another free energy difference between A3 and RCAM A3, ΔGSS, D1⇌D2 −ΔGSR, D1⇌D2, sets up a thermodynamic cycle between the oxidized and reduced, expanded and compact denatured state ensembles illustrated in Fig. 9 and defines the thermodynamic contribution of a disulfide bond to the denatured state collapse transition in the absence of urea. Eq. 14 states that the free energy difference between A3 and RCAM A3 for denatured state collapse is equal to the free energy difference of crosslinking (oxidizing) the compact and expanded denatured states.
Figure 9.
Thermodynamic behavior of the A3 Domain in its oxidized (SS) and reduced states (SR).
| (14) |
Fig. 8B demonstrates that over much of the water liquid range of temperatures, the free energy of denatured state collapse, ΔGD1⇌D2, for A3 is more favorable than for RCAM A3. In the range of 280–360K, ΔΔG averages ~−12.7 ± 1.2 kJ/mol demonstrating that a restraining disulfide bond makes a favorable contribution to denatured state collapse. Therefore, the thermodynamic cycle and Eq. 14 necessitate that the free energy of introducing a disulfide bond into the expanded denatured state, D1, must therefore be greater than crosslinking the compact denatured state, D2, as one should expect.
The entropic contributions of the disulfide bond to collapse (Eq. 15) always exceed (are either more positive or less negative) the enthalpic contributions (Fig. 8C).
| (15) |
From a theoretical perspective, a disulfide crosslink introduced into a randomly coiled denatured polypeptide chain will increase its free energy by decreasing the conformational entropy and therefore stabilize the collapsed state. In the direction of denatured state collapse, this favorable ΔΔGD1⇌D2 would arise from a positive ΔΔSD1⇌D2 in the absence of enthalpic contributions. Fig. 8C demonstrates that TΔΔS is positive only at high and low temperatures. The entropy is compensated by the enthalpy, ΔΔH, over the full temperature range such that between 300–345K, both contributions of the disulfide bond become negative and counter to theoretical expectations in the absence of enthalpy and heat capacity effects. In this temperature range, the favorable enthalpy (ΔΔH < TΔΔS) is balanced by an unfavorable loss in entropy to the free energy.
Based on polymer theory developed by Schellman, Flory, Poland and Scheraga [24, 25, 26], Pace introduced a simplified equation for calculating the stabilization of a protein by a disulfide bond [27] given the number of residues (N) between the disulfide bonded cysteines. Eq. 16 is Pace’s original equation put in units of J/mol and placed in the context of the folding direction (e.g. in this case, denatured state collapse) rather than stabilization against unfolding [40].
| (16) |
ΔΔScalc in Eq. 16 evaluates to 74 kJ/mol/K for N=187 residues. Through comparison with the experimentally derived 3-state model, Eq. 16 predicts temperatures where the enthalpic contributions of the free energy are zero (gray areas of Fig. 8C). The temperatures at which the experimental ΔΔH = 0 occur at ~296.5K and ~346.5K. Comparison of TΔΔScalc with the experimental TΔΔSD1⇌D2 in Fig. 8C indicates that these two functions are equal at ~295K and ~352K. Despite the experimental compensation between enthalpy and entropy in the denatured state, the close agreement between these experimental and predicted zero enthalpy temperatures provides a measure of confidence in theoretical entropic solutions derived from probabilities that ends of a polymer chain will simultaneously occur in the same volume element.
5 Discussion
Application of the Clausius–Clapeyron equation links two cooperativity parameters for protein unfolding, m and ΔH. The Transfer Model demonstrates that the urea cooperativity of unfolding, m, is equal to the summed contributions of protein group transfer free energies from water to urea weighted by the amount of solvent accessible surface area [41] that is newly exposed on unfolding [42, 43, 44]. The connection of m to ΔH through the slope of the phase diagram (∂cm/∂T) via Clausius–Clapeyron, Eq. 2, establishes that enthalpy and its temperature derivatives [41, 45] are also proportional to changes in solvent accessible surface area in part through the temperature dependence of transfer free energies. Using the methods described in Auton & Bolen [43], the Transfer Model predicts an m–value = −9.9 kJ/mol/M for disulfide–intact A3 that is in agreement with the experimental m–value = −9.6±0.3 kJ/mol/M at 25°C. Given the experimental slope of the phase diagram at 25°C (~0.021) and the calculated m–value from the Transfer model, the calculated enthalpy of the transition (−62.8 kJ/mol) is in expected agreement with the Clausius–Clapeyron derived ΔH = −61±2 kJ/mol. This predictive agreement between the Transfer Model and the experimental cooperativity in addition to a temperature independent m–value over the temperature range of 265–305K indicates that within this temperature range, the unfolding of both A3 and RCAM A3 behave macroscopically two–state.
Comparatively, one might expect the cooperativity of RCAM A3 unfolding by urea to be greater than the disulfide–intact A3, since the urea–denatured state is more expanded with a greater Stokes radius. This is because the denatured state of RCAM A3 has the potential to expose more surface area, and thus a larger change in solvent accessible surface area would be expected, corresponding to a larger m–value [41]. However, the overall cooperativity of unfolding (Fig. 5B & C) is attenuated due to the enhanced native state flexibility of RCAM A3, as observed by time dependent trypsinolyis mass spectrometry (Fig. 2), which increases the average native state solvent accessibility. Even though the urea–denatured state of RCAM A3 is more expanded (Fig. 3B), the urea–denatured state of the disulfide–intact A3 may already be sufficiently exposed to have minimal change in solvent accessibility upon reducing the disulfide bond.
As the temperature is raised, the cooperativity of unfolding switches dramatically, indicating an alternative state in the phase diagram at high temperature. Although CD spectroscopy and size exclusion chromatography data demonstrate that the additional transition is between the urea and temperature denatured states, could it, in principle, be possible that the sudden changes in m–value, ΔH, ΔG are due to another state in the native region, rather than the denatured region of the phase diagram? The typical expectation would be that the non–two–state observations described here are a result of intermediates populated en route from the native state to a common denatured state which decrease the observed cooperativity [46]. The possibility of intermediates can be ruled out based on thermodynamic considerations of the phase diagram. The fact that both the m–value (= ∂cμD − ∂cμN) and ΔH (= HD − HN) between N and D transition to less negative and more positive values, respectively (Fig. 5B & C), as temperature is increased indicates a positive slope of the phase separation line between states, i.e. the alternative state becomes populated as temperature is increased and urea concentration is decreased. Accordingly, ΔH and the m–value for this transition to an alternative state must be positive (Eqns.6 & 7). From the data in Fig. 5B & C one can derive that the opposite would be true if there was an alternative native state transition to an intermediate. If true, then ∂cμN must decrease, i.e. the m–value for the putative N1 ⇌ N2 would be negative. Similarly, also the ΔH for this transition must be negative. Thus, considering the different properties of the phase diagram data, one comes to self-contradictory results, viz. that one and the same m–value must be simultaneously positive and negative; and also ΔH must simultaneously be both positive and negative.
Only a denatured state transition from D1 to D2, is thermodynamically self-consistent with the experimental phase diagram (Fig. 7). D1 is simply the urea–denatured state at low temperature and D2 is a thermally–denatured state at low urea concentration. To corroborate the thermodynamics, we have used urea/temperature combinations in Fig. 6 to poise the system so that the native state (1%) is not significantly populated, offering the best chance for a direct observation of “cooperative collapse” of the denatured state. Experimental proof of a first–order transition from D1 to D2 for the disulfide–intact A3 domain using size–exclusion chromatography (SEC) demonstrates this “cooperative collapse” as the temperature is raised and the urea concentration lowered. This collapse transition has a 4Å change in hydrodynamic radius and occurs concomitantly within a range of circular dichroic ellipticities characteristic of denatured state ensembles (Fig. 6).
Temperature dependent curvature in m–values suggests the presence of multiple thermodynamically distinct denatured states in other proteins [47], but the large body of published work has observed the denatured state as a continuous ensemble distribution of conformations. Expansion and contraction of random coil denatured states and thermally–denatured states can be modulated by urea and protecting osmolytes [21, 48, 22, 23]. Significant efforts using single molecule FRET, FCS and SAXS have been employed to directly observe the equilibrium and kinetic collapse of denatured states [49, 50, 51] upon the removal of urea or GndHCl [52, 53, 54] or by raising the temperature [55] when ensemble based methods are limited to conditions in which the native state population is low [49]. Although the kinetic collapse of denatured states is not obligatory for folding [56, 57], when it has been observed, the “collapsed” denatured state is not a thermodynamically different state because the equilibrium ensemble continuously redistributes upon gradually changing the temperature or denaturant concentration, resulting in a smooth contraction or expansion of the macromolecular dimensions. The energetic effect of these ensemble redistributions must therefore be small, otherwise the collapse would carry with it some cooperative behavior in the traditional thermodynamic sense that either ΔH or the m–value are not negligible. Alternatively, it is possible that the collapse is cooperative, but energetically invisible without the use of phase diagrams to identify conditions that give rise to denatured state phase transitions. In the case of A3, a transition is directly visible in both CD and SEC, and indirectly observed in the thermodynamics of the phase diagram.
The contraction of the urea–denatured state (D1) concomitant with a decreasing circular dichroic ellipticity as temperature is raised is consistent with the conversion of Polyproline II (PII) helix to extended β secondary structure. Peptides show a preference for PII over random coil at low temperature that switches to β–strand at high temperature [58, 59, 60] and urea is known to increase PII content [61]. However, the negative ellipticity observed at 222nm is consistent with the overall accumulation of β–sheet, β–turns and α–helical secondary structures at high temperature characteristic of a premolten globule state [37]. Contraction concomitant with enhanced premolten globule secondary structure has also been observed in the presence of protecting osmolytes, but without a “cooperative collapse” [23]. Thus, the cooperativity observed by CD, SEC and the phase diagram could be due to collapse to a molten globule state in which much of the secondary structure elements in the premolten globule state coalesce to form the supersecondary and loose tertiary structure environment reminiscent of the native fold. Indeed, the thermally denatured state of α-lactalbumin is molten with similar properties as its molten globule state at low pH or intermediate concentrations of GndHCl [62, 63, 64].
The cumulative phase diagram evidence for the disulfide–intact and disulfide–free variants of the VWF A3 domain demonstrates that the collapse of D1 to D2 is a “cooperative collapse” and therefore subject to the traditional laws of thermodynamics. Moreover, this transition is energetically in the same order of magnitude as the denaturation itself. The collapse of D1 to D2 is thermodynamically favorable at high temperature where the “collapsed” denatured state is populated and unfavorable at low temperature where the “expanded” denatured state is populated (inset of Fig. 8B). The free energy of “cooperative collapse” is composed of positive compensating enthalpic and entropic contributions, demonstrating that the collapse to D2 is enthalpically disfavored, but, counterintuitively, has a higher entropy than the expanded D1 state (inset of Fig. 8C).
Given the unique three–state denaturation of A3 to collapsed and expanded denatured states, the energetic effect of constraining the denatured state with a single disulfide bond was assessed through comparison of the phase diagram energetics between disulfide–intact and carboxyamidated A3. Illustrated in Fig. 9, the disulfide bond contributes a favorable free energy to the collapse of the denatured state from D1 to D2 (Fig. 8B). Stated differently, forming a disulfide bond in the collapsed D2 state is favored over the expanded D1 state. The entropy always exceeds the enthalpic contributions of the disulfide bond to the free energy of collapse. Two cases arise. 1) When the ΔΔH and TΔΔS are positive, both contributions disfavor collapse with entropy dominating the enthalpy to yield a favorable free energy. 2) When both are negative, collapse of the denatured state is enthalpically driven. These energetic conclusions are in line with computational simulations that the formation disulfide bonds proceeds the early formation of collapsed structures [65]. The energetic effect of the disulfide bond is small, but entails highly compensating contributions from enthalpy and entropy.
A unique outcome of this study is that considering only the interconversion between denatured state ensembles provides a verifiable test of statistical mechanics theory of crosslinked polymers. Eq. 16 specifies that a disulfide bond should decrease the entropy of a denatured state and, therefore, stabilize proteins [27]. This relationship has been used to calculate the stability enhancement of native proteins with mixed results [27, 40, 66, 67, 68, 69, 36, 70, 71], but the original theory did not consider entropic stabilization in the context of denatured state collapse or protein folding where enthalpic contributions are significant. Comparison of the calculated entropy associated with placing a disulfide bond into a denatured state with the experimental entropic contribution of the disulfide to the D1 ⇌ D2 transition provides a reasonable prediction of temperature ranges where the enthalpic contributions are close to zero even though enthalpy and entropy compensate each other.
6 Conclusions
In any equilibrium protein unfolding transition, the salient experimental observables are the midpoints and cooperativities of the transition. For protein chemical and thermal denaturation, these parameters are cm, Tm, the m–value (−m/RT) and enthalpy, ΔH. Proper application of the Clausius–Clapeyron relation and the criteria developed here enables a rigorous evaluation of two–state character and the elucidation of additional states that contribute to a protein’s thermodynamic behavior without assuming anything beyond these direct observables. To reiterate the criteria, 1) sigmoidicity in the unfolding cooperativity is a clear non–two–state indicator, 2) the definition of the partition function should reproduce the experimentally observed phase diagram, and 3) the existence of all phase boundaries should be experimentally demonstrable. It should be noted that applying this method and its criteria validates the two–state character of other globular proteins for which phase diagram data are available [18, 72, 36]. The observations described here demonstrate that cooperative conformational transitions within the denatured state need to be seriously considered as significant thermodynamic contributors to protein denaturation transitions and the many diversified functions intrinsically disordered proteins perform in the cell [73, 74].
Supplementary Material
Acknowledgments
We dedicate this manuscript to the memory, friendship and mentorship of Jack Aviv. This work was supported by the National Heart Lung and Blood Institute of the NIH grant HL109109 to M.A. and the National Institute of General Medical Sciences of the NIH grant GM049760 to J.R.
Abbreviations Used
- vWF
von Willebrand Factor
- CD
Circular Dichroism
- FL
Fluorescence
Footnotes
Author Contributions: AT expressed, purified and carboxyamidated the A3 domain. AT performed the spectroscopy, size-exclusion chromatography, trypsin proteolysis, mass-spectrometry and analyzed the primary data. VRM performed and analyzed the SPR experiments. JR and MA designed the phase diagram analysis. MA, JR and AT wrote the manuscript. MA and JR designed the research.
References
- 1.Atkins P. Physical Chemistry. New York: W.H. Freeman & Company; 1994. [Google Scholar]
- 2.Mosselman C, Van Vugt WH, Vos H. Exactly integrated clapeyron equation. its use to calculate quantities of phase change and to design vapor pressure-temperature relations. J Chem Eng Data. 1982;27(3):246–251. [Google Scholar]
- 3.Sánchez-Lavega A, Pérez-Hoyos S, Hueso R. Clouds in planetary atmospheres: A useful application of the clausius–clapeyron equation. Am J Phys. 2004;72(6):767–774. [Google Scholar]
- 4.O’Gorman PA, Muller CJ. How closely do changes in surface and column water vapor follow clausius–clapeyron scaling in climate change simulations. Environ Res Lett. 2010;5(2):025207. [Google Scholar]
- 5.Hawley S. Reversible pressure–temperature denaturation of chymotrypsinogen. Biochemistry. 1971;10(13):2436–2442. doi: 10.1021/bi00789a002. [DOI] [PubMed] [Google Scholar]
- 6.Zhang J, Peng X, Jonas A, Jonas J. Nmr study of the cold, heat, and pressure unfolding of ribonuclease a. Biochemistry. 1995;34(27):8631–8641. doi: 10.1021/bi00027a012. [DOI] [PubMed] [Google Scholar]
- 7.Lassalle M, Yamada H, Akasaka K. The pressure-temperature free energy-landscape of staphylococcal nuclease monitored by (1)h nmr. J Mol Biol. 2000;298(2):293–302. doi: 10.1006/jmbi.2000.3659. [DOI] [PubMed] [Google Scholar]
- 8.Smeller L. Pressure–temperature phase diagrams of biomolecules. Biochim Biophys Acta. 2002;1595(1–2):11–29. doi: 10.1016/s0167-4838(01)00332-6. [DOI] [PubMed] [Google Scholar]
- 9.Clausius R. Über die bewegende kraft der wärme und die gesetze, welche sich daraus für die wärmelehre selbst ableiten lassen. Annalen der Physik. 1850;155:500–524. [Google Scholar]
- 10.Clapeyron E. Mémoire sur la puissance motrice de la chaleur. Journal de l’Ecole Royale Polytechnique Paris. 1834:153–190. vol. De l’Imprimerie Royale. Vingt-troisiéme Cahier Tome XIV. [Google Scholar]
- 11.Rösgen J, Hinz H-J. Phase diagrams: A graphical representation of linkage relations. J Mol Biol. 2003;328(1):255–271. doi: 10.1016/s0022-2836(03)00246-8. [DOI] [PubMed] [Google Scholar]
- 12.Ferreon A, Ferreon J, Bolen D, Rösgen J. Protein phase diagrams ii: nonideal behavior of biochemical reactions in the presence of osmolytes. Biophys J. 2007;92(1):245–256. doi: 10.1529/biophysj.106.092262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Permyakov EA, Morozova LA, Burstein EA. Cation binding effects on the ph, thermal and urea denaturation transitions in alpha-lactalbumin. Biophys Chem. 1985;21(1):21–31. doi: 10.1016/0301-4622(85)85003-1. [DOI] [PubMed] [Google Scholar]
- 14.Holthauzen L, Auton M, Sinev M, Rösgen J. Protein stability in the presence of cosolutes. Methods Enzymol. 2011;492:61–125. doi: 10.1016/B978-0-12-381268-1.00015-X. [DOI] [PubMed] [Google Scholar]
- 15.Privalov P, Khechinashvili N. A thermodynamic approach to the problem of stabilization of globular protein structure: A calorimetric study. J Mol Biol. 1974;86(3):665–684. doi: 10.1016/0022-2836(74)90188-0. [DOI] [PubMed] [Google Scholar]
- 16.Pace CN, Hermans J. The stability of globular proteins. CRC Critical Reviews in Biochemistry. 1975;3(1):1–43. doi: 10.3109/10409237509102551. [DOI] [PubMed] [Google Scholar]
- 17.Pace C, Shaw K. Linear extrapolation method of analyzing solvent denaturation curves. Proteins. 2000;(Suppl 4):1–7. doi: 10.1002/1097-0134(2000)41:4+<1::aid-prot10>3.3.co;2-u. [DOI] [PubMed] [Google Scholar]
- 18.Nicholson E, Scholtz J. Conformational stability of the escherichia coli hpr protein: test of the linear extrapolation method and a thermodynamic characterization of cold denaturation. Biochemistry. 1996;35:11369–11378. doi: 10.1021/bi960863y. [DOI] [PubMed] [Google Scholar]
- 19.Hermans J, Jr, Scheraga HA. Structural studies of ribonuclease. v. reversible change of configuration1-3. J Am Chem Soc. 1961;83(15):3283–3292. [Google Scholar]
- 20.Tischer A, Auton M. Urea-temperature phase diagrams capture the thermodynamics of denatured state expansion that accompany protein unfolding. Protein Sci. 2013;22(9):1147–1160. doi: 10.1002/pro.2301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Qu Y, Bolen C, Bolen D. Osmolyte-driven contraction of a random coil protein. Proc Natl Acad Sci U S A. 1998;95(16):9268–9273. doi: 10.1073/pnas.95.16.9268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Auton M, Ferreon A, Bolen D. Metrics that differentiate the origins of osmolyte effects on protein stability: a test of the surface tension proposal. J Mol Biol. 2006;361(5):983–992. doi: 10.1016/j.jmb.2006.07.003. [DOI] [PubMed] [Google Scholar]
- 23.Holthauzen L, Rösgen J, Bolen D. Hydrogen bonding progressively strengthens upon transfer of the protein urea-denatured state to water and protecting osmolytes. Biochemistry. 2010;49(6):1310–1318. doi: 10.1021/bi9015499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schellman J. The stability of hydrogen-bonded peptide structures in aqueous solution. Comptes rendus des travaux du Laboratoire …. 1954;29:230–259. [PubMed] [Google Scholar]
- 25.Flory PJ. Theory of elastic mechanisms in fibrous proteins. J Am Chem Soc. 1956;78(20):5222–5235. [Google Scholar]
- 26.Poland DC, Scheraga HA. Statistical mechanics of noncovalent bonds in polyamino acids. viii. covalent loops in proteins. Biopolymers. 1965;3(4):379–399. [Google Scholar]
- 27.Pace C, Grimsley G, Thomson J. Conformational stability and activity of ribonuclease t1 with zero, one, and two intact disulfide bonds. J Biol Chem. 1988;263(24):11820–11825. [PubMed] [Google Scholar]
- 28.Pace C, Vajdos F, Fee L, Grimsley G, Gray T. How to measure and predict the molar absorption coefficient of a protein. Protein Sci. 1995;4(11):2411–2423. doi: 10.1002/pro.5560041120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Weber G, Young LB. Fragmentation of bovine serum albumin by pepsin i. the origin of the acid expansion of the albumin molecule. J Biol Chem. 1964;239(5):1415–1423. [PubMed] [Google Scholar]
- 30.Lakowicz J. Principles in Fluorescence Spectroscopy. New York: Plenum Press; 1986. [Google Scholar]
- 31.Kelly S, Price N. The use of circular dichroism in the investigation of protein structure and function. Curr Prot Pept Sci. 2000;1(4):349–384. doi: 10.2174/1389203003381315. [DOI] [PubMed] [Google Scholar]
- 32.Yang M, Liu D, Bolen D. The peculiar nature of the guanidine hydrochloride-induced two-state denaturation of staphylococcal nuclease: a calorimetric study. Biochemistry. 1999;38(34):11216–11222. doi: 10.1021/bi9909400. [DOI] [PubMed] [Google Scholar]
- 33.Yang M, Ferreon A, Bolen D. Structural thermodynamics of a random coil protein in guanidine hydrochloride. Proteins. 2000;(Suppl 4):44–49. doi: 10.1002/1097-0134(2000)41:4+<44::aid-prot40>3.3.co;2-z. [DOI] [PubMed] [Google Scholar]
- 34.Ferreon A, Bolen D. Thermodynamics of denaturant-induced unfolding of a protein that exhibits variable two-state denaturation. Biochemistry. 2004;43(42):13357–13369. doi: 10.1021/bi048666j. [DOI] [PubMed] [Google Scholar]
- 35.Becktel W, Schellman J. Protein stability curves. Biopolymers. 1987;26(11):1859–1877. doi: 10.1002/bip.360261104. [DOI] [PubMed] [Google Scholar]
- 36.Baskakov I, Bolen D. The paradox between m values and delta cp’s for denaturation of ribonuclease t1 with disulfide bonds intact and broken. Protein Sci. 1999;8(6):1314–1319. doi: 10.1110/ps.8.6.1314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Uversky V, Fink A. The chicken-egg scenario of protein folding revisited. FEBS Lett. 2002;515(1–3):79–83. doi: 10.1016/s0014-5793(02)02441-9. [DOI] [PubMed] [Google Scholar]
- 38.Tiffany M, Krimm S. Effect of temperature on the circular dichroism spectra of polypeptides in the extended state. Biopolymers. 1972;11:2309–2316. doi: 10.1002/bip.1972.360111109. [DOI] [PubMed] [Google Scholar]
- 39.Sharp K. Entropy-enthalpy compensation: fact or artifact. Protein Sci. 2001;10(3):661–667. doi: 10.1110/ps.37801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Doig AJ, Williams DH. Is the hydrophobic effect stabilizing or destabilizing in proteins. J Mol Biol. 1991;217(2):389–398. doi: 10.1016/0022-2836(91)90551-g. [DOI] [PubMed] [Google Scholar]
- 41.Myers J, Pace C, Scholtz J. Denaturant m values and heat capacity changes: relation to changes in accessible surface areas of protein unfolding. Protein Sci. 1995;4(10):2138–2148. doi: 10.1002/pro.5560041020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Auton M, Bolen D. Predicting the energetics of osmolyte-induced protein folding/unfolding. Proc Natl Acad Sci U S A. 2005;102(42):15065–15068. doi: 10.1073/pnas.0507053102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Auton M, Bolen D. Application of the transfer model to understand how naturally occurring osmolytes affect protein stability. Methods Enzymol. 2007;428:397–418. doi: 10.1016/S0076-6879(07)28023-1. [DOI] [PubMed] [Google Scholar]
- 44.Auton M, Rösgen J, Sinev M, Holthauzen L, Bolen D. Osmolyte effects on protein stability and solubility: a balancing act between backbone and side-chains. Biophys Chem. 2011;159(1):90–99. doi: 10.1016/j.bpc.2011.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hilser V, Gómez J, Freire E. The enthalpy change in protein folding and binding: refinement of parameters for structure-based calculations. Proteins. 1996;26(2):123–133. doi: 10.1002/(SICI)1097-0134(199610)26:2<123::AID-PROT2>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 46.Lumry R, Biltonen R. Validity of the “two-state” hypothesis for conformational transitions of proteins. Biopolymers. 1966;4(8):917–944. doi: 10.1002/bip.1966.360040808. [DOI] [PubMed] [Google Scholar]
- 47.Zweifel M, Barrick D. Relationships between the temperature dependence of solvent denaturation and the denaturant dependence of protein stability curves. Biophys Chem. 2002;101–102:221–237. doi: 10.1016/s0301-4622(02)00181-3. [DOI] [PubMed] [Google Scholar]
- 48.Baskakov I, Bolen D. Monitoring the sizes of denatured ensembles of staphylococcal nuclease proteins: implications regarding m values, intermediates, and thermodynamics. Biochemistry. 1998;37(51):18010–18017. doi: 10.1021/bi981849j. [DOI] [PubMed] [Google Scholar]
- 49.Ziv G, Thirumalai D, Haran G. Collapse transition in proteins. Phys Chem Chem Phys. 2009;11(1):83–93. doi: 10.1039/b813961j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Haran G. How, when and why proteins collapse: the relation to folding. Curr Opin Struct Biol. 2012;22(1):14–20. doi: 10.1016/j.sbi.2011.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sosnick T, Barrick D. The folding of single domain proteins–have we reached a consensus. Curr Opin Struct Biol. 2011;21(1):12–24. doi: 10.1016/j.sbi.2010.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Schuler B, Lipman E, Eaton W. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature. 2002;419(6908):743–747. doi: 10.1038/nature01060. [DOI] [PubMed] [Google Scholar]
- 53.Sherman E, Haran G. Coil-globule transition in the denatured state of a small protein. Proc Natl Acad Sci U S A. 2006;103(31):11539–11543. doi: 10.1073/pnas.0601395103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Arai M, Kondrashkina E, Kayatekin C, Matthews C, Iwakura M, Bilsel O. Microsecond hydrophobic collapse in the folding of escherichia coli dihydrofolate reductase, an alpha/beta-type protein. J Mol Biol. 2007;368(1):219–229. doi: 10.1016/j.jmb.2007.01.085. [DOI] [PubMed] [Google Scholar]
- 55.Nettels D, Müller-Späth S, Küster F, Hofmann H, Haenni D, Rüegger S, Reymond L, Hoffmann A, Kubelka J, Heinz B, Gast K, Best R, Schuler B. Single-molecule spectroscopy of the temperature-induced collapse of unfolded proteins. Proc Natl Acad Sci U S A. 2009;106(49):20740–20745. doi: 10.1073/pnas.0900622106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Plaxco K, Millett I, Segel D, Doniach S, Baker D. Chain collapse can occur concomitantly with the rate-limiting step in protein folding. Nat Struct Biol. 1999;6:554–556. doi: 10.1038/9329. [DOI] [PubMed] [Google Scholar]
- 57.Jacob J, Krantz B, Dothager R, Thiyagarajan P, Sosnick T. Early collapse is not an obligate step in protein folding. J Mol Biol. 2004;338(2):369–382. doi: 10.1016/j.jmb.2004.02.065. [DOI] [PubMed] [Google Scholar]
- 58.Makarov A, Adzhubei I, Protasevich I, Lobachov V, Fasman G. Melting of the left-handed helical conformation of charged poly-l-lysine. Biopolymers. 1994;34(8):1123–1124. doi: 10.1002/bip.360340816. [DOI] [PubMed] [Google Scholar]
- 59.Shi Z, Olson CA, Rose GD, Baldwin RL, Kallenbach NR. Polyproline ii structure in a sequence of seven alanine residues. Proceedings of the National Academy of Sciences. 2002;99(14):9190–9195. doi: 10.1073/pnas.112193999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Yang W, Larios E, Gruebele M. On the extended beta-conformation propensity of polypeptides at high temperature. J Am Chem Soc. 2003;125(52):16220–16227. doi: 10.1021/ja0360081. [DOI] [PubMed] [Google Scholar]
- 61.Whittington S, Chellgren B, Hermann V, Creamer T. Urea promotes polyproline ii helix formation: implications for protein denatured states. Biochemistry. 2005;44(16):6269–6275. doi: 10.1021/bi050124u. [DOI] [PubMed] [Google Scholar]
- 62.Dolgikh D, Gilmanshin R, Brazhnikov E, Bychkova V, Semisotnov G, Venyaminov S, Ptitsyn O. Alpha-lactalbumin: compact state with fluctuating tertiary structure. FEBS Lett. 1981;136(2):311–315. doi: 10.1016/0014-5793(81)80642-4. [DOI] [PubMed] [Google Scholar]
- 63.Dolgikh D, Abaturov L, Bolotina I, Brazhnikov E, Bychkova V, Gilmanshin R, Lebedev Y, Semisotnov G, Tiktopulo E, Ptitsyn O. Compact state of a protein molecule with pronounced small-scale mobility: bovine alpha-lactalbumin. Eur Biophys J. 1985;13(2):109–121. doi: 10.1007/BF00256531. [DOI] [PubMed] [Google Scholar]
- 64.Ptitsyn O. How the molten globule became. Trends Biochem Sci. 1995;20(9):376–379. doi: 10.1016/s0968-0004(00)89081-7. [DOI] [PubMed] [Google Scholar]
- 65.Qin M, Wang W, Thirumalai D. Protein folding guides disulfide bond formation. Proc Natl Acad Sci U S A. 2015;112(36):11241–11246. doi: 10.1073/pnas.1503909112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Betz S. Disulfide bonds and the stability of globular proteins. Protein Sci. 1993;2(10):1551–1558. doi: 10.1002/pro.5560021002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Zhang T, Bertelsen E, Alber T. Entropic effects of disulphide bonds on protein stability. Nat Struct Biol. 1994;1(7):434–438. doi: 10.1038/nsb0794-434. [DOI] [PubMed] [Google Scholar]
- 68.Hinck A, Truckses D, Markley J. Engineered disulfide bonds in staphylococcal nuclease: effects on the stability and conformation of the folded protein. Biochemistry. 1996;35(32):10328–10338. doi: 10.1021/bi960309o. [DOI] [PubMed] [Google Scholar]
- 69.Johnson C, Oliveberg M, Clarke J, Fersht A. Thermodynamics of denaturation of mutants of barnase with disulfide crosslinks. J Mol Biol. 1997;268(1):198–208. doi: 10.1006/jmbi.1997.0928. [DOI] [PubMed] [Google Scholar]
- 70.Zavodszky M, Chen C, Huang J, Zolkiewski M, Wen L, Krishnamoorthi R. Disulfide bond effects on protein stability: designed variants of cucurbita maxima trypsin inhibitor-v. Protein Sci. 2001;10(1):149–160. doi: 10.1110/ps.26801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Dombkowski A, Sultana K, Craig D. Protein disulfide engineering. FEBS Lett. 2014;588(2):206–212. doi: 10.1016/j.febslet.2013.11.024. [DOI] [PubMed] [Google Scholar]
- 72.Felitsky D, Record M. Thermal and urea-induced unfolding of the marginally stable lac repressor dna-binding domain: a model system for analysis of solute effects on protein processes. Biochemistry. 2003;42(7):2202–2217. doi: 10.1021/bi0270992. [DOI] [PubMed] [Google Scholar]
- 73.Dyson H, Wright P. Intrinsically unstructured proteins and their functions. Nat Rev Mol Cell Biol. 2005;6(3):197–208. doi: 10.1038/nrm1589. [DOI] [PubMed] [Google Scholar]
- 74.Wright P, Dyson H. Linking folding and binding. Curr Opin Struct Biol. 2009;19(1):31–38. doi: 10.1016/j.sbi.2008.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.