Abstract
The wide tissue distribution of the adrenergic β3 receptor makes it a potential target for the treatment of multiple pathologies such as diabetes, obesity, depression, overactive bladder (OAB), and cancer. Currently, there is only one drug on the market, mirabegron, approved for the treatment of OAB. In the present study, we have carried out an extensive structure-activity relationship analysis of a series of 41 aryloxypropanolamine compounds based on three-dimensional quantitative structure-activity relationship (3D-QSAR) techniques. This is the first combined comparative molecular field analysis (CoMFA) and comparative molecular similarity index analysis (CoMSIA) study in a series of selective aryloxypropanolamines displaying anti-diabetes and anti-obesity pharmacological profiles. The best CoMFA and CoMSIA models presented values of r2ncv = 0.993 and 0.984 and values of r2test = 0.865 and 0.918, respectively. The results obtained were subjected to extensive external validation (q2, r2, r2m, etc.) and a final series of compounds was designed and their biological activity was predicted (best pEC50 = 8.561).
Keywords: β3-adrenergic receptor, obesity, diabetes, overactive bladder, aryloxypropanolamines, mirabegron, vibegron, 3D-QSAR, CoMFA, CoMSIA
1. Introduction
The β3 adrenergic receptor (β3-AR) is a transmembrane protein that belongs to the superfamily of G protein-coupled receptors [1,2]. There are three subtypes of β adrenergic receptors. The β1 adrenergic receptor is mainly located in the cardiovascular system, where it is the target of selective blockers such as atenolol or bisoprolol, which are used for the treatment of hypertension [3]. The β2 adrenergic receptor is mainly located in smooth muscles, where their activation by agonists such as salbutamol or salmeterol enables asthma treatment [4]. On the other hand, the β3-AR is widely distributed in the human body. It is present in the brain [5], the cardiovascular system [6], colon, bladder, and adipose tissue [7]. Therefore, it could be a therapeutic target for the treatment of diseases such as depression [8], hypertension, heart failure [9], overactive bladder (OAB) syndrome [10], colon cancer [11], metabolic syndrome, and obesity [12].
Until now, the pharmacophore for the design and synthesis of new β3-AR ligands has been the ethanolamine chain. Most of the compounds are of the phenylethanolamine or aryloxypropanol-amine type. To achieve β3 adrenergic selectivity, the insertion of bulky groups on the right-hand side (RHS) of the molecule is favorable (Figure 1). However, since the approval of mirabegron in 2012, few selective agonist compounds for the β3-AR receptor have been reported [13,14,15]. Selective β3 adrenergic agonists include CL 316,243 [16], amibegron (SR58611A) [17,18], mirabegron (YM-178) [10], and vibegron (RVT-901) [19] (Figure 1). CL 316,243 has anti-obesity and anti-diabetic profiles [20]. Amibegron presents antidepressant effects in animal models [21]. Mirabegron is the only selective β3 drug currently approved by the U.S. Food and Drug Administration for the treatment of OAB syndrome [22], however, there have been reports of upper airway angioedema following the administration of mirabegron [23]. On the other hand, recent studies have shown that mirabegron raises blood pressure and prolongs the QTc interval in electrocardiograms [24]. This information calls into question the continuity of mirabegron in the market. In this scenario, Merck Laboratories reported in 2016 the discovery of vibegron (Figure 1), a new potent and selective β3-AR agonist, which is currently under development in human clinical trials for the treatment of OAB [19].
Figure 1.
Structures of CL 316,243, amibegron, mirabegron, vibegron and the general structure of the aryloxypropanolamines studied here.
From the works of Cramer and Klebe [25,26], comparative molecular field analysis (CoMFA) and comparative molecular similarity index analysis (CoMSIA) are considered useful methodologies to understand the pharmacological properties of a series of compounds. Contour maps generated from CoMFA and CoMSIA show regions of the molecular structure where modifications in the steric, electrostatic, hydrophobic, and H-bond properties generate a favorable or unfavorable change in biological activity. Therefore, the contour maps obtained help to: (a) understand the nature of ligand-receptor interactions; (b) predict biological activity; and (c) aid in the rational design of new compounds.
In the last 10 years, there have been only two reports of quantitative structure-activity relationship (QSAR) studies on selective compounds for the β3-AR [27,28], one of which was conducted by our research group [28]. In both cases, the studies were carried out on phenylethanolamine-type compounds. Since then, there have been no reports of QSAR studies on aryloxypropanolamines. In the present work, we present a three-dimensional (3D)-QSAR study of a series of potent and selective human β3-AR agonists [29,30]. The reported compounds showed an interesting profile as potential drugs for the treatment of obesity and noninsulin-dependent (type II) diabetes. The compounds have a wide structural variability on both the RHS and left-hand side (LHS) of the general aryloxypropanolamine structure (Figure 1). The information obtained from the CoMFA and CoMSIA contour maps was systematized in a useful structural-activity relationship diagram. With this information, we finally reported the design of new compounds with promising β3 adrenergic activity.
2. Results and Discussion
2.1. Statistical Results
A summary of the statistical results for CoMFA and CoMSIA are presented in Table 1. Details of all possible combinations are given in Table S1 (Supplementary Material).
Table 1.
Statistical parameters and Field combinations for CoMFA and CoMSIA a.
| Model | q 2 | N | SEP | SEE | r 2 ncv | F | r 2 | Field Contributions | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | E | H | D | A | ||||||||
| CoMFA-SE | 0.537 | 6 | 0.544 | 0.067 | 0.993 | 525.4 | 0.865 | 0.412 | 0.588 | |||
| CoMSIA-SE | 0.566 | 7 | 0.539 | 0.101 | 0.985 | 193.0 | 0.002 | 0.299 | 0.701 | |||
| CoMSIA-SEHA | 0.674 | 6 | 0.456 | 0.119 | 0.978 | 161.3 | 0.790 | 0.174 | 0.335 | 0.215 | 0.276 | |
| CoMSIA-SEA | 0.651 | 5 | 0.462 | 0.151 | 0.963 | 118.7 | 0.760 | 0.245 | 0.395 | 0.360 | ||
| CoMSIA-SEDA | 0.601 | 7 | 0.517 | 0.103 | 0.984 | 185.5 | 0.816 | 0.229 | 0.324 | 0.190 | 0.257 | |
| CoMSIA-SD | 0.551 | 6 | 0.536 | 0.217 | 0.926 | 46.2 | 0.347 | 0.470 | 0.530 | |||
| CoMSIA-SHD | 0.561 | 9 | 0.570 | 0.095 | 0.988 | 172.1 | 0.237 | 0.312 | 0.398 | 0.289 | ||
| CoMSIA-EHA | 0.598 | 6 | 0.507 | 0.136 | 0.971 | 123.0 | 0.765 | 0.427 | 0.299 | 0.274 | ||
| CoMSIA-EHDA | 0.508 | 7 | 0.574 | 0.111 | 0.982 | 160.3 | 0.716 | 0.375 | 0.261 | 0.156 | 0.208 | |
| CoMSIA-ALL | 0.669 | 6 | 0.460 | 0.101 | 0.984 | 225.9 | 0.918 | 0.165 | 0.279 | 0.181 | 0.159 | 0.215 |
aq2 = the square of the leave-one-out (LOO) cross-validation (CV) coefficient; N = the optimum number of components; SEP = standard error of prediction; SEE is the standard error of estimation of non-CV analysis; r2ncv is the square of the non CV coefficient; F is the F-test value; r2 is the predictive r2 for test set compounds; S, E, H, D and A are the steric, electrostatic, hydrophobic, hydrogen-bond donor, and hydrogen-bond acceptor contributions respectively.
The best models were searched through successive field combinations. The first parameter to evaluate the statistical robustness of a QSAR model is the value of q2, which must be greater than 0.5. q2 is an indicator of the internal predictive capacity of a QSAR model. For CoMFA, the model that considered both field contributions (CoMFA-SE) presented the highest value (0.537), while with CoMSIA, several models presented a significant q2 value. The CoMSIA steric + electrostatic + hydrophobic + acceptor (CoMSIA-SEHA) and CoMSIA steric + electrostatic + acceptor (CoMSIA-SEA) models generated similar values for this coefficient (0.674 and 0.651, respectively). However, the value of r2, which evaluates the external predictive capacity of the model, allowed for discrimination between the models. In this case, the CoMSIA model that considered all the field contributions (CoMSIA-All) presented the highest value of r2 (0.918). The best models also had a low SEE and a high r2. The optimal number of components (N) is also low in all models presented (N = 6 for the best CoMFA and CoMSIA model). Ideally, a good model should have as few components as possible (N should be less than one-third of the total number of compounds studied), which ensures that the predictions will be based on meaningful information from field contributions, rather than on overtraining of the model. There is also a balance in the percentages of field contribution (approximately 50% for each field in CoMFA-SE and approximately 20% for each field in CoMSIA-All), which supports the reliability of the conclusions obtained from each contour map.
Table 2 presents a summary of the external validation of the CoMFA-SE and CoMSIA-All models (hereafter they are referred to as “CoMFA” and “CoMSIA” models). Both models have a high value for r2 (0.865 and 0.918, respectively), which is an indication of an adequate external predictive capacity. However, according to Golbraikh and Tropsha [31,32], high values of q2 and r2 (conditions 1 and 2) are necessary but not sufficient conditions for the validation of a model. For a QSAR model to have a reliable predictive capability, the line for experimental versus predicted activity should be as close as possible to the line y = x. This is observed in the fulfillment of conditions 3a or 3b, 4a or 4b, 5a or 5b, and 6 listed in Table 2. Finally, condition 7, known as r2m metrics, is a quantitative measure to determine the proximity between the observed and the predicted activity for the test set. The CoMFA and CoMSIA models reported here fulfilled all the conditions for internal and external validation and, in general, the CoMSIA model displays better statistical parameters than CoMFA.
Table 2.
Summary of external validation parameters for CoMFA and CoMSIA.
| Condition | Parameters | Threshold Value | CoMFA | CoMSIA |
|---|---|---|---|---|
| 1 | >0.5 | 0.537 | 0.669 | |
| 2 | >0.6 | 0.865 | 0.918 | |
| 3a | Close to value of | 0.864 | 0.911 | |
| 3b | Close to value of | 0.834 | 0.885 | |
| 4a | 0.85 < < 1.15 | 1.002 | 0.996 | |
| 4b | 0.85 < k < 1.15 | 0.937 | 1.004 | |
| 5a | <0.1 | 0.001 | 0.007 | |
| 5b | <0.1 | 0.036 | 0.034 | |
| 6 | <0.3 | 0.031 | 0.027 | |
| 7 | >0.5 | 0.793 | 0.843 |
q2 and r2 are the same parameters as listed in Table 1; and k are the correlation coefficient between the experimental (x) versus predicted activities (y) for test set through the origin and the respective slope of regression; and and k are the correlation coefficient between the predicted (y) versus experimental activities (x) for test set through the origin and the respective slope of regression. was defined in Equation (6).
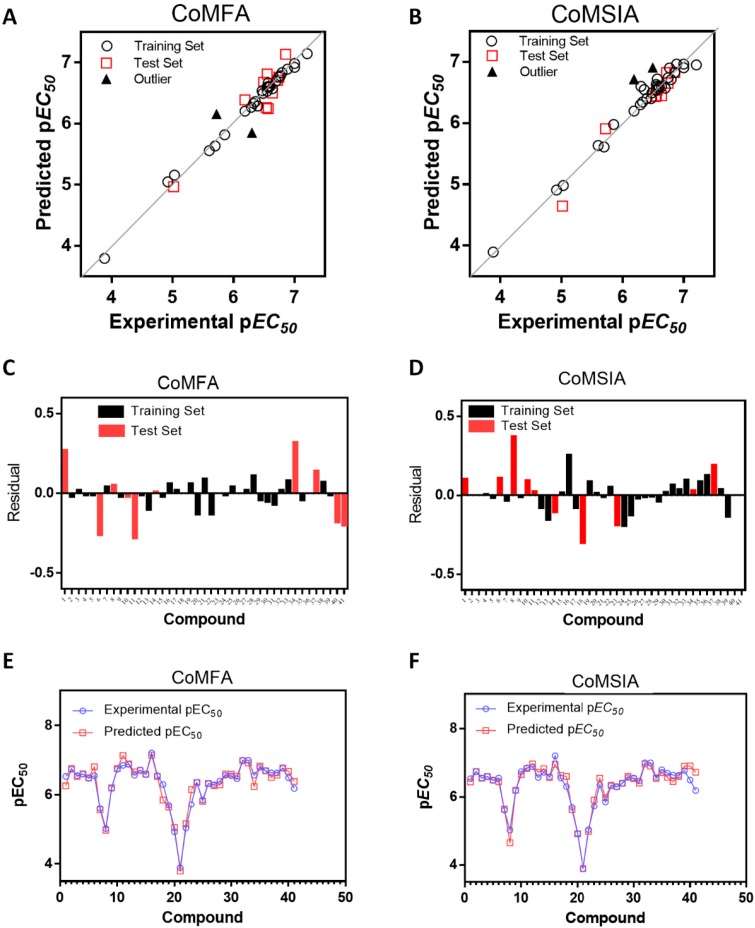
The values of experimental activity, predicted activity, and residual values for the best CoMFA and CoMSIA models are shown in Table 3. All the compounds showed low residual values and deviations in the predicted activity over a logarithmic unit were not observed. Figure 2A,B show the graphs of experimental versus predicted activity, from which it can be seen that the data distribution is close to the y = x line. Both models show a good balance in terms of predictive capacity. The CoMFA model presents 21 compounds with negative residual values and 20 with positive deviations (Figure 2C), while the CoMSIA model presents 19 compounds with negative residual values and 22 with positive deviations (Figure 2D). The residual ranges were −0.44 to 0.45 for CoMFA and −0.53 to 0.37 for CoMSIA. As shown in Figure 2E,F, the CoMFA and CoMSIA models show a satisfactory predictive capability throughout the whole set of data (training and test set) as well as a good predictive power for both, less active (8, 20, and 21) and most active compounds (16, 32, and 33).
Table 3.
Experimental and predicted pEC50 and residual values for analyzed compounds according to CoMFA and CoMSIA.
| CoMFA | CoMSIA | ||||
|---|---|---|---|---|---|
| Molecule | Experimental pEC50 | Predicted pEC50 | Residual | Predicted pEC50 | Residual |
| 1 t | 6.538 | 6.263 | 0.27 | 6.435 | 0.10 |
| 2 | 6.745 | 6.760 | −0.02 | 6.743 | 0.00 |
| 3 | 6.553 | 6.532 | 0.02 | 6.552 | 0.00 |
| 4 | 6.602 | 6.610 | −0.01 | 6.596 | 0.01 |
| 5 | 6.482 | 6.494 | −0.01 | 6.496 | −0.01 |
| 6 t | 6.553 | 6.811 | −0.26 | 6.444 | 0.11 |
| 7 | 5.602 | 5.559 | 0.04 | 5.635 | −0.03 |
| 8 t | 5.018 | 4.969 | 0.05 | 4.646 | 0.37 |
| 9 | 6.187 | 6.205 | −0.02 | 6.197 | −0.01 |
| 10 t | 6.745 | 6.761 | −0.02 | 6.651 | 0.09 |
| 11 t | 6.854 | 7.136 | −0.28 | 6.830 | 0.02 |
| 12 | 6.886 | 6.893 | −0.01 | 6.965 | −0.08 |
| 13 | 6.569 | 6.667 | −0.10 | 6.721 | −0.15 |
| 14 t | 6.721 | 6.707 | 0.01 | 6.826 | −0.10 |
| 15 | 6.585 | 6.601 | −0.02 | 6.569 | 0.02 |
| 16 | 7.208 | 7.144 | 0.06 | 6.953 | 0.26 |
| 17 | 6.553 | 6.530 | 0.02 | 6.632 | −0.08 |
| 18 t,a | 6.301 | 5.853 | 0.45 | 6.601 | −0.30 |
| 19 | 5.699 | 5.636 | 0.06 | 5.613 | 0.09 |
| 20 | 4.921 | 5.049 | −0.13 | 4.908 | 0.01 |
| 21 | 3.886 | 3.794 | 0.09 | 3.894 | −0.01 |
| 22 | 5.032 | 5.157 | −0.13 | 4.980 | 0.05 |
| 23 t,a | 5.721 | 6.157 | −0.44 | 5.908 | −0.19 |
| 24 | 6.357 | 6.362 | −0.01 | 6.549 | −0.19 |
| 25 | 5.854 | 5.818 | 0.04 | 5.979 | −0.13 |
| 26 | 6.328 | 6.331 | 0.00 | 6.345 | −0.02 |
| 27 | 6.292 | 6.269 | 0.02 | 6.303 | −0.01 |
| 28 | 6.398 | 6.288 | 0.11 | 6.404 | −0.01 |
| 29 | 6.569 | 6.604 | −0.04 | 6.605 | −0.04 |
| 30 | 6.553 | 6.601 | −0.05 | 6.534 | 0.02 |
| 31 | 6.469 | 6.539 | −0.07 | 6.403 | 0.07 |
| 32 | 7.000 | 6.984 | 0.02 | 6.964 | 0.04 |
| 33 | 7.000 | 6.921 | 0.08 | 6.904 | 0.10 |
| 34 t | 6.569 | 6.244 | 0.32 | 6.539 | 0.03 |
| 35 | 6.796 | 6.835 | −0.04 | 6.710 | 0.09 |
| 36 | 6.699 | 6.696 | 0.00 | 6.572 | 0.13 |
| 37 t | 6.638 | 6.503 | 0.14 | 6.448 | 0.19 |
| 38 | 6.638 | 6.570 | 0.07 | 6.601 | 0.04 |
| 39 | 6.770 | 6.781 | −0.01 | 6.902 | −0.13 |
| 40 t,b | 6.495 | 6.678 | −0.18 | 6.910 | −0.42 |
| 41 t,b | 6.187 | 6.390 | −0.20 | 6.718 | −0.53 |
t Test set compounds; a CoMFA outliers; b CoMSIA outliers.
Figure 2.
Plots of experimental versus predicted pEC50 values for the training and test set molecules for CoMFA (A) and CoMSIA (B) models. Residual plots between predicted and experimental values for CoMFA (C) and CoMSIA (D); CoMFA (E) and CoMSIA (F) predictions for every molecule in the complete set.
Furthermore, to assess the robustness of the model, the Y-randomization test [33] was applied (see Table S2 of the Supplementary Material for randomizations). The dependent variable (biological activity) was randomly shuffled and a new QSAR model was developed using the original independent variable matrix. If after multiple randomizations the new values of q2 and r2ncv are negative or below the limit of acceptability (q2 < 0.5, r2ncv < 0.6), then it is corroborated that the results obtained in the formulation of the final models are not by chance. In our case, the new QSAR models (after several repetitions) have low q2 and r2ncv values (Table 4).
Table 4.
q2 and r2ncv values after several Y-randomization tests.
| CoMFA | CoMSIA | |||
|---|---|---|---|---|
| Iteration | q 2 | r 2 ncv | q 2 | r 2 ncv |
| random_1 | −0.927 | 0.263 | −0.392 | 0.210 |
| random_2 | −0.111 | 0.321 | −0.075 | 0.204 |
| random_3 | −0.348 | 0.543 | −0.116 | 0.181 |
| random_4 | −0.315 | 0.427 | −0.036 | 0.259 |
| random_5 | −0.192 | 0.343 | −0.075 | 0.216 |
| random_6 | −0.192 | 0.332 | −0.171 | 0.154 |
| random_7 | −0.303 | 0.361 | −0.769 | 0.399 |
| random_8 | −0.051 | 0.345 | −0.004 | 0.283 |
| random_9 | −0.262 | 0.374 | −0.166 | 0.310 |
| random_10 | −0.001 | 0.339 | −0.092 | 0.175 |
In summary, the best CoMFA and CoMSIA models were selected based on their statistical robustness and good validated external predictability. In the case of CoMFA, both potentials contribute equally to biological activity (41.2% for the steric field and 58.8% for the electrostatic field). In the case of CoMSIA there is a homogeneous contribution of each field to the activity, however, the electrostatic field presents a slightly higher contribution (27.9%), so its contribution to biological activity is more important.
2.2. Contour Maps Analysis
2.2.1. CoMFA
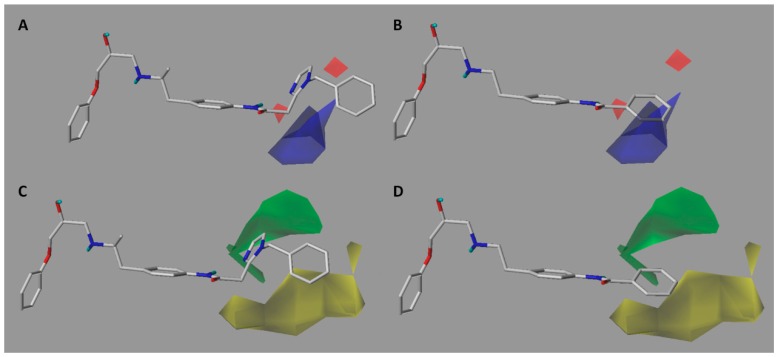
In the electrostatic contour map (Figure 3A), we can see a blue polyhedron around the methylene connector that connects the amide with imidazole ring. This suggests that the replacement of this connector by electropositive groups would be favorable for activity. For example, groups such as CONH, CO(NH)2, or a protonated amino group (projecting the proton towards the blue polyhedron) could be evaluated. This could explain why compounds 32 and 33 are among the most active since they project the polar proton of the urea function towards the blue zone, while compounds 8 and 20 present low activities due to the absence of said function. On the other hand, as seen in Figure 3B, the most inactive compound of the series (compound 21) intersects the blue polyhedron. Therefore, one way to improve the activity of this type of derivative would be to increase the electronic deficiency of the benzene ring. This could be achieved by inserting electronic attractor groups into the ring or by inserting groups such as OH or NH that project the hydrogen atom to the blue region.
Figure 3.
CoMFA electrostatic (A,B) and steric (C,D) contour maps around compounds 16 (left) and 21 (right), the most active and less active of the series respectively. Electropositive favored (blue) and electronegative favored (red). Sterically favored (green) and disfavored (yellow).
In the steric contour map around the most active compound 16 (Figure 3C), a green polyhedron is seen around position 5 of the imidazole ring. Therefore, the insertion of bulky substituents in that position would be favorable. This could explain the high activities reported for compounds 12 and 32, which project a benzyl and nitro group, respectively, to the green region. In Table 5, the proposals 1x to 5x were based on this observation. These compounds contain OH, NH, F, and acetyl groups in that position. The use of more voluminous halogens did not generate better predictions (e.g., Cl, Br, or I). On the other hand, in the less active compounds 7, 20, and 21 (Figure 3D), the benzene ring intersects the yellow region, which could explain the low activity of these compounds.
Table 5.
The proposed structures of new molecules and their predicted pEC50 values using the best model.
| Entry | Structure | Predicted pEC50 |
|---|---|---|
| 1x |
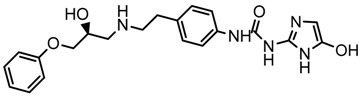
|
7.186 |
| 2x |
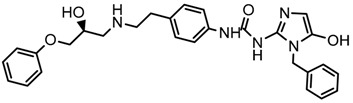
|
8.442 |
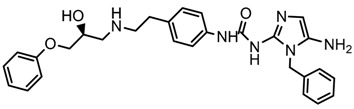
| 3x |
|
8.561 |
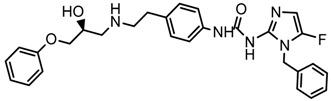
| 4x |
|
8.021 |
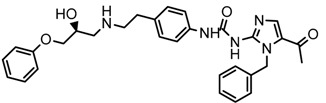
| 5x |
|
7.960 |
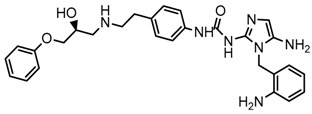
| 6x |
|
8.100 |
| 7x |
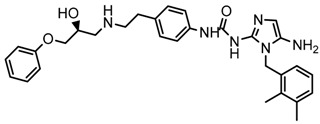
|
8.520 |
| 8x |
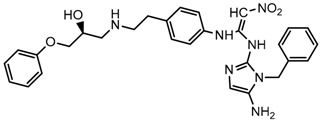
|
7.590 |
| 9x |
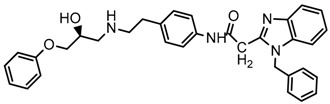
|
7.260 |
| 10x |
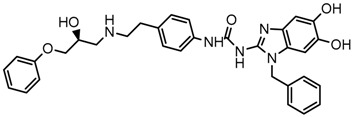
|
7.680 |
| 11x |
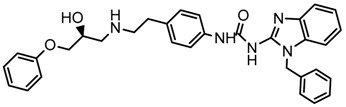
|
7.580 |
| 12x |
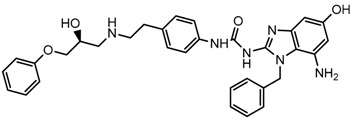
|
8.000 |
2.2.2. CoMSIA
The CoMSIA electrostatic contour map (Figure 4A,B) is similar to that obtained for CoMFA (Figure 3A,B). A blue polyhedron is visible near the methylene linker (Figure 4A). The concordance of this information in both models led us to propose the insertion of a urea group, after which we obtained derivatives with high predicted activity (Table 5). As in CoMFA, the less active compound 21 intersects the blue polyhedron in the benzene region, therefore the insertion of electropositive functions before the ring would be most favorable for activity.
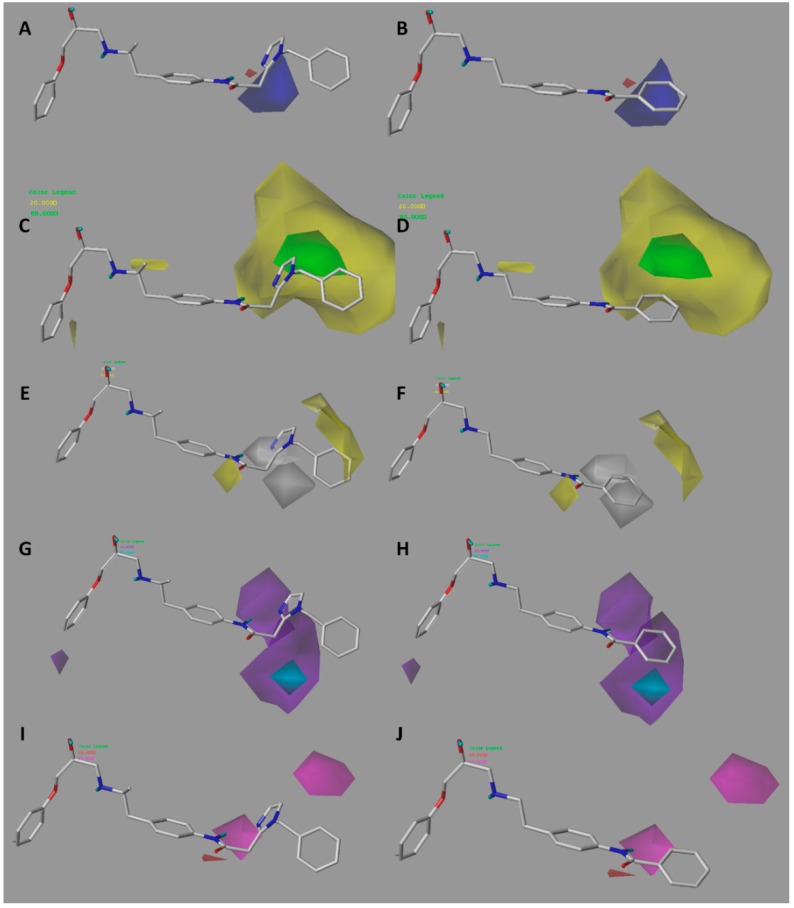
Figure 4.
CoMSIA electrostatic (A,B); steric (C,D); hydrophobic (E,F); donor (G,H) and acceptor (I,J) contour maps around compounds 16 (left) and 21 (right), the most active and less active of the series respectively. The colors in A–D have the same meaning as in the CoMFA contour maps. Hydrophobic favored areas are in yellow and unfavorable areas in grey (E,F). Donor and acceptor favored areas are in cyan and magenta respectively, and donor and acceptor unfavorable areas are in purple and red, respectively (G–J).
Like the CoMFA map (Figure 3C), the steric contour map shows a green region intersecting position 5 of the imidazole ring of compound 16 (Figure 4C). However, on the CoMSIA map, a yellow region surrounds the green region, therefore the increase in volume should be explored with caution. In fact, in the proposal for new structures, it was found that the insertion of large groups in position 5, such as Br and Cl, generated a reduction in biological activity, however, the insertion of medium-volume groups such as OH, NH2, and F improved activity considerably. This also suggests that the increase in molar refractivity is not favorable for activity.
The hydrophobic contour map (Figure 4E,F) shows two yellow polyhedrons, one near the carbonyl oxygen and the other near the benzene ring. This indicates that the presence of lipophilic groups in these regions would be favorable for activity. The high activity reported for compounds 32, 33, 35, and 39 could be explained by this fact since they position the sulfur atom of the sulfonylurea linker towards the smaller yellow polyhedron. In addition, in those same derivatives, the proton of the NH group at the right of the connector is directly positioned towards a grey polyhedron, which suggests that the presence of hydrophilic groups in that area is favorable. On the other hand, around the most active compound 16, there is a second grey polyhedron intersecting the imidazole ring (Figure 4E), which implies that this ring could be replaced by other hydrophilic isostere rings, but not by systems such as benzene or thiophene. Finally, the second yellow polyhedron intersects the benzene ring of the most active compound 16, but not the benzene ring of the least active compounds 19–23 (Figure 4F), which may in part explain the lower activity observed for these derivatives.
A large purple polyhedron surrounding the imidazole ring and the ortho position of benzene around the most active compound 16 (Figure 4G) is shown on the H-bond donor map (Figure 4G,H), suggesting that the presence of H-bond donor groups in these positions is not favorable for activity. This may explain the low activity of compound 8 (which is among the series of compounds 5–18) because it directly positions the NH group of the imidazole ring to the upper purple region. On the other hand, a smaller cyan polyhedron in the lower area suggests that the selective insertion of H-bond donor groups in the methylene connector area of imidazole would be beneficial. This is corroborated by the fact that the most active compounds 32, 33, and 35 position the NH group of the sulfonylurea towards this polyhedron. Finally, a small purple polyhedron on the LHS of the molecule suggests that the presence of NH groups of the dihydrobenzimidazolone and indole ring systems would not be beneficial for activity.
The H-bond acceptor contour map (Figure 4I,J) shows two magenta polyhedra close to position 3 and 5 of the imidazole ring, which means that incorporation of H-bond acceptor atoms in these positions is favorable. In fact, compounds 32 and 33 position the oxygen atoms from nitro groups to the magenta region. Other groups that could be inserted are F, OH, and pyridine rings.
2.3. Outliers
In the CoMFA model, compounds 18 and 23 were outliers. Compound 18 has a pEC50 = 6.3010 and unlike its analog 16 (the most active compound in the series), it has an alkylation in the N of the amide. Therefore, the spatial conformation of the imidazole ring may be altered. On the other hand, alkylation of the ethyl chain in compound 18 restricts rotation and could fix a different conformation within the target. With respect to the underestimation of activity for compound 23, this may be because CoMFA does not consider the favorable effects of the presence of the urea group. Effects that are considered by the hydrophobic and H-bond acceptor maps of CoMSIA, where compounds 18 and 23 were not outliers.
The outlier compounds in CoMSIA were 40 and 41, for which the model predicts greater activity than the real one. This imprecision may be because, in the case of compound 40, it positions a sulfonamide group towards the magenta polyhedral of the H-bond acceptor map, which is favorable for activity. However, this group falls into the yellow region of the steric map, but the greater contribution of the H-bond acceptor potential to the activity overestimates the predicted activity. In the case of compound 41, the overestimation of the biological activity value may be due to the reduction in the electronic density of the benzene ring, given by the thiourea group, which has the highest percentage of contribution to biological activity.
2.4. Applicability Domain
The applicability domain (AD) is a theoretical region in chemical space encompassing both the model descriptors and modeled response, which allows one to estimate the uncertainty in the prediction of a compound based on how similar it is to the training compounds employed in the model development. In this work, we used the method developed by Roy et al. [34] for the determination of AD. This method is based on the basic theory of the standardization approach.
The calculation was carried out using the free application available on the author’s page, after which it was obtained that all compounds were within the domain of applicability, except compound 18. This reinforces what was described in the previous section, that alkylation of the urea connector could result in significant changes in receptor binding. For this reason, none of the designed compounds (see next section) included alkyl groups in the urea connector.
2.5. Design of Novel Derivatives
Based on the information provided by CoMFA and CoMSIA, we have designed a series of structures of the aryloxypropanolamine type. In Table 5, we present the best derivatives with their predicted pEC50 value by the best model (CoMSIA, r2 = 0.918). The first proposed molecule 1x was as active as compound 16 (pEC50 = 7.208). The other structures (2x–12x) are more active than compound 16. The best candidates are compounds 3x (pEC50 = 8.561) and 7x (pEC50 = 8.520). The presence of polar functions like OH, NH2, and F at position 5 of the imidazole ring yielded good candidates. Other interesting proposals are the replacement of imidazole with a benzimidazole ring (comp. 9x–12x), in which the presence of polar functions improves the activity.
3. Materials and Methods
3.1. Selection of Conformers and Molecular Alignment
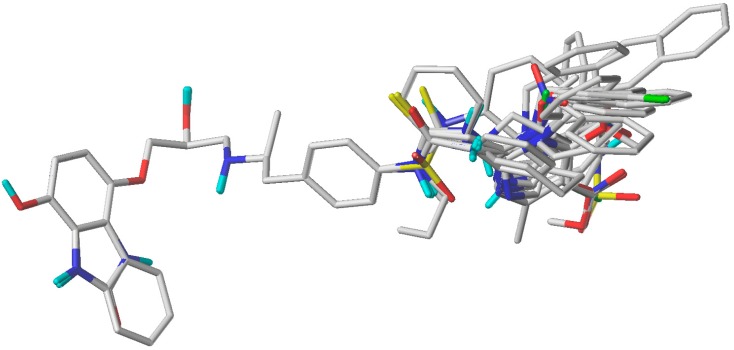
CoMFA and CoMSIA studies were performed with Sybyl X-1.2 software (1.2, Tripos International, St. Louis, MS, USA) installed in a Windows 10 environment on a PC with an Intel Core i7 CPU. To acquire the best conformers for each molecule, every compound was drawn in ChemDraw and subjected to a preliminary geometry optimization using MM2 molecular mechanics as is implemented in ChemBio3D software (15.1.0, PerkinElmer, Waltham, MA, USA). Following this, the structure of compound 16 (the most active of the series) was further minimized by quantum mechanics using the DFT B3LYP/6.311+g** method in Gaussian software (09, Gaussian Inc., Wallingford, CT, USA). This structure was used as a template for the alignment. The mol2 structures were imported to Sybyl and MMFF94 charges were assigned to each atom. The minimized structures were superimposed by the atom-by-atom fit method choosing the aryloxypropanolamine nucleus as the common scaffold for alignment (Figure 5). In addition, a minimization was carried out based on the Powell method [35] (as implemented in Sybyl, Figure S1 in the Supplementary Material). However, the statistical results were much lower than those reported by the method used in this manuscript (Table S3 in the Supplementary Material).
Figure 5.
The superimposed structures of all compounds used in the CoMFA/CoMSIA models.
3.2. CoMFA and CoMSIA Field Calculation
To derive the CoMFA and CoMSIA descriptor fields, the aligned training set molecules were placed in a three-dimensional cubic lattice with a grid spacing of 2 Å in the x, y, and z directions such that the entire set was included in it. The CoMFA steric and electrostatic field energies were calculated using an sp3 carbon probe atom with a van der Waals radius of 1.52 Å and a charge of +1.0. Cut-off values for both steric and electrostatic fields were set to 30.0 kcal/mol. For CoMSIA analysis, the standard settings (probe with charge +1.0, radius 1 Å, hydrophobicity +1.0, H-bond donating +1.0, and H-bond accepting +1.0 [26]) were used to calculate five different fields: steric, electrostatic, hydrophobic, donor, and acceptor. Gaussian-type distance dependence was used to measure the relative attenuation of the field position of each atom in the lattice and led to a much smoother sampling of the fields around the molecules when compared to CoMFA. The default value of 0.3 was set for attenuation factor α.
3.3. Data Set Selection and β3-Adrenergic Activity
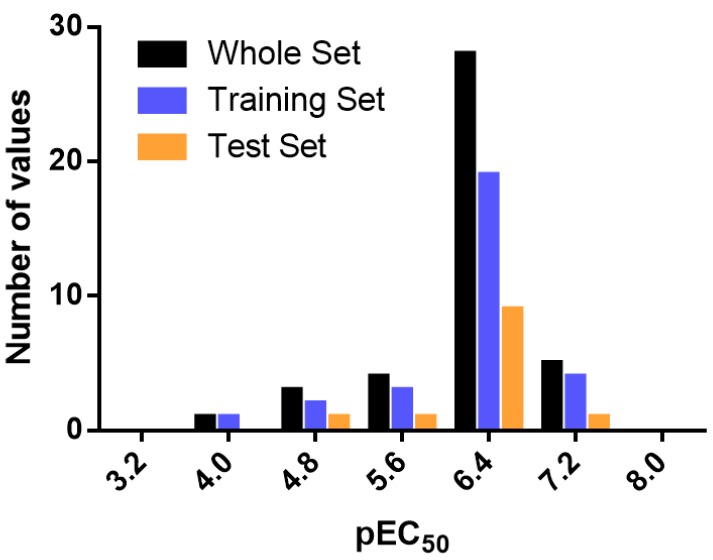
CoMFA and CoMSIA studies were performed on a set of 41 phenoxypropanolamine derivatives reported by Astellas Pharma [29,30] (Table 6). The derivatives displayed potent agonistic activity at the β3-AR. Agonistic activity (EC50) was assessed by measuring cAMP accumulation in CHO cells expressing β3-ARs. The EC50 values were converted to pEC50 (−logEC50). Several combinations of training and test sets were evaluated. The compounds were manually and randomly divided into training (29 compounds, 70%) and test sets (12 compounds, 30%), ensuring that both sets contained structurally diverse compounds with high, medium, and low activity, and a uniform distribution to avoid possible problems during external validation. For this purpose, most of the test set compounds were randomly extracted from the range of 6–8 logarithmic units of pEC50, while a smaller number were randomly selected from the range of 4–6 logarithmic units. Several test set groups were evaluated. For the construction of the final models, the test set that generated the highest r2 value in each case (CoMFA and CoMSIA) was finally selected. The distribution of pEC50 values for the whole set, the training set, and the test set is shown in Figure 6. In all three cases, the biological activity followed a Gaussian distribution. The range of the biological activities spans 3.5 log units, from 3.89 to 7.37.
Table 6.
Chemical structures and pEC50 values of the studied β3-adrenergic ligands a.
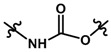
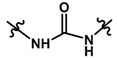
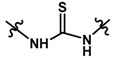
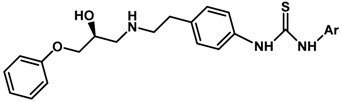
| Entry | Structure | EC50 (μM) | pEC50 | |
|---|---|---|---|---|
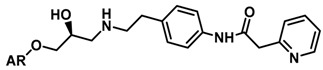
|
||||
| 1 |
|
0.29 | 6.538 | |
| 2 |
|
0.18 | 6.745 | |
| 3 |
|
0.28 | 6.553 | |
| 4 |
|
0.25 | 6.602 | |
|
||||
| 5 |
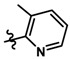
|
0.33 | 6.481 | |
| 6 |
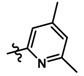
|
0.28 | 6.553 | |
| 7 |
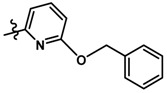
|
2.50 | 5.602 | |
| 8 |
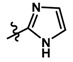
|
9.60 | 5.018 | |
| 9 |
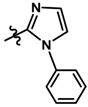
|
0.65 | 6.187 | |
| 10 |
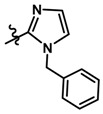
|
0.18 | 6.745 | |
| 11 |
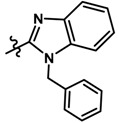
|
0.14 | 6.854 | |
| 12 |
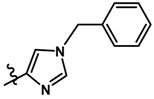
|
0.13 | 6.886 | |
| 13 |
|
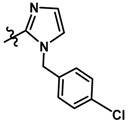
0.27 | 6.569 | |
| 14 |
|
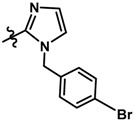
0.19 | 6.721 | |
| 15 |
|
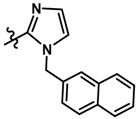
0.26 | 6.585 | |
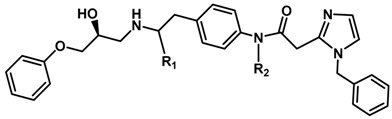
|
||||
| R1 | R2 | |||
| 16 | (S)-Me | H | 0.062 | 7.208 |
| 17 | H | Me | 0.28 | 6.553 |
| 18 | H | Propyl | 0.50 | 6.301 |
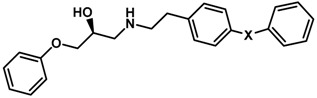
|
||||
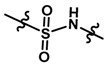
| 19 |
|
2.0 | 5.699 | |
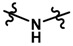
| 20 |
|
12.0 | 4.921 | |
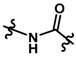
| 21 |
|
130 | 3.886 | |
| 22 |
|
9.30 | 5.032 | |
| 23 |
|
1.90 | 5.721 | |
| 24 |
|
0.44 | 6.357 | |
|
5.854 | |||
| 25 |
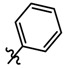
|
1.40 | 6.328 | |
| 26 |
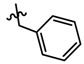
|
0.47 | 6.292 | |
| 27 |
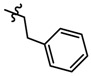
|
0.51 | 6.398 | |
| 28 |
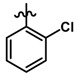
|
0.40 | 5.854 | |
| 29 |
|
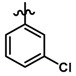
0.27 | 6.569 | |
| 30 |
|
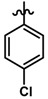
0.28 | 6.553 | |
| 31 |
|
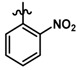
0.34 | 6.469 | |
| 32 |
|
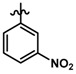
0.10 | 7.000 | |
| 33 |
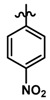
|
0.10 | 7.000 | |
| 34 |
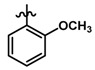
|
0.27 | 6.569 | |
| 35 |
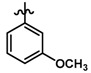
|
0.16 | 6.796 | |
| 36 |
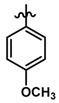
|
0.20 | 6.699 | |
| 37 |
|
0.23 | 6.638 | |
| 38 |
|
0.23 | 6.638 | |
| 39 |
|
0.17 | 6.770 | |
| 40 |
|
0.32 | 6.495 | |
| 41 |
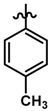
|
0.65 | 6.187 | |
a EC50 = Half maximal effective concentration; pEC50 = −logEC50; M = molL−1.
Figure 6.
Histogram of frequency distribution data.
3.4. Internal Validation and Partial Least Squares (PLS) Analysis
PLS analysis was used to construct a linear correlation between the CoMFA and CoMSIA descriptors (independent variables) and the activity values (dependent variables) [36]. To select the best model, the cross-validation analysis was performed using the leave-one-out (LOO) method (and sample distance PLS [SAMPLS]), which generates the square of the cross-validation coefficient (q2) and the optimum number of components (N). The non-cross validation was performed with a column filter value of 2.0 to speed up the analysis and reduce the noise. The q2, which is a measure of the internal quality of the models, was obtained according to the following Equation (1):
| (1) |
where , , and are observed, mean, and predicted activity in the training set, respectively.
3.5. External Validation
The models were subjected to external validation criteria according to the proposed test by Golbraikh and Tropsha [31,32], which considers a QSAR model predictive, if the following conditions are satisfied:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
It has been demonstrated [31] that all of the above criteria are indeed necessary to adequately assess the predictive ability of a QSAR model.
Furthermore, the external predictive power of the developed 3D-QSAR models using the test set was examined by considering metrics as shown below [37]:
| (7) |
where and are the squared correlation coefficients between the observed and predicted activities of the test set with and without the (0,0) intercept, respectively. For a significant external model validation, the value of should be greater than 0.5.
3.6. Applicability Domain Calculation
The AD was evaluated based on the simple standardization method reported by Roy et al. [34]. First, each descriptor “i” for each compound “k” is standardized (Sik). Every compound must have a maximum value [Si]max(k) ≤ 3. In the case that [Si]max(k) > 3 and its minimum value [si]min(k) < 3, then the Snew(k) parameter must be calculated and has to fulfill the condition: Snew(k) = , where is the mean of Sik values for compound k and is the standard deviation for such values. The software is available free of charge on the authors’ website: http://dtclab.webs.com/software-tools and http://teqip.jdvu.ac.in/QSAR_Tools/.
4. Conclusions
In the present article, we presented the construction of two QSAR models in aryloxypropanolamines with selective potency for the β3-AR. The CoMFA and CoMSIA models presented good internal (q2 = 0.537 and 0.669 for CoMFA and CoMSIA, respectively) and external (r2 = 0.865 and 0.918 for CoMFA and CoMSIA, respectively) validation. The models were further validated following the criteria given by Tropsha and Roy [31,32,37], and were determined to be statistically reliable and robust. In both models, there was an equilibrium among the steric, electrostatic, hydrophobic, H-bond acceptor, and H-bond donor contribution to the activity. With this information, a new series of compounds was designed. The predicted biological activity for the new derivatives is high and, in general, the presence of polar groups and cycles like the benzimidazole ring on the RHS are predicted to improve activity. This could be due the presence of polar functions may be important for interaction with the Arg315 residue, and aromatic rings may establish pi-stacking interactions with a Phe198 residue as it is reported in literature [38].
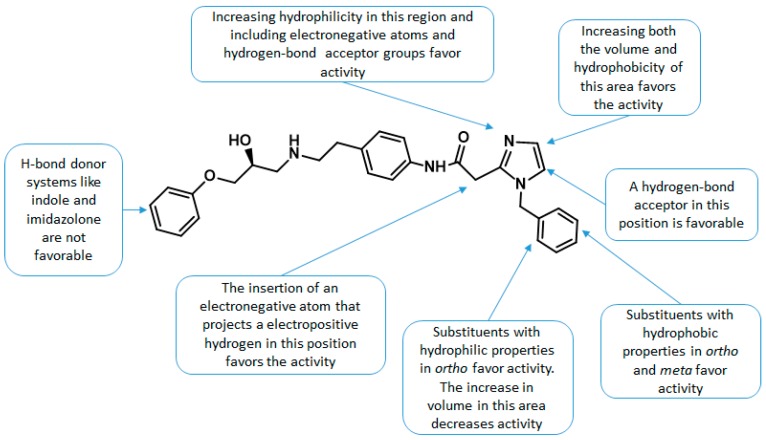
Taking into account the information derived from the CoMFA and CoMSIA studies, we have summarized the principal structure-activity relationships for the studies series of compounds in Figure 7. This information will be useful for the design of new compounds with promising therapeutic applications in several pathological disorders such as obesity, diabetes, OAB, depression, and cancer.
Figure 7.
Main structure-activity relationships found in this study.
Acknowledgments
This work was supported by FONDECYT No. 11130701. We would also like to thank DTCLab for the free availability of the software required to calculate the AD (http://dtclab.webs.com/software-tools and http://teqip.jdvu.ac.in/QSAR_Tools/). SDG.
Supplementary Materials
The following are available online, Figure S1: Distill-based alignment of optimized molecules by Powell method, Table S1: q2 and N values for all field combinations of CoMFA and CoMSIA, Table S2: Randomizations of biological activity for the execution of the Y-random test, Table S3: Statistical parameters for CoMFA and CoMSIA based in the Powell minimization method
Author Contributions
C.M.-V., D.V.-V., J.A.-L., and J.C.-S. Collected and processed data. J.S.-D. and G.R.-G. performed the DFT calculations. M.L. performed the statistical analysis and constructed the CoMFA and CoMSIA models. J.M. conducted the study and wrote the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Sample Availability: Not Available.
References
- 1.Tan S., Curtis-Prior P.B. Characterization of the beta-adrenoceptor of the adipose cell of the rat. Int. J. Obes. 1983;7:409–414. [PubMed] [Google Scholar]
- 2.Emorine L.J., Marullo S., Briend-Sutren M.M., Patey G., Tate K., Delavier-Klutchko C., Strosberg A.D. Molecular characterization of the human beta 3-adrenergic receptor. Science. 1989;245:1118–1121. doi: 10.1126/science.2570461. [DOI] [PubMed] [Google Scholar]
- 3.Heel R.C., Brogden R.N., Speight T.M., Avery G.S. Atenolol: A review of its pharmacological properties and therapeutic efficacy in angina pectoris and hypertension. Drugs. 1979;17:425–460. doi: 10.2165/00003495-197917060-00001. [DOI] [PubMed] [Google Scholar]
- 4.Paterson J.W., Evans R.J., Prime F.J. SElectivity of broncholidlator action of salbutamol in asthmatic patients. Br. J. Dis. Chest. 1971;65:21–38. doi: 10.1016/0007-0971(71)90002-7. [DOI] [PubMed] [Google Scholar]
- 5.Rodriguez M., Carillon C., Coquerel A., Le Fur G., Ferrara P., Caput D., Shire D. Evidence for the presence of beta 3-adrenergic receptor mRNA in the human brain. Brain Res. Mol. Brain Res. 1995;29:369–375. doi: 10.1016/0169-328X(94)00274-I. [DOI] [PubMed] [Google Scholar]
- 6.Gauthier C., Tavernier G., Charpentier F., Langin D., Le Marec H. Functional beta3-adrenoceptor in the human heart. J. Clin. Investig. 1996;98:556–562. doi: 10.1172/JCI118823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Krief S., Lonnqvist F., Raimbault S., Baude B., Van Spronsen A., Arner P., Strosberg A.D., Ricquier D., Emorine L.J. Tissue distribution of beta 3-adrenergic receptor mRNA in man. J. Clin. Investig. 1993;91:344–349. doi: 10.1172/JCI116191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Stemmelin J., Cohen C., Terranova J.P., Lopez-Grancha M., Pichat P., Bergis O., Decobert M., Santucci V., Francon D., Alonso R., et al. Stimulation of the beta3-Adrenoceptor as a novel treatment strategy for anxiety and depressive disorders. Neuropsychopharmacology. 2008;33:574–587. doi: 10.1038/sj.npp.1301424. [DOI] [PubMed] [Google Scholar]
- 9.Gauthier C., Rozec B., Manoury B., Balligand J.L. Beta-3 adrenoceptors as new therapeutic targets for cardiovascular pathologies. Curr. Heart Fail. Rep. 2011;8:184–192. doi: 10.1007/s11897-011-0064-6. [DOI] [PubMed] [Google Scholar]
- 10.Takasu T., Ukai M., Sato S., Matsui T., Nagase I., Maruyama T., Sasamata M., Miyata K., Uchida H., Yamaguchi O. Effect of (R)-2-(2-aminothiazol-4-yl)-4′-{2-[(2-hydroxy-2-phenylethyl)amino]ethyl} acetanilide (YM178), a novel selective beta3-adrenoceptor agonist, on bladder function. J. Pharmacol. Exp. Therm. 2007;321:642–647. doi: 10.1124/jpet.106.115840. [DOI] [PubMed] [Google Scholar]
- 11.Perrone M.G., Notarnicola M., Caruso M.G., Tutino V., Scilimati A. Upregulation of beta3-adrenergic receptor mRNA in human colon cancer: A preliminary study. Oncology. 2008;75:224–229. doi: 10.1159/000163851. [DOI] [PubMed] [Google Scholar]
- 12.Van Baak M.A., Hul G.B., Toubro S., Astrup A., Gottesdiener K.M., DeSmet M., Saris W.H. Acute effect of L-796568, a novel beta 3-adrenergic receptor agonist, on energy expenditure in obese men. Clin. Pharmacol. Ther. 2002;71:272–279. doi: 10.1067/mcp.2002.122527. [DOI] [PubMed] [Google Scholar]
- 13.Moyes C.R., Berger R., Goble S.D., Harper B., Shen D.M., Wang L., Bansal A., Brown P.N., Chen A.S., Dingley K.H., et al. Design, synthesis, and evaluation of conformationally restricted acetanilides as potent and selective beta3 adrenergic receptor agonists for the treatment of overactive bladder. J. Med. Chem. 2014;57:1437–1453. doi: 10.1021/jm4017224. [DOI] [PubMed] [Google Scholar]
- 14.Maruyama T., Onda K., Suzuki T., Hayakawa M., Takahashi T., Matsui T., Takasu T., Nagase I., Ohta M. Synthesis and evaluation of N-phenyl-(2-aminothiazol-4-yl)acetamides with phenoxypropanolamine moiety as selective beta3-adrenergic receptor agonists. Chem. Pharm. Bull. 2012;60:647–658. doi: 10.1248/cpb.60.647. [DOI] [PubMed] [Google Scholar]
- 15.Hertzberg R., Monreal Santiago G., Moberg C. Synthesis of the beta3-adrenergic receptor agonist solabegron and analogous N-(2-ethylamino)-beta-amino alcohols from O-acylated cyanohydrins-expanding the scope of minor enantiomer recycling. J. Org. Chem. 2015;80:2937–2941. doi: 10.1021/acs.joc.5b00322. [DOI] [PubMed] [Google Scholar]
- 16.Bloom J.D., Dutia M.D., Johnson B.D., Wissner A., Burns M.G., Largis E.E., Dolan J.A., Claus T.H. Disodium (R,R)-5-[2-[[2-(3-chlorophenyl)-2-hydroxyethyl]-amino]propyl]-1,3-benzodioxole-2,2-dicarboxylate (CL 316,243). A potent beta-adrenergic agonist virtually specific for beta 3 receptors. A promising antidiabetic and antiobesity agent. J. Med. Chem. 1992;35:3081–3084. doi: 10.1021/jm00094a025. [DOI] [PubMed] [Google Scholar]
- 17.Bianchetti A., Manara L. In vitro inhibition of intestinal motility by phenylethanolaminotetralines: Evidence of atypical beta-adrenoceptors in rat colon. Br. J. Pharmacol. 1990;100:831–839. doi: 10.1111/j.1476-5381.1990.tb14100.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Manara L., Bianchetti A. Further heterogeneity of the beta-adrenoceptor. The phenylethanolaminotetralines: New selective agonists for atypical beta-adrenoceptors. Trends Pharmacol. Sci. 1990;11:229–230. doi: 10.1016/0165-6147(90)90247-6. [DOI] [PubMed] [Google Scholar]
- 19.Edmondson S.D., Zhu C., Kar N.F., Di Salvo J., Nagabukuro H., Sacre-Salem B., Dingley K., Berger R., Goble S.D., Morriello G., et al. Discovery of Vibegron: A Potent and Selective beta3 Adrenergic Receptor Agonist for the Treatment of Overactive Bladder. J. Med. Chem. 2016;59:609–623. doi: 10.1021/acs.jmedchem.5b01372. [DOI] [PubMed] [Google Scholar]
- 20.Collins S., Daniel K.W., Petro A.E., Surwit R.S. Strain-specific response to beta 3-adrenergic receptor agonist treatment of diet-induced obesity in mice. Endocrinology. 1997;138:405–413. doi: 10.1210/endo.138.1.4829. [DOI] [PubMed] [Google Scholar]
- 21.Overstreet D.H., Stemmelin J., Griebel G. Confirmation of antidepressant potential of the selective beta3 adrenoceptor agonist amibegron in an animal model of depression. Pharmacol. Biochem. Behav. 2008;89:623–626. doi: 10.1016/j.pbb.2008.02.020. [DOI] [PubMed] [Google Scholar]
- 22.Gras J. Mirabegron for the treatment of overactive bladder. Drugs Today. 2012;48:25–32. doi: 10.1358/dot.2012.48.1.1738056. [DOI] [PubMed] [Google Scholar]
- 23.Myrbetriq. [(accessed on 10 May 2018)]; Available online: https://www.myrbetriqhcp.com/
- 24.Van Gelderen M., Stolzel M., Meijer J., Kerbusch V., Collins C., Korstanje C. An Exploratory Study in Healthy Male Subjects of the Mechanism of Mirabegron-Induced Cardiovascular Effects. J. Clin. Pharmacol. 2017;57:1534–1544. doi: 10.1002/jcph.952. [DOI] [PubMed] [Google Scholar]
- 25.Cramer R.D., Patterson D.E., Bunce J.D. Comparative molecular field analysis (CoMFA). 1. Effect of shape on binding of steroids to carrier proteins. J. Am. Chem. Soc. 1988;110:5959–5967. doi: 10.1021/ja00226a005. [DOI] [PubMed] [Google Scholar]
- 26.Klebe G., Abraham U., Mietzner T. Molecular similarity indices in a comparative analysis (CoMSIA) of drug molecules to correlate and predict their biological activity. J. Med. Chem. 1994;37:4130–4146. doi: 10.1021/jm00050a010. [DOI] [PubMed] [Google Scholar]
- 27.Telvekar V.N., Patel D.J., Jadhav N.C., Mishra S.J. Three-dimensional QSAR and pharmacophore mapping of biphenyl benzoic acid derivatives as selective human β3-adrenergic receptor agonists. Med. Chem. Res. 2010;19:1174–1190. doi: 10.1007/s00044-009-9261-1. [DOI] [Google Scholar]
- 28.Apablaza G., Montoya L., Morales-Verdejo C., Mellado M., Cuellar M., Lagos C.F., Soto-Delgado J., Chung H., Pessoa-Mahana C.D., Mella J. 2D-QSAR and 3D-QSAR/CoMSIA Studies on a Series of (R)-2-((2-(1H-Indol-2-yl)ethyl)amino)-1-Phenylethan-1-ol with Human beta(3)-Adrenergic Activity. Molecules. 2017;22:404. doi: 10.3390/molecules22030404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Maruyama T., Onda K., Hayakawa M., Seki N., Takahashi T., Moritomo H., Suzuki T., Matsui T., Takasu T., Nagase I., et al. Synthesis and evaluation of novel phenoxypropanolamine derivatives containing acetanilides as potent and selective beta3-adrenergic receptor agonists. Bioorg. Med. Chem. 2009;17:3283–3294. doi: 10.1016/j.bmc.2009.03.044. [DOI] [PubMed] [Google Scholar]
- 30.Maruyama T., Seki N., Onda K., Suzuki T., Kawazoe S., Hayakawa M., Matsui T., Takasu T., Ohta M. Discovery of novel thiourea derivatives as potent and selective beta3-adrenergic receptor agonists. Bioorg. Med. Chem. 2009;17:5510–5519. doi: 10.1016/j.bmc.2009.06.031. [DOI] [PubMed] [Google Scholar]
- 31.Golbraikh A., Tropsha A. Beware of q2! J. Mol. Graph. Model. 2002;20:269–276. doi: 10.1016/S1093-3263(01)00123-1. [DOI] [PubMed] [Google Scholar]
- 32.Tropsha A. Best Practices for QSAR Model Development, Validation, and Exploitation. Mol. Inform. 2010;29:476–488. doi: 10.1002/minf.201000061. [DOI] [PubMed] [Google Scholar]
- 33.Rucker C., Rucker G., Meringer M. y-Randomization and its variants in QSPR/QSAR. J. Chem. Inf. Model. 2007;47:2345–2357. doi: 10.1021/ci700157b. [DOI] [PubMed] [Google Scholar]
- 34.Roy K., Kar S., Ambure P. On a simple approach for determining applicability domain of QSAR models. Chemometr. Intell. Lab. Syst. 2015;145:22–29. doi: 10.1016/j.chemolab.2015.04.013. [DOI] [Google Scholar]
- 35.Powell M.J.D. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 1964;7:155–162. doi: 10.1093/comjnl/7.2.155. [DOI] [Google Scholar]
- 36.Clark M., Cramer R.D., Van Opdenbosch N. Validation of the general purpose Tripos 5.2 force field. J. Comput. Chem. 1989;10:982–1012. doi: 10.1002/jcc.540100804. [DOI] [Google Scholar]
- 37.Roy K., Chakraborty P., Mitra I., Ojha P.K., Kar S., Das R.N. Some case studies on application of “r(m)2” metrics for judging quality of quantitative structure-activity relationship predictions: Emphasis on scaling of response data. J. Comput. Chem. 2013;34:1071–1082. doi: 10.1002/jcc.23231. [DOI] [PubMed] [Google Scholar]
- 38.Saxena A.K., Roy K.K. Hierarchical virtual screening: Identification of potential high-affinity and selective beta(3)-adrenergic receptor agonists. SAR QSAR Environ. Res. 2012;23:389–407. doi: 10.1080/1062936X.2012.664824. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.