Abstract
There is considerable evidence that the cerebellum plays a vital role in motor learning by constructing an estimate of the sensory consequences of movement. Theory suggests this estimate is compared with the actual sensory feedback to drive motor learning. However, direct proof for the existence of this comparison is still lacking. Here we carried out a trial-by-trial analysis of cerebellar neurons during the execution and adaptation of voluntary head movements, and found that neuronal sensitivities dynamically track the comparison of predictive and feedback signals. When the relationship between the motor command and resultant movement was altered, neurons robustly responded to sensory input as if the movement was externally-generated. Neuronal sensitivities then declined with the same time course as the concurrent behavioral learning. These findings demonstrate the output of an elegant computation in which rapid updating of an internal model enables the motor system to learn to expect unexpected sensory inputs.
Keywords: sensory coding, self-motion, response selectivity, cerebellum, fastigial nucleus, efference copy, voluntary movement, vestibular, neck proprioception, learning
Introduction
How does the brain allow us to acquire new skills and maintain mastered skills in response to changes in the external environment and our motor systems? There are many reasons to believe that it does this by computing a sensory prediction error signal that represents the difference between the expected and actual sensory consequences of a given motor command. First, the intrinsic delays of sensory feedback make it impossible for sensory signals alone to account for many aspects of motor learning1–5. Second, theoretical investigations have demonstrated that the computation of sensory prediction errors is essential for fine-tuning motor behavior, including its on-line control and motor adaptation6, 7. Third, behavioral studies in humans suggest that errors induced by external perturbations are interpreted as sensory prediction errors8, 9.
The cerebellum, a structure that is well-conserved across vertebrates, plays a vital role in motor learning. Numerous studies have focused on understanding the information represented by the activity of cerebellar Purkinje cells, whose axons encode the output of the cerebellar cortex, during motor learning (reviewed in10, 11). While progress has been limited by the inherent challenge of systematically dissociating motor commands and movement kinematics, recent experiments demonstrate that Purkinje cells encode signals consistent with a forward model (i.e., the predicted sensory consequence of movement) rather than actual movement12, 13. Theoretically, sensory prediction errors will occur if there is a mismatch between the sensory expectation computed by the cerebellum’s forward model and actual sensory feedback (see Figure 1A). This error signal has been hypothesized to fine-tune the cerebellum’s forward model, as well as the consequent motor command, to ensure accurate motor learning (reviewed in14, 15). While the finding that cerebellar patients exhibit deficits in the predictive control of movement16–18 is consistent with this proposal, the existence of an explicit neural representation of such an error signal has not yet been demonstrated.
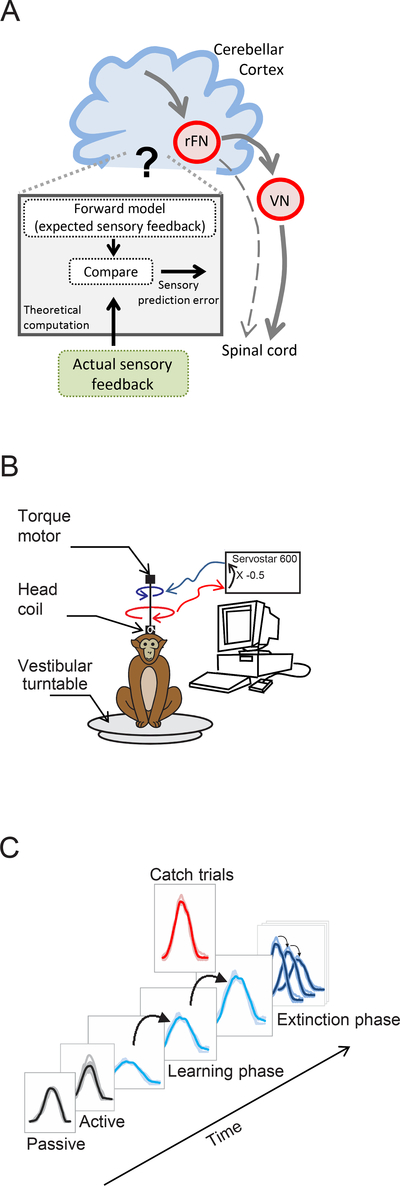
Figure 1:
Experimental design: A. Schematic shows the prevailing model of the proposed circuit for motor learning in which the cerebellum computes an estimate of the expected sensory consequence of the brain’s motor command (i.e., forward model). This estimate is then compared with the actual sensory feedback to compute the sensory prediction error. Single unit recordings were made in the rostral fastigial nucleus (rFN) which constitutes a major output target of the cerebellar cortex as well as vestibular nuclei (VN), which project to the spinal cord. B. Experimental set-up for learning paradigm in which resistive torque was applied to reduce head motion initially by one-half. C. Sequence of learning task. First, head movements and neuronal responses (not shown) were recorded before learning in both passive and active conditions. Second, the load was applied and held constant for the learning phase. Third, after the learning phase, the motor was randomly turned off for single ‘catch’ trials. Finally, the motor was completely turned off for the extinction phase.
Thus, to date, the question of where and how the brain compares expected and actual sensory feedback during the process of motor learning remains open. One recent line of work reported that components of Purkinje cell activity encode both predictive signals and actual sensory feedback during manual tracking13, 19. However this work stopped short of linking neuronal activities to sensory prediction errors, because the predictive and feedback representations in individual Purkinje cells were separated by several hundred milliseconds. Accordingly, here we examined whether there might be evidence for the comparison between predictive and feedback signals required for the computation of sensory prediction errors downstream of Purkinje cells - at the level of the deep cerebellar nuclei.
We took advantage of a relatively simple sensory-motor pathway with a well-described organization to gain new insight into the computations performed by the cerebellum to drive motor learning. The most medial of the deep cerebellar nuclei (rostral fastigial nucleus [rFN]), constitutes a major output target of the cerebellar cortex20 and in turn this nucleus sends strong projections to the vestibular nuclei, reticular formation, and spinal cord20–23 for postural control. We recorded the activity of single neurons in this deep cerebellar nucleus while monkeys made voluntary head movements to orient to visual targets. We then unexpectedly applied a load to the head while continuing to record the activity of these cerebellar neurons. Initially, there was a marked attenuation in the voluntary head movements made by monkeys that was subsequently accompanied by an increase in neuronal response. We measured head movement parameters and neuronal responses while monkeys learned to accommodate this new mechanical constraint on their head motion, and found that head movement trajectories showed rapid (within ~40 movements) updating to adjust to this loaded condition. Cerebellar nuclei neuronal responses, like the behavior, adapted to this new mechanical constraint over the same period and displayed responses consistent with the initial introduction of a sensory prediction error as well as its subsequent decline throughout motor learning. We further revealed corresponding parallel changes in the responses of neurons downstream in the vestibular nuclei, thereby directly linking observed changes in cerebellar output to sensory-motor adaptation during voluntary head motion. Finally, we found that when the externally applied load was removed, the responses of neurons at both stages of motor processing were again initially consistent with the introduction of a new sensory prediction error and then subsequently declined following the same time course as learning extinction. Our results provide the first support, at the level of single neurons, for the required dynamic and rapid comparison between predictive and feedback signals as the motor system learns to expect unexpected sensory input.
Results
To study the neural basis of motor learning during voluntary head movements, we recorded from single neurons (n=41) in the rostral fastigial nucleus (rFN) and quantified their sensitivity to passively applied stimulation of the vestibular system and neck proprioceptors24. Because the present study focuses on head movement motor learning, we targeted our analyses on the responses of unimodal rFN neurons (hereafter referred to simply as rFN neurons, n=21) – since these neurons respond to head motion. Bimodal rFN neurons instead responded to body motion, consistent with previous results24, and are presented in supplementary figures for comparison. Recordings were also made from neurons in the vestibular nuclei (VN) that responded to passive vestibular stimulation, but were insensitive to eye movements as well as passive neck stimulation, consistent with previous characterizations of VN vestibular-only neurons25.
Deep cerebellar nuclei during learning: evidence for computation of sensory prediction error
Recent studies have suggested that the responses of Purkinje cells in the cerebellum encode signals consistent with a forward model (i.e., the predicted sensory consequence of movement) rather than actual movement12, 13. The difference between this prediction and actual sensory feedback (termed a sensory prediction error) is commonly thought to drive motor learning. However as reviewed above, to date, no evidence for the comparison between the predicted and actual sensory feedback has been identified at the level of cerebellar Purkinje cells13, 19. Accordingly, we asked whether there is evidence for this comparison at the next stage of processing, specifically in the deep cerebellar nuclei that constitute the major output target of the cerebellar cortex. To test this, we analyzed changes in the responses of rFN neurons and changes in head velocity at the same time during a motor learning task. In a typical learning experiment, monkeys initially made active head movements between two alternating targets located 50 degrees apart. After the monkeys had made at least 20 of these control movements, we introduced a load to the head by applying resistive torque (Fig. 1B) proportional to head velocity adjusted to produce an initial reduction in peak head velocity of about 50%. The monkey then made >60 learning trials under the new biomechanical constraints imposed by this new load (i.e., learning phase; Fig. 1C, light blue traces). After 50 learning trials, occasional ‘catch trials’ (Fig. 1C, red traces) were introduced to assess neuronal responses when the load was unexpectedly removed for a single trial. Finally, the load was permanently removed and the monkey continued to make orienting movements during the learning extinction phase (Fig. 1C, dark blue traces). Below we establish the link between the monkey’s behavior and cerebellar rFN neuronal responses throughout the course of these components of the learning protocol.
In conditions that do not involve motor learning, rFN neurons encode passively generated, but not self-produced (i.e., active), vestibular sensory signals26. The responses of a typical neuron to passive and active stimulation before learning are shown in the first two columns of Figure 2A. Consistent with previous work26, the striking difference in the modulation of this representative neuron during passive (Fig. 2A first column; 0.43±0.04 (sp/s)/(°/s)) and active (Fig. 2A second column; 0.05±0.04 (sp/s)/(°/s)) head motion was typical of our population. Overall, the sensitivity of rFN neurons was significantly reduced (~70%) during active motion (0.10±0.01 vs. 0.35±0.03 (sp/s)/(°/s); Wilcoxon test p<0.05). Thus, these neurons preferentially respond to exafferent (externally generated) as compared to the reafferent (self-generated) sensory effects of self-motion, consistent with the coding of unexpected sensory input. If rFN neuronal responses are updated in a manner consistent with the computation of sensory prediction error signals, we hypothesized that they should robustly encode reafferent sensory input when the relationship between motor commands and resulting head motion is altered, but their sensitivity should then decrease with learning. Specifically neurons should (i) show an increased sensitivity to head motion when the load is initially applied, and (ii) show markedly decreased head-velocity sensitivity once adaptation occurs, consistent with the brain’s updating of the predicted sensory consequence of movement.
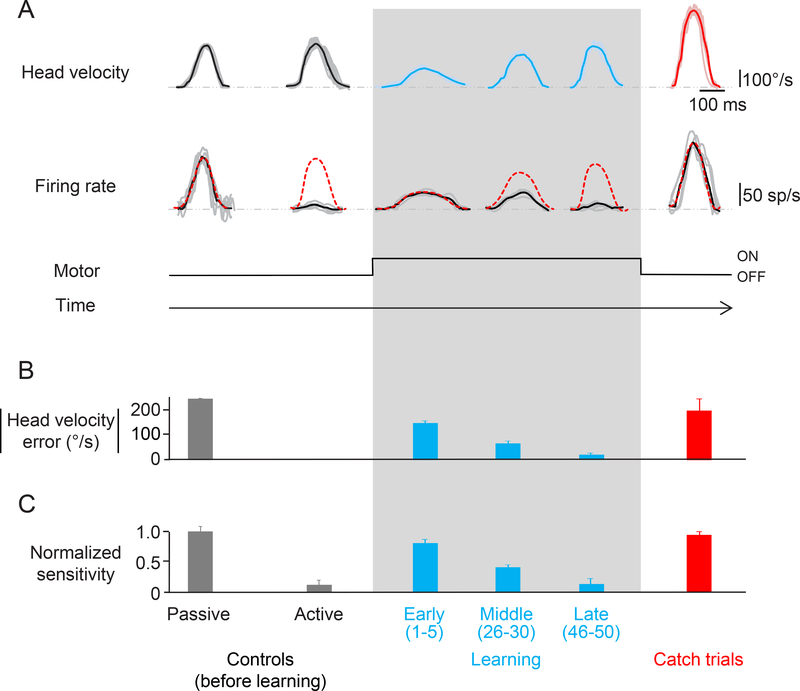
Figure 2:
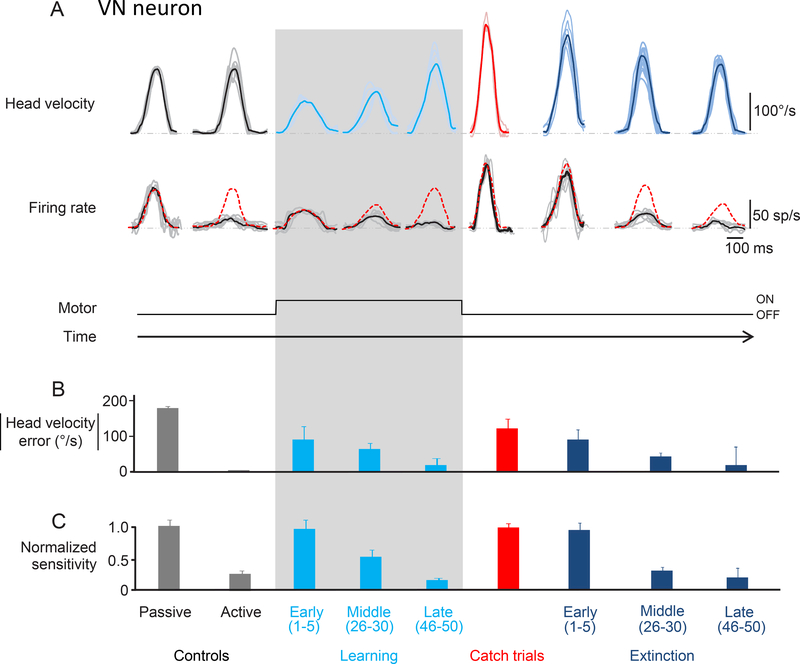
Learning paradigm. A. Activity of an rFN example neuron during the learning phase and catch trials. Top row shows the head velocity during control trials, learning phase and catch trials overlaying a minimum of 5 trials. Second row shows the firing rates corresponding to the head movements above. Grey lines show individual trials and black lines show the average. The red dashed lines superimposed on the firing rates are a prediction based on the neuron’s sensitivity to passive whole-body rotation. B. Head velocity error magnitude during learning and catch trials. When the load was applied, the monkey initially made slower head movements as quantified by a significant head velocity error. As learning progressed, head velocity increased nearing control values as indicated by the striking decrease in head velocity error magnitude (light blue bars). C. Normalized sensitivity to corresponding head movements shown above. During the learning phase, the neuronal sensitivity gradually decreased from that measured during passive head motion to the suppressed response observed during active motion (light blue bar). Neuronal sensitivity during catch trials (red) is comparable to the neuronal sensitivity during early learning and passive head movements.
To test these hypotheses, we analyzed changes in the trial-by-trial motor behavior and neuronal responses during the learning phase of our paradigm (Fig. 2A; shaded box). While the monkey’s peak head velocity was initially reduced by approximately 50% in the presence of resistive torque (64±4°/s vs 173±12°/s), it progressively increased - reaching values that were not significantly different from those of control movements (161±8°/s for the 46st-50th movements versus 173±12°/s, respectively, Wilcoxon test p>0.05). Thus, the monkey successfully modified its head motor command to account for the new relationship between motor command and movement. The second row of Figure 2A illustrates the simultaneously recorded activity of the example rFN neuron for these same movements. Remarkably, when the torque was initially applied, the example rFN neuron robustly responded to active motion. Indeed, the neuron’s sensitivity to vestibular stimulation resulting from passive head motion provided an excellent prediction of its response to active head motion during the early phases of learning (red dashed line), but this prediction increasingly overestimated the neuron’s response for head movements made in the middle and later phases of learning, (Fig. 2A; compare red dashed lines and black lines overlaying the firing rates). Notably, the neuron’s head-velocity sensitivity progressively decreased such that it was nearly negligible once the monkey adapted to the new load by ~trial 50; as the magnitude of the difference between expected and actual sensory input (i.e., head velocity error) approached zero, neuronal sensitivity progressively decreased (compare Figs. 2B and C, respectively). Thus, in agreement with our prediction, the example rFN neuron responded robustly to reafferent sensory input when the relationship between motor command and movement was initially altered, followed by a markedly decreased modulation once motor adaptation had occurred.
In motor learning studies, experimenters often introduce ‘catch’ trials where the perturbation (i.e., the applied load) is unexpectedly removed27–30 to establish whether the brain’s internal model has been updated to account for the imposed perturbation. The reasoning is that if an internal model has been updated such that the motor command accounts for the new load, then movements should approximate the mirror image of the deviation initially caused by the mechanical perturbation when it is removed. Our analysis of behavior showed that motor learning occurs in our adaptation paradigm. Specifically, because the head motor system had incorporated the applied resistive load into its motor plan, monkeys made substantially faster head movements when the load was unexpectedly removed (Fig. 2A, red trace showing the average of 5 catch trials: 281±11°/s). Moreover, neurons again showed robust responses to reafferent sensory input when the load was removed. Indeed, the example neuron was typical in that its response to vestibular stimulation resulting from passive head motion again provided an excellent prediction of its response to active head motion during catch trials (Fig. 2A, right column; compare red dashed line and black line overlaying the firing rate), indicating the vestibular sensitivity was comparable to that observed for passive rotations (Fig. 2B, right column; Wilcoxon test p>0.05). Thus, following the introduction of a large sensory prediction error by either i) application of the load to induce learning or ii) removal of the load during catch trials, neurons initially respond with the same sensitivity as during passive motion - regardless of the error’s sign (i.e., less versus more head velocity than expected, respectively). For completeness, a comparable analysis was also carried out on bimodal neurons (Figure S1) confirming the expected lack of response before, during, and after learning since these neurons respond to body rather than head motion24.
The observations shown in Figure 2 were representative and are summarized in Figures 3A and B for our population. Consistent with our experimental design, passively applied head velocities were comparable to active head movements made prior to the induction of learning (Fig. 3A, grey bars; 165±10 versus 180±20°/s, respectively; Wilcoxon test p>0.05). Moreover, similar to the behavior recorded simultaneously with the example neuron in Fig. 2, the peak head velocity of active head movements i) dropped by ~50% when the load was first applied to the head, ii) then steadily increased returning to control values after ~50 movements (Fig. 3A, light blue trace), and iii) nearly doubled for catch trials (Fig. 3A, red bar). Importantly, these changes in head movement were consistently linked to changes in neuronal responses across our population of neurons (Fig. 3B). Neuronal responses to active movements were minimal before learning, but immediately after the onset of learning they were robust and were in fact characterized by sensitivities comparable to those estimated for passive motion (0.28±0.04 vs 0.35±0.03(sp/s)/(°/s); Wilcoxon test p>0.05, gray bars). As learning progressed, neurons displayed increasingly reduced vestibular sensitivities (light blue trace) that returned to control values for active motion (gray bar) within 50 trials (0.09±0.01(sp/s)/(°/s); Wilcoxon test p>0.05). Additionally, comparison of neuronal responses during catch trials revealed sensitivities comparable to those measured during passively applied motion (0.33±0.05(sp/s)/(°/s); Wilcoxon test p>0.05; Fig. 3B, red bar). As expected, a comparable analysis of our population of bimodal rFN neurons, which encode body rather than head motion, did not show any changes in response sensitivity during head movement learning (See Supplemental Figure 2). Thus, taken together these results suggest a tight linkage between the learning of new relationships between motor commands and actual head movements and changes in the response sensitivity of neurons in the deep cerebellum that is consistent with the coding of unexpected sensory input.
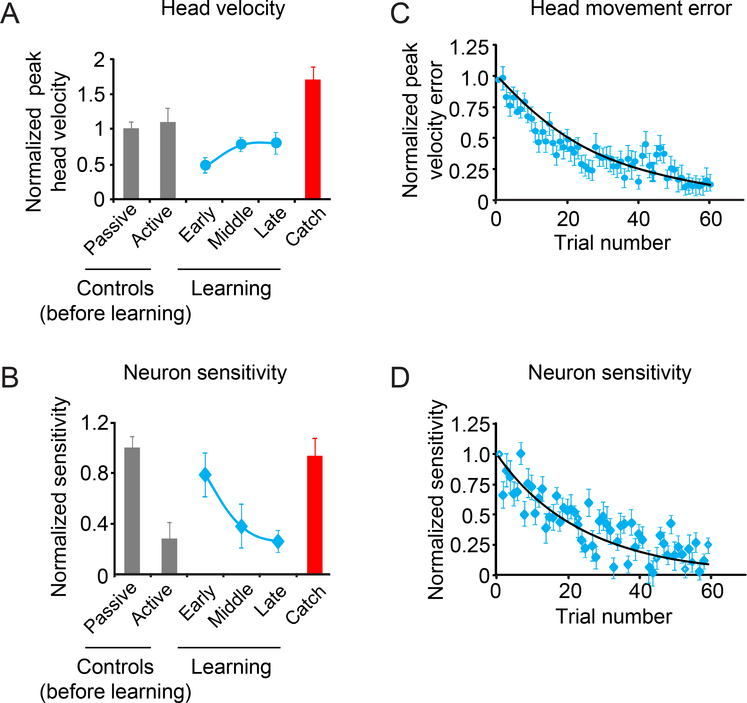
Figure 3:
Average head velocity and sensitivity for our population of rFN neurons during the learning phase. A. Normalized head velocity for control trials before learning, learning phase and catch trials. B. Normalized neuronal sensitivity for control trials, the learning phase and catch trials. Data show average and error bars are ±SEM. C. Scatter plot of peak head velocity errors over time for each trial during the learning phase. D. Scatter plot of normalized neuronal sensitivity over time for each trial during the learning phase. Black lines show exponential fits to the data.
Dynamics of the time course of adaptation:
Previous studies of motor learning have shown that adaptation can take place within 10 repetitions of a task (e.g. compensation for coriolis forces when reaching in a rotating environment28, 31) or require much more prolonged exposure (e.g. reaching while forces dependent on the motion state of the hand are applied32). To determine the time course of behavioral learning and corresponding changes in neuronal activity in our motor learning task, we next performed a trial-by-trial analysis of each single neuron’s response (Fig. S3A,B). We quantified the time course of the change in peak head velocity and compared it to that of the accompanying decrease in neuronal sensitivity by fitting both data sets with exponential curves (see Methods). Figures 3C-D illustrate the average normalized change in velocity (see methods; Fig. 3C) and normalized neuronal sensitivities for each trial in the learning phase (Fig. 3D) across our population of rFN neurons. Over our population, the average time constant of the increase in peak velocity toward control values was remarkably similar to the average time constant for the coincident decrease in neuronal sensitivity (34±7 versus 24±8 trials, respectively; Wilcoxon test p>0.05). Thus, these results demonstrate that the decreased neuronal sensitivity of deep cerebellar nuclei neurons tracks the detailed time course of behavioral changes as learning progresses.
Neuronal responses during extinction:
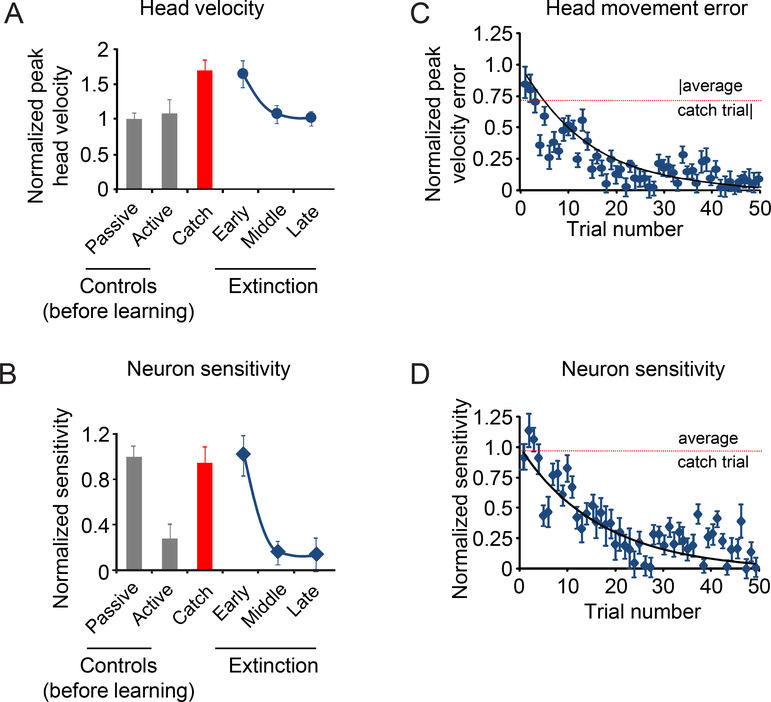
Our original hypothesis was: If rFN neuronal responses are updated in a manner consistent with the computation of sensory prediction error signals, then they should respond robustly to reafferent sensory input when the relationship between motor commands and resulting head motion is altered, but then their sensitivity should markedly decrease with learning, consistent with the brain updating its prediction of the sensory consequence of movement. The analysis of learning and catch trials described above was consistent with this proposal. We next addressed whether this hypothesis was further supported when the relationship between motor command and movement was altered after learning had occurred and the load was permanently removed (i.e., during the extinction phase of learning, Fig. 4A dark blue traces). We found that head movements were initially (i.e., the first 5 movements made in the extinction phase) larger than control head movements (274±11°/s vs 173±12°/s, Wilcoxon test, p<0.05) as would be expected since these trials were effectively equivalent to catch trials (Fig. 4B; Catch trials). When the monkey then continued to make active movements without the load, peak head velocity returned to normal (Fig. 4B; Extinction). This leads to the question: Do changes in rFN neuron responses mirror the extinction of this learned behavior? We found that this was the case. Figure 4B illustrates the responses of the same example neuron shown above in Figure 2 during learning extinction (Fig. 4B, second row; compare red dashed lines and black lines overlaying the firing rates). In the early phases of extinction, the example neuron’s response gain was comparable to its sensitivity to passive stimulation (0.34±0.08 vs 0.43±0.04(sp/s)/(°/s), respectively, Fig. 4D). In contrast, in the late stages of extinction, its response gain was substantially reduced and comparable to its sensitivity to active rotations made before learning (0.05±0.05 vs. 0.05±0.04(sp/s)/(°/s), respectively, Fig. 4D). Thus, these findings are consistent with the idea that rFN neuronal sensitivity dynamically tracks the comparison of expected and actual head movement; response gain was initially comparable to that observed for passive motion, and then rapidly decreases to levels observed during actively generated head movements in a manner that closely parallels the reduction in head velocity error (compare Fig. 4C and4D).
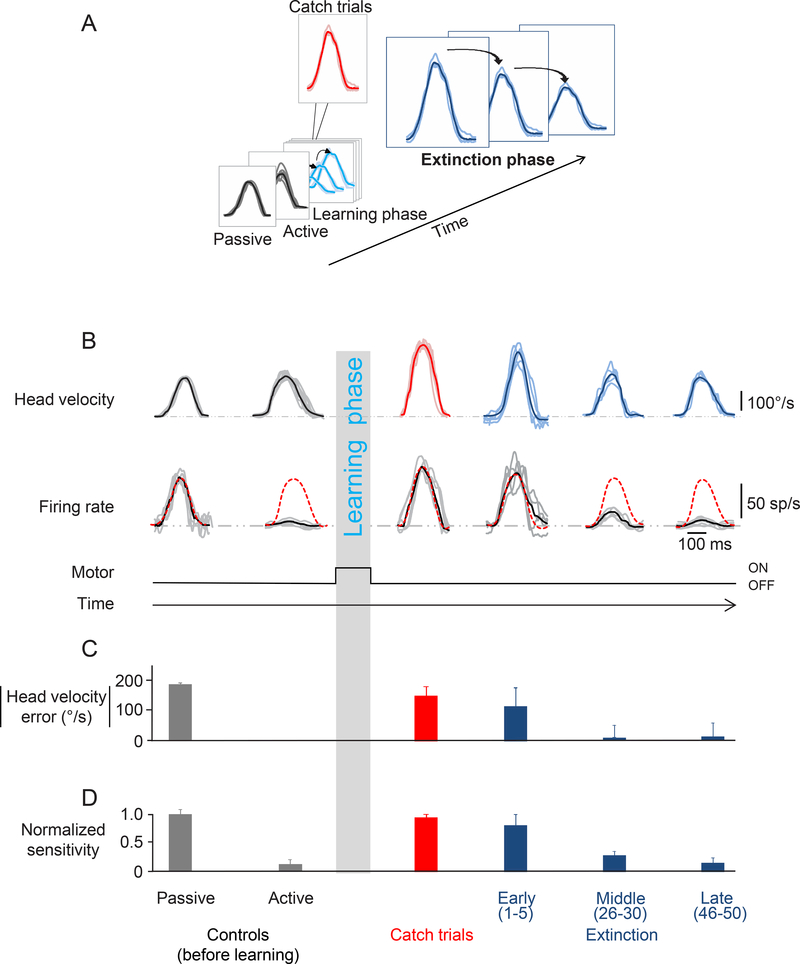
Figure 4:
Extinction phase. A. This figure focuses on the last phase of the paradigm during which the torque motor is turned off (extinction phase). B. Activity of the same example neuron as in Figure 2 during the extinction phase. Top row shows the head velocity during the extinction phase overlaying a minimum of 5 trials. Second row shows the firing rates corresponding to the head movements above. Grey lines show individual trials and black lines show the average. The dashed red lines superimposed on the firing rates are a prediction based on the sensitivity estimated during passively-applied whole body rotation. C. Head velocity error magnitude during learning extinction. When the load was removed, the monkey initially made faster head movements, and then head velocity error progressively decreased as head velocity approached control values (dark blue bars). D. Normalized neuronal sensitivity for the extinction phase. Data show average and error bars are ±SEM. Data from the control (before learning) and catch trials are reproduced here for comparison.
The observations shown in Figure 4 were representative and are summarized in Figures 5A and B for our population. When the torque was initially removed, peak head velocity increased (Fig. 5A; ‘early’ extinction), but then steadily decreased until it reached near control values (Fig. 5A; ‘late’ extinction). As expected, the peak head velocities observed during the first few movements after the torque had been removed (i.e., ‘early’ extinction) and catch trials were not significantly different (274±19°/s vs 281±18°/s; Wilcoxon test p>0.05). Notably, changes in neuronal sensitivity mirrored these behavioral changes. Initially, the vestibular sensitivities of rFN neurons were comparable to those measured in response to passively applied motion (0.35±0.04(sp/s)/(°/s); 5B; ‘early’ extinction; Wilcoxon test p>0.05). Then once the learned behavior was extinguished (i.e., the peak velocity of head movement returned to control values), response sensitivities were markedly reduced and, in fact, comparable to those measured for active movements in the control condition (0.05±0.01(sp/s)/(°/s); Fig. 5B ‘late’ extinction; Wilcoxon test p>0.05).
Figure 5:
Average head velocity and sensitivity for our population of rFN neurons during the extinction phase. A. Normalized head velocity for control trials before learning, catch trials and extinction phase. B. Normalized neuronal sensitivity for control trials before learning, catch trials and extinction phase. Data show average and error bars are ±SEM. C. Scatter plot of peak head velocity error over time for each trial during the extinction phase. D. Scatter plot of normalized neuronal sensitivity over time for each trial during the extinction phase. Black lines show exponential fits to the data. Dashed lines are the average values for the catch trials.
Previous studies of motor learning generally find that the extinction of learning is faster than the processes involved in the initial learning (reviewed in33). We thus quantified the time course of extinction and the corresponding changes in rFN neuronal activity to see whether this was the case for head-control motor learning. We again performed a trial-by-trial analysis of each single neuron’s response and compared it to the time course of the change in peak head velocity (Fig. S3C,D). Figures 5C and D illustrate the average normalized change in velocity (see Methods; Fig. 5C) and normalized neuronal sensitivities for each trial in the extinction phase across our population of rFN neurons (Fig. 5D). To facilitate comparison with the time course of learning (Fig. 3C and D), both data sets were fit with exponential curves (see Methods). Over our population of rFN neurons, the average time constant of the decrease in peak velocity toward control values was comparable to the average time constant for the coincident decrease in neuronal sensitivity (21±8 versus 16±7, trials, respectively; Wilcoxon test p>0.05). Furthermore, comparisons with the time course of behavioral and neuronal changes in the learning phase revealed that both were indeed significantly shorter (~30 %) for extinction (paired Wilcoxon tests p<0.05). For completeness, comparable testing and analyses were carried out on bimodal neurons (Figures S4 and S5) that confirmed the expected lack of response throughout the entire time course of extinction. In summary, our trial-by-trial analysis shows that the time course of the extinction of learning is linked to changes in the responses of rFN neurons in the deep cerebellar nuclei – providing evidence that the output of the cerebellum signals the mismatch between the expected and actual sensory consequences of head movement during the extinction as well as acquisition of learning.
Vestibular nuclei neurons mirror rFN neurons during motor learning
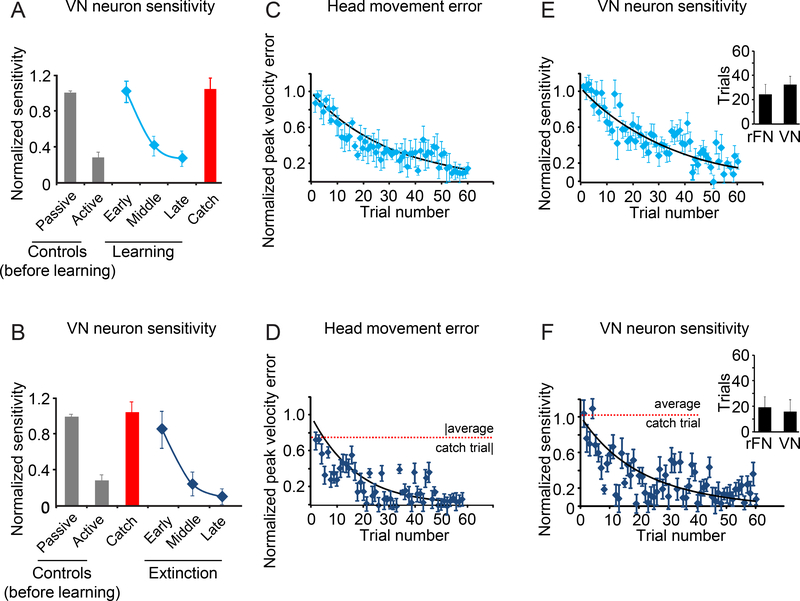
The deep cerebellar nuclei neurons of the rFN serve a vital role in regulating vestibulo-spinal reflexes to ensure accurate postural control. Given that the vestibular nuclei (VN) receive direct input from the rFN20–23, we hypothesized that the modulation of VN neurons that mediate vestibulo-spinal pathways would similarly reflect the updating of the forward model predicting the sensory consequences of head motion – thereby encoding a continuously updated representation of unexpected motion that could be used to maintain postural stability. To directly test this hypothesis, we examined whether the time course of changes in the head-velocity sensitivity of VN neurons was linked on a trial-by-trial basis to the learning and extinction of new relationships between active motion and vestibular reafference. Before learning, VN neurons were sensitive to vestibular stimulation resulting from passive motion, however their sensitivities were greatly reduced when motion was self-generated (N=20, 0.46±0.01 vs 0.13±0.03(sp/s)/(°/s))), as has been previously reported25, 34.
Figure 6 illustrates the responses of a typical VN neuron before learning, during learning and catch trials, and lastly during the extinction of learning. Consistent with our hypothesis, the trial-by-trial modulation of VN neurons similarly represents the updating of the internal model predicting the sensory consequences of head motion. Figure 7 illustrates the comparison of the population response during the learning (Fig. 7A,C,E) and extinction (Fig. 7B,D,F) phases of learning. Consistent with the first part of our hypothesis, neuronal sensitivities increased upon the application of the load and then decreased during learning. Specifically, in the early stages of learning, sensitivities to vestibular stimulation produced by active motion were comparable to those produced by passive motion (0.46±0.05 vs 0.46±0.01(sp/s)/(°/s); Wilcoxon test p>0.05) and by the late phase of learning, sensitivities to active motion were again suppressed to control levels (0.13±0.04(sp/s)/(°/s); Wilcoxon test p>0.05). During catch trials, vestibular sensitivities were again comparable to those measured during passively applied motion (0.48±0.06(sp/s)/(°/s), Wilcoxon test p>0.05). Notably, as seen above for rFN neurons, VN neuronal sensitivity progressively decreased as the magnitude of the difference between expected and actual sensory input (i.e., head velocity error) approached zero (compare Figs. 7C and E, respectively). Moreover, the time constant of the decay in neuronal response was equivalent to that observed above for rFN neurons (32±7 versus 24±8 trials, Wilcoxon test p>0.05, Fig. 7E inset). Thus, neurons in the vestibular nuclei, like those in the deep cerebellar nuclei, demonstrate rapid updating in the sensitivities of their sensory responses as the motor system learns to expect unexpected vestibular input.
Figure 6:
Activity of an example neuron recorded in the vestibular nuclei. A. Top row shows the head velocity during control trials, learning phase, catch trials and extinction phase overlaying a minimum of 5 trials. Bottom row shows the firing rates corresponding to the head movements above. Grey lines show individual trials and black lines show the average. The red dashed lines superimposed on the firing rates are a prediction based on the sensitivity estimated during passive whole-body rotation. B. The magnitude of head velocity error during control, learning, catch, and extinction trials. During the learning phase, the magnitude of head velocity error decreased (as head velocity increased) to approach control values (light blue bars). During the extinction phase (dark blue bars), the magnitude of head velocity error again decreased (this time as head velocity decreased) to approach control values (dark blue bars). C. Normalized sensitivity to corresponding head movements shown above. During the learning phase, neuronal sensitivity gradually decreased from that observed during passive motion to the suppression seen for active motion (light blue bars). Neuronal sensitivity during catch trials (red) is comparable to the neuronal sensitivity during early learning and passive head movements. During the extinction phase, neuronal response sensitivity again gradually decreased from that observed during passive motion to the suppression observed for active motion (dark blue bars).
Figure 7:
Average head velocity and neuronal sensitivity for our population of neurons recorded in the vestibular nuclei. A. Normalized neuronal sensitivity for control trials before learning, the learning phase and catch trials. B. Normalized neuronal sensitivity for control trials before learning, catch trials and extinction phase. C,D. Scatter plots of head velocity error magnitude for each trial during learning (C) and the extinction of learning (D). The dashed line denotes the average value for the catch trials. E,F. Scatter plot of normalized neuronal sensitivity over time for each trial during learning (E) and the extinction phase (F). The dashed line denotes the average value for the catch trials. Insets compare time constants for learning (E) and extinction (F) with those computed for our population of rFN neurons. Data show average and error bars are ±SEM.
Additionally, when the load was removed after learning, consistent with the second part of our initial hypothesis, we found a marked and immediate increase in neuronal sensitivity. Neuronal sensitivities then decreased to control levels for active head movements with the same time course as the extinction of the learned behavior (Fig. 7B). Initially, neuronal sensitivities to active movements were comparable to those measured for passive motion (0.39±0.09(sp/s)/(°/s); Wilcoxon test p>0.05), but by the late phase of extinction vestibular sensitivities were suppressed to control levels (0.05±0.02(sp/s)/(°/s); Wilcoxon test p>0.05). Our trial-by-trial based analysis (Fig. S6) further established that neuronal sensitivities progressively decreased during extinction as the magnitude of the difference between expected and actual sensory input (i.e., head velocity error) approached zero (compare Figs. 7D and F, respectively). The time constant of this decrease was equivalent to that observed above for rFN neurons during the extinction of learning (inset, Fig. 7F; 16±7vs13±8 for VN vs rFN respectively). Thus, in the extinction phase, following the introduction of a large sensory prediction error by removal of the load, neurons again initially responded with the same sensitivity as during passive motion. Moreover, as was the case for rFN neurons, VN neuronal sensitivities increased to robustly encode sensory reafference when a sensory prediction error was introduced regardless of direction of the error (i.e., during learning initiation as well as catch trials and extinction initiation). Taken together, our findings show that the sensory responses of individual neurons in the vestibular nuclei, like those in the deep cerebellar nuclei, reflect the dynamic computation of sensory prediction error as motor learning (and unlearning) progresses.
Discussion
Our central finding is that rapid updating in the primate cerebellum consistent with the dynamic comparison between expected and actual sensory feedback enables the motor system to learn to expect unexpected sensory input. Specifically, we provide direct evidence that the sensitivity of individual cerebellar output neurons tracks the difference between predictive and feedback signals consistent with the computation of sensory prediction error during motor learning. This conclusion is based on the trial-to-trial evaluation of neuronal responses and behavior before, during and after learning.
By applying a constant load while monkeys generated voluntary head movements, we were able to systematically alter the relationship between the motor command to move the head and its actual motion. Our findings establish that neuronal and behavioral responses were tightly linked, consistent with the idea that cerebellar learning is based on the continual updating of an internal model of the sensory consequences of self-motion. Specifically, when the load was first applied, the initial resulting reduction in head motion was accompanied by a marked increase in neuronal sensitivity relative to what was observed for control active movements. Then during the adaptation process, neuronal sensitivity steadily decreased as head motion returned to normal. This reduction in response gain had the same temporal dynamics as the reduction in the head motion error. Notably, analysis of trial-by-trial changes in neuronal responses revealed the rapid but gradual (i.e., not a switch-like transition) updating of an internal model consistent with the resultant behavioral learning. Furthermore, as predicted, i) neurons again immediately showed increased vestibular sensitivity with the introduction of a new challenging sensory prediction error when the load was removed in catch trials, and ii) during learning extinction neuronal response gain declined with the same time course as that of the behavior. Thus, taken together, our findings reveal for the first time the output of an elegant computation by which the cerebellum compares expected and unexpected sensory inputs to fine-tune behavior during motor learning.
Evidence for the updating of a forward model predicting the sensory consequences of voluntary motion
The computation of sensory prediction errors has emerged as an important theoretical concept in motor control (reviewed in14, 15). In this context, the cerebellum has been proposed as a likely candidate site for a forward model that predicts the expected sensory consequences of self-generated action. Changes in motor apparatus and/or environment will cause a mismatch between the cerebellum’s prediction and the actual resulting sensory stimulation. This mismatch is the sensory prediction error, which is thought to update both the forward model and motor program during motor learning to ensure that sensory-motor pathways remain calibrated. A major contribution of our study is that it provides answers to the fundamental question of whether the brain actually compares predictive and feedback sensory signals during motor learning and if so, whether there is evidence for this computation at the level of the output neurons of the cerebellum.
Behavioral and lesion studies provide clear evidence that the cerebellum plays a fundamental role in motor learning. Notably, patients with cerebellar pathologies display impaired performance during sensory-motor adaptation tasks, characterized by persistent error and attenuated after-effects18, 35–37. Targeted lesions of the cerebellum in primates similarly impair adaptation of voluntary eye movements and the vestibulo-ocular reflex38, 39. Motor adaptation studies in humans further suggest that learning requires updating of forward models, and that the errors produced by external perturbations are interpreted as sensory prediction errors rather than target errors8, 9. Indeed, when high quality sensory feedback is available, adaptation of motor commands appears to be almost exclusively driven by sensory prediction errors40. The cerebellum is required for this computation, since patients show selective deficits in sensory-motor learning, consistent with a cerebellar-dependent adaptation process based on minimizing such errors17.
By assessing trial-by-trial changes in firing rate, we were able to show that the sensory sensitivities of neurons in the deep cerebellar nuclei are dynamically modulated based on the difference between predictive and feedback signals consistent with the computation of sensory prediction error during motor learning. Prior single-unit recording studies have shown that these same neurons robustly encode vestibular sensory inputs during passively applied motion24, 41, 42, but are not sensitive to the same vestibular sensory input when it is the result of self-generated motion26. Given that the sensory stimulation produced by passive motion is not expected, this led to the suggestion that, in the presence of sensory prediction errors, these neurons respond to vestibular input as if it were externally generated. However, in contrast with the present study, prior studies did not consider conditions that require motor learning. Here we show that neuronal responses are correspondingly consistent with the trial-by-trial updating of a forward model, which minimizes the mismatch between expected and actual sensory input with the same temporal dynamics observed in the fine-tuning of motor commands required by the learning process. Thus, during motor learning, the responses of neurons in the deep cerebellar nuclei, which constitute a major output of the cerebellar cortex, suggest that the dynamic computation of a sensory prediction error signal underlies the brain’s ability to both i) distinguish between expected and unexpected sensory inputs as well as ii) learn new expected consequences of self-motion when unexpected sensory input becomes expected.
Neuronal computations that drive motor learning
While it is generally agreed that the cerebellar cortex is required for initially driving motor learning and then ensuring that movements remain accurately calibrated over time (reviewed in 14, 43), its precise contribution remains controversial10, 11. Nevertheless, the recent demonstration that cerebellar Purkinje cells encode the predicted consequence of movement rather than actual movement12, 44 provides strong support for the idea that the cerebellar cortex acts as a forward model. If motor learning is driven by the error signal computed by comparing this forward model’s prediction of sensory feedback with the actual sensory feedback, then it follows that there should be evidence for such a computation. Notably, the computation of sensory prediction error theoretically requires that these two sensory-related signals be aligned in time as well as within the same neuronal location4. Accordingly, if these two representations are temporally offset within individual Purkinje cells, as recently suggested by Popa et al.13, 19, then it follows that sensory prediction error is likely computed downstream of the Purkinje cells. This then raises the question of where and how does this computation occur?
We think our experimental findings provide new insight into this question by establishing that, during motor learning, neurons at the next stage of cerebellar processing (i.e., in the deep cerebellar nuclei) robustly encode sensory reafference following the introduction of a sensory prediction error, such that they respond as if the stimuli were externally generated. Specifically, when the motor requirements change, as was the case when we applied resistive torque to the head during voluntary movements (i.e., learning) or removed it following learning (i.e., extinction), there is initially a mismatch between the brain’s prediction of the sensory consequences of the voluntary head motion and actual sensory feedback. Trial-by-trial analysis of rFN neuronal responses further revealed that the dynamic computation of sensory prediction error rapidly updated neuronal responses (expressed as a relative decrease in sensitivity) as the motor system learned to expect unexpected sensory input, suggesting successful temporal alignment between an internal estimate of the sensory consequences of self-generated head motion (i.e., forward model) and its actual sensory feedback. As a result, neurons again displayed suppression to self-generated sensory input within ~40 movements. Interestingly, neuronal responses were then characterized by a decrease in sensitivity (i.e., response gain) as the difference between expected and actual sensory input was minimized during both learning and extinction. Thus while neuronal responses provide evidence for the dynamic computation of sensory prediction error, they do not explicitly encode the difference between expected and actual sensory input. Ultimately, further studies of how deep cerebellar nuclei neurons integrate convergent input from cerebellar Purkinje cells during motor learning will be required to provide a deeper understanding of the specific mechanisms that underlie this temporally precise computation. Indeed, based on the findings of prior anatomical and physiological studies, we speculate that future experiments focused on neurons in the anterior vermis will likely provide important insight into this open question. Notably, neurons in this region of the cerebellar cortex project to the fastigial nucleus and integrate proprioceptive and labyrinthine information during passive motion (45). To date, however, the responses of neurons in this region have not been studied during voluntary head movements.
Implications for the maintenance of accurate postural control
Finally, our present results have direct implications for behavior, since neurons in the fastigial deep cerebellar nucleus send descending projections to vestibular nuclei neurons that mediate vestibulo-spinal reflexes46. Given that these reflexes are essential for maintaining posture and balance, our ability to adapt their descending commands in the face of changes to either the motor apparatus or external environment is crucial. This is true both for continuous changes in the motor system (e.g., changes in muscle fatigability, muscle fiber composition) as well as for more abrupt changes in the external world. Indeed, our trial-by-trial analysis of learning-induced modulation of response sensitivity revealed the same temporal characteristics for neurons in the deep cerebellar and vestibular nuclei. These changes in neuronal activity occurred in a continuous but rapid manner with approximately the same time constant as the adaptive change in behavior. Moreover, consistent with previous studies, the extinction of learning occurs faster than the initial learning itself (reviewed in32). Theoretical studies suggest that motor learning is not one process, but several processes that act at different time scales47–49. In the analysis of human motor learning, these multiple time scales have been used to explain the phenomena of savings (i.e., faster learning upon a second exposure to the learning protocol) and anterograde interference (i.e., slower learning upon a second exposure to the learning protocol)49. Interestingly, quantification of the time course of adaptation in our study in primates did not reveal multiple time scales of adaptation; a single time constant fit the data well. Furthermore, consistent with Smith et al.’s proposal49, exposure to our learning protocol did not result in savings or anterograde inference in either the neuronal or behavioral responses, even when the learning protocol was experienced again within the same recording session (i.e., on the same day). Although it is unclear why we did not observe these characteristics in our data, it is possible that savings may have been initially present in early behavioral training sessions (i.e., before we began our neural recordings and quantification of head movement). Taken together this suggests that, in monkeys, the learning required to accurately predict the sensory consequences of voluntary head movement - after movement dynamics have been altered - operates at a single time scale.
The ability to control posture and estimate unexpected self-motion depends strongly on the integration of vestibular, proprioceptive, and motor-related signals and is significantly disrupted in cerebellar patients50. Notably, the rFN receives descending projections from the anterior vermis of the cerebellum20, and it in turn projects to vestibular neurons, reticular formation, and spinal cord20–23. Vestibular sensory inputs produced by volitional movement (i.e., sensory reafference) are markedly suppressed in descending pathways that mediate postural reflexes at the level of both the rFN and vestibular nuclei, suggesting that postural reflex pathways are themselves suppressed during voluntary motion26, 34. Hypothetically, this suppression is functionally advantageous, since an intact reflex would be counterproductive to the intended movement. Specifically, following the introduction of a large sensory prediction error (for example, if we slip on ice) vestibular reflex pathways are robustly activated to maintain balance. However, when vestibular sensory feedback is persistently altered in relation to a voluntary motor command (as during the motor learning in the present study) these same corrective reflexes would be counterproductive. Accordingly, in such conditions it would be behaviorally advantageous to reduce the efficacy of vestibular sensory-motor reflexes. Indeed, the results of the present study show that when unexpected sensory input becomes expected, the mechanism underlying the suppression of sensory reafference is rapidly and accurately updated to re-enable this distinction between self-generated and applied stimulation. We posit that the rapid updating observed at the level of single cerebellar output neurons reveals the computation of the sensory prediction error signal required for ensuring stable perception and accurate motor control during our everyday activities.
METHODS:
Two adult male rhesus monkeys (Macaca mulatta) were prepared for chronic extracellular recording using aseptic surgical techniques. Monkeys were housed in pairs and kept on a 12 hour dark/light cycle. All experimental protocols were approved by the McGill University Animal Care Committee and were in compliance with the guidelines of the Canadian Council on Animal Care.
Surgical procedures
Surgical techniques were similar to those previously described by Brooks and Cullen24. Briefly, under aseptic conditions and surgical levels of isoflurane an 18 mm diameter eye coil (3 loops of Teflon-coated stainless steel wire) was attached to the sclera beneath the conjunctiva of one eye. In addition, a dental acrylic implant was fastened to the animal’s skull using stainless steel screws. The implant held in place a stainless steel post used to restrain the animal’s head, and a stainless steel recording chamber positioned to access the rostral fastigial nuclei (rFN) and vestibular nuclei (VN) (posterior and lateral angles of 28° and 30°, respectively). Animals were given 2 weeks to recover from the surgery before any experiments were performed.
Data acquisition
During the experiments, conducted during the light period of the light/dark cycle, monkeys sat comfortably in a primate chair located on a vestibular turntable, and the animal’s head was centered within a stationary 1-m3 magnetic field coil system (CNC Engineering). Extracellular single-unit activity was recorded using enamel-insulated tungsten microelectrodes (7–10 MΩ impedance, Frederick-Haer Co., Bowdoinham, ME). The location of the rFN and VN was determined relative to the abducens nucleus, which was identified based on its stereotypical neuronal responses during eye movements. Turntable velocity was measured using an angular velocity sensor (Watson Industries, Eau Claire, WI). Gaze and head positions were measured using the magnetic search coil technique as previously described24, 25. During experiments, unit activity, horizontal gaze, head, and target positions, and table velocity were recorded on DAT tape for later playback. Action potentials were discriminated during playback using a windowing circuit (BAK) that was manually set to generate a pulse coincident with the rising phase of each action potential. Gaze, head, and target position and table velocity signals were low-pass filtered at 250 Hz (8 pole anti-aliasing Bessel filter) and sampled at 1000 Hz.
Behavioral paradigms:
Head-restrained paradigms:
Monkeys were trained to follow a target light (HeNe laser) that was projected, via a system of two galvanometer controlled mirrors, onto a cylindrical screen located 60 cm away from the monkey’s head. Target, turntable motion, torque motor, and data displays were controlled on-line by a UNIX-based real-time data-acquisition system (REX, Laboratory of Sensorimotor Research, The National Institutes of Health). Consistent with previous studies of rFN and VN, all neurons were sensitive to passive vestibular stimulation but not to eye movements41. Accordingly, to verify that neurons were unresponsive to eye movements, neuronal activity was recorded during saccades and periods of fixation when head-restrained monkeys followed a target that stepped between horizontal positions over a range of ±30°. Neuronal responses were also recorded during smooth pursuit eye movements made to track sinusoidal target motion (0.5 Hz, 40°/s peak velocity).
Neuronal sensitivities to vestibular stimulation were verified by passively rotating monkeys about an earth vertical axis in the dark (whole-body rotation) and also during a paradigm in which they suppressed the vestibulo-ocular reflex (VOR) by fixating a laser target that moved with the vestibular turntable (termed VOR cancellation (VORc)). The responses of neurons in both the rFN and VN were comparable during VOR and VORc (p>0.05), consistent with these neurons’ insensitivity to eye motion. We characterized responses to whole-body rotation using two types of stimulation: i) a 1Hz sine wave with peak velocity of ±40 °/s and ii) a typical head velocity trajectory generated during active gaze shifts in the head-unrestrained condition, termed ‘active-like motion’ profile. The latter stimulus was used to facilitate comparison of neuronal responses during passive and active (see below) head rotations.
Head-unrestrained paradigms:
After a neuron was fully characterized in the head-restrained condition, the monkey’s head was slowly and carefully released to maintain isolation. Once released, the monkey was able to only rotate its head in the yaw axis (i.e., earth-vertical rotation) with no pitch or roll rotation or translations. The response of the same neuron was then recorded during the voluntary head movements made while orienting to a laser target projected on a screen in front of the monkey for a juice reward. The target alternated from between a position 25 degrees to the right and one 25 degrees to the left of midline. Monkeys were required to remain on target at the end of the head movement for 500 ms to receive a reward.
Next, using a torque motor (Kollmorgen), we applied a resistive torque to the head while the monkeys made active head movements (see Fig. 1b). This torque was proportional to head velocity and was calibrated such that initially head velocity was reduced by approximately half that observed during control active head movements. One trial consisted of a leftward and then rightward head rotation. For simplicity, we show responses in the neuron’s preferred direction. The resistive torque was then kept constant while the monkey learned to adjust his head movements to acquire the target (Fig. 1c; learning phase). During the last third of the learning phase, we introduced random trials, during which no resistive torque was applied (Fig. 1c; termed catch trials). Finally we stopped applying the resistive torque for an extended period of time while the monkey continued to orient to the targets and once again needed to change his head movements in order to acquire the target (Fig. 1c; extinction phase).
Analysis of neuronal discharges:
Data were imported into the Matlab (The MathWorks, Natick MA) programming environment for analysis. Recorded gaze and head position signals were digitally filtered with zero-phase at 60 Hz using a 51st order finite-impulse-response (FIR) filter with a Hamming window. Eye position was calculated from the difference between gaze and head position signals. Gaze, eye, and head position signals were digitally differentiated to produce velocity signals. Neural firing rate was represented using a spike density function in which a Gaussian was convolved with the spike train SD of 5ms as previously described24, 25.
To determine whether a unit could be classified as a VO neuron, we first verified that it was unresponsive to eye position and/or velocity by analyzing periods of steady fixation and saccade-free smooth pursuit using a multiple regression analysis24, 25. In addition, spike trains were assessed to confirm that neurons neither paused nor burst during saccades. Prior characterizations of these same neurons have shown that their responses to head motion are well described by a second order head-velocity based equation24, 25. Accordingly, a least-squared regression analysis was then used to describe each unit’s response to head motion stimulation during passive and active head rotations:
| (1) |
where is the estimated firing rate, Sv and Sa are coefficients representing sensitivities to head velocity and acceleration, b is a bias term, and and are head velocity and head acceleration, respectively. Note that this equation could be used during passive or active motion as well as during the learning and extinction protocols.
To quantify the ability of the linear regression analysis to model neuronal discharges, we determined variance-accounted-for (VAF) provided by each regression equation. The VAF was computed as:
| (2) |
where represents the modeled firing rate (i.e., regression equation estimate) and fr represents the actual firing rate.
The regression analyses were first applied to data collected in the control passive and active motion conditions to obtain estimates of neuronal sensitivity in each condition before learning. The regression analyses were then applied to data collected during the learning phase to estimate average sensitivities for the first 5, middle 5 (26 to 30) and last 5 (46 to 50) head movements to calculate estimates of the average peak head velocity and neuronal sensitivity for the early, middle and late phases of learning (the average peak head velocity was normalized relative to the passive peak head velocity). Finally, to quantify the detailed time course of the changes in behavior and neuronal sensitivity, we applied the regression analysis to individual head movements as well as obtained the peak velocity for each head movement.
To facilitate comparison across neurons, we normalized both peak head velocity and neuronal sensitivity. Peak head velocity during the learning paradigm was normalized using the following equation:
| (3) |
where is the normalized error in peak velocity, Ha is the head velocity during the control active phase, Hn is the head velocity on a given trial and H1 is the head velocity on the first trial. This equation results in values near 0 when peak head velocity is comparable to that produced for control active movements before learning and of 1 when the resistive torque is initially applied and head velocity is most drastically attenuated. Similarly, peak head velocity (Hpk) during learning extinction was normalized using the following equation:
| (4) |
and neuronal sensitivities during learning and extinction were normalized using following equation:
| (5) |
Where N is the normalized sensitivity, x is the sensitivity on a given trial and P is the sensitivity during passive head motion. Equation (5) results in values near 1 when the sensitivity is the same as during passive head movements. We then fit this trial-by-trial data with an exponential curve and calculated a time constant for changes in both peak head velocity and neuronal sensitivity. Before statistical analysis, normality of distribution was evaluated using Kolmogorov-Smirnov test. Statistical significance (p<0.05) was determined using non-parametric analysis with either two-tailed Wilcoxon signed-rank or rank-sum test. Data are expressed as mean ± SEM. Note that only data for which the firing rate was greater than 20 sp/s were included in regression analyses.
Supplementary Material
Supplementary Figure 1: A typical bimodal neuron is unresponsive during control active head-on-body motion, and remains so during learning and catch trials. A. Top row shows the head velocity during control trials, learning phase and catch trials overlaying a minimum of 5 trials. Bottom row shows the firing rates corresponding to the head movements above. Grey lines show individual trials and black lines show the average responses. B. The magnitude of head velocity error during control, learning, and catch trials. During the learning phase, the monkey initially made slower head movements as quantified by an increase in head velocity error. As learning further progressed, head velocity increased nearing control values as indicated by the striking decrease in head velocity error magnitude (light blue bars). C. Normalized sensitivity to corresponding head movements shown above. During the learning phase, the neuron remained insensitive as predicted by its response to active head-on-body motion before learning (light bluebars). Similarly, the minimal response for catch trials (red), was comparable to that measured for active head on body movements in the control condition and during learning (p>0.05).
Supplementary Figure 2: Average head velocity and sensitivity for our population of bimodal neurons during the learning phase. A. Normalized head velocity for control trials before learning, learning phase and catch trials. B. Normalized neuronal sensitivity for control trials, the learning phase and catch trials. Data show average and error bars are ±SEM. C. Scatter plot of peak head velocity errors over time for each trial during the learning phase. D. Scatter plot of normalized neuronal sensitivity over time for each trial during the learning phase. Black lines show exponential fits to the data.
Supplementary Figure 3: Trial-by trial analysis of single rFN neuron responses. A,B. Exponential fits to the head movement error (A) and neuronal sensitivity data (B) for each cell collected during learning (Grey lines). C,D. exponential fits to the head movement error and neuronal sensitivity data collected for each cell collected during learning extinction. Finally, for each panel, the data for the individual example cell is superimposed (blue circles).
Supplementary Figure 4: A typical bimodal neuron remains unresponsive during the extinction of learning. A. Top row shows the head velocity during the extinction phase overlaying a minimum of 5 trials. Bottom row shows the firing rates corresponding to the head movements above. Grey lines show individual trials and black lines show the average. B. Magnitude of head velocity error during the extinction phase. C. Normalized neuronal sensitivity to head motion during the extinction phase. Data show average and error bars are ±SEM. Data from the control (before learning) and catch trials are reproduced here for comparison.
Supplementary Figure 5: Average head velocity and sensitivity for our population of bimodal neurons during the extinction phase. A. Normalized head velocity for control trials before learning, catch trials and extinction phase. B. Normalized neuronal sensitivity for control trials before learning, catch trials and extinction phase. Data show average and error bars are ±SEM. C. Scatter plot of peak head velocity error over time for each trial during the extinction phase. D. Scatter plot of normalized sensitivity over time for each trial during the extinction phase. Black lines show exponential fits to the data.
Supplementary Figure 6: Trial-by trial analysis of single VN neuron responses. A,B. Exponential fits to the head movement error (A) and neuronal sensitivity data (B) for each cell during learning (Grey lines). C,D. exponential fits to the head movement error and neuronal sensitivity data for each cell collected during learning extinction. Finally, for each panel, the data for the individual example cell is superimposed (blue circles).
Acknowledgements:
We thank Maurice Chacron, Mohsen Jamali, Diana Mitchelle, Alexis Dale, and Isabelle Mackrous for helpful discussions and critically reading this manuscript. This study was supported by grants from the Canadian Institute of Health Research (CIHR), US National Institutes of Health (R01 DC002390) and from the Fonds québécois de la recherche sur la nature et les technologies (FQRNT) to J.X.B.
References
- 1.Bhushan N & Shadmehr R Computational nature of human adaptive control during learning of reaching movements in force fields. Biological cybernetics 81, 39–60 (1999). [DOI] [PubMed] [Google Scholar]
- 2.Kawato M Internal models for motor control and trajectory planning. Current opinion in neurobiology 9, 718–727 (1999). [DOI] [PubMed] [Google Scholar]
- 3.Shadmehr R, Smith MA & Krakauer JW Error correction, sensory prediction, and adaptation in motor control. Annual review of neuroscience 33, 89–108 (2010). [DOI] [PubMed] [Google Scholar]
- 4.Wolpert DM & Ghahramani Z Computational principles of movement neuroscience. Nature neuroscience 3 Suppl, 1212–1217 (2000). [DOI] [PubMed] [Google Scholar]
- 5.Wolpert DM & Miall RC Forward Models for Physiological Motor Control. Neural networks : the official journal of the International Neural Network Society 9, 1265–1279 (1996). [DOI] [PubMed] [Google Scholar]
- 6.Berniker M & Kording K Estimating the sources of motor errors for adaptation and generalization. Nature neuroscience 11, 1454–1461 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Todorov E & Jordan MI Optimal feedback control as a theory of motor coordination. Nature neuroscience 5, 1226–1235 (2002). [DOI] [PubMed] [Google Scholar]
- 8.Mazzoni P & Krakauer JW An implicit plan overrides an explicit strategy during visuomotor adaptation. The Journal of neuroscience : the official journal of the Society for Neuroscience 26, 3642–3645 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wong AL & Shelhamer M Sensorimotor adaptation error signals are derived from realistic predictions of movement outcomes. Journal of neurophysiology 105, 1130–1140 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ebner TJ, Hewitt AL & Popa LS What features of limb movements are encoded in the discharge of cerebellar neurons? Cerebellum 10, 683–693 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Medina JF The multiple roles of Purkinje cells in sensori-motor calibration: to predict, teach and command. Current opinion in neurobiology 21, 616–622 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pasalar S, Roitman AV, Durfee WK & Ebner TJ Force field effects on cerebellar Purkinje cell discharge with implications for internal models. Nature neuroscience 9, 1404–1411 (2006). [DOI] [PubMed] [Google Scholar]
- 13.Popa LS, Hewitt AL & Ebner TJ Predictive and feedback performance errors are signaled in the simple spike discharge of individual Purkinje cells. The Journal of neuroscience : the official journal of the Society for Neuroscience 32, 15345–15358 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Krakauer JW & Mazzoni P Human sensorimotor learning: adaptation, skill, and beyond. Current opinion in neurobiology 21, 636–644 (2011). [DOI] [PubMed] [Google Scholar]
- 15.Wolpert DM, Goodbody SJ & Husain M Maintaining internal representations: the role of the human superior parietal lobe. Nature neuroscience 1, 529–533 (1998). [DOI] [PubMed] [Google Scholar]
- 16.Bastian AJ Learning to predict the future: the cerebellum adapts feedforward movement control. Current opinion in neurobiology 16, 645–649 (2006). [DOI] [PubMed] [Google Scholar]
- 17.Taylor JA, Klemfuss NM & Ivry RB An explicit strategy prevails when the cerebellum fails to compute movement errors. Cerebellum 9, 580–586 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tseng YW, Diedrichsen J, Krakauer JW, Shadmehr R & Bastian AJ Sensory prediction errors drive cerebellum-dependent adaptation of reaching. Journal of neurophysiology 98, 54–62 (2007). [DOI] [PubMed] [Google Scholar]
- 19.Popa LS, Hewitt AL & Ebner TJ Purkinje cell simple spike discharge encodes error signals consistent with a forward internal model. Cerebellum 12, 331–333 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Batton RR 3rd, Jayaraman A, Ruggiero D & Carpenter MB Fastigial efferent projections in the monkey: an autoradiographic study. The Journal of comparative neurology 174, 281–305 (1977). [DOI] [PubMed] [Google Scholar]
- 21.Carleton SC & Carpenter MB Afferent and efferent connections of the medial, inferior and lateral vestibular nuclei in the cat and monkey. Brain research 278, 29–51 (1983). [DOI] [PubMed] [Google Scholar]
- 22.Homma Y, Nonaka S, Matsuyama K & Mori S Fastigiofugal projection to the brainstem nuclei in the cat: an anterograde PHA-L tracing study. Neuroscience research 23, 89–102 (1995). [PubMed] [Google Scholar]
- 23.Shimazu H & Smith CM Cerebellar and labyrinthine influences on single vestibular neurons identified by natural stimuli. Journal of neurophysiology 34, 493–508 (1971). [DOI] [PubMed] [Google Scholar]
- 24.Brooks JX & Cullen KE Multimodal integration in rostral fastigial nucleus provides an estimate of body movement. The Journal of neuroscience : the official journal of the Society for Neuroscience 29, 10499–10511 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Roy JE & Cullen KE Selective processing of vestibular reafference during self-generated head motion. The Journal of neuroscience : the official journal of the Society for Neuroscience 21, 2131–2142 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Brooks JX & Cullen KE The primate cerebellum selectively encodes unexpected self-motion. Current biology : CB 23, 947–955 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kluzik J, Diedrichsen J, Shadmehr R & Bastian AJ Reach adaptation: what determines whether we learn an internal model of the tool or adapt the model of our arm? Journal of neurophysiology 100, 1455–1464 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lackner JR & DiZio P Adaptation to Coriolis force perturbation of movement trajectory; role of proprioceptive and cutaneous somatosensory feedback. Advances in experimental medicine and biology 508, 69–78 (2002). [DOI] [PubMed] [Google Scholar]
- 29.Scheidt RA, Conditt MA, Secco EL & Mussa-Ivaldi FA Interaction of visual and proprioceptive feedback during adaptation of human reaching movements. Journal of neurophysiology 93, 3200–3213 (2005). [DOI] [PubMed] [Google Scholar]
- 30.Zago M, et al. Fast adaptation of the internal model of gravity for manual interceptions: evidence for event-dependent learning. Journal of neurophysiology 93, 1055–1068 (2005). [DOI] [PubMed] [Google Scholar]
- 31.Lackner JR & DiZio PA Adaptation to rotating artificial gravity environments. Journal of vestibular research : equilibrium & orientation 13, 321–330 (2003). [PubMed] [Google Scholar]
- 32.Shadmehr R & Mussa-Ivaldi FA Adaptive representation of dynamics during learning of a motor task. The Journal of neuroscience : the official journal of the Society for Neuroscience 14, 3208–3224 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shadmehr R Control of movements and temporal discounting of reward. Current opinion in neurobiology 20, 726–730 (2010). [DOI] [PubMed] [Google Scholar]
- 34.Roy JE & Cullen KE Dissociating self-generated from passively applied head motion: neural mechanisms in the vestibular nuclei. The Journal of neuroscience : the official journal of the Society for Neuroscience 24, 2102–2111 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rabe K, et al. Adaptation to visuomotor rotation and force field perturbation is correlated to different brain areas in patients with cerebellar degeneration. Journal of neurophysiology 101, 1961–1971 (2009). [DOI] [PubMed] [Google Scholar]
- 36.Smith MA & Shadmehr R Intact ability to learn internal models of arm dynamics in Huntington’s disease but not cerebellar degeneration. Journal of neurophysiology 93, 2809–2821 (2005). [DOI] [PubMed] [Google Scholar]
- 37.Werner S, Bock O & Timmann D The effect of cerebellar cortical degeneration on adaptive plasticity and movement control. Experimental brain research. Experimentelle Hirnforschung. Experimentation cerebrale 193, 189–196 (2009). [DOI] [PubMed] [Google Scholar]
- 38.Barash S, et al. Saccadic dysmetria and adaptation after lesions of the cerebellar cortex. The Journal of neuroscience : the official journal of the Society for Neuroscience 19, 10931–10939 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rambold H, Churchland A, Selig Y, Jasmin L & Lisberger SG Partial ablations of the flocculus and ventral paraflocculus in monkeys cause linked deficits in smooth pursuit eye movements and adaptive modification of the VOR. Journal of neurophysiology 87, 912–924 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Izawa J & Shadmehr R Learning from sensory and reward prediction errors during motor adaptation. PLoS computational biology 7, e1002012 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gardner EP & Fuchs AF Single-unit responses to natural vestibular stimuli and eye movements in deep cerebellar nuclei of the alert rhesus monkey. Journal of neurophysiology 38, 627–649 (1975). [DOI] [PubMed] [Google Scholar]
- 42.Shaikh AG, Ghasia FF, Dickman JD & Angelaki DE Properties of cerebellar fastigial neurons during translation, rotation, and eye movements. Journal of neurophysiology 93, 853–863 (2005). [DOI] [PubMed] [Google Scholar]
- 43.Lisberger SG Internal models of eye movement in the floccular complex of the monkey cerebellum. Neuroscience 162, 763–776 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hewitt AL, Popa LS, Pasalar S, Hendrix CM & Ebner TJ Representation of limb kinematics in Purkinje cell simple spike discharge is conserved across multiple tasks. Journal of neurophysiology 106, 2232–2247 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Barresi M, Bruschini L, Li Volsi G & Manzoni D Effects of leg-to-body position on the responses of rat cerebellar and vestibular nuclear neurons to labyrinthine stimulation. Cerebellum 11, 212–222 (2012). [DOI] [PubMed] [Google Scholar]
- 46.Wilson VJ, Yamagata Y, Yates BJ, Schor RH & Nonaka S Response of vestibular neurons to head rotations in vertical planes. III. Response of vestibulocollic neurons to vestibular and neck stimulation. Journal of neurophysiology 64, 1695–1703 (1990). [DOI] [PubMed] [Google Scholar]
- 47.Criscimagna-Hemminger SE, Donchin O, Gazzaniga MS & Shadmehr R Learned dynamics of reaching movements generalize from dominant to nondominant arm. Journal of neurophysiology 89, 168–176 (2003). [DOI] [PubMed] [Google Scholar]
- 48.Sing GC & Smith MA Reduction in learning rates associated with anterograde interference results from interactions between different timescales in motor adaptation. PLoS computational biology 6 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Smith MA, Ghazizadeh A & Shadmehr R Interacting adaptive processes with different timescales underlie short-term motor learning. Plos Biol 4, e179 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kammermeier S, Kleine J & Buttner U Vestibular-neck interaction in cerebellar patients. Annals of the New York Academy of Sciences 1164, 394–399 (2009). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figure 1: A typical bimodal neuron is unresponsive during control active head-on-body motion, and remains so during learning and catch trials. A. Top row shows the head velocity during control trials, learning phase and catch trials overlaying a minimum of 5 trials. Bottom row shows the firing rates corresponding to the head movements above. Grey lines show individual trials and black lines show the average responses. B. The magnitude of head velocity error during control, learning, and catch trials. During the learning phase, the monkey initially made slower head movements as quantified by an increase in head velocity error. As learning further progressed, head velocity increased nearing control values as indicated by the striking decrease in head velocity error magnitude (light blue bars). C. Normalized sensitivity to corresponding head movements shown above. During the learning phase, the neuron remained insensitive as predicted by its response to active head-on-body motion before learning (light bluebars). Similarly, the minimal response for catch trials (red), was comparable to that measured for active head on body movements in the control condition and during learning (p>0.05).
Supplementary Figure 2: Average head velocity and sensitivity for our population of bimodal neurons during the learning phase. A. Normalized head velocity for control trials before learning, learning phase and catch trials. B. Normalized neuronal sensitivity for control trials, the learning phase and catch trials. Data show average and error bars are ±SEM. C. Scatter plot of peak head velocity errors over time for each trial during the learning phase. D. Scatter plot of normalized neuronal sensitivity over time for each trial during the learning phase. Black lines show exponential fits to the data.
Supplementary Figure 3: Trial-by trial analysis of single rFN neuron responses. A,B. Exponential fits to the head movement error (A) and neuronal sensitivity data (B) for each cell collected during learning (Grey lines). C,D. exponential fits to the head movement error and neuronal sensitivity data collected for each cell collected during learning extinction. Finally, for each panel, the data for the individual example cell is superimposed (blue circles).
Supplementary Figure 4: A typical bimodal neuron remains unresponsive during the extinction of learning. A. Top row shows the head velocity during the extinction phase overlaying a minimum of 5 trials. Bottom row shows the firing rates corresponding to the head movements above. Grey lines show individual trials and black lines show the average. B. Magnitude of head velocity error during the extinction phase. C. Normalized neuronal sensitivity to head motion during the extinction phase. Data show average and error bars are ±SEM. Data from the control (before learning) and catch trials are reproduced here for comparison.
Supplementary Figure 5: Average head velocity and sensitivity for our population of bimodal neurons during the extinction phase. A. Normalized head velocity for control trials before learning, catch trials and extinction phase. B. Normalized neuronal sensitivity for control trials before learning, catch trials and extinction phase. Data show average and error bars are ±SEM. C. Scatter plot of peak head velocity error over time for each trial during the extinction phase. D. Scatter plot of normalized sensitivity over time for each trial during the extinction phase. Black lines show exponential fits to the data.
Supplementary Figure 6: Trial-by trial analysis of single VN neuron responses. A,B. Exponential fits to the head movement error (A) and neuronal sensitivity data (B) for each cell during learning (Grey lines). C,D. exponential fits to the head movement error and neuronal sensitivity data for each cell collected during learning extinction. Finally, for each panel, the data for the individual example cell is superimposed (blue circles).