Inferring Parsimonious Migration Histories for Metastatic Cancers

Abstract

Metastasis is the migration of cancerous cells from a primary tumor to other anatomical sites. While metastasis was long thought to result from monoclonal seeding, or single cellular migrations, recent phylogenetic analyses of metastatic cancers have reported complex patterns of cellular migrations between sites, including polyclonal migrations and reseeding. However, accurate determination of migration patterns from somatic mutation data is complicated by intra-tumor heterogeneity and discordance between clonal lineage and cellular migration. We introduce MACHINA, a multi-objective optimization algorithm that jointly infers clonal lineages and parsimonious migration histories of metastatic cancers from DNA sequencing data. MACHINA analysis of data from multiple cancers reveals that migration patterns are often not uniquely determined from sequencing data alone, and that complicated migration patterns among primary tumors and metastases may be less prevalent than previously reported. MACHINA’s rigorous analysis of migration histories will aid in studies of the drivers of metastasis.

Cancer is an evolutionary process where somatic mutations accumulate in a population of cells, yielding a heterogeneous primary tumor composed of multiple cellular subpopulations with different complements of mutations. During cancer progression, cancerous cells may migrate to other anatomical sites, seeding new metastases at these sites. Since metastasis causes up to 90% of deaths from solid tumors¹, understanding this process is of critical importance in improving the diagnosis and treatment of cancer^2–5.

Until recently, the dominant model of metastasis was the monoclonal theory, which posits that each metastasis is founded by a single founder cell⁶. Recent analyses of high-throughput DNA sequencing data have suggested more complex migration patterns between primary tumors and metastases^6–8. In particular, several studies^4,9–13 have reported polyclonal seeding, where cancer cells from one or more anatomical sites seed a metastasis, and reseeding where cancer cells migrate from a metastasis back to the primary tumor or back to other metastases. Such complex migration patterns can result in highly heterogeneous metastases with aggressive phenotypes^2,14. Polyclonal seeding may be explained by either the simultaneous migration, or comigration, of multiple cells from distinct clones, or by multiple waves of migrating cells, each wave composed of cells from the same anatomical site⁸. Intriguingly, evidence from mouse models suggests that cancer cells migrate together in clusters, and that these cell clusters may be more efficient at forming metastases than single cells^14–20.

Many recent analyses infer a migration history for an individual patient from phylogenetic trees constructed from the somatic mutations measured in multiple anatomical sites. In most cases, this inference relies on a combination of two assumptions that do not generally hold in cancer sequencing data. The first assumption, sample homogeneity, assumes that each sequenced sample is a homogeneous population of cells with identical somatic mutations. Many published analyses of bulk sequencing data from matched primary tumors and metastases^9,13,21–38 implicitly rely on this assumption by employing standard phylogenetic techniques such as neighbor-joining, maximum parsimony or maximum likelihood to the mutations measured at each sequenced region (Fig. 1a). However, it is well established that tumors exhibit extensive intra-tumor heterogeneity^6,39,40 and thus it is unlikely that a bulk tumor sample is homogeneous. Multi-region sequencing²¹ reduces, but does not eliminate, this heterogeneity, as each region remains a mixture of cells. The assumption of sample homogeneity can result in the construction of phylogenetic trees that have surprising implications for tumor evolution such as suspiciously high rates of homoplasy, or convergent evolution⁴¹ (Supplementary Fig. 1). To avoid the assumption of sample homogeneity, one can identify subpopulations of cells with the same somatic mutations, or clones, by clustering mutations according to their variant allele frequencies^42,43. One then uses specialized phylogenetic algorithms to construct clone trees from mixed samples^39,44–50 (Fig. 1b). However, these specialized techniques have been used only sporadically in the analysis of metastasis⁶.

Figure 1. Phylogenetic analysis of metastatic tumors.

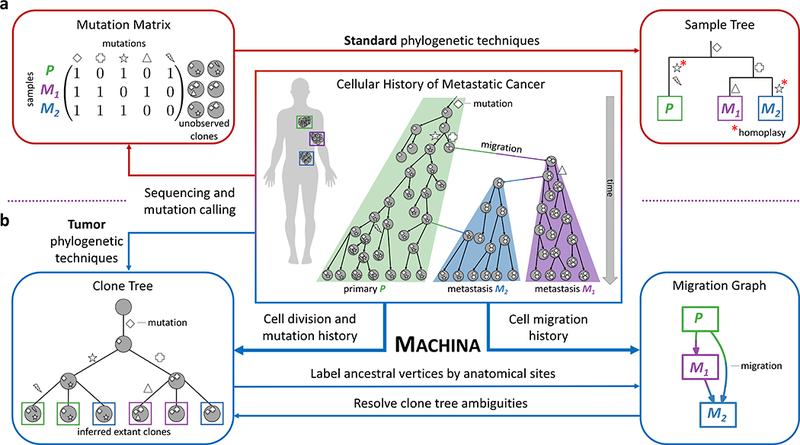
(Center) Accurate analysis of the history of metastases requires the consideration of two distinct processes: (1) Cell division and acquisition of mutations; (2) Cell migration between anatomical sites. (a) Standard phylogenetic tree reconstruction algorithms applied to mutations measured in distinct anatomical sites (or regions within a site) result in a sample tree that does not accurately model either of these two processes. This approach relies on the assumption of sample homogeneity that is generally not true for bulk tissue samples. (b) Specialized tumor phylogenetic techniques construct a clone tree that describes the heterogeneity within each site. However, the structure of the clone tree does not directly determine the migration history; falsely assuming mutation-migration concordance may result in incorrect conclusions about the pattern of migration. MACHINA (Metastatic And Clonal History INtegrative Analysis) jointly infers parsimonious clone trees and migration histories from sequencing data of a metastatic cancer. MACHINA labels the internal vertices of a clone tree by anatomical sites resulting in a migration graph whose topology records the migration number and migration pattern (e.g. monoclonal vs. polyclonal, single-source vs. multi-source seeding). MACHINA finds all parsimonious migration histories with distinct migration patterns. At the same time, MACHINA uses constraints from the migration history to resolve ambiguities in clone trees, including polytomies and uncertainties in bulk sequencing data.

The second assumption, mutation-migration concordance, states that a tree constructed from the mutations present in clones at multiple anatomical sites determines the history of cellular migrations. In other words, the migration history follows directly from the topology and branch lengths of a phylogenetic tree constructed from mutations. The mutation-migration concordance assumption underlies many recent analyses of metastatic cancers^{9,23–25,27–29,34–36,38}, as well as a recent method, Treeomics⁵¹, for reconstructing clone trees given sequencing data of metastatic tumors^52,53. However, there are two problems with the mutation-migration concordance assumption. First, the migration history does not uniquely follow from the structure of a phylogenetic tree because the phylogenetic tree does not encode the anatomical sites of ancestral clones, as has been noted previously^51,54. Second, while somatic mutations can be used as a marker for cellular lineage, mutations do not directly model the history of cellular migrations between anatomical sites. In particular, while cellular lineage is appropriately modeled as a tree – since a cell divides into two daughter cells – migrations do not necessarily follow a tree topology (Fig. 1, center panel). Indeed, complex migration patterns, such as polyclonal seeding or reseeding, cannot be modeled by a tree.

An essential missing ingredient for evaluating different hypotheses about the migration pattern that occurred in metastasis is an explicit model that evaluates how well each hypothesis fits the observed sequencing data. Here, we introduce a rigorous computational model that represents migration patterns using a migration graph, a directed multi-graph describing migration of cells between anatomical sites (Fig. 1b). We introduce a taxonomy of migration patterns, streamlining the ambiguous language in the literature. Importantly, we show that minimizing the number of migrations is insufficient to distinguish different migration patterns, and that additional biologically-motivated criteria are necessary to distinguish parsimonious migration histories.

Our computational model forms the basis for Metastatic And Clonal History INtegrative Analysis (MACHINA), an algorithm that does not assume sample homogeneity and mutation-migration concordance. MACHINA operates in three distinct modes. In the first mode, MACHINA infers parsimonious migration histories (PMH) for a given clone tree. In the second mode, MACHINA infers parsimonious migration histories and simultaneously resolves uncertainties in a given clone tree (PHM-TR). In the third mode, MACHINA jointly infers a parsimonious migration history and a clone tree that best fit measured mutation frequencies (PMH-TI). On simulated metastatic cancers, we show that MACHINA more accurately recovers clone trees and migration histories than existing approaches that assume sample homogeneity and/or use limited models of migration. On DNA sequencing data from metastatic ovarian¹², prostate¹¹, breast¹⁰ and skin⁴ cancer, we demonstrate that MACHINA provides a rigorous approach to evaluate alternative migration histories. We show that some previous reports of metastasis-to-metastasis migrations, polyclonal migrations, reseeding, or multi-source seeding are not well supported by the data. By improving the analysis of migration histories, MACHINA will enable further studies of the drivers and mechanisms of metastasis.

Results

A Computational Model for Migration Histories

Suppose we measure all clones that are present in m anatomical sites of a metastatic cancer. These clones are distinguished by their somatic mutations and their anatomical locations. A clone tree T describes the cell division history, or cell lineage, of the clones and the mutations that accumulated over these cell divisions (Fig. 1b). However, a clone tree does not describe the migration history, the process by which cells/clones moved between anatomical sites. This is because while we know the anatomical sites of the measured, present-day clones (leaves of T), we do not know the anatomical sites of ancestral clones (internal vertices of T). The migration history is determined by a labeling ℓ of each vertex of the clone tree by an anatomical site; a migration is an edge connecting vertices labeled with different anatomical sites (Fig. 2).

Figure 2. The migration number μ does not determine the migration pattern.

A clone tree T describes the relationships between clones from a primary tumor P and two metastases M₁ and M₂. Every labeling ℓ of the vertices of T induces a migration graph G whose topology determines the migration pattern. In clone tree T, we observe two clones present in each site (indicated by colored leaves). (a-d) Four maximum parsimony labelings of the internal vertices of T, each with the minimum possible migration number μ* = 4 but different migration patterns, which are explained in Fig. 3.

Distinguishing different labelings ℓ of a clone tree T requires a biologically-motivated scoring function. In the simplest model, we assume that each migration between anatomical sites is monoclonal, comprising cells from a single clone. The migration number μ(T, ℓ) counts the number of such monoclonal migrations. We assume that migrations are rare events in the evolutionary history of the cancer, and that migrations between all pairs of anatomical sites are equally likely. Thus, we appeal to the maximum parsimony principle and aim to find a labeling with the minimum migration number μ*(T) = min_ℓ μ(T, ℓ). Finding the minimum migration labeling is an instance of the small phylogeny problem and can be solved using the Sankoff algorithm⁵⁵, as noted by Slatkin and Maddison⁵⁶, and later by McPherson et al.¹²

Importantly, the maximum parsimony labeling is not unique and there are typically many vertex labelings of T with the same minimum migration number μ*(T ) but strikingly different structures of migration between anatomical sites (Fig. 2). We introduce the migration graph G as a mathematical representation of this structure. The vertices of G are anatomical sites, and directed edges indicate migrations between anatomical sites. From a vertex labeling ℓ of a clone tree T we obtain the migration graph G by collapsing all vertices labeled by the same anatomical site into a single vertex and removing any self-loops that connect the same vertex. Formally, the migration graph is a multi-graph, as there may exist multiple directed edges between the same pair of anatomical sites.

We classify a migration graph G according to its migration pattern, which is defined by two criteria (Fig. 3a). The first criterion is the presence of a single edge between a pair of anatomical sites, indicating a monoclonal migration, versus the presence of multiple edges between a pair of anatomical sites, indicating a polyclonal migration. We say that a migration graph is polyclonal (p) if the graph contains at least one multi-edge; otherwise the graph is monoclonal (m). The second criterion classifies the topology of migration graph G into three types: (1) single-source seeding (S) where for each anatomical site all migrations into the site originate from a single anatomical site, and thus G is a tree; (2) multi-source seeding (M) where at least one anatomical site has clones that originate from different anatomical sites but no migrations return to originating sites, and thus G is a directed acyclic graph; (3) reseeding (R), where at least one migration returns to an originating anatomical site, and thus G has a directed cycle. We denote a migration pattern by combining the two criteria, e.g. mS denotes monoclonal (m) single-source seeding (S).

Figure 3. Migration history analysis requires evaluation of tradeoffs between migration pattern, migration number and comigration number.

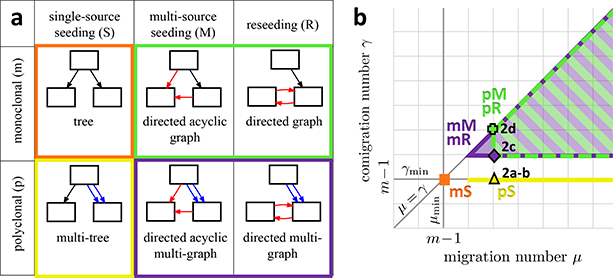
(a) The taxonomy of migration patterns is defined using two different criteria. First, the migration graph G is polyclonal (p) if it contains multi-edges; otherwise the graph is monoclonal (m). Second, the topology of the migration graph defines the migration pattern. In single-source seeding (S), each anatomical site is seeded by clones originating from at most one anatomical site, and the migration graph G is a tree. In multi-source seeding (M), at least one anatomical site is seeded by clones originating from more than one site; however, the migration graph G is acyclic. In reseeding (R), clones migrate back and forth between anatomical sites, and the migration graph has a directed cycle. (b) The 2D plot shows that each migration pattern constrains the migration number μ and the comigration number γ. Note that μ ≥ γ, since the comigration model allows for simultaneous migrations of clones. Moreover, with m anatomical sites, the minimum possible comigration number γ_min is m − 1, and is achieved only by a single-source seeding (S) pattern. Additionally, the monoclonal single-source seeding (mS) pattern also has the minimum possible migration number μ_min = m − 1. In contrast, M and R patterns have comigration number γ ≥ m, with the polyclonal pM and pR patterns having migration numbers μ ≥ m + 1. Labels of individual points on the graph indicate the scores of the corresponding clone tree labelings in Fig. 2.

Recent experimental evidence suggests that tumor cells can simultaneously travel in groups through the bloodstream or lymphatic system and settle at other anatomical sites^14–20, suggesting that polyclonal migrations may not be unusual. Thus, we introduce a second model, the comigration model, which counts simultaneous, or polyclonal, migration of multiple clones between the same anatomical sites, as a single event. We define the comigration number γ(T, ℓ) as the smallest number of monoclonal and polyclonal migrations incurred by vertex labeling ℓ of a clone tree T. While the migration number μ(T, ℓ) equals the number of edges in the migration graph G, the comigration number γ(T, ℓ) equals the number of multi-edges in the case G is acyclic. (See Supplementary Note for the precise definition of γ(T, ℓ).

Each migration pattern constrains the migration number μ and comigration number γ in a few ways (Fig. 3b). First, since each metastasis is seeded by at least one migrating clone, any vertex labeling of a clone tree T with m anatomical sites must have a migration number of least μ_{min =} m − 1 and a comigration number of at least γ_min = m − 1. Second, a vertex labeling ℓ of T corresponds to an S pattern if and only if γ(T, ℓ) = γ_min = m − 1. In general, vertex labelings with an S pattern always exist. If such a labeling also has the minimum possible migration number μ_min, then the labeling corresponds to an mS pattern; otherwise the labeling is a pS pattern. Finally, vertex labelings ℓ correspond to M and R patterns if and only if the comigration number γ(T, ℓ) is greater than γ_min.

The interplay between the migration pattern, the migration number, and the comigration number imply that the analysis of migration histories is a constrained multi-objective optimization problem. However, parsimonious vertex labelings found by the Sankoff algorithm⁵⁵ optimize only a single objective, the migration number, and do not consider tradeoffs between the migration pattern, the migration number, and the comigration number. We develop an algorithm, Metastatic And Clonal History INtegrative Analysis (MACHINA) that solves three constrained multi-objective optimization problems: the Parsimonious Migration History (PMH) problem, the Parsimonious Migration History with Tree Resolution (PMH-TR) problem, and the Parsimonious Migration History with Tree Inference (PHM-TI) problem (Fig. 4). We validate MACHINA using simulated metastatic tumors (Fig. 5). See Online Methods for further details.

Figure 4. The MACHINA algorithm for joint clone tree inference and migration history analysis.

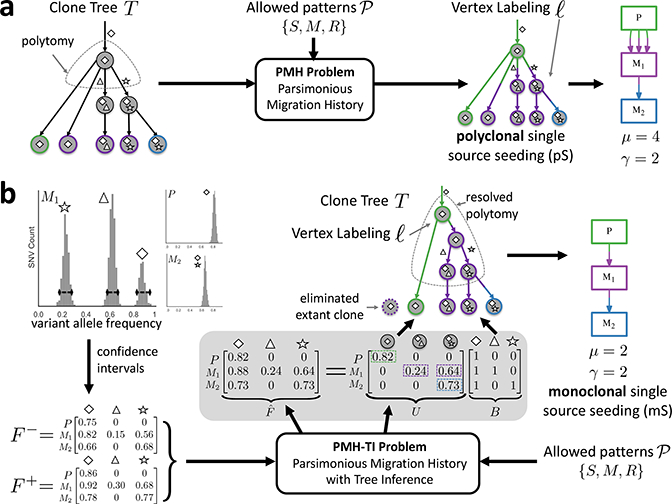
(a) One mode of MACHINA solves the PMH problem. Here, one is given a set $\mathcal{P}$ of allowed migration patterns and a clone tree T whose leaves correspond to extant clones and where each leaf is labeled by the anatomical site where the clone is present. The task is to infer a vertex labeling ℓ of T that minimizes the migration number μ and comigration number γ. (b) Another mode of MACHINA solves the PMH-TI problem. Here, one does not directly observe the clone tree, but only mutation frequencies, whose uncertainty is recorded as confidence intervals with corresponding frequency matrices (F^−,F⁺). In addition, one is given a set $\mathcal{P}$ of allowed migration patterns. The task is to infer a frequency matrix $\widehat{F}$, a clone tree T, and vertex labeling ℓ of T that minimize the migration number μ and comigration number γ.

Figure 5. MACHINA accurately infers clone trees and migration histories on simulated data.

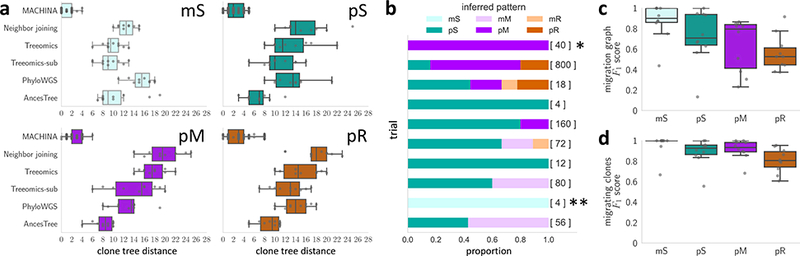
(a) Distance between simulated clone trees and clone trees inferred by MACHINA, neighbor joining⁶⁶, Treeomics⁵¹, PhyloWGS⁴⁴ and AncesTree⁴⁷. The simulated tumors have monoclonal single-source seeding (mS), polyclonal single-source seeding (pS), polyclonal multi-source seeding (pM) and polyclonal reseeding (pR). By jointly inferring parsimonious migration and clonal histories, MACHINA recovers the simulated clone trees more accurately than existing methods that disregard migration histories. (b) The proportion of inferred migration patterns from the minimum migration vertex labelings for 10 simulated pS tumors. The number of minimum migration labelings is shown in square brackets. The fractions of minimum migration labelings with the correct pS pattern ranges from 0 to 1, with a median of 0.52. (*) On this simulated tumor, by enforcing single-source seeding (S), MACHINA finds a pS migration pattern with migration number μ = 12, one more than the minimum migration number μ* = 11. (**) On this simulated tumor, the simulated vertex labeling is not the most parsimonious vertex labeling. (c) MACHINA identifies the migration graph with high precision and recall for mS and pS patterns, as summarized by the F₁ score. More complicated pM and pR patterns are more difficult to infer, with MACHINA often reporting simpler migration patterns. (d) MACHINA identifies the clones that migrate to different anatomical sites with high precision and recall across all migration patterns. Only MACHINA results are shown in (c) and (d), as the other methods do not infer a vertex labeling and migration graph.

Comigrations in Ovarian Cancer

We use MACHINA to analyze the migration history of seven metastatic ovarian cancer patients from McPherson et al.¹². These data include whole-genome and targeted sequencing on a total of 68 samples from different anatomical sites, including the left (LOv) and right ovary (ROv) and various metastases. McPherson et al.¹² constructed a clone tree T for each patient by clustering mutations that have similar cell frequencies across different anatomical sites, and then determined the evolutionary relationships between the clusters using a Dollo parsimony model. Next, they found a minimum migrating labeling, a labeling of the internal vertices of T by anatomical sites with the minimum migration number μ*(T ). Since the anatomical site of the primary tumor is unknown, McPherson et al.¹² selected the primary to be the anatomical site that incurred the fewest number of migrations. For six of the seven patients, the primary was inferred as either the left or right ovary; however, for one patient the primary was inferred to be the right uterosacral ligament.

We use MACHINA (in PMH mode) to find a parsimonious migration history for the reported clone tree T for each patient. For all patients, we find that the reported vertex labeling is among the vertex labelings output by MACHINA (Supplementary Table 5). Strikingly, we find that three of the seven patients (patients 1, 3 and 7) admit multiple vertex labelings that achieve the minimum migration number μ*(T), but differ considerably in the comigration number and the structure of migrations. For example, McPherson et al.¹² report vertex labeling ℓ_C for patient 1 with migration number μ(T, ℓ_C) = μ*(T) = 13, designating ROv as the primary tumor (Fig. 6a). This labeling has comigration number γ(T,ℓ_C) = 10 (Fig. 6b-c). MACHINA finds two additional vertex labelings ℓ_D and ℓ_E with the same minimum migration number μ*(T) = 13 but smaller comigration number γ(T,ℓ_D) = γ(T,ℓ_E) = 7 (Fig. 6d-e).

Figure 6. Joint analysis of migrations and comigrations leads to more parsimonious migration histories in metastatic ovarian cancer.

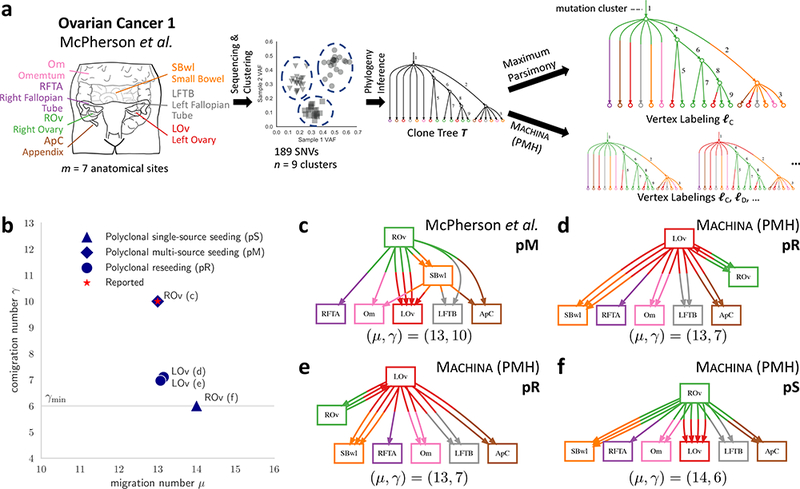
(a) McPherson et al.¹² report a clone tree T for patient 1 with n = 9 clones over m = 7 anatomical sites with 189 single nucleotide variants (SNVs). They also report a vertex labeling ℓ_C of T with the minimum migration number μ*(T) = 13. (b) MACHINA finds multiple vertex labelings (ℓ_C,ℓ_D,ℓ_E) with the minimum migration number μ*(T) = 13 but with different comigration number γ. Points are different labelings of the clone tree and are annotated by corresponding figure panel and inferred site of primary tumor. Shapes correspond to different migration patterns. (c) The migration graph obtained from the reported vertex labeling ℓ_C has comigration number γ(T,ℓ_C) = 10, and a complex pM migration pattern, with multi-source seeding of the left ovary (LOv), and metastasis-to-metastasis migrations from the small bowel (SBwl) metastasis. SBwl is both a destination for clones from the right ovary (ROv) and a source of clones for multiple anatomical sites, including the left ovary (LOv) and several other metastases. (d-e) Two additional migration graphs found by MACHINA with comigration number γ(T,ℓ_D) = γ(T,ℓ_E) = 7, and polyclonal reseeding (pR) migration patterns. LOv is the primary tumor which directly seeds all the metastases. (f) Constraining MACHINA to find a single-source seeding (S) migration pattern yields vertex labeling ℓ_F with minimum comigration number γ_min = 6, and migration number μ(T,ℓ_F) = 14. This is only one more than the minimum migration number μ*(T) = 13, indicating the tradeoff between minimizing the migration number and the comigration number.

In addition to different designations of the primary tumor, these different labelings produce migration graphs with different migration patterns (Fig. 6b-e). For example, the authors report that the left ovary (LOv) is polyphyletic, i.e. composed of clones from distinct phylogenetic branches, which they report to be indicative of polyclonal migration. Indeed, in our nomenclature, the migration graph corresponding to ℓ_C has a polyclonal multi-source seeding (pM) pattern, with multi-source seeding of LOv from multiple clones from ROv and a single clone from the small bowel (SBwl). Moreover, SBwl is both a destination of clones from the ROv primary and a source of clones for various anatomical sites, including LOv and several metastases (Fig. 6c). In contrast, vertex labelings ℓ_D and ℓ_E found by MACHINA are much simpler than reported: there are no metastasis-to-metastasis migrations, and the only reseeding is between left and right ovary (Fig. 6d-e). While the reported clone trees do not allow one to further distinguish between these two reseeding migration patterns, the simpler migration patterns suggest that the left ovary is more likely the anatomical site of the primary than the right ovary.

By constraining MACHINA to consider only single-source seeding (S) migration patterns, we find a vertex labeling ℓ_F for patient 1 with the minimum comigration number γ(T,ℓ_F) = γ_min = 6, and with μ(T,ℓ_F) = 14 migrations, one more than the minimum migration number μ*(T) = 13 (Fig. 6f). This illustrates the tradeoff between optimizing the migration number vs. the comigration number and demonstrates that different migration patterns are possible with only a small increase in the number of migrations. Without further information on the relative likelihood of different migration patterns one cannot definitively determine the true migration history of this tumor.

Similarly, applying MACHINA to ovarian patient 3 from this dataset results in a simpler migration history lacking the metastasis-to-metastasis migrations and multi-source seeding that was reported in McPherson et al. (Supplementary Note). For ovarian cancer patient 7, the authors designate the right uterosacral ligament as the primary tumor based on a clone tree T with four polytomies. MACHINA, run in PMH-TR mode, resolves these polytomies yielding a clone tree T′ with two migration histories that have the same minimum migration number μ*(T′) = 11 but with either of the two ovarian anatomical sites (LOv or ROv) as the site of the primary tumor. These alternative explanations of the data demonstrate that the inference of migration histories can help resolve ambiguities in clone trees (Supplementary Note).

Metastasis-to-Metastasis Migrations in Prostate Cancer

We apply MACHINA (in PHM-TR mode) to clone trees of ten metastatic prostate cancers reported in Ref. 11. MACHINA’s analysis supports the reported polyclonal migrations in these patients. However, the evidence for metastasis-to-metastasis migrations is not conclusive. For three of the eight patients where Gundem et al.¹¹ reported metastasis-to-metastasis migrations (A10, A31 and A32), MACHINA finds alternative migration histories with parallel seeding of all metastases from the primary tumor that are also consistent with the data (Supplementary Note).

Joint Clone Tree and Migration Inference in Breast Cancer

We apply MACHINA (in PMH-TI mode) to whole-genome sequencing data from two metastatic triple-negative breast cancers from Hoadley et al.¹⁰, who reported that metastases in both patients resulted from “multiclonal seeding instead of a single cell of origin”.

For patient A7, Hoadley et al.¹⁰ sequenced m = 6 anatomical sites, and identified 10 clusters of somatic mutations using SciClone⁴² (Fig. 7a). There is considerable uncertainty in the variant allele frequency (VAF) for each mutation (Fig. 7b), and this uncertainty propagates through the construction of the clone tree, and the clonal composition of each sequenced anatomical site. Ignoring this uncertainty, Hoadley et al.¹⁰ report a clone tree with 22 extant clones (Fig. 7c). Using manual analyses, the authors describe two different migration histories, both of which are recovered by MACHINA (Fig. 7d). The migration history with the smallest migration number (μ = 12) corresponds to a polyclonal multi-source seeding (pM) pattern (γ = 6), where the lung is seeded by clones from the rib and breast, and polyclonal migrations occur from lung to brain and from liver to kidney (Fig. 7e).

Figure 7. Joint analysis of mutations and migrations reveals a monoclonal single-source migration history for a metastatic breast cancer patient.

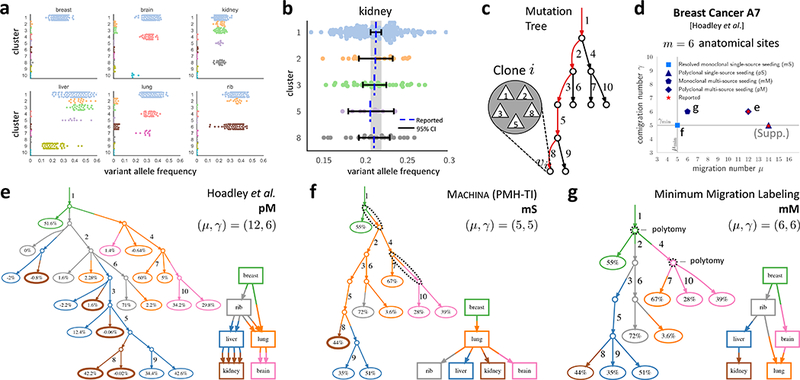
(a) Variant allele frequencies (VAFs) for ten mutation clusters across six anatomical sites reported in patient A7 from Hoadley et al.¹⁰. (b) 95% confidence intervals for the VAFs of each cluster in kidney; overlapping intervals indicate presence of a single clone in kidney. (c) The reported¹⁰ mutation tree: each edge is labeled by a mutation cluster; each vertex corresponds to a clone comprised of the mutation clusters on the unique path to the root. (d) Migration number, comigration number and migration pattern for migration histories reported in Ref. 10 (e), reported by MACHINA (f), and identified by the minimum migration labeling (g). (e) The reported¹⁰ migration history has migration number μ = 12, comigration number γ = 6, and a polyclonal multi-source seeding (pM) pattern. Each leaf label is the proportion of the extant clone in the corresponding anatomical site; small or negative proportions are due to analysis of mutation clusters and not clones in the published work. Note that the clone tree has many polytomies. (f) MACHINA infers a monoclonal single-source seeding (mS) migration history, the simplest possible migration history, implying that the sequencing data does not strongly support complicated polyclonal migration patterns in this patient. (g) Without MACHINA’s polytomy resolution, a minimum migration labeling of the unresolved clone tree selects one of possible labelings that minimize the migration number μ, leading to more complicated migration history with multi-source seeding of the lung.

We use MACHINA (in PMH-TI mode) to jointly infer the clone tree and migration history from confidence intervals on the VAFs derived from the SciClone clustering. We obtain a clone tree with only nine extant clones and a monoclonal single-source seeding (mS) migration pattern with migration number μ_min = 5 and comigration number γ_min = 5 (Fig. 7f). This finding contradicts the reports of polyclonal migrations in patient A7.

For comparison, we also ran Treeomics⁵¹ on these data. Treeomics is unable to identify the two subclones that MACHINA detected in the liver and brain (Supplementary Fig. 2g). To demonstrate the advantages of MACHINA’s ability to resolve polytomies, we ran the minimum migration labeling method on the unresolved clone tree inferred by MACHINA. This method infers a more complex monoclonal multi-source seeding (mM) history with migration number μ = 6 and comigration number γ = 6, due to two polytomies in the clone tree, which are resolved by MACHINA (Fig. 7f), but not by the minimum migration labeling (Fig. 7g).

For patient A1, MACHINA identifies more parsimonious clone trees and migration histories than previously reported¹⁰ for patient A1 (Supplementary Note). Our results on these two patients show that ambiguities in the sequencing data and inaccuracies in the clone tree may lead to the inference of unnecessarily complex migration patterns. By accounting for uncertainty in bulk sequencing data and jointly inferring parsimonious clone trees and migration histories, MACHINA finds simpler migration histories that explain the observed mutation data.

Metastatic Progression in Melanoma

We applied MACHINA (in PMH-TI mode) to eight metastatic melanoma patients from Sanborn et al.⁴ MACHINA recapitulates the findings reported by Sanborn et al.⁴ and identifies parsimonious migration histories where multiple anatomical sites are seeded directly from the primary tumor. These results provide additional support for Sanborn et al.’s rejection of the commonly-accepted serial progression model in melanoma, where migration proceeds from primary tumor to regional metastases to distant metastases (Supplementary Note).

Discussion

The increasing availability of DNA/RNA sequencing from matched primary and metastases samples provides data to improve our understanding of the drivers of metastasis. Recent phylogenetic analyses revealed that the process of metastasis may be more complicated than monoclonal migration of individual cells between anatomical sites, with polyclonal migrations of cells, multi-source seeding and reseeding between the primary tumor and metastases^4,9–13. Here we showed that deriving such conclusions about migration patterns without a precise quantitative model is a risky endeavor and can lead to statements about migration patterns that are not adequately supported by the data. In particular, the simplest migration model, monoclonal single-source seeding, should be definitively ruled out before invoking more complicated migration patterns to explain the data.

We introduced MACHINA (Metastatic And Clonal History INtegrative Analysis), a multi-objective optimization algorithm that jointly infers the cell division/mutation and migration history from DNA sequencing data while simultaneously resolving uncertainty in bulk samples. MACHINA is based on a mathematical model that distinguishes the process of cell division from the process of cell migration. This model evaluates migration histories according to three criteria: the migration pattern, the migration number, and the comigration number, the latter motivated by experimental evidence describing clusters of tumor cells simultaneously migrating and seeding metastases^14–20. We used MACHINA to analyze sequencing data from metastatic ovarian¹², prostate¹¹, breast¹⁰ and skin⁴ cancers. Importantly, in each case we find that multiple migration histories are consistent with the sequencing data, and that in many cases, these migration histories are simpler than those reported. These alternative migration histories contradict reports in some patients regarding metastasis-to-metastasis migrations, the anatomical site of a primary tumor, or the occurrence of polyclonal migrations.

MACHINA fills a critical need in studies of metastases, enabling researchers to rigorously assess the validity of different migration patterns in individual patients and evaluate the prevalence of these patterns across large cohorts of patients and tumor types. However, we note several limitations of our analyses. First, while MACHINA relaxes the assumption of sample homogeneity, the subpopulations of cells, or clones, inferred by MACHINA are not homogeneous: complete homogeneity is obtained only at the level of individual cells. At the same time, we emphasize that single-cell sequencing alone does not resolve migration histories: even with perfect cell trees, the anatomical site of ancestral cells remains unknown. The PMH and PHM-TR modes of MACHINA are directly applicable to cell trees derived from single-cell sequencing data. Second, while MACHINA allows for uncertainty in the frequencies of the mutation clusters, MACHINA does not account for uncertainty in the composition of the clusters themselves. Inferred migration patterns may be affected by such uncertainty, and we evaluated how the number, purity and sequencing depth of samples affect the inference of migration patterns (Supplementary Note). Third, copy-number aberrations are an additional source of uncertainty as they lead to a divergence between the fraction of cancer cells containing a mutation (often called the cancer cell fraction (CCF)) and the variant allele frequency of the mutation^4,11,39. While CCFs cannot be uniquely determined from sequencing data⁴⁹, one might be able to jointly infer CCFs, mutation clusters, clone trees and migration histories by extending the parsimony objectives we have introduced here. Fourth, there is evidence that primary tumors from different tissues are biased in the anatomical sites of metastasis⁵⁷. One can encode such information as different weights in the current MACHINA algorithm (Supplementary Note).

There are additional future directions. Other types of data can be used to infer migration histories, including DNA methylation, circulating tumor DNA and circulating tumor cells. In addition, the computational model of migrations introduced here could be used to study spatial heterogeneity and cellular migrations during the growth of a tumor in a single anatomical site. Another possibility is to apply MACHINA to non-cancer data, e.g. to analyze migrations of individuals and pathogens between geographically isolated populations, where previous work has constrained migrations to particular topologies^58,59. Finally, on the theoretical side, the computational complexity of the PMH, PHM-TR and PMH-TI problems is unknown.

High-throughput DNA sequencing has revolutionized studies of cancer evolution. The complexity, subtlety, and unique features of this data necessitates the use of robust and reproducible analysis approaches based on quantitative models. In particular, such models allow researchers to evaluate the evidence for simple explanations for the data before proposing complex evolutionary scenarios. Just as it is necessary to rigorously examine the evidence for neutral evolution in a tumor before one can reliably conclude that selection has occured⁶⁰, it is also necessary to rigorously evaluate the evidence for simple migration patterns in a metastatic cancer before concluding that complex migration patterns have occurred. In the coming years, the marriage of high-throughput genomics and epigenomics data with appropriate quantitative analysis will further elucidate the mysteries of metastasis.

Online Methods

We develop an algorithm, Metastatic And Clonal History INtegrative Analysis (MACHINA) to solve three versions of the migration analysis problem. Each version is a constrained multi-objective optimization problem. In the following sections, we describe these three versions, and provide validation and benchmarking results.

Parsimonious Migration History

The first version of the migration analysis problem is the Parsimonious Migration History (PMH) problem. In this problem, we are given in input a clone tree T, which has been derived from some other data, such as bulk-sequencing data or single-cell sequencing data. We are also given a set $\mathcal{P}$ of allowed migration patterns. Our goal is to find a labeling ℓ of the vertices of T by anatomical sites that first minimizes the migration number μ(T,ℓ) and then minimizes the comigration number γ(T,ℓ).

Parsimonious Migration History (PMH).

Given a clone tree T and a set $\mathcal{P}$ of allowed migration patterns, find a vertex labeling ℓ with the minimum migration number μ*(T) and subsequently the smallest comigration number $\widehat{\gamma }\left(T\right)$.

We consider three different sets $\mathcal{P}$ of allowed migration patterns: (1) $\mathcal{P}$ = {S}, requiring the migration graph G to be a single-source (S) migration pattern; (2) $\mathcal{P}$ = {S,M}, requiring the migration graph to be either an S or M pattern; (3) $\mathcal{P}$ = {S,M,R} meaning that G is unrestricted. Note that because these cases are nested, the migration number decreases monotonically from case (1) to case (2) to case (3). In contrast, the most restrictive case $\mathcal{P}$ = {S} leads to the minimum comigration number γ_min. Thus, by using different sets of allowed migration patterns, one can explore the tradeoff between the migration pattern, migration number and comigration number. For example, one could assess the evidence for reseeding (migration pattern R) by examining the difference in number of migrations reported when $\mathcal{P}$ = {S,M,R} versus when $\mathcal{P}$ = {S,M} which restricts the migration graph to either an S or M pattern.

Parsimonious Migration History with Tree Resolution

The second version of the problem, the Parsimonious Migration History with Tree Resolution (PHM-TR) problem, aims to infer a migration history while simultaneously resolving polytomies of a given clone tree T, where a polytomy is an internal vertex of T with more than two children. As cells divide into exactly two daughter cells, such polytomies reflect uncertainty in the ancestral relationships of clones (Fig. 4). The PHM-TR problem is useful for analyzing DNA sequencing data from both bulk tumors and single cells, as polytomies are common in both datasets; e.g. most current published clone trees derived from single-cell data are not fully resolved and contain polytomies^61–64.

Parsimonious Migration History with Tree Resolution (PHM-TR).

Given a clone tree T and a set $\mathcal{P}$ of allowed migration patterns, find a refinement T′ of T and vertex labeling ℓ of T′ with the minimum migration number μ*(T′), and subsequently smallest comigration number $\hat{\gamma }\left(T\mathrm{\text{'}}\right)$.

The resolution of polytomies has been previously studied in species phylogenetics, and Maddison⁶⁵ provides an exponential time algorithm for resolving polytomies. In our context, this algorithm would minimize the migration number μ, but does not consider the comigration number γ.

Parsimonious Migration History with Tree Inference

The third version of the problem, the Parsimonious Migration History with Tree Inference (PMH-TI) problem, jointly infers a clone tree and a migration history directly from bulk sequencing data. In bulk sequencing data, there is often substantial uncertainty in the clone tree due to the fact that the sequenced samples are generally not homogeneous, but instead are mixtures of populations of cells, or clones, with different complements of somatic mutations. Analyzing these mixed samples using standard phylogenetic techniques, such as neighbor-joining⁶⁶, maximum parsimony⁶⁷ or maximum likelihood⁶⁸, yields phylogenetic trees with high rates of homoplasy. Thus, many specialized deconvolution algorithms that model bulk samples as mixtures have been proposed for inferring clone trees^{39,44–49,69,70}. The computational problem that these approaches solve can be viewed as a constrained matrix factorization problem⁴⁷. The input is a mutation frequency matrix F = [f_s,i], where f_s,i is the proportion of cells in anatomical site s that have mutation i. Given F, the goal is to find a nonnegative mixture matrix U = [u_s,j] and a binary mutation matrix B = [b_j,i] such that F = UB. Here, b_j,i = 1 if and only if mutation i is present in clone j, and b_j,i = 0 otherwise. Entry u_s,j is the proportion of clone j in anatomical site s; clone j is present in an anatomical site s if and only if u_s,j > 0.

Most deconvolution methods assume the absence of homoplasy, i.e. they require mutations to only occur once in the clone tree and never to be lost. This no-homoplasy assumption (also known as the infinite sites assumptions) has two important implications for the computational problem^47,49. First, given F and B, there is only one matrix U such that F =UB. Second, under this assumption there is a 1–1 correspondence between mutation matrices B and mutation trees $\overline{T}$, which describe ancestral relationships between mutations. In contrast to a clone tree, the leaves of a mutation tree are not labeled by anatomical sites. From $\overline{T}$ and U, we obtain a clone tree T by attaching a leaf w to vertex v_j of $\overline{T}$ and setting the label ℓ(w)≔ s for each entry u_s,j > 0, i.e. clone j is present in anatomical site s. Thus, to determine the presence of clones in anatomical sites one must know both the mutation tree $\overline{T}$ (or equivalently matrix B) and U.

Deciding whether there exists a mutation tree $\overline{T}$ respecting the no-homoplasy assumption that explains F (i.e. whether there exists a mutation matrix B corresponding to $\overline{T}$ and a mixture matrix B with nonnegative entries satisfying F = UB) is NP-complete⁴⁷. Moreover, when such a tree exists, the problem is typically underdetermined; that is, there may exist many trees that explain F⁴⁹. As described previously^46,47, mutations trees $\overline{T}$ that explain the observed mutation frequencies F are constrained spanning trees of a directed acyclic graph obtained from F that satisfy the sum condition (SC), defined as

$$f_{s,i}\mathrm{ }\ge \mathrm{ }\sum _{v_j\text{child}\text{of}{v}_i}^{}{f}_{s,j}$$

for each vertex v_i and anatomical site s.

In practice, there is extensive uncertainty in the mutation frequencies in F, as these frequencies must be estimated from the proportion of DNA sequence reads that contain a mutation at a locus. One way to model this uncertainty is to define confidence intervals $[f_{s,i}^{-},f_{s,i}^{+}]$ for each mutation i in sample s. Given confidence intervals $F^{-}=\left[f_{s,i}^{-}\right],F^{+}=\left[f_{s,i}^{+}\right]$ for the frequency of each mutation i in each sample s and a mutation matrix B = [b_j,i], there may be many mixture matrices U = [u_s,j] such that $\sum _j{u}_{s,j}\cdot b_{j,i}\in [f_{s,i}^{-},f_{s,i}^{+}]$. Thus, in addition to many mutation trees $\overline{T}$ explaining the observed data, each mutation tree $\overline{T}$ may correspond to multiple mixture matrices U. As such, the presence of clones in anatomical sites is no longer fully determined given a mutation tree $\overline{T}$ (or mutation matrix B). Moreover, many different mutation trees may explain the observed (F⁻,F⁺). This leads to the following problem (Fig. 4b).

Parsimonious Migration History with Tree Inference (PHM-TI).

Given a set $\mathcal{P}$ of allowed migration patterns and mutation frequency confidence intervals ${(F}^{-}=\left[f_{s,i}^{-}\right],F^{+}=\left[f_{s,i}^{+}\right])$, find a frequency matrix $\hat{F}=\left[{\hat{f}}_{s,i}\right]$, a clone tree T, and a vertex labeling ℓ of T such that: (1) ${\hat{f}}_{s,i}\in [f_{s,i}^{-},f_{s,i}^{+}]$; (2) $\hat{F}$ satisfies the sum condition for T; and (3) vertex labeling ℓ of T has minimum migration number μ*(T) and subsequently smallest comigration number $\widehat{\gamma }\left(T\right)$.

In practice, one typically does not have enough resolution in bulk sequencing data to determine the ancestral relationships for all pairs of mutations. Thus, instead of solving the PHM-TI problem for individual mutations, we consider clusters of mutations with similar frequencies across samples. Several specialized methods have been developed specifically to cluster mutations in the context of tumor sequencing^{42,43,71–73}. It is important to note that the resulting mutation clusters do not directly correspond to clones; instead, they correspond to edge labels of an unknown mutation tree (Supplementary Fig. 3). A clone contains not only the mutations introduced on its incoming edge, but also all the mutations present in all its ancestral clones. From the output of a clustering algorithm, we obtain confidence intervals (F⁻,F⁺) for the frequencies of each cluster per anatomical site. These mutation frequency confidence intervals are input to the PHM-TI problem.

MACHINA: Algorithm for Metastatic And Clonal History INtegrative Analysis.

We solve the unrestricted PMH problem by adapting the backtrace step of the Sankoff algorithm. We solve the restricted variants of the PMH problem as well as all variants of the PHM-TR and PMH-TI problems using (mixed) integer linear programming with the Gurobi Optimizer (see URLs). See Supplementary Note for additional details.

Validation of MACHINA on Simulated Data

We assess the performance of MACHINA on simulated metastatic tumors, which we generate by extending an existing agent-based simulation of tumor growth⁷⁷ to include cell migration. In this simulation, tumor cells may migrate to an existing anatomical site or seed a new anatomical site following a user-defined migration pattern (mS, pS, pM and pR) and a number m of anatomical sites. For simplicity, we simulate only single-nucleotide mutations and exclude copy-number aberrations. Each simulation results in a clone tree T*, a vertex labeling ℓ* and migration graph G*, which together describe the clonal and migration history of the simulated tumor. We generated 40 simulated tumors with either m = 5 or m = 8 anatomical sites and varying migration patterns. For each simulated tumor, we generated DNA sequencing data from a single bulk sequencing sample from each metastasis and two bulk samples from the primary tumor. Each sample has a purity of 1 and a target DNA sequence coverage of 200X corresponding to a typical whole-exome sequencing experiment.

We first benchmark MACHINA (run in PMH-TI mode) against four other methods that construct phylogenetic trees from metastatic tumors: (1) neighbor joining⁶⁹, a standard approach for constructing phylogenetic trees that has been used frequently for analysis of recent metastatic sequencing data sets (e.g. Ref. 25,37,38); (2) Treeomics⁵¹, a recent phylogenetic reconstruction algorithm designed for analyzing metastatic samples; (3) PhyloWGS⁴⁴ and (4) AncesTree⁴⁷, two methods for tumor phylogeny reconstruction from mixed bulk samples. Importantly, each of these four methods outputs a phylogenetic tree, but they do not infer a vertex labeling or migration graph and thus differ considerably from MACHINA. Moreover, both neighbor joining and Treeomics assume sample homogeneity, as they record each mutation as present (1) or absent (0) in each sample, by thresholding of variant allele frequencies (VAFs). Specifically, Treeomics finds the most likely ‘error corrections’ required to transform the 0–1 valued mutation matrix into a perfect phylogeny matrix that describes an evolutionary tree with no homoplasy (i.e. infinite sites assumption). Additionally, Treeomics provides an optional heuristic, denoted as Treeomics-sub, that detects subclones by resolving violations of the infinite sites assumption using a variation of the ‘split row’ operation that was previously described⁷⁵. In contrast, PhyloWGS and AncesTree analyze VAFs and infer subclones within a sample. Further details of the simulations and the mutation clustering algorithm in MACHINA are in Supplementary Note.

We find that the clone trees identified by MACHINA better resemble the simulated clone trees than those inferred by neighbor joining, Treeomics, PhyloWGS and AncesTree across all migration patterns. Fig. 5a shows that the distance between the inferred clone tree T and the simulated clone tree T* on simulations with m = 8 anatomical sites is substantially smaller for MACHINA. (Supplementary Fig. 4 shows similar results with m = 5 anatomical sites.) Here, we use a modified Robinson-Foulds distance⁷⁹ to compute the distance between trees. This demonstrates the deficiency of the sample homogeneity assumption on heterogeneous data. Treeomics-sub does not assume sample homogeneity and performs better than Treeomics. However, Treeomics-sub cannot match the performance of MACHINA and AncesTree, likely because these latter two methods use variant allele frequencies to deconvolve mixed samples and thus are better able to detect subclones. PhyloWGS achieves similar performance to Treeomics-sub but performs worse than AncesTree and MACHINA. Importantly, MACHINA outperforms both PhyloWGS and AncesTree, thus showing that MACHINA’s advantage is not only a result of its analysis of subclones but also because of its simultaneous inference of clone trees and migration histories.

Next, we examined whether the goal of minimizing migrations, as done in McPherson et al.¹² using the Sankoff algorithm, was sufficient to determine the correct migration pattern. For simulated polyclonal single-source seeding (pS) migration patterns, we found that simulated clone trees typically have multiple vertex labelings with the same minimum number of migrations but varying migration patterns that are more complex than pS, such as pM and pR (Fig. 5b). The fraction of minimum migration labelings of the correct clone tree that were pS ranged from 0 to 1, with a median of 0.52 across the 10 simulated instances. Thus, choosing one of the minimum migration labelings will often not result in the correct migration pattern. Moreover, one of the trials, indicated by ‘*’ in Fig. 5b, does not admit a minimum-migration vertex labeling with a pS pattern. However, by solving the PMH problem with a single-source seeding constraint, MACHINA determines that a vertex labeling with such a pS pattern requires only one additional migration. These findings demonstrate the importance of more sophisticated scoring functions that account for the complexity of the resulting migration pattern. See Supplementary Note for corresponding results for mS, pM and pR patterns.

Finally, we assess MACHINA’s ability to infer the correct migration graph and to identify the clones that migrate and seed anatomical sites. Fig. 5c shows migration graph G inferred by MACHINA closely resembles the simulated migration graph G* for the mS and pS simulations. The more complicated pM and pR patterns are more difficult to infer correctly, with MACHINA sometimes inferring simpler migration patterns than simulated (Supplementary Fig. 5). This may be due to the resolution of the data not allowing us to detect the minor subclones involved in more complex seeding events. Finally, Fig. 5d shows that MACHINA identifies the mutations present in migrating clones with high precision and recall for all simulated migration patterns. Accurate identification of such mutations is an important prerequisite for further experimental validation of the mutations that drive metastatic progression. In summary, our simulations show that MACHINA accurately infers clone trees and migration histories, outperforming existing methods.

In Supplementary Note, we show that MACHINA continues to outperform existing clone tree inference methods when given mutation clusters from different clustering algorithms. Moreover, we show that MACHINA benefits from having more samples and higher coverage sequencing, with the number of samples having the largest impact, followed by the depth of sequencing and the sample purity. Finally, we performed subsampling experiments running MACHINA on subsets of mutations from simulated WGS data. We found that MACHINA performs well, given only a small subset (< 5%) of mutations, demonstrating that MACHINA can accurately infer migration patterns given only whole-exome sequencing (WES) data.