An analytic expression for the Ultimate Intrinsic SNR in a uniform sphere

Abstract

Purpose

The ultimate intrinsic signal-to-noise ratio (UISNR) is normally calculated using electrodynamic simulations with a complete basis of modes. Here we provide an exact solution for the UISNR at the center of a dielectric sphere, and assess how accurately this solution approximates UISNR away from the center.

Methods

We performed a mode analysis to determine which modes contribute to central UISNR – ζ(r → 0). We then derived an analytic expression to calculate ζ(r → 0) and analyzed its dependence on main magnetic field strength, sample geometry and electrical properties. We validated the proposed solution against an established method based on dyadic Green’s function simulations.

Results

Only one divergence-free mode contributes to ζ(r → 0). The UISNR given by the exact solution matched the full simulation results for various parameter settings, while calculation speed was approximately 1000 times faster. We showed that the analytic expression can approximate the UISNR with < 5% error at positions as much as 10–20% of the radius away from the center.

Conclusion

The proposed formula enables rapid and direct calculation of UISNR in the central region of a sphere. The resulting UISNR value may be used, for example, as an absolute reference to assess the performance of head coils with spherical phantoms.

INTRODUCTION

Ultimate intrinsic signal-to-noise ratio (UISNR) is the largest SNR allowed by electrodynamic theory for a given sample geometry and set of electrical properties, independent of the particulars of radiofrequency (RF) coil design (1–4). Therefore, UISNR provides an absolute benchmark for evaluating the performance of RF detector coils (5,6). The UISNR can be calculated, for example, via a current mode expansion and dyadic Green's functions (DGF) (3,7–9). Such a method also enables derivation of the ideal current patterns associated with UISNR (7), which constitute the best possible arrangement of currents on a specified surface encircling a body, and which can be used as guidelines to optimize coil design (10,11).

Uniform dielectric spheres with average brain electrical properties have been used as approximations of the human head in UISNR simulations (1,7–9). In fact, analytic solutions for the electromagnetic field can be found in the case of a simple object geometry, which results in rapid electrodynamic simulations. While numerical simulations can handle a realistic heterogeneous head model, they are time consuming, and their numerical complexity grows as the number of modeled sources increases, which generally precludes their use with a full basis to calculate the UISNR. Recently, a novel approach based on volume integral equations (VIE) has been proposed to calculate the UISNR in a realistic head model (12). Although relatively rapid, the VIE-based calculations require a graphics processing unit (GPU) to handle the ultimate basis set, as well as proficiency with the MARIE (MAgnetic Resonance Integral Equation suite) open source software (13,14). Furthermore, the results described in (12) suggest that a uniform sphere with average brain electrical properties is a good approximation of a human head for UISNR calculations. However, even performing DGF simulations with a uniform sphere could be challenging without access to existing software and/or experience in using it. Kopanoglu et al. derived an analytic formula to approximate the UISNR in an homogenous sample of arbitrary shape (15). However, the proposed formula is applicable only when the distance of the voxel of interest from the sample surface is smaller than the wavelength, which limits its validity to superficial positions, therefore preventing most practical use, since coil designers are usually interested in assessing and maximizing central SNR.

Initial work on ideal current patterns (7) showed that the optimal current distribution resulting in maximum SNR at the center of a uniform sphere consists of two large distributed loops rotating around the z axis (i.e., the direction of the main magnetic field B₀) at the Larmor frequency. Further, it was shown that the shape of these ideal current patterns did not change with B₀. This suggests that only few modes likely contribute to the UISNR in the central region, compared to thousands of modes at other voxel positions (1,16). Following this observation, the aim of this work was to perform a mode analysis to establish which current modes maximize SNR at the center of the sphere, and to determine whether it is possible to use these modes to derive an analytic expression for the UISNR at the center of the sphere.

THEORY

Given a complete basis set of current modes K_l,m,

$${\mathit{K}}_{l,m}={\mathrm{\sum }}_{l=0}^{\infty }{\mathrm{\sum }}_{m=-l}^l{W}_{l,m}^{(M)}{\mathit{X}}_{l,m}(\theta ,\varphi )+W_{l,m}^{(E)}\widehat{\mathit{r}}\times {\mathit{X}}_{l,m}(\theta ,\varphi ),$$ [1]

defined on a spherical surface of radius b, the resulting electric (E) field inside a dielectric sphere of radius a < b can be calculated as E(r) = iωμ∫_AḠ(r,r′) · K(r′)dA′ (17). In these expressions, i is the imaginary unit, l, m are the expansion indices, X_l,m is a vector spherical harmonic of order (l,m), ω is the angular frequency, μ is the magnetic permeability of the dielectric material composing the sphere, Ḡ(r,r′) is the branch of the DGF corresponding to the region indicated by r, and $W_{l.m}^{(M)}$ and $W_{l.m}^{(E)}$ are the series expansion coefficients representing divergence-free and curl-free surface current contributions, respectively. The left circularly polarized component of the magnetic field (B) can be derived from E by using Maxwell’s equations and, defining ${\mathit{W}}^T=[\begin{array}{cc}{W}_{l,m}^{(M)}& W_{l,m}^{(E)}\end{array}]$, can be written as (7)

$$\begin{gathered} B_1^{-}(\mathit{r})=B_x(\mathit{r})-i{B}_y(\mathit{r}) \\ =-i{\mu }_0{k}_0{k}_{\text{in}}{b}^2\sum _{l=0}^{\infty }\sum _{m=-l}^l{\mathit{W}}^T\mathit{T}\left(\begin{array}{c}{\mathit{N}}_{l,m}{(k_{\text{in}},\mathit{r})}_x-i{\mathit{N}}_{l,m}{(k_{\text{in}},\mathit{r})}_y\\ {\mathit{M}}_{l,m}{(k_{\text{in}},\mathit{r})}_x-i{\mathit{M}}_{l,m}{(k_{\text{in}},\mathit{r})}_y\end{array}\right) \\ =\sum _{l=0}^{\infty }\sum _{m=-l}^l{\mathit{W}}^T\mathit{S}. \end{gathered}$$ [2]

where, T is a transformation matrix that accounts for boundary conditions at the surface of the sphere, S is a matrix that contains the complex signal sensitivities associated with each mode, $k_0^2={\omega }^2{\mu }_0{\epsilon }_0$ and $k_{\text{in}}^2={\omega }^2{\epsilon }_r{\epsilon }_0\mu +i\omega {\mu }_0\sigma$ are the complex wave numbers in free space and inside the sphere, respectively, where ε₀ is the electric permittivity of free space, and ε_r and σ are the relative permittivity and the electric conductivity of the dielectric material composing the sphere, respectively. We approximated the permeability μ of the dielectric sphere with the permeability μ₀ in free space, μ~μ₀, which is a valid assumption for common in vivo situation. Note that harmonic time variation is assumed for all fields and currents, although the common factor e^−iωt is omitted from the equations for convenience.

The vector wave functions M_l,m and N_l,m in Eq. [2] are defined as (7)

$$\begin{gathered} {\mathit{M}}_{l,m}(k_{\text{in}},\mathit{r})=\frac{1}{-i\sqrt{l(l+1)}}(\mathbf{\nabla }\times j_l(k_{\text{in}}r)Y_l^m(\theta ,\varphi )\mathit{r}), \\ =j_l(k_{\text{in}}r){\mathit{X}}_{l,m}(\theta ,\varphi ), \end{gathered}$$ [3a]

$${\mathit{N}}_{l,m}(k_{\text{in}},\mathit{r})=\frac{1}{k_{\text{in}}}\mathbf{\nabla }\times {\mathit{M}}_{l,m}(k_{\text{in}},\mathit{r}),$$ [3b]

where j_l is a spherical Bessel function of order l, r (radial), θ (polar), and ϕ (azimuthal) are spherical coordinates, and $Y_l^m$ is a scalar spherical harmonic of order (l, m). From Eq. [2] we see that, since the matrix T is diagonal (7), the divergence-free component of the signal sensitivity (S) depends only on N_l,m, whereas the curl-free component depends only on M_l,m.

The UISNR ζ at any position r₀ inside the sphere can be calculated as (1):

$$\zeta ({\mathit{r}}_{\mathbf{0}})~\frac{{\omega }_0{M}_0}{\sqrt{4k_B{T}_S·{\left(\mathit{S}{(\mathit{r})}^H{\mathit{\Psi }}_{\text{mode}}^{-1}\mathit{S}(\mathit{r})\right)}_{0,0}^{-1}}},$$ [4]

where M₀ is the equilibrium magnetization, ω₀ is the Larmor frequency, k_B is Boltzmann’s constant, T_S is the absolute temperature of the sample, and Ψ_mode is the modes’ noise covariance matrix associated with the noise equivalent resistance. The “0,0” subscript indicates the diagonal element corresponding to target position r₀. The ideal current patterns corresponding to ζ(r₀) can be derived by performing a weighted sum of the individual current modes K_l,m using the SNR-optimal reconstruction weights ${\mathrm{W}}_{\text{opt}}={\left({\mathit{S}}^{\mathrm{H}}{\mathit{\Psi }}_{\text{mode}}^{-1}\mathit{S}\right)}^{-1}{\mathit{S}}^{\mathrm{H}}{\mathit{\Psi }}_{\text{mode}}^{-1}$ (7).

Mode analysis and analytic formula for the UISNR at the center of the sphere

The signal sensitivity (Eq. [2]) inside the dielectric sphere is determined by the vector wave functions M_l,m and N_l,m in Eq. [3]. At the sphere center (r → 0), it can be shown (Appendix A) that M_l,m(r → 0) = 0,∀(l,m) and N_l,m(r → 0) = 0,∀(l,m), except for the three modes (1,1), (1,0) and (1,−1), for which the following expressions hold:

$${\mathit{N}}_{1,1}(r\to 0)=\sqrt{\frac{1}{6\pi }}\left(\frac{-i}{\sqrt{2}},\frac{1}{\sqrt{2}},0\right),$$ [5a]

$${\mathit{N}}_{1,0}(r\to 0)=\sqrt{\frac{1}{6\pi }}(0,0,i),$$ [5b]

$${\mathit{N}}_{1,-1}(r\to 0)=\sqrt{\frac{1}{6\pi }}\left(\frac{i}{\sqrt{2}},\frac{1}{\sqrt{2}},0\right).$$ [5c]

However, substituting these quantities into Eq. [2], we see that only N_1,1 contributes to the signal sensitivity at the center, which means that the corresponding UISNR ζ(r → 0) is completely determined by one divergence-free current mode. This explains why the ideal current patterns for a voxel at the sphere center do not change shape with field strength, but only differ by an azimuthal phase shift (Figure 1): the patterns must always conform to the mode pattern, multiplied by a complex scalar weight that changes with field strength and other parameters.

Figure 1.

A time snapshot of the ideal current patterns associated with the UISNR at the center of a sphere, for B₀ = 1.5 T, 3 T, 7 T, and 11 T. The ideal current patterns form two large distributed loops, centered on the x–y plane (θ = 90°) and separated by 180 degrees in the azimuthal direction, which rotate in the same sense about an axis that precesses around the direction of the main magnetic field (z). Ideal currents are the same in all cases, except for a phase shift, which is clearly visible in the 2D “unwrapped” view of the spherical surface (bottom row).

The fact that only one mode survives at the center of sphere enables derivation of an analytic expression for ζ(r → 0), which is given by

$$\zeta (r\to 0)=\frac{{\omega }_0{M}_0}{\sqrt{4k_B{T}_S·3\pi ·\frac{\sigma {\omega }_0^2}{{\mid k_{\text{in}}\mid }^2}·{\int }_0^a{\mid j_1(k_{\text{in}}r)\mid }^2{r}^{2}dr}}.$$ [6]

The solution of the integral in Eq. [6] is given by

$$\underset{0}{\overset{a}{\int }}{\mid j_1(kr)\mid }^2{r}^{2}dr=\frac{a^2\{k^{\ast }{j}_0(k^{\ast }a)j_1(ka)-k{j}_0(ka)j_1(k^{\ast }a)\}}{k^2-k^{\ast 2}}.$$ [7]

Details of the derivation are provided in Appendix B. The analytic expression in Eq. [6] explicitly shows the dependence of ζ(r → 0) on the sphere radius (a) and on the electrical properties of the sphere (via the wave number).

METHODS

To validate the analytic solution, we investigated the dependence of ζ(r → 0) on main magnetic field strength B₀ and compared the results with corresponding DGF simulation results, with expansion order l_max = 55 (6,272 modes in total, evenly distributed between curl-free and divergence-free modes). The dielectric properties of the sphere, ε_r and σ (1,7,18), were calculated as the average of gray and white matter properties for each operating frequency (Table 1). We also tested the case with conductivity σ equal to 10⁻⁵ Ω⁻¹·m⁻¹ to approximate the lossless condition as in (1). Furthermore, we used the analytic expression to study the dependence of ζ(r → 0) on the sphere radius (a) and the radius of the surface where the current distribution is defined (b). We then investigated how the UISNR ζ(r) varies with the distance r from the center, either in the x–y plane or along the z-axis (direction of B₀), and determined the extent of the region within which the UISNR could be approximated by the analytic solution at the center, ζ(r → 0). Finally, we computed an experimental performance map for a 32-element 3 Tesla head coil array by approximating the UISNR at every voxel with the central UISNR obtained with the analytic formula. We compared the result with an accurate performance map based on full DGF simulations, to evaluate the error of the approximation in a practical situation. The experimental SNR map of the 32-element array was available from previous work (5), whereas the scaling factors needed to calculate the performance maps are described in Appendix C.

Table 1.

Dielectric properties of the average brain tissue (white and gray matters) (1,7,18)

B0 (T)	1	3	5	7	9	11	14	20
Larmor frequency (MHz)	42.6	127.7	212.9	298.1	383.2	468.4	596.1	851.5
Dielectric constant εr	102.5	63.1	55.3	52	50	48.8	47.5	46
Conductivity σ (Ω−1·m−1)	0.36	0.46	0.51	0.55	0.59	0.62	0.66	0.75

RESULTS

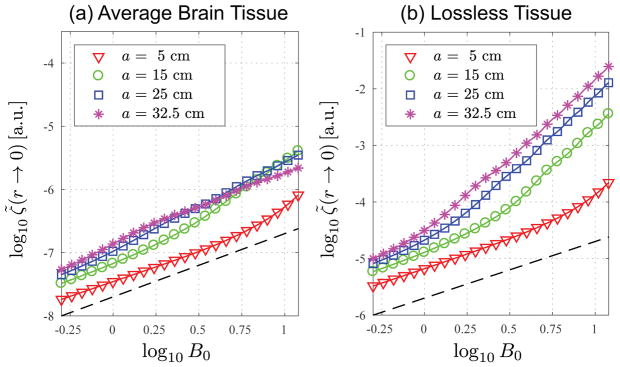
Figure 2 shows the double-logarithmic plots of ζ̃(r → 0) vs. B₀ for B₀ = 0.5 – 12 T, replicating the plots in fig. 6 of Ref (1). The tilde in ζ̃ indicates that the UISNR values were normalized by (2a)³ before plotting (Appendix C). Note that the behavior of ζ̃(r → 0) based on the analytic solution (solid lines) was consistent, up to a scaling factor (Appendix C), with the results in (1), which were computed using a multipole field expansion. Furthermore, the values obtained with the analytic solution traced exactly the values calculated with full DGF simulations (data points). Figure 2 shows that ζ̃(r → 0) is approximately linear with respect to B₀ at low B₀ values, and increases nonlinearly as ~(B₀)ⁿ with an exponent n > 1 at high B₀ values, which is compatible with published results (1). In the case of average brain tissue (Figure 2a), this effect was more pronounced for a small sphere radius, whereas for the large spheres (a = 25 cm and 32.5 cm) the relationship remained approximately linear also at ultra-high field.

Figure 2.

UISNR at the sphere center as a function of main magnetic field strength B₀, calculated using the analytic formula (solid lines) and full DGF simulations (data points). The radius of the dielectric sphere a was set to 5, 15, 25 and 32.5 cm. Surface current radius b was kept constant at 35 cm. The dashed line is a reference line with a slope n = 1. Dielectric properties of the sphere were set to (a) average brain tissue, or (b) approximately lossless conditions (σ = 10⁻⁵ Ω⁻¹·m⁻¹). The tilde in ζ̃(r → 0) indicates that the UISNR ζ(r → 0) was normalized by (2a)³ (Appendix C) to validate the plots against those shown in fig. 6 of previous work (1), which calculated central UISNR with multipole expansions. The plots were found to be identical, except for a scaling factor ~ 7 × 10⁴ .

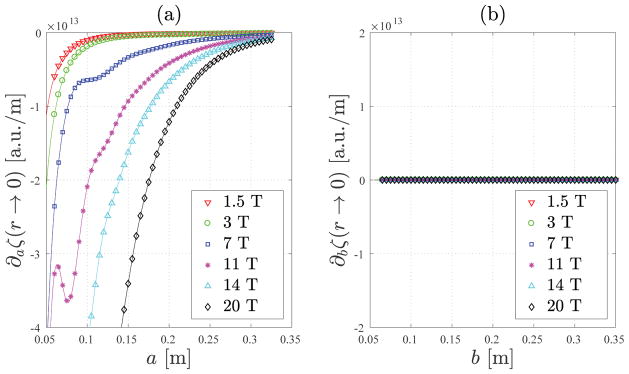
The sensitivity of the central UISNR with respect to changes in sphere radius ∂_aζ(r → 0) and current radius ∂_bζ(r → 0) is shown in Figure 3. These quantities can be calculated directly from the analytic formula in Eq. [6]:

$${\partial }_a\zeta (r\to 0)=-\zeta (r\to 0)·\frac{{\mid j_1(k_{\text{in}}a)\mid }^2{a}^2}{2{\int }_0^a{\mid j_1(k_{\text{in}}r)\mid }^2{r}^{2}dr},$$ [8a]

$${\partial }_b\zeta (r\to 0)=0,$$ [8b]

Figure 3.

(a) ∂_aζ(r → 0) with a fixed b = 35 cm and (b) ∂_bζ(r → 0) with a fixed a = 5 cm based on analytic solutions (solid lines) and full DGF simulations (data points). The dielectric properties were set to values in the average brain tissue. At high field ≥ 7 T, ∂_aζ(r → 0) oscillates for small sphere radii a, probably due to wavelength effects. At 14 and 20 T, the oscillation happens at a very negative ∂_aζ(r → 0)~ −10¹⁴, and was not shown in this figure (a).

Note that also in this case the analytic results (solid lines) agree with the results from full DGF simulations (data points). For B₀ < 7 T, the rate of change of the central UISNR with respect to the sphere radius (∂_aζ(r → 0)) increases monotonically until ζ(r → 0) reaches a minimum and remains constant for larger object size (Figure 3a). For B₀ ≥ 7 T, ∂_aζ(r → 0) instead oscillates for small sphere radii, likely due to wavelength effects, and the higher the field strength, the larger is the sphere radius for which ζ(r → 0) reaches its minimum values. On the other hand, ζ(r → 0) is constant with respect to the radius (b) at which the surface current distribution is defined (Figure 3b), as predicted by the analytic solution (Eq. [8b]).

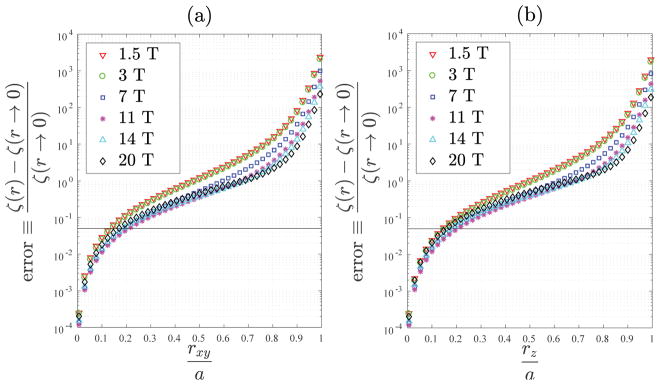
Figure 4 shows that using the formula for the UISNR at the center to approximate the UISNR for a voxel at an intermediate position $r(0<\frac{r}{a}<1)$ on the x–y plane (Figure 4a), or along the z-axis (Figure 4b), yields an error < 5 % if $\frac{r}{a}<10-20\%$. At high field, the range of $\frac{r}{a}$ with an error < 5 % is similar to the case at low field. In other words, at high field, the UISNR at the center can approximate the UISNR at an intermediate position within a region comparable to the case at low field. The error grows approximately exponentially as the voxel of interest approaches the surface of the sphere.

Figure 4.

The error $\equiv \frac{\zeta (r)-\zeta (r\to 0)}{\zeta (r\to 0)}$ associated with using the analytic expression for the central voxel to approximate UISNR at positions away from the center. The error is shown as a function of the normalized distance $\frac{r}{a}$ from the sphere center. The dielectric properties were set to values in the average brain tissue. The dielectric sphere radius a was set to 8.5 cm, and the surface current radius b was set to 9.5 cm. The normalized distance $\frac{r}{a}$ was varied either along the (a) x–y plane or (b) z axis. The horizontal solid line indicates an error of 5%.

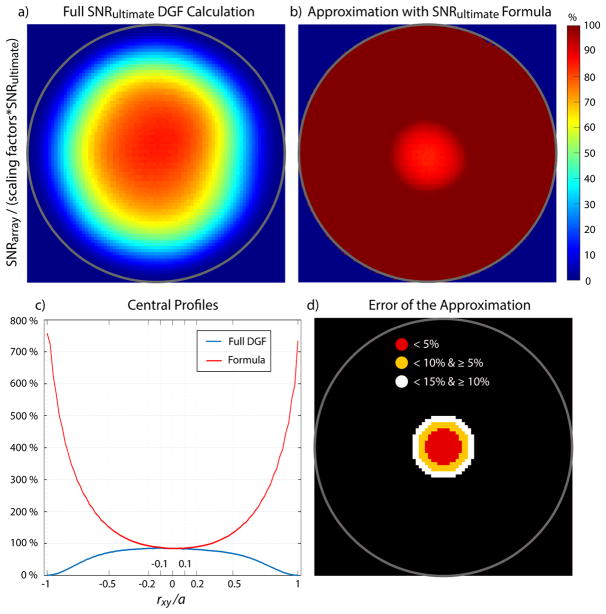
Figure 5 compares experimental coil performance maps for a 32-element head coil array (5), obtained with a full DGF simulation (Figure 5a) or by approximating UISNR at every voxel with the value provided by the exact solution (Figure 5b). The profile plots in Figure 5c indicates that the analytic formula is accurate in a region surrounding the center, whereas the error grows exponentially closer to the surface, as predicted by the simulation results in Figure 4, and shown by Figure 5d.

Figure 5.

Coil performance of a 32-element head array as a percentage of the UISNR for a central axial slice through a homogeneous spherical phantom (σ = 0.97 Ω⁻¹·m⁻¹, ε_r = 81.3) at 3 Tesla. (a) Coil performance map where each pixel represents the experimental SNR divided by its corresponding UISNR value, scaled to account for sequence and system related parameters (5). (b) Approximated performance map, where the experimental SNR at every pixel is divided by the UISNR value at the center, calculated using the exact formula and scaled appropriately. The scaling factor is discussed in Appendix C. The approximated map provides an accurate estimate of coil performance along an extended central region, with less than 5% error for pixels that are within ~14% of the sphere radius a (c,d).

DISCUSSION

Here we have derived an analytic expression to directly calculate the UISNR at the center of a dielectric sphere. This analytic formula allows one to explicitly investigate UISNR behavior as a function of main magnetic field strength, sample geometry and electrical properties. For example, note that the radius of the surface current distribution (b) does not appear in the formula, and full DGF simulation results confirm that ζ(r → 0) is, in fact, constant with respect to b. This is a potentially counterintuitive result, since, according to traditional “fill-factor” arguments or common experience with close-fitting coil arrays, one might expect deep-lying SNR to decrease with increasing distance of the receive coil surface from the body. The fact that central UISNR does not depend upon the radius of the receiving surface can be understood considering that a) the electric conductivity of air is zero, therefore expanding the gap between the sample and the current-carrying surface does not introduce additional losses that would reduce UISNR, and b) any change in body noise with changing b is directly canceled by a corresponding change in signal for the single surviving mode (see Appendix B). Note that this result is valid only for UISNR at the center and when the current-bearing surface completely encircles the object. (At some point, it should be noted, coil noise would become significant, and SNR would be degraded in practice, for large current-carrying surfaces with large stretches of conductive material, but this degradation relates to concrete considerations of coil engineering rather than to fundamental electrodynamics (19).) The radius-independence (for receiving surface b) of central UISNR is in fact a more general result which applies to a range of geometries other than the current spherical configuration (3,19), but it arises in a comparatively transparent fashion in our analytical formula for the sphere. Recent work has shown that moving the current surface away from the sample only affects the phase of the ideal current patterns, due to propagation delay (20). In fact, the shape of the ideal current patterns cannot change with increasing b, since it is always the same current mode that contributes to the UISNR at the sphere center, as we have mathematically proven in this work. Pfrommer and Henning have also reported that the UISNR in a dielectric sphere does not depend on the radius of the surface current distribution (9). They have also shown that UISNR is not affected by the presence of an encircling RF shield, independently of the shield radius and electric conductivity.

Our derivation demonstrates that there are no curl-free contributions to ζ(r → 0), as it was previously shown using full DGF simulations (9). This, and the fact that the only mode contributing to ideal current patterns associated with UISNR at the center of a sphere forms large distributed loops (Figure 1), suggests that arrays of loop coils are a reasonable choice to maximize central SNR for head imaging at all field strengths (8). This observation is valid only if the current distribution is defined on a spherical surface, as in this work. In fact, recent work (21) has shown that since in a spherical geometry all points on the surface are equidistant from a central spin, the optimal receive currents that maximize performance at the center are closed and create loop-like patterns at all field strengths. Nevertheless, electric dipoles, which also have a divergence-free component (6,22), can still capture a substantial portion of the available central SNR at ultra-high field, if the current-bearing surface is not a complete sphere (23,24). At ultra-high field, electric dipole arrays can even exceed loops’ performance in maximizing central SNR in the case of body-size objects, for which the receive elements are normally arranged on a cylindrical surface (6,7,21).

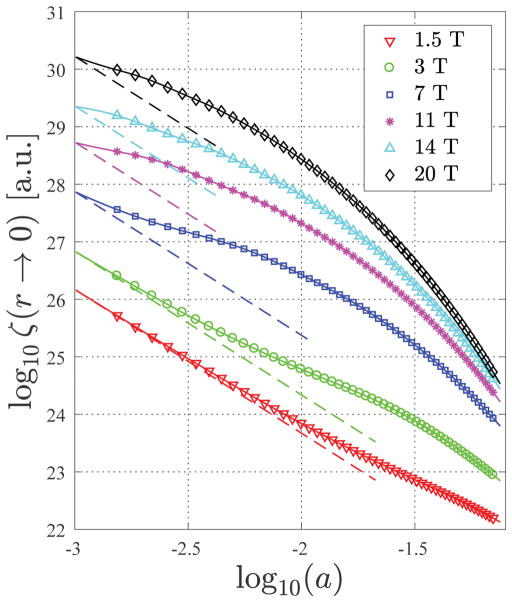
Kopanoglu et al. suggested UISNR ∝ a^−2.5 to approximate the dependence of UISNR on the sphere radius a (15), in cases where wavelength effects are small, i.e. where $\frac{a}{\lambda }\ll 1$, with λ being the wavelength of electromagnetic field inside the sample. This simple power law can also be derived by performing Taylor expansions of spherical Bessel functions in Eq. [7] with respect to ka for |ka| ≪ 1. To further demonstrate this relationship, we used the simulation results from Figure 3 to show how ζ(r → 0) varies with a in a logarithmic scale (Figure 6). At low field (long λ), ζ(r → 0) is, in fact, approximately proportional to a^−2.5, as shown by the red dashed line in Figure 6. On the other hand, at high field (short λ on the order of a), ζ(r → 0) completely deviates from the simple power law, due to significant wavelength effects.

Figure 6.

UISNR ζ(r → 0) at the sphere center as a function of sphere radius a with a fixed b = 35 cm for B₀ = 1.5 T, 3 T, 7 T, 11 T, 14 T and 20 T, based on the analytic formula (solid lines) and full DGF simulations (data points). The dielectric properties were set to values in the average brain tissue. Dashed lines show the approximate dependence of UISNR on ~ a^−2.5, suggested by Kopanoglu et al for low field strengths. (15).

We showed that the formula for ζ(r → 0) could be used to approximate the UISNR in a region surrounding the center with an acceptable error < 5 % (Figure 4). By properly scaling the formula in Eq. [6] to account for pulse sequence and system parameters (5), it is possible to assess the absolute SNR performance of actual head coils at the center of a spherical phantom, without running any simulations. In fact, Figure 5 shows that an accurate estimate of the performance of a 32-element head coil can be obtained over an extended region surrounding the center. Since coil designers are often interested in maximizing central SNR, the proposed UISNR formula could be useful to predict or evaluate the performance of coils being developed, by using simulated or experimental SNR maps, respectively. Furthermore, the analytic expression for the UISNR enables one to rapidly investigate UISNR as a function of various parameters, such as magnetic field strength, sphere radius and electrical properties, providing additional insights for coil design. Although the same information could be derived from full DGF simulations, our proposed formula can be used by anyone, without the need for simulation software, and it is approximately a thousand times faster than DGF in calculating UISNR.

Although a uniform dielectric sphere is a common and useful model for the human head, differences between realistic heads (25) and sphere models have been observed in simulation results (12), which showed that the UISNR increases faster with B₀ in the sphere than in the head model. However, these differences were negligible for a voxel at the center, suggesting that our proposed analytic formula could closely approximate the UISNR behavior at the center of a realistic human head model. A better estimation of the UISNR at other positions in the human head could be achieved using a symmetric ellipsoid, which is a better approximation of the actual geometry than a sphere. This would require deriving the DGF in a symmetric dielectric ellipsoid in prolate or oblate spheroidal coordinates, for which the wave function is separable (i.e., it can be calculated via separation of variables). Future work will focus on this derivation to investigate whether the UISNR in dielectric spheres or cylinders can be expressed as special cases of the general solution for the symmetric ellipsoid.

CONCLUSION

We introduced an analytic formula to calculate the UISNR at the center of a dielectric sphere, which is rapid, accurate, and enables direct analysis of the dependence on B₀, sample geometry and electrical properties. The analytic expression can approximate the UISNR near the center with an acceptable error: for a typical spherical phantom with radius equal to 8.5 cm, the UISNR would be valid within a central volume of approximately 2.6 cm³. This work can enable people to rapidly calculate UISNR without running complex simulations and use it, for example, as an absolute reference to assess the performance at depth of head coils with tissue-mimicking spherical phantoms (5). The source code to calculate ζ(r → 0) based on Eq. [6] can be freely downloaded from http://cai2r.net/resources/software/ultimate-intrinsic-snr-uniform-sphere.

APPENDIX A

Mode analysis at the sphere center

By performing the curl operations in Eq. [3], the vector wave functions M_l,m and N_l,m in a spherical coordinate can be rewritten as:

$${\mathit{M}}_{l,m}=\frac{1}{-i\sqrt{l(l+1)}}\left\{\widehat{\mathit{\theta }}\left[\frac{j_l(kr)}{sin\theta }{\partial }_{\varphi }{Y}_l^m\right]-\widehat{\mathit{\varphi }}[j_l(kr){\partial }_{\theta }{Y}_l^m]\right\},$$ [A1a]

$${\mathit{N}}_{l,m}=\frac{1}{-i\sqrt{l(l+1)}}\{\widehat{\mathit{r}}·\frac{j_l(kr)}{kr}\left[-cot\theta {\partial }_{\theta }{Y}_l^m-{\partial }_{\theta }^2{Y}_l^m-\frac{1}{{sin}^2\theta }{\partial }_{\varphi }^2{Y}_l^m\right]+\widehat{\mathit{\theta }}\left[\frac{j_l(kr)}{kr}+{\partial }_{kr}{j}_l(kr)\right]{\partial }_{\theta }{Y}_l^m+\widehat{\mathit{\varphi }}\left[\frac{j_l(kr)}{kr}+{\partial }_{kr}{j}_l(kr)\right]·\frac{{\partial }_{\varphi }{Y}_l^m}{sin\theta }\},$$ [A1b]

where r̂, θ̂, and ϕ̂ are unit vectors in radial, polar, and azimuthal directions in the spherical coordinate system.

It is straightforward to prove that M_l,m(r → 0) = 0,∀(l,m) at the sphere center. By substituting ${\partial }_{\varphi }{Y}_0^0=0$ and ${\partial }_{\theta }{Y}_0^0=0$ into the Eq. [A1a], we obtain M_0,0(r → 0) = 0. For the cases when l > 0, M_l,m(r → 0) = 0 since $\underset{x\to 0^{+}}{lim}{j}_l(x)={\delta }_{0l}$, where δ is a Kronecker delta function. Hence, M_l,m(r → 0) = 0 and, therefore, M_l,m(r → 0)_x − iM_l,m(r → 0)_y is always also zero, which means that none of the curl-free modes contribute to the signal sensitivity (Eq. [2]) at the center of the sphere.

The calculation of N_l,m(r → 0) will be separated into three cases: (a) l = 0, (b) l > 1, and (c) l = 1.

For l = 0, since $Y_0^0$ is a constant, ${\partial }_{\theta }{Y}_0^0={\partial }_{\theta }^2{Y}_0^0={\partial }_{\varphi }{Y}_0^0={\partial }_{\varphi }^2{Y}_0^0=0$, which, when substituted into Eq. [A1b], yields N_0,0(r → 0) = 0.

For l > 1, $\underset{x\to 0^{+}}{lim}\frac{j_l(x)}{x}=0$, since $j_l(x)\simeq \frac{x^l}{(2l+1)!!}\left(1-\frac{x^2}{2(2l+3)}\right)$ when x → 0⁺. Substituting into Eq. [A1b], we find N_l>1,m(r → 0) = 0.

Finally, for l = 1, $\underset{x\to 0^{+}}{lim}\frac{j_1(x)}{x}=\frac{1}{3}$. Therefore, substituting into Eq. [A1b], we obtain

$${\mathit{N}}_{1,m}(r\to 0)=\frac{1}{-i\sqrt{2}}\left\{\widehat{\mathit{r}}·\frac{1}{3}\left[-cot\theta {\partial }_{\theta }{Y}_1^m-{\partial }_{\theta }^2{Y}_1^m-\frac{1}{{sin}^2\theta }{\partial }_{\varphi }^2{Y}_1^m\right]+\widehat{\mathit{\theta }}·\frac{2}{3}{\partial }_{\theta }{Y}_1^m+\widehat{\mathit{\varphi }}·\frac{2}{3}\frac{{\partial }_{\varphi }{Y}_1^m}{sin\theta }\right\}.$$ [A2]

Eq. [A2] shows that N_1,m(r → 0) is non-zero at the sphere center and has a spurious orientation dependence on θ and ϕ. Since the unit vectors r̂, θ̂, and ϕ̂ also depend on θ and ϕ, to further simplify Eq. [A2], we can convert r̂, θ̂, and ϕ̂ to a fixed basis î, ĵ, and k̂ in Cartesian coordinates using the following relationships:

$$\begin{gathered} \widehat{\mathit{r}}=sin\theta cos\varphi \widehat{\mathit{i}}+sin\theta sin\varphi \widehat{\mathit{j}}+cos\theta \widehat{\mathit{k}}, \\ \widehat{\mathit{\theta }}=cos\theta cos\varphi \widehat{\mathit{i}}+cos\theta sin\varphi \widehat{\mathit{j}}-sin\theta \widehat{\mathit{k}}, \\ \widehat{\mathit{\varphi }}=-sin\varphi \widehat{\mathit{i}}+cos\varphi \widehat{\mathit{j}}. \end{gathered}$$ [A3]

Substituting Eqs. [A3] into Eq. [A2], and using the definition of spherical harmonic functions ( $Y_1^1=\sqrt{\frac{3}{8\pi }}sin\theta e^{i\varphi },Y_1^0=\sqrt{\frac{3}{4\pi }}cos\theta$, and $Y_1^{-1}=-Y_1^{1\ast }$), we obtain a simplified expression for the three non-zero DGF modes at the sphere center shown in Eq. [5], which are constant vectors. Since the signal sensitivity is proportional to (N_l,m)_x − i(N_l,m)_y (Eq. [2]), there is only one divergence-free mode contributing to it at the sphere center: ${\mathit{N}}_{1,1}{(r\to 0)}_x-i{\mathit{N}}_{1,1}{(r\to 0)}_y=\frac{-i}{\sqrt{3\pi }}$.

APPENDIX B

Analytic expression for the UISNR at the sphere center

The most important step in deriving an analytic expression for the UISNR is to calculate the term ${\left({\mathit{S}}^H{\mathit{\Psi }}_{\text{mode}}^{-1}\mathit{S}\right)}_{0,0}^{-1}$ in the denominator of Eq. [4]. The noise covariance matrix can be expressed as Ψ_mode = TR_LT^T, where (7,8)

$${\mathit{R}}_L=\sigma {\mid \omega {\mu }_0{k}_0{b}^2\mid }^2\left(\begin{array}{cc}\underset{0}{\overset{a}{\int }}{\mid j_l(k_{\text{in}}r)\mid }^2{r}^{2}dr& 0\\ 0& \frac{1}{{\mid k_{\text{in}}\mid }^2}\underset{0}{\overset{a}{\int }}\{{\mid {\partial }_r[r{j}_l(k_{\text{in}}r)]\mid }^2+l(l+1){\mid j_l(k_{\text{in}}r)\mid }^2\}dr\end{array}\right).$$ [B1]

Since both T and R_L are diagonal matrices, then also Ψ_mode is diagonal. We can rewrite

$${\left({\mathit{S}}^H{\mathit{\Psi }}_{\text{mode}}^{-1}\mathit{S}\right)}_{0,0}^{-1}={\mid {\mu }_0{k}_0{k}_{\text{in}}{b}^2\mid }^{-2}{({\mathit{F}}^H{\mathit{R}}_L^{-1}\mathit{F})}_{0,0}^{-1},$$ [B2]

where we have used S = (−iμ₀k₀k_inb²)TF (see Eq. [2]). Since only the N_1,1 mode contributes to the signal sensitivity at the sphere center (Appendix A), we can simplify the previous expression as:

$${{\left({\mathit{S}}^H{\mathit{\Psi }}_{\text{mode}}^{-1}\mathit{S}\right)}_{0,0}^{-1}\mid }_{r\to 0}=3\pi ·\frac{\sigma {\omega }^2}{{\mid k_{\text{in}}\mid }^2}·\underset{0}{\overset{a}{\int }}{\mid j_1(k_{\text{in}}r)\mid }^2{r}^{2}dr.$$ [B3]

Substituting into Eq. [4], we obtain the expression for the UISNR at the sphere center shown in Eq. [6].

Note that the solution of the integral in Eq. [7] is valid only for k ∉ ℝ. For the case of k ∈ ℝ, the solution is:

$$\underset{0}{\overset{a}{\int }}{\mid j_1(kr)\mid }^2{r}^{2}dr=\frac{2^{-4}\pi a^3{(ka)}^2}{5{\left[\mathrm{\Gamma }\left(\frac{5}{2}\right)\right]}^2}·{{}_{2}F}_3\left(2,\frac{5}{2};\frac{5}{2},\frac{7}{2},4;-{(ka)}^2\right),$$ [B4]

where ₂F₃ is the generalized hypergeometric function.

Appendix C

Scaling factors between the plots in Figure 2 and those in fig. 6 of Wiesinger et al. (1)

Based on Eq. [25], Eq. [B7] and Eq. [B8] in Ref.(1), the quantity plotted by Wiesinger et al. in their fig. 6, ζ_Wiesinger, relates to the UISNR, ζ, in our Eq. [4] via

$${\zeta }_{\text{Wiesinger}}=\zeta ·\frac{{\text{FOV}}^3\sqrt{n_k·4k_B{T}_s}}{\gamma \left(\frac{M_0}{B_0}\right)},$$ [C1]

where the field-of-view FOV is equal to the dielectric sphere’s diameter (FOV = 2a), n_k is the number of k-space samples, γ is the gyromagnetic ratio of the water hydrogen proton, and the constant

$$\frac{M_0}{B_0}=\frac{N{\gamma }^2{\hslash }^{2}I(I+1)}{3k_B{T}_s},$$

where N = 6.691 × 10²⁸ m⁻³ is the number of water hydrogen per unit volume, ħ is Planck’s constant divided by 2π, and I = 1/2 is the spin quantum number of the water hydrogen proton. Since in (1) the value of n_k is not given, the exact scaling factor in Eq. [C1] cannot be calculated. For this reason the values on the y-axis of Figure 2 (normalized central UISNR ζ̃ = ζ·FOV³) are different from those in fig. 6 of Ref (1), although the shape of the plots is identical.

Scaling factors used to compare simulated UISNR with experimental SNR in Figure 5

To compare the SNR obtained by experiments with the simulated UISNR, we scaled UISNR values by the system and sequence-related parameters in Table 2, following the method described in (5):

$${\zeta }^{\prime }({\mathit{r}}_{\mathbf{0}})=\zeta ({\mathit{r}}_{\mathbf{0}})·\frac{V_{\text{voxel}}\sqrt{N_{\text{acq}}\text{NEX}}sin\theta }{F\sqrt{\mathrm{\Delta }f}},$$

where V_voxel is the voxel volume, N_acq is the number of the sampled k-space data, NEX is the number of the signal averages, θ is the flip angle, F is the system noise factor, and Δf is the receiver bandwidth.

Table 2.

Dielectric properties, constants and scaling factors (5) used to calculate ζ(r → 0) in Eq. [6] and compare it with the experimental SNR of a 32-element head array (Figure 5).

Larmor frequency	$\frac{{\omega }_0}{2\pi }$	123.22	MHz
Equilibrium magnetization	M0	9.03 × 10−3	A·m−1
Boltzmann constant	kB	1.381 × 10−23	J·K−1
Sample temperature	Ts	298	K
Conductivity	σ	0.97	Ω−1·m−1
Relative permittivity	εr	81.3	-
Vacuum permittivity	ε0	8.85 × 10−12	C2·N−1·m−2
Magnetic permeability	μ~μ0	1.2566 × 10−6	Wb·A−1·m−1
Voxel volume	Vvoxel	1.2 × 10−8	m3
Receiver bandwidth	Δf	51.2	kHz
Flip angle	θ	0.3421	rad
Noise factor	F	1.22	-
Signal averages	NEX	1	-
Acquired data points	Nacq	256 × 128	-