A fast exact functional test for directional association and cancer biology applications

Abstract

Directional association measured by functional dependency can answer important questions on relationships between variables, for example, in discovery of molecular interactions in biological systems. However, when one has no prior information about the functional form of a directional association, there is not a widely established statistical procedure to detect such an association. To address this issue, here we introduce an exact functional test for directional association by examining the strength of functional dependency. It is effective in promoting functional patterns by reducing statistical power on non-functional patterns. We designed an algorithm to carry out the test using a fast branch-and-bound strategy, which achieved a substantial speedup over brute-force enumeration. On data from an epidemiological study of liver cancer, the test identified the hepatitis status of a subject as the most influential risk factor among others for the cancer phenotype. On human lung cancer transcriptome data, the test selected 1049 transcription start sites of putative noncoding RNAs directionally associated with lung cancers, stronger than 95% of 589 curated cancer genes. These predictions include non-monotonic interaction patterns, to which other routine tests were insensitive. Complementing symmetric (non-directional) association methods such as Fisher’s exact test, the exact functional test is a unique exact statistical test for evaluating evidence for causal relationships.

1 Introduction

Uncovering casual mechanisms to explain a phenomenon is central to scientific endeavors. In cancer research, one is often charged with identifying environmental factors or genes that can be responsible for tumor development using data generated from observational studies. Complex non-monotonic functional relationships (Fig. 1) from gene to cancer have been increasingly observed. Abate-Shen and colleagues suggested a model of prostate cancer progression as a non-monotonic function of p27 gene dosage [1]; indeed, genes in many cancer pathways showed a low-high-low expression pattern in response to an increasing p27 dosage in mouse papillomas [2]. In breast cancer, the SKI gene can be either pro- or anti-oncogenic [3], depending on the status of the TGFβ signaling pathway. Many studies also implicated the TLR4 gene to have both pro and anti-cancer effects [4]. Detecting such non-monotonic functional patterns requires statistical methods sensitive to directional association. We focus on evaluating directional association via the functional dependency of a dependent variable (child) on independent variables (parents). We categorize a parent-child pattern into three types: (1) functional, (2) dependent non-functional, and (3) independent. In a functional pattern, the child is strictly a non-constant function of the parents. In a dependent non-functional pattern, the child can not be a function of the parents but they must be statistically dependent on each other. In an independent pattern, the child and the parents are statistically independent. Parametric regression [5] reveals functional dependencies among random variables but requires prior knowledge about the functional forms—often unavailable in not well-understood biological systems. Nonparametric regression [6] such as smoothing splines [7] relies on the given parametric form of splines. To be free from parametric assumptions, one can discretize continuous random variables, form contingency tables, and test associations using the classical Pearson’s chi-square [8] or Fisher’s exact test [9], [10] (Supplementary Note 1, 2). These tests, however, are insensitive to the direction of association. Sharply differing from previous methods, a recently developed asymptotic functional chi-square test (FunChisq) [11] uncovers directional functional dependencies among discrete random variables. The test statistic follows an asymptotic null chi-square distribution and has a unique property of asymmetric functional optimality (Theorem 8 [11]) that benefits causal inference. These theoretical properties of the asymptotic FunChisq may explain its outstanding performance at HPN-DREAM Breast Cancer Network Inference Challenges [12].

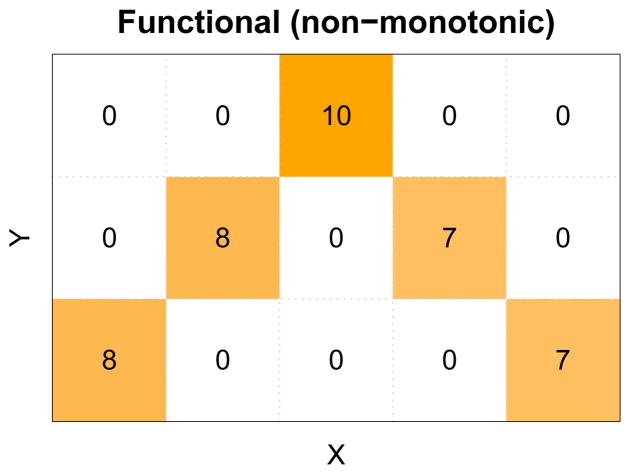
Fig. 1. A discrete non-monotonic functional pattern represented as a contingency table.

A non-monotonic function exists from X to Y, whose inverse is not a mathematical function. The number in each cell is the frequency that a specific combination of X and Y is observed.

However, the inexact chi-square null distribution may prevent FunChisq from achieving a high statistical power when the sample size is modest. This motivated us to design a new exact functional test using the multivariate hypergeometric distribution for the null hypothesis to complement the FunChisq test. This distribution allows the calculation of the exact significance level (p-value) of functional dependency, by summing up the probabilities of those contingency tables from the null population that are no less extreme than the observed table. Next, we developed a practically efficient branch-and-bound algorithm to compute the exact p-value, attaining a substantial speedup over brute-force enumeration. The run time is reduced by taking advantage of the lower and upper bounds that we established for the test statistic. Our simulation study shows that the exact functional test promotes functional patterns over dependent non-functional patterns, by suppressing the statistical power on the latter. This is in contrast to Fisher’s exact test which performs similarly to the exact functional test in absolute statistical power for functional patterns, but has a higher statistical power for non-functional patterns than the exact functional test. This distinction enables the exact functional test to favor functional over non-functional patterns more than Fisher’s exact test. In addition, on independent patterns, the exact functional test maintains a similar level of type I error to Fisher’s exact test.

Then we applied the exact functional test to reveal complex patterns in cancer biology. On data from a previous epidemiological study on four environmental or genetic risk factors to liver cancer, the test revealed hepatitis as the most important risk factor to the CpG island methylator phenotype of several tumor suppressor genes—an indicator of liver cancer; while such directional associations were not available in the original report [13] that used Fisher’s exact test and Pearson’s chi-square test. We further demonstrate the utility of the exact functional test by identifying 1049 potential noncoding RNA genes that are directionally associated with lung cancer phenotypes from FANTOM5 data [14]. The significance levels of these candidate genes are higher than 95% of 589 curated cancer genes from COSMIC Cancer Gene Census [15]. Several cases of gene-lung cancer association show non-monotonic patterns, suggesting a possible context-dependent role of these genes ranging from oncogenic to tumor suppressing in lung cancer; meanwhile, routine tests including t-test or logistic regression cannot detect such non-monotonic patterns. With both the theoretical arguments and experimental evidence, the exact functional test is uniquely advantageous in evaluating asymmetric functional dependency. Given the importance of functional dependency as evidence for causality [16], when asymptotic tests become inadequate, the exact functional test can serve as a useful instrument for exposing directional associations in many scientific applications beyond cancer biology.

2 Methods

2.1 Problem statement and notation

The problem is to test whether there is a functional relationship Y = f(X) from discrete random variable X to Y. The input data is a contingency table with observed counts of variable X and Y. The outcome of the test is the statistical significance of the functional relationship Y = f(X). Here X can be a compound variable composed of multiple variables and is called the parent variable, and Y is the child variable.

A contingency table is an r × c matrix O, where the r rows represent the levels of parent variable X and the c columns are levels of child variable Y. Let O_i,j at row i and column j of matrix O represent the sample count when X = i and Y = j. Let n be the sample size or the total number of observations in table O. Let O_i. be the sum of row i and O_.j be the sum of column j in O, respectively defined as $O_{i·}={\sum }_{j=1}^c{O}_{i,j}$ and $O_{·j}={\sum }_{i=1}^r{O}_{i,j}$.

The asymptotic functional chi-square test (FunChisq) determines directionality of interactions and represents a paradigm shift from Pearson’s chi-square test [8]. FunChisq differentiates the parent-to-child from child-to-parent functional dependencies. The functional chi-square statistic of observed table O is defined by [11]

$${\chi }_f^2(O)=\left[\sum _{i=1}^r\sum _{j=1}^c\frac{{(O_{i,j}-O_{i·}/c)}^2}{O_{i·}/c}\right]-\sum _{j=1}^c\frac{{(O_{·j}-n/c)}^2}{n/c}$$ (1)

which asymptotically follows a chi-square distribution [11] with (r − 1) × (c − 1) degrees of freedom under the null hypothesis of X and Y being statistically independent and the assumption that Y is uniformly distributed. The statistical significance can thus be computed by the upper-tail probability of the chi-square distribution. The optimality of ${\chi }_f^2(O)$ for functional dependencies has also been established [11].

However, the chi-square distribution approximates the p-value well only when the sample size is sufficiently large, and is inexact when the sample size is small. This is a major motivation to develop an exact functional test.

2.2 The exact functional test

We describe a novel exact test for functional dependency using an exact null distribution, of the test statistic also applied in the FunChisq test. We assume that the row and column sums of the contingency tables in the population are fixed to those of the observed contingency table O. The null hypothesis is that the parent and child variables are statistically independent. Thus, the probability of observing a table under the null hypothesis follows a multivariate hypergeometric distribution.

Let 𝒜 be the set of all null contingency tables with the same row and column sums of O:

$$\mathcal{A}=\{A\mid A_{i·}=O_{i·},i\in [1,r]\text{and}{A}_{·j}=O_{·j},j\in [1,c]\}$$ (2)

where the row and column sums of A are defined as $A_{i·}={\sum }_{j=1}^c{A}_{i,j}$ and $A_{·j}={\sum }_{i=1}^r{A}_{i,j}$. The probability of observing A ∈ 𝒜 can be exactly described by a multivariate hypergeometric distribution for sampling without replacement [10]:

$$Pr(A)=\frac{{\prod }_{i=1}^r{A}_{i·}!·{\prod }_{j=1}^c{A}_{·j}!}{n!·{\prod }_{i=1}^r{\prod }_{j=1}^c{A}_{i,j}!}$$ (3)

which is true under the null hypothesis of the exact functional test. Table A is no less extreme than O if A has a functional chi-square statistic no less than O. Let 𝒜_e(O) denote the set of all such extreme tables:

$${\mathcal{A}}_e(O)=\left\{A|{\chi }_f^2(A)\ge {\chi }_f^2(O)\text{and}A\in \mathcal{A}\right\}$$ (4)

The statistical significance of O is defined exactly by the one-sided p-value

$$p\text{-value}=\sum _{A\in {\mathcal{A}}_e(O)}Pr(A)$$ (5)

The only non-constant functional pattern of a 2×2 table O is linear functions. As the inverse of a linear function is another linear function, it implies that the transposed table O^⊤ has the same strength of functional dependency with O. Indeed, we proved in Theorem 1 (Supplementary Note 3) that the exact functional test on any 2×2 table always returns a significance level equal to its transpose.

2.3 A fast and exact algorithm by branch and bound

To compute the exact p-value by definition, one must enumerate all tables in the null population 𝒜. To reduce the burden of brute-force enumeration, we present a branch-and-bound algorithm (Supplementary Note 4) to speed up the calculation by skipping or including an entire branch of tables. The fast algorithm took advantage of both mathematical upper and lower bounds for the FunChisq test functional chi-square statistic when a table is only partially enumerated. The two bounds were established based on Theorem 2 (Supplementary Note 5) and Theorem 3 (Supplementary Note 6) on quadratic programming, respectively.

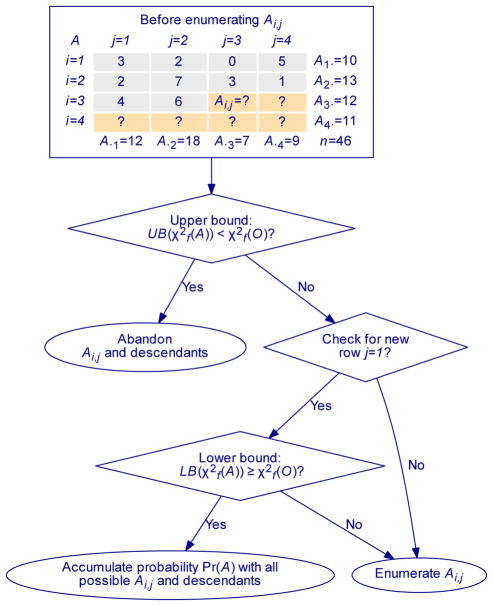
The strategy is illustrated by Fig. 2. A table A of with given row and column sums is enumerated element-wise and row by row. The descendants of A_i,j are the values of unenumerated elements after cell (i, j) in A. Let ${\chi }_f^2(A)$ be the functional chi-square statistic on table A. Considering elements in A to be enumerated, we determine both an upper bound $UB({\chi }_f^2(A))$ and a lower bound $LB({\chi }_f^2(A))$ of ${\chi }_f^2(A)$. Let O be the observed contingency table. We skip the entire branch to be enumerated if the upper bound is less than ${\chi }_f^2(O)$; and accumulate the probability of the entire branch if the lower bound is greater than or equal to ${\chi }_f^2(O)$. When an instance of A is fully enumerated, we will accumulate the probability Pr(A) if and only if ${\chi }_f^2(A)\ge {\chi }_f^2(O)$.

Fig. 2. The branch-and-bound algorithm for the exact functional test.

The contingency table A is enumerated element wise and row-by-row, such that it has the same row and column sums of the observed table O. If upper bound $UB({\chi }_f^2(A))<{\chi }_f^2(O)$, A_i,j will not lead to any A with ${\chi }_f^2(A)\ge {\chi }_f^2(O)$ and this branch is abandoned. Otherwise, it is promising to enumerate A_i,j. If this branch has a lower bound $LB({\chi }_f^2(A))\ge {\chi }_f^2(O)$, all instances of A_i,j and its descendants (other unenumerated cells) will guarantee ${\chi }_f^2(A)\ge {\chi }_f^2(O)$. The total probability contributed by all tables under this branch will be calculated by evaluating a single formula, and then the enumeration of the entire branch is completed. Otherwise, A_i,j will be enumerated and the probabilities of those instances of A with ${\chi }_f^2(A)\ge {\chi }_f^2(O)$ are summed table-by-table to compute the exact p-value.

The run time of the branch-and-bound algorithm depends on sample size n, table size r × c, and also the given marginal sums {A_i.} and {A_.j }. Let T (n, r, c, {A_i.}, {A_.j }) be the total number of tables the algorithm has to examine. It is bounded above by the total number of unique tables with the given marginal sums. This total number, however, does not have a closed form and must be computed iteratively [17]. A less tight upper bound is the total number of unique ways of drawing n samples to generate tables with fixed marginal sums, as given below:

$$T(n,r,c,\{A_{i·}\},\{A_{·j}\})\le \frac{n!}{{\prod }_{i=1}^r{A}_{i·}!}·\frac{n!}{{\prod }_{j=1}^c{A}_{·j}!}$$ (6)

This upper bound is also no greater than (r × c)ⁿ, the total number of unique ways of drawing n points into the r × c table without marginal sum constraints. This upper bound is exponential in n and polynomial in r and c.

2.4 Simulating noisy discrete patterns

We used a simulator implemented in the function simulate_tables [18] from R package FunChisq [19] to produce noisy random contingency tables with functional, dependent non-functional, or independent patterns. The first two pattern types have a uniform row marginal distribution for the parents. In independent tables both row and column sums are uniformly distributed. The simulator generates noise-free patterns first and then applies noise on the tables using the discrete house noise model [20], defined in Supplementary Note 7 and visualized in Supplementary Figure 1. To evaluate the performance of the exact functional test, we generated 8,100 contingency tables of three sizes (2×3, 3×3, and 4×4) and three sample sizes (30, 40, and 50) at three noise levels (0, 0.1, 0.5), covering three pattern types (functional, dependent non-functional, and independent), with 100 table instances for each unique setup.

3 Results

3.1 Performance evaluation

Exact functional test favored functional patterns by demoting non-functional patterns

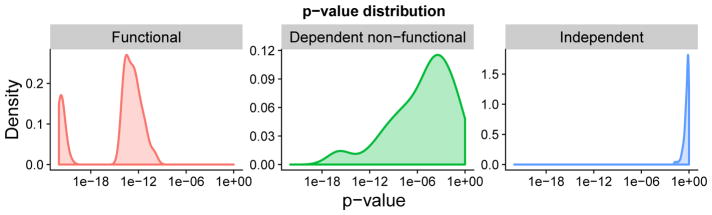
We first applied the exact functional test on noise-free 3×3 tables of sample size 50 to illustrate the statistical power for functional, dependent non-functional patterns and the null distribution for independent patterns. Distributions of p-values calculated for the three pattern types are shown in Figure 3. They suggest that the exact functional test is most powerful on functional patterns, much less powerful on non-functional patterns, and most insensitive to independent patterns.

Fig. 3. The exact functional test can effectively separate functional, non-functional, and independent patterns.

The p-value distributions of the exact functional test on three types of pattern are shown. On the left, the p-value distribution suggests the test has the highest power on functional patterns. In the middle, the test is less powerful on dependent non-functional patterns than functional patterns. On the right, the test is least sensitive to independent patterns, with p-values approaching 1 as expected. Exactly 100 noise-free tables of size 3×3 and sample size 50 were simulated to generate each distribution.

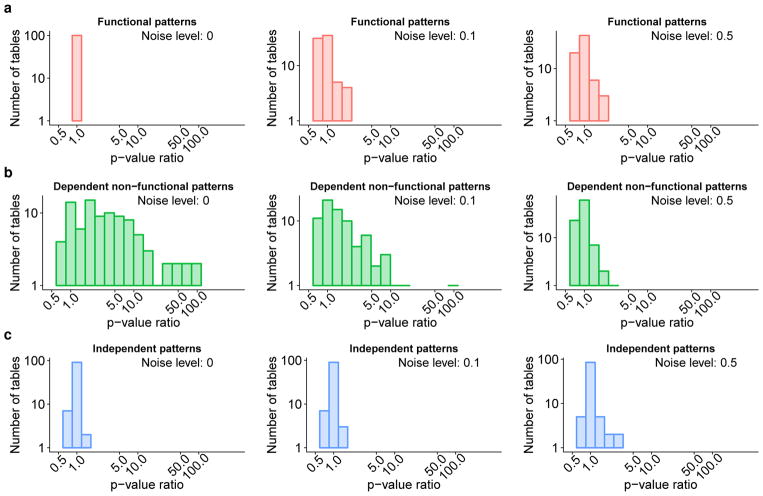
Next, we compared the exact functional test and Fisher’s exact test [9] [10]. We applied both tests on each of the 8,100 tables to calculate two p-values (one for the exact functional test and one for Fisher’s exact test). Figure 4 shows histograms of p-value ratios of the exact functional test over Fisher’s exact test on 3×3 tables of sample size 50, for functional, dependent non-functional and null independent patterns. Fig. 4a suggests both tests promote functional patterns with a comparable level of statistical power. However, the positive skewness of the ratio distributions in Fig. 4b suggests that the exact functional test more heavily demotes dependent non-functional patterns, implying that exact functional test is more specific to differ functional and dependent non-functional patterns than Fisher’s exact test. In Fig. 4c, both tests have similar p-value distributions with ratios close to 1 for independent patterns representing the null hypothesis, suggesting comparable type I error rates. At the noise level of 0.5, both tests performed comparably in all three types as the noise has destroyed the patterns.

Fig. 4. The effectiveness of exact functional test is in reduced statistical power on dependent non-functional patterns over Fisher’s exact test.

The histograms show distributions of p-value ratios of the exact functional test over Fisher’s exact test on three types of pattern. Exactly 100 tables of size 3×3 and sample size 50 were simulated to generate each distribution. Each type of table was subjected to house noise at three levels of 0, 0.1 and 0.5. (a) On functional patterns, the ratio distributions are tightly centered around 1, suggesting similar p-values of both tests with a comparable statistical power. (b) On dependent non-functional patterns, the right-skewed ratios for most tables are higher than 1 and some can be as high as 100, indicating that the exact functional test is less sensitive to non-functions with a lower statistical power than Fisher’s exact test. (c) On independent patterns from the null hypothesis, both tests have a similar p-value distribution, indicating a comparable type-I error rate.

Supplementary Files 2, 3, and 4 show p-value distributions on all three table sizes and all three sample sizes. The behaviors of the two tests are consistent with Fig. 4 for 3×3 tables at a sample size of 50. Moreover, the p-value ratio on non-functional patterns shifted to greater values with increased sample sizes on tables of the same sizes. This suggests that the exact functional test demotes nonfunctional patterns more heavily when the sample size is large. No such strong effects are observed for functional or independent patterns.

Therefore, although both tests are similar in absolute statistical power for functional patterns, the exact functional test suppressed the statistical power for non-functional patterns more than Fisher’s exact test. This gives the exact functional test a distinct advantage in promoting functional patterns.

Branch-and-bound reduced empirical run time

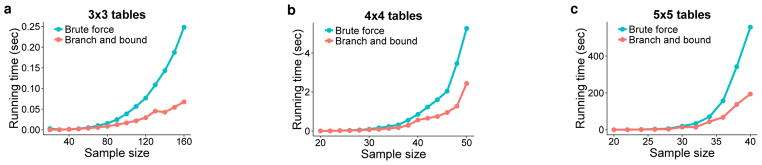
We evaluated the computational efficiency of the branch-and-bound algorithm over a brute-force implementation. We ran both implementations on 840 random contingency tables with increasing table and sample sizes. Fig. 5 shows the average run time as a function of sample size for the two implementations on 3×3, 4×4 and 5×5 contingency tables. As the sample size increases, the run time of the brute-force implementation becomes practically intractable. However, the fast branch-and-bound implementation remarkably reduced the run time for all table sizes and is practical on large tables. This indicates that a large number of branches could be cut or included during table enumeration in calculating the exact p-value.

Fig. 5. Empirical run time of the exact functional test by brute force and branch-and-bound.

We recorded the average empirical run time for the two implementations on 840 random contingency tables with increasing table and sample sizes. The fluctuations in run time were due to the randomness of table marginals. The empirical run time as a function of sample size is shown for (a) 3×3, (b) 4×4, and (c) 5×5 contingency tables.

The more extreme an observed table is, the more the run time will decrease, as more branches can be avoided. The worst-case run time of branch-and-bound is exponential, with very few branches to be cut, and comparable to brute-force enumeration. The best case for branch-and-bound occurs when the p-value approaches either 0 or 1, with the run time enormously reduced due to the extremity of the test statistic.

3.2 Evaluating liver cancer risk factors

To illustrate how directional functional dependency can extend an association study further, we examined an epidemiology study [13] that investigated four risk factors for hepatocellular carcinoma, a type of liver cancer. The risk factors of a person include (1) p53 mutation, (2) cirrhosis, (3) hepatitis, and (4) country risk, called country of origin by Shen et al [13]. The variable of country risk takes a value of low if a patient was from a country or region of a low liver-cancer risk, including the United Kingdom, Europe, and the United States; otherwise, the value is high if a patient was from China, Egypt, or East Asia countries of a high liver-cancer risk. These four factors were studied for their effects on the CpG island methylator phenotype (CIMP). CpG islands are genomic regions enriched of CG nucleotide pairs on one DNA strand. The CIMP status is a global measure of CpG island hypermethylation in promoter regions of multiple tumor suppressor genes [13]. The level of CIMP was used as a direct measure of liver cancer risk, where an elevated CIMP level is associated with carcinogenesis. CIMP is negative (no methylated tumor suppressor genes), intermediate (1 or 2 methylated genes), or positive (>2 methylated genes). Table 1 gives the original data set as contingency tables formed between all risk factor-CIMP pairs. Using Pearson’s chi-square or Fisher’s exact test, the original study reported statistically significant associations between CIMP and all risk factors (Table 2).

TABLE 1.

Clinicopathology correlates of CpG island methylator phenotype (CIMP) status. This table is adapted from Shen et al [13].

	CpG Island Methylator Phenotype (CIMP)
	Negative	Intermediate	Positive
Hepatitis
Negative	12	12	8
Positive	5	22	22
p53 mutation
No	12	26	18
Yes	0	8	12
Country risk
Low risk	14	17	14
High risk	3	19	18
Cirrhosis
Negative	12	16	10
Positive	5	18	21

TABLE 2.

Statistical significance (p-value) of the non-directional association between the CIMP status and liver cancer risk factors [13].

Non-directional Association	p-value
Hepatitis ↔ CIMP	0.010* (Pearson’s chi-square test)
p53 mutation ↔ CIMP	0.017* (Fisher’s exact test)
Country risk ↔ CIMP	0.021* (Fisher’s exact test)
Cirrhosis ↔ CIMP	0.038* (Pearson’s chi-square test)

The p-values highlighted in bold with * are no more than 0.05. The last column is p-values from either Pearson’s chi-square or Fisher’s exact test. If the expected counts in all cells are greater than or equal to 5, Pearson’s chi-square test was applied; otherwise, Fisher’s exact test was used.

However, the statistical methods used in the original study [13] are not designed to provide evidence for directional associations. We therefore performed the exact functional test on the tables separately in each direction from risk factors to CIMP (Table 3) and from CIMP to risk factors (Table 4). The results are consistent with the association tests (Table 2) in that at least one direction of each pair is statistically significant. All significant (p-value ≤ 0.05) directional interactions obtained by the exact functional test constitute a dependency network shown in Fig. 6.

TABLE 3.

Directional association: statistical significance (p-value) of the CIMP status as a function of liver cancer risk factors.

Directional Association	Exact functional test
Hepatitis → CIMP	0.0301*
p53 mutation → CIMP	0.0426*
Country risk → CIMP	0.0716
Cirrhosis → CIMP	0.0706

TABLE 4.

Directional association: statistical significance (p-value) of liver cancer risk factors as a function of the CIMP status.

Directional Association	Exact functional test
CIMP → Hepatitis	0.0108*
CIMP → p53 mutation	0.0273*
CIMP → Country risk	0.0243*
CIMP → Cirrhosis	0.0424*

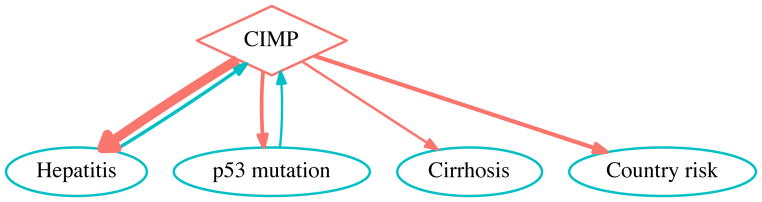
Fig. 6. CIMP-risk factor functional dependency network for liver cancer.

The CIMP status (diamond node) is an epigenetic feature summarizing the number of tumor suppressor genes methylated in their promoter regions leading to function impairment. The oval nodes are risk factors of liver cancer. The edges pointing to CIMP represent the influence of risk factors on the CIMP status—the primary objective of the original study. The edges originating from CIMP represent its predictive power on the risk factors. The network was obtained by the exact functional test and includes only interactions with p-value ≤ 0.05. More significant interactions are indicated by wider directed edges.

In the direction of primary interest (risk factor to CIMP), directional associations from both hepatitis and p53 mutation to CIMP are statistically significant, consistent with the logistic regression analysis result [13]. The exact functional test is more general as it does not assume a parametric form, while the logistic regression assumed the log odd as a linear function of the risk factors. With the lowest p-value, hepatitis is the most significant risk factor for liver cancer among the four. p53 mutation is the only other risk factor that is also significant. Meanwhile, country risk with the highest p-value is an insignificant risk factor. Although the original study [13] concluded that geographic factors, i.e. “country of origin”, may have influenced the methylation of tumor suppressor genes, our analysis suggests that the microenvironment created by hepatitis or p53 mutation may have a much stronger impact on CIMP than country risk.

In the direction of secondary interest from CIMP to risk factors, all risk factors are strongly functionally dependent on CIMP, with CIMP to hepatitis the most significant. A possible causal explanation for the directional association from CIMP to country risk would be that an elevated CIMP of citizens in a country may cause the country to be classified as of high liver-cancer risk.

3.3 Novel noncoding transcripts directionally associated with lung cancer

We sought to identify unannotated transcripts as potential novel noncoding RNAs on which cancer phenotypes functionally depend. FANTOM5 [14] offers an atlas of whole-body human gene expression at the promoter resolution and includes a large number of normal and pathological human cells and tissues. Using a published tissue catalog [21] on FANTOM5 samples, we selected a total of 32 samples classified as lung: 17 lung cancer samples were from cell lines covering 11 lung cancer subtypes; 15 normal lung samples included 12 samples of four types of primary lung cell and also three normal lung tissues. FANTOM5 used CAGE technology to capture a short sequence expressed from each transcription start site (TSS) [14].

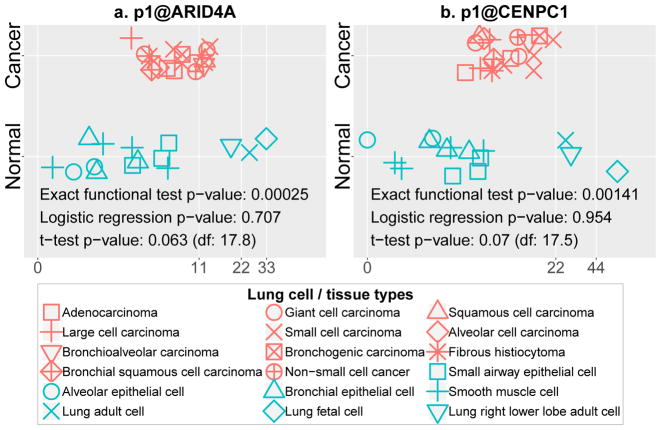
We first applied the exact functional test on two genes known to be associated with lung cancer: ARID4A and CENPC1. ARID4A, a chromatin remodeling gene [22], may be either an oncogene or a tumor suppressor depending on the context [23]. ARID4A has been identified as a suppressor gene in mice leukemia [22] and an associated antigen in human breast cancer [24], [25]. However, Wu et al [26] showed that ARID4A mutation may also promote cancer development by cooperating with the PI3K/Akt pathway. Disruption of CENPC1 (CENP-C ) function was suggested as a cause of some human cancers [27]. CENPC1 is associated with MAD2 expression; MAD2 is a tumor suppressor in human somatic cells [28] and can also promote tumorigenesis in mice [29]. We examined the abundance of two TSSs p1@ARID4A and p1@CENPC1, where p1 specifies the most transcribed promoter of a gene. Figure 7 shows the expression of both TSSs in normal and cancer lung samples. The TSSs in normal samples, similarly distinguishable from those in the cancer samples, show non-monotonicity, suggesting diverse gene expression programs among lung cancer subtypes represented by the different lung cancer cell lines. Figure 7 also indicates how well the expression of both TSSs can predict lung cancer using three methods including the exact functional test, logistic regression, and t-test. The latter two were chosen because both are widely used to identify interesting gene candidates. Logistic regression was applied to the original continuous values of gene expression and unpaired t-test with unequal variance on the normalized continuous data. In both cases, the exact functional test reported significant p-values (<0.05), but logistic regression and t-test missed both. This outcome is expected because neither logistic regression nor t-test was designed to detect non-monotonic patterns.

Fig. 7. Non-monotonic functional dependency of lung cancer phenotype on the expression level of two known cancer genes.

The horizontal axis is the abundance of TSS in a sample in tags per million. We compared the exact functional test with unpaired t-test (unequal variance) and logistic regression in finding cancer associations with these genes. (a) Non-monotonic functional dependency of lung cancer on gene p1@ARID4A. (b) Non-monotonic functional dependency of lung cancer on gene p1@CENPC1.

Next, we used the exact functional test to screen potential noncoding RNAs involved in lung cancer from 91,213 unannotated but robustly expressed TSSs in FANTOM5. We found 1049 unannotated TSSs on which lung cancer phenotypes exhibited stronger dependencies than 95% of the 589 curated cancer genes from COSMIC Cancer Gene Census [15]. Supplementary File 7 lists all detected 1049 unannotated TSSs with coordinates based on the human reference genome version hg19; these TSSs constitute our hypotheses of novel noncoding RNAs associated with lung cancer. The main steps of this screening are described in Supplementary Note 8.

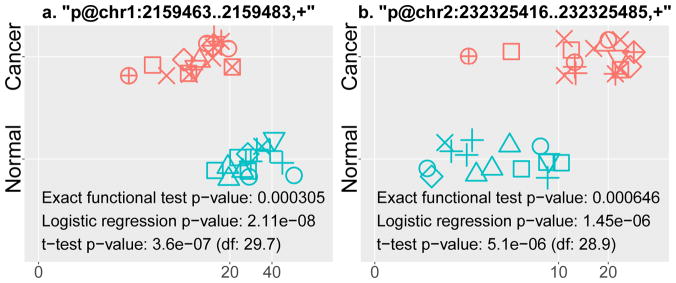
Figure 8 highlights the expression pattern of two of the 1049 TSSs in lung cancer cell-lines versus normal lung tissues. The first TSS (p@chr1:2159463..2159483,+) in Fig. 8a is located in a DNase hypersensitive genomic region on a CpG island along the forward strand of chromosome 1. On human reference genome assembly hg19 in UCSC Genome Browser [30] with regulatory elements from ENCODE [31], twenty transcription factors bind to this site, with POLR2A and TAF1 having the strongest binding signals. POLR2A has been identified to be an indispensable gene in the proximity of cancer gene TP53 [32]. TAF1 mutation has been reported to be associated with multiple cancer types including lung cancer [33]. Furthermore, histone mark H3K27ac is observed at and around this TSS site, suggesting active enhancers among those marked by H3K4me1 only [34]. In addition, the gene SKI, noted for its role in breast cancer [3], is 651bp downstream of this TSS. Its proximity to a cancer gene adds additional evidence to its tumor involvement. Figure 8b presents another TSS (p@chr2:232325416..232325485,+) that is antisense exonic to gene NCL on chromosome 2. Antisense long non-coding RNAs (lncRNAs) can play a role in regulating their neighboring genes [35]. Moreover, NCL was observed to be highly expressed on the surface of lung cancer cells, and its NCL-targeting aptamer (aptNCL ) was considered to be a promising tumor cell-specific targeting carrier to recognize the NCL-expressing cells [36]. Given the strong lung-cancer specific expression patterns and supporting evidence from the literature, we hypothesize both unannotated TSSs may be putative lung cancer-associated non-coding transcripts and merit further biological investigation.

Fig. 8. Two putative noncoding RNAs with unannotated transcript start sites that are directionally associated with lung cancer phenotype.

The legend is the same with Fig. 7. (a) An intergenic TSS repressed in cancer is located on the forward strand of chromosome 1. (b) An antisense exonic TSS, induced in cancer, is located within known cancer gene NCL on the forward strand of chromosome 2.

4 Discussion

We have presented a novel exact functional test to detect functional dependency in contingency tables based on the exact null multivariate hypergeometric distribution. It is the only exact statistical inference instrument for directional association as far as we are aware. Our simulation studies have also shown that the exact functional test outperformed Fisher’s exact test in reducing statistical power on nonfunctional patterns to favor functional patterns.

As Fisher’s exact test detects symmetric—instead of directional—association among discrete random variables, it is sensitive to both dependent non-functional and functional patterns, limiting its effectiveness on recognizing functional relationships.

The fast branch-and-bound algorithm for the exact functional test is practically efficient to use—the more extreme the true p-value is, the more remarkable the run time reduction. The table enumeration problem is considered to be challenging, where a specific exact test involving Pearson’s chi-square was proved to be NP-hard [37]. We thus postulate that the exact functional test may also be NP-hard.

The two cancer biology applications not only revealed key liver cancer risk factors and new potential biomarkers for lung cancers, but also illustrated how the exact functional test addressed complex pattern recognition questions not easily answered by existing statistical association tests. We anticipate the exact functional test to become an important methodology, to be used in conjunction with or in place of Fisher’s exact test, for scientific discovery via directional associations.

Software availability

The exact functional test is implemented as the fun.chisq.test(…, method=“exact”, …) function within the R package FunChisq (≥2.4.3) in Comprehensive R Archive Network. The branch-and-bound algorithm is internally coded in C++. The package is freely downloadable from https://CRAN.R-project.org/package=FunChisq

Supplementary Material

Supplementary File 1. Supplementary File 1—”S1-EFT-sup.pdf”.

Supplementary Note 1: Pearson’s chi-square test of association.

Supplementary Note 2: Fisher’s exact test.

Supplementary Note 3: Symmetry of the exact functional test on 2-by-2 contingency tables.

Supplementary Note 4: A fast and exact algorithm by branch and bound.

Supplementary Note 5: Upper bound of sum of squares with linear inequality constraints.

Supplementary Note 6: Lower bound of sum of squares with linear inequality constraints.

Supplementary Note 7: The house noise model.

Supplementary Note 8: Screening putative noncoding RNAs on which lung cancer phenotypes functionally depends.

Supplementary Figure 1: An example of the house noise model.

Supplementary File 2. Supplementary File 2—”S2_functional.pdf”.

On noisy functional patterns, the exact functional test and Fisher’s exact test have a similar statistical power. The p-value ratio distributions of the two tests are shown. Exactly 100 tables for each of size 2×3 to 4×4 and sample size 30 to 50 were simulated to generate each distribution. Each type of table was subjected to house noise at three levels of 0, 0.1 and 0.5.

Supplementary File 3. Supplementary File 3—”S3_dependent_non_functional.pdf”.

On noisy dependent non-functional patterns, the exact functional test has a lower statistical power than Fisher’s exact test. The p-value ratio distributions of the two tests are shown. Exactly 100 tables for each of size 2×3 to 4×4 and sample size 30 to 50 were simulated to generate each distribution. Each type of table was subjected to house noise at three levels of 0, 0.1 and 0.5.

Supplementary File 4. Supplementary File 4—”S4_independent.pdf”.

On noisy independent patterns, the exact functional test and Fisher’s exact test show similar significance level distributions. The p-value ratio distributions of the two tests are shown. Exactly 100 tables for each of size 2×3 to 4×4 and sample size 30 to 50 were simulated to generate each distribution. Each type of table was subjected to house noise at three levels of 0, 0.1 and 0.5.

Supplementary File 5. Supplementary File 5—”EFT_lung_cancer_genes.R”.

This R source code file contains a script to apply three methods, including the functional exact test, t-test, and logistic regression on two known lung cancer cancer-associated genes (ARIDA4A, CENPC1) in Fig. 7 and two unannotated genes in Fig. 8.

Supplementary File 6. Supplementary File 6—”Gene_expression.txt”.

This is the input data file for the R script file given as Supplementary File 5. This file contains the abundance of transcription start sites for ARID4A and CENPC1 in Fig. 7 and the two unannotated genes in Fig. 8 extracted from FANTOM5.

Supplementary File 7. Supplementary File 7—”Novel_unannotated_cancer_TSSs.tsv”.

A list of 1049 unannotated transcription start sites directionally associated with lung cancer, at a significance level higher than 95% of all 589 well-known cancer genes. Coordinates are within human reference genome hg19 or GRCh37. Most of these are likely to be novel putative noncoding RNAs directionally associated with lung cancer.

Biographies

Hua Zhong received the BS degree in computer science from both Nanjing University of Posts and Telecommunications and New York Institute of Technology. He received the MS degree in computer science from New Mexico State University, where he is a PhD candidate in the Department of Computer Science. His research interests include algorithm design for network inference and next-generation sequencing data analysis. He has contributed to the statistical computing R package FunChisq and developed computer programs to discovery cancer molecular patterns and detect plant genome duplication events.

Mingzhou Song received the BS degree in electrical engineering from Beijing University of Posts and Telecommunications, the MS and PhD degrees from the Department of Electrical Engineering at the University of Washington at Seattle. He was an assistant professor in the Department of Computer Science at Queens College of City University of New York. In 2005, he joined the New Mexico State University, where he is a professor in the Department of Computer Science. His research interests include statistical foundations for pattern discovery, data science algorithms for network inference, and applications to molecular biological systems. Two software packages (FunChisq and Ckmeans.1d.dp) developed by his lab have been downloaded worldwide over 106,000 times and are available in seven programming languages.