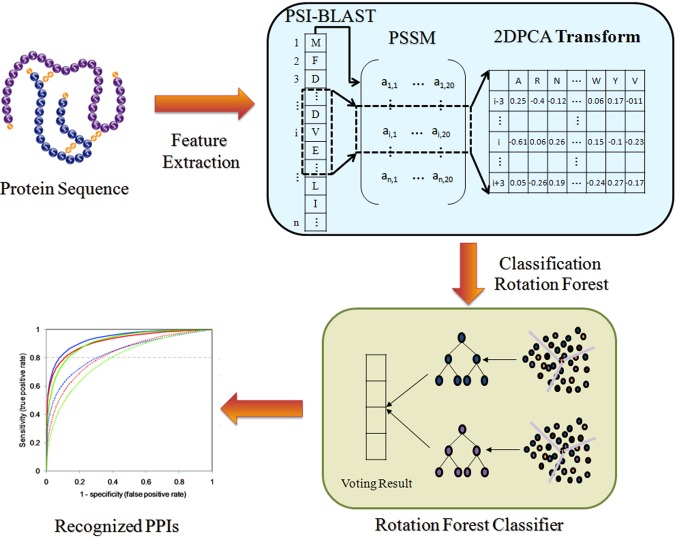
Abstract
The interaction among proteins is essential in all life activities, and it is the basis of all the metabolic activities of the cells. By studying the protein-protein interactions (PPIs), people can better interpret the function of protein, decoding the phenomenon of life, especially in the design of new drugs with great practical value. Although many high-throughput techniques have been devised for large-scale detection of PPIs, these methods are still expensive and time-consuming. For this reason, there is a much-needed to develop computational methods for predicting PPIs at the entire proteome scale. In this article, we propose a new approach to predict PPIs using Rotation Forest (RF) classifier combine with matrix-based protein sequence. We apply the Position-Specific Scoring Matrix (PSSM), which contains biological evolution information, to represent protein sequences and extract the features through the two-dimensional Principal Component Analysis (2DPCA) algorithm. The descriptors are then sending to the rotation forest classifier for classification. We obtained 97.43% prediction accuracy with 94.92% sensitivity at the precision of 99.93% when the proposed method was applied to the PPIs data of yeast. To evaluate the performance of the proposed method, we compared it with other methods in the same dataset, and validate it on an independent datasets. The results obtained show that the proposed method is an appropriate and promising method for predicting PPIs.
Introduction
Since the interactions among proteins play an extremely important role in almost all biological processes, many researchers have designed innovative techniques for detecting Protein-Protein Interactions (PPIs) in post genome era1,2. Over the past several decades, various high-throughput techniques have been proposed and designed, including yeast two-hybrid (Y2H) system2–4, microarray analysis5, and mass spectrometry4,6, for large-scale and systematic prediction of PPIs. However, the PPIs determined from these traditional biological experiment methods only accounts for a small proportion of the PPIs network7–9. In addition, the high-throughput experiment methods are usually expensive and time-consuming with high ratio of both false-positives and false-negatives10–13. To predict the PPIs more efficiently and at low cost, various computational-based approaches have been proposed so far to solve this problem14–19. These computational approaches can be roughly classified into structure based methods, literature knowledge based methods, network topology based methods, and genome based methods, according to the information they perform on their tasks20. However, the application of these approaches is restricted, because they can hardly be practiced if the pre-knowledge of the proteins is unavailable19,21,22.
More recently, researchers have become increasingly interested in determining whether proteins interact by using information obtained directly from the protein amino acid sequence13,23–26. Numerous studies have indicated that the information extracted from protein amino acid sequences alone is sufficient to predict the interactions of proteins27,28. Pitre et al. proposed the PIPE algorithm based on the hypothesis that some of the protein interactions are mediated by a limited number of short polypeptide sequences. In the detection of yeast protein interactions PIPE realized an overall accuracy of 75% with 61% sensitivity and a specificity of 89%29. Shen et al. using only protein sequences information developed a method for PPIs prediction. The method combines the conjoint triad feature for describing amino acids and learning algorithm based on support vector machine (SVM). In the five-fold cross-validation, they achieved an accuracy of 83.90%30. Guo et al. combined the automatic covariance features extracted from the protein amino acid sequences and the support vector machine classifier to predict the interaction among proteins. This method has obtained an average accuracy of 86.55% when performed on the Saccharomyces cerevisiae dataset7.
In this article, we develop a new sequence-based approach to predict PPIs using the matrix-based protein sequence descriptors combined with the Rotation Forest (RF). In detail, we first represent the protein sequence as the Position-Specific Scoring Matrix (PSSM) and use the two-dimensional Principal Component Analysis (2DPCA) algorithm to extract numerically descriptor to characterize the protein amino acid sequence. We then construct the feature vector of the protein pair by coding two protein vectors in this pair. Finally, the feature vectors of these protein pairs are sent to the RF classifier for classification. In order to assess the ability of the proposed model to predict PPIs, we use Yeast and Helicobacter pylori datasets to verify it. In the experiment, our model achieved 97.43% and 88.07% prediction accuracy with 94.92% and 78.20% sensitivity at the specificity of 99.93% and 97.44% on these two datasets. Furthermore, we evaluated the ability of the proposed model on independent datasets (C.elegans, E.coli, H.sapiens and M.musculus), where 91.43%, 99.93%, 92.00% and 90.73% of the prediction accuracy were generated, respectively.
Results and Discussions
Evaluation Criteria
In this study, we use five-fold cross-validation technique to verify the predictive power of our model. All samples are randomly divided into almost the same number of 5 subsets, each subset containing interacting and non-interacting protein pairs. Four subsets are used as training sets each time, and the remaining one subset is used as a test set, the process is repeated five times so that every subset is used as a test set once. The performance of the method is the average of the 5 sets performances. Several evaluation criteria used in our study to estimate the predictive power of our model including accuracy (Accu.), sensitivity (Sen.), precision (Prec.), and Matthews correlation coefficient (MCC). The calculation formulas are listed below:
| 1 |
| 2 |
| 3 |
| 4 |
where True Positive (TP) represents the number of correct classification of positive samples, False Positive (FP) represents the number of incorrect classification of positive samples, True Negative (TN) represents the number of correct classification of negative samples, and False Negative (FN) represents the number of incorrect classification of negative samples.
We also produce Receiver Operating Characteristic (ROC) curves31 to estimate the performance of the classifier. Typically, the random classification threshold of the two-class classifier is 0.5. When the new classification results are accepted, the threshold will change along with the true positive rate and the false positive rate, and this change will be plotted in the form of graphics. In addition, the Area Under a Curve (AUC) is calculated in the experiment. The performance of different prediction methods can be expressed directly with AUC values, which is considered to be better than the other method when the AUC value of one method is greater than the value of another method.
Evaluation of model predictive ability
We appraise the ability of our model using the Golden Standard Datasets. To ensure the stability of the experimental results, the five-fold cross-validation is exploited in the experiment. The parameters of the rotation forest (feature subset number K and decision trees number L) were tested within the range of values by the grid search method to expect to achieve better performance. Considering the accuracy rate and time cost of the rotation forest, as a result the best parameter we get K is 20 and L is 2.
The experimental results of the RF classifier and the matrix-based protein amino acids sequences representation is summarized in Table 1. As seen from the Table 1 that the average accuracy of our approach is as high as 97.43%. In order to more fully show the predicted results of our approach, we also calculated the values of precision, sensitivity, MCC, and AUC. From Table 1, we can see that our model has achieved good experimental results, the sensitivity value of 94.92%, the precision value of 99.93%, the MCC value of 94.97%, and the AUC value of 97.51%. Furthermore, it can be seen from the table that the standard deviation of accuracy, sensitivity, precision, MCC, and AUC is 0.30%, 0.43%, 0.17%, 0.59% and 0.47%, respectively. Figure 1 plots the ROC curve generated by our method on the Yeast dataset. X-axis expresses false positive rate (FPR) and Y-axis expresses true positive rate (TPR) in the figure.
Table 1.
The five-fold cross-validation results achieved on the Yeast dataset using the proposed method.
| Testing set | Accu. (%) | Sen. (%) | Prec. (%) | MCC (%) | AUC (%) |
|---|---|---|---|---|---|
| 1 | 97.50 | 95.04 | 100.00 | 95.11 | 97.27 |
| 2 | 96.92 | 94.32 | 99.63 | 93.98 | 96.88 |
| 3 | 97.63 | 95.22 | 100.00 | 95.37 | 97.89 |
| 4 | 97.68 | 95.38 | 100.00 | 95.46 | 97.46 |
| 5 | 97.41 | 94.66 | 100.00 | 94.94 | 98.05 |
| Average | 97.43 ± 0.30 | 94.92 ± 0.43 | 99.93 ± 0.17 | 94.97 ± 0.59 | 97.51 ± 0.47 |
Figure 1.
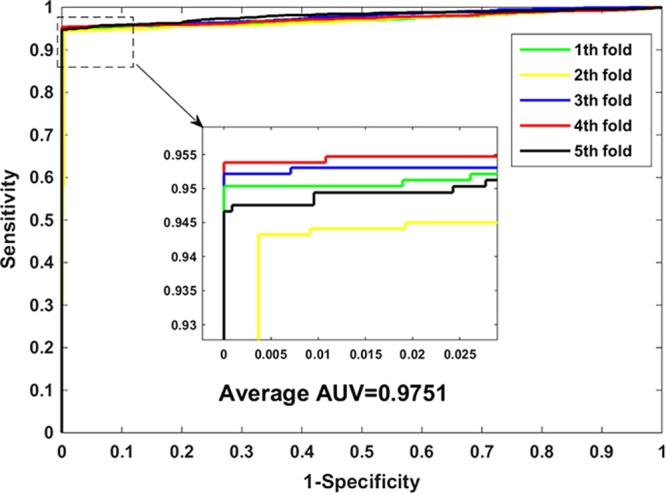
The ROC curves performed on the Yeast dataset using the proposed method.
In order to further evaluate the ability of our approach to predict PPIs, we tested it against the H. pylori dataset. In the experiment, the same classifier parameters and feature extraction algorithm are used. Table 2 lists the experimental results of cross-validation. We achieved the high accuracy of 88.07%, the sensitivity value of 78.20%, the precision value of 97.44%, the MCC value of 77.66%, and the AUC value of 88.76% on the H. pylori dataset. In addition, from Table 2 we can also observe that the standard deviation of accuracy, sensitivity, precision, MCC, and AUC is 0.77%, 0.97%, 0.90%, 1.46% and 1.32%, respectively. Figure 2 plots the ROC curve generated by our method on the H. pylori dataset.
Table 2.
The five-fold cross-validation results achieved on the H. pylori dataset using the proposed method.
| Testing set | Accu. (%) | Sen. (%) | Prec. (%) | MCC (%) | AUC (%) |
|---|---|---|---|---|---|
| 1 | 88.68 | 79.23 | 96.98 | 78.51 | 88.36 |
| 2 | 86.79 | 77.03 | 96.20 | 75.21 | 86.71 |
| 3 | 88.68 | 79.12 | 98.33 | 79.00 | 90.22 |
| 4 | 88.16 | 78.05 | 97.39 | 77.76 | 89.18 |
| 5 | 88.01 | 77.55 | 98.28 | 77.83 | 89.33 |
| Average | 88.07 ± 0.77 | 78.20 ± 0.97 | 97.44 ± 0.90 | 77.66 ± 1.46 | 88.76 ± 1.32 |
Figure 2.
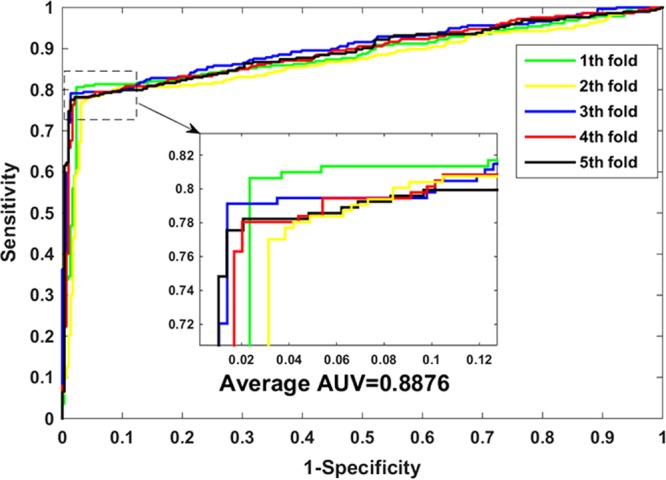
The ROC curves performed on the H. pylori dataset using the proposed method.
Comparison of the proposed model with different classifiers and descriptors
Machine learning has been successfully and reliably applied to predictive PPIs. Wherein, SVM is one of the famous algorithms based on statistical learning theory. To verify the predictive ability of our approach, we compare the RF classifier with the SVM classifier based on the same feature extraction method. For the SVM classifier, the LIBSVM we used can be downloaded at www.csie.ntu.edu.tw/~cjlin/libsvm, which was originally proposed by Chang and Lin32. The grid search method is used to optimize SVM parameters and the optimal parameters c and g on this dataset are 0.1 and 0.5, respectively.
The experimental prediction results of the SVM combined with the protein sequence descriptor are listed in Table 3. It can be observed from Table 3 that the accuracy of SVM on the Yeast dataset is 87.29%, wherein the results of five experiments are 87.84%, 85.47%, 87.71%, 89.23%, and 86.21%. However, the rotation forest classifier achieves an average accuracy of 97.43%. To show the prediction ability of our approach more comprehensively, we calculated the values of precision, sensitivity, MCC, and AUC. As seen from the Table 3, the prediction result of the SVM classifier with the sensitivity value of 84.42%, precision value of 89.58%, MCC value of 74.73%, and AUC value of 94.59%. Furthermore, we can see in detail from Table 3 that the standard deviation of accuracy, sensitivity, precision, MCC, and AUC is 1.48%, 1.88%, 2.02%, 2.93% and 0.56%, respectively. The accuracy, sensitivity, precision, MCC and AUC of the RF classifier is 10.14%, 10.50%, 10.35%, 20.24% and 2.92% higher than that of the SVM classifier. From the comparison of experimental results we can see that the evaluation criteria based on SVM classifier are all lower than those of our model. The ROC curves performed by support vector machine classifier on Yeast dataset were shown in Fig. 3.
Table 3.
The five-fold cross-validation results achieved on the Yeast dataset using the SVM classifier.
| Testing set | Accu. (%) | Sen. (%) | Prec. (%) | MCC (%) | AUC (%) |
|---|---|---|---|---|---|
| 1 | 87.84 | 85.37 | 90.00 | 75.79 | 94.80 |
| 2 | 85.47 | 81.48 | 89.20 | 71.27 | 94.13 |
| 3 | 87.71 | 83.84 | 90.63 | 75.60 | 94.41 |
| 4 | 89.23 | 86.41 | 91.71 | 78.59 | 95.47 |
| 5 | 86.21 | 85.00 | 86.36 | 72.38 | 94.16 |
| Average | 87.29 ± 1.48 | 84.42 ± 1.88 | 89.58 ± 2.02 | 74.73 ± 2.93 | 94.59 ± 0.56 |
| Our method | 97.43 ± 0.30 | 94.92 ± 0.43 | 99.93 ± 0.17 | 94.97 ± 0.59 | 97.51 ± 0.47 |
Figure 3.
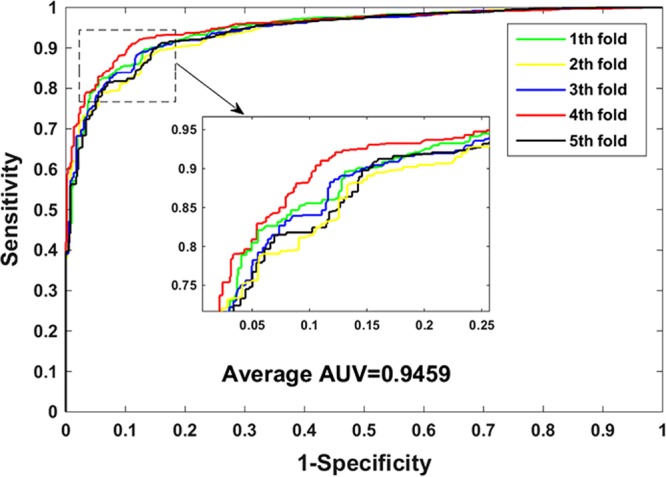
The ROC curves performed on the Yeast dataset using the SVM classifier.
To further evaluate the performance of our approach, we also compared it with different descriptors. In the experiment, we selected feature extraction algorithms including Auto Covariance (AC) and Discrete Cosine Transform (DCT) to perform experiments on the Yeast dataset. The introduction of these feature extraction algorithms can be viewed in the supplementary file.In addition, we also verified the protein descriptors without feature extraction. Table 4 summarizes the comparison results of the proposed feature descriptor with the above three descriptors. It can be seen from Table 4 that our feature descriptors have obtained the best results on accuracy, sensitivity, and MCC. The precision is only 0.07% lower than the highest AC descriptor and DCT descriptor. This indicates that the 2DPCA algorithm can effectively extract the features of the protein and help improves the prediction performance of the model.
Table 4.
The performance comparison among different descriptor on the Yeast dataset.
| Descriptor | Accu. (%) | Sen. (%) | Prec. (%) | MCC (%) |
|---|---|---|---|---|
| AC | 93.14 ± 0.69 | 86.28 ± 1.23 | 100.00 ± 0.00 | 87.10 ± 1.20 |
| DCT | 93.65 ± 0.67 | 87.30 ± 1.41 | 100.00 ± 0.00 | 88.02 ± 1.21 |
| Original | 81.50 ± 0.62 | 70.55 ± 0.51 | 90.33 ± 1.94 | 64.57 ± 1.65 |
| 2DPCA | 97.43 ± 0.30 | 94.92 ± 0.43 | 99.93 ± 0.17 | 94.97 ± 0.59 |
Comparison with Existing Method
In the past few years, many research teams have put forward a variety of computational methods to solve the problem of PPI prediction. By comparison with these models on the Yeast and H. pylori datasets, we can more clearly evaluate the proposed method. We selected accuracy, precision, sensitivity, and MCC as evaluation indicators that are listed in Tables 5 and 6. Table 5 summarizes the experimental results of different approaches on the Yeast dataset. From the table we can clearly see that the range of accuracy generated by the other methods is from 75.08% to 89.33%, the range of sensitivity generated is from 75.81% to 89.93%, the range of precision generated is from 74.75% to 90.24%, and corresponding experimental results we generated were 97.43%, 94.92%, 99.93%, 94.97%, these results are lower than what we have achieved. Table 6 shows the performance of different models on the H. pylori dataset. It can be seen that the range of accuracy generated by the other approaches is from 75.80% to 87.50%, the range of sensitivity obtained is from 69.80% to 88.95%, the range of precision obtained is from 80.20% to 86.15%, and the corresponding experimental results we obtained were 88.07%, 78.20%, 97.44%, and 77.66%. Except for the precision and MCC slightly lower, the accuracy and sensitivity are higher than the highest value.
Table 5.
The performance comparison between different methods on the Yeast dataset.
| Author | Model | Accu. (%) | Sen. (%) | Prec. (%) | MCC (%) |
|---|---|---|---|---|---|
| Guos’ work7 | ACC | 89.33 ± 2.67 | 89.93 ± 3.68 | 88.87 ± 6.16 | N/A |
| AC | 87.36 ± 1.38 | 87.30 ± 4.68 | 87.82 ± 4.33 | N/A | |
| Zhous’ work40 | SVM + LD | 88.56 ± 0.33 | 87.37 ± 0.22 | 89.50 ± 0.60 | 77.15 ± 0.68 |
| Yangs’ work41 | Cod1 | 75.08 ± 1.13 | 75.81 ± 1.20 | 74.75 ± 1.23 | N/A |
| Cod2 | 80.04 ± 1.06 | 76.77 ± 0.69 | 82.17 ± 1.35 | N/A | |
| Cod3 | 80.41 ± 0.47 | 78.14 ± 0.90 | 81.86 ± 0.99 | N/A | |
| Cod4 | 86.15 ± 1.17 | 81.03 ± 1.74 | 90.24 ± 0.45 | N/A | |
| Yous’ work42 | PCA-EELM | 87.00 ± 0.29 | 86.15 ± 0.43 | 87.59 ± 0.32 | 77.36 ± 0.44 |
| Our method | RF + PSSM | 97.43 ± 0.30 | 94.92 ± 0.43 | 99.93 ± 0.17 | 94.97 ± 0.59 |
Table 6.
The performance comparison of different methods on the H. pylori dataset.
| Model | Accu. (%) | Sen. (%) | Prec. (%) | MCC (%) |
|---|---|---|---|---|
| Signature products34 | 83.40 | 79.90 | 85.70 | N/A |
| Ensemble ELM42 | 87.50 | 88.95 | 86.15 | 78.13 |
| Phylogentic bootstrap43 | 75.80 | 69.80 | 80.20 | N/A |
| HKNN44 | 84.00 | 86.00 | 84.00 | N/A |
| Ensemble of HKNN45 | 86.60 | 86.70 | 85.00 | N/A |
| Boosting46 | 79.52 | 80.37 | 81.69 | 70.64 |
| Our method | 88.07 | 78.20 | 97.44 | 77.66 |
Prediction Ability on Independent Datasets
To further estimate the proposed model, we decided to verify its performance on an independent datasets. We apply all of the 11188 pairs from the Yeast dataset as the training set in our final prediction model, the test set is composed of C.elegans, E.coli, H.sapiens and M.musculus datasets from the DIP database. The number of protein pairs they contained was 4013, 6954, 1413, and 313, respectively. In the experiment, we utilize the same matrix representation and feature extraction algorithm for these datasets, and we also use the same parameters for rotation forest classification. Table 7 lists the prediction results of four independent datasets based on our method. We can observe from Table 7 that the high accuracy of 91.43% was acquired on the C.elegans dataset, 99.93% accuracy on the E.coli dataset, 92.00% accuracy on the H.sapiens dataset, and 90.73% accuracy on the M.musculus dataset. All of these results demonstrate that our approach is a suitable method for predicting the interactions of other species.
Table 7.
Predictive results of four species based on the proposed method.
| Species | Test pairs | Accu. (%) |
|---|---|---|
| C.elegans | 4013 | 91.43 |
| E.coli | 6954 | 99.93 |
| H.sapiens | 1412 | 92.00 |
| M.musculus | 313 | 90.73 |
Conclusions
In this article, we develop an efficient and practical prediction approach, which utilizes protein sequence information combined with feature descriptors to accurately predict protein interactions at high speed. It is well known that the most important challenge of sequence-based algorithm is to find appropriate features to adequately represent the information of protein interactions. For this purpose, we transform the protein sequences into the PSSM and use the 2DPCA algorithm to extract their features, extracting as much as possible the hidden information in the primary sequence of the protein. Then the rotation forest is applied to guarantee the reliability of prediction. In comparison with the SVM classifier and other approaches, our model has achieved excellent results. Furthermore, we validate our model on the independent datasets. The excellent results show that our model performed well in the prediction of protein interactions. In future research, we will focus on finding better ways to describe protein sequences to accurately identify interacting and non-interacting protein pairs.
Materials and Methodology
Golden Standard Datasets
In the experiments we used the real Yeast PPIs dataset, which was collected from Saccharomyces cerevisiae core subset of Database of Interacting Proteins (DIP)33 by Guo et al.7. A total of 5966 interaction protein pairs are included in the Saccharomyces cerevisiae core subset. In order to remove the redundant in the dataset, we deleted protein pairs with the sequence identity of more than 40% or protein pairs with the protein residue of less than 50. The number of these redundant protein pairs is 372. Therefore, the remaining 5594 protein pairs constitute the positive dataset of golden standard. To construct the negative dataset, we in accordance with the hypothesis that the proteins do not interact with each other in different subcellular compartments, and strictly according to Guo’s work procedure, we finally obtained 5594 protein pairs. Therefore, the complete Yeast PPIs dataset contains 11188 pairs, half of which are from the positive dataset and half from the negative dataset. Another dataset we used was the Helicobacter pylori dataset collected by Martin et al.34 consisting of 2916 pairs. There are interacting protein pairs and non-interacting protein pairs each accounted for fifty percent.
Position-Specific Scoring Matrix
Position-Specific Scoring Matrix (PSSM) is proposed by Gribskov et al.35 to detect distantly related protein. The structure of PSSM is a matrix of N rows and 20 columns. Suppose and each matrix is represented as follows:
| 5 |
where εi,j in the i row of PSSM mean that the probability of the ith residue being mutated into type j of 20 native amino acids during the procession of evolutionary in the protein from multiple sequence alignments.
In our experiment, we introduced the Position-Specific Iterated BLAST (PSI-BLAST) tool26,36 and the SwissProt database to create the PSSM for each protein amino acid sequence. The PSI-BLAST is a highly sensitive protein sequence alignment program that is effective in discovering new members of protein family and similar proteins in distantly related species. To obtain more homologous sequences, we set the e-value to 0.001, the number of iterations to 3, and the default value of the other parameters. We can download the SwissProt database and PSI-BLAST tool from, http://blast.ncbi.nlm.nih.gov/Blast.cgi.
Two-dimensional Principal Component Analysis
Two-dimensional Principal Component Analysis (2DPCA)37,38 is an effective feature extraction algorithm based on two-dimensional matrix, which has been universally used in a variety of fields. It can be directly applied to the two-dimensional matrix and significantly reduces the computational complexity and the probability of singularity in feature extraction. The 2DPCA does not need to convert the matrix into a row vector or a column vector first, but directly uses the two-dimensional projection method for feature extraction. Studies have shown that extracting features directly from the matrix mode without vectorization preprocessing can not only reduce the computational complexity, but also improve performance in subsequent classification based on nearest neighbor rules. Therefore, the 2DPCA algorithm has the advantages of feature extraction directly, less generated feature data and less time consuming. The 2DPCA algorithm is described as follows.
Assuming that the sample number is N and the ith matrix is Vi (i = 1, 2, …, N), this means can be calculated as follows:
| 6 |
In the 2DPCA algorithm, the matrix V is projected onto the optimal projection matrix, so we can get the following formula:
| 7 |
Thus we can get an M-dimensional projection vector F. The optimal projection axis X is determined by the dispersion of eigenvector F, and uses the following equation:
| 8 |
where Sx denotes the covariance matrix of the projection eigenvector F, and trace (Sx) denotes the trace of Sx. The purpose of the maximizing criterion is to search for an optimal projection direction to maximize the total scatter matrix of the training samples. The covariance matrix Sx is represented as:
| 9 |
so,
| 10 |
Define total scatter matrix Gt as:
| 11 |
The formula for calculating Gt is:
| 12 |
Therefore, the criterion function can be written as:
| 13 |
where X is a unit column vector. The first d maximum eigenvalues of the covariance matrix corresponding to the orthogonal eigenvectors constitute the optimal projection axis X1, X2, …, Xd. The matrix V is projected onto the vector X1, X2, …, Xd, and extract its features, let
| 14 |
A new set of eigenvectors F1, F2, …, Fd, can be obtained by calculation (14), which is the principal component of matrix V. In the 2DPCA algorithm, we expect to find the appropriate number of projection axes so that it can reduce the dimensionality of the data without losing useful information.
Rotation Forest
Rotation forest16 is a popular ensemble classifier which has been proposed recently. RF first divides the attributes set of samples randomly, and transforms the attribute subsets by means of linear transformation to increase the difference between the subsets. Then use the transformed attribute subsets to train different classifiers and finally obtain reliable classification results39.
Assume that {xi, yi} contains T samples, of which xi = (xi1, xi2, …, xin) is an n-dimensional feature vector. Let X be the training sample set, Y be the label set and S be the feature set. X is a training set containing T training samples, forming a matrix of T × n. Suppose the number of decision trees is D, then the decision trees can be represented as F1, F2, …, Fd. The rotation forest algorithm is implemented as follows.
Select the suitable parameter K, randomly divide S into K parts of the disjoint subsets, the number of features that each subset contains is .
Let Si,j be the j-th feature subset and use it for classifier Fi training. For each feature subset, a non-empty subset is randomly selected and repeatedly sampled in a certain proportion, forming a sample subset .
Principal component analysis is performed on to obtain Mi,j principal components.
The coefficients obtained in the matrix Mi,j are constructed a sparse rotation matrix Gi, which is expressed as follows:
| 15 |
During the prediction period, a test sample x generated by the classifier Fi of is provided to determine that x belongs to class yi. Next, the class of confidence is calculated by means of the average combination, and the formula is as follows:
| 16 |
Then assign the category with the largest λj(x) value to x. The flow chart of our approach is shown as Fig. 4.
Figure 4.
Flow chart of the proposed method.
Electronic supplementary material
Acknowledgements
This work is supported in part by the National Science Foundation of China, under Grants 61373086, 61572506, 61702444, in part by Guangdong Natural Science Foundation, under Grant 2014A030313555 and in part by the Pioneer Hundred Talents Program of Chinese Academy of Sciences, and in part by the CCF-Tencent Open Fund. The authors would like to thank all anonymous reviewers for their constructive advices.
Author Contributions
L.W., Z.Y. and X.Y. conceived the algorithm, carried out the analyses, prepared the data sets, carried out experiments, and wrote the manuscript. S.X., F.L., L.L., W.Z. and Y.Z. designed, performed and analyzed experiments and wrote the manuscript. All authors read and approved the final manuscript.
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Lei Wang and Zhu-Hong You contributed equally.
Contributor Information
Lei Wang, Email: leiwang@cumt.edu.cn.
Zhu-Hong You, Email: zhuhongyou@xjb.ac.cn.
Electronic supplementary material
Supplementary information accompanies this paper at 10.1038/s41598-018-30694-1.
References
- 1.Zhang, Q. C. et al. Structure-based prediction of protein-protein interactions on a genome-wide scale. Nature490, 556-+, 10.1038/nature11503 (2012). [DOI] [PMC free article] [PubMed]
- 2.Krogan NJ, et al. Global landscape of protein complexes in the yeast Saccharomyces cerevisiae. Nature. 2006;440:637–643. doi: 10.1038/nature04670. [DOI] [PubMed] [Google Scholar]
- 3.Ito T, et al. A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:4569–4574. doi: 10.1073/pnas.061034498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ho Y, et al. Systematic identification of protein complexes in Saccharomyces cerevisiae by mass spectrometry. Nature. 2002;415:180–183. doi: 10.1038/415180a. [DOI] [PubMed] [Google Scholar]
- 5.Templin MF, et al. Protein microarrays: Promising tools for proteomic research. Proteomics. 2003;3:2155–2166. doi: 10.1002/pmic.200300600. [DOI] [PubMed] [Google Scholar]
- 6.Trinkle-Mulcahy L, et al. Identifying specific protein interaction partners using quantitative mass spectrometry and bead proteomes. Journal of Cell Biology. 2008;183:223–239. doi: 10.1083/jcb.200805092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Guo Y, Yu L, Wen Z, Li M. Using support vector machine combined with auto covariance to predict proteinprotein interactions from protein sequences. Nucleic Acids Research. 2008;36:3025–3030. doi: 10.1093/nar/gkn159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.You, Z.-H., Yin, Z., Han, K., Huang, D.-S. & Zhou, X. A semi-supervised learning approach to predict synthetic genetic interactions by combining functional and topological properties of functional gene network. Bmc Bioinformatics11, 10.1186/1471-2105-11-343 (2010). [DOI] [PMC free article] [PubMed]
- 9.Zhu, L., You, Z.-H., Huang, D.-S. & Wang, B. LSE: A Novel Robust Geometric Approach for Modeling Protein-Protein Interaction Networks. Plos One8, 10.1371/journal.pone.0058368 (2013). [DOI] [PMC free article] [PubMed]
- 10.Xia JF, You ZH, Wu M, Wang SL, Zhao XM. Improved Method for Predicting pi-Turns in Proteins Using a Two-Stage Classifier. Protein and Peptide Letters. 2010;17:1117–1122. doi: 10.2174/092986610791760315. [DOI] [PubMed] [Google Scholar]
- 11.You ZH, Lei YK, Gui J, Huang DS, Zhou XB. Using manifold embedding for assessing and predicting protein interactions from high-throughput experimental data. Bioinformatics. 2010;26:2744–2751. doi: 10.1093/bioinformatics/btq510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.You ZH, Li LP, Yu HJ, Chen SF, Wang SL. Increasing Reliability of Protein Interactome by Combining Heterogeneous Data Sources with Weighted Network Topological Metrics. Advanced Intelligent Computing Theories and Applications. 2010;6215:657–663. doi: 10.1007/978-3-642-14922-1_82. [DOI] [Google Scholar]
- 13.Lei, Y. K., You, Z. H., Ji, Z., Zhu, L. & Huang, D. S. Assessing and predicting protein interactions by combining manifold embedding with multiple information integration. Bmc Bioinformatics13, 10.1186/1471-2105-13-s7-s3 (2012). [DOI] [PMC free article] [PubMed]
- 14.Zhang QC, et al. Structure-based prediction of protein-protein interactions on a genome-wide scale (vol 490, pg 556, 2012) Nature. 2013;495:127–127. doi: 10.1038/nature11977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.You ZH, Yu JZ, Zhu L, Li S, Wen ZK. A MapReduce based parallel SVM for large-scale predicting protein-protein interactions. Neurocomputing. 2014;145:37–43. doi: 10.1016/j.neucom.2014.05.072. [DOI] [Google Scholar]
- 16.Gao, Z. G. et al. Ens-PPI: A Novel Ensemble Classifier for Predicting the Interactions of Proteins Using Autocovariance Transformation from PSSM. Biomed Research International8, 10.1155/2016/4563524 (2016). [DOI] [PMC free article] [PubMed]
- 17.Zhao XM, Wang Y, Chen LN, Aihara K. Protein domain annotation with integration of heterogeneous information sources. Proteins-Structure Function and Bioinformatics. 2008;72:461–473. doi: 10.1002/prot.21943. [DOI] [PubMed] [Google Scholar]
- 18.Huang Y-A, et al. Construction of reliable protein–protein interaction networks using weighted sparse representation based classifier with pseudo substitution matrix representation features. Neurocomputing. 2016;218:131–138. doi: 10.1016/j.neucom.2016.08.063. [DOI] [Google Scholar]
- 19.Wang L, et al. An ensemble approach for large-scale identification of protein-protein interactions using the alignments of multiple sequences. Oncotarget. 2017;8:5149. doi: 10.18632/oncotarget.14103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yang YD, Faraggi E, Zhao HY, Zhou YQ. Improving protein fold recognition and template-based modeling by employing probabilistic-based matching between predicted one-dimensional structural properties of query and corresponding native properties of templates. Bioinformatics. 2011;27:2076–2082. doi: 10.1093/bioinformatics/btr350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yin, Z. et al. Using iterative cluster merging with improved gap statistics to perform online phenotype discovery in the context of high-throughput RNAi screens. Bmc Bioinformatics9, 10.1186/1471-2105-9-264 (2008). [DOI] [PMC free article] [PubMed]
- 22.Yang YD, Zhou YQ. Specific interactions for ab initio folding of protein terminal regions with secondary structures. Proteins-Structure Function and Bioinformatics. 2008;72:793–803. doi: 10.1002/prot.21968. [DOI] [PubMed] [Google Scholar]
- 23.Chen, W., Feng, P. M., Lin, H. & Chou, K. C. iRSpot-PseDNC: identify recombination spots with pseudo dinucleotide composition. Nucleic Acids Research41, 10.1093/nar/gks1450 (2013). [DOI] [PMC free article] [PubMed]
- 24.Lin H. The modified Mahalanobis Discriminant for predicting outer membrane proteins by using Chou’s pseudo amino acid composition. Journal of Theoretical Biology. 2008;252:350–356. doi: 10.1016/j.jtbi.2008.02.004. [DOI] [PubMed] [Google Scholar]
- 25.Wang L, et al. Advancing the prediction accuracy of protein-protein interactions by utilizing evolutionary information from position-specific scoring matrix and ensemble classifier. Journal Of Theoretical Biology. 2017;418:105–110. doi: 10.1016/j.jtbi.2017.01.003. [DOI] [PubMed] [Google Scholar]
- 26.Wang, L. et al. An improved efficient rotation forest algorithm to predict the interactions among proteins. Soft Computing, 1–9 (2017).
- 27.Luo, X. et al. A Highly Efficient Approach to Protein Interactome Mapping Based on Collaborative Filtering Framework. Scientific Reports5, 10.1038/srep07702 (2015). [DOI] [PMC free article] [PubMed]
- 28.Zhao, X. M., Wang, Y., Chen, L. N. & Aihara, K. Gene function prediction using labeled and unlabeled data. Bmc Bioinformatics9, 10.1186/1471-2105-9-57 (2008). [DOI] [PMC free article] [PubMed]
- 29.Pitre S, et al. PIPE: a protein-protein interaction prediction engine based on the re-occurring short polypeptide sequences between known interacting protein pairs. Bmc Bioinformatics. 2006;7:15. doi: 10.1186/1471-2105-7-365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shen J, et al. Predictina protein-protein interactions based only on sequences information. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:4337–4341. doi: 10.1073/pnas.0607879104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zweig MH, Campbell G. Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine. Clinical chemistry. 1993;39:561–577. [PubMed] [Google Scholar]
- 32.Chang, C.-C. & Lin, C.-J. LIBSVM: A Library for Support Vector Machines. Acm Transactions on Intelligent Systems and Technology2, 10.1145/1961189.1961199 (2011).
- 33.Xenarios I, et al. DIP, the Database of Interacting Proteins: a research tool for studying cellular networks of protein interactions. Nucleic Acids Research. 2002;30:303–305. doi: 10.1093/nar/30.1.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Martin S, Roe D, Faulon JL. Predicting protein-protein interactions using signature products. Bioinformatics. 2005;21:218–226. doi: 10.1093/bioinformatics/bth483. [DOI] [PubMed] [Google Scholar]
- 35.Gribskov M, McLachlan AD, Eisenberg D. Profile analysis: detection of distantly related proteins. Proceedings of the National Academy of Sciences of the United States of America. 1987;84:4355–4358. doi: 10.1073/pnas.84.13.4355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Altschul SF, et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic acids research. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Yang J, Zhang D, Frangi AF, Yang JY. Two-dimensional PCA: A new approach to appearance-based face representation and recognition. Ieee Transactions on Pattern Analysis and Machine Intelligence. 2004;26:131–137. doi: 10.1109/TPAMI.2004.1261097. [DOI] [PubMed] [Google Scholar]
- 38.Yang J, Yang JY. From image vector to matrix: a straightforward image projection technique - IMPCA vs. PCA. Pattern Recognition. 2002;35:1997–1999. doi: 10.1016/S0031-3203(02)00040-7. [DOI] [Google Scholar]
- 39.Wang L, et al. RFDT: A Rotation Forest-based Predictor for Predicting Drug-Target Interactions Using Drug Structure and Protein Sequence Information. Current Protein & Peptide Science. 2018;19:445–454. doi: 10.2174/1389203718666161114111656. [DOI] [PubMed] [Google Scholar]
- 40.Zhou YZ, Gao Y, Zheng YY. Prediction of Protein-Protein Interactions Using Local Description of Amino Acid Sequence. Advances in Computer Science and Education Applications, Pt Ii. 2011;202:254–262. doi: 10.1007/978-3-642-22456-0_37. [DOI] [Google Scholar]
- 41.Yang L, Xia J-F, Gui J. Prediction of Protein-Protein Interactions from Protein Sequence Using Local Descriptors. Protein and Peptide Letters. 2010;17:1085–1090. doi: 10.2174/092986610791760306. [DOI] [PubMed] [Google Scholar]
- 42.You, Z.-H., Lei, Y.-K., Zhu, L., Xia, J. & Wang, B. Prediction of protein-protein interactions from amino acid sequences with ensemble extreme learning machines and principal component analysis. Bmc Bioinformatics14, 10.1186/1471-2105-14-s8-s10 (2013). [DOI] [PMC free article] [PubMed]
- 43.Bock JR, Gough DA. Whole-proteome interaction mining. Bioinformatics. 2003;19:125–134. doi: 10.1093/bioinformatics/19.1.125. [DOI] [PubMed] [Google Scholar]
- 44.Nanni L. Hyperplanes for predicting protein-protein interactions. Neurocomputing. 2005;69:257–263. doi: 10.1016/j.neucom.2005.05.007. [DOI] [Google Scholar]
- 45.Nanni L, Lumini A. An ensemble of K-local hyperplanes for predicting protein-protein interactions. Bioinformatics. 2006;22:1207–1210. doi: 10.1093/bioinformatics/btl055. [DOI] [PubMed] [Google Scholar]
- 46.Liu, B. et al. QChIPat: a quantitative method to identify distinct binding patterns for two biological ChIP-seq samples in different experimental conditions. Bmc Genomics14, 10.1186/1471-2164-14-s8-s3 (2013). [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.