Evolutionary route to diploidy and sex

Abstract

By using a bit-string model of evolution, we find a successful route to diploidy and sex in simple organisms. Allowing the sexually reproducing diploid individuals to also perform mitosis, as they do in a haploid-diploid cycle, leads to the complete takeover of the population by sexual diploids. This mechanism is so robust that even the accidental conversion and pairing of only two diploids give rise to a sexual population.

The evolution of sex through Darwinian selection despite the seeming odds with respect to asexual reproduction through cloning is still an unresolved problem (1–3) that has attracted a great deal of recent activity (4, 5). We present here results from a very simple model based on unicellular organisms in which sex seems to have first emerged without any complicating factors such as the cost of male-female differentiation, parental care, mating preferences, maternity periods, and so on, which we assume only to have arisen in higher organisms. These factors may be responsible for the differentiation, modification, or even at times reversal [as in meiotic parthenogenesis (2)] of the patterns that may have become established accidentally in the remote evolutionary past. Unicellular organisms are not only simpler to model, but this choice also imposes more stringent conditions on the establishment of a sexual population, because it severly limits the number of viable offspring that a pair of parent cells can have. By confining ourselves to “worst-case scenarios” we hope to be able to obtain plausible lower bounds to the feasibility of sex as a reproductive mechanism.

Sexual reproduction as we know it today in higher plants and animals can be regarded as a haploid-diploid cycle (HDC) with a highly abbreviated haploid phase in which the (haploid) gametes typically do not perform mitosis (1, 2). These haploids are not viable unless two of them fuse and once more make a diploid cell, which then multiplies by mitosis and eventually forms the mature individual.

The HDC, which under unfavorable conditions causes the population to become diploid, is found in many species (6, 7) and was the motivation behind the hypothesis of Jan, Stauffer, and Moseley (JSM, ref. 8), who proposed that diploidy and sex may have arisen first as a way to escape death when a simple unicellular individual is threatened by too many deleterious mutations. The fitness is taken to be a step function of the number of mutations, also setting the threshold for conversion to diploidy and sex. Here the number of deleterious mutations can be read as the distance from the ideal case, called the wild type, which can be altered as a result of a change in the environment such that the individual is not as well adapted as before the change.

In previous work (9, 10) we showed that the JSM hypothesis indeed leads to a steady source of diploid sexuals, given a population of haploids that multiply by mitosis. This process leads to a steady-state distribution of coexisting haploids and diploids in a constant population. The premises adopted in ref. 10 were very restrictive. Two sexual parent cells were allowed to have only one offspring, after which they died. In case one considers a greater number of offspring by allowing a greater number of viable gametes to be formed, as indeed is possible in many unicellular organisms (ref. 6), one finds that the diploid, sexual population completely takes over.

In the same paper (10) we also considered the situation in which conversion to sex occurred with a constant probability σ (which we varied between 0 and 1) independent of the fitness of the individual. This strategy also gave rise to a sexual population making up a small but macroscopic fraction of the total such that the JSM threshold mechanism for conversion to sex did not prove to be necessary, although it was more successful. On the other hand the JSM hypothesis has the additional attraction of providing a mechanism that could trigger the fusion of two haploid cells to form a diploid: it is known (1) that extensive genetic damage can lead to gene repair via genetic transmission between two haploid cells; the fusion of two haploids could be seen as an extreme form of such behavior. An alternative means of forming a diploid from a haploid cell is via endomitosis (2) as in the first step in meiotic parthenogenesis. Endomitosis is the process whereby the genetic material in a cell is duplicated without subsequent cell division as in normal mitosis. Again, it is not implausible that this process originated as a result of grave genetic damage that precluded the successful completion of mitosis (1).

In the present paper we show that if the diploid cells, once formed, are also allowed to multiply by mitosis, as indeed they do in an HDC, the whole population is taken over by diploid cells, which perform facultative sex if they are once more threatened by extinction because of too many deleterious mutations. Moreover we show that even an episodic conversion to sex involving as few as only two individuals who survive to mate leads to a steady-state made up solely of sexual types.

In the next section we briefly describe our algorithms and report the simulation results. In the last section we provide a discussion and some pointers for future research.

Bit-String Model for the Conversion to Sex: Algorithms and Simulation Results

The type of model we consider here is the same as that described in ref. 10. Below we recall the definitions. We also introduce new rules to test the autonomous viability of sexual populations.

Each haploid one-celled organism consists, for our purposes, of a 15-bit string of “0”s and “1”s representing the genetic code in a 16-bit computational word (11–13). We use the bit defining the “sign” to specify whether the individual is asexual (+) or sexual (−). A mutation entails the flipping of a randomly chosen bit, except the sign bit, with a constant probability Γ for each individual per generation. Because the genetic difference between individuals of the same species typically is less than 10% (1), this rather short string for the genetic code may be considered as a coarse-grained model for the complete genome of the individual, which we divide up into different zones retaining a 0 where there are no mutations and flipping the bit to 1 when there are one or more mutations in this zone. The wild type is a string of all 0s. Therefore, at each locus, a 1 corresponds to a deleterious mutation (which we will call “mutation” for short, where this usage is not liable to lead to any confusion). Diploid organisms have two bit strings, which are allowed to be different. The number of deleterious mutations m is simply the number of 1s for a haploid individual. For a diploid, the number of “expressed” deleterious mutations is the number of loci at which both homologous alleles are set to 1, i.e., we assume that deleterious mutations are recessive.

The total population is fixed at N = 10³, and we have chosen Γ = 1/N. This corresponds to a mutation rate per allele per generation of ≈6 × 10⁻⁵, which is comparable to the typical mutation rates encountered in eukaryotes (2).

The probability of survival (or fitness) as a function of m is given by a Fermi-like distribution (14),

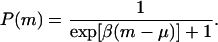1

For large β (or “low temperatures,” in the language of statistical mechanics), P(m) behaves like a step function. Individuals with m > μ die, those with m < μ survive, and those with m = μ survive with a probability of 1/2. In the simulations we confined ourselves to low temperatures (β = 10). We chose μ = 4, which just allows us enough variability without leading to totally unrealistic mutational loads.

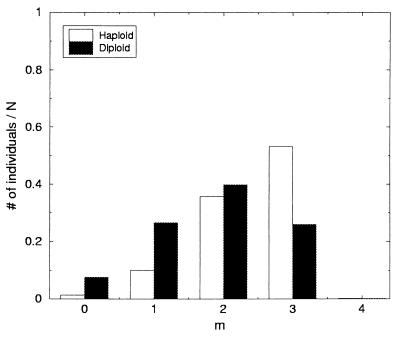
We start with a set of N asexual (haploid) wild types. In each generation, ≈ΓN individuals suffer mutations; they are killed off or retained according to the fitness function (Eq. 1), and the population is restored to N by once cloning as many randomly chosen survivors as necessary. The population of haploid asexuals settles down to a minimally stable (15) steady-state distribution (see Table 1) as shown in Fig. 1, independent of the value of Γ, for Γ ≥ 1/N (9, 10).

Table 1.

The distribution of expressed deleterious mutations and death rates for the models discussed in Bit-String Model for the Conversion to Sex

Model	Population	m = 0	m = 1	m = 2	m = 3	m = 4	Death rate
Pure haploid		1	10	36	53	0	0 (10−4)
Pure diploid		7	27	40	26	0	0 (10−5)
Diploid sexuals	Mitotic	7	27	40	26	0	0 (10−5)
Diploid sexuals	Episodic	7	27	40	26	0	0 (10−5)
Model A—nonhereditary*	Asex	1	11	37	51	0	0 (10−4)
Model A—nonhereditary*	Sex	11	33	36	20	0	0 (10−4)
Model A—hereditary*	Asex	1	11	36	52	0	0 (10−4)
Model A—hereditary*	Sex	10	50	40	0	0	0 (10−2)

The m distributions are percentages (±1%) computed over each type if coexisting; the death rates are per capita per generation. 

^*See ref. 10. 

Figure 1.

The steady-state distribution of pure haploids with respect to the number of deleterious mutations m compared with the distribution of asexual diploids over the number of expressed mutations m. The histograms are normalized to unity.

For comparison, we also performed simulations on a diploid population reproducing asexually according to the same rules as stated in the previous paragraph. We found that the diploid population reaches a steady state with an m distribution peaking at m = 2 rather than m = 3 as found for haploids (see Fig. 1 and Table 1).

Conversion to Sex.

Let us briefly summarize our algorithm for conversion to sex, which we also used in our previous study (see Model A in ref. 10).

We choose the steady state of the haploid population as our initial state from which to start the conversion to sex, because that would be a most likely “natural state” encountered at this stage. Once the haploid population reaches a steady state, we allow those individuals that are threatened by extinction to convert to diploidy and sex by implementing the following rule at each generation: if an asexual individual with m = 4 has survived, it is converted to an active sexual individual by deterministically and irreversibly switching its sign bit to −. It performs endomitosis and becomes diploid. If there are already sexual, diploid organisms in the population, they also will be made active if m, the number of their expressed mutations, is ≥4 (otherwise they do not participate in the reproduction cycle; hence the conversion to sex may be termed nonhereditary). Finally, all the active sexual organisms pair randomly and engage in sexual reproduction, where they each contribute one gamete (formed via one step meiosis) toward a single diploid sexual offspring. If we denote the genotypes of parents as {Aa} and {Bb} respectively, then the genotype of the offspring is either {AB}, {Ab}, {aB}, or {ab}. No crossover occurs during this one-step meiosis. If there is only one active sexual individual at a certain time step then it must wait subsequent generations until it either finds a partner or dies. We keep the population constant (16) by cloning randomly selected haploid individuals to make up the deficit. The consequences of the conversion to hereditary and obligatory sex can be found in ref. 10.

Mitotic Diploid Sexuals Win over Haploids.

In the previous subsection we described a scenario in which too big a mutation load meant conversion to diploidy and sex if the individual survived. It should be realized that in this scheme the haploids, which multiply by cloning, provide a steady source for the diploid sexuals, whose numbers are halved every time they mate. Now we want to test whether the diploid, sexual population can survive autonomously if the sexuals are also allowed to perform mitosis themselves.

Once a steady state with coexisting haploid and diploid populations is reached via the algorithm described above, we switch off the conversion of haploid organisms to diploidy and sex. The diploid individuals mate when they face extinction because of too many mutations. We now keep the total population constant by making up for the deficit in the population at each step by cloning randomly selected individuals regardless of whether they are sexual or asexual. In colonies undergoing an HDC, it quite frequently is the case (6) that the diploid phase of the cycle also involves multiplication by mitosis.

The result is that the diploid, sexual individuals completely win over the population. The haploids that now cannot compete with the sexuals become extinct. Here we find that the haploid phase of the HDC becomes abbreviated to the point that haploids appear only as gametes that do not perform mitosis. This is exactly the situation in highly evolved sexual organisms.

Episodic Conversion to Diploidy and Sex Leads to Sexual Steady State.

One also can think of a scenario in which conversion to sex takes place accidentally over a short period after the asexual population settles down to a steady state. In fact, this is probably the most realistic situation given the random nature of the mutations.

The way we actually implemented this scenario in the computer code was by deterministically switching the sign bits of the first two asexual individuals to survive with m = 4 and then turning off the possibility of further conversion. These then form two sexual individuals by endomitosis, and if the first survives long enough to mate with the second, it will give rise to one sexual offspring.

The rest of the rules are as explained before; in each generation we clone randomly chosen individuals to make up the deficit in the population regardless of whether they are asexuals or sexuals. We allow the diploid individuals to mate when they face extinction in the course of their lives.

Suprisingly, the sexuals capture the population in 95% of the performed runs. (In the rest the single diploid, which is still at the threshold of extinction with an m value of 4, may not survive until a partner arrives.)

Relative Fitness.

The steady-state m distributions for the sexual populations are much better than those for the haploid distribution. However, they are identical with the distribution for asexual diploids (see Table 1 and Fig. 1), i.e. as soon as diploidy is achieved, it is so successful in screening the effects of deleterious mutations that once diploid, the organism practices sex very infrequently, making these three distributions identical.

The diploid m distribution in Fig. 1 should be contrasted with the results of ref. 10. (Model A, nonhereditary and hereditary; see above), in which cloning of the sexuals is not allowed, but there is a steady influx of new sexuals from the haploids (see Table 1). In the nonhereditary model, the m distribution has shifted nearer the wild type than in the purely diploid case (although the peak is again at m = 2 ); in the hereditary model, the peak has shifted to m = 1. Thus, the frequency with which sex is practiced has a salutary effect on the distribution of expressed deleterious mutations in the population.

On the other hand it should be noted that with the Fermi-like fitness function (Eq. 1) for large β, to which we have confined ourselves, the survival probability is about constant for m < μ and therefore does not discriminate between steady-state populations that differ solely in the shape of their m distributions for m < μ. A better measure might be the death rate, namely, the average number of individuals that are eliminated at each step under the criterion given in Eq. 1.

Our findings, which are rather revealing, are summarized in Table 1. Because the fluctuations were very large, we have only reported order-of-magnitude results for the death rates. Pure diploids have the lowest death rate, which is an order of magnitude smaller than pure haploids. Mitotic (including the “episodic” case) sexuals are very close to diploids. For nonhereditary sexuals the rates are comparable with asexuals, but hereditary sexuals have a death rate that is 2 orders of magnitude larger than asexuals. We infer from this that the success of hereditary sexuals in lowering their mutation load is because of the much greater rate at which they can select-out highly mutated genes through death.

Thus it is seen that the clear advantage of sex over asex (haploid or diploid) in our model can become manifest only with a sufficiently high frequency of sexual reproduction, which is driven by the mutation rate Γ and moreover in situations that can discriminate between the different adaptabilities (smaller typical m) of the different modes of reproduction such as time-varying environments. This effect is similar to the finding of Pekalski (17), who has considered environments (wild types) that vary over time and found that the benefits of sexual reproduction are enhanced by higher birth rates. For lower birth rates, meiotic parthenogenesis, which can be compared with diploid asex, has a slight advantage over sex, a difference from our results that can be ascribed to the exponential fitness function the author uses.

Discussion

This paper is a culmination of a series of studies in which we have considered very stringent rules for the survival and propagation of diploid, sexual individuals in competition with haploids. Here we have been able finally to show that a pair of simple unicellular organisms who have converted accidentally to diploidy and subsequently engage in sexual reproduction, begetting one sexual offspring, can give rise to a population of sexual types that totally take over a finite population, provided they also are allowed to multiply by mitosis, on an equal footing with the haploids in the population. They engage in sex when the going gets tough, that is, when the number of their expressed deleterious mutations exceeds a certain number. This success seems to vindicate the hypothesis of JSM (8), which states that sex could have been a mechanism of last resort when simple organisms were faced with extinction.

It is interesting to pose the question of what happens if we do not allow the diploids to clone themselves but, on the other hand, allow the gametes under special conditions to enter a haploid phase in which they multiply by mitosis. Eventually these haploids will be allowed once more to fuse and give rise to diploids. Within the present scheme, because the haploids convert to diploidy only at the threshold, m = 4, the gametes of the diploid individuals have m ≥ 4, i.e., they are not viable. Therefore the extension of the haploid phase calls for a modification of the rules in such a way as to allow the gametes to survive nevertheless, e.g., by forming “spores.”

One way the parameters of the present model could be modified is to take the threshold for survival to be different (greater) than the threshold for the conversion to (or practice of) sex. Then if a haploid gamete were to be considered as a member of the haploid population and subjected to the same rules for selection and reproduction, it would seem as if one would get haploid phases of arbitrary duration. However, after closer inspection we see that this is not true; because the gamete comes from a diploid organism that engages in sex because of an excess mutational load, it already has deleterious mutations in excess of (or at least equal to) the sex threshold. (For the diploid organism to have m expressed mutations, both of its genetic strings must have at least that many.) Thus, according to the rules that we have adopted, the abbreviated haploid cycle is automatically selected, because within this scheme the gamete would immediately seek a mate. The lengthening of the haploid phase would call for further evolution, e.g., such mutations as would lead to the enhancement of the fitness of the haploid gametes with m in excess of the sexual threshold [say by the formation of spores, to survive in an environment that has become disfavorable (3, 4)]. Because the survival and multiplication of the gametes will provide a mechanism for the diploids once more to make up for the reduction in their numbers caused by the single-offspring mating rule, we expect this HDC to win out over the haploid, asexual population.

To understand the seemingly contradictory results from similar models investigating the phenomenon of the selection of sex as the dominant mode of reproduction, it is of interest to compare our model with that of Redfield (16) and Cui et al. (18). The former employs a more complex system in which there is sexual differentiation between males and females, with the additional feature of a much greater mutation rate for males than for females, eventually making meiotic parthenogenesis safer than sex. Redfield has used three different “selection functions” (survival probabilities), falling off exponentially (no “epistasis” or correlation between the effects of successive mutations), quadratically (some positive epistasis), or as a step function (extreme positive epistasis) with m (19). The fact that the step-function (“truncation”) survival probability alone leads to a much better fitness resulting from sex tells us that the form of the survival probability that is adopted determines the outcome very strongly. The step function favors sex because it does not punish small deviations from the wild type, thereby allowing genetic diversity, whereas it penalizes large deviations severely and helps to eliminate highly mutated individuals.

This insight enables us to understand the results of Cui et al. (18), who have considered a diploid population reproducing either asexually or sexually depending on a fixed probability. There is a constant mutation rate. The survival probability is chosen to be of the “independent mutation,” i.e., exponential type. These authors find that the diploid population accumulates such a large number of deleterious mutations (which, however, do not get expressed) that sexual reproduction, i.e., the random pairing of gametes from different parents, results in a disasterous reduction in the fitness of the offspring. Moreover, sexually reproducing diploid populations are susceptible to invasion by asexually reproducing ones, whereas the converse is not true, i.e., asexually reproducing diploid populations are not invaded by sexually reproducing ones. These results change drastically in favor of sex when they introduce cell senescence, which means that a cell can clone itself only a certain number of times before it stops dividing and dies unless it engages in sexual reproduction, which resets the senescence clock.

We argue that in the model of Cui et al. (18), introducing cell senescence is very much like turning on a “truncation-like” survival function, which, as in our model, also controls the switch to sexual reproduction. In the presence of a constant mutation rate, the number of times a cell has cloned is another way to measure its (mean) mutation load, which in an asexual haploid population of course gets expressed directly, whereas for diploid individuals it hides behind the dominant unmutated alleles. Introducing a cell senescence threshold, beyond which the individual is either killed off or has to engage in sexual reproduction, is therefore equivalent in an average way to the JSM criterion applied to a diploid population. Seen in this way, it is very gratifying that the Cui et al. model in fact corraborates our findings regarding the greater fitness of diploid populations that frequently engage in sex, given a step function-like survival probability.

Very recently, two variants of the Redfield model that assign “harsher selection” to males (rather than relatively higher mutation rates) have been considered (20, 21). These studies both find that the mutational load on the whole population decreases as a result, and that the relative fitness of sexual females is increased by more than enough to compensate for the 2-fold cost of sex in anisogamous populations, at least for extremely high values of the average mutation rate. Agrawal finds that this can happen even in the absence of synergystic epistasis in his model. Meanwhile, Wilke et al. (22) have found that high mutation rates select for low replication rates and flat regions of the fitness surface.

It should be noted that the Fermi-type fitness function (Eq. 1) adopted here (8–10, 14) extrapolates for finite temperatures (smaller values of β) between highly synergistic (step function) and independent (exponential) survival probabilities (23) as a function of m. A recent study by Peck and Waxman (24) indicates that competition for limited resources can lead to synergy between successive mutations, leading to truncation or step function-like survival probabilities, which they also find favors sexual populations.

In this paper we have presented numerical results for a model involving unicellular organisms, which may shed light on how sex and diploidy emerged and established a foothold in the protozoon world. Many different mechanisms have been proposed thus far via which sex may prove advantageous or otherwise, in more highly evolved organisms. We believe that care should be taken while proposing any single mechanism such as an adaptation to resist infestation by parasites (25, 26) for the preferance of sex by organisms that range from the unicellular eukaryotes to trees or human beings (27). More complex organisms may have elaborated much more complex survival mechanisms and behaviorial patterns, which stabilize or destabilize already evolved traits.

Abbreviation

HDC

haploid-diploid cycle