Characterization of Pulmonary Nodules Based on Features of Margin Sharpness and Texture

Abstract

Lung cancer is the leading cause of cancer-related deaths in the world, and one of its manifestations occurs with the appearance of pulmonary nodules. The classification of pulmonary nodules may be a complex task to specialists due to temporal, subjective, and qualitative aspects. Therefore, it is important to integrate computational tools to the early pulmonary nodule classification process, since they have the potential to characterize objectively and quantitatively the lesions. In this context, the goal of this work is to perform the classification of pulmonary nodules based on image features of texture and margin sharpness. Computed tomography scans were obtained from a publicly available image database. Texture attributes were extracted from a co-occurrence matrix obtained from the nodule volume. Margin sharpness attributes were extracted from perpendicular lines drawn over the borders on all nodule slices. Feature selection was performed by different algorithms. Classification was performed by several machine learning classifiers and assessed by the area under the receiver operating characteristic curve, sensitivity, specificity, and accuracy. Highest classification performance was obtained by a random forest algorithm with all 48 extracted features. However, a decision tree using only two selected features obtained statistically equivalent performance on sensitivity and specificity.

Introduction

Lung cancer is the most common cause of cancer-related deaths, with a 5-year overall survival rate of only 15% [1]. The evaluation of pulmonary nodules is clinically important because they may be an early manifestation of lung cancer [2]. The diagnosis of lung cancer may be a complex task to radiologists and it presents some challenges. One of them is to classify pulmonary nodules in diagnostic imaging. Nodule classification in malignant or benign depends on several aspects [3]: for instance, its growth rate and change in size from two time-separated computed tomography (CT) scans; and subjective, qualitative aspects of the lesion, e.g., “moderate heterogeneity,” “highly spiculated,” “large necrotic core” [4].

To aid radiologists in the diagnosis of lung cancer, it is important to integrate the computer-based assistance into the processes of imaging pattern recognition and pulmonary nodule classification [5, 6]. The purpose of computer-aided diagnosis (CAD) is to improve the accuracy and consistency of medical image diagnosis through computational support used as reference [7]. In particular, the automation of pattern classification process may considerably reduce the time and effort required by the analysis and, at the same time, improve its repeatability and reliability [8].

Some works have performed computer-aided classification of pulmonary nodules, using different classifiers and CT image features to improve the diagnosis of lung cancer (“Related Works”) [1, 9–14]. However, very few have used margin sharpness descriptors, which are important to differentiate nodules in terms of potential malignancy because malignant tumors grow into neighboring tissues [15]. Therefore, pulmonary nodule classification systems based on 3D image descriptors of margin sharpness along with traditional features, such as second-order texture [16], are still immature and need to be more evaluated.

In this context, the goal of this work is to classify pulmonary nodules in malignant and benign and to evaluate margin sharpness and texture imaging features extracted from CT scans. The proposed evaluation relies on five steps: the development of a pulmonary nodule image database, the extraction of 3D shape-based features of margin sharpness and second-order texture attributes, the selection of the most relevant attributes from the feature vector using different methods, the classification of the pulmonary nodules in terms of potential malignancy using different established machine learning algorithms, and the performance assessment of the malignant-benign classification using the well-known statistical parameters of accuracy, sensitivity, specificity, and area under the receiver operating characteristic curve (AUC).

The remainder of this paper is organized as follows: “Related Works” presents related works of pattern recognition on malignant-benign pulmonary nodules. “Materials and Methods” describes the materials and methods used in this work, including the development of the pulmonary nodule database in “Pulmonary Nodule Database,” the image feature extraction in “Image Feature Extraction,” the image feature selection in “Image Feature Selection,” the pulmonary nodule classification in “Pulmonary Nodule Database” and performance evaluation details in “Performance Evaluation.” “Results” and “Discussion” present the results and discussion of this work, respectively. “Conclusions” concludes this paper.

Related Works

Wu et al. used a back-propagation artificial neural network for the classification of malignant and benign pulmonary nodules with Lasso-type regularization to select radiological and textural CT features. The authors used a local CT image repository to extract the features and obtained sensitivity of 0.960, specificity of 0.800, and AUC of 0.910 [1].

Tartar et al. extracted geometric features from basic morphological shape information and statistical attributes from a two-dimensional principal component analysis. The authors used a local CT image collection to extract the features and selected the best ones with the minimum redundancy maximum relevance method. The random forest (RF) algorithm also was employed as classifier and obtained classification accuracy of 0.837, sensitivity of 0.854, specificity of 0.816, and AUC of 0.908 [9].

Reeves et al. extracted morphological, density, surface curvature, and margin gradient features from the pulmonary nodules, and evaluated them with support vector machine (SVM) classifiers with a polynomial kernel and with a radial basis function kernel. The Early Lung Cancer Action Program and the National Lung Cancer Screening Trial image datasets were used in the experiments. Both SVM classifiers obtained AUC of 0.772 [10].

Dilger et al. analyzed the lung parenchyma surrounding the nodule and extracted parenchymal and nodule intensity, shape, border, and texture features from images of the National Lung Screening Trial and the Chronic Obstructive Pulmonary Disease Genetic Epidemiology datasets. Feature selection was performed by statistical analysis and stepwise forward selection method. An artificial neural network classified the pulmonary nodules with accuracy of 0.920, sensitivity of 0.909, specificity of 0.928, and AUC of 0.935 [11].

Zhang et al. extracted intensity, texture, and gradient CT attributes from well-circumscribed, vascularized, juxta-pleural, and pleural-tail pulmonary nodules provided by the Early Lung Cancer Action Program. Classification was performed with a combination of SVM and probabilistic latent semantic analysis, with a classification rate of 0.880 [12].

Kaya et al. used a weighted rule based classification approach to distinguish pulmonary nodules presented on the Lung Image Database Consortium images. The authors employed ensemble classifiers of linear discriminant classifier, SVM, k-nearest neighbors (KNN), adaboost, and RF. They extracted 2D and 3D image features of shape, size, and texture, and selected the most relevant attributes using a weighing and ranking method combined. Ensemble RF obtained the highest classification accuracy of 0.849 with sensitivity of 0.831 and specificity of 0.921 [13].

Ferreira Jr et al. extracted 3D image features of margin sharpness and texture of pulmonary nodules provided by the Lung Image Database Consortium. The authors selected the most relevant attributes using a wrapper and classified the nodules with the KNN algorithm using different values for k. Feature selection improved nodule classification using nine nearest neighbors and texture features of inverse difference moment at orientations 0^∘ and 135^∘ and correlation at 90^∘ with accuracy of 0.792 and AUC of 0.816 [14]. In this present work, we extended the evaluation of Ferreira Jr et al. by employing different datasets, classifiers, feature selection algorithms, and performance measures.

Materials and Methods

Pulmonary Nodule Database

The Lung Image Database Consortium (LIDC) project provided the CT scans used in this work [17, 18]. A publicly available pulmonary nodule database was used to allow reproducible research and cross-validation with other CAD method implementations through the use of a single image resource to compare the results with the same testbed [19].

LIDC is a reference database for the medical imaging research community that consists of images with marked-up annotated lesions. It has associated specialists annotations, including nodule outlines and subjective nodule characteristic ratings, and is now composed with 1010 patients, 1018 CT exams, and 244,527 images. LIDC required four experienced radiologists to review each image of a CT exam and to outline lesions that they considered to be a nodule with greatest in-plane dimension in the range 3–30 mm. Full description of the image interpretation and reading process of the radiologists to evaluate the lesions is available at the original LIDC references [17, 18]. For the purposes of this work, only the reading of the radiologist that identified the highest number of nodules was used [19].

Each specialist was also asked to subjectively set an integer value (on a 1–5 scale) to the nodule’s likelihood of malignancy, in which 1 is high probability to be benign, 2 is moderate probability to be benign, 3 is indeterminate probability, 4 is moderate probability to be malignant, and 5 is high probability to be malignant. However, pulmonary nodules with likelihood of malignancy 3 were discarded due to its indeterminate rating. For the purposes of this work, nodules with likelihood of malignancy 4 and 5 were considered malignant, and nodules with likelihood of malignancy 1 and 2 were considered benign.

Experiments were performed with two datasets (one unbalanced and one balanced) to prevent bias to the majority class (benign), and hence to improve sensitivity. The total number of nodules of the unbalanced dataset was 1171, which 745 of them were benign and 426 were malignant nodules. The total number of nodules of the randomly balanced dataset was 600, equally split in 300 malignant and benign cases.

Image Feature Extraction

The pulmonary nodule feature vector was composed of 48 image attributes of texture and margin sharpness, explained as follows.

A 3D texture analysis was applied to manually segmented pulmonary nodules to extract textural features. All nodules had lesion images segmented using the radiologist’s marks. After the segmentation, texture attributes were extracted from the voxels using a 3D extended version of the gray level co-occurrence matrix (GLCM). The 3D GLCM method obtains from a single image volume: the occurrence probability of pairs of voxels with spacing between them of Δx, Δy, and Δz in the dimensions x, y, and z, respectively, given a distance d and orientation 𝜃. Second-order histogram statistics are computed from the GLCM producing the texture attributes. Texture attributes used in this work were energy, entropy, inverse difference moment (IDM), inertia, variance, shade, promenance, correlation, and homogeneity, suggested by Haralick et al. [20]. The texture feature vector was obtained by means of the calculation of the nine attributes computed from the co-occurrence matrices in orientations 0^∘, 45^∘, 90^∘, and 135^∘, and distance of 1 voxel. In this case, each nodule was associated with a 36-dimension texture feature vector.

A 3D margin sharpness analysis was also implemented to characterize pulmonary nodules, in which a data statistical analysis was performed by extracting attributes from a sorted array composed of the gray level intensities of the pixels from perpendicular lines that drew over the borders on all nodule slices. The margin sharpness feature vector was composed by the simple statistics attributes of difference of the two ends of the array, sum of values, sum of squares, sum of logs, arithmetic mean, geometric mean, population variance, sample variance, standard deviation, Kurtosis measure, Skewness measure, and second central moment (SCM). Therefore, each nodule is characterized as a 12-dimension margin sharpness feature vector.

Image Feature Selection

Feature selection process extracts a subset of image attributes from the feature vector to improve the classification accuracy. The main purposes of feature selection are: (a) to reduce the dimensionality of the input data by removing irrelevant information, and (b) to improve the chances of avoiding overfitting, whose probability increases with the dimension of the feature space [8].

Three feature selection methods were employed in this work: a statistical significance analysis, a correlation-based filtering method, and a wrapper.

The statistical analysis was performed with p values to test the statistical significance of the features across the two classes (malignant and benign). According to Almeida et al. [21], p ≥ 0.05 implies that the differences in the feature are not significant to distinguish between the two classes, 0.01 ≤p < 0.05 implies the existence of statistical significance in the differences of the feature, and p < 0.01 implies high significance.

The correlation-based feature selection filter searches for subsets of features that are highly correlated with the class while having low intercorrelation are preferred [22]. It evaluates the worth of a subset of attributes by considering the individual predictive ability of each feature along with the degree of redundancy between them. Correlation-based method needs to use a search method to find a local optimum feature subset in the search space. The search method used in this work was the best first, which searches the space of attribute subsets by greedy hillclimbing augmented with a backtracking facility [23]. Best first was employed with a forward search, which starts with the empty subset of attributes, to find a small subset of relevant features.

The wrapper method evaluates attribute subsets using a learning scheme and uses cross-validation to estimate the accuracy of the learning scheme for a subset of attributes [24]. In order to do that, it uses a classifier to estimate the accuracy of the subsets and a search method. It is important that the classifier used in the wrapper method be the same as the classifier used in the classification process due to the performance of the learning scheme. Therefore, the classifier used in the wrapper method is presented in the pulmonary nodule classification “Pulmonary Nodule Database” using tenfolds to estimate the accuracy of the subset. The search method of the wrapper was also the best first with forward search.

Statistical analysis was performed using an unpaired Student’s t test. Correlation and wrapper feature selection methods were performed using a stratified tenfold cross-validation. Therefore, after the execution of the tenfolds, a list of attributes and their occurrences on selection is generated. Relevance can be measured by the number of occurrences on the cross-validation. For instance, if an attribute is selected on tenfolds of the cross-validation, then it may have high relevance on pulmonary nodule characterization. If an attribute is not selected on any fold, then it may have low (or none) relevance on pulmonary nodule characterization, and hence may decrease classification performance.

Pulmonary Nodule Classification

In order to classify the pulmonary nodules, we used seven traditional machine learning algorithms, one for each different classification method, as follows:

• ZeroR (ZR): it selects the majority class in the dataset (independently of the feature vector) and can be used as baseline for the experiment, which all algorithms can be compared to;

• k-nearest neighbors (KNN): also known as instance-based learning algorithm, it chooses the majority class among k neighbors to classify the unknown test instance. The Euclidean distance was used as distance function, and the value of k was defined as 9;

• Support vector machine (SVM): a classifier that aims to find a hyperplane that separates a dataset in discrete classes. The SVM used a nu-support vector type with radial basis function kernel;

• Naive Bayes (NB): a probabilistic classifier based on Bayes’ theorem with features independence assumption;

• Radial basis function (RBF): a radial basis function-based artificial neural network. In this work, RBF neural network training was performed by k-means clustering to provide the radial units. The number of clusters was defined as 2;

• J48: the Java implementation of the C4.5 decision tree that selects more descriptive attributes using information entropy for the classification. The confidence factor was 0.25;

• Random forest (RF): an ensemble learning classifier that operates by bagging ensembles of random decision trees. The number of random trees was 100.

Performance Evaluation

Classification was performed using a stratified tenfold cross-validation. The machine learning classifiers used different nodule attributes to perform the binary classification. All nodule descriptors were previously extracted from all database cases (“Image Feature Extraction”). Each pulmonary nodule was characterized by four feature vectors. The first vector has all 48 texture and margin sharpness attributes combined. The second vector has selected features from the statistical significance analysis with p < 0.05 (“Image Feature Selection”). The third vector has selected attributes from the correlation-based method. The fourth vector has selected attributes from the wrapper. The threshold value for the feature occurrence on the cross-validation was 4, hence all features that appeared at least on fivefolds of the cross-validation were used. The value of 4 was employed to exclude attributes that may have low or none relevance on distinguishing pulmonary nodules. All attributes were normalized in a range from 0 to 1.

In order to assess the efficiency of the pulmonary nodule classification, the following statistical parameters were used: accuracy, sensitivity, specificity, and area under the receiver operating characteristic (ROC) curve (AUC). Accuracy refers to the proportion of correctly classified instances (1). Sensitivity refers to the proportion of positives that are correctly classified as such Eq. 2. Specificity refers to the proportion of negatives that are correctly classified as such Eq. 3. The ROC curve is defined as a plot of test sensitivity as the y coordinate versus its 1-specificity or false-positive rate as the x coordinate, and the AUC is the area under the ROC curve [25].

$$\text{Accuracy}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}},$$ 1

$$\text{Sensitivity}=\frac{\text{TP}}{\text{TP}+\text{FN}},$$ 2

$$\text{Specificity}=\frac{\text{TN}}{\text{TN}+\text{FP}},$$ 3

where TP, TN, FP, and FN are the numbers of true positives, true negatives, false positives, and false negatives, respectively.

Results

Table 1 presents the results of the feature selection by the statistical significance analysis, the correlation-based method, and the wrapper described in “Image Feature Selection.” Statistical significance analysis was performed for each feature independently. Correlation-based feature selection was performed once for each dataset, since it does not rely on a specific classifier. Feature selection by the wrapper method was performed once for each dataset and classifier, except for the ZeroR, because it does not use imaging attributes to perform pulmonary nodule classification.

Table 1.

Statistical significance of the features and attribute occurrences on feature selection using the correlation-based method and classifiers wrappers

Attribute	p value	Correlation	KNN	SVM	NB	RBF	J48	RF
Difference of two ends	0.3367	10 ∣ 10	0 ∣ 10	10 ∣ 10	8 ∣ 10	10 ∣ 10	8 ∣ 10	10 ∣ 10
Sum of values	< 0.0001	0 ∣ 0	0 ∣ 0	7 ∣ 5	2 ∣ 1	9 ∣ 0	2 ∣ 0	3 ∣ 1
Sum of squares	< 0.0001	0 ∣ 1	1 ∣ 1	6 ∣ 7	0 ∣ 2	0 ∣ 1	3 ∣ 0	6 ∣ 0
Sum of logs	< 0.0001	0 ∣ 0	0 ∣ 2	3 ∣ 5	7 ∣ 0	0 ∣ 0	2 ∣ 1	4 ∣ 3
Arithmetic mean	0.2876	10 ∣ 1	0 ∣ 0	10 ∣ 6	6 ∣ 6	8 ∣ 9	1 ∣ 0	4 ∣ 3
Geometric mean	0.0073	0 ∣ 0	0 ∣ 0	6 ∣ 3	8 ∣ 5	0 ∣ 3	2 ∣ 0	2 ∣ 2
Population variance	0.6129	2 ∣ 1	0 ∣ 2	5 ∣ 2	7 ∣ 5	1 ∣ 0	1 ∣ 1	1 ∣ 1
Sample variance	0.6491	4 ∣ 3	0 ∣ 1	3 ∣ 3	8 ∣ 4	3 ∣ 0	1 ∣ 0	4 ∣ 3
Standard deviation	0.6491	0 ∣ 0	0 ∣ 0	4 ∣ 4	5 ∣ 5	2 ∣ 1	0 ∣ 0	0 ∣ 4
Kurtosis measure	< 0.0001	10 ∣ 10	0 ∣ 3	1 ∣ 5	1 ∣ 8	4 ∣ 6	1 ∣ 0	8 ∣ 3
Skewness measure	< 0.0001	6 ∣ 3	0 ∣ 0	3 ∣ 5	3 ∣ 8	10 ∣ 2	2 ∣ 1	3 ∣ 2
SCM	< 0.0001	0 ∣ 1	0 ∣ 3	2 ∣ 1	0 ∣ 0	0 ∣ 0	0 ∣ 0	1 ∣ 0
Energy at 0∘	0.1215	0 ∣ 0	0 ∣ 0	1 ∣ 0	3 ∣ 5	1 ∣ 1	1 ∣ 1	1 ∣ 1
Entropy at 0∘	< 0.0001	8 ∣ 3	2 ∣ 0	3 ∣ 2	0 ∣ 0	0 ∣ 0	1 ∣ 1	0 ∣ 7
Inertia at 0∘	< 0.0001	10 ∣ 10	0 ∣ 9	5 ∣ 5	8 ∣ 0	8 ∣ 9	1 ∣ 0	2 ∣ 3
Homogeneity at 0∘	< 0.0001	0 ∣ 0	2 ∣ 1	4 ∣ 1	0 ∣ 0	0 ∣ 0	2 ∣ 1	0 ∣ 4
Correlation at 0∘	< 0.0001	0 ∣ 0	1 ∣ 0	3 ∣ 3	3 ∣ 5	0 ∣ 0	1 ∣ 0	0 ∣ 2
Shade at 0∘	< 0.0001	0 ∣ 0	3 ∣ 0	0 ∣ 1	0 ∣ 0	0 ∣ 0	2 ∣ 2	3 ∣ 0
Promenance at 0∘	< 0.0001	10 ∣ 4	4 ∣ 0	0 ∣ 2	0 ∣ 0	0 ∣ 0	0 ∣ 0	1 ∣ 0
Variance at 0∘	< 0.0001	0 ∣ 0	2 ∣ 0	1 ∣ 0	0 ∣ 0	2 ∣ 3	1 ∣ 0	0 ∣ 0
IDM at 0∘	< 0.0001	9 ∣ 3	5 ∣ 5	3 ∣ 4	0 ∣ 0	6 ∣ 0	3 ∣ 3	5 ∣ 3
Energy at 45∘	0.0017	6 ∣ 1	0 ∣ 0	2 ∣ 0	4 ∣ 0	2 ∣ 0	1 ∣ 0	0 ∣ 1
Entropy at 45∘	< 0.0001	0 ∣ 0	0 ∣ 0	1 ∣ 2	0 ∣ 0	0 ∣ 0	0 ∣ 2	2 ∣ 5
Inertia at 45∘	< 0.0001	6 ∣ 1	0 ∣ 5	3 ∣ 1	0 ∣ 1	7 ∣ 5	3 ∣ 0	5 ∣ 4
Homogeneity at 45∘	< 0.0001	0 ∣ 0	1 ∣ 0	3 ∣ 1	0 ∣ 0	0 ∣ 0	0 ∣ 2	1 ∣ 1
Correlation at 45∘	< 0.0001	0 ∣ 0	0 ∣ 0	3 ∣ 5	2 ∣ 0	0 ∣ 0	0 ∣ 0	0 ∣ 3
Shade at 45∘	< 0.0001	0 ∣ 0	2 ∣ 0	1 ∣ 2	0 ∣ 0	0 ∣ 0	1 ∣ 0	2 ∣ 0
Promenance at 45∘	< 0.0001	4 ∣ 0	0 ∣ 0	1 ∣ 1	0 ∣ 0	0 ∣ 0	0 ∣ 0	0 ∣ 1
Variance at 45∘	< 0.0001	0 ∣ 0	0 ∣ 0	0 ∣ 1	0 ∣ 0	0 ∣ 0	0 ∣ 1	2 ∣ 2
IDM at 45∘	< 0.0001	10 ∣ 5	3 ∣ 0	1 ∣ 3	0 ∣ 0	3 ∣ 0	2 ∣ 0	3 ∣ 1
Energy at 90∘	0.0424	0 ∣ 2	0 ∣ 0	0 ∣ 6	2 ∣ 5	4 ∣ 5	1 ∣ 3	3 ∣ 0
Entropy at 90∘	< 0.0001	2 ∣ 0	1 ∣ 0	2 ∣ 1	0 ∣ 0	0 ∣ 0	1 ∣ 0	1 ∣ 2
Inertia at 90∘	< 0,0001	1 ∣ 1	0 ∣ 2	1 ∣ 5	1 ∣ 6	7 ∣ 4	0 ∣ 3	0 ∣ 0
Homogeneity at 90∘	< 0.0001	0 ∣ 0	1 ∣ 0	1 ∣ 3	0 ∣ 0	0 ∣ 0	1 ∣ 0	1 ∣ 0
Correlation at 90∘	< 0.0001	0 ∣ 0	5 ∣ 0	1 ∣ 4	7 ∣ 5	5 ∣ 1	0 ∣ 1	2 ∣ 4
Shade at 90∘	< 0.0001	0 ∣ 0	0 ∣ 0	0 ∣ 3	0 ∣ 0	0 ∣ 0	0 ∣ 2	1 ∣ 0
Promenance at 90∘	< 0.0001	10 ∣ 10	0 ∣ 0	1 ∣ 0	0 ∣ 0	0 ∣ 0	1 ∣ 0	1 ∣ 0
Variance at 90∘	< 0.0001	0 ∣ 3	0 ∣ 0	1 ∣ 3	0 ∣ 0	1 ∣ 1	5 ∣ 1	1 ∣ 3
IDM at 90∘	< 0.0001	9 ∣ 8	1 ∣ 3	1 ∣ 4	0 ∣ 0	5 ∣ 0	0 ∣ 0	1 ∣ 1
Energy at 135∘	0.0030	10 ∣ 3	0 ∣ 0	0 ∣ 0	6 ∣ 8	10 ∣ 3	1 ∣ 2	0 ∣ 2
Entropy at 135∘	< 0.0001	0 ∣ 0	0 ∣ 0	1 ∣ 3	0 ∣ 0	0 ∣ 0	1 ∣ 1	0 ∣ 1
Inertia at 135∘	< 0.0001	8 ∣ 5	0 ∣ 7	4 ∣ 5	2 ∣ 0	8 ∣ 4	3 ∣ 1	0 ∣ 3
Homogeneity at 135∘	< 0.0001	0 ∣ 2	0 ∣ 1	4 ∣ 4	0 ∣ 0	0 ∣ 0	2 ∣ 2	2 ∣ 3
Correlation at 135∘	< 0.0001	0 ∣ 0	0 ∣ 0	2 ∣ 5	2 ∣ 0	0 ∣ 0	0 ∣ 0	3 ∣ 0
Shade at 135∘	< 0.0001	0 ∣ 0	2 ∣ 0	1 ∣ 2	0 ∣ 0	0 ∣ 0	1 ∣ 0	0 ∣ 2
Promenance at 135∘	< 0.0001	10 ∣ 0	1 ∣ 0	1 ∣ 0	0 ∣ 0	0 ∣ 0	0 ∣ 0	1 ∣ 0
Variance at 135∘	< 0.0001	0 ∣ 0	0 ∣ 0	2 ∣ 2	0 ∣ 0	0 ∣ 0	1 ∣ 0	1 ∣ 1
IDM at 135∘	< 0.0001	8 ∣ 5	6 ∣ 2	1 ∣ 5	0 ∣ 0	4 ∣ 0	3 ∣ 7	5 ∣ 4

Occurrences are displayed in pairs x ∣y, where x and y correspond to the number of occurrences of an attribute on the tenfold cross-validation using the unbalanced and the balanced datasets, respectively

In “Experimental Results with the Unbalanced Dataset,” Table 2 presents the results of classification efficiency using the unbalanced dataset, and Fig. 1a–d illustrates its diagnostic performance using ROC curves. In “Experimental Results with the Balanced Dataset,” Table 3 presents the results of classification efficiency using the balanced dataset, and Fig. 2a–d illustrates the diagnostic performance using ROC curves. Sensitivity and specificity values in Tables 2 and 3 are related to the point in the ROC curve that presents highest accuracy. A performance comparison between the two datasets is presented in “Performance Comparison Based on Datasets.’’

Table 2.

Classification results with the unbalanced dataset

		ZR	KNN	SVM	NB	RBF	J48	RF
All features	Accuracy	0.636	0.763	0.773	0.703	0.691	0.753	0.800
	Sensitivity	0.000	0.596	0.493	0.244	0.209	0.617	0.702
	Specificity	1.000	0.859	0.933	0.965	0.966	0.831	0.856
	AUC	0.496	0.827	0.713	0.769	0.695	0.735	0.858
Features	Accuracy	0.636	0.756	0.774	0.702	0.683	0.762	0.786
selected by	Sensitivity	0.000	0.563	0.491	0.242	0.350	0.636	0.685
statistics	Specificity	1.000	0.866	0.936	0.965	0.874	0.834	0.843
	AUC	0.496	0.794	0.713	0.749	0.702	0.747	0.847
Features	Accuracy	0.636	0.766	0.765	0.703	0.740	0.777	0.781
selected by	Sensitivity	0.000	0.559	0.495	0.223	0.392	0.650	0.655
correlation	Specificity	1.000	0.885	0.919	0.977	0.940	0.850	0.854
	AUC	0.496	0.811	0.707	0.778	0.709	0.771	0.846
Features	Accuracy	0.636	0.792	0.784	0.769	0.761	0.786	0.788
selected by	Sensitivity	0.000	0.664	0.531	0.502	0.505	0.575	0.662
wrapper	Specificity	1.000	0.866	0.929	0.921	0.907	0.906	0.860
	AUC	0.496	0.816	0.730	0.792	0.752	0.710	0.843

Italicized values are the highest for each row

Fig. 1.

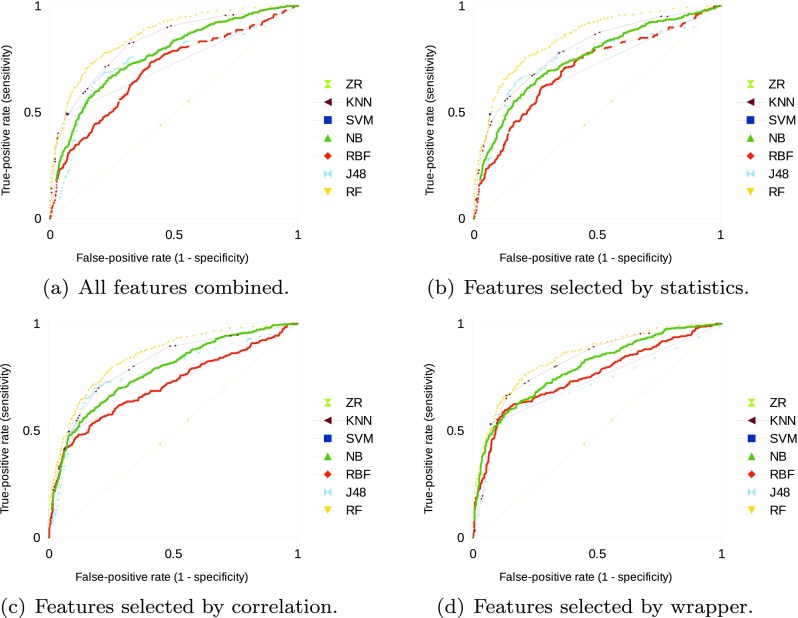
ROC curves for diagnostic performance of the classifiers using the unbalanced dataset

Table 3.

Classification results with the balanced dataset

		ZR	KNN	SVM	NB	RBF	J48	RF
All features	Accuracy	0.500	0.738	0.777	0.608	0.635	0.688	0.760
	Sensitivity	1.000	0.663	0.700	0.247	0.643	0.680	0.750
	Specificity	0.000	0.813	0.853	0.970	0.627	0.697	0.770
	AUC	0.500	0.806	0.777	0.734	0.685	0.720	0.856
Features	Accuracy	0.500	0.727	0.747	0.605	0.608	0.720	0.760
selected by	Sensitivity	1.000	0.683	0.677	0.240	0.593	0.707	0.780
statistics	Specificity	0.000	0.770	0.817	0.970	0.623	0.733	0.740
	AUC	0.500	0.791	0.747	0.711	0.667	0.747	0.856
Features	Accuracy	0.500	0.748	0.627	0.610	0.698	0.717	0.728
selected by	Sensitivity	1.000	0.703	0.643	0.247	0.497	0.660	0.733
correlation	Specificity	0.000	0.793	0.610	0.973	0.900	0.773	0.723
	AUC	0.500	0.820	0.627	0.765	0.736	0.746	0.819
Features	Accuracy	0.500	0.738	0.773	0.692	0.747	0.758	0.747
selected by	Sensitivity	1.000	0.687	0.697	0.607	0.600	0.693	0.753
wrapper	Specificity	0.000	0.790	0.850	0.777	0.893	0.823	0.740
	AUC	0.500	0.796	0.773	0.752	0.784	0.751	0.809

Italicized values are the highest for each row

Fig. 2.

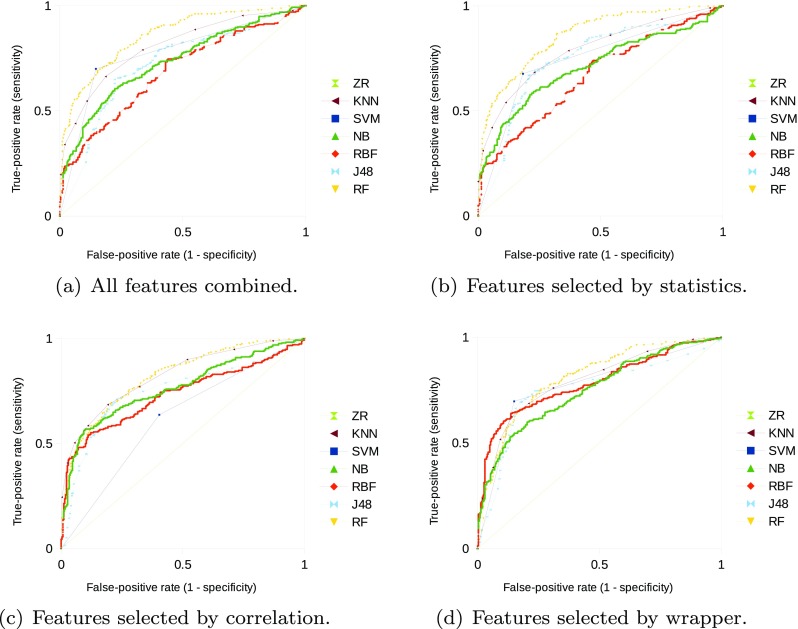
ROC curves for diagnostic performance of the classifiers using the balanced dataset

Experimental Results with the Unbalanced Dataset

All classifiers presented higher performance in comparison to the baseline ZeroR (ZR) on the unbalanced dataset, independently of the set of attributes used. Lowest classification performance was obtained by the radial basis function (RBF) neural network with all attributes, but higher than the baseline. Random forest (RF) classifier obtained highest performance with the feature vector presenting all attributes. Figure 1a illustrates the diagnostic performance of the classifiers with all the extracted features using ROC curves.

Classification performance was not improved by selecting only the statistically significant attributes in comparison to all features combined. RF obtained highest classification performance on this scenario, but no statistically significant difference was identified in comparison to the performance of the complete feature vector (95% confidence interval—consider this confidence level for the remainder of the statistical analysis). Figure 1b illustrates the diagnostic performance of the classifiers with the statistically significant attributes.

Selecting the attributes by the correlation method also did not improve classification efficiency with the majority of classifiers. However, RBF classification accuracy with those 17 selected attributes increased 5 percentage points in comparison to the complete feature vector, with statistically significant difference on sensitivity between them. J48 accuracy and AUC on this scenario obtained a mean increase of three percentage points in comparison to all features combined, but no statistically significant difference was identified. Figure 1c illustrates the diagnostic performance of the classifiers with the selected attributes by the correlation-based method.

Selecting the attributes by the wrapper improved classification performance (accuracy or AUC) with the majority of classifiers. Highest differences on accuracy, in comparison to the complete feature vector, were obtained by RBF (using 12 features) and Naive Bayes (NB, using 10 attributes) with a mean increase of seven percentage points for both classifiers and statistically significant differences on sensitivity and specificity. RF and k-nearest neighbors (KNN) classifiers with six and three selected attributes, respectively, obtained highest classification performance on this scenario, but no statistically significant differences between them and in comparison to the complete feature vectors. Figure 1d illustrates the diagnostic performance of the classifiers with the selected attributes by the wrapper.

Experimental Results with the Balanced Dataset

All classifiers presented higher performance in comparison to the baseline ZeroR on the balanced dataset, independently of the subset of attributes used. Lowest classification performance was obtained by the SVM with selected attributes by correlation with AUC of 0.627, but higher than the baseline with AUC of 0.500.

RF obtained highest diagnostic performance with AUC of 0.846, and the SVM obtained highest classification accuracy with 0.777 and the feature vector presenting all attributes. No statistically significant difference was identified on RF and SVM classification performances. Figure 2a illustrates the diagnostic performance of the classifiers with all the extracted features and the balanced dataset.

Classification efficiency was not improved by selecting only the statistically significant attributes in comparison to all features combined. J48 classification performance with those 42 selected attributes increased in comparison to the complete feature vector, but no statistically significant difference was identified. RF obtained highest classification performance on this scenario, but no statistically significant difference was identified in comparison to all features combined and to the J48 performance. Figure 2b illustrates the diagnostic performance of the classifiers with the statistically significant attributes.

Selecting the attributes by the correlation method improved classification performance with the majority of classifiers. RBF classification with those eight selected attributes was improved in comparison to the complete feature vector, with statistically significant difference on both sensitivity and specificity. However, no statistically significant difference was identified on the performances of the KNN, NB, and J48 classifiers with this scenario. Figure 2c illustrates the diagnostic performance of the classifiers with the selected attributes by the correlation-based method.

Selecting the attributes by the wrapper improved diagnostic performance with the majority of classifiers. NB classification with 13 attributes was improved, with statistically significant differences on both sensitivity and specificity. RBF with six attributes and J48 with two attributes improved classification performance, with statistically significant difference on specificity with both classifiers. Figure 2d illustrates the diagnostic performance of the classifiers with the selected attributes by the wrapper.

Performance Comparison Based on Datasets

Statistically significant improvements on sensitivity, which is important on malignant vs. benign classification problems [25], were identified on several scenarios when balancing the number of cases in the database (Table 4).

Table 4.

Occurrence of statistically significant difference on sensitivity using the datasets

	KNN	SVM	NB	RBF	J48	RF
All features combined		X		X
Features selected by statistics	X	X		X
Features selected by correlation	X	X
Features selected by wrapper		X			X

RBF with all features combined obtained highest sensitivity improvement with a mean increase of 43 percentage points in comparison to the unbalanced dataset. RF and NB were the only classifiers that did not present statistically significant improvement on sensitivity with any subset of features. SVM presented statistically significant difference on sensitivity with all subsets of features.

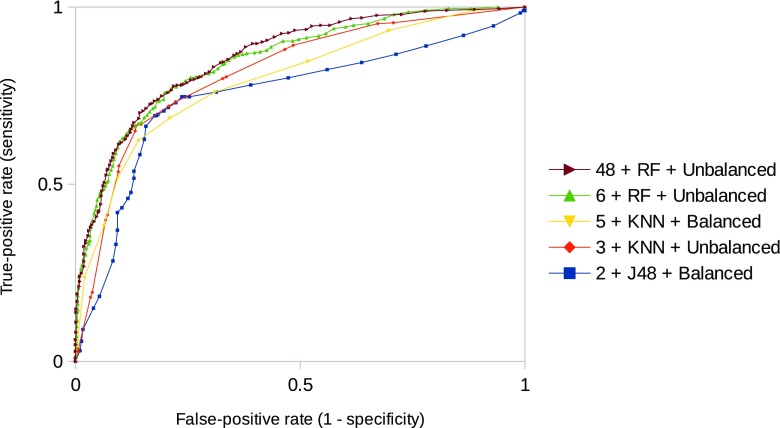
RF with all attributes combined and the unbalanced dataset obtained highest classification performance overall scenarios with AUC of 0.858. However, no statistically significant differences on sensitivity and specificity were identified in comparison to some combination scenarios of classifiers, features selected by the wrapper method, and dataset employed. Table 5 and Fig. 3 present sensitivity, specificity, and ROC curves for some of those combination scenarios (most relevant ones according to high efficiency and small number of selected features by the wrapper method) of classification.

Table 5.

Classification scenarios with no statistically significant difference identified on sensitivity and specificity (95% confidence intervals)

Number of features	Classifier	Dataset	Sensitivity	Specificity
48	RF	Unbalanced	(0.656, 0.744)	(0.829, 0.880)
6	RF	Unbalanced	(0.615, 0.706)	(0.833, 0.884)
5	KNN	Balanced	(0.630, 0.738)	(0.739, 0.834)
3	KNN	Unbalanced	(0.617, 0.709)	(0.839, 0.889)
2	J48	Balanced	(0.637, 0.744)	(0.774, 0.864)

Fig. 3.

ROC curves of relevant classification scenarios with no statistically significant difference identified on sensitivity and specificity. Scenarios are presented with the number of features + classifier + dataset used

Discussion

Computer recognition of medical image patterns is important in that it can assist the clinical decision process of distinguishing pulmonary nodules according to their malignancy [1, 9, 12]. However, it depends on extracting image features to characterize the pulmonary nodules, selecting the most relevant attributes to better discriminate the lesions, and on an efficient machine learning algorithm that can use those relevant features to classify malignant and benign pulmonary nodules. In this work, we aimed to recognize CT image features of second-order texture, which is traditional and relevant to scientific literature [4, 11, 13], and margin sharpness, which is important in diagnosing lung cancer nodules [15] and has less dependence of the radiologist’s ground truth mark of the nodule border.

Regarding to the results obtained from the experiments, balancing the number of cases of each class in the database partially solved the problem of low sensitivity of some classification scenarios using the unbalanced dataset, as “Performance Comparison Based on Datasets” presented. Therefore, in some cases, it is advisable to employ a balanced database for training and classification purposes; for instance, with SVM using any set of features of margin sharpness and texture (Table 4).

The selection of statistically significant features did not present neither relevant performance improvement, nor relevant dimensionality reduction of the feature space. Only six features were excluded from the feature vector (difference of two ends, arithmetic mean, population variance, sample variance, standard deviation, and energy at 0^∘), which represented a reduction of 13% of the feature space. Therefore, the attribute selection by statistical analysis of each feature apparently did not present any classification relevance for computational or diagnostic purposes.

However, correlation and wrapper methods were able to improve classification performance in several scenarios, or at least, reduce the dimensionality of the feature space. For instance, correlation method selected 17 features using the unbalanced dataset (difference of two ends, arithmetic mean, kurtosis measure, skewness measure, entropy at 0^∘, inertia at 0^∘, promenance at 0^∘, IDM at 0^∘, energy at 45^∘, inertia at 45^∘, IDM at 45^∘, promenance at 90^∘, IDM at 90^∘, energy at 135^∘, inertia at 135^∘, promenance at 135^∘, and IDM at 135^∘), which corresponded a reduction of 65% of the feature space, and eight features using the balanced dataset (difference of two ends, kurtosis measure, inertia at 0^∘, IDM at 45^∘, promenance at 90^∘, IDM at 90^∘, inertia at 135^∘, and IDM at 135^∘), which corresponded a reduction of 83% of the feature space. Moreover, those selected features with the RBF neural network increased classification performance with a mean increase of five and three percentage points on accuracy and AUC, respectively, in comparison to the complete feature vector for both datasets, with statistically significant difference on sensitivity for both datasets and on specificity for the balanced one.

Furthermore, since the wrapper needs to use a classifier to perform the feature selection, each classifier used in this work selected a different subset of features. For instance, Naive Bayes wrapper selected 13 features using the balanced dataset (difference of two ends, arithmetic mean, geometric mean, population variance, standard deviation, kurtosis measure, skewness measure, energy at 0^∘, correlation at 0^∘, energy at 90^∘, inertia at 90^∘, correlation at 90^∘, and energy at 135^∘) and ten features using the unbalanced dataset (difference of two ends, sum of logs, arithmetic mean, geometric mean, population variance, sample variance, standard deviation, inertia at 0^∘, correlation at 90^∘, and energy at 135^∘), and obtained a mean increase of seven and two percentage points on accuracy and AUC, respectively, in comparison to the complete feature vector, with statistically significant differences on sensitivity and specificity on both datasets.

Highest number of attributes selected by a wrapper was obtained by SVM using the balanced dataset of 14 features (difference of two ends, sum of values, sum of squares, sum of logs, arithmetic mean, kurtosis measure, skewness measure, inertia at 0^∘, correlation at 45^∘, energy at 90^∘, inertia at 90^∘, inertia at 135^∘, correlation at 135^∘, and IDM at 135^∘), which corresponded a reduction of 71% of the feature space, and no statistically significant differences on sensitivity and specificity were obtained in comparison to the complete feature vector. Lowest number of attributes selected by a wrapper was obtained by the decision tree J48 using both datasets of two features (difference of two ends and IDM at 135^∘ for the balanced dataset, and difference of two ends and variance at 90^∘ for the unbalanced dataset), which corresponded a reduction of 96% of the feature space, and statistically significant difference on specificity in comparison to the complete feature vector.

Despite the fact that the wrapper is able to reduce the dimensionality more effectively than the correlation method, the former takes much more time than the latter to perform feature selection. This happens because, for each feature subset examined by the wrapper, a training model is built for each of the tenfolds of the cross-validation. Therefore, for some classifier wrappers, it takes several hours to select the most relevant attributes out of the 48 extracted features, while the correlation method selects them in just a few seconds.

As stated before, the RF algorithm with all 48 combined features and the unbalanced dataset obtained highest classification efficiency overall scenarios. However, the J48 decision tree using the balanced dataset and only two features selected by the wrapper (difference of two ends and IDM at 135^∘), which corresponded a reduction of 96% of the feature space, obtained equivalent classification performance with no statistically significant differences on sensitivity and specificity, despite the higher AUC of RF in comparison to J48 (0.858 vs. 0.751, Fig. 3).

Besides the attributes of difference of two ends and IDM at 135^∘ selected by the J48 wrapper with the balanced dataset, we also highlight the attribute of IDM at 0^∘ as relevant to distinguish the pulmonary nodules as malignant or benign, due to its occurrence on the other three classification scenarios that did not present statistically significant difference in comparison to the scenario that presented highest classification efficiency (48 + RF + unbalanced dataset, Table 5).

Results from the RF with the unbalanced dataset are promising when comparing to the results found in literature with different image features and datasets (Table 6) [1, 9–14]. RF obtained higher AUC in comparison to the Reeves et al. and Ferreira Jr et al., higher specificity than the approaches of Wu et al. and Tartar et al., and at least equivalent accuracy than Ferreira Jr et al. “Related Works” presents details from those works.

Table 6.

Comparison on random forest classification efficiency (using the unbalanced dataset) with the literature

Proposal	Accuracy	Sensitivity	Specificity	AUC
Wu et al. [1]	–	0.960	0.800	0.910
Tartar et al. [9]	0.837	0.854	0.816	0.908
Reeves et al. [10]	–	–	–	0.772
Dilger et al. [11]	0.920	0.909	0.928	0.935
Zhang et al. [12]	0.880	–	–	–
Kaya et al. [13]	0.849	0.831	0.921	–
Ferreira Jr et al. [14]	0.792	–	–	0.816
48 combined features	0.800	0.702	0.856	0.858
6 selected features	0.788	0.662	0.860	0.843

Furthermore, quantifying the margin sharpness and texture of the pulmonary nodules differently may increase classification performance, for instance, with Levman and Martel attribute of margin sharpness [15], Tamura features for texture characterization [26], or by wavelet transforms and fractal dimension analysis [27, 28]. Attribute weighing and principal components analysis may also enhance the performance of the pulmonary nodule classification by updating the feature weights or filtering the noise attributes [23, 29]. For last, classification performance may be improved by employing a more robust learning algorithm to classify the pulmonary nodules, e.g., using deep convolutional neural networks [30].

One limitation of this work is the lack of clinical diagnosis to be used as gold standard for benign and malignant pulmonary nodules. LIDC has a limited number of lesions with final diagnosis, either by biopsy, surgical resection, review of radiological images to show two years of stable nodule or progression/response [18]. In this work, we prioritized a high number of cases for the analysis, and hence, we used only the radiological evaluation as gold standard (likelihood of malignancy in a 1–5 scale), as other studies also used this approach [13, 14, 29]. However, it is important to perform further experiments to validate the results and findings of this work with the clinically proven pulmonary nodules.

Other limitation of this work is the lack of association between the image features and histopathological subtype of the malignant lesions and other clinical outcomes (process known as radiomics [4]). Therefore, further investigation is necessary to assist specialists with, not only the diagnosis, but also the prognosis of lung cancer.

Conclusions

This paper presented the malignant-vs-benign classification of pulmonary nodules based on imaging features of margin sharpness and second-order texture in CT scans. Classification was performed with a publicly available pulmonary nodule image database, which enabled reproducible research and cross-validation between others researchers and CAD methods. The selection of the most relevant attributes from the feature vector used different feature selection methods, and the classification of the pulmonary nodules was performed in terms of potential malignancy, with different machine learning algorithms to find the best approach to identify image patterns in pulmonary nodules.

All extracted features combined with the RF classifier and an unbalanced dataset for training presented highest classification performance and promising results for future works. However, the J48 decision tree with only two features (difference of highest and lowest gray level intensities from perpendicular lines of the nodule, and inverse difference moment computed from the 135^∘ gray level co-occurrence matrix) selected by a wrapper is a low cost computational solution for a possible end-user CAD software, with statistically equivalent performance in comparison to the RF. Therefore, the first scenario may be a better solution for diagnostic purposes, while the second scenario is more appropriate to reduce computational costs that the complete feature vector may introduce to a pulmonary nodule classification software. Furthermore, texture and margin sharpness image features and decision-tree-based classifiers present potential to predict malignancy of pulmonary nodules.

Further experiments need to be performed in terms of evaluation and in clinical practice as a CAD tool to radiologists. Our pulmonary nodule feature vector is in a developing stage, and we aim at improving its efficiency on characterization and classification in order to improve the diagnosis of lung cancer.

Funding Information

This study was funded by Fundação de Amparo à Pesquisa do Estado de Alagoas and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (grant no. 20130603-002-0040-0063)

Conflict of interests

The authors declare that they have no conflict of interest.

Ethical approval

For this type of study formal consent is not required. This study used a public image database (10.7937/K9/TCIA.2015.LO9QL9SX), which all protected health information (PHI) contained within the DICOM headers of the images were removed in accordance with Health Insurance Portability and Accountability Act (HIPAA) guidelines.