Graphical Models for Quasi-experimental Designs

Abstract

Randomized controlled trials (RCTs) and quasi-experimental designs like regression discontinuity (RD) designs, instrumental variable (IV) designs, and matching and propensity score (PS) designs are frequently used for inferring causal effects. It is well known that the features of these designs facilitate the identification of a causal estimand and, thus, warrant a causal interpretation of the estimated effect. In this article, we discuss and compare the identifying assumptions of quasi-experiments using causal graphs. The increasing complexity of the causal graphs as one switches from an RCT to RD, IV, or PS designs reveals that the assumptions become stronger as the researcher’s control over treatment selection diminishes. We introduce limiting graphs for the RD design and conditional graphs for the latent subgroups of com-pliers, always takers, and never takers of the IV design, and argue that the PS is a collider that offsets confounding bias via collider bias.

Introduction

Randomized experiments and quasi-experimental designs play an important role in inferring cause–effect relationships in evaluating treatments and programs in psychology, education, sociology, economics, and other fields of the social and behavioral sciences. In implementing (quasi)-experiments with a treatment and a control condition, researchers frequently follow Campbell’s tradition (Shadish, Cook, and Campbell 2002; Wong et al. 2012) in ruling out all plausible threats to internal validity, including selection, maturation, history, or instrumentation effects. Depending on a study’s capacities and limitations, a researcher may choose to implement a randomized controlled trial (RCT), a regression discontinuity (RD) design, an instrumental variable (IV) design, a nonequivalent control group design (matching design), or an interrupted time series design (difference-indifferences design). If the corresponding design is perfectly implemented, threats to validity are successfully ruled out by the specific design such that the causal effect of the treatment or program is identified and estimable using a consistent or unbiased estimator. In comparison to model-based analyses of observational data (e.g., regression or structural equation modeling of register or survey data), RCTs and quasi-experimental designs require fewer or weaker assumptions for identifying the causal effect of interest and, thus, frequently offer a stronger warrant for a causal interpretation of the estimated treatment or program effect.

However, (quasi)-experimentation is only one way for inferring cause–effect relationships. Alternatively, one can use substantive theory in order to derive a structural causal model (SCM) that reflects the causal mechanism in which researchers believe given the gathered empirical evidence (Heckman 2005; Pearl 2009; Spirtes, Glymour, and Scheines 2000). On grounds of the theory-based SCM, a researcher can then determine which covariates need to be measured in an observational study so that the causal effect of interest is identified conditional on the presumed SCM. The SCM can be depicted in a nonparametric and nonlinear causal graph which considerably facilitates the identification task. One of the main advantages of causal graphs is that they make explicit most assumptions needed for identifying a causal effect. Pearl (2009) and others (Brito and Pearl 2002b; Shpitser and Pearl 2006; Shpitser, VanderWeele, and Robins 2013) developed an exhaustive set of graphical identification criteria (e.g., the backdoor and front-door criteria) that allows one to probe a causal effect’s identification from a causal graph alone. Causal graphs and the corresponding SCMs represent a researcher’s qualitative causal knowledge or belief about the data generating mechanism which also includes aspects of the study design (like matching), measurement, and the data collection procedure. A brief introduction to causal graphs is given in Online Appendix A. For a more thorough introduction see, for instance, Elwert (2013), Hernán and Robins (2014), Morgan and Winship (2014), or Pearl (2010). Shadish and Sullivan (2012) contains a comparison between Campbell’s tradition of (quasi)-experimentation, the Rubin Causal Model, and SCMs including causal graphs.

The aim of this article is to represent experimental and quasi-experimental designs as causal graphs and to demonstrate that strong designs result in simple graphs. Typically, a simple graph implies easier identification of causal treatment effects. The causal graphs of RCTs, RD, IV, matching and propensity score (PS) designs make it very clear, at least from a theoretical point of view, that the design assumptions underlying an RCT are weaker than for an RD design, which themselves are weaker than for an IV or PS design.¹ The increased complexity of IV and PS graphs directly reflects the stronger assumptions needed for identification. We also use causal graphs to illustrate that different designs identify different causal quantities. While RCTs and PS designs allow for an identification of the average treatment effect (ATE), the basic RD and IV designs only identify a local ATE: the ATE at the cutoff and the ATE for compliers, respectively.

While all the arguments about the relative strength and weakness of RCTs and quasi-experimental designs are not new, the causal graphs we present for RD, IV, and PS designs have never been shown and discussed before. It is maybe not surprising then, that the graphical formalization of quasi-experiments results in new insights and a clearer understanding of the designs and their assumptions. For instance, contrary to the general belief, we show that the PS is a collider variable that offsets the confounding bias via collider bias. Or, in introducing a limiting graph for the RD design, we clearly see that RD is a randomized experiment at the cutoff. Or, in using conditional graphs for the latent subpopulations of compliers, always takers, and never takers, it becomes apparent that the treatment effect is only identified for the compliers.

Given that this article focuses on the graphical representation of (quasi)-experimental designs and their identifying assumptions, we do not discuss or compare the designs’ practical advantages or limitations with respect to estimation, implementation, or generalization. Instead we exclusively focus on the nonparametric identification of ATEs, that is, whether a causal treatment effect can be obtained from perfect data (i.e., if we would have an infinitely large target population) without making any functional form or distributional assumptions. Estimating the ATE from a finite sample requires the choice of an estimator and additional assumptions like functional form assumptions. Estimators and their underlying assumptions are covered in many introductory books and articles on causal inference, for instance, Angrist and Pischke (2008), Morgan and Winship (2014), or Wong et al. (2012).

The remainder of the article is organized as follows. The first section gives a brief introduction to causal graphs, SCMs, and potential outcomes and motivates the use of RCTs and quasi-experiments. The second section discusses the causal graph for an RCT and the third section focuses on the RD design. The fourth section elaborates on the IV design and is followed by the application of the IV design to RCT and RD designs with noncompliance in the fifth section. The sixth section discusses the causal graphs for matching and PS designs. Finally, in the discussion section, we compare the different designs and highlight their advantages and limitations.

Causal Graphs, Structural Causal Models, and Potential Outcomes

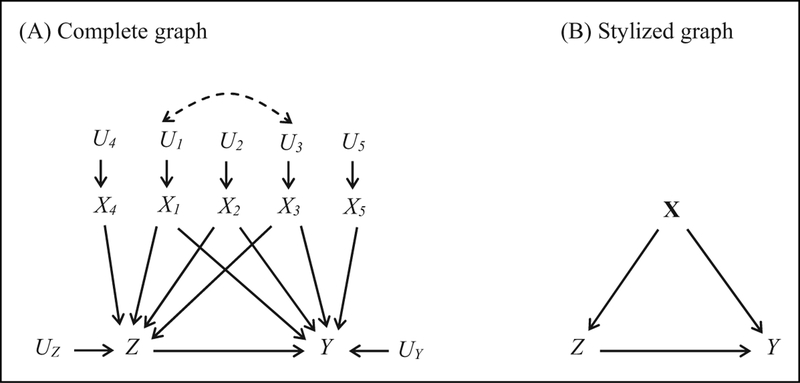
Figure 1A shows an example of how the data from an observational study might have been generated. The nodes in the causal graph represent variables or constructs, and the arrows indicate causal relations between the variables. The absence of an arrow between two variables signifies that the two variables have no direct causal connection (see Online Appendix A for a short introduction to causal graphs). In our causal graph, Z represents a dichotomous treatment variable, where Z = 1 indicates exposure to the treatment condition and Z = 0 indicates exposure to the control or an alternative treatment condition, and Y is the outcome variable of interest. For example, treatment Z might indicate a student’s participation in a remedial math program and Y might be a math achievement score. We are interested in identifying the average causal effect of the remedial math program on the math outcome, that is, the average effect of the path Z ⟶ Y. However, as the graph reveals, the direct identification of the treatment effect is hindered by the presence of (correlated) pretreatment variables X₁–X₃ which confound the relationship between Z and Y because they simultaneously determine treatment Z and outcome Y, that is, Z ⟵ X_j ⟶ Y, for j = 1, 2, 3. The confounders X₁–X₃ might represent students’ ability, sex, and socioeconomic status, which are believed to determine the selection into the remedial math program (Z) but also the math outcome (Y) which is measured after the end of the program. Thus, the simple difference in the treatment and control group’s expectation, E(Y | Z 1) E(Y | Z = 0), is contaminated with confounding bias. For example, if students with a low ability and low socioeconomic status select into the math program, the unadjusted difference in means would be downward biased and, thus, underestimate the causal effect of the program. The simple difference in the treatment and control group’s expectation is biased because the confounding backdoor paths Z ⟵ X_j ⟶Y, for j = 1, 2, 3, are unblocked.

Figure 1.

Causal graph of an observational study: complete and stylized representation.

In addition to confounders, the causal graph also shows variables X₄ and X₅ that exclusively affect Z and Y, respectively, and error terms U₁–U₅, U_Z, and U_Y that represent unobserved but exogenous variables (or disturbances) with respect to the Xs, Z, and Y. Except for U₁ and U₃, all errors are assumed to be independent. The dashed, bidirected arrow between U₁ and U₃ indicates that common causes create an association between the error terms and, as a consequence, variables X₁ and X₃ are associated with each other. In order to simplify the graphical representation, we summarize all confounders (in our case X₁–X₃) into a confounder vector X and absorb the independent exogenous variables X₄ and X₅ in the corresponding error terms U_Z and U_Y, respectively.² The confounders X might be observed or unobserved (for drawing a causal graph this does not make a difference, though it is of crucial importance when we discuss the identification of the treatment effect). Since the error terms for X, Z, and Y are independent, we no longer show them in the stylized graph in Figure 1B—this does not mean that they are absent, but as long as they are independent they do not affect identification. The SCM that corresponds to the stylized graph in Figure 1B is given by:

$$\begin{gathered} {\text{X}}_i=f_i^{\text{X}}\left({\text{U}}_i^{\text{X}}\right) \\ {Z}_i=f_i^Z\left({\text{X}}_i,U_i^Z\right) \\ {Y}_i=f_i^Y\left({\text{X}}_i,Z_i,U_i^Y\right), \end{gathered}$$ (1)

where $f_i^{\text{X}}$ , $f_i^Z$ and $f_i^Y$ are functions generating the confounder vector X, treatment Z and outcome Y, respectively. The subscripts i indicate that the functions may vary across the i = 1, …, N subjects of some (in)finite target population. In particular, this implies that the treatment effect may be heterogeneous. ${\text{U}}_i^{\text{X}}$ , ${\text{U}}_i^Z$ and ${\text{U}}_i^Y$ are independent error terms representing the variation due to exogenous variables (not shown in the stylized graph). Because all error terms are random variables, confounders X, treatment Z, and the outcome Y are stochastic with joint probability distribution P_M. The causal graphs in Figure 1 and the SCM in equation (1) describe a stable and autonomous data generating mechanism. Autonomy implies that a real-world intervention on one variable or a change of one variable’s data generating mechanism does not perturb the data generating mechanism of the other variables (that is why the causal model is called “structural”). Stability refers to the faithfulness of the joint probability distribution’s independence structure as encoded in the causal graph and SCM, that is, the independence relations as reflected by the missing paths remain invariant to changes in the parameters of the data generating SCM (see Online Appendix A for more details; see also Pearl 2009; Pearl and Verma 1991; Spirtes et al. 2000).

Based on the SCM, we can derive potential outcomes for each subject and define the major causal quantities of interest. Following Rubin (1974) and Holland (1986), each subject i has two potential outcomes (see also Balke and Pearl 1994; Pearl 2009): a potential control outcome $Y_i^0$ , which would be observed if the subject is in the control condition, and a potential treatment outcome $Y_i^1$ , which would be observed if the subject is in the treatment condition. Using the outcome equation of the SCM in equation (1), we obtain the potential control outcome by setting Z_i = 0, $Y_i^0=f_i^Y\left({\text{X}}_i,Z_i=0,U_i^Y\right)$, and the potential treatment outcome by setting $Z_i=1,Y_i^1=f_i^Y\left({\text{X}}_i,Z_i=1,U_i^Y\right)$.³

Since the SCM in equation (1) consists of autonomous structural equations, the structural definition of the potential outcomes implies that the three conditions of the stable-unit-treatment values assumption (SUTVA) are met (Rubin 1990; West, Biesanz, and Pitts 2000): (1) There is only one unique version of the treatment; (2) A subject’s potential outcomes do not depend on the treatment status of other subjects; and (3) The assignment or selection process does not affect the potential outcomes. For the remedial math program example, SUTVA implies that (1) all treatment students receive the same math training and control students do not receive any part of it; (2) a student’s potential outcomes are neither affected by the presence of peers nor by a student’s knowledge about whether his friends do or do not participate in the program; and (3) whether a student chose on his own to participate in the remedial math training or whether parents or teachers did so has no effect on the potential outcomes either.

The causal graphs in Figure 1 and the potential outcomes help us to define causal quantities of interest and to check whether they are identifiable. In this article, we are mostly interested in one causal quantity: the ATE of the path Z ⟶ Y, averaged across the entire population. Using the potential outcomes notation, we can define the ATE as:

$$\text{ATE}=E\left(Y_i^1-Y_i^0\right)=E\left(Y_i^1\right)-E\left(Y_i^0\right)=E\left(f_i^Y\left({\text{X}}_i,Z_i=1,U_i^Y\right)\right)-E\left(f_i^Y\left({\text{X}}_i,Z_i=0,U_i^Y\right)\right),$$ (2)

that is, the expected difference between the potential treatment outcomes and the potential control outcomes. We can conceive of this definition as a thought intervention where we first expose all subjects to the treatment condition and then to the control condition, holding everything else constant.⁴

Using Pearl’s backdoor criterion, one can show that the effect Z ⟶ Y is identified in the causal graphs of Figure 1 if all the confounders X are observed such that the backdoor path Z ⟵ X ⟶ Y can be blocked. The back-door criterion states that all backdoor paths into Z need to be blocked, which is achieved if we condition on X (see Online Appendix A for more details). In probabilistic terms, the backdoor criterion corresponds to the conditional independence or strong ignorability assumption: Conditional on confounders X, potential outcomes are independent of treatment Z, (Y⁰; Y¹)⊥ Z | X, and thus, ATE is identified (for details, see the section on matching jand PS designs). However, if we do not observe all confounders X or fail to reliably measure them, the backdoor path Z ⟵ X ⟶ Y is not completely blocked and ATE is not identified. For instance, in our remedial math program example, students’ ability is a confounder that is typically unobserved or unreliably measured when a math pretest is used as a proxy measure for students’ ability. Thus, conditioning on a set of observed covariates (instead of the theorized confounders) might not remove all the confounding bias.

The causal graphs in Figure 1 illustrate the main problem with observational studies: First, our substantive theories are frequently not elaborate enough such that we would know all variables X that confound the relation Z ⟶ Y. Second, even if we have a strong theory we might lack measures for all confounders or only have fallible measures of them (Steiner, Cook, and Shadish 2011). Thus, in order to avoid overly strong assumptions with regard to the identification of ATE, one may resort, if possible, to randomized experiments or quasi-experimental designs like RD designs or IV designs. Since all the assumptions required for a valid design are encoded in the corresponding causal graphs, the comparison of (quasi)-experimental graphs strikingly highlights the advantages and disadvantages of different designs.

Randomized Controlled Trial

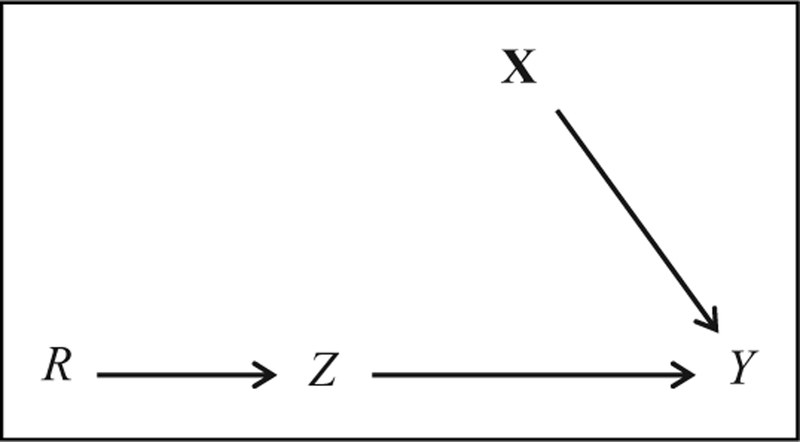
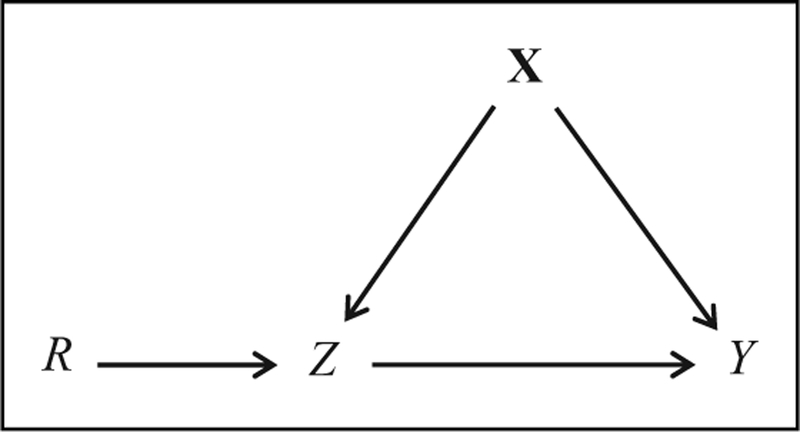
RCTs are considered as the simplest and most powerful experimental designs for identifying the causal effect of a treatment on an outcome (Shadish et al. 2002). RCTs work because the researcher controls the assignment mechanism and the implementation of the treatment. Randomization into treatment conditions can also occur as a “natural” process (natural experiment) that is not under the control of the researcher but known by the researcher (Gerber and Green 2012). With respect to the example of the remedial math program, administrators might randomly sort the list of target students and then assign the first 50 percent of listed students to the math program. Randomly assigning subjects to the treatment and control condition creates groups that are equivalent in expectation and, thus, rules out any confounding biases. The causal graph in Figure 2 shows the data generating model for an RCT, where R is the dichotomous random variable indicating treatment assignment (R = 0 indicates assignment to the control condition, R = 1 assignment to the treatment condition); Z, the corresponding dichotomous indicator of treatment exposure; and Y, the outcome. Due to the exogenous intervention via randomization, observed and unobserved pretreatment variables X have no effect on Z, and they only determine the outcome and, thus, do not confound the relation Z ⟶ Y. The SCM of a perfectly implemented RCT is given by:

$${\text{X}}_i=f_i^{\text{X}}\left({\text{U}}_i^{\text{X}}\right)$$

$$R_i=f_i^R\left(U_i^R\right)$$

$$Z_i=f^z\left(R_i\right)$$

$$Y_i=f_i^Y\left(Z_i,{\text{X}}_i,U_i^Y\right)$$

where the treatment exposure Z_i = f^Z(R_i) is a function of the treatment assignment R_i, which itself is determined by some independent noise $U_i^R$ (e.g., toss of a coin or dice and its environmental factors, or the algorithm of a random number generator). Besides SUTVA, which requires that the randomization process has no effect on the outcome Y except via treatment Z, the sole design assumption is that the RCT is perfectly implemented. That is, (1) random assignment is correctly carried out such that each subject has a known positive probability of being in the treatment and control group, P(Z_i = 1) > 0 (positivity assumption), (2) all subjects comply with the assigned treatment status R (thus, f^Z is the identity function for all subjects), and (3) no attrition occurs. The assumptions are directly reflected in the RCT graph in Figure 2. There is no arrow R ⟶ Y because randomization must not have a direct effect on Y (SUTVA), and there are no confounders X due to perfect compliance and absence of attrition (i.e., there is no arrow X ⟶ Z). Also note that there is no arrow R ⟶ X because randomization should not affect the (measurement of) pretreatment covariates X (thus all covariates are ideally measured before treatment assignment). Consequently, there are no open backdoor paths that could confound the relation Z ⟶ Y. Under these conditions, the potential outcomes are independent! of treatment Z, (Y⁰, Y¹)⊥ Z, and the ATE of Z ⟶ Y as defined in equation (2)is identified because $E\left(Y_i|Z_i=1\right)-E\left(Y_i|Z_i=0\right)=E\left(Y_i^1|Z_i=1\right)-E\left(Y_i^0|Z_i=0\right)=E\left(Y_i^1\right)-E\left(Y_i^0\right)=\text{ATE}$. It is important to note that the simplicity of the RCT graph and the relative ease of identification are due to the researcher’s control over the data generating mechanism, in particular the researcher’s control over the assignment mechanism of randomly assigning subjects to treatment conditions, but also the control over the treatment implementation which makes SUTVA more likely to be met. However, random assignment is not always possible due to ethical or practical reasons. Instead, an RD design might be still feasible where subjects are deterministically assigned on the basis of a continuous assignment variable.

Figure 2.

Data generating graph of a randomized controlled trial.

Regression Discontinuity Design

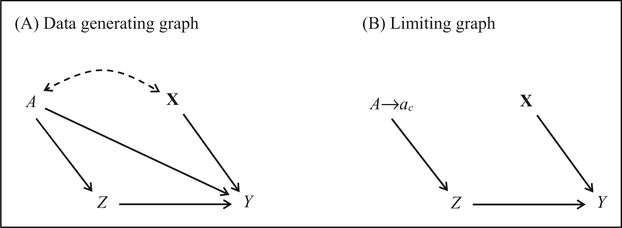
The causal graph in Figure 3A represents the data generating model for a perfectly implemented RD design, where A is a continuous assignment variable which directly determines the treatment status Z (A ⟶ Z). Assignment is based on a cutoff score a_C such that subjects that score below the cutoff, A < a_C, get assigned to the treatment condition and subjects that score above or equal to the cutoff, A ≥ a_C, get assigned to the control condition (or vice versa). For example, A could be a math pretest measure used to assign students to a remedial math program. Students with a pretest score below the cutoff of 100 attend the remedial math program, and students who score 100 or above are assigned to the control group and receive no treatment. The assignment variable may also affect the outcome Y (A ⟶ Y) and, moreover, can be related to a set of variables X as indicated by the dashed bi-headed arrow. Note that the treatment status is exclusively determined by the assignment rule but completely independent of variables X given A, thus, there is no arrow X ⟶ Z. The SCM that corresponds to the RD graph is given by:

$${\text{X}}_i=f_i^{\text{X}}\left({\text{U}}_i^{\text{X}}\right)$$

$$A_i=f_i^A\left(U_i^A\right)$$

$$Z_i=f^z\left(A_i\right)={\{}_{\text{0 if }{A}_i\ge a_C}^{\text{1 if }{A}_i\text{< }{a}_C}$$

$$Y_i=f_i^Y\left(Z_i,A_i,{\text{X}}_i,U_i^Y\right),$$

where the error terms ${\text{U}}_i^{\text{X}}$ and ${\text{U}}_i^A$ may be correlated.⁵ The RD graph and structural model clearly indicate that the assignment variable confounds the relation Z ⟶ Y because A affects both Z and Y. In addition, since all subjects scoring below the cutoff get assigned to the treatment condition and those scoring above or equal to the cutoff get assigned to the control condition, we never observe control subjects with a score below a_C or treated subjects with a score above or equal to a_C. Thus, since P(Z = 0 | A = a) = 0 for all subjects scoring below the cutoff (a < a_C) and P(Z = 1 | A = a) = 0 for all subjects scoring or at cutoff (a ≥ a_C) positivity assumption (i.e., P(Z = z | A = a) = 0) is violated for all possible values a of the assignment variable and ATE is neither identified for the treated subjects nor for the control subjects. Thus, conditioning on A in the graph of Figure 3A does not identified ATE via the backdoor criterion because, conditional on a specific assignment value A = a, there is no longer any variation in Z and Y that is caused by A. For this reason, the graph for the subpopulation with A = a would contain neither variable A nor arrows A ⟶ Z, A ⟶ Y and . Moreover, since Z constant conditional on A = a, the arrow Z ⟶ Y disappears as well, making the identification of ATE impossible for any assignment score a. A more thorough discussion of conditioning on a value of a variable is given in Online Appendix A. It is important to note that this is a nonparametric identification result. If one would be willing to make strong functional form assumptions that allow for an extrapolation of the treatment and control functions into the respective regions of nonoverlap, ATE would be parametrically identified.

Figure 3.

Causal graphs of a regression discontinuity (RD) design. (A) Data generating graph. (B) Limiting graph for A = a_C ± ε with ε ⟶ 0.

However, even without making any functional form assumptions, we can identify ATE for the subjects that score in an (infinitesimally) close neighborhood around the cutoff. More formally, ATE is identified at the limiting cutoff value A ⟶ a_C, that is, for subjects in the interval [a_C – ε; a_C + ε] as ε approaches zero (ε ⟶ 0).⁶ Identification at the limiting cutoff score is ppossible because the cutoff score is the sole point where treatment and control subjects overlap in the limit. The ATE at the limiting cutoff (ATEC) is defined as

$$\text{ATEC}{=}_{a\uparrow a_C}^{\text{lim}}E\left(Y_i^1|A_i=a\right){-}_{a\downarrow a_C}^{\text{lim}}E\left(Y_i^0|A_i=a\right){=}_{a\uparrow a_C}^{\text{lim}}E\left(Y_i|A_i=a\right){-}_{a\downarrow a_C}^{\text{lim}}E\left(Y_i|A_i=a\right).$$

The difference in limits represents the discontinuity (i.e., the treatment effect) at the cutoff a_C as we approach the cutoff from below (a ↑ a_C) and above (a ↓ a_C). The limiting graph for the subpopulation with A ⟶ a_C is shown in Figure 3B. Two design assumptions besides SUTVA are required for the identification of ATEC (Hahn, Todd, and van der Klaauw 2001; Imbens and Lemieux 2007; Lee and Lemieux 2010). First, the assignment rule is implemented perfectly such that the probability of receiving treatment drops at the cutoff from 1 to 0: ${}_{a\uparrow a_C}^{\text{lim}}E\left(Z_i|A_i=a\right){-}_{a\downarrow a_C}^{\text{lim}}E\left(Z_i|A_i=a\right)=1$. Thus, the limiting RD graph shows an arrow A ⟶ Z indicating that Z is solely determined by A. Note that this is different to the previous discussion of conditioning on A = a, where the arrow A ⟶ Z would vanish (see Online Appendix A).

Second, the potential outcomes must be continuous at the cutoff (i.e., there is no discontinuity at the cutoff), ${}_{a\uparrow a_C}^{\text{lim}}E\left(Y_i^0|A_i=a\right){\text{= }}_{a\downarrow a_C}^{\text{lim}}E\left(Y_i^0|A_i=a\right)$ and ${}_{a\uparrow a_C}^{\text{lim}}E\left(Y_i^1|A_i=a\right){\text{= }}_{a\downarrow a_C}^{\text{lim}}E\left(Y_i^1|A_i=a\right)$. That is, the expected potential outcomes for the treatment and control subjects need to be connected at the cutoff (the limits from below and above the cutoff score are identical). This assumption assures that no threats to validity like differential instrumentation, competing treatments, or manipulation of the assignment score around the cutoff are present. In the limiting RD graph (Figure 3B), the continuity assumption is reflected by the absence of the arrow A ⟶ Y because, at the limiting cutoff a_C, the assignment variable A has no longer a direct effect on Y (i.e., the limits from below and above in the expected potential outcomes are identical). From the continuity assumption and the SCM also follows that A is unrelated to X in the limit, that is, ${}_{a\uparrow a_C}^{\text{lim}}E\left({\text{X}}_i|A_i=a\right){=}_{a\downarrow a_C}^{\text{lim}}E\left({\text{X}}_i|A_i=a\right);$ otherwise, the discontinuity in X would result in discontinuous potential outcomes.

From the limiting RD graph in Figure 3B, it is apparent that ATEC is identified because the causal relation Z ⟶ Y is neither confounded by A nor by X. Not surprisingly, the limiting RD graph is identical to the RCT graph in Figure 2. At the limit a_C, assigning subjects according to A is equivalent to random assignment since an infinitesimally small amount to the left and the right of the cutoff the covariate and potential outcomes distributions are identical (Lee and Lemieux 2010). However, the main limitation of an RD design is that, without making functional form assumptions, only a very local ATE—for the population in the very close vicinity of the cutoff score—is identified.

Instrumental Variable Design

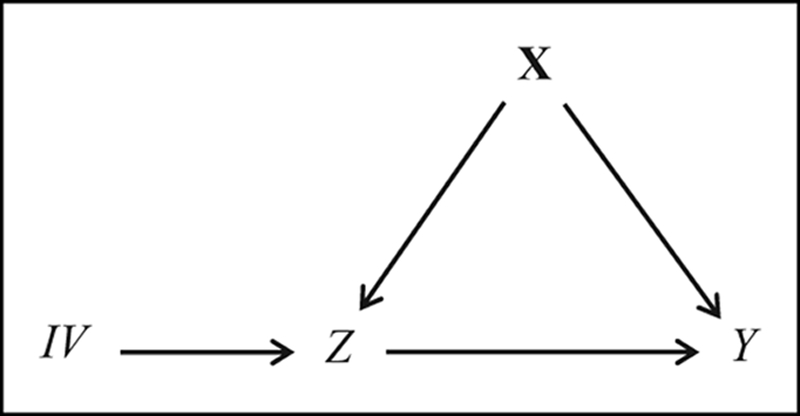
Although RCTs and RD designs are strong designs for causal inference in practice, the assignment of subjects to treatment and control conditions might be, due to noncompliance issues, not fully under the researcher’s control or entirely infeasible because of ethical or practical reasons. In both cases, the lack of control over treatment assignment results in confounding bias with respect to the relation Z ⟶ Y, which can only be removed if all the con founding variables are observed (see the section on matching and PS designs). However, even if all the confounding variables X are not known or unobserved, the effect of Z on Y is identifiable if we are in the possession of an IV, that is, a variable that is predictive of treatment Z but has no direct or indirect effect on the outcome Y except via Z (Angrist, Imbens, and Rubin 1996; Angrist and Pischke 2008; Brito 2010; Brito and Pearl 2002a). An IV might be available because it is part of the intervention, like in an RCT with noncompliance or an encouragement design (Holland 1988), or it is passively observed and identified after the data were collected. The causal graph in Figure 4 shows the basic data generating structure of the IV design where confounders X are assumed to be (partially) unobserved. Besides SUTVA, the two crucial design features of the IV design are: (1) the IV must be predictive of treatment Z and (2) the IV must be independent of the potential outcomes, IV ⊥ (Y⁰, Y¹) (exclusion restriction). These two assumptions are also clearly reflected in the causal graph and the corresponding SCM:

Figure 4.

Data generating graph of an instrumental variable design.

$$\begin{gathered} {\text{X}}_i=f_i^{\text{X}}\left({\text{U}}_i^{\text{X}}\right) \\ I{V}_i=f_i^{\text{IV}}\left({\text{U}}_i^{IV}\right) \\ {Z}_i=f_i^Z\left({\text{X}}_i,I{V}_i,U_i^Z\right) \\ {Z}_i=f_i^Y\left({\text{X}}_i,Z_i,U_i^Y\right). \end{gathered}$$ (3)

First, the IV affects the treatment Z as shown by the arrow IV ⟶ Z and, thus, the IV is predictive of Z.⁷ Second, the IV has no effect on the outcome Y other than through the path IV ⟵ Z ⟶Y. Thus, the structural equation for the outcome $f_i^Y\left({\text{X}}_i,{\text{Z}}_i,U_i^Y\right)$ but also the error term $U_i^Y$ are independent of IV. The exclusion of paths other than IV ⟵ Z ⟶ Y implies that the IV represents a source of exogenous variation (like random assignment in an RCT). Continuing our example on the remedial math program, some of the confounders X might actually be unknown or unobserved like students’ ability such that we cannot condition on X. But we might be able to find an IV. If the remedial math program is offered during summer, participation in the program might also be determined by the distance between a student’s home and the school offering the program. Students living far away from the school might have a lower likelihood in participating than students living closer to the school. If we believe that the distance between a student’s home and school neither affects the math outcome directly nor indirectly, except via program participation (i.e., we believe that the exclusion restriction holds), then we can use the distance as an IV. In the following, we assume that the IV and treatment Z are dichotomous variables, where a value of 1 indicates treatment assignment and treatment receipt, respectively, and a value of 0 indicates assignment and receipt of the control condition.

We cannot remove the bias that confounds the relation Z ⟶ Y by conditioning on X because the confounders X in Figure 4 are (partially) unobserved—thus, ATE is not identifiable via the backdoor criterion. However, since the IV is related to the outcome only via treatment Z but is otherwise completely unrelated to Y (exclusion restriction), we are at least able to identify the average effect of the IV (AIVE) on Y, AIVE = E(Y | IV = 1) – E(Y | IV = 0). For RCT with noncompliance where random assignment is an IV, this effect is known as intent-to-treat effect (ITT). In addition, also the average effect of IV on Z is identified because the relation IV ⟶ Z is unconfounded due to the IV’s exogeneity.

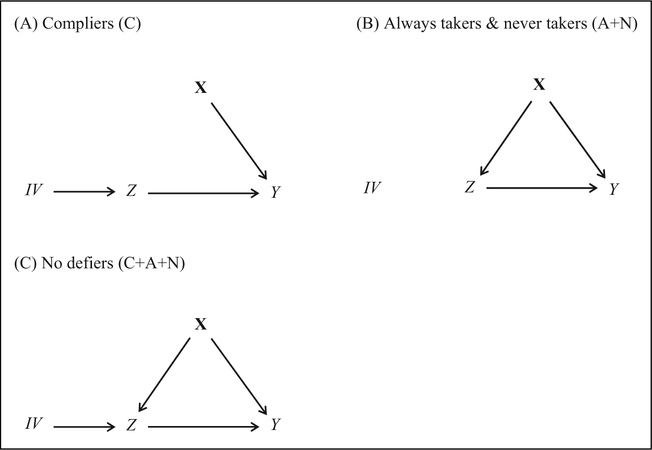
Although AIVE can be of its own interest, we also would like to identify ATE, that is, the average effect of Z ⟶ Y in Figure 4. However, Z ⟶ Y is not identified unless we can reasonably assume monotonicity in addition to the two design assumptions discussed above (Angrist et al. 1996; Brito 2010).⁸ In order to discuss the monotonicity assumption, also called no-defiers assumption, we need to distinguish between four latent subgroups (S), com-pliers, always takers, never takers, and defiers, where the latent group status is determined by (unobserved) confounders X and an independent error term: $S_i=f_i^S\left({\text{X}}_i,U_i^S\right)$.⁹ For instance, a subject’s sociodemographic characteristics, health status, or attitudes might determine group membership. Each of the four subgroups is characterized by a different compliance behavior with respect to the IV, that is, how the IV determines a subject’s treatment status Z. Subjects whose treatment status is exclusively determined by the IV such that they take treatment if IV = 1 and take the control condition if IV = 0 are called compliers (S_i = C) because they always comply with the treatment status suggested by the IV: Z = 1 if IV = 1 and Z = 0 if IV = 0. Because the compliers’ treatment status Z is exclusively determined by the IV, $Z_i=f_i^Z\left(I{V}_i\right)$, Z is independent of X (and U^Z) as shown in the complier graph in Figure 5A (the arrow X ⟶ Z is missing). Always takers (S_i = A) always select into the treatment group irrespective of their IV status:Z = 1 if IV = 0 and Z = 1 if IV = 1. Never takers (S_i = N) always show up in the control condition independent of their IV status: Z = 0 if IV = 0 and Z = 0 if IV = 1. Thus, the treatment status of always takers and never takers is solely determined by X and U^Z and is independent of IV. That is, $Z_i=f_i^Z\left({\text{X}}_i,U_i^Z\right)$ is a function of X and U^Z alone, as shown in the corresponding graph for always and never takers in Figure 5B (the independence is reflected by the missing arrow IV ⟶ Z). Finally, defiers (S_i = D) always do the opposite to what the IV indicates: Z = 0 if IV = 1 and Z = 1 if IV = 0. As with compliers, the defiers’ treatment status is exclusively determined by the IV but, for identification reasons, we need to assume that no defiers are present, that is, P(S_i = D) = 0 (as becomes clear from the proofs in Online Appendix B). The absence of defiers is referred to as monotonicity (no-defiers) assumption. For our remedial math example, the monotonicity assumption implies the absence of students that would not participate in math training if the program school is close but participate if the school is far away. The population of compliers consists of students that would participate in the math training if the program school is close but would not participate if the school is remote.

Figure 5.

Data generating IV graphs for (A) compliers, (B) always takers and never takers, and (C) compliers, always takers and never takers together (i.e., no defiers).

With regard to the causal graphs in Figure 5, a couple of remarks are indicated.¹⁰ First, for always takers and never takers, (1) the effect Z ⟶ Y is not identified because we neither observe X nor will an always taker ever be observed in the control condition and a never taker in the treatment condition, and (2) the effect IV ⟶ Y is zero because the IV is unrelated to Z and Y. Second, for compliers, (1) the effect Z ⟶ Y is identified because X does not confound the relation Z ⟶ Y and (2) the effect IV ⟶ Y is equivalent to the effect Z ⟶ Y and, thus, identified. This is so, because treatment status Z is solely determined by the IV (i.e., Z = IV). Also note that the complier graph is identical to the RCT graph in Figure 2. Third, though we are theoretically able to identify the causal effect Z ⟶ Y for compliers from the complier graph in Figure 5A, it is practically impossible because the latent subgroup of compliers is not observable (as are the subgroups of always takers and never takers). The group of compliers cannot be empirically determined because the subjects in the treatment condition (Z = 1) with IV = 1 consist of and always takers, and subjects with Z = 0 and IV = 0 consist of compliers and never takers, making it impossible to empirically separate compliers from always takers and never takers. Thus, the identification of the complier average treatment effect (CATE) must be based on the causal graph for the observable but mixed population of compliers, always takers and never takers together (C + A + N). Because defiers are assumed to be absent, we refer to the mixed population as no-defiers population (Figure 5C). Interestingly, the ATE for compliers is still identified from the nodefiers graph. The main argument can already be seen from the causal graphs in Figure 5. Since only the group of compliers has a nonzero effect IV ⟶ Z, the effect of the IV on Z and Y in the no-defiers graph can only be due to compliers and no other latent group.

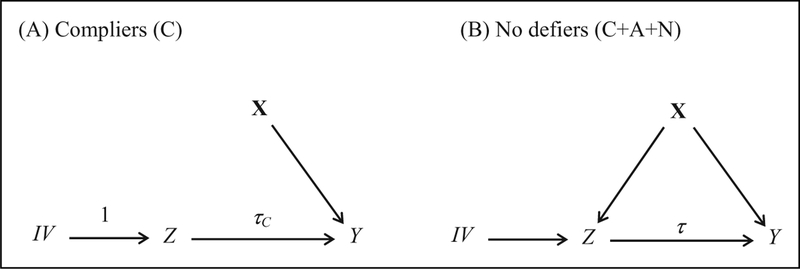
The SCM for the no-defiers population (i.e., the population of compliers, always takers and never takers) is the same as in equation (3) but now with defiers excluded. Again, note that the subscript i in $f_i^Y$ of the structural outcome model indicates that the treatment effects may vary across subjects, implying that the ATEs for the latent subgroups of compliers, always takers, and never takers can be different. Assuming monotonicity, the CATE (Z ⟶ Y in the complier graph) is then defined as

$$\begin{gathered} \text{CATE}=E\left(Y_i^1|S_i=C\right)-E\left(Y_i^0|S_i=C\right)=E\left(Y_i^1-Y_i^0|S_i=C\right) \\ =E\left(f_i^Y\left({\text{X}}_i,Z_i=1,U_i^Y\right)-f_i^Y\left({\text{X}}_i,Z_i=0,U_i^Y\right)|S_i=C\right) \\ =E\left({\tau }_i|S_i=C\right)={\tau }_C, \end{gathered}$$

where the expectation is taken over all units in the complier population. The CATE, τ_C, is shown in the complier graph in Figure 6A. Since the effect IV ⟶ Z is equal to 1 (because Z = IV) the average effect of IV on Y is also τ_C (the formal proof is given in proof 1 in Online Appendix B).

Figure 6.

IV graphs for (A) compliers and (B) compliers, always takers, and never takers together (i.e., no defiers).

We now show how CATE can be identified from the no-defiers graph in Figure 6B. The identification argument involves three steps:

• (1)The average effect IV ⟶ Z in the no-defiers graph is given by the complier probability γ = P(S_i = C).
• (2)The AIVE on Y, IV ⟵ Z ⟶ Y, is the product of the complier probability and CATE, that is, γτ_C.
• (3)Using the results from steps (1) and (2), CATE is then given by the ratio of the effects of IV ⟵ Z ⟶ Y and IV ⟶ Z, that is, $\frac{{\text{γτ}}_C}{\text{γ}}={\text{τ}}_C$

First, using the IV’s independence of X, proof 2 of Online Appendix B shows that the effect IV ⟶ Z is given by complier probability γ = E(Z_i | IV_i = 1) – E(Z_i | IV_i = 0) = p(S_i = C). This is also clear from the causal graphs Figure 5. For the complier graph, the path IV ⟶ Z is equal to one (γ = 1) because all subjects comply with the treatment indicated by the instrument, while in the always-taker and never-taker graph the corresponding effect is zero (γ = 0). Thus, in the no-defiers graph in Figure 6B, γ represents the weighted average of the effects IV ⟶ Z across the three latent subgroups: 1 × P(S_i = C) + 0 × P(S_i = A) + 0 × P(S_i = N) = P(S_i = C) with P(S_i = C) + P(S_i = A) + P(S_i = N) = 1.

Second, due to the IV’s exogeneity, the AIVE on Y is identified in the no-defiers graph and is given by γτ_C:

$$\begin{gathered} \text{AIVE}=E\left(Y_i|I{V}_i=1\right)-E\left(Y_i|I{V}_i=0\right)= \\ =P\left(S_i=C\right)\left\{E\left(Y_i^1|S_i=C\right)-E\left(Y_i^0|S_i=C\right)\right\} \\ =\gamma {\tau }_C. \end{gathered}$$ (4)

This result is formally proven in proof 3 of Online Appendix B, but it is also clear from the causal graphs in Figure 5. Since the IV has no effect on Y for always takers and never takers, the IV’s effect on Y in the no-defiers graph can only be due to the compliers whose effect is τ_C. Thus, AIVE is obtained as the weighted average τ_C P(S_i = C) + 0 × p(S_i = A) + 0 × p(S_i = N) = γτ_C, and CATE is obtained as the ratio of AIVE and the complier probability:

$$\text{CATE}=\frac{\text{AIVE}}{P\left(S_i=C\right)}=\frac{{\text{γτ}}_C}{\text{γ}}={\text{τ}}_C$$

With the mechanics of the IV design in hand, we now revisit the RCT and RD designs and discuss the identification of CATEs in the case of noncompliance.

Randomized Experiment and RD Design With Noncompliance

RCTs and RD designs are frequently not perfectly implemented since it is common for some subjects not to comply with the assigned treatment or control condition. In this case, ATE is generally not identified but CATE still is because the treatment status assigned can be used as an IV. We first discuss the RCT with noncompliance and then the RD design. The causal graph in Figure 7 represents the data generating mechanism of an RCT with noncompliance. Due to noncompliance, treatment status $Z_i=f_i^Z\left(R_i,{\text{X}}_i,U_i^Z\right)$ is now also determined by confounders X (X ⟶ Z) and factors U^Z (the latter are unrelated to the outcome Y and not shown in the graph). Since the confounders X are in general unobserved, the average effect Z ⟶ Y is not identified. However, since the randomly assigned treatment status R usually meets the IV assumptions (predictive first stage, exclusion restriction, and no-defiers), CATE is identified. Note that the causal graph in Figure 7 is identical to the IV graph in Figure 4, thus, identification is analogous. For the case of one-sided noncompliance (i.e., there are no always takers such that noncompliance is only due to never takers), one can show that the ATE on the treated (ATT) is identified (Bloom 1984; Frölich and Melly 2008).

Figure 7.

Causal graph of the randomized controlled trial with noncompliance.

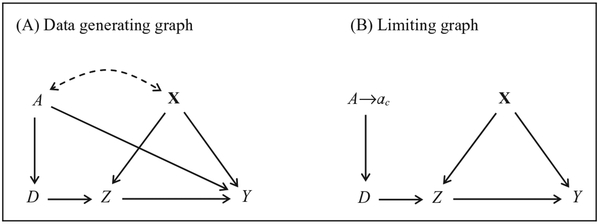
The graph in Figure 8A displays the data generating mechanism for the RD design with noncompliance, also called fuzzy RD design. In comparison to the RD graph with full compliance (Figure 3), we now have an additional variable D in the graph, which indicates the assigned treatment status, while Z indicates treatment received. The structural equations for D and Z are:

Figure 8.

Causal graphs for the fuzzy regression discontinuity (RD) design. (A) Data generating graph. (B) Limiting graph for A = a_C ± ε with ε ⟶ 0.

$$D_i=f^D\left(A_i\right)={\{}_{\text{0 if }{A}_i\ge a_C}^{\text{1 if }{A}_i\text{< }{a}_C}{Z}_i=f_i^Z\left(D_i,{\text{X}}_i,U_i^Z\right).$$

As for the RCT with noncompliance, X now directly confounds the relation Z ⟶ Y, even after conditioning on the limiting cutoff a_C (Figure 8B). Thus, without observing X, ATE at the cutoff is no longer identified. However, as the limiting graph in Figure 8B indicates, we can use the assignment status D as an instrument for identifying CATE at the cutoff. Again, in case of one-sided noncompliance (i.e., no always takers are present) ATT at the cutoff is identified.

Matching and Propensity Score Designs

Although RCT, RD, and IV designs are strong designs for causal inference, they might not be feasible in practice because treatment assignment is not always under the researcher’s control and an IV might not be available or unambiguously identifiable (i.e., whether the exclusion restriction and the monotonicity assumption actually hold might be in doubt). However, if a researcher has reliable knowledge about the selection mechanism and reliable measures of all variables X that confound the relation between treatment Z and the outcome Y, the average causal effect of Z ⟶ Y is identified. More general, identification requires a set of variables X that blocks all confounding paths. Instead of a confounder X_j one can measure any intermediate variable X_m lying on the confounding path Z ⟵ X_j ⟶ Y, that is, Z ⟵ X_j ⟶ X_m ⟶ Y or Z ⟵ X_m ⟵ X_j ⟶ Y). For simplicity reasons, we only confounders in our structural models and causal graphs. With respect to our remedial math example, identification requires that all confounders like student’s ability, sex, or socioeconomic status are known and reliably measured. The causal graph in Figure 9A shows the presumed data generating structure. The corresponding SCM is given by:

$${\text{X}}_i=f_i^{\text{X}}\left({\text{U}}_i^{\text{X}}\right)$$

$$Z_i=f_i^Z\left({\text{X}}_i,U_i^Z\right)$$

$$Y_i=f_i^Y\left({\text{X}}_i,{\text{Z}}_i,U_i^Y\right)$$

which is identical to equation (1) discussed in the introduction section. The ATE of Z on Y (Z ⟶ Y) is identified if two assumptions in addition to SUTVA are met: First, all confounders X must be observed and reliably measured such that, conditional on X, the potential outcomes are independent of treatment selection (Y⁰; Y¹)⊥ Z | X. Second, the conditional probability of receiving the treatment given the confounders must be strictly between zero and one, 0 < P(Z = 1| X) < 1 (positivity assumption). These two assumptions are frequently referred to as strong ignorability (Rosenbaum and Rubin 1983). In the data generating graph in Figure 9A, the first part of the strong ignorability assumption is reflected by the absence of any backdoor path via an unobserved confounder or a latent construct that has been unreliably measured—only backdoor paths via X exist where all confounders X are assumed to be known and reliably measured. The second part of strong ignorability, 0 < P(Z = 1| X) < 1, cannot directly be seen from the causal graph but the assumption requires that ATE is identified for all subpopulations with X = x^′, where x^′ takes on all possible combinations of x values. Thus, for each realization x^′, there must be variation in Z; otherwise, the effect Z ⟶ Y would not be identified for X = x^′. That is, if all subjects with X = x^′ always end up in the treatment condition such that P(Z = 1 | X = x^′) = 1it then impossible infer their outcomes under the control condition because not even a single subject will ever be in the control condition. For such a subpopulation with P(Z = 1 | X = x^′) = 1 we would neither draw the arrow X ⟶ Z nor Z ⟶ Y because there is neither variation in X nor in Z (analogous for P(Z = 1 | X = x^′) = 0).

Figure 9.

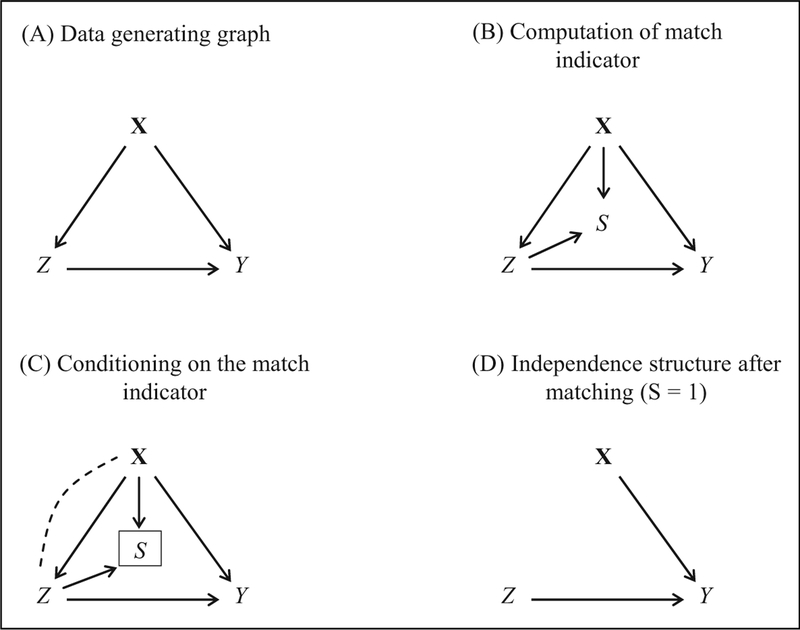
Causal graphs for a matching design (with constant matching ratio).(A) Data generating directed acyclic graph. (B) Computation of match indicator S.(C) Conditioning on the match indicator S. (D) The independence structure after matching (S = 1).

Given strong ignorability, the data generating graph in Figure 9A ensures that the average effect Z ⟶ Y is identified via the backdoor criterion (Pearl 2009). Conditioning on confounders X blocks the backdoor path Z ⟵ X ⟶ Y and, thus, ATE is identified. In terms of potential outcomes, we get $E\left(E\left(Y_i|Z_i=1,{\text{X}}_i\right)\right)-E\left(E\left(Y_i|Z_i=0,{\text{X}}_i\right)\right)=E\left(E\left(Y_i^1|Z=1,\text{X}\right)\right)-E\left(E\left(Y_i^0|Z_i=0,\text{X}\right)\right)=E\left(Y_i^1\right)-E\left(Y_i^0\right)=\text{ATE}$.

If strong ignorability is met, one can directly estimate the treatment effect parametrically via standard regression methods or nonparametrically via multivariate stratification. Alternatively, one can employ a matching design before estimating the treatment effect. Since matching is a procedure that constrains the naturally occurring data generating process (i.e., unmatched data are removed), the matching step needs to be reflected by the causal graph. Figure 9 represents the graphs for the matching design where the match indicator S indicates whether a subject got matched (S = 1) or not matched (S = 0). If matching is done before treatment implementation, unmatched cases do not become a part of the study. If subjects are matched after treatment exposure and the collection of outcome data, unmatched cases are removed from the data. Since matching treatment and control cases on observed confounders requires knowledge of both Z and X, that is, S is causally determined by Z and X, the arrows in Figure 9B point from Z and X into S, making S a collider on the path Z ⟶ S ⟵ X (Mansournia, Hernán, and Greenland 2013; Shahar and Shahar 2012). Because S is a collider, conditioning on the match status S introduces an association (collider bias) between Z and X as shown in Figure 9C by the dashed path. The box around S symbolizes the conditioning. If matching is implemented with a constant matching ratio (i.e., 1:1 or 1:k matching), then the collider bias X---Z exactly offsets the confounding relation X ⟶ Z in the matched data with S = 1 (Mansournia et al. 2013; Shahar and Shahar 2012). For the matched data, the graph in Figure 9D shows that X and Z are no longer related to each other (S is no longer shown because it is a constant in the matched data set, S = 1; see Online Appendix A for further explanations). Since the graph for the matched data is identical to the RCT graph (Figure 2), one can say that a matching design tries to mimic an RCT—though on observed covariates only. Given the independence of X and Z, the ATE, in this case the ATT, is identified without any further adjustments. Importantly, the ATT is identified not because all the confounding backdoor paths have been blocked but because matching with a constant matching ratio offsets the confounding relation between X and Z via collider bias.

We now extend this identification result for matching designs with a constant matching ratio (Mansournia et al. 2013; Shahar and Shahar 2012) to PS designs (for an introduction to PS methods, see Schafer and Kang 2008; Steiner and Cook 2013). We demonstrate that collider bias not only offsets the confounding relation in PS matching designs (with constant matching ratio) but more generally also in PS designs that use full matching, stratification or inverse-propensity weighting. This general result is obtained because the PS itself is a collider variable and, thus, conditioning on the PS offsets the confounding relation X ⟶ Z regardless of the choice of a specific PS design—matching, stratification, or weighting. The PS is defined as the conditional probability of receiving the treatment, given observed variables X: PS_i = P_X;Z(Z_i = 1| X = x_i). The PS is a balancing score that balances the baseline differences between the treatment and control group in observed confounders X such that the conditional distribution of X given PS is the same for treated and control subjects, P(X | Z; PS) = P(X | PS). Conse quently, X is independent of Z given PS, X ⊥Z | PS. Rosenbaum and Rubin (1983) showed that if selection is strongly ignorable given X, it is also ignorable given the PS alone: (Y⁰; Y¹)⊥Z | PS. That is, ATE or ATT is identified by conditioning on the PS alone—once the PS is determined, variables X are not longer needed for identifying ATE or ATT. However, other than for conditioning on confounders X, conditioning on the PS does not identify ATE via blocking the confounding backdoor path Z ⟵ X ⟶ Y because the PS does not lie on the backdoor path. Instead, the PS removes the confounding effect of X by offsetting the relation X ⟶ Z via collider bias. Since this is in contrast to explanations of other authors who argue that the PS essentially blocks the backdoor path (Baker and Lindeman 2013; Shrier 2008, 2009; Sjölander 2009), a more thorough discussion of the PS is required.¹¹

Consider how the PS is generated for a finite target population of size N. Since the PS is inherently unknown and defined as a function of observed covariates (Rosenbaum and Rubin 1983), the joint distribution of X and Z has to be determined in a first step: $P_{\text{X},Z}\left(X=\text{x},Z=\text{z}\right)=\frac{F\left(X=\text{x},Z=\text{z}\right)}{N}$ where F(.) is the frequency function. Then, using the distribution function P_X,Z, a single subject’s PS is determined as the conditional probability of being in the treatment group (Z = 1), given the observed covariates x_i:

$$\begin{gathered} P{S}_i=f_{\text{X},Z}^{PS}\left({\text{X}}_i\right)=P_{\text{X},Z}\left(Z=1|\text{X}={\text{x}}_i\right) \\ =\frac{P_{\text{X},Z}\left(\text{X}={\text{x}}_i,Z=1\right)}{P_{\text{X},Z}\left(\text{X}={\text{x}}_i,Z=0\right)+P_{\text{X},Z}\left(\text{X}={\text{x}}_i,Z=1\right)} \end{gathered}$$

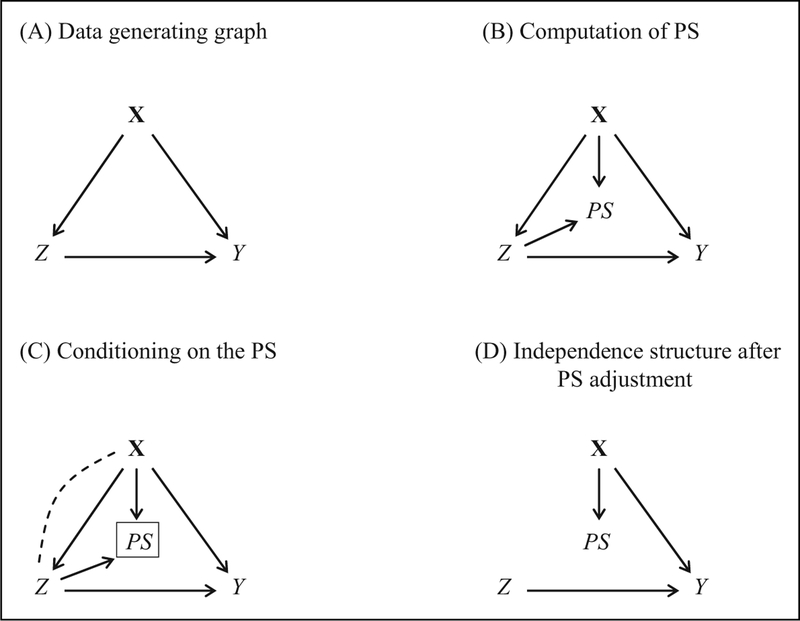
It is important to realize that (1) the PS function $f_{\text{X},Z}^{PS}$ has subscripts X and Z because it can only be determined after the joint probability function Px,z has been determined from population data X and Z and that (2) $f_{\text{X},Z}^{PS}$ is the same for all subjects (i.e., the PS function does not have a subscript i like the other structural equations of the SCM). Thus, the PS function $f_{\text{X},Z}^{PS}$ is constant across subjects but depends on the population’s realized values of X and Z. Once Px,z and thus $f_{\text{X},Z}^{PS}$ is known, the PS is only a function of x, $P{S}_i=f_{\text{X},Z}^{PS}$ because the PS for a treated and control subject with identical covariate values x_i is the same. However, because the computation of the PS first requires the determination of P_X,Z from population data X and Z, the PS is necessarily a function of both X and Z as shown in Figure 10B where two arrows point into PS, Z ⟶ PS ⟵ X.

Figure 10.

Causal graphs for propensity score designs. (A) Data generating directed acyclic graph. (B) Computation of the propensity score (PS). (C) Conditioning on the PS. (D) The independence structure after PS adjustment.

This definition of the PS as a function of X and Z deviates from the usual practice of defining the PS as a function of observed covariates X alone, PS_i = e(x_i) (e.g., Rosenbaum and Rubin 1983). Such a definition neglects the fact that the PS cannot be determined without observing Z because the PS has to balance group differences in the observed covariate distribution caused by selection $Z_i=f_i^Z\left({\text{X}}_i,U_i^Z\right)$ In order for the PS to be a balancing score, it necessarily has to change whenever one intervenes on covariates X or the selection mechanism $f_i^Z\left({\text{X}}_i,U_i^Z\right)$. Thus, the PS is causally determined by both X and Z.¹²

Because $PS=f_{\text{X},Z}^{PS}\left(\text{x}\right)$ is many-to-one function of X, that is, different x values result in the same PS (i.e., for some X′ ≠ X*, $f_{\text{X},Z}^{PS}\left({\text{X}}^{\prime }\right)=f_{\text{X},Z}^{PS}\left(X*\right)$), conditioning on the PS does not fully block the backdoor path Z ⟵ X ⟶Y (see also Pearl 2009, footnote 7 on p. 348).¹³ That is, conditional on a single PS = s, confounders X still vary and thus transmit information to Z and Y. But since this conditional variation no longer confounds the relation Z ⟶ Y, one could argue that the PS filters out or blocks that part of X’s variation that is responsible for the confounding while the variation in X that does not confound the relation Z ⟶ Y remains unblocked. However, we argue that conditioning on the PS induces a collider bias that exactly offsets the confounding relation X ⟶ Z. This is so, because the PS is defined as a balancing score that balances the baseline differences between the treatment and control group in observed confounders X. The collider argument also holds if one would believe that a latent PS instead of X directly determines Z, that is, Y ⟵ Z ⟵ PS ⟵X ⟶ Y. Because such a latent PS is inherently unobservable, the balancing PS also needs to be determined from both X and Z.¹⁴

The causal graph in Figure 10B shows the PS as a collider on the path Z ⟶ PS ⟵ X ⟶ Y. Conditioning on PS in order to identify the ATE of Z on Y actually induces a spurious relation between X and Z as shown by the dashed path in the conditional graph in Figure 10C. The spurious relation created by conditioning on the PS exactly offsets the effect X ⟶ Z because the PS is a balancing score such that X ⊥Z | PS More formally, though X and Z are marginally dependent, P(X; Z) ≠ P(X) P (Z), conditional on the PS they are independent: P(X,Z | PS) = P(X | PS)P(Z | PS) If the PS were not a balancing score, | PS, but any other derived from X and Z (or X alone) it would not offset the relation X ⟶ Z; bias in the outcome would remain or even increase (e.g., the collider bias might go into the same direction as the confounding bias and, thus, increase the overall bias).

The independence structure resulting from conditioning on the PS via any type of PS matching, PS stratification, or inverse-propensity weighting is reflected by the graph in Figure 10D. The relations X ⟶ Z and Z ⟶ PS are no longer present because of the PS’s balancing property which also implies that Z is independent of PS given X: Z⊥PS | X, that is,P(Z | X, PS) = P(Z | X).¹⁵ Thus, after the PS adjustment the effect Z ⟶ Y is identified without any further conditioning. In this sense, PS designs create a matched, stratified, or weighted data set that mimics a randomized experiment—the RCT graph in Figure 2 is essentially identical to the graph in Figure 10D. A causal search algorithm like IC (Inductive Causation), PC (Peter Clark, named after Peter Spirtes and Clark Glymour), or FCI (Fast Causal Inference; Pearl and Verma 1991; Spirtes et al. 2000; Spirtes, Meek, and Richardson 1999) would exactly reveal these independencies in the matched or weighted data set.

However, the two conditional independencies X⊥Z | PS and Z⊥ PS | X encoded in the causal graph (Figure 10D) are unfaithful because slight changes in or misspecifications of the PS model would immediately induce a dependence not only between X and Z but also between Z and PS.¹⁶ This reveals an essential difference between observational studies and an RCT: While an RCT establishes a faithful independence structure via randomization (i.e., a natural data generating process), a PS-adjusted observational study relies on unfaithful independencies that need to be established via a computational procedure using observed covariates X and treatment Z. Moreover, the PS adjustment only establishes independence with regard to the observed covariates X but not with regard to unobserved or unreliably measured confounders (in our discussion, we assumed that all confounders are reliably measured, i.e., strong ignorability is met).

Discussion

In this article, we presented the causal graphs of randomized experiments and quasi-experimental designs for inferring causal effects from experimental and observational data. The graphical representation of experimental and quasi-experimental designs has the advantage that it makes the crucial design assumptions explicit and facilitates determining whether a treatment effect is identified. In introducing the concepts of limiting and conditional graphs and by explicitly including the PS in the graph, we were able to graphically demonstrate that both the RD and IV designs identify only local ATEs and that the PS is a collider that offsets confounding bias via collider bias. Overall, we believe that the graphical representation of quasi-experiments will help practitioners in getting a better understanding of the designs’ assumptions and limitations and, finally, in doing better causal studies.

In comparing the causal graphs of the discussed designs, it becomes clear that RCTs rely on the weakest and fewest assumptions for identifying the ATE. The RD graph reveals that deterministic assignment on the basis of an assignment variable typically results in confounding bias. However, in limiting the causal graph to the close vicinity around the cutoff score, the RD graph reduces to an RCT graph and, thus, allows the ATEC to be identified. A major disadvantage of the RD design is that it only identifies a very local treatment effect (at the cutoff) that is not generalizable to the overall target population without further assumptions (particularly functional form assumptions).

The IV design results in a series of causal graphs highlighting the design’s complexities. Although an IV represents a source of exogenous variation just like random assignment, other factors might simultaneously determine the treatment status and the outcome and confound the treatment effect. However, assuming monotonicity, it is possible to identify the ATE for the latent subgroup of compliers from the observable no-defiers population (i.e., com-pliers, always takers, and never takers). Again, because the graph for the latent subpopulation of compliers is identical to an RCT graph, the CATE is identified, though not directly observable. Thus, in comparison to an RCT, the IV design requires stronger assumptions and it only identifies the ATE for the latent subpopulation of compliers which depends on the instrument chosen.

Although the data generating graphs of the matching and PS designs are similar to the data generating IV graph, the two designs differ completely in their identification strategy. While the IV design tries to identify the CATE via an exogenous source of variation, matching and PS designs aim to identify the ATE by neutralizing the confounding backdoor paths via collider bias. However, the ATE is identified only if all confounders have been reliably measured, which is not required for the IV design. The graphs resulting from matching or conditioning on the PS mimic an RCT graph—there are no longer any confounders present that could confound the treatment effect.

From a theoretical point of view, the causal graphs highlight that the identifying assumptions become stronger as a researcher’s control over treatment selection diminishes. The active interventions associated with RCTs and RD designs result in fewer assumptions for identifying causal effects than passive observations which are typically used in IV, matching, and PS designs. This suggests that one should prefer RCTs and RD designs over IV, matching, and PS designs. However, from a practical point of view, it is frequently not possible to directly control the assignment of subjects to treatment and control conditions, so a researcher needs to rely on observational data. In that case, IV, matching, and PS designs are viable designs given that one is either in the possession of an IV or of reliable measures of all the confounding variables.

The causal graphs discussed in this article only represent the basic RCT and quasi-experimental designs for cross-sectional data with respect to the effect of a single treatment on a single outcome. The causal graphs can naturally be extended to reflect more complex designs that address plausible threats to validity, for instance, RD designs with a matched comparison group (Wing and Cook 2013), conditional or multiple IV designs (Brito 2010), PS matching designs with the added design elements of multiple nonequivalent comparison groups or nonequivalent outcomes (Shadish et al. 2002), or comparative interrupted time series (difference-in-differences) designs (Lechner 2010; Wong, Cook, and Steiner, 2015).

Causal graphs also can and need to reflect violations or relaxations of SUTVA, attrition issues, measurement errors, nonresponse problems, or more complex treatment regimes (including mediated effects). Not surprisingly, these graphs will almost always indicate that the identification of causal treatment effects requires stronger and an increased number of assumptions that are most likely not met in practice. Thus, we claim that strong causal inferences should rely on studies whose basic designs are associated with simple and credible causal graphs—well-implemented randomized trials and quasi-experiments, in particular RD designs, may meet this claim.

Author Biographies

Peter M. Steiner is an assistant professor in the Department of Educational Psychology, University of Wisconsin–Madison. His research interests focus are in causal inference, particularly in experimental and quasi-experimental designs, including propensity score matching designs, interrupted time series designs, and regression discontinuity designs.

Yongam Kim is a PhD student in the Quantitative Methods program in Educational Psychology, University of Wisconsin–Madison.

Courtney E. Hall is a statistical analyst at the Bureau of Assessment, Accountability and Evaluation, New Mexico Public Education Department, Santa Fe, NM.

Dan Su is a PhD student in the Quantitative Methods program in Educational Psychology, University of Wisconsin–Madison.