Abstract
Reward prediction errors track the extent to which rewards deviate from expectations, and aid in learning reward predictions. How do such errors in prediction interact with memory for the rewarding episode? Existing findings point to both cooperative and competitive interactions between learning and memory mechanisms. Here, we investigated whether learning about rewards in a high-risk context, with frequent, large prediction errors, gives rise to higher fidelity memory traces for rewarding events than learning in a low-risk context. Experiment 1, showed that recognition was better for items associated with larger absolute prediction errors during reward learning. Larger prediction errors also led to higher rates of learning about rewards. Interestingly, we did not find a relationship between learning rate for reward and recognition memory accuracy for items, suggesting that these two effects of prediction errors were due to separate underlying mechanisms. Experiment 2, replicated these results with a longer task that posed stronger memory demands and allowed for more learning. We also showed improved source and sequence memory for items within the high-risk context. Experiment 3 controlled for the difficulty of reward learning in the risk environments, again replicating the previous results. Moreover, this control revealed that the high-risk context enhanced item recognition memory beyond the effect of prediction errors. In summary, our results show that prediction errors boost both episodic item memory and incremental reward learning, but the two effects are likely mediated by distinct underlying systems.
Keywords: reward prediction error, risk, memory, reinforcement learning, surprise
If you receive a surprising reward, would you remember the event better or worse than if that same reward were expected? And what if it was a surprising punishment? Surprising rewards or punishments cause “prediction errors” that are important for learning which outcomes to expect in the future, but it is unclear how these prediction errors affect episodic memory for the details of the surprising event. Theories of learning suggest that outcomes are integrated across experiences, yielding an average expected value for the rewarding source. Alternatively, we could use distinct episodic memories of past events and their outcomes to help guide us towards rewarding experiences and away from punishing ones. Incremental learning and episodic memory systems can collaborate during decision making, for example, when both the expected value of an option and a distinct memory of a previously experienced outcome influences a decision (Biele, Erev, & Ert, 2009; Duncan & Shohamy, 2016). The two systems can also compete for processing resources: compromised feedback-based learning has been associated with enhanced episodic memory, both behaviorally and neurally (Foerde, Braun, & Shohamy, 2012; Wimmer, Braun, Daw, & Shohamy, 2014). Here, we study the nature of the interaction between incremental learning and episodic memory by investigating the role of reward prediction errors – rapid and transient reinforcement signals that track the difference between actual and expected outcomes – in the formation of episodic memory for rewarding events.
Reward prediction errors play a well-established role in updating stored information about the values of different choices, and are known to modulate dopamine release. When a reward is better than expected, there is an increase in the firing of dopamine neurons, and conversely, when the reward is worse than expected, there is a dip in dopaminergic firing (Schultz & Dickinson, 2000; Schultz, Dayan, & Montague, 1997). Dopamine, in turn, modulates plasticity in the hippocampus, a key structure for episodic memory (Lisman & Grace, 2005). This dopaminergic link therefore provides a potential neurobiological mechanism for reward prediction errors to affect episodic memory. However, there are several ways by which reward prediction errors could potentially influence episodic memory. First, if memory formation is affected by this signed prediction error, then we would expect an asymmetric effect on memory, such that a positive prediction error (leading to an increase in dopaminergic firing) would improve memory whereas a negative prediction error (leading to a decrease in dopaminergic firing) would worsen it.
A second possibility is that the magnitude of the prediction error could influence episodic memory regardless of the sign of the error, enhancing memory for events that are either much better or much worse than expected. Outside of reward learning, surprising feedback has been linked to better memory for both the content and source of feedback events in studies investigating the “hypercorrection” effect, where high confidence errors are more likely to be corrected and remembered (Butterfield & Mangels, 2003; Butterfield & Metcalfe, 2001; Fazio & Marsh, 2009, 2010). The same memory benefit for high-confidence errors has also been shown for low-confidence correct feedback, and one can envision both high-confidence errors and low-confidence correct trials as generating a large (unsigned) prediction error. These putative “high prediction-error events” have also been shown to modulate attention, as measured by impaired performance on a secondary task; the degree of this attentional capture in turn predicts subsequent memory enhancement for the feedback content (Butterfield & Metcalfe, 2006).
The effects of unsigned prediction errors are thought to be mediated by the locus-coeruleus-norepinephrine (LC-NE) system, which demonstrates a transient response to unexpected changes in stimulus-reinforcement contingencies in both reward and fear learning (that is, regardless of sign; for a review, see Sara, 2009), and modulates increases in learning rate, i.e. the extent to which a learner updates their values, following large unsigned prediction errors (Behrens, Woolrich, Walton, & Rushworth, 2007; McGuire, Nassar, Gold, & Kable, 2014; Nassar et al., 2012; Pearce & Hall, 1980). Importantly, recent evidence also indicates that the locus coeruleus co-releases dopamine with norepinephrine, giving rise to dopamine-dependent plasticity in the hippocampus (Kempadoo, Mosharov, Choi, Sulzer, & Kandel, 2016; Takeuchi et al., 2016). This latter pathway thereby provides a mechanism whereby unsigned prediction errors could affect episodic memory, by modulating hippocampal plasticity.
In the following experiments, we therefore tested whether signed or unsigned prediction errors influence learning rate and episodic memory, and whether these two effects are correlated. Correlated effects on learning of values and memory for events would suggest a common mechanism underlying both effects, whereas two uncorrelated effects are consistent with separate underlying mechanisms.
We also wanted to measure the effect of risk context (i.e., whether unsigned prediction errors were large or small, on average, in a particular environment) on episodic memory. Previous work on the effects of risk context show that dopamine signals scale to the reward variance of the learning environment (Tobler, Fiorillo, & Schultz, 2005), allowing for greater sensitivity to prediction errors in lower variance contexts. Moreover, behavioral learning rate and BOLD responses in the dopaminergic midbrain and striatum reflect this adaptation, with higher learning rates and increased striatal response to prediction errors when the reward variance is lower (Diederen, Spencer, Vestergaard, Fletcher, & Schultz, 2016). We therefore expected higher learning rates in a low-risk context, but it was unclear whether this effect would interact with episodic memory. If anything, for memory we expected opposite effects, such that a high-risk context would induce better episodic memory, as salient feedback (like experiencing high magnitude prediction errors) is thought to increase autonomic arousal and encoding of those events (Clewett, Schoeke, & Mather, 2014). The mnemonic effects of higher magnitude prediction errors may also “spill over” to surrounding items, boosting memory for those items as well, again predicting better memory for events experienced in the high-risk context (Duncan, Sadanand, & Davachi, 2012; Mather, Clewett, Sakaki, & Harley, 2015).
To investigate the effect of prediction errors and risk context on the structure of memory, we asked participants to learn by trial and error which of two types of images, indoor or outdoor scenes, leads to larger rewards. Trial-unique indoor and outdoor images were presented in two different contexts or ‘rooms,’ with each room associated with a different degree of outcome variance. The average values of the scene categories in the two rooms were matched. Participants were instructed to learn the average (expected) value of each type of image (indoor or outdoor scenes), given the variable individual outcomes experienced for each scene, as is typically done in reinforcement learning tasks (e.g. O’Doherty, Dayan, Friston, Critchley, & Dolan, 2003; Wimmer et al., 2014).
Specifically, we asked participants to explicitly estimate, on each trial, the average value of the category of the current scene. The deviation between this estimate and the outcome on that trial defined the trial-specific subjective prediction error. These prediction errors were then used to calculate trial-by-trial learning rates for the average values of the categories, as well as to predict future memory for the specific scenes presented on each trial. At a later stage, memory for the individual scenes was assessed through recognition memory (‘item’ memory), identification of the room the item belonged to (‘source’ or context memory; Exp. 2–3), and the ordering of a pair of items (‘sequence’ memory). Given that both category-value learning and individual scene memory were hypothesized to depend on the same prediction errors, we also characterized the relationship between learning about the average rewards in the task and episodic memory for the individual rewarding events.
Experiment 1
In Experiment 1, we assessed whether reward prediction errors interact with episodic memory for rewarding episodes. Participants learned the average reward values of images from two categories (indoor or outdoor scenes) in two learning contexts (‘rooms’). The two learning contexts had the same mean reward, but different degrees of reward variance (‘risk’) such that the rewards associated with scenes in the ‘high-risk room’ gave rise to higher absolute prediction errors than in the ‘low-risk room’. We then assessed participants’ recognition for the different scenes in a surprise memory test, to test how prediction errors due to the reward associated with each episode affected memory for that particular scene.
Method
Participants
Two hundred participants initiated an online task using Amazon Mechanical Turk (MTurk), and 174 completed the task. We obtained informed consent online, and participants had to correctly answer questions checking for their understanding of the instructions before proceeding (see supplementary material); procedures were approved by Princeton University’s Institutional Review Board. Participants were excluded if they (1) had a memory score (A′: Sensitivity index in signal detection; Pollack & Norman, 1964) of less than 0.5 based on their hit rate and false alarm rate for item recognition memory, or (2) missed more than three trials. These criteria led to the exclusion of ten participants, leading to a final sample of 164 participants. Although we do not have demographic information for the mTurk workers who completed these experiments, an online demographic tracker reports that during the time we collected data, the samples were approximately 55% female; 40% were born before 1980, 40% were born between 1980 and 1990, and 20% were born between 1990–1999 (Difallah, Catasta, Demartini, Ipeirotis, & Cudré-Mauroux, 2015; Ipeirotis, 2010).
Procedure
Participants learned by trial and error the average value of images from two categories (indoor or outdoor scenes) in two rooms defined by different background colors (see Figure 1). In each room, one type of scene was worth 40¢ on average (low-value category) and the other worth 60¢ (high-value category). The average values of the categories were matched across rooms, but the reward variance of the high-risk room was more than double that of the low-risk room (high-risk σ = 34.25, low-risk σ = 15.49). The order of the rooms (high-risk and low-risk) was randomized across participants. In an instruction phase, participants were explicitly told (through written instructions; see supplementary material) that in each room one scene category is worth more than the other (a ‘winning’ category) and were asked to indicate the winner after viewing all images in a room. They were not told the reward distributions of the rooms, nor that the rooms would have different levels of variance. In addition, to motivate participants to pay attention to individual scenes and their outcomes, participants were told that later in the experiment they would have the opportunity to choose between these same scenes and receive the rewards associated with them as per their choices.
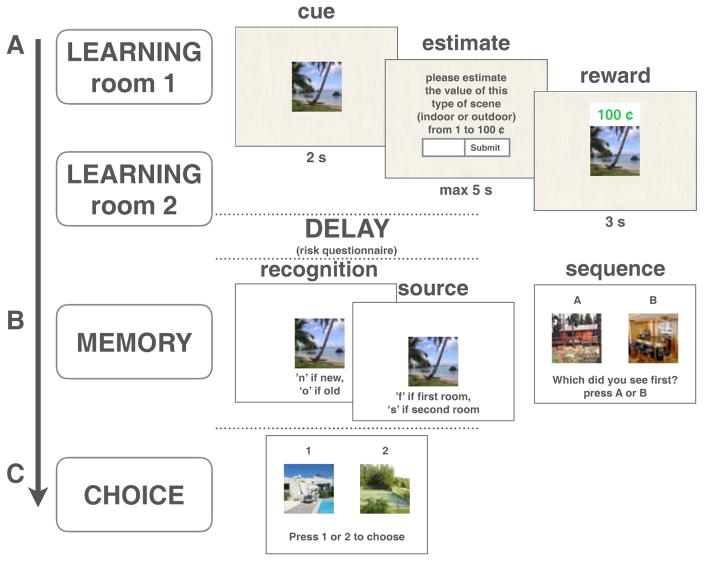
Figure 1.
Task Design. A: Example learning trial. On each trial, participants were shown an image (“cue”), and were asked to estimate how much on average that type of scene (indoor or outdoor) was worth (“estimate”). They then saw the image again with a monetary outcome (“reward”). Each image appeared on one trial only. B: Memory tests. Participants completed item recognition, source (Exp. 2,3) and sequence memory tasks. C: Choice task. Participants chose between previously seen images that were matched for reward outcome, risk context, and/or scene category value.
After the two learning blocks (one high-risk and one low-risk), participants completed a risk attitude questionnaire (DOSPERT, Weber, Blais, & Betz, 2002) that served to create a 5–10 minute delay between learning and memory tests. Participants then completed a surprise item-recognition task (i.e., participants were never told that their memory for scenes would be tested, apart from instructions about the choice task as detailed above), as well as a sequence memory task. After the memory tests, participants made choices between previously seen images.
Learning
On each trial, participants were shown a trial-unique image (either an indoor or outdoor scene) for 2 seconds. Participants then had up to 5 seconds to estimate how much that type of scene is worth on average in that room (from 1 to 100 cents). In other words, participants were asked to provide their estimate of the average, or expected value, of the scene category based on the previous (variable) outcomes they had experienced from that scene category within the room. The scene was then presented again for 3 seconds along with its associated reward (see Figure 1A). In the instructions (see supplementary material), participants had been told that although trial-unique images can take on different rewards, each scene category had a stable mean reward, and on average one scene category was worth more than the other. Note that participants were not asked to estimate the exact outcome they would receive on that trial, but instead were estimating the average expected reward from that scene category. Accordingly, participants had also been told that their payment was not contingent on how accurate their guesses were relative to the reward on that trial. Instead, their payment was solely determined by the rewards they received, to ensure that rewards were meaningful for the participant. This task structure was chosen to ensure that participants would continue to experience prediction errors on each trial (i.e., for individual scenes) even after correctly estimating the expected values of the categories, as is commonly done in reinforcement learning tasks (e.g. Niv, Edlund, Dayan, & O’Doherty, 2012).
There were 16 trials in each room (8 outdoor and 8 indoor). Rewards were 20¢, 40¢, 80¢, 100¢ (twice each) for the high-risk–high-value category, 0¢, 20¢, 60¢, 80¢ for the high-risk–low-value category, 45¢, 55¢, 65¢, 75¢ for the low-risk–high-value category and 25¢, 35¢, 45¢, 55¢ for the low-risk–low-value category. All participants experienced the same sequence of rewards within each room, with the order of the rooms randomized.
Memory
After completing the risk questionnaire, participants were presented with a surprise recognition memory test in which they were asked whether different scenes were old or new (Figure 1) as well as their confidence for that memory judgment (from 1 ‘guessing’ to 4 ‘completely certain’). There were 32 test trials, including 16 old images (8 from each room) and 16 foils. Participants were then asked to sequence 8 pairs of previously seen scenes (which were not included in the recognition memory test) by answering ‘which did you see first?’ (Figure 1) and by estimating how many trials apart the images had been from each other. Each pair belonged to either the low (4 pairs) or the high-risk room (4 pairs).
Choice
In the last phase of the experiment, to verify that participants had encoded and remembered the individual outcomes associated with different scenes, participants were asked to choose between pairs of previously seen scenes for a chance to receive their associated reward again (see Figure 1C). The pairs varied in either belonging to the same room or different rooms and some were matched for reward and/or average scene value in order to test for the effects of factors such as risk context on choice preference. The choices were presented without feedback.
Statistical Analysis
Analyses were conducted using paired t-tests, repeated measures ANOVAs, and generalized linear mixed-effects models (lme4 package in R; Bates et al., 2015). All results reported below (t-tests and ANOVAs) were confirmed using linear or generalized mixed-effects models treating participant as a random effect (for both the intercept and slope of the fixed effect in question). We note that in all experiments, our results held when controlling for the between-subjects variable of room order (for brevity, we only explicitly report these results in Experiment 1, see below).
Results
Learning
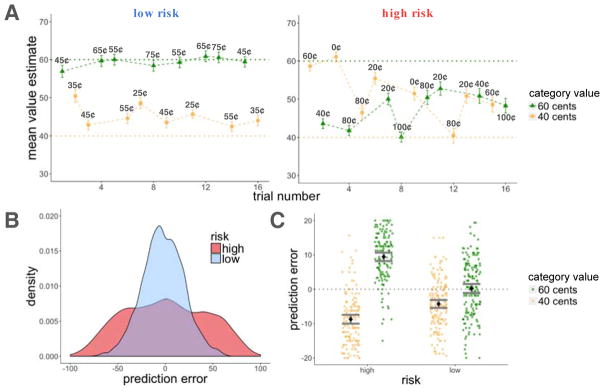
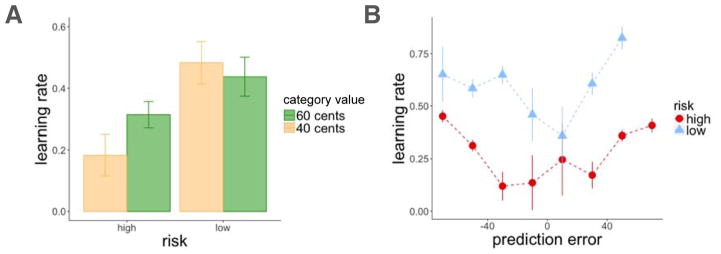
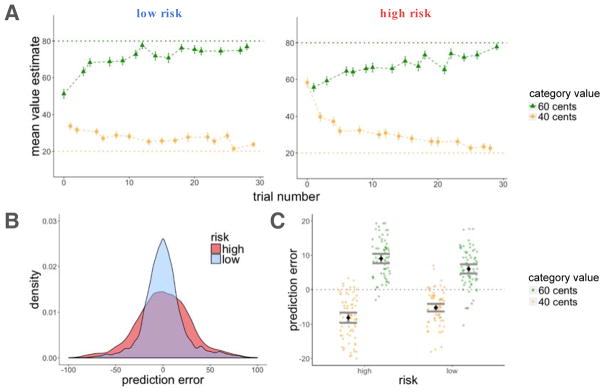
Participants learned the average values of the high- and low-value categories better in the low-risk than in the high-risk room, as assessed by the deviation of their value estimates from the true averages of the scene categories (t(163) = 14.52, p < 0.001; Figure 3A). We then calculated, for every scene, the prediction error (PEt associated with that scene by subtracting participants’ value estimates (Vt) from the reward outcome they observed (Rt; see Figure 2). This showed that, as we had planned, there were more high-magnitude prediction errors in the high-risk room as compared to the low-risk room (t(163) = 36.77, p < 0.001, within-subject comparison of average absolute prediction errors between the two rooms; Figure 3B).
Figure 3.
Experiment 1, learning results. A: Average estimates for the high and low-value categories as a function of trial number for the high and low-risk rooms. Participants learned better in the low-risk room, indicated by the proximity of their guesses to the true values of the scenes (dashed horizontal lines). Cent values represent the outcome participants received on that trial (after entering their value estimate). B: Density plot of prediction errors (PEt) in each room. There were more high-magnitude prediction errors in the high-risk in comparison to the low-risk room. C: There was an interaction for positive and negative prediction errors between risk context and category value, such that participants overestimated the value of the low-value category and underestimated the value of the high-value category to a greater extent in the high-risk room. Error bars represent standard error of the mean.
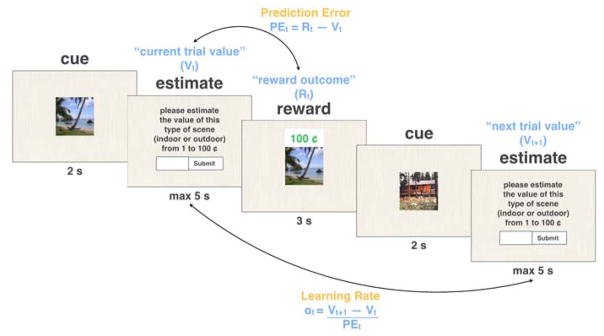
Figure 2.
Schematic of prediction error (PE) and learning rate (α) calculation for two consecutive trials that involve the same scene category, in the learning phase of the experiment. Based on the learning equation Vt+1 = Vt + αt* PEt, we calculated the trial-by-trial learning rate as (Vt+1 − Vt) / PEt. Note that all components of this equation are measured explicitly: Vt and Vt+1 are two consecutive estimates of the value of a scene from a single category (e.g., outdoor scenes), and the prediction error on trial t is the difference between the reward given on that trial, and the participants’ estimate of the value of scene on the same trial. We assume here that separate values are learned and updated for each of the scene categories.
Moreover, there was an interaction between risk and scene category such that participants overestimated the value of low-value scene category (resulting in negative prediction errors, on average) and underestimated the value of high-value scene category (resulting in positive prediction errors, on average) to a greater extent in the high-risk room than in the low-risk room (F(1,163) = 141.2, p < 0.001 for a within-subject interaction of the effects of room and scene category on the average signed prediction error; Figure 3C). This demonstrates more difficulty in separating the values of the categories in the high-risk room, consistent with previous findings showing that when people estimate the means of two largely overlapping distributions, they tend to average across the two distributions, thereby grouping them into one category instead of separating them into two (Gershman & Niv, 2013). Despite greater difficulty in separating the values of the high and low value categories within the high-risk room, most participants correctly guessed the “winner”, or the high-value scene category, within both the high-risk (88%) and the low-risk (89%) rooms.
Memory by Risk and Prediction Error
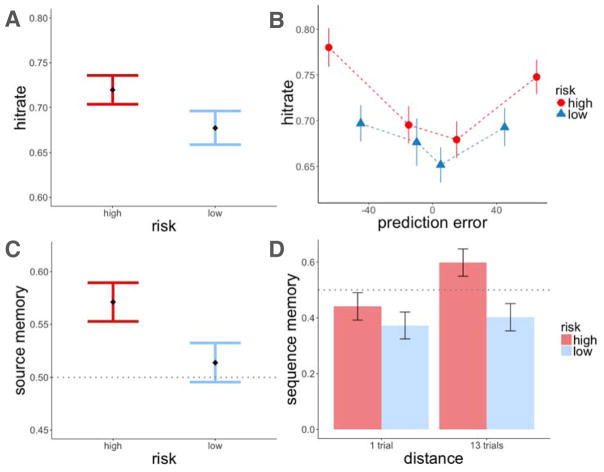
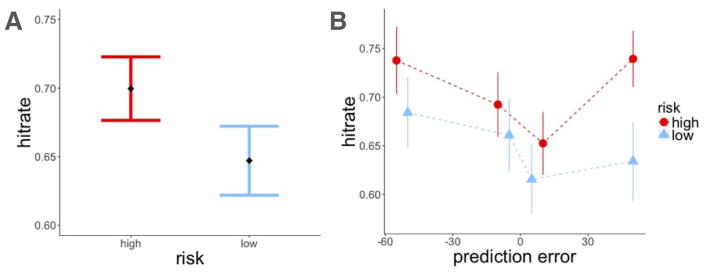
We found that items within the high-risk room were recognized better than items within the low-risk room (z = 2.37, p = 0.02, β = 0.31; Figure 4A). To test the effect of reward prediction errors on item-recognition memory, we ran two separate mixed-effects logistic regression models of memory accuracy, one testing for the effect of signed and the other the effect of unsigned (absolute) prediction errors on recognition memory. Both models also included a risk-level regressor to test for the effects of risk and prediction error separately, and treated participants as a random effect. We did not find signed prediction errors to influence recognition memory beyond the effect of risk (signed prediction error (PEt): z = 0.71, p = n.s., β = 0.04; risk: z = 2.29, p = 0.02, β = 0.30). Instead, we found that larger prediction errors enhanced memory regardless of the sign of the prediction error, which also explained the modulation of memory by risk (absolute prediction error (|PEt|) : z = 3.36, p < 0.001, β = 0.23; risk: z = 0.9, p = n.s., β = 0.10; Figure 4B).
Figure 4.
Experiment 1, recognition memory results. A: Recognition memory was better for items within the high-risk room. B: There was better recognition memory for items associated with a higher absolute prediction error. Item memory was binned by the quartile values of prediction errors within each risk room. Each dot represents the average value within that quartile. Error bars represent standard error of the mean.
We ran two subsequent models testing for confounds, one including the effect of value estimates and the other the actual reward outcomes associated with the items, along with the effect of absolute prediction errors. Absolute prediction error had a significant effect on recognition memory when controlling for reward outcome (|PEt| : z = 3.94, p < 0.001, β = 0.26; Rt: z = 0.45, p = n.s., β = 0.02) and value estimates (|PEt| : z = 3.93, p < 0.001, β = 0.26; Vt: z = −0.09, p = n.s., β = −0.005). This effect also held when modeling recognition memory for items in the high and low-risk rooms separately (high-risk: z = 1.90, p = 0.05, β = 0.18; low-risk: z = 2.17, p = 0.03, β = 0.24), and in a model of the effects of absolute prediction errors on recognition memory that controlled for room order (|PEt| : z = 3.90, p < 0.001, β = 0.25; room order: z = 1.95, p = 0.05, β = 0.33). Although room order itself did affect recognition memory (participants who experienced the low-risk room first showed better memory accuracy overall), all of our main findings (including learning rate, see below) held when controlling for this effect.
Reward prediction errors therefore affected recognition memory, such that larger deviations from one’s predictions, in any direction, enhanced memory for items. Finally, we tested for the effect of risk on sequence memory (the correct ordering of two images seen during learning) and found no difference in sequence memory between pairs of images seen in the high and low-risk rooms (z = 0.11, p = n.s., β = 0.02).
Learning Rate by Risk and Prediction Error
We also examined the effects of risk and prediction errors on the reward learning process itself. For this we calculated a trial-by-trial learning rate αt as the proportion of the current prediction error PEt = Rt − Vt that was applied to update the value for the next encounter of the same type of scene, Vt+1 (see Figure 2 for schematic representing learning rate calculation). That is, we derived the trial-specific learning rate directly from the standard reinforcement-learning update equation Vt+1 = Vt + αt(Rt − Vt), as .
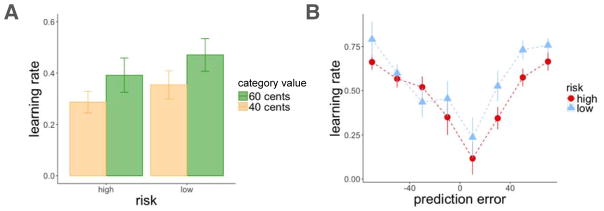
In agreement with recent findings (e.g. Diederen et al., 2016), we found that average learning rate was higher in the low-risk room than in the high-risk room (t(163) = 3.37, p < 0.001 within-subjects test; Figure 5A). Moreover, higher absolute prediction errors increased trial-by-trial learning rates (αt) above and beyond the effect of risk (mixed-effects linear model, effect of absolute prediction error: t = 3.30, p = 0.001, β = 0.07; risk: t = 4.67, p < 0.001, β = 0.16; Figure 5B). We did not find participant room order to influence learning rate (t = 0.31, p = n.s., β = −0.03). These results show that larger absolute prediction errors enhance value updating, and further, that learning rates adapt to the reward variance such that there is greater sensitivity to prediction errors in a lower-risk environment.
Figure 5.
Experiment 1, learning rate results. A: Learning rate was higher in the low-risk context. Average learning rate plotted by risk context and category value. B: Both absolute prediction errors and a low-risk context increased learning rate. Learning rates were binned by prediction errors that occurred on the same trial (each dot represents the average prediction error within the binned range). Error bars represent standard error of the mean.
We next ran a mixed-effects regression model to test whether trial-by-trial learning rates predicted recognition memory for scenes at test. Controlling for absolute prediction error, we did not find that learning rate on trial t predicted memory on that same trial (αt : z = 0.85, p = n.s., β = 0.08; |PEt| : z = 3.42, p < 0.001, β = 0.20), nor on the subsequent trial, (effect of αt−1 on recognition memory for the scene on trial t: z = 0.56, p = n.s., β = 0.05; |PEt| : z = 3.06, p = 0.002, β = 0.19, where t enumerates over trials within a room). This demonstrates that increases in learning rate were not correlated with better (or worse) memory, even though both learning rate and recognition memory were enhanced by larger prediction errors.
Choice by Reward and Value Difference
Finally, in a manipulation test, participants were asked to make choices between pairs of previously-seen scenes. Choices between scenes with different reward outcomes served to test whether participants encoded the rewards associated with the images. Participants chose the image associated with the larger outcome more often (mixed-effects logistic regression model predicting choice based on outcome: z = 6.40, p < 0.001, β = 0.54), suggesting that they did indeed encode and remember the rewards associated with the scenes.
Some choices were between items that were associated with the same outcome feedback. Here we sought to test whether features of the environment such as the risk context biased participants away from indifference. We did not find risk level, whether the scene was from the low rewarding or high rewarding category, or the difference in absolute prediction error between the images, to additionally influence choice preference. We instead found that participants were more likely to choose the scene that they had initially guessed a higher value for (z = 3.74, p < 0.001, β = 0.01). We additionally found that even when the two options had led to different reward outcomes, the difference in initial value estimates for the scene was a significant predictor of choice, above and beyond the difference in actual reward outcome (value estimate difference: z = 2.27, p = 0.02, β = 0.16; reward difference: z = 7.25, p < 0.001, β = 0.52). This suggests that participants remembered not only the outcomes for different scenes, but also their initial estimates.
Discussion
In Experiment 1, we showed that the greater the magnitude of the prediction error experienced during value learning, the more likely participants were to recognize items associated with those prediction errors. We also demonstrated that both risk context and absolute prediction errors influenced the extent to which people updated values for the scene categories, i.e. their item-by-item learning rate fluctuated according to prediction errors and was influenced by context. In particular, learning rate was higher in the low-risk environment, suggesting greater sensitivity to prediction errors when the variance of the environment was lower. Further, in both contexts, higher absolute prediction errors increased learning rate. Although absolute prediction errors enhanced both recognition memory and learning rate, we did not find learning rate to predict recognition memory, suggesting that absolute prediction errors affect learning and memory through distinct mechanisms.
Experiment 2
In Experiment 2, we allowed for more learning in both rooms, which posed stronger memory demands. We also tested for other types of episodic memory. Notably, different from standard reinforcement-learning paradigms, Experiment 1 involved only 16 trials of learning in each context, 8 for each category. The initial phase of learning, which we were effectively testing, is characterized by increased prediction errors and uncertainty relative to later learning, which might affect the relationship between prediction errors and episodic memory. Additionally, participants in Experiment 1 all experienced the same reward sequence, which inadvertently introduced regularities in the learning curves that could have also influenced initial learning and memory results. Finally, in this relatively short experiment, average recognition memory performance was near ceiling (A′ = 0.90). In Experiment 2, we therefore sought to replicate the results of Experiment 1 while increasing the number of learning and memory trials and randomizing reward sequence. With more trials, we were also able to test for sequence memory for items that were presented further apart in time, and we included a measure of source memory (i.e., which room the item belonged to)—a marker of episodic memory—for the context of the probed item.
Method
Participants
Two hundred participants initiated an online task run on Amazon Mechanical Turk, and 148 completed the task. Following the same protocol as in Experiment 1, twelve participants were excluded from the analysis leading to a final sample of 136 participants.
Procedure
The procedure was the same as in Experiment 1 but with some changes to learning, memory and choice. As in Experiment 1, rewards had a mean of 60¢ for the high-value category and 40¢ for the low-value category (high-risk–high-value scenes: 20¢, 40¢, 60¢, 80¢, 100¢; high-risk–low-value scenes: 0¢, 20¢, 40¢, 60¢, 80¢; low-risk–high-value scenes: 40¢, 50¢, 60¢, 70¢, 80¢; low-risk–low-value scenes: 20¢, 30¢, 40¢, 50¢, 60¢). However, we increased the number of learning trials from 16 to 30 trials per room, and we pseudo-randomized the reward sequence such that the rewards were drawn at random and were sampled three times without replacement.
During the item memory test, we also asked participants to indicate whether items identified as ‘old’ belonged to the first or second room (see Figure 1B), to measure source memory. Additionally, given that sequence memory improves with greater distance between events (DuBrow & Davachi, 2013), here we asked participants to order items that were as far as 13–14 trials apart, in contrast to the maximum of 8 trials apart in Experiment 1. Finally, satisfied by the manipulation check in the choice tasks in Experiment 1, we asked participants to choose only between pairs of scenes matched for reward outcome.
Results
Learning
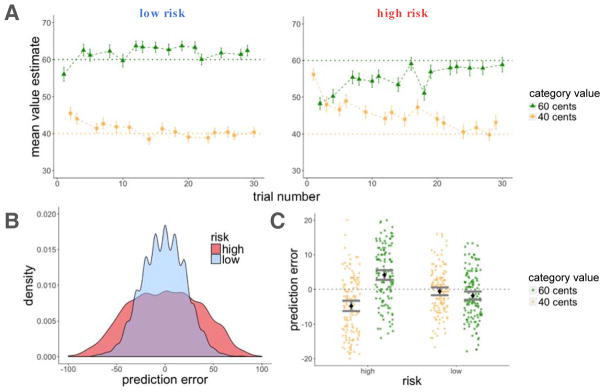
As in Experiment 1, participants learned better in the low-risk than in the high-risk room (assessed by the average deviation of participants’ value estimates from the true means of the category values; t(135) = 13.11, p < 0.001; Figure 6A). They experienced larger absolute prediction errors in the high-risk room (t(135) = 39.65, p < 0.001; Figure 6B), and there was again an interaction between risk and scene category value such that in the high-risk room, participants overestimated the value of the low-value scene category and underestimated the value of the high-value scene category to a greater extent than in the low-risk room (F(1,135) = 77.5, p < 0.001; interaction of the effects of room and category on average prediction error experienced; Figure 6C). Again, participants guessed the high-value scene category at the end of each room equally well in the high-risk (90%) and low-risk (89%) rooms.
Figure 6.
Experiment 2, learning results. A: Average estimates for the high and low-value categories as a function of trial number for the high and low-risk rooms. Participants learned better in the low-risk room, indicated by the proximity of their guesses to the true values of the scenes (dashed horizontal lines). B: Density plot of prediction errors (PEt) in each room. There were more high-magnitude prediction errors in the high-risk in comparison to the low-risk room. C: There was an interaction for positive and negative prediction errors between risk context and category value, such that participants overestimated the value of the low-value category and underestimated the value of the high-value category to a greater extent in the high-risk room. Error bars represent standard error of the mean.
Memory by Risk and Prediction Error
By increasing the number of learning and memory trials, we significantly reduced average recognition memory performance from Experiment 1 (A′ = 0.86, t(275.23) = 3.04, p = 0.003 when comparing overall memory performance between Experiment 1 and 2). We nevertheless replicated the main results of Experiment 1: items from the high-risk room were better recognized than items from the low-risk room (z = 2.51, p = 0.01, β = 0.19 when testing for the effect of risk on item-recognition memory; Figure 7A). In a separate model, higher absolute prediction errors enhanced recognition memory for scenes, while again explaining the effect of risk (|PEt| : z = 3.44, p < 0.001, β = 0.16; risk: z = 1.76, p = 0.08, β = 0.14, Figure 7B). Like in Experiment 1, in subsequent models testing for potential confounds, this effect was significant when controlling for the outcomes associated with the items (|PEt| : z = 4.14, p < 0.001, β = 0.18; outcome Rt: z = −1.71, p = n.s., β = −0.06) as well as for the value estimate for the scene category (|PEt| : z = 4.15, p < 0.001, β = 0.19; estimate Vt: z = −1.16, p = n.s., β = −0.04).
Figure 7.
Experiment 2, memory results. A: Recognition memory was better for items within the high-risk context. B: Absolute prediction errors enhanced recognition memory for the scenes. Item memory was binned by the quartile values of prediction errors within each risk room, each dot represents the average value within that quartile. C: For correctly remembered items, source memory was better for items within the high-risk context. D: A high-risk context and distance between items (number of trials between pairs) increased sequence memory. Error bars represent the standard error of the mean.
In addition, for the scenes correctly identified as old, we found better source memory for scenes from the high-risk room (z = 2.05, p = 0.04, β = 0.25 in a mixed-effects logistic regression model testing for the effect of risk on source memory; Figure 7C). This effect was not modulated by absolute prediction error. Rather, it was a context effect: the source of a recognized image was better remembered if that item was seen in the high-risk room (absolute prediction errors: z = −0.60, p = n.s., β = −0.03; risk: z = 2.17, p = 0.03, β = 0.27). To verify that participants were not simply attributing remembered items to the high-risk context, we looked at the proportion of high-risk source judgments for recognition hits and false alarms separately. We did not find a greater proportion of high-risk source judgments for false alarms, indicating that participants were not biased to report that remembered items belonged to a high-risk context (for high-risk hits: mean = 0.57, standard error = 0.02; for false alarms: mean = 0.49, standard error = 0.04; chance response is 0.50).
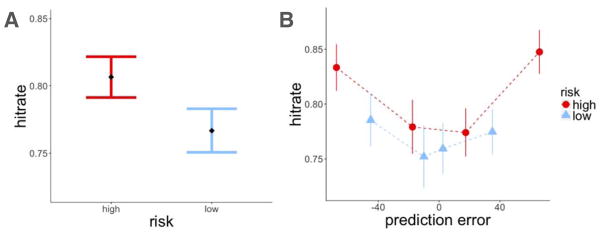
Participants also exhibited better sequence memory for pairs from the high-risk room (z = 2.70, p = 0.007, β = 0.56 in a mixed-effects logistic regression model testing for the effect of risk on sequence memory; Figure 7D). Although we did not see this effect in Experiment 1, the longer training in Experiment 2 allowed us to test pairs that were more distant from each other (the most distant items were 13 and 14 trials apart). Indeed, in a model additionally testing for the effect of distance between tested pairs, greater distance predicted better sequence memory, controlling for risk (distance: z = 1.92, p = 0.05, β = 0.39; risk: z = 2.70, p = 0.006, β = 0.56). We therefore replicated our original results and further showed that other forms of episodic memory—source and sequence memory—were also enhanced in a high-risk context.
Learning Rate by Risk and Prediction Error
We replicated the results of Experiment 1 with respect to learning rates as well: participants had higher learning rates for the low-risk relative to the high-risk room, and higher absolute prediction errors additionally increased learning rates in a mixed-effects regression model testing for the effect of risk and absolute prediction error on learning rate (absolute prediction error: t = 5.12, p < 0.001, β = 0.09; risk: t = 7.01, p < 0.001, β = 0.18; Figure 8A–B). Controlling for absolute prediction error, we again did not find learning rate to predict recognition memory on the current trial (αt : z = −0.29, p = n.s., β = −0.01; |PEt| : z = 4.44, p < 0.001, β = 0.20), nor the subsequent trial (αt−1 : z = 0.68, p = n.s., β = 0.03; |PEt| : z = 3.53, p < 0.001, β = 0.17).
Figure 8.
Experiment 2, learning rate results. A: Learning rate was higher in the low-risk context. Average learning rate plotted by risk context and category value. B: Both absolute prediction errors and a low-risk context increased learning rate. Learning rates were binned by prediction errors that occurred on the same trial (each dot represents the average prediction error within the binned range). Error bars represent standard error of the mean.
Choice by Value Difference
In this experiment, all choices were between images with matched reward outcomes. We replicated the results of Experiment 1 such that choice was predicted by the difference in participants’ initial value estimates for the scenes (z = 2.78, p = 0.005, β = 0.18, Figure 9). In particular, even in this better-powered test (12 choice trials as compared to 4 choice trials with matched outcomes in Experiment 1), there was no evidence for preference for images from one risk context versus the other (z = −1.56, p = n.s., β = −0.08).
Figure 9.
Experiment 3, learning results. A: Average estimates for the high and low-value categories as a function of trial number, separately for the high-risk and low-risk rooms. Participants learned better in the low-risk room (although the difference in learning between risk rooms was smaller than in Exp. 1 & 2). B: Density plot of experienced prediction errors (PEt) in each room. Compared to Exp 1 & 2, there were higher-magnitude prediction errors in the low-risk room, making the range of prediction errors more similar between rooms. C: Prediction errors show an interaction between risk context and category value, such that participants overestimated the value of the low-value category and underestimated the value of the high-value category to a greater extent in the high-risk room. Error bars represent the standard error of the mean.
Discussion
In Experiment 2, we doubled the number of training trials and replicated the results of Experiment 1, showing that large prediction errors increase learning rate and improve recognition memory, but that higher learning rates do not predict better item recognition. In fact, like in Experiment 1, learning rates were higher in the low-risk room, but item recognition was better in the high-risk room. Moreover, in this experiment, we demonstrated additional risk-context effects on episodic memory by showing better sequence and source memory for items that were encountered in the high-risk learning context. These results were separate from the effect of absolute prediction errors, but perhaps point to general memory enhancement for events occurring in a putatively more arousing environment.
Experiment 3
A possible confound of the effects of risk on memory and learning in Experiments 1 and 2 is that there was higher overlap between the outcomes for the two categories in the high-risk context as compared to the low-risk context. The distributions of outcomes for the indoor and outdoor scenes shared values from 20¢ to 80¢ (Exp. 1 & 2) in the high-risk room, but only 45¢ to 55¢ (Exp. 1) and 40¢ to 60¢ (Exp. 2) in the low-risk room. This greater overlap in the high-risk context could have made learning more difficult in comparison to the low-risk room, and therefore influenced the effects of absolute prediction error on subsequent memory. To test for this possibility, in Experiment 3 we made the learning conditions in the two rooms more similar by eliminating any overlap between the outcomes of the two categories.
Method
Participants
We conducted a simulation-based power analysis of the effect of absolute prediction errors on item-recognition memory. This revealed that we would have sufficient power (80% probability) to replicate the results of Experiments 1 and 2 with as few as 55 participants. As a result, we had 100 participants initiate the study, of which 86 completed the task. Three participants were excluded based on our exclusion criteria (see Experiment 1) leaving a final sample of 83 participants.
Procedure
We followed the same procedure as in Experiment 2 but changed the rewards such that they had a mean of 80¢ for the high-value category and 20¢ for the low-value category, and there was no overlap between the outcomes for scenes from the two categories (high-risk–high-value scenes: 60¢, 70¢, 80¢, 90¢, 100¢; high-risk–low-value scenes: 0¢, 10¢, 20¢, 30¢, 40¢; low-risk–high-value scenes: 70¢, 75¢, 80¢, 85¢, 90¢; low-risk–low-value scenes: 10¢, 15¢, 20¢, 25¢, 30¢).
Results
Learning
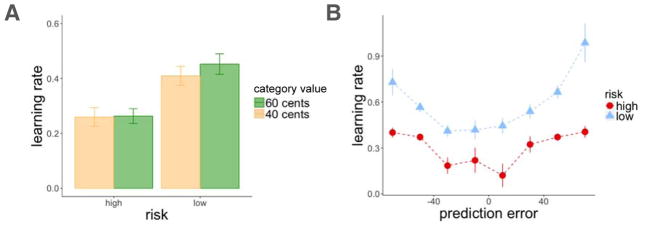
As in Experiment 1 and 2, participants learned better in the low-risk than in the high-risk room (t(82) = 6.28, p < 0.001 in a paired t test comparing the average deviation of estimates from the true means of the categories across rooms; Figure 9A). However, learning in the two rooms was more similar here than in Experiment 2, as assessed by first computing the difference in learning (average deviation of estimates from the true means of the scene categories) between the high and low-risk rooms for each participant, and then comparing this value between participants in Experiments 2 and 3 (t(148.98) = 1.84, p = 0.03). The range of prediction errors in the two rooms was also more similar in comparison to Experiment 1 and 2 (Figure 9B), allowing us to better assess the effects of risk context on learning and memory, when controlling for prediction errors (see below). As in previous experiments, there was an interaction between risk and scene category such that participants overestimated the low-value category and underestimated the high-value category more in the high-risk than in the low-risk room, (F(1,82) = 23.02, p < 0.001; Figure 9C). Nonetheless, participants correctly guessed the high-value category equally well (and at a higher proportion than in Experiment 1 and 2) in the high-risk (95%) and low-risk (96%) rooms.
Memory by Risk and Prediction Error
We replicated the results of Experiments 1 and 2, and further found separate effects of context and unsigned prediction error on recognition memory. A high-risk context and larger absolute prediction errors enhanced recognition memory for scenes, even with both predictors in the same model, indicating independent effects (|PEt| : z = 2.24, p = 0.02, β = 0.12; risk: z = 2.58, p = 0.009, β = 0.24, Figure 10A–B). This effect was again significant when controlling for reward outcome (|PEt| : z = 2.72, p = 0.007, β = 0.15; Rt: z = −0.38, p = n.s., β = −0.02) and value estimates (|PEt| : z = 2.70, p = 0.007, β = 0.15; Vt: z = −0.74, p = n.s., β = −0.03). Similar to Experiment 2, we again found better sequence memory for items within the high-risk context, while controlling for the effect of distance (risk: z = 2.47, p = 0.01, β = 0.57; distance: z = 2.36, p = 0.02, β = 0.55). For source memory, we did not have the power to detect the effect in Experiment 2, and this difference was not statistically significant although it was in the same direction.
Figure 10.
Experiment 3, recognition memory results. A: Recognition memory was better for scenes that were encountered in the high-risk context. B: Both absolute prediction errors and a high-risk context independently enhanced recognition memory for scenes. Item memory was binned by the quartile values of prediction errors within each risk room. Each dot represents the average value within that quartile. Error bars represent the standard error of the mean.
It is worth noting here that there was a stronger effect of context in modulating recognition memory than in Experiments 1 and 2 (the context effect remained when controlling for absolute prediction errors, unlike in Experiments 1 and 2). That is, when learning was more similar in the two rooms, an independent effect of risk in increasing recognition memory became apparent. One possible explanation for this finding is that memory-boosting effects of reward prediction errors might “spill over” to adjacent trials, enhancing memory for those items as well. To test for these “spill over” effects in the high-risk context, we measured whether immediately previous and subsequent absolute prediction errors proactively or retroactively strengthened recognition memory for a scene, while controlling for the absolute prediction error experienced for that particular scene. We ran two mixed-effects logistic-regression models testing for the effect of adjacent absolute prediction errors (one for previous and one for subsequent prediction error) on recognition memory. We did not find any effect of adjacent prediction errors (|PEt−1| : z = −1.71, p = n.s., β = −0.13; |PEt+1| : z = −0.93, p = n.s., β = −0.08), suggesting that the memory-enhancing effect of the high-risk context may be due to general enhanced memory for items experienced in a high-risk, and potentially more arousing, environment.
Learning Rate by Risk and Prediction Error
As in Experiments 1 and 2, absolute prediction errors increased learning rates in both rooms, and there was a trend for higher learning rates in the low-risk room (|PEt|: t = 3.33, p < 0.001, β = 0.06; risk: t = 1.84, p = 0.06, β = 0.06; Figure 11A–B). We again did not find learning rate for values to predict recognition memory for the scene on the current trial (z = −0.26, p = n.s., β = −0.01), nor the subsequent trial (z = −1.22, p = n.s., β = −0.08), while controlling for the effect of absolute prediction error on the current trial.
Figure 11.
Experiment 3, learning rate results. A: There was a trend for higher average learning rates in the low-risk context. B: Absolute prediction errors increased learning rate. Learning rates were binned by prediction errors on the same trial (each dot represents the average prediction error within the binned range). Error bars represent standard error of the mean.
Choice by Value Difference
As in Experiment 2, all choices (12 trials) were between scenes that had matched reward outcomes. Here too we replicated the results of Experiment 1 and 2, such that participants were more likely to choose the scene that they had initially guessed a higher value for (z = 3.98, p < 0.001, β = 0.29).
Discussion
In Experiment 3, we eliminated all overlap between the reward outcomes of the high and low-value categories in both rooms—a potential confound in Experiment 1 and 2—and replicated our previous results. Additionally, given the more similar range of prediction errors in the high and low-risk contexts, we were able to detect an independent effect of risk context on recognition memory. Improved recognition memory in the high-risk room, like the better source and sequence memory observed for high-risk events in Experiment 2, points to general memory enhancement for events experienced in an environment with greater reward variance.
General Discussion
Our aim was to determine how reward prediction errors influence episodic memory, above and beyond their known influence on learning. In Experiment 1, we demonstrated that unsigned, or absolute prediction errors enhanced recognition memory for a rewarding episode. That is, trial-unique scenes that were accompanied by a large reward prediction error, whether positive (receiving much more reward than expected) or negative (receiving much less reward than expected) were better recognized in a subsequent surprise recognition test. We additionally found that risk context and absolute prediction errors modulated the trial-by-trial rate by which participants used the rewards to update their estimate of the general worth of that category of scenes. In particular, learning rate was higher in a low-risk environment, and there was more learning from rewards that generated larger prediction errors. Notably, although large prediction errors increased learning from rewards on that specific trial, and enhanced memory for the scene in the trial, we did not find a trial-by-trial relationship between learning rate and memory accuracy. In fact, the high-risk context led to lower learning rates but better recognition memory on average, suggesting separate mechanisms underlying these two effects of prediction errors.
In Experiment 2, we increased the number of trials therefore allowing for more learning in each context, and placing more demands on memory. We replicated all the effects from Experiment 1, and further showed that source and sequence-memory were better for images encountered in the high-risk context. In Experiment 3, we eliminated a potential confound by equating learning difficulty in the high-risk and low-risk contexts, again reproducing the original results. This manipulation also resulted in a more similar range of prediction errors in both risk contexts, which uncovered a separate effect of risk on episodic memory, above and beyond that of absolute prediction errors.
Previous work has shown both a collaboration between learning and memory systems, such as boosting of memory for items experienced during reward anticipation (Adcock et al., 2006) including oddball events (Murty & Adcock, 2014), as well as a competition between the systems, where the successful encoding of items experienced prior to reward outcome is thought to interfere with neural prediction errors (Wimmer et al., 2014). Here, in all three experiments, we showed that incremental learning and episodic memory systems collaborate, as learning signals. Specifically, large reward prediction errors both increase learning rate for the value of the rewarding source and enhance memory for the scene that led to the prediction error. However, the fact that the effects of prediction errors on learning rate and episodic memory were uncorrelated suggests that these effects are mediated by somewhat separate neural mechanisms.
Although we only tested behavior, the impetus for our experiments were neurobiological accounts adjudicating between the effects of signed and unsigned reward prediction errors on memory. Neurally, reward prediction error modulation of dopamine signaling provides a strong putative link between trial-and-error learning and dopamine-induced plasticity in the hippocampus. Such an effect of (signed) dopaminergic prediction errors from the ventral tegmental area (VTA) to the hippocampus would have predicted an asymmetric effect on memory, such that memories benefit from a positive prediction error (signaled by an increase in dopaminergic firing from the VTA), but not a negative prediction error (signaled by decreased dopaminergic firing). Instead, we found that the absolute magnitude of prediction errors, regardless of the sign, enhanced memory. This mechanism perhaps explains the finding that extreme outcomes are recalled first, are perceived as having occurred more frequently, and increase preference for a risky option (Ludvig, Madan, & Spetch, 2014; Madan, Ludvig, & Spetch, 2014).
In our task, each outcome was sampled with equal probability (uniform distributions), meaning that extreme outcomes were not rare. However, the mnemonic effects that we identified could potentially also contribute to the well-demonstrated phenomenon of nonlinear responses to reward probability in choice and in the brain, characterized by the overweighting of low-probability events and the underweighting of high-probability ones (Hsu, Krajbich, Zhao, & Camerer, 2009; Kahneman & Tversky, 1979). In particular, large prediction errors due to the occurrence of rare events would mean that these events affect learning and memory disproportionately strongly. Similarly, the underweighting of very common events could arise from the rare cases in which the common event does not occur, giving rise to large and influential prediction errors. Our results suggest that these distortions of weighting would be especially prominent when episodic memory is used in performing the task.
The influence of unsigned reward prediction errors on recognition memory is also reminiscent of work demonstrating better memory for surprising feedback outside of reinforcement learning, such as a recent study showing improved encoding of unexpected paired associates (Greve, Cooper, Kaula, Anderson, & Henson, 2017). Another potentially related paradigm is the hypercorrection effect (Butterfield & Metcalfe, 2001), where high-confidence errors and low-confidence correct feedback (both potentially generating large prediction errors) lead to greater attentional capture and improved memory (Butterfield & Metcalfe, 2006).
Neuroscientific work has linked surprising feedback to increases in arousal and the noradrenergic locus coeruleus (LC; Clewett et al., 2014; Mather et al., 2015; Miendlarzewska, Bavelier, & Schwartz, 2016). Our finding that absolute prediction errors influenced subsequent memory is in line with a mechanism (also described in the Introduction) whereby the LC-norepinephrine system responds to salient (surprising) events, and dopamine co-released with norepinephrine from LC neurons strengthens hippocampal memories (Kempadoo et al., 2016; Takeuchi et al., 2016). This proposed mechanism would seem to imply that increases in learning rate (previously linked to norepinephrine release) and enhanced episodic memory (linked to dopamine release) should be correlated across trials, given the hypothesized common cause of LC activation. However, we found that increases in learning rate were uncorrelated with enhanced memory, suggesting that the actual mechanism may involve additional (or different) steps from the one described above.
In our task, learning rate not only increased with the magnitude of prediction error, but also changed with the riskiness of the environment. In line with our results, recent work shows that learning rate scales inversely with reward variance, with higher learning rates in lower variance contexts (Diederen & Schultz, 2015; Diederen et al., 2016). Greater sensitivity to the same magnitude prediction errors in a low versus a high-variance environment demonstrates adaptation to reward statistics, where in a low-risk context, even small prediction errors are more relevant to learning than they would be when there is greater reward variance. This heightened sensitivity to unexpected rewards in the low-risk environment, however, was not associated with improved episodic memory in any of our experiments. In fact, in Experiment 3, we found that memory was better for items experienced in the high-risk context, even when controlling for the magnitude of trial-by-trial reward prediction errors. The opposing effects of risk on learning rate and episodic memory again suggest distinct underlying mechanisms, in agreement with work characterizing learning and memory systems as separate and even antagonistic (Foerde et al., 2012; Wimmer et al., 2014).
To explain the beneficial effect of high-risk environments on episodic memory, we hypothesized that better memory for large-prediction-error events could potentially “spill over” to surrounding items, in line with work showing that inducing an “encoding” state (such as through the presentation of novel items) introduces a lingering bias to encode subsequent items (Duncan & Shohamy, 2016; Duncan et al., 2012). These effects, however, did not explain how risk context modulated memory in our task, as we did not find prediction error events to additionally improve memory for adjacent items. Instead, we speculate that this context effect is due to improved encoding when in a putatively more aroused state, although future studies should more directly characterize the link between arousal and enhanced memory in risky environments.
Finally, we did not find effects of absolute prediction error or risk context on preferences in a later choice test. It remains, however, to be determined whether memories enhanced by large prediction errors may still bias decisions by prioritizing which experiences are sampled or reinstated during decision making.
In conclusion, we show that surprisingly large or small rewards and high-risk contexts improve memory, revealing that prediction errors and risk modulate episodic memory. We further demonstrated that absolute prediction errors have dissociable effects on learning rate and memory, pointing to separate influences on incremental learning and episodic memory processes.
Supplementary Material
Acknowledgments
This work was supported by the Ellison Foundation (Y.N.), grant R01MH098861 from the National Institute for Mental Health (Y.N.), grant W911NF-14-1-0101 from the Army Research Office (Y.N.), and the National Science Foundation’s Graduate Research Fellowship Program (N.R.).
References
- Adcock RA, Thangavel A, Whitfield-Gabrieli S, Knutson B, Gabrieli JDE. Reward-Motivated Learning: Mesolimbic Activation Precedes Memory Formation. Neuron. 2006;50(3):507–517. doi: 10.1016/j.neuron.2006.03.036. [DOI] [PubMed] [Google Scholar]
- Bates D, Maechler M, Bolker B, Walker S, Christensen RHB, Singmann H, … Grothendieck G. Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software. 2015;67(1):1–48. https://doi.org/10.18637/jss.v067.i01. [Google Scholar]
- Behrens TEJ, Woolrich MW, Walton ME, Rushworth MFS. Learning the value of information in an uncertain world. Nature Neuroscience. 2007;10(9):1214–21. doi: 10.1038/nn1954. [DOI] [PubMed] [Google Scholar]
- Biele G, Erev I, Ert E. Learning, risk attitude and hot stoves in restless bandit problems. Journal of Mathematical Psychology. 2009;53:155–167. doi: 10.1016/j.jmp.2008.05.006. [DOI] [Google Scholar]
- Butterfield B, Mangels JA. Neural correlates of error detection and correction in a semantic retrieval task. Cognitive Brain Research. 2003;17(3):793–817. doi: 10.1016/s0926-6410(03)00203-9. Retrieved from http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=14561464. [DOI] [PubMed] [Google Scholar]
- Butterfield B, Metcalfe J. Errors committed with high confidence are hypercorrected. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27(6):1491–1494. doi: 10.1037/0278-7393.27.6.1491. [DOI] [PubMed] [Google Scholar]
- Butterfield B, Metcalfe J. The correction of errors committed with high confidence. Metacognition and Learning. 2006;1(1):69–84. doi: 10.1007/s11409-006-6894-z. [DOI] [Google Scholar]
- Clewett D, Schoeke A, Mather M. Locus coeruleus neuromodulation of memories encoded during negative or unexpected action outcomes. Neurobiology of Learning and Memory. 2014;111:65–70. doi: 10.1016/j.nlm.2014.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diederen KMJ, Schultz W. Scaling prediction errors to reward variability benefits error-driven learning in humans. Journal of Neurophysiology. 2015;114:1628–1640. doi: 10.1152/jn.00483.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diederen KMJ, Spencer T, Vestergaard MD, Fletcher PC, Schultz W. Adaptive Prediction Error Coding in the Human Midbrain and Striatum Facilitates Behavioral Adaptation and Learning Efficiency. Neuron. 2016;90:1127–1138. doi: 10.1016/j.neuron.2016.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Difallah DE, Catasta M, Demartini G, Ipeirotis PG, Cudré-Mauroux P. The Dynamics of Micro-Task Crowdsourcing: The Case of Amazon MTurk. Proceedings of the 24th International Conference on World Wide Web; Republic and Canton of Geneva, Switzerland: International World Wide Web Conferences Steering Committee; 2015. pp. 238–247. [DOI] [Google Scholar]
- DuBrow S, Davachi L. The influence of context boundaries on memory for the sequential order of events. Journal of Experimental Psychology: General. 2013;142(4):1277–86. doi: 10.1037/a0034024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan KD, Sadanand A, Davachi L. Memory’s Penumbra: Episodic Memory Decisions Induce Lingering Mnemonic Biases. Science. 2012;337 doi: 10.1126/science.1221936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan KD, Shohamy D. Memory States Influence Value-Based Decisions. Journal of Experimental Psychology: General. 2016;145(9):3–9. doi: 10.1037/xge0000231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fazio LK, Marsh EJ. Surprising feedback improves later memory. Psychonomic Bulletin & Review. 2009;16(1):88–92. doi: 10.3758/PBR.16.1.88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fazio LK, Marsh EJ. Correcting False Memories. Psychological Science. 2010;21(6):801–803. doi: 10.1177/0956797610371341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foerde K, Braun EK, Shohamy D. A Trade-Off between Feedback-Based Learning and Episodic Memory for Feedback Events: Evidence from Parkinson’s Disease. Neurodegenerative Diseases. 2012;11(2):93–101. doi: 10.1159/000342000. [DOI] [PubMed] [Google Scholar]
- Gershman SJ, Niv Y. Perceptual estimation obeys Occam’s razor. Frontiers in Psychology. 2013;4:623. doi: 10.3389/fpsyg.2013.00623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greve A, Cooper E, Kaula A, Anderson MC, Henson R. Does prediction error drive one-shot declarative learning? Journal of Memory and Language. 2017;94:149–165. doi: 10.1016/j.jml.2016.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu M, Krajbich I, Zhao C, Camerer CF. Neural Response to Reward Anticipation under Risk Is Nonlinear in Probabilities. Journal of Neuroscience. 2009;29(7):2231–2237. doi: 10.1523/JNEUROSCI.5296-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ipeirotis PG. Analyzing the Amazon Mechanical Turk Marketplace. XRDS. 2010;17(2):16–21. doi: 10.1145/1869086.1869094. [DOI] [Google Scholar]
- Kahneman D, Tversky A. An analysis of decision under risk. Econometrica. 1979;47(2):263–292. Retrieved from http://www.jstor.org/stable/1914185. [Google Scholar]
- Kempadoo KA, Mosharov EV, Choi SJ, Sulzer D, Kandel ER. Dopamine release from the locus coeruleus to the dorsal hippocampus promotes spatial learning and memory. Proceedings of the National Academy of Sciences. 2016;113(51) doi: 10.1073/pnas.1616515114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludvig EA, Madan CR, Spetch ML. Extreme Outcomes Sway Risky Decisions from Experience. Journal of Behavioral Decision Making. 2014;27:146–156. doi: 10.1002/bdm.1792. [DOI] [Google Scholar]
- Madan CR, Ludvig EA, Spetch ML. Remembering the best and worst of times: Memories for extreme outcomes bias risky decisions. Psychonomic Bulletin & Review. 2014;21(3):629–636. doi: 10.3758/s13423-013-0542-9. [DOI] [PubMed] [Google Scholar]
- Mather M, Clewett D, Sakaki M, Harley CW. Norepinephrine ignites local hot spots of neuronal excitation: How arousal amplifies selectivity in perception and memory. Behavioral and Brain Sciences. 2015;1 doi: 10.1017/S0140525X15000667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuire JT, Nassar MR, Gold JI, Kable JW. Functionally Dissociable Influences on Learning Rate in a Dynamic Environment. Neuron. 2014;84(4):870–881. doi: 10.1016/j.neuron.2014.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miendlarzewska EA, Bavelier D, Schwartz S. Influence of reward motivation on human declarative memory. Neuroscience and Biobehavioral Reviews. 2016;61:156–176. doi: 10.1016/j.neubiorev.2015.11.015. [DOI] [PubMed] [Google Scholar]
- Murty VP, Adcock RA. Enriched encoding: Reward motivation organizes cortical networks for hippocampal detection of unexpected events. Cerebral Cortex. 2014;24(8):2160–2168. doi: 10.1093/cercor/bht063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassar MR, Rumsey KM, Wilson RC, Parikh K, Heasly B, Gold JI. Rational regulation of learning dynamics by pupil-linked arousal systems. Nature Neuroscience. 2012;15(7):1040–1046. doi: 10.1038/nn.3130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niv Y, Edlund JA, Dayan P, O’Doherty JP. Neural Prediction Errors Reveal a Risk-Sensitive Reinforcement-Learning Process in the Human Brain. Journal of Neuroscience. 2012;32(2):551–562. doi: 10.1523/JNEUROSCI.5498-10.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Doherty JP, Dayan P, Friston K, Critchley H, Dolan RJ. Temporal difference models and reward-related learning in the human brain. Neuron. 2003;38(2):329–337. doi: 10.1016/S0896-6273(03)00169-7. [DOI] [PubMed] [Google Scholar]
- Pearce JM, Hall G. A Model for Pavlovian Learning: Variations in the Effectiveness of Conditioned But Not of Unconditioned Stimuli. Psychological Review. 1980;87(6):532–552. [PubMed] [Google Scholar]
- Pollack I, Norman DA. A non-parametric analysis of recognition experiments. Psychonomic Science. 1964;1(1–12):125–126. doi: 10.3758/BF03342823. [DOI] [Google Scholar]
- Sara SJ. The locus coeruleus and noradrenergic modulation of cognition. Nature Reviews Neuroscience. 2009;10 doi: 10.1038/nrn2573. [DOI] [PubMed] [Google Scholar]
- Takeuchi T, Duszkiewicz AJ, Sonneborn A, Spooner PA, Yamasaki M, Watanabe M, … Morris RGM. Locus coeruleus and dopaminergic consolidation of everyday memory. Nature. 2016;537(7620):1–18. doi: 10.1038/nature19325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobler PN, Fiorillo CD, Schultz W. Adaptive Coding of Reward Value by Dopamine Neurons. Science. 2005;307(5715):1642–1645. doi: 10.1126/science.1105370. [DOI] [PubMed] [Google Scholar]
- Weber EU, Blais AR, Betz NE. A domain-specific risk-attitude scale: measuring risk perceptions and risk behaviors. Journal of Behavioral Decision Making. 2002;15(4):263–290. doi: 10.1002/bdm.414. [DOI] [Google Scholar]
- Wimmer GE, Braun EK, Daw ND, Shohamy D. Episodic memory encoding interferes with reward learning and decreases striatal prediction errors. The Journal of Neuroscience. 2014;34(45):14901–14912. doi: 10.1523/JNEUROSCI.0204-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.