Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Jul 20;12(8):8540–8546. doi: 10.1021/acsnano.8b04080

Statistical Analysis of Scanning Fluorescence Correlation Spectroscopy Data Differentiates Free from Hindered Diffusion

Falk Schneider †, Dominic Waithe ‡,⊥, B Christoffer Lagerholm ‡, Dilip Shrestha †, Erdinc Sezgin †, Christian Eggeling †,‡,§, Marco Fritzsche †,∥,*
PMCID: PMC6117752  PMID: 30028588

Abstract

graphic file with name nn-2018-04080r_0003.jpg

Cells rely on versatile diffusion dynamics in their plasma membrane. Quantification of this often heterogeneous diffusion is essential to the understanding of cell regulation and function. Yet such measurements remain a major challenge in cell biology, usually due to low sampling throughput, a necessity for dedicated equipment, sophisticated fluorescent label strategies, and limited sensitivity. Here, we introduce a robust, broadly applicable statistical analysis pipeline for large scanning fluorescence correlation spectroscopy data sets, which uncovers the nanoscale heterogeneity of the plasma membrane in living cells by differentiating free from hindered diffusion modes of fluorescent lipid and protein analogues.

Keywords: Brownian, scanning FCS, free and trapped diffusion, actin cytoskeleton, hindered diffusion dynamics, diffusion modes

Quantification of molecule diffusion dynamics in the plasma membrane of living cells is essential for the understanding of their function.1−3 Most fluorescence-based methodologies for examining the heterogeneity of lipid and protein diffusion dynamics, such as single-particle tracking,4,5 fluorescence recovery after photobleaching,6,7 or fluorescence correlation spectroscopy (FCS)1,2 and their advancements, especially super-resolution stimulated emission depletion (STED) FCS,8−10 either necessitate specialized hardware, sophisticated fluorescence labeling, or constrain themselves to quantification with limited spatial and temporal sensitivity. Together, these issues remain to pose practical challenges for the quantification of diffusion dynamics in living cells.

Important advancements in fluorescence acquisition and/or analysis pipelines drew attention to the power of simple measurement equipment like total internal reflection setups, which can be used for camera-based FCS variants.11−13 For instance, for the disclosure of large spatial diffusion maps, the methodology of image mean square displacement (iMSD) analysis provides robust detection of free Brownian and non-Brownian hindered diffusion modes.14,15 Unfortunately, these camera-based acquisitions often limit the accessible diffusion time scales.16

Yet, scanning FCS (sFCS) measurements acquired with confocal laser scanning microscopes offer a good compromise in terms of equipment, adaptability (e.g., combination with iMSD), and high spatiotemporal sensitivity with statistical accuracy and flexibility by combining conventional instrumentation and standard fluorescence labeling.14,17−19 Specifically, the large number of simultaneously acquired FCS curves (>50 curves) and well-established fitting and bleaching correction procedures ensure high confidence in the data analysis.20−22 Although sFCS measurements are often performed in biological membranes at the equatorial plane of cells or vesicles,23,24 they can, in principle, flexibly be applied anywhere in the cell volume.19,22,25 From the biological point of view, it is important to differentiate three main parameters for the complete characterization of molecular diffusion dynamics: the total number of diffusion processes, the fraction of molecules contributing to each diffusion mode, and their respective diffusion time scales. Such a parametrization allows one to infer whether molecules undergo free Brownian or hindered diffusion, revealing deeper insights into cellular signaling and function. For example, during the activation of immune cells, well-defined fractions of immune receptors are thought to form receptor clusters through transient trapping of their intracellular domains.29,30 In turn, certain lipids such as 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE) and the transferrin receptor have been shown to undergo hindered hop diffusion within the dense cortical actin network beneath the cell membrane.4,25−27 Conventional sFCS recordings theoretically contain all the kinetic information on such hindered diffusion of fluorescent particles, including hop and trapped diffusion modes within the observed probe ensemble. However, this information is mostly lost due to averaging during the analysis process because, traditionally, only the average diffusion coefficients and their standard errors are computed, assuming a normal distribution of the sFCS data sets. Consequently, conventional sFCS quantification analysis does not usually allow for the direct disclosure of diffusion modes, such as for differentiating hindered from free Brownian diffusion, precluding perhaps the discovery of lipid or protein clustering, hopping, or trapping.

Here, we introduce a pipeline for the statistical analysis of sFCS data recorded by confocal microscopy, yielding the systematic and robust quantification of diffusion modes in living cells. The protocol allows a systematic mathematical characterization of the distribution of sFCS diffusion data, involving fitting analysis and the calculation of the biological-relevant parameters, and a quantitative evaluation of the results using weighted fitting residuals and maximum likelihood estimations. Applying this framework to the free and non-Brownian diffusion dynamics of lipids and glycosylphosphatidylinositol (GPI)-anchored proteins demonstrates the power of the method and allows a comprehensive characterization of well-known molecular particle diffusion in computer-simulated data sets, supported lipid bilayers (SLBs), and the plasma membrane of living cells. Combining this analysis pipeline with conventional confocal sFCS experiments may offer alternative avenues for systematic studies of the mechanisms by which living cells adjust their molecular membrane dynamics to their physiological needs.

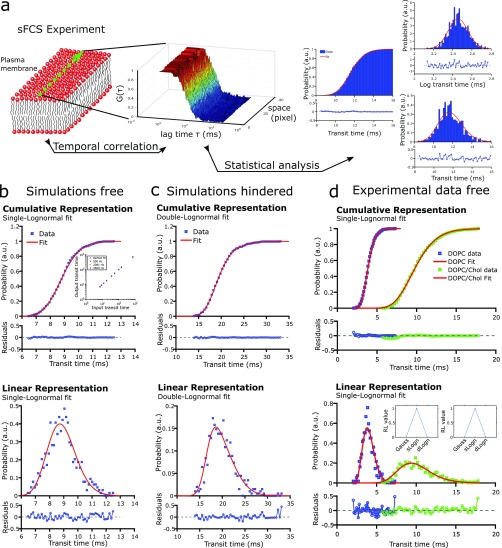
Analysis of sFCS experiments conventionally involves two steps: (i) simultaneous acquisition of a multitude of FCS curves acquired by repeatedly scanning few-micrometer-long lines, and (ii) obtaining the transit times of the diffusing molecules through the observation spot from fitting the respective time-correlated data for each pixel of the line to specific diffusion models, yielding a value of an average transit time and a standard error. To improve sFCS analysis, we aimed to examine the full kinetic information provided by all the correlation curves. Consequently, our strategy comprised a third step, wherein we computed and analyzed the transit time histograms to extract further information on the diffusion modes (Figure 1a), exploiting the statistical power of large ensemble measurements independent of local spatial heterogeneities.

Figure 1.

Figure 1

Open in a new tab

(a) Schematic of the experiment principle. (Left) sFCS data are recorded by scanning the laser (green dots) along a micrometer line in the membrane (lipids with red headgroups and gray tails), thereby creating (through temporal correlations) FCS data (decaying curves G(τ) from red to blue against correlation time τ) for each pixel along the line (space). (Right) All FCS data are fitted to obtain values of transit times through the observation spot, in which histograms (blue, probability distributions; right, cumulative; top right, logarithmic values; bottom right, linear representation) are fitted by the LogNorm (red line), with weighted residuals in the respective bottom panels. (b–d) Cumulative (top panels) and linear (bottom panels) transit time histograms (blue) and LogNorm fits (red, single- or double-LogNorm fit as labeled) with weighted residuals (respective bottom panels) for simulated sFCS data of (b) freely (input: D = 0.80 μm2/s, recovered D = 0.82 μm2/s) and (c) hindered diffusion (input: Dfree = 0.80 μm2/s, Dtrapped = 0.1 × 10–9 μm2/s, and ptrap_on = ptrap_off = 0.001, recovered D1 = 0.39 μm2/s, D2 = 0.31 μm2/s, and A = 0.73), and (d) for experimental data of DPPE-Abberior STAR Red in pure DOPC (blue; μ = 4.2 ms, D = 2.45 μm2/s) and DOPC/Chol (green; μ = 9.7 ms, D = 1.1 μm2/s) SLBs (see Supporting Information Table S1). Inset (b): Fit results μ of the LogNorm fits (output values) against the transit times implemented in the sFCS simulations of free diffusion, indicating an accurate recovery of values. Insets (d): Relative likelihood (RL) values of Gaussian (Gauss) and single (sLogn) and double (dLogn) LogNorm fits to the experimental data of pure DOPC (left) and DOPC/Chol (right) SLBs, indicating accurate fitting by a single-LogNorm model.

Results and Discussion

We first set out to statistically evaluate the distribution of transit time values obtained from a large ensemble of computer-simulated sFCS data (see the Methods section and the Supporting Information). Consistent with previous findings, the histograms over a wide range of transit time values displayed non-Gaussian distributions (Supporting Information Figure S1a). The broadness and asymmetry toward longer transit times of the distribution depended on the magnitude of the measured transit time values, because the error of the measurements increased exponentially with the transit times, accompanied by respective changes in the signal-to-noise and fitting standard deviation (Supporting Information Figure S1b,c). Specifically, slow diffusing particles experienced larger errors than faster particles, primarily depending on the finite scanning frequency but also on other factors such as the finite acquisition time. To this end, the total acquisition time determined the number of points for correlation, limiting the convergence of the corresponding FCS curves.20 Computing the logarithm of the corresponding transit time histograms revealed a normal distribution, indicating, together with exponentially distributed signal-to-noise and fitting standard deviation, that sFCS data were log-normally distributed (Figure 1a and Supporting Information Figure S1b,c). The variance of the distributions increased with increasing transit time (Supporting Information Figure S1a).

In the following, we exploited the mathematical properties of a log-normal distribution, hereafter referred to as LogNorm. Statistical analysis of the sFCS data was achieved by fitting the cumulative, logarithmic, and linear representation of the histograms using analytical forms of the LogNorm (Figure 1a and Supporting Information Figure S2a). LogNorm functions are well-defined through their two characteristic parameters, μ and σ, which can mathematically be related to the mean and standard deviation of a normal distribution in its logarithmic representation. Consequently, the analysis involves the fitting of three representations to obtain two free parameters. Large ensemble acquisitions of sFCS curves (>400 per condition) ensured sufficient bin counts (30–80 bins). The bins of a given transit time histogram reflected the number of fitting points. Empirically, we found that the LogNorm fitting accurately recovered the input diffusion parameters in the computer simulations of free diffusion over a wide range of transit times (inset of Figure 1b and Supporting Information Figure S2b–d).

Next, we introduced hindered trapped diffusion (transient halts in the diffusion path; see stochastic trapping model in the Methods section and Supporting Information Figure S3a,b) as a second process in addition to free diffusion in the computer simulations. Using our statistical analysis, we found deviations from the single-LogNorm behavior as indicated by the weighted residuals. These transit time histograms were accurately fitted with a double-LogNorm fitting model in all three representations (Figure 1c and Supporting Information Figure S3c). Consistently, the statistical analysis indeed revealed two LogNorm transit time histograms reporting on free Brownian and non-Brownian trapped diffusion.

To confirm the findings of the computer simulations, we further measured the diffusion of fluorescently labeled lipids in SLBs. As expected, analysis of the diffusion dynamics of a fluorescent DPPE analogue (1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine labeled with Abberior STAR Red) in a fluid SLB of DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine) accurately detected free diffusion (i.e., best representation of the data by a single-LogNorm fit), with an overall decrease in mobility depending on the cholesterol content (Figure 1d). In contrast to the computer simulations, we did not have any prior knowledge of the diffusion modes. We hence complemented our weighted residual evaluation for the quality of the fitting and model selection with maximum likelihood estimations, employing the Bayesian information criterion (from which we could calculate the relative likelihood (RL) value for any given model; see the Methods section and Supporting Information Figure S4a).33−35 Consistent with the weighted residuals, the RL values confirmed free diffusion for the lipids in the SLB by best representing the data with a single-LogNorm fit (insets in Figure 1d and Supporting Information Figure S4a and Table S1). Note, in the following, the most likely model (RL value equals 1) was selected as the appropriate fitting model. The weighted residuals were employed to evaluate the quality of the single- or double-LogNorm fits in all experiments.

Next, we investigated the well-described nanoscale diffusion dynamics of fluorescent lipid analogues in living Ptk2 cells. Consistent with previous reports using advanced FCS technologies such as super-resolution STED-FCS,10,26,28,36,37 the phospholipid analogue PE (Atto647N-DPPE) diffused freely, and the sphingomyelin (SM) analogue (Atto647N-SM) showed hindered trapped diffusion, as revealed by either single- and double-LogNorm fits to the transit time distributions (Figure 2a,b and Supporting Information Figure S4b), respectively. Trapping sites of SM were also illustrated by the occurrence of the heterogeneities in the unprocessed sFCS data (correlation carpets) of SM compared to PE (Figure 2a,b).26,28 Consequently, the statistical analysis of large ensemble sFCS data acquired with a conventional confocal microscope yielded the detection of a small fraction of molecules undergoing trapped diffusion.

Figure 2.

Figure 2

Open in a new tab

Correlation carpets (left panels, decaying curves G(τ) from red to blue for each pixel against correlation lag time τ) and (right panels) cumulative and linear transit time histograms (blue, as labeled) with LogNorm fits (red, single- or double-LogNorm fit as labeled, best fit in red and respective inaccurate fit in magenta and brackets) with respective weighted residuals (respective bottom panels) for experimental data of (a) DPPE, (b) SM, and (c) GPI-GFP in live Ptk2 cells and (d) GPI-GFP in Ptk2-cell-derived giant plasma membrane vesicles (GPMVs) (see Supporting Information and Table S2 for fitted parameters).

To further demonstrate the applicability of our approach, we examined the diffusion of GPI-anchored proteins (GPI-AP) fluorescently labeled with green fluorescent protein (GFP) and compared the results of our sFCS analysis to those from the diffusion dynamics of the GPI-APs in giant plasma membrane vesicles (GPMVs). While GPI-AP diffusion appeared to be trapped in the cells, likely due to the interactions with the cortical actin cytoskeleton, it was seemingly free in actin-depleted GPMVs (Figure 2c,d and Supporting Information Figure S4c) as previously demonstrated.31 The statistical analysis was therefore able to detect free and trapped diffusion of GFP-tagged GPI-APs in the cell membrane.

Finally, we explored the ability of our analysis pipeline to detect hindered hop diffusion. To this end, we produced spatial random mesh maps with an average boundary distance L in the simulations (Supporting Information Figure S5a) mimicking the cortical actin network beneath the membrane. The particles were able to undergo free motion within the boundaries of the individual meshes and random hop transitions for crossing the confinement barriers with the probability phop (Supporting Information Figure S5a). To fully characterize the motion conditions of the particles, we calculated the phase diagram of those particles experiencing hop diffusion for a range of hopping probabilities and characteristic average length scale of mesh sizes for a given input diffusion coefficient (Supporting Information Figure S5b,c). Consistent with the previous hindered trapped diffusion simulations, the hop diffusion simulations revealed two processes in the transit time histograms, with the second process dominant on short time scales. Statistical analysis involving fitting and the maximum likelihood estimations of the transit time histogram uncovered a combination of a LogNorm and an exponential probability distribution function reporting on the combination of free Brownian diffusion and a random hop diffusion process, respectively (Supporting Information Figure S5d). Note that the same model selection criteria using the RL values were applied (Supporting Information). Consequently, the statistical analysis of large ensemble sFCS data also allowed the detection of a fraction of molecules undergoing hop diffusion.

Conclusions

In this work, we highlighted how different diffusion dynamics of lipids and proteins in the plasma membrane of living cells can be disclosed using conventional confocal microscopy. Revisiting well-established experiments, we demonstrated how this statistical analysis pipeline of scanning FCS data systematically and robustly differentiates free from hindered diffusion. Whereas single-LogNorm quantifications allowed the determination of free Brownian diffusion, double-LogNorm or LogNorm and exponential analysis enabled the detection of hindered trapped and hop diffusion dynamics.

In conclusion, the statistical analysis provides a broadly applicable methodology that revealed findings, which could previously only be characterized by dedicated equipment and experimental procedures such as spot variation or STED-FCS. Expanding the statistical analysis further to quantification of full reaction diffusion dynamics including transient binding and molecular cluster formation might offer one technique for a more complete characterization of lipid and protein dynamics in the near future. For example, reaction processes such as transient binding events of transmembrane proteins to associated structures such as the actin cytoskeleton or the extracellular matrix could also be quantified with the analysis pipeline. In light of the broad applicability, straightforward implementation, usage of standard fluorescent dyes at turn-key microscopes, we envisage statistical sFCS analysis to become an important tool for characterizing nanoscale heterogeneity of diffusion dynamics in the plasma membrane of living cells.

Methods

Preparation of Supported Lipid Bilayers

SLBs were prepared by spin-coating as described elsewhere.31

A solution of 1 mg/mL total lipid concentration (either 100% DOPC (Avanti Polar Lipids, USA) or 50% DOPC/50% cholesterol (Avanti Polar Lipids)) both doped with DPPE-Abberior STAR Red (Abberior, Germany) at a weight on weight ratio of 1:2000 in 1:2 methanol/chloroform was spin-coated at 3200 rpm onto a clean 25 mm #1.5 glass coverslip (VWR, UK). The resulting lipid film was hydrated with SLB buffer (150 mM NaCl, 10 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) pH 7.4) and washed multiple times.

Glass coverslips were cleaned using piranha edging (3:2 sulfuric acid/hydrogen peroxide) for 2 h and not stored for longer than a week.

Cell Culture, Labeling, and Plasmid Transfection

Potorous tridactylus epithelial kidney (Ptk2) cells were cultured in DMEM (Sigma-Aldrich, UK) supplemented with 15% fetal bovine serum (Sigma-Aldrich) and 1% l-glutamine (Sigma-Aldrich).

For microscopy experiments, the cells were seeded onto 25 mm glass coverslips and allowed to grow to a confluence of about 75%. For sFCS experiments, the cells were labeled with Atto647N-DPPE or Atto647N-sphingomyelin (AttoTec, Germany) by incubating the cells at a lipid analogue concentration of 0.4 μg/μL in L15 (Sigma-Aldrich) at room temperature for 15 min. After cells were washed twice with L15, the experiments were performed at 37 °C. The diffusion of the lipid analogues in the cellular membrane was measured in the periphery of the cell at its bottom membrane.

Transfections of Ptk2 cells with GPI-anchored green fluorescent protein were performed using Lipofectamine 3000 (Thermo Fisher) according to the manufacturer’s protocol. The GPI-GFP plasmid was obtained from Kai Simons’ Lab (Max Planck Institute of Molecular Cell Biology and Genetics, Dresden, Germany).

Preparations of Giant Plasma Membrane Vesicles

GPMVs from Ptk2 cells were prepared as described previously.31 Cells were allowed to grow to a confluence of about 75%. Cells were washed once with hypotonic (30%) then with 100% GPMV buffer (containing 150 mM NaCl, 10 mM HEPES, 2 mM CaCl2, pH 7.4) and incubated for 3 h in 2 mM dithiothreitol and 25 mM paraformaldehyde at 37 °C. The GPMV-containing supernatant was harvested, and for microscopy, the GPMVs were dropped onto poly-l-lysine (PLL)-coated 25 mm coverslips. PLL coating was performed by incubating the coverslip with 0.01% PLL solution (Sigma-Aldrich) for 1 h at room temperature. The coverslips were washed three times with GPMV buffer. GPMVs were allowed to sink down and equilibrate for 15 min at 37 °C. The diffusion was measured at the top membrane of the GPMVs.

Microscopy

All imaging and sFCS data were acquired on a Zeiss 780 confocal laser scanning microscope (Carl Zeiss, Germany) equipped with a 40× C-Apochromat NA 1.2 W Corr FCS objective (Carl Zeiss). All sFCS experiments were performed using the GaAsP detector (Channel S) in photon counting mode, and the pinhole was set to 1 airy unit. For the GFP experiments, fluorescence was excited using a 488 nm argon laser, and a single 488 dichroic was chosen; for the Atto647N-labeled lipids, the fluorescence was excited using a 633 nm He–Ne laser, and the 488/594/633 MBS was used. sFCS experiments were acquired in line scan mode at a zoom of 40 with maximum time-lapse repetitions at highest scanning speed. These settings resulted in a line of 52 pixels (with a pixel size of 100 nm), a scanning frequency of 2081 Hz, a pixel dwell time of 3.94 μs, and an overall measurement time t of about 47 s. The measurements were saved as .lsm5 files.

Simulations

Computer simulations were performed as Monte Carlo simulations in the programming language Python using the nanosimpy repository on GitHub.20,38 For free Brownian diffusion, we generated random tracks in a box of 2 μm × 8 μm. One hundred particles were randomly distributed, and their movement was simulated with diffusion coefficients D varying from 0.01 to 1.00 μm2/s. The tracks were simulated for t = 45 s with time steps of 3.94 μs (same as the pixel dwell time) using periodic boundary conditions. The scanned line of the sFCS experiments (hereafter referred to as sFCS line) was placed in the center of the simulation box (microns away from the boundaries). The sFCS line consisted of 52 pixels (length of 5.2 μm), where at every time step the molecules were passed through a Gaussian-shaped observation spot (resembling the microscopes’ point spread function) to generate the intensity fluctuations. The full width at half-maximum (FWHM) of the Gaussian-shaped observation spot was set to 200 nm to mimic confocal recordings. sFCS simulations were sampled at 500, 2081, and 3500 Hz. The obtained transit times, τD (from fitting the correlation curves), are related to the diffusion coefficients implemented in the simulations according to the following equation:

graphic file with name nn-2018-04080r_m001.jpg

To demonstrate the capabilities of our statistical analysis approach of sFCS data to identify nanoscale heterogeneous non-Brownian diffusion, we also employed simulations on hindered diffusion modes. For trapped and hop hindered diffusion, we adapted the simulations from point STED-FCS31 to our needs in sFCS. For trapped diffusion, again tracks of 100 molecules for 45 s using time steps of 3.94 μs were created and passed through a Gaussian-shaped observation spot, and sFCS was sampled at 2081 Hz. The stochastic trapping model by molecular complex formation is outlined in Supporting Information Figure S3a. At every time step, diffusing particles were re-evaluated whether they continued free diffusion with a diffusion coefficient of 0.8 μm2/s or trap with a probability ptrap_on and a diffusion coefficient of 0.1 × 10–9 μm2/s, being basically immobile, or discontinued trapping with the probability ptrap_off, respectively. Moreover, to ensure the simulations resembled the trapping behavior (which was previously only recovered using super-resolved STED-FCS recordings), we additionally to the confocal recordings (200 nm FWHM observation spot) simulated STED recordings with an observation spot with a FWHM of 80 nm and determined the diffusion coefficients Dconf and DSTED from fitting the confocal and STED-FCS data, respectively. Notably, the ratio of DSTED and Dconf, the so-called Drat value, equals 1 for free diffusion and is smaller than 1 for hindered trapped diffusion and greater than 1 for hindered hop diffusion. Supporting Information Figure S3b shows a parameter estimation of the trapping probabilities (with ptrap_on = ptrap_off) using the Drat value.

For the simulations of hindered hop diffusion, we adapted the previously described point STED-FCS simulations for sFCS.31,32 To this end, we calculated a random meshwork with distinct barriers using Voronoi transformation of randomly seeded points. This spatial hopping map was superimposed with the diffusion simulation box and the sFCS measurement (compare Supporting Information Figure S5a). Particles at the boundary had a given probability (phop) to transition to the neighboring compartment or to reside in the same mesh compartment. For a diffusion coefficient of D = 0.2 μm2/s, we explored the parameter space employing shorter (30 s) scanning STED-FCS measurements with a fwhm of 40 nm in STED (yielding Drat) with 100 particles in the simulation. Ultimately, we simulated hop hindered diffusion with phop = 0.01, with a characteristic length scale of the mesh size of L = 100 nm (yielding a Voronoi region size given as √area of 186 nm) of 150 particles for 45 s at a scanning frequency of 2081 Hz and a pixel dwell time of 3.94 μs. The respective intensity carpets from the simulations were outputted as .tiff files.

Acknowledgments

The WIMM is acknowledged for infrastructure support. We thank the Wolfson Imaging Centre Oxford and the MICRON Advanced Bioimaging Unit Oxford (supported by the Wellcome Trust Strategic Award 091911) for access to equipment and assistance with data acquisition and analysis. The work was supported by the Wolfson Foundation, the Medical Research Council (MRC, Grant No. MC UU 12010/unit programmes G0902418 and MC UU 12025), MRC/BBSRC/EPSRC (Grant No. MR/K01577X/1), and internal University of Oxford funding (John Fell Fund).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.8b04080.

  • Detailed description of the analysis of sFCS data: data fitting and statistical analysis; supporting Figures S1–S5 and Tables S1 and S2 (PDF)

Author Contributions

M.F. designed and supervised the research. F.S. planned and executed the experiments and analysis. D.W. assisted with writing the computer simulations. D.S., B.C.L., and E.S. helped with experiments and C.E. with supervision. F.S. and M.F. wrote the manuscript.

The authors declare no competing financial interest.

Supplementary Material

nn8b04080_si_001.pdf (12.9MB, pdf)

References

  1. Fahey P.; Koppel D.; Barak L.; Wolf D.; Elson E.; Webb W. Lateral Diffusion in Planar Lipid Bilayers. Science (Washington, DC, U. S.) 1977, 195, 305–306. 10.1126/science.831279. [DOI] [PubMed] [Google Scholar]
  2. Schwille P.; Korlach J.; Webb W. W. Fluorescence Correlation Spectroscopy with Single-Molecule Sensitivity on Cell and Model Membranes. Cytometry 1999, 36, 176–182. . [DOI] [PubMed] [Google Scholar]
  3. Kusumi A.; Nakada C.; Ritchie K.; Murase K.; Suzuki K.; Murakoshi H.; Kasai R. S.; Kondo J.; Fujiwara T. Paradigm Shift of the Plasma Membrane Concept from the Two-Dimensional Continuum Fluid to the Partitioned Fluid: High-Speed Single-Molecule Tracking of Membrane Molecules. Annu. Rev. Biophys. Biomol. Struct. 2005, 34, 351–378. 10.1146/annurev.biophys.34.040204.144637. [DOI] [PubMed] [Google Scholar]
  4. Schmidt T.; Schutz G. J.; Baumgartner W.; Gruber H. J.; Schindler H. Imaging of Single Molecule Diffusion. Proc. Natl. Acad. Sci. U. S. A. 1996, 93, 2926–2929. 10.1073/pnas.93.7.2926. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Fujiwara T.; Ritchie K.; Murakoshi H.; Jacobson K.; Kusumi A. Phospholipids Undergo Hop Diffusion in Compartmentalized Cell Membrane. J. Cell Biol. 2002, 157, 1071–1081. 10.1083/jcb.200202050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Schlessinger J.; Axelrod D.; Koppel D.; Webb W.; Elson E. Lateral Transport of a Lipid Probe and Labeled Proteins on a Cell Membrane. Science (Washington, DC, U. S.) 1977, 195, 307–309. 10.1126/science.556653. [DOI] [PubMed] [Google Scholar]
  7. Fritzsche M.; Charras G. Dissecting Protein Reaction Dynamics in Living Cells by Fluorescence Recovery after Photobleaching. Nat. Protoc. 2015, 10, 660–680. 10.1038/nprot.2015.042. [DOI] [PubMed] [Google Scholar]
  8. Wawrezinieck L.; Rigneault H.; Marguet D.; Lenne P.-F. Fluorescence Correlation Spectroscopy Diffusion Laws to Probe the Submicron Cell Membrane Organization. Biophys. J. 2005, 89, 4029–4042. 10.1529/biophysj.105.067959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hebert B.; Costantino S.; Wiseman P. W. Spatiotemporal Image Correlation Spectroscopy (STICS) Theory, Verification, and Application to Protein Velocity Mapping in Living CHO Cells. Biophys. J. 2005, 88, 3601–3614. 10.1529/biophysj.104.054874. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Eggeling C.; Ringemann C.; Medda R.; Schwarzmann G.; Sandhoff K.; Polyakova S.; Belov V. N.; Hein B.; von Middendorff C.; Schönle A.; Hell S. W. Direct Observation of the Nanoscale Dynamics of Membrane Lipids in a Living Cell. Nature 2009, 457, 1159–1162. 10.1038/nature07596. [DOI] [PubMed] [Google Scholar]
  11. Huang H.; Simsek M. F.; Jin W.; Pralle A. Effect of Receptor Dimerization on Membrane Lipid Raft Structure Continuously Quantified on Single Cells by Camera Based Fluorescence Correlation Spectroscopy. PLoS One 2015, 10, e0121777. 10.1371/journal.pone.0121777. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Petersen N. O.; Höddelius P. L.; Wiseman P. W.; Seger O.; Magnusson K. E. Quantitation of Membrane Receptor Distributions by Image Correlation Spectroscopy: Concept and Application. Biophys. J. 1993, 65, 1135–1146. 10.1016/S0006-3495(93)81173-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Sankaran J.; Manna M.; Guo L.; Kraut R.; Wohland T. Diffusion, Transport, and Cell Membrane Organization Investigated by Imaging Fluorescence Cross-Correlation Spectroscopy. Biophys. J. 2009, 97, 2630–2639. 10.1016/j.bpj.2009.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Di Rienzo C.; Gratton E.; Beltram F.; Cardarelli F. Fast Spatiotemporal Correlation Spectroscopy to Determine Protein Lateral Diffusion Laws in Live Cell Membranes. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 12307–12312. 10.1073/pnas.1222097110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Moens P. D. J.; Digman M. A.; Gratton E. Modes of Diffusion of Cholera Toxin Bound to GM1 on Live Cell Membrane by Image Mean Square Displacement Analysis. Biophys. J. 2015, 108, 1448–1458. 10.1016/j.bpj.2015.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Sankaran J.; Bag N.; Kraut R. S.; Wohland T. Accuracy and Precision in Camera-Based Fluorescence Correlation Spectroscopy Measurements. Anal. Chem. 2013, 85, 3948–3954. 10.1021/ac303485t. [DOI] [PubMed] [Google Scholar]
  17. Ruan Q.; Cheng M. A.; Levi M.; Gratton E.; Mantulin W. W. Spatial-Temporal Studies of Membrane Dynamics: Scanning Fluorescence Correlation Spectroscopy (SFCS). Biophys. J. 2004, 87, 1260–1267. 10.1529/biophysj.103.036483. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ries J.; Chiantia S.; Schwille P. Accurate Determination of Membrane Dynamics with Line-Scan FCS. Biophys. J. 2009, 96, 1999–2008. 10.1016/j.bpj.2008.12.3888. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Wachsmuth M.; Waldeck W.; Langowski J. Anomalous Diffusion of Fluorescent Probes inside Living Cell Investigated by Spatially-Resolved Fluorescence Correlation Spectroscopy. J. Mol. Biol. 2000, 298, 677–689. 10.1006/jmbi.2000.3692. [DOI] [PubMed] [Google Scholar]
  20. Waithe D.; Schneider F.; Chojnacki J.; Clausen M. P.; Shrestha D.; de la Serna J. B.; Eggeling C. Optimized Processing and Analysis of Conventional Confocal Microscopy Generated Scanning FCS Data. Methods 2018, 140-141, 62. 10.1016/j.ymeth.2017.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Ries J.; Schwille P. Studying Slow Membrane Dynamics with Continuous Wave Scanning Fluorescence Correlation Spectroscopy. Biophys. J. 2006, 91, 1915–1924. 10.1529/biophysj.106.082297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Baum M.; Erdel F.; Wachsmuth M.; Rippe K. Retrieving the Intracellular Topology from Multi-Scale Protein Mobility Mapping in Living Cells. Nat. Commun. 2014, 5, 4494. 10.1038/ncomms5494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Dunsing V.; Mayer M.; Liebsch F.; Multhaup G.; Chiantia S. Direct Evidence of Amyloid Precursor–like Protein 1 Trans Interactions in Cell–cell Adhesion Platforms Investigated via Fluorescence Fluctuation Spectroscopy. Mol. Biol. Cell 2017, 28, 3609–3620. 10.1091/mbc.e17-07-0459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Dörlich R. M.; Chen Q.; Niklas Hedde P.; Schuster V.; Hippler M.; Wesslowski J.; Davidson G.; Nienhaus G. U. Dual-Color Dual-Focus Line-Scanning FCS for Quantitative Analysis of Receptor-Ligand Interactions in Living Specimens. Sci. Rep. 2015, 5, 10149. 10.1038/srep10149. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Digman M. A.; Gratton E. Lessons in Fluctuation Correlation Spectroscopy. Annu. Rev. Phys. Chem. 2011, 62, 645–668. 10.1146/annurev-physchem-032210-103424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Honigmann A.; Mueller V.; Ta H.; Schoenle A.; Sezgin E.; Hell S. W.; Eggeling C. Scanning STED-FCS Reveals Spatiotemporal Heterogeneity of Lipid Interaction in the Plasma Membrane of Living Cells. Nat. Commun. 2014, 5, 5412. 10.1038/ncomms6412. [DOI] [PubMed] [Google Scholar]
  27. Hedde P. N.; Dörlich R. M.; Blomley R.; Gradl D.; Oppong E.; Cato A. C. B.; Nienhaus G. U. Stimulated Emission Depletion-Based Raster Image Correlation Spectroscopy Reveals Biomolecular Dynamics in Live Cells. Nat. Commun. 2013, 4, 2093. 10.1038/ncomms3093. [DOI] [PubMed] [Google Scholar]
  28. Maraspini R.; Beutel O.; Honigmann A. Circle Scanning STED Fluorescence Correlation Spectroscopy to Quantify Membrane Dynamics and Compartmentalization. Methods 2018, 140-141, 188. 10.1016/j.ymeth.2017.12.005. [DOI] [PubMed] [Google Scholar]
  29. Fritzsche M.; Fernandes R. A.; Chang V. T.; Colin-York H.; Clausen M. P.; Felce J. H.; Galiani S.; Erlenkämper C.; Santos A. M.; Heddleston J. M.; Pedroza-Pacheco I.; Waithe D.; de la Serna J. B.; Lagerholm B. C.; Liu T.; Chew T.; Betzig E.; Davis S. J.; Eggeling C.; et al. Cytoskeletal Actin Dynamics Shape a Ramifying Actin Network Underpinning Immunological Synapse Formation. Sci. Adv. 2017, 3, e1603032. 10.1126/sciadv.1603032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Blouin C. M.; Hamon Y.; Gonnord P.; Boularan C.; Kagan J.; Viaris de Lesegno C.; Ruez R.; Mailfert S.; Bertaux N.; Loew D.; Wunder C.; Johannes L.; Vogt G.; Contreras F.-X.; Marguet D.; Casanova J.-L.; Galès C.; He H.-T.; Lamaze C. Glycosylation-Dependent IFN-ΓR Partitioning in Lipid and Actin Nanodomains Is Critical for JAK Activation. Cell 2016, 166, 920–934. 10.1016/j.cell.2016.07.003. [DOI] [PubMed] [Google Scholar]
  31. Schneider F.; Waithe D.; Clausen M. P.; Galiani S.; Koller T.; Ozhan G.; Eggeling C.; Sezgin E. Diffusion of Lipids and GPI-Anchored Proteins in Actin-Free Plasma Membrane Vesicles Measured by STED-FCS. Mol. Biol. Cell 2017, 28, 1507–1518. 10.1091/mbc.e16-07-0536. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Andrade D. M.; Clausen M. P.; Keller J.; Mueller V.; Wu C.; Bear J. E.; Hell S. W.; Lagerholm B. C.; Eggeling C. Cortical Actin Networks Induce Spatio-Temporal Confinement of Phospholipids in the Plasma Membrane – a Minimally Invasive Investigation by STED-FCS. Sci. Rep. 2015, 5, 11454. 10.1038/srep11454. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Burnham K. P.; Anderson D. R. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociol. Methods Res. 2004, 33, 261–304. 10.1177/0049124104268644. [DOI] [Google Scholar]
  34. Lagerholm B. C.; Andrade D. M.; Clausen M. P.; Eggeling C. Convergence of Lateral Dynamic Measurements in the Plasma Membrane of Live Cells from Single Particle Tracking and STED-FCS. J. Phys. D: Appl. Phys. 2017, 50, 063001. 10.1088/1361-6463/aa519e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Schwarz G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. 10.1214/aos/1176344136. [DOI] [Google Scholar]
  36. Mueller V.; Ringemann C.; Honigmann A.; Schwarzmann G.; Medda R.; Leutenegger M.; Polyakova S.; Belov V. N. N.; Hell S. W. W.; Eggeling C. STED Nanoscopy Reveals Molecular Details of Cholesterol- and Cytoskeleton-Modulated Lipid Interactions in Living Cells. Biophys. J. 2011, 101, 1651–1660. 10.1016/j.bpj.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Regmi R.; Winkler P. M.; Flauraud V.; Borgman K. J. E.; Manzo C.; Brugger J.; Rigneault H.; Wenger J.; García-Parajo M. F. Planar Optical Nanoantennas Resolve Cholesterol-Dependent Nanoscale Heterogeneities in the Plasma Membrane of Living Cells. Nano Lett. 2017, 17, 6295–6302. 10.1021/acs.nanolett.7b02973. [DOI] [PubMed] [Google Scholar]
  38. Waithe D. GitHub Nanosimpy Repository, https://github.com/dwaithe/nanosimpy (accessed July 19, 2018).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn8b04080_si_001.pdf (12.9MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES