All four subunits of HCN2 channels contribute to the activation gating in an additive but intricate manner

HCN pacemaker channels are dually gated by hyperpolarizing voltages and cyclic nucleotide binding. Sunkara et al. show that each of the four binding sites promotes channel opening, most likely by exerting a turning momentum on the tetrameric intracellular gating ring.

Abstract

Hyperpolarization-activated cyclic nucleotide–modulated (HCN) channels are tetramers that elicit electrical rhythmicity in specialized brain neurons and cardiomyocytes. The channels are dually activated by voltage and binding of cyclic adenosine monophosphate (cAMP) to their four cyclic nucleotide-binding domains (CNBDs). Here we analyze the effects of cAMP binding to different concatemers of HCN2 channel subunits, each having a defined number of functional CNBDs. We show that each liganded CNBD promotes channel activation in an additive manner and that, in the special case of two functional CNBDs, functionality does not depend on the arrangement of the subunits. Correspondingly, the reverse process of deactivation is slowed by progressive liganding, but only if four and three ligands as well as two ligands in trans position (opposite to each other) are bound. In contrast, two ligands bound in cis positions (adjacent to each other) and a single bound ligand do not affect channel deactivation. These results support an activation mechanism in which each single liganded CNBD causes a turning momentum on the tetrameric ring-like structure formed by all four CNBDs and that at least two liganded subunits in trans positions are required to maintain activation.

Hyperpolarization-activated cyclic nucleotide–modulated (HCN; Gauss et al., 1998; Ludwig et al., 1998; Santoro et al., 1998) ion channels produce electrical rhythms in specialized neuronal (Banks et al., 1993; Ingram and Williams, 1996; Saitow and Konishi, 2000; Santoro et al., 2000; Cuttle et al., 2001; Moosmang et al., 2001; Chan et al., 2004; Notomi and Shigemoto, 2004) and cardiac cells (Brown et al., 1979; Ludwig et al., 1999; Gauss and Seifert, 2000; Biel et al., 2009). They are activated by membrane hyperpolarization (DiFrancesco, 1986; Santoro and Tibbs, 1999) in the repolarization phase of the action potential, thereby evoking the pacemaker current I_h (I_f, I_q). In an organism, stimulation of the sympathetic part of the autonomous nerve system leads to an enlargement and an acceleration of I_h, resulting in an acceleration of the respective electrical rhythms. On the molecular level, this effect is mediated by an increase of the second messenger cAMP, directly binding to the channels (DiFrancesco, 1999; Wang et al., 2001, 2002; Robinson and Siegelbaum, 2003; Craven and Zagotta, 2006).

Structurally, HCN channels belong to the superfamily of tetrameric voltage-gated ion channels (Clapham, 1998). In these channels, each subunit contains a voltage-sensor domain and a pore domain contributing to the wall of a common pore. In contrast to most other members of this superfamily, HCN channel subunits contain a cyclic nucleotide-binding domain (CNBD) in the C terminus (Santoro et al., 1997). In mammals, four HCN isoforms have been identified to encode for the subunits HCN1 to HCN4 (Santoro and Tibbs, 1999; Kaupp and Seifert, 2001), which all can form functional homotetrameric channels (Santoro et al., 2000; Ishii et al., 2001; Stieber et al., 2005).

The structure of isolated CNBDs has been resolved by crystals and x-ray analysis for three of the four mammalian HCN isoforms (Zagotta et al., 2003; Xu et al., 2010; Lolicato et al., 2011; Goldschen-Ohm et al., 2016). These structures are fourfold symmetric, in both the absence and presence of cAMP. Very recently, cryo-electron microscopy has been successfully used to resolve the full structure of the HCN1 isoform at 3.5-Å resolution, also in the absence and presence of cAMP (Lee and MacKinnon, 2017). According to these structural results, the authors proposed a scenario for the duality of voltage- and cAMP-induced activation and, moreover, for the unusual reversed polarity of activation compared with the other channels in this superfamily, which are activated not by hyperpolarization but by depolarization. For the depolarized voltage sensor of HCN1, three facts are supposed to stabilize the gate in a closed position: (1) an unusually long S4 helix touching the C-linker, (2) a special packing arrangement of the S4 to S6 helices, and (3) a unique 3-α-helical HCN domain preceding the S1 helix. Furthermore, hyperpolarization has been supposed to drive the S4 helix in a downward direction, thereby disrupting the stabilizing effects and causing movement of the S6 helices, opening the gate. For HCN2 channels, similar scenarios have been proposed using functional approaches (Chen et al., 2001a; Macri et al., 2009). Concerning the activating effect of cAMP, its binding to the CNBD would evoke a concerted rotation of the tetrameric ring-like CNBD, thereby enhancing opening of the gate by promoting the disruption of the stabilizing effects. These ideas of the cAMP effect are in line with an earlier study, suggesting a binding-induced relief of autoinhibition caused by the CNBD (Wainger et al., 2001).

Despite these recent structural insights, many questions about channel function remain open, in particular, how the successive binding of four cyclic nucleotides is transmitted to change the operation of the channels and how the two stimuli, hyperpolarization and cAMP binding, are interlinked.

Progress in the understanding of voltage-evoked activation of HCN channels has been achieved in related spHCN channels by combining voltage activation and monitoring conformational changes of the S4 segment by changes of the fluorescence intensity (Bruening-Wright et al., 2007). One of the results was that the channels open after only two S4 segments have moved and that the voltage sensors of the four subunits act independently of each other. In another approach measuring gating currents in SpHCN channels, locked in either the open or the closed state (Kwan et al., 2012), Ryu and Yellen (2012) proposed a weak coupling between voltage sensors and the activation gate, with the consequence that only a low amount of energy is required from cAMP binding to shift the voltage dependence of activation. However, spHCN channels are not only structurally but also functionally distant to mammalian HCN channels, because they show a pronounced slow mode shift (Elinder et al., 2006) that is not observed in HCN channels (Männikkö et al., 2005).

In contrast to the idea of an independent action of the subunits, previous results of our group upon cAMP-induced activation in homotetrameric HCN2 channels suggest pronounced cooperativity for cAMP binding. By monitoring cAMP binding and activation gating in parallel using confocal patch-clamp fluorometry and a fluorescent cAMP derivative (Biskup et al., 2007; Kusch et al., 2010) we suggested an intricate type of cooperativity with the sequence positive-negative-positive for the second, third, and fourth binding step, respectively (Kusch et al., 2011). Negative cooperativity for the binding of cyclic nucleotides binding has been also demonstrated for isolated binding sites (Chow et al., 2012; Ng et al., 2016; Hayoz et al., 2017). The four-state kinetic model, on which our suggestions were based, gave us also information about the rate and equilibrium constants of the closed-open isomerizations at each degree of liganding. The result was that the equilibria of the closed-open isomerizations became progressively shifted to the open states at increased liganding. However, for the sake of convergence of the model fit, several rate constants at three and four occupied binding sites had to be equated, which compromised the conclusiveness concerning the equilibria of the closed-open isomerizations.

Herein we used concatemeric HCN2 channels, containing a defined number and position of disabled CNBDs, to systematically study the effects of the remaining functional binding domains on channel gating. Respective HCN2 concatemers have been shown previously to produce functional channels with properties similar to those of channels formed by the self-assembly of four subunits (Ulens and Siegelbaum, 2003). In the presence of saturating cAMP, this approach allowed us to quantify voltage-dependent gating for all degrees of liganding at both equilibrium and in time. Moreover, in case of two functional CNBDs, the effects of the cis and trans position of the functional subunits could be considered. With these results, we provide new insight into the role of the subunits for the phenomenon that occupation of two binding sites suffices to evoke the maximum current response, but not the full shift in the Boltzmann relationship (Kusch et al., 2010). In the present study, the effects of the functional subunits are surprisingly simple: their effects on activation are additive and independent of the position of the functional subunits within the tetramer, suggesting that each liganded subunit exerts a turning momentum on the channel’s tetrameric CNBD. In contrast, the open probability at maximum hyperpolarization is reached after only two subunits are liganded, and slowing of deactivation requires at least two functional subunits in trans position. The results are discussed in the context of the channel structure.

Materials and methods

Xenopus laevis oocytes

The surgical removal of oocytes was performed from adult females of X. laevis under anesthesia (0.3% tricaine; MS-222). The oocytes were treated with collagenase A (3 mg/ml; Roche) for 105 min in Ca²⁺-free Barth’s solution containing (in mM) 82.5 NaCl, 2 KCl, 1 MgCl₂, and 5 HEPES, pH 7.5. After this procedure, oocytes of stages IV and V were manually dissected and injected with cRNA encoding mHCN2 channels of Mus musculus (NM_008226) and concatemers thereof (Table 1). After injection with cRNA, the oocytes were cultured at 18°C for 2–10 d in Barth’s solution containing (in mM) 84 NaCl, 1 KCl, 2.4 NaHCO₃, 0.82 MgSO₄, 0.41 CaCl₂, 0.33 Ca(NO₃)₂, 7.5 Tris, cefuroxime, and penicillin/streptomycin, pH 7.4. The procedures had approval from the authorized animal ethics committee of the Friedrich-Schiller University Jena. The methods were performed in accordance with the approved guidelines. Oocytes harvested in our own laboratory were complemented with ready-to-use oocytes purchased from Ecocyte Bioscience.

Table 1. Constructs used in the experiments and steady-state parameters.

Construct	Vh,cont	zδcont	Vh,cAMP	zδcAMP	Vh,cont Vh,cAMP
Nonconcatenated subunits
w4	−116.5 ± 1.8	6.57 ± 0.40	−94.8 ± 1.5	6.42 ± 0.48	21.6 ± 1.1
m4	−120.7 ± 1.6	6.64 ± 0.44	−121.5 ± 1.2	6.67 ± 0.42	0.04 ± 0.7
Dimeric concatemers
ww2	−125.3 ± 2.0	6.36 ± 0.50	−104.5 ± 2.2	7.56 ± 0.30	20.9 ± 1.4
mm2	−130.9 ± 0.6	6.11 ± 0.21	−131.8 ± 1.7	6.26 ± 0.17	−0.94 ± 1.3
wm2	−115.3 ± 1.2	7.09 ± 0.32	−105.6 ± 1.0	6.42 ± 0.32	9.0 ± 0.7
Tetrameric concatemers
wwww	−123.9 ± 2.3	6.41 ± 0.26	−103.9 ± 3.0	6.43 ± 0.26	21.1 ± 1.1
wwwm	−116.7 ± 1.0	6.00 ± 0.31	−102.0 ± 0.8	6.64 ± 0.26	14.8 ± 1.1
wmwm	−120.2 ± 1.2	6.07 ± 0.39	−111.7 ± 1.6	6.09 ± 0.34	9.7 ± 1.6
mwmw	−119.7 ± 0.8	9.03 ± 0.81	−109.9 ± 0.8	8.79 ± 0.50	9.8 ± 0.6
mmww	−130.9 ± 0.9	6.20 ± 0.20	−121.5 ± 0.9	5.25 ± 0.17	9.4 ± 0.5
wwmm	−127.6 ± 1.2	6.02 ± 0.69	−119.3 ± 1.2	5.12 ± 0.42	10.3 ± 1.7
mmmw	−126.6 ± 0.9	6.44 ± 0.46	−122.5 ± 1.1	6.30 ± 0.37	4.8 ± 1.1
mmmm	−126.1 ± 1.5	6.27 ± 0.44	−128.8 ± 1.4	6.38 ± 0.75	−2.2 ± 0.8

The sequence of either two or four w or m denotes a concatemer with the respective subunit arrangement reading from N terminus to C terminus. The data points were fitted with the Boltzmann function (Eq. 1), yielding the effective gating charge zδ and the voltage of half-maximum activation V_h. The errors are given as SEM. w, wild-type subunit; m, subunit carrying the mutation R591E; w₄ and m₄, channels formed from nonligated subunits.

Molecular biology

The dimers wm and mm and the tetramers mmmm, mmmw, wmwm, mmww, and wwwm were provided by S.A. Siegelbaum (Columbia University, New York, NY). The constructs mm, mmmm, mmmw, and mmww were modified at position 481 of each subunit by replacing a histidine residue with a tyrosine residue according to the databank sequence NM_008226. The other tetrameric mouse HCN2 concatemers wwww, mwmw, and wwmm were assembled by interlinking two HCN2 subunit dimers into a single open reading frame as described previously (Ulens and Siegelbaum, 2003). The dimer wm was digested using BglII restriction enzyme, and the pGEM-HCN2 BglII/BglII fragment was re-ligated, yielding a R591E mutant HCN2 single subunit in pGEMHEnew. Likewise, the tetramer mmww was cut and the pGEM-HCN2 BglII/BglII fragment was re-ligated, yielding a single wild-type HCN2 subunit in pGEMHEnew. From this, the remaining dimers, ww and mw, were assembled using a previously described strategy (Ulens and Siegelbaum, 2003). Initially, the unique MfeI restriction site was introduced in front of the stop codon of the wild-type and R591E mutant HCN2 in-frame with the EcoRI restriction site present in the vector pGEMHEnew 5′ of the HCN2 start codon (Ulens and Siegelbaum, 2003). Dimers were subsequently constructed by inserting an EcoRI/MfeI fragment of w or m at the XbaI/MfeI site of pGEM-HCN2 (w or m). This resulted in a short linker sequence, SPFLA, between the subunits. MfeI and EcoRI have compatibly cohesive ends. Ligation thus removed the MfeI restriction site between the cojoint subunits plus the last amino acid at the end of the C terminus of the subunit 5′ of the linkage. To obtain tetramers, two dimers were joined via the same approach yielding the wwww, mwmw, and wwmm concatemers.

The resulting HCN2 constructs were checked by restriction digestion and subsequent gel electrophoreses as well as partial sequencing. cRNAs were transcribed from cDNAs using the mMESSAGE mMACHINE T7 kit (Ambion).

Electrophysiology

Ionic currents were measured with the patch-clamp technique in inside-out macropatches excised from the oocytes. The patch pipettes were pulled from quartz tubing (P-2000; Sutter Instrument) whose outer and inner diameter were 1.0 and 0.7 mm, respectively (Vitrocom). The pipette resistance was 0.9–1.8 MΩ. The bath solution contained (in mM) 100 KCl, 10 EGTA, and 10 HEPES, pH 7.2 (Table S1), and the pipette solution contained (in mM) 120 KCl, 10 HEPES, and 1.0 CaCl₂, pH 7.2. Following Ulens and Siegelbaum (2003), for part of the experiments, 50 µM cAMP (Sigma-Aldrich) was added to the bath solution. Saturation of the activating effect of 50 µM cAMP was demonstrated for the construct mmmw by comparing the cAMP-induced shift of V_h (ΔV_h) and the percentage of cAMP-induced current increase at 50 µM with the respective data at 3 mM. ΔV_h was 4.8 ± 1.1 and 2.4 ± 0.5, and the percentage of current increase was 7.8 ± 0.6% and 4.2 ± 1.2%, for 50 µM and 3 mM, respectively. The respective differences were not significant (t test, P < 0.05).

An Axopatch 200A amplifier (Axon Instruments) was used for current recording. Pulsing and data recording were controlled by the ISO2 hard- and software (MFK). The sampling rate was 10 kHz, and the recordings were on-line filtered at 2.5 kHz using the four-pole Bessel filter of the amplifier. The holding potential was generally −30 mV. Each recording was started 3–4 min after patch excision to avoid artifacts caused by excision-induced channel rundown (Thon et al., 2013, 2015; Hummert et al., 2018).

Previously, it has been shown that the rundown caused by patch excision is at least partially caused by the dephosphorylation of PI(4,5)P₂, which can be opposed by the action of a lipid kinase typically remaining associated with the membrane in cell-free patches (Pian et al., 2006). In case the phosphorylation status of PI(4,5)P₂ is also an issue under our recording conditions, the presence of Mg²⁺ ions should support the kinase action, thereby diminishing the rundown. For the two constructs tested, wmwm and mmww, channel activation was not altered by 1 mM MgCl₂, indicating that the phosphorylation status of PI(4,5)P₂ was not relevant herein.

Quantification and statistical analysis

Boltzmann relationships were fitted with OriginPro 9.0G by

$$I/I_{max}=1/\left\{1+exp\left[z\delta F\left(V-V_h\right)/RT\right]\right\},$$ (1)

where V_h is the voltage of half-maximum activation and zδ the effective gating charge. F, R, and T are the Faraday constant, the molar gas constant, and the temperature in Kelvin, respectively. I is the actual current amplitude and I_max the maximum current amplitude at the saturating hyperpolarizing voltage of −150 mV specified for each patch. All current amplitudes in the absence of cAMP were additionally normalized to I_max at saturating cAMP.

The time courses of current activation and deactivation were fitted with a single exponential starting after an initial delay:

$$I\left(t\right)=A\ast exp\left[-t/\tau \right],$$ (2)

where A is the amplitude, t the time, and τ the time constant for either activation or deactivation.

Experimental data are given as mean ± SEM.

Online supplemental material

For the constructs wmwm and mmww, we show in Table S1 that Mg²⁺ ions did not affect channel gating. Fig. S1 compares the V_h values in the absence of cAMP for all tested constructs to study the effect of the R591E mutations on steady-state activation. Supplemental Results shows that prepulse-induced closed-state inactivation exist in HCN2 wild-type channels but that this inactivation is not cAMP-dependent and therefore in the focus of this study (Fig. S2).

Results

Effects of ligation on steady-state activation

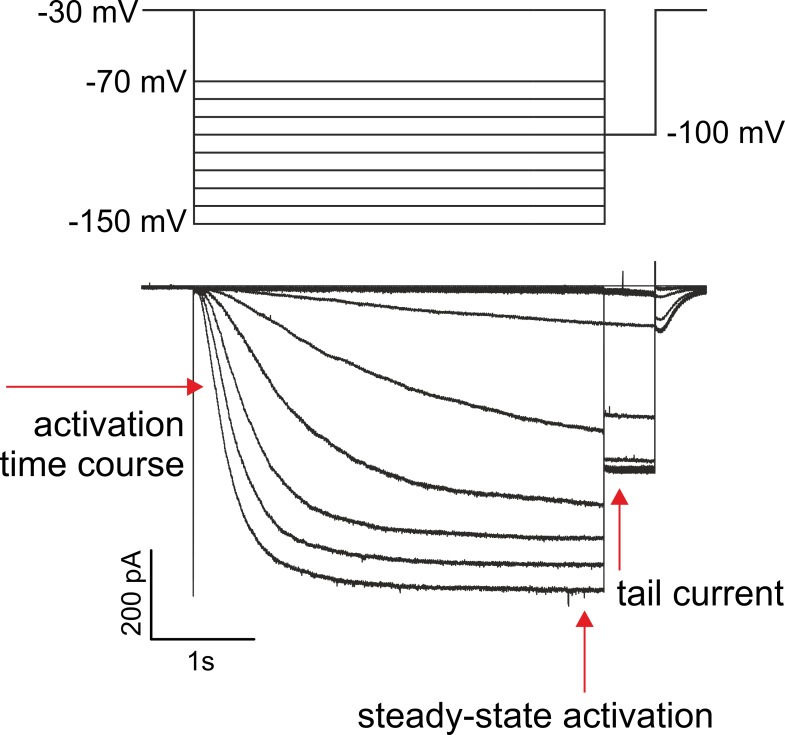
Ion currents were measured with series of hyperpolarizing pulses followed by test pulses to −100 mV (Fig. 1). The pulse duration was set to 4 s to complete activation at the most hyperpolarizing voltages. We first tested to what extent subunit ligation disturbs steady-state activation by comparing the wild-type concatemers ww₂ (dimer) and wwww (tetramer) with channels formed by nonligated wild-type subunits, w₄ (Fig. 2). The steady-state activation relationships of both concatemers showed the typical sigmoidal shape (Santoro et al., 1998) described previously for w₄ HCN2 channels (Altomare et al., 2001) and showed also a shift to less negative voltages and a current increase at saturating hyperpolarizing voltages by saturating cAMP (Fig. 2, A and B). All current amplitudes I were normalized with respect to I_max at −150 mV and 50 µM cAMP, resulting for w₄ at −150 mV and without cAMP in I/I_max = 0.83. To ease further comparison, I/I_max = 0.83 was used generally as scaling factor for all constructs.

Figure 1.

Series of representative currents generated by the wwww concatemer for recording steady-state activation. The pulse protocol is shown above the traces. The channels were activated in the sequence to more hyperpolarizing voltages. The amplitude of the tail current at −100 mV was evaluated.

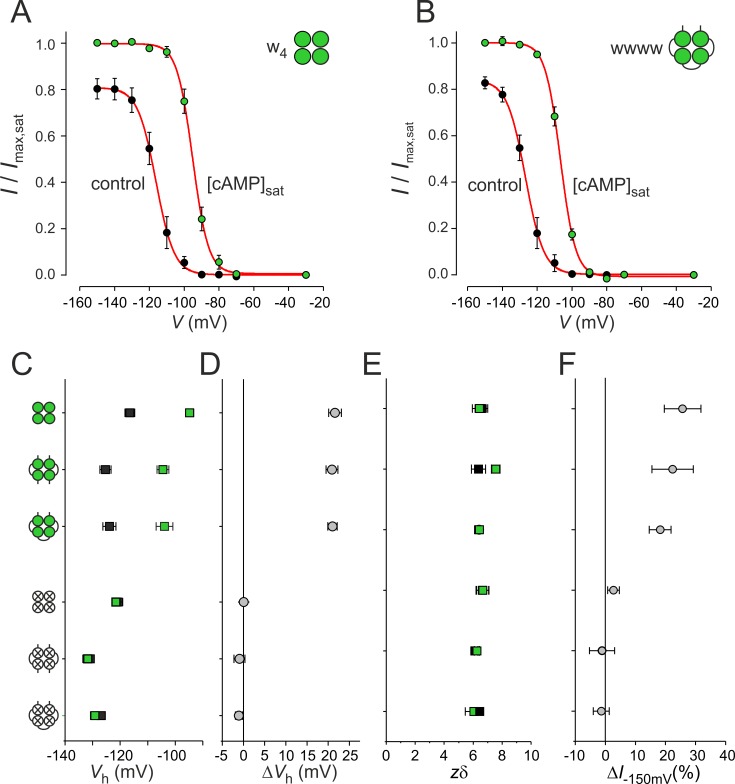
Figure 2.

Function of concatenated homotetrameric channels. (A) Steady-state activation relationships in the absence and presence of 50 µM cAMP for w₄ channels. The data points were fitted with Eq. 1, yielding for the parameters V_h and zδ −116.5 ± 1.8 mV (n = 10) and 6.57 ± 0.40 (n = 10); −94.8 ± 1.5 mV (n = 9) and 6.42 ± 0.48 (n = 9), respectively. (B) Same as A for wwww channels. The respective parameters for V_h and zδ are −123.9 ± 2.3 mV (n = 17) and 6.41 ± 0.26 (n = 17); −103.9 ± 3.0 mV (n = 12) and 6.43 ± 0.26 (n = 12). (C) Comparison of the V_h values for the three wild-type and three mutated channels; 0 cAMP (control), black squares, 50 µM cAMP, green squares. (D) Comparison of the cAMP-induced voltage shift of V_h, ΔV_h. (E) Comparison of zδ. Symbols correspond to C. (F) Comparison of cAMP-evoked current increase, ΔI_−150mV. 4–17 recordings per data point were included for analyses in C to F. In the cartoons here and below, green circles represent functional binding sites, whereas empty crossed circles represent mutated binding sites. Error bars indicate SEM.

The data points of the steady-state activation relationships (Fig. 2, A and B) were fitted with a Boltzmann function (Eq. 1), yielding the voltage of half-maximum activation, V_h, and the effective gating charge, zδ. Ligation had a decent hyperpolarizing effect on V_h by ∼10 mV (upper half of Fig. 2 C), which suggests a stronger autoinhibitory effect of the CL-CNBD portion, possibly by slightly restricting the conformational movement of the N and C terminus. In all three cases (w₄, ww₂, and wwww), however, cAMP consistently shifted V_h to depolarized potentials by an equal amount of 20 mV, which becomes evident when considering ΔV_h (upper half of Fig. 2 D). cAMP also consistently increased the current amplitude at saturating hyperpolarizing voltage (ΔI_{−150 mV}; Fig. 2 F). Respective constructs with mutated binding sites, disabled to bind cAMP (see below), showed a similar effect of ligation on V_h, and as expected, cAMP had no respective effects (lower half of Fig. 2, C, D, and F). The effective gating charge, zδ, for all wild-type and mutated constructs either with or without cAMP, was indistinguishable (Fig. 2 E). Together, these results show that ligation of the subunits does not disturb the effects of cAMP on wild-type channel gating, making the concatemers thus a useful experimental tool to study the effects of the individual subunits in detail.

Effects of cAMP binding to individual subunits on steady-state activation

We studied the effects of cAMP binding to specific HCN2 subunits on steady-state activation by analyzing currents in tetrameric concatemers with defined constellations of functional and disabled CNBDs. Following previous studies, the CNBDs were disabled by the mutation R591E located in the β-roll of the CNBD (Chen et al., 2001b; Ulens and Siegelbaum, 2003). This resulted in concatemers with 0 to 4 wild-type subunits (w) and, correspondingly, 4 to 0 mutated subunits (m). In total, we included in the analysis six tetrameric concatemers with mixed subunits together with the two homotetramers wwww and mmmm (Table 1; see Materials and methods). Comparison of half-maximum activation at 0 cAMP for the tetrameric constructs showed a scatter within ∼10 mV (Fig. S1).

The result for the eight concatemers was that ΔV_h was shifted to more depolarized voltages in a systematic—and moreover, approximately proportional—way (Fig. 3 A); that is, the effect of liganding a further subunit adds to the effects of other already liganded subunits. In case of two functional subunits, two cases can be distinguished, a trans (opposite) and a cis (neighbored) position. With pulse durations of 1 s, a larger ΔV_h value has been reported previously for a trans than for a cis concatemer (Ulens and Siegelbaum, 2003). Under our conditions with pulses of 4-s duration, presumably closer to an equilibrium, we observed indistinguishable ΔV_h values, which was substantiated by two constructs each, and for the trans channel also by the dimeric channels wm₂.

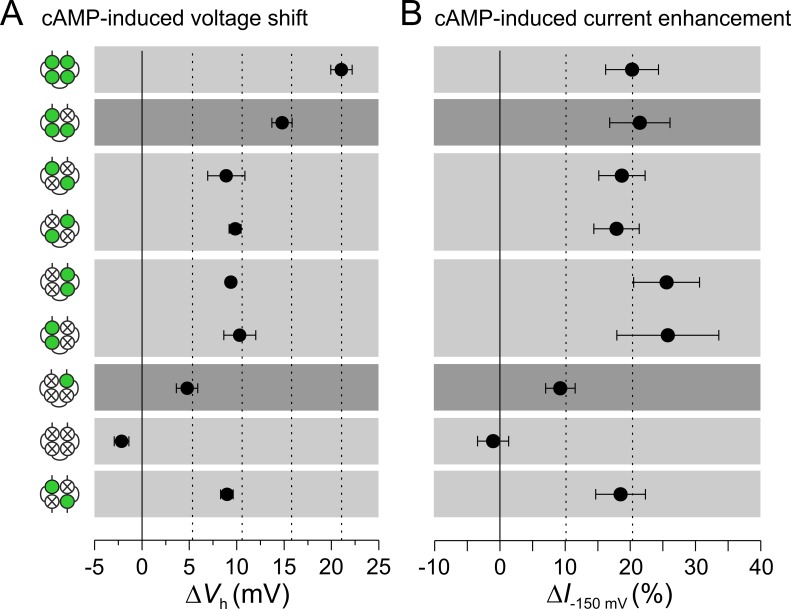
Figure 3.

Effect of different combinations of liganded subunits on steady-state activation. Eight tetrameric and one dimeric concatemer are compared. cAMP is applied at a saturating concentration of 50 µM. (A) cAMP-induced voltage shift ΔV_h (mV), determined as described for Fig. 2A by using Eq. 1. The amount of voltage shift by liganded subunits is additive. In channels with two functional CNBDs, the cis and the trans position are indistinguishable. (B) Effect of saturating cAMP on current increase at the saturating voltage of −150 mV, ΔI_−150mV. Two liganded subunits suffice to generate the maximum effect. Data points contain 8–17 recordings. Error bars indicate SEM.

Together, an occupied CNBD exerts an effect on ΔV_h irrespective of its position to the other liganded CNBDs. We suggest that a liganded CNBD causes a turning momentum on the tetrameric CNBD and that these turning momenta are additive.

Concerning the cAMP-induced current increase at saturating hyperpolarizing voltage, the situation differs notably. If two subunits are liganded, the effect is already maximal (Fig. 3 B), suggesting that the proposed turning momentum generated by two subunits together with the energy delivered by the strong hyperpolarization suffices to generate the maximum open probability, P_o. The effect of the dimeric trans channel wm₂ further supports this notion. These data are also in agreement with previous data by Zhou and Siegelbaum (2007) showing that the shift of V_h required higher cAMP concentrations than the increase of current amplitude (EC₅₀ = 0.1 µM vs. 0.035 µM).

Subunit-evoked acceleration of activation is also additive

After quantifying the contribution of the individual subunits to steady-state activation, we tested their accelerating effects on the activation time course (shown for wwww in Fig. 4 A). In the absence of cAMP, all used concatemers showed the typical acceleration of the activation time course at more hyperpolarizing potentials (shown for wwww in Fig. 4 B; Altomare et al., 2001; Wang et al., 2002). Activation was measured with pulses of 4-s duration and quantified by fitting a single exponential (Eq. 2) to the time courses starting after the initial delay, yielding the time constants τ_a,cont for cAMP-free conditions and τ_a,cAMP for cAMP saturation. For comparing the accelerating effects in all constructs, we focused on data obtained at −140 mV (Fig. 4 C), because after 4 s, activation could be considered approximately complete. To minimize the variability between the activation time courses among the patches, we specified for each patch the ratio τ_a,cont/τ_a,cAMP to measure the extent of cAMP-dependent acceleration. Comparison of these ratios gave a pattern similar to that observed for steady-state activation (Fig. 4 C): one through four functional subunits accelerated activation in an additive manner. Moreover, the four concatemers with two functional CNBDs showed that there was also no difference between the cis and the trans position, and again, the dimeric trans channel wm₂ produced an acceleration of the activation time course similar to the respective tetramers. Apparently, the difference between three and two functional subunits was larger than the other differences. This might correspond to an earlier study showing that the third ligand binding causes the major activating effect on HCN2 channels (Kusch et al., 2011). The results of this section further support the notion that the ligand-evoked activating effects of the subunits are additive and that the cis and the trans position in constructs with two functional binding sites produce a similar effect.

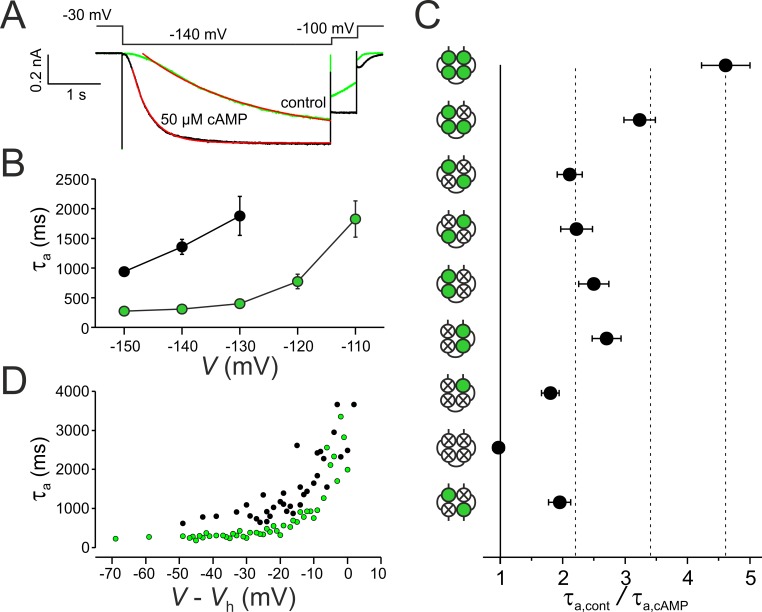
Figure 4.

Effects of subunit liganding on activation kinetics. (A) Superimposition of activation time courses in the presence and in the absence of cAMP at −140 mV for wwww and illustration of determining the activation time constant τ_a (monoexponential fits are shown in red). Late currents are normalized. (B) Voltage dependence of τ_a and effect of cAMP for wwww (n = 13–17 recordings per data point). Green and black symbols show values obtained at 50 µM and zero cAMP, respectively. (C) Comparison of τ_a for the eight tetrameric concatemers and the dimeric concatemer wm₂ at hyperpolarization to −140 mV. Data points contain 9–17 recordings. (D) τ_a values in dependence on normalized voltage. Shown are individual data points. Green and black symbols show values obtained at 50 µM and zero cAMP, respectively. Normalization was performed by the respective V_h value of the individual recordings. Error bars indicate SEM.

To test whether at the strongest hyperpolarizing voltages the activation speed is indeed maximal, we plotted the activation time constants of all individual wwww recordings versus the normalized voltage (V − V_h) for both cAMP-free and saturating cAMP conditions (Fig. 4 D). The data suggest that at the strongest hyperpolarizing voltages applied herein, the activation speed is maximal and that it is faster in the presence than in the absence of cAMP (Chen et al., 2007).

Two liganded subunits in trans but not cis position are required to slow down deactivation

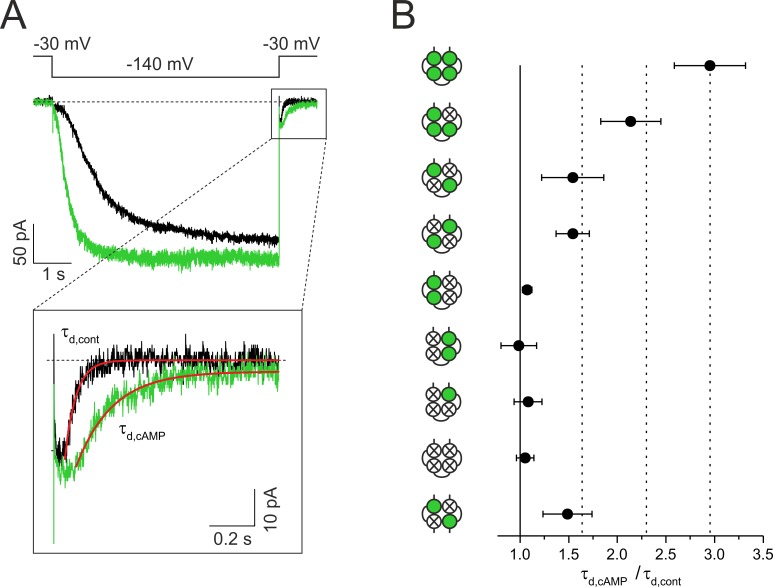
Compared with activation kinetics, deactivation kinetics provide information that is more closely related to conformational changes associated with the pore action. Accordingly, the deceleration of deactivation by cAMP (Wang et al., 2002) means that cAMP stabilizes the open pore. To attribute this effect to the action of specific subunits, we compared the time courses of deactivation in our concatemers. Deactivation time courses were measured generally at −30 mV after a hyperpolarizing pulse to −140 mV in the presence and absence of cAMP (shown for wwww in Fig. 5 A). Quantification of the deactivation speed was performed again by approximating a single exponential (Eq. 2) to the time courses after the delay, yielding the time constants τ_d,cont for the cAMP-free conditions and τ_d,cAMP for saturating cAMP. In analogy to activation, the decelerating effect of cAMP was calculated by τ_d,cAMP/τ_d,cont for each concatemer (Fig. 5 B).

Figure 5.

Effects of subunit liganding on deactivation kinetics. The currents were activated by pulses of 6-s duration to −140 mV, and deactivation was measured at a subsequent pulse to −30 mV. (A) Superimposition of two current time courses of the concatemer wwww in the absence and presence of cAMP and expanded deactivation time courses at −30 mV. Determination of the time of half-maximum deactivation t_hd is illustrated. (B) Comparison of τ_d,cAMP/τ_d,cont for the eight tetrameric concatemers and the dimeric concatemer wm₂ (see text). At least two liganded subunits in trans position are required to decelerate deactivation. Data points contain 3–32 recordings. Error bars indicate SEM.

The result was again a step-like effect of cAMP on deceleration, although the effects are more complex: as expected, deceleration was maximal for the wwww concatemer and became decreased by the wwwm concatemer and further by the wmwm, mwmw, and wm₂ concatemers—that is, in the concatemers with two functional CNBDs in trans position. In contrast, the concatemers with two functional CNBDs in cis position, wwmm and mmww, were ineffective to decelerate deactivation, as was the concatemer mmmw, containing only one functional CNBD.

Together, these results show that at least two subunits in the trans position have to be liganded to decelerate deactivation, that the third and fourth liganded subunits further decelerate deactivation, and that liganding of two subunits in cis position or a single subunit only are ineffective to decelerate deactivation, or in other words, to stabilize the open pore.

Prepulse-induced inactivation does not bias the cAMP effects

It has been suggested previously that HCN2 channels undergo a prepulse-induced closed-state inactivation and that this inactivation is independent of cAMP (Shin et al., 2004). To rule out that the cAMP effects observed herein somehow superimpose with this prepulse-induced inactivation, we tested for respective effects on the activation of w₄ channels under our recording conditions. We quantitatively confirmed that prepulse-induced inactivation is cAMP independent (Supplemental Results and Fig. S2). Hence, we conclude that prepulse-induced inactivation is present in our channels but does not bias the cAMP effects.

Discussion

In this study, we analyzed how liganding of specified functional subunits in HCN2 channels affects voltage-dependent gating using channel constructs with concatenated subunits, in which a specified number of CNBDs were disabled by a point mutation (Chen et al., 2001b; Ulens and Siegelbaum, 2003). The main results are as follows. (a) Each CNBD occupied by cAMP exerts an additional shift of steady-state activation to more depolarized voltages, irrespective of how many CNBDs are already occupied. (b) In case of two functional CNBDs, their trans or cis position causes an equal voltage shift. (c) In contrast, at saturating hyperpolarizing voltages, two liganded subunits cause the maximum current increase. (d) The activation time course becomes accelerated by subunit liganding in a respectively additive manner. (e) The deactivation time course becomes decelerated by progressive liganding if at least two subunits in the trans position are liganded, whereas liganded subunits in the cis position are ineffective. Together, these results argue for an activation mechanism in which each single liganded CNBD causes a turning momentum on the tetrameric ring-like CNBD, thereby stabilizing the open pore. For keeping this effect, at least two subunits in trans position have to be liganded.

Each CNBD exerts a turning momentum on the tetrameric gating ring upon ligand binding

As expected from functional studies (Shin et al., 2001; Rothberg et al., 2002) the HCN1 channel structure (Lee and MacKinnon, 2017) suggests that the channel gate is formed by the bottom parts of the S6-helices, building a right-handed helix bundle, which is tightly packed at depolarizing voltages. The authors proposed a scenario in which in the closed state, the extraordinarily long S4 segment exerts a force onto the C-linker disk, twisting it in a direction that wraps the right-handed helical bundle into a closed conformation. During hyperpolarization, the S4 segments move, thereby releasing the constraints on the S6 helix bundle. As a consequence, the C-linker disk rotates leftward, thereby unwrapping the S6 helix bundle and opening the gate. For cAMP binding, the authors propose a concerted rotation of the tetrameric CNBD-CL region, evoking a displacement of the S6 helices in the same direction as caused by voltage. Consequently, cAMP binding would support voltage-induced opening of the gate.

Our results on functional channels substantiate such a concerted rotation of the tetrameric CNBD-CL region at cAMP binding because the effect of cAMP on concatemers with one to four functional subunits provided additive effects on both steady-state activation (Fig. 3 A) and the activation time course (Fig. 4 C). Additionally, in all concatemers with two functional CNBDs, the effects are indistinguishable irrespective of their position (Figs. 3 A and 4 C). This suggests that it is not a functional dimer of neighbored subunits that exerts a specific cAMP effect, but that the gating ring acts as a whole. Hence, the most plausible explanation is that each individual CNBD exerts a turning momentum on the tetrameric CNBD-CL region upon ligand binding.

With part of the concatemers used herein, a previous study showed a significantly larger voltage shift ΔV_h (ΔV_1/2) of 8–9 mV in the trans concatemer wmwm compared with a 5-mV shift in the cis concatemer mmww, leading the authors to the conclusion that the channel operates as a system of two functional dimers (Ulens and Siegelbaum, 2003). Our results did not reproduce this observation. To verify this, we investigated two further concatemers not included in the mentioned study (Ulens and Siegelbaum, 2003), mwmw and wwmm, which fully confirmed our results. We measured steady-state activation from tail currents after hyperpolarizing pulses of 4-s duration, whereas in the previous study, the duration of the hyperpolarizing pulses had a duration of only 1 s. Our data are therefore closer to equilibrium. However, when repeating the experiments for wmwm and mmww with a pulse length of 1 s, the ΔV_h values were lower, and thus closer to the published values of Ulens and Siegelbaum (2003). Nevertheless, we could not verify a significant difference for the two constructs (ΔV_h = 6.7 ± 0.7 mV for wmwm and ΔV_h = 5.5 ± 0.9 mV for mmww). Moreover, additivity of the subunit effects on activation was further substantiated by the activation time courses.

Another relevant point with respect to earlier work is that the additivity of the ligand binding on channel activation seems to conflict with the results of our own previous study substantiating the remarkable cooperativity sequence positive-negative-positive for the second, third, and fourth binding steps of the tetrameric channel (Kusch et al., 2011). However, herein we applied exclusively a high cAMP concentration that saturates all functional CNBDs independent of differences in their affinity. We therefore assume that the complex cooperativity in the ligand binding is also present in the used concatemers.

Interplay between voltage- and ligand-induced activation

It has been previously reported that at strong hyperpolarization, unliganded HCN channels generate a current amplitude clearly below that in fully liganded HCN channels (Seifert et al., 1999). Using single-channel analysis, we showed that in the presence of cAMP, the open probability P_o is close to unity (Thon et al., 2013). Using patch-clamp fluorometry with a fluorescently tagged cAMP derivative, we further showed that at strong hyperpolarization, two occupied binding sites are sufficient to cause the maximum P_o (Kusch et al., 2010, 2011). This finding is substantiated by a completely different approach used herein: for all constructs with two functional binding sites only, the cAMP-induced increase of current amplitude at saturating voltages was similar to the constructs with three and four functional binding sites (Fig. 3 B).

This indicates that the proposed turning momentum generated by two subunits together with the energy delivered by the strong hyperpolarization suffices to generate the maximum P_o. Hence, the energies delivered by hyperpolarizing voltage and cAMP binding are in part additive: the energy provided by binding the third and fourth ligand can be replaced by strong hyperpolarizing voltage. However, strong hyperpolarization cannot replace the energy provided by binding of ligand numbers one and two, which is reflected by the maximum open probability in the absence of cAMP being lower than unity. Conversely, cAMP-evoked activation cannot replace voltage-evoked activation, because at depolarized voltages even the highest cAMP concentrations are ineffective to open the channels.

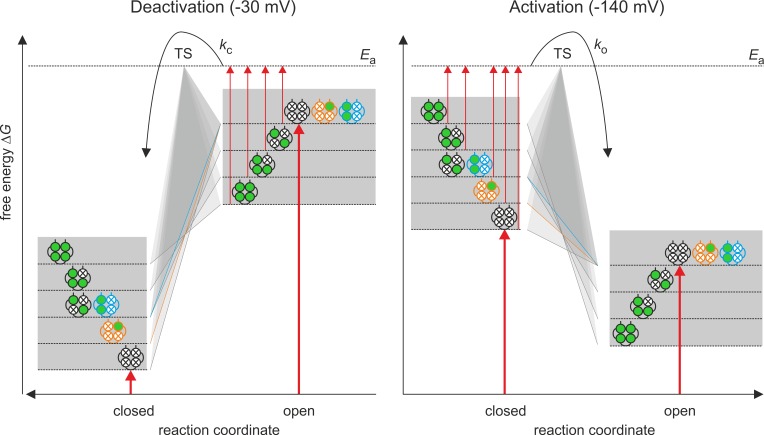
Energetics

The interplay between both types of activation, including the role of the individual liganded subunits, is illustrated qualitatively by a cartoon of an energy barrier for the deactivating voltage of −30 mV and the activating voltage of −140 mV (Fig. 6). Despite the gating of HCN channels by voltage (Männikkö et al., 2005; Elinder et al., 2006) and cAMP (Kusch et al., 2011; Benndorf et al., 2012a,b) being a complex process involving multiple states, it is assumed for the following considerations that a channel can either be in one closed (C) or one open (O) state. According to the transition state theory by Eyring (Glasstone et al., 1941), transition from one of these states to the other requires the activation energy E_a to reach the transition state (TS) and pass to the other state.

Figure 6.

Cartoon model for the energetics of activation by voltage and cAMP in a HCN2 channel. A channel is assumed to adopt only one open (O) and one closed (C) state. According to the Eyring rate theory (Glasstone et al., 1941), the transition between the two states requires an amount of free energy ΔG to reach the activation energy E_a of the transition state TS. The major effect on activation is that of voltage (thick red arrows): At −30 mV, ΔG is much higher in O than in C, whereas at −140 mV, ΔG is moderately higher in C than in O. The binding of cAMP to the four subunits (green circles) is assumed to increase and decrease ΔG in the closed and open state, respectively. In the closed state, the energy contributions for the four binding steps are additive, whereas in the open state, these energy contributions are only additive for the quadruple, triple, and trans-double ligated channel and the cis-double and the single ligated channel do not change ΔG with respect to the empty channel.

The free energies ΔG of C and O are controlled by two stimuli, the membrane voltage and the occupancy of the binding sites. Of these, the membrane voltage is the major stimulus (thick red arrows): in the absence of cAMP, the ΔG value at −30 mV is much lower for the closed than for the open state (P_o→0), whereas at −140 mV, the situation is opposite (the ΔG value is lower in the open than the closed state) although the difference is smaller (P_o = 0.83). The effect of cAMP binding would add to the dominating voltage effect: at −140 mV, increased cAMP would increase ΔG (decrease E_a) to reach the transition state TS (thin red arrows), thus accelerating the activation time course and promoting steady-state activation. The reverse reaction, channel closure, is made less likely by cAMP binding than by voltage alone.

The situation at −30 mV is basically opposite that at −140 mV: channel closing is favored over channel opening. Increased liganding at quadruple, triple, and double liganded channels in trans position decreases ΔG (increases E_a) to reach the transition state TS (thin red arrows), thus decelerating the deactivation time course. The reverse reaction, channel opening, is made unlikely by voltage to such an extent that the increase of ΔG (decrease of E_a) by cAMP binding is functionally irrelevant. Notably, although the effects of cAMP binding are fully additive at all degrees of liganding, they are not entirely additive for deactivation: the mono-liganded channel and the double-liganded channel in cis position generate a deactivation time course that is as fast as that of the nonliganded channel (ocher and blue profiles). Despite this latter specialty, the reciprocal effect of cAMP binding on the closed and open state indicates that it predominantly affects ΔG of the closed and the open state but does not preferentially diminish E_a.

The graded effects of two bound ligands in trans position, three and four bound ligands to accelerate activation and concomitantly to decelerate deactivation, strongly argues for an intimate coupling between voltage and ligand-induced activation. One possible mechanism for this coupling is a direct interaction between the voltage-sensor domain and the CNBD-CL, as shown previously by our group when studying the kinetics of ligand binding and activation gating in parallel (Kusch et al., 2010). The dissociation of the effects between activation and deactivation in case of the binding of one ligand or two ligands in cis position might provide valuable information in future studies about the interaction of the subunits.

Trajectories for deactivation and activation are different

In contrast to channel activation, the effects of liganded CNBDs were not generally additive in slowing down depolarization-induced deactivation. They are additive from two occupied CNBDs in trans position to four occupied CNBDs, whereas two CNBDs in cis position and one occupied CNBD did not slow down deactivation kinetics (Fig. 5). Thus, the trajectories for activation and deactivation are different. This is in agreement with earlier studies using unbranched Purkinje fibers from calf hearts (DiFrancesco, 1984) or heterologously expressed HCN2 channels (Chen et al., 2007).

According to Lee and MacKinnon (2017), depolarization moves the voltage sensor in an outward direction, thereby forcing the C-linker disk in a rightward rotation, keeping the gate closed. In contrast, ligand binding forces the C-linker disk into a leftward movement, the direction of gate opening. These two opposing voltage-controlled forces must also form the energetic framework for the slowed deactivation at progressive liganding. According to Fig. 6, our data suggest that channels with two occupied binding sites in trans position, and even more with three and four occupied CNBDs, require a higher activation energy E_a for inducing the process of the rightward movement of the C-linker disk at a depolarizing step. In contrast, two occupied CNBDs in cis position, or even only one occupied CNBD, do not affect this activation energy.