Abstract
Pulsed high intensity focused ultrasound was shown to enhance chemotherapeutic drug uptake in tumor tissue through inertial cavitation, which is commonly assumed to require peak rarefactional pressures to exceed a certain threshold. However, recent studies have indicated that inertial cavitation activity also correlates with the presence of shocks at the focus. The shock front amplitude and corresponding peak negative pressure (p−) in the focal waveform are primarily determined by the transducer F-number: less focused transducers produce shocks at lower p−. Here, the dependence of inertial cavitation activity on the transducer F-number was investigated in agarose gel by monitoring broadband noise emissions with a coaxial passive cavitation detector (PCD) during pulsed exposures (pulse duration 1 ms, pulse repetition frequency 1 Hz) with p− varying within 1–15 MPa. Three 1.5 MHz transducers with the same aperture, but different focal distances (F-numbers 0.77, 1.02, 1.52) were used. PCD signals were processed to extract cavitation probability, persistence, and mean noise level. At the same p−, all metrics indicated enhanced cavitation activity at higher F-numbers; specifically, cavitation probability reached 100% when shocks formed at the focus. These results provide further evidence supporting the excitation of inertial cavitation at reduced p− by waveforms with nonlinear distortion and shocks.
I. INTRODUCTION
The mechanical effects produced by ultrasound when combined with ultrasound contrast agents (UCAs) have been extensively, and successfully, investigated in recent years for application to the delivery of chemotherapeutic drugs to solid malignancies (Sennoga et al., 2017). This approach addresses multiple anatomical and physiological barriers that prevent effective drug delivery from the vasculature to tumors, including the presence of dense interstitial structures (cellular and/or fibrous), abnormal blood and lymph vessel networks, and elevated interstitial fluid pressures (Lammers et al., 2012). To some extent, these barriers are present across most malignancies, including those of liver, pancreas, breast, and prostate. The limitation of UCAs is that they are generally confined to vessels and perivascular spaces, thereby localizing therapeutic effects only to these regions. Thus, while current use of UCAs provides cavitation within the vascular space, giving some degree of vessel and perivascular space permeabilization, poorly vascularized areas of the tumor remain unaffected (Rapoport et al., 2011).
The induction of de novo cavitation throughout the tumor using pulsed high intensity focused ultrasound (pHIFU) exposures, especially in the dense interstitial structures, may thus circumvent the limitations of UCAs. The effectiveness of this approach has been confirmed in a series of studies harnessing pHIFU-induced inertial cavitation to increase the concentration of doxorubicin or Evans Blue Dye (EBD) in murine pancreatic tumors and porcine kidneys, respectively (Li et al., 2015, Zhou et al., 2016). An important observation from these studies included the presence of a substantial discrepancy in peak negative pressure levels required for inducing inertial cavitation activity. Specifically, in the study by Li et al. (2015), two highly focused pHIFU transducers (F-numbers 0.75 and 1, frequencies 1.5 and 1.1 MHz, correspondingly) were used, and the treatment was only successful under high peak negative focal pressures (14.5–16.5 and 9–11 MPa, correspondingly). In the study by Zhou et al. (2016), a less focused 1.1 MHz transducer (F-number 1.4) was used, and the peak negative focal pressure necessary for successful treatment was found to be much lower −6.8 MPa. Similar discrepancies in cavitation threshold across transducers with different form-factors have been reported by another group during continuous high intensity focused ultrasound (HIFU) exposures (ter Haar et al., 2014).
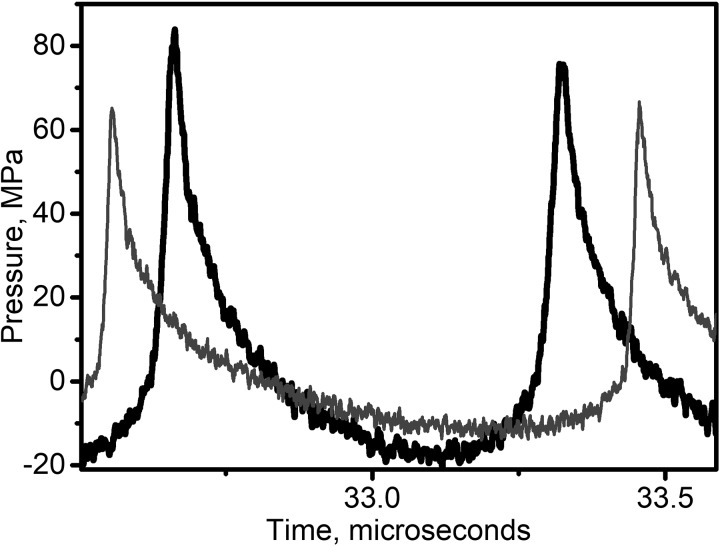
Importantly, although not consistently reported in the aforementioned studies, the pHIFU output level required for generating a therapeutic effect coincided with the formation of shocks in the in situ focal waveform. The therapeutic effect, as defined qualitatively (fluorescence imaging, Li et al., 2015) or quantitatively (fluorimetric analysis, Zhou et al., 2016) by the enhancement of a delivered substance concentration in the treated areas, exhibited a threshold-like behavior within the range of outputs that corresponded to shock formation at the focus. For example, Fig. 1 shows representative focal waveforms measured in water produced by the two different pHIFU transducers in Li et al. (2015) that corresponded to the threshold for the therapeutic effect. As seen, peak pressures are very different in the two waveforms, but the common attribute is that both waveforms are substantially nonlinearly distorted, and contain a shock front. The same was true for the waveforms derated into murine tumor tissue (Li et al., 2015). Indeed, as recently reported (Rosnitskiy et al., 2017), peak positive and negative pressures corresponding to shock formation at the focus are primarily determined by the F-number of a HIFU transducer. Less focused transducers generate shocks at lower peak negative pressure values.
FIG. 1.
Representative focal waveforms measured in water by fiber-optic probe hydrophone (FOPH) from two HIFU transducers with different F-numbers (F-number 1, frequency 1.1 MHz—thin grey line, F-number 0.75, frequency 1.5 MHz—thick black line) from the studies by Li et al., 2014 and Li et al., 2015. The output levels corresponding to these waveforms were required of the two transducers to induce consistent inertial cavitation activity during pHIFU and enhanced drug uptake in murine pancreas tumors. Note that peak pressures in the two waveforms are substantially different (specifically, p− = 16.5 MPa for F-number 0.75 and 11 MPa for F-number 1), but both waveforms contain a shock front.
Here it is hypothesized that the threshold for, and the characteristics of, inertial cavitation activity are critically dependent on the level of nonlinear distortion of the focal waveform in the form of the presence of shock fronts. The goal of this work was to provide experimental confirmation for this hypothesis through characterization of inertial cavitation activity induced in a tissue mimicking gel phantom by transducers with the same operating frequency and aperture, but different focal lengths (i.e., different F-numbers).
II. MATERIALS AND METHODS
A. HIFU transducers and driving electronics
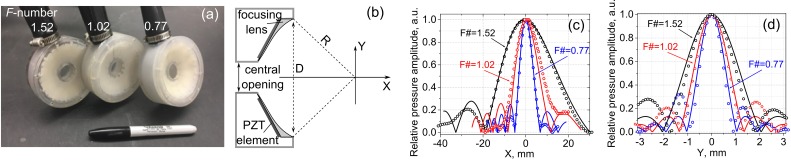
The HIFU sources used in this study were spherically focused, 1.5 MHz 12-element sector arrays with F-numbers of 0.77, 1.02, and 1.52 [Fig. 2(a)]. The sources were fabricated in house using flat, trapezoidal piezoelectric elements bonded with an adhesive acoustic matching layer to a rapid prototyped plastic lens [Fig. 2(b)]. All transducers had a nearly identical aperture D (73, 75, and 78 mm, respectively), and a central opening of 20 mm in diameter to allow for in-line passive cavitation detection. However, the focal distances R were different (56, 76.6, and 118 mm, respectively). The transducers were powered by a custom-built class D amplifier that is capable of delivering up to 26 kW pulse average electrical power in pulses lasting up to 10 ms. The input waveform to the amplifier was generated by a computer-controlled field-programmable gate array (FPGA) board (Maxwell et al., 2017). The total acoustic output power for all three transducers was measured using an acoustic radiation force balance over the relevant power source voltage range (Maruvada et al., 2007). The acoustic power, Wac, was the same for the three transducers within 10% accuracy and depended on the power source output voltage, V, as follows:
| (1) |
Here the power and the voltage are given in watts and volts, respectively.
FIG. 2.
(Color online) (a) A photograph and (b) a schematic of the three 1.5 MHz HIFU transducer arrays with varying F-numbers—1.52, 1.02, and 0.77—used in the experiments. The arrays consisted of 12 air-backed sector elements bonded with tungsten epoxy to a rapid-prototyped acoustic lens. The transducers had a varying focal distance, R, but were otherwise identical. The central opening for in-line imaging or cavitation detection was 20 mm in diameter. (c) Axial and (d) transverse pressure distributions in the linear beam measured with a hydrophone in water (symbols) and numerically calculated (curves) based on the equivalent source model for the transducers with F-numbers 1.52, 1.02, and 0.77.
B. Acoustic characterization of nonlinear fields generated by the transducers
Each of the three transducers was characterized by a set of hydrophone measurements in conjunction with numerical modeling. First, low output measurements of acoustic pressure amplitude (linear propagation regime) were performed along the beam axis and in the focal plane using a calibrated capsule hydrophone (HGL-0200 hydrophone with an AH-2020 preamplifier set at 0 dB gain, 1−20 MHz bandwidth, 200 μm aperture, Onda Corp., Sunnyvale, CA). These low amplitude pressure scans were used to define an axially symmetric boundary condition at the apex plane for each transducer; the equivalent source represented by each boundary condition was then used as a basis for modeling nonlinear propagation with the Khokhlov-Zabolotskaya-Kuznetsov (KZK) equation (Canney et al., 2008; Rosnitskiy et al., 2016; Rosnitskiy et al., 2017). Parameters of the equivalent sources such as their focal distance, aperture, and initial pressure amplitude were determined by matching the modeled axial distributions of the pressure amplitude in the focal region of the linear beam to those measured in water with the hydrophone at low source output (Canney et al., 2008; Bessonova and Wilkens, 2013). The focal distance of the equivalent source was determined by matching the location of the pressure maximum on the beam axis, the equivalent aperture was found by matching the length of the focal lobe determined at the −6 dB level, and the equivalent pressure amplitude was calculated by matching pressure levels at the focus. The measured and modeled field scans are presented in Figs. 2(c) and 2(d). Such an approach for setting a boundary condition to the parabolic KZK model has been shown to provide accurate results for predicting pressure levels at the focus of nonlinear beams generated even by strongly focused HIFU transducers (Rosnitskiy et al., 2016; Rosnitskiy et al., 2017).
Another set of measurements was performed at the focus of the beam at high output levels using a fiber-optic probe hydrophone (FOPH2000, 100 μm fiber tip diameter, 100 MHz bandwidth, RP Acoustics, Leutenbach, Germany). The measurement location on the beam axis was determined by finding the position with the maximum peak positive pressure at the highest power output at which measurements were possible. At this location, focal pressure waveforms were measured at increasing source outputs starting from the low power level used in the linear beam scans. Nonlinear modeling was then performed at increasing source outputs using axially symmetric nonlinear KZK equation with the equivalent source boundary condition determined as described above (Rosnitskiy et al., 2016; Rosnitskiy et al., 2017). Simulated focal pressure waveforms were compared to direct measurements made in water with the fiber-optic probe hydrophone.
C. Experimental arrangement and phantom preparation
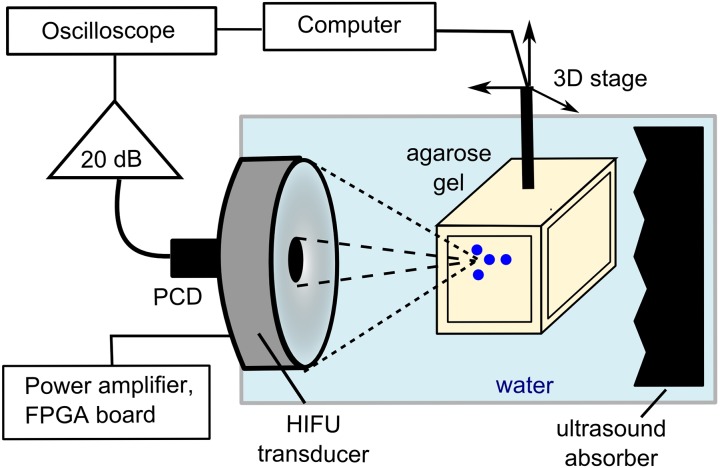
The diagram of the experimental setup used for passive measurements of cavitation activity in tissue-mimicking gel phantoms is presented in Fig. 3. A single-element, spherically focused 5 MHz transducer with 12 mm aperture and 63 mm radius of curvature (Olympus NDT) was inserted in the central opening of the HIFU transducer and served as a passive cavitation detector (PCD). The HIFU transducer and the PCD were mounted in a degassed, deionized water tank. The signals received by the PCD were amplified by 20 dB (Panametrics PR5072, Waltham, MA) and recorded by a digital oscilloscope (Keysight DSOX3034A) at a sampling frequency of 50 MHz and 10-bit vertical resolution. Note that the PCD and the HIFU transducers were aligned coaxially, but not confocally, due to the difference in the focal distances of the three transducers. The geometric focus of the PCD was closest to that of the most focused transducer with F-number 0.77; the geometric foci of two other transducers were located axially further away than that of the PCD.
FIG. 3.
(Color online) Diagram of the experimental setup for passive cavitation measurements. The same PCD fitted in the central opening of the HIFU transducer and coaxially aligned with it was used in the measurements with all three transducers. The axial position of the PCD focus coincided with that of the transducer with the F-number 0.77, but the not the foci of the two other transducers (F-numbers 1.02 and 1.52) that were located further due to the difference in the focal distances.
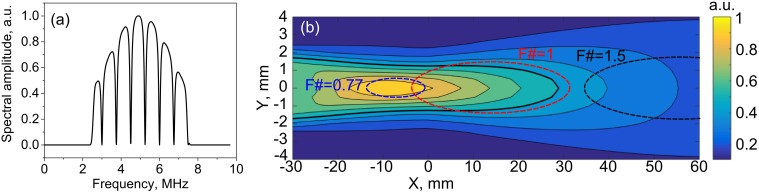
To quantitatively estimate the PCD sensitivity map and its position relative to the focal regions of the three transducers, the following approach was used. To model the acoustic signal produced by an inertially collapsing bubble, a short 1-ns uni-polar pulse emitted by a point source located at an arbitrary point in the axial plane of the transducer was considered. The impulse response of the PCD to such a signal was then calculated using the Rayleigh integral. The impulse response was then filtered in the frequency domain by a combination of a band-pass 1000th order Hamming filter within 2.5–7.5 MHz (matlab function fir1) and a second order IIR comb filter with a notch bandwidth of 100 kHz (matlab function iirnotch) applied at the HIFU frequency of 1.5 MHz and its harmonics [Fig. 4(a)]. The filtering was the same as that applied to signals recorded by the PCD during a HIFU pulse (following Li et al., 2014) to suppress the backscattered HIFU waves along with associated harmonics and ultraharmonics, thereby retaining only the broadband noise from inertial cavitation. The peak amplitude of this filtered impulse response in the time domain was then used as the metric for PCD sensitivity at any given point in the XY plane. The PCD sensitivity map obtained in this way is presented in Fig. 4(b), along with the relative positions of the focal regions of the three transducers at the first null level.
FIG. 4.
(a) (Color online) A combination of a band-pass filter (2.5 –7.5 MHz) and a notch-shaped comb filter applied to each PCD signal in the frequency domain to suppress the harmonics and ultraharmonics of HIFU backscattered by the gel, yet retain the broadband noise emitted by inertially collapsing bubbles. (b) Theoretically estimated distribution of the PCD sensitivity over the frequency range of the filter and relative positions of the focal regions (at the null level) of the three HIFU transducers. The thick black contour denotes the −6 dB level in the PCD sensitivity map. X = 0 corresponds to the geometric focus of the PCD.
Agarose gel (1.5% wt./vol.) was selected as a suitable tissue-mimicking gel material because it is non-toxic, easily fabricated, and has been used in multiple prior studies of cavitation dynamics (Maxwell et al., 2010; Li et al., 2014).The other advantage is that agarose gel has negligible attenuation at 1.5 MHz frequency, and its parameter of nonlinearity is close to that of water (Zeqiri et al., 2015; Culjat et al., 2010); therefore, the focal HIFU waveforms in the gel were expected to be the same as those measured in water. Agarose powder (UltraPure Agarose; Invitrogen) was added to deionized water (1.5% wt./vol. agarose/water). The resulting solution was placed into a microwave oven and allowed to boil for 10 min to displace any dissolved gases. The solution was then immediately poured into a plastic mold (5 cm × 5 cm × 8 cm) and rapidly cooled down by placing the mold into a large reservoir filled with room-temperature water. After polymerization, the phantom was transferred into a sample holder with acoustic windows on four sides and positioned in the water tank using a computer-controlled three dimensional (3D) positioning stage. The samples were positioned such that the HIFU transducer focus was 2 cm deep in the phantom, and the acoustic window edges were well outside of the beam path to avoid reflections. A large ultrasound absorber made of neoprene rubber was positioned behind the sample to prevent the reverberations within the water tank.
D. Pulsed HIFU exposures and PCD signal processing
All pHIFU exposures used in this study had the same pulsing protocol as that used in our prior studies (1 ms pulse duration, 1 Hz pulse repetition frequency, 60 pulses applied per focus location), differing only in the focal pressure levels (Li et al., 2014; Li et al., 2015). The rationale for this choice of the pulse length and low duty cycle (0.001) was based on an intent to avoid substantial heat deposition, especially at the higher pressure levels for which shocks formed. The pHIFU peak focal pressures were varied over the achievable range for each transducer, as characterized by hydrophone measurements and numerical modeling.
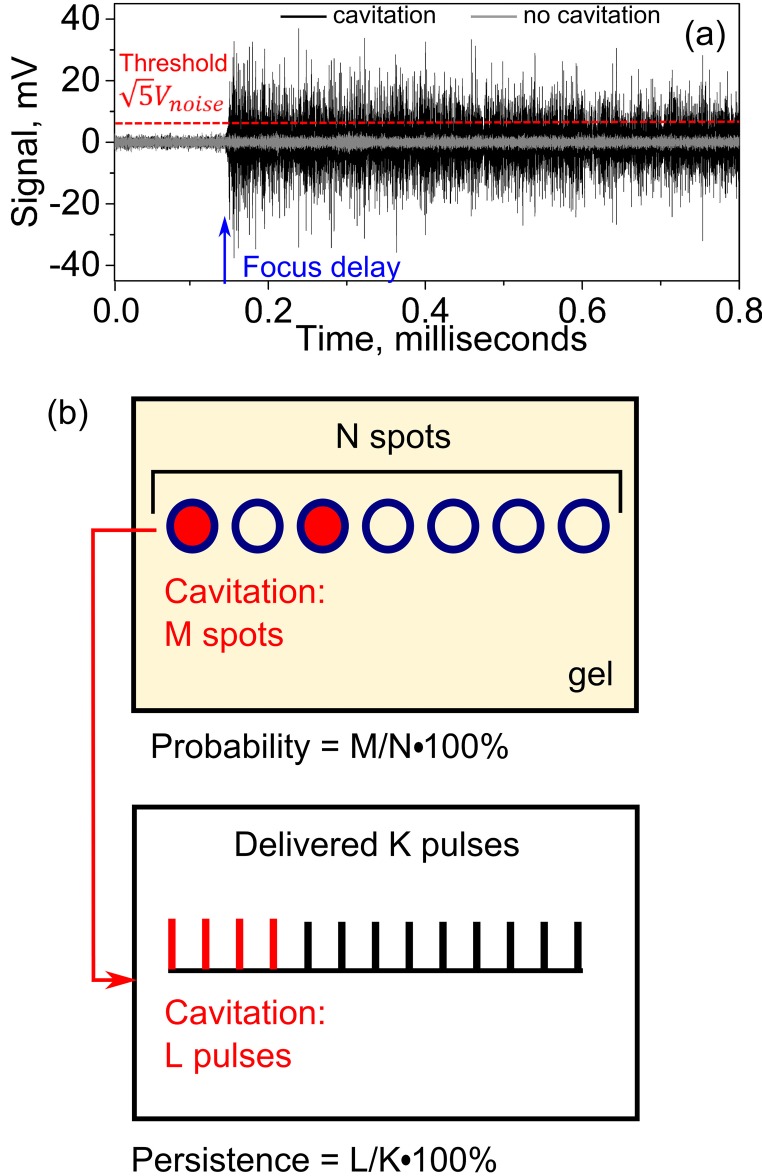
Processing and interpretation of the recorded and filtered PCD signals were undertaken as described by Li et al., 2014 and are illustrated in Fig. 5. Each filtered PCD signal was analyzed in the time domain to determine whether a cavitation event took place within each HIFU pulse [Fig. 5(a)]. The part of the signal arriving before the time point corresponding to the position of the HIFU transducer focus was considered as background noise, which was almost entirely electrical and was similar for the transducers of different F-numbers under the same output power. A cavitation event was considered to be observed if the peak signal value exceeded the peak value of the background noise by a factor of —the Rose criterion which ensures that the signal is distinguishable from the background noise (Rose, 1974). This approach allows to identify the axial location of the spot where cavitation starts, as well as to ensure the absence of prefocal cavitation that would manifest itself as cavitation signal arriving earlier than the signal from the focus. In this study, no prefocal cavitation was noted in any of the signals.
FIG. 5.
(Color online) PCD signal processing. (a) Two examples of a filtered PCD signals in the time domain. Focus delay is the time of ultrasound wave propagation from the pHIFU transducer surface to its focus and back to the PCD. A cavitation event was considered observed if the signal after the focus delay was larger than the noise preceding the focus delay by a factor of (Rose criterion)—the dashed horizontal line. The black and grey curves correspond to the PCD signals collected at the same output level of a HIFU transducer, with and without observed cavitation event. (b) Definition of cavitation probability and persistence. In the current studies 60 HIFU pulses at the same pressure level were applied to each of the 20 spots in the gel. Thus, N = 20 and K = 60.
The pHIFU exposures that corresponded to a given peak negative pressure at the focus of each HIFU transducer were applied to 20 points in total, with each focal spot being treated only once. Within a single gel sample, target sites were separated by 3 mm, so that the focal regions in the neighboring sites would not overlap [the largest focal region considered was 3.2 mm wide, Fig. 2(d)]. Two or three gel samples were used for each transducer. The collected PCD signals were processed as described above, and three cavitation metrics were extracted: cavitation probability, cavitation persistence, and broadband noise level. Cavitation probability at each pressure level was defined as the percentage of positions at which at least one cavitation event was observed. It therefore describes the percentage of regions containing nuclei with appropriate dimension to undergo inertial cavitation. Cavitation persistence was defined as the percentage of the HIFU pulses that induced a cavitation event among all pulses delivered at a single treatment position [see Fig. 5(b)]—i.e., it describes how well sustained the cavitation at a given treatment position across multiple pulses was. The mean and standard error values of the cavitation persistence were calculated over the 20 focal points corresponding to the same focal pressure levels. If for a given HIFU pulse a cavitation event was identified, broadband noise amplitude was calculated in the time domain as the root-mean-square (RMS) value of the filtered PCD signal, representing the broadband noise emitted by collapsing bubbles. The RMS calculation was performed starting from the time delay corresponding to the HIFU focus, and over the HIFU pulse duration. The broadband noise amplitude at a given focal pressure level was averaged over all HIFU pulses delivered to the 20 treatment locations.
III. RESULTS
A. Effect of transducer F-number on nonlinear distortion of the focal waveform
Figure 6(a) shows the dependence of the measured and modeled peak pressures in the focal waveforms on the power source voltage. As demonstrated, the measurement and modeling results are in a good agreement. Peak negative pressure exhibits monotonic growth as a function of input voltage; however, this growth is much slower than it would be if nonlinear propagation effects can be neglected. Conversely, peak positive pressure levels grow in a more complex way with source input voltage: slow linear growth initially, followed by rapid growth that ultimately slows at the highest voltages. As shown in our previous studies, the range of outputs where peak positive pressure increases rapidly corresponds to the formation of shock fronts in the pressure waveform at the focus; above this range, saturation is caused by absorption at the shocks that start to form prefocally (Bessonova and Wilkens, 2013).
FIG. 6.
(Color online) Experimental (circles) and theoretical (curves) peak positive and negative focal pressures (a) and shock amplitudes (b) for the transducers with F-numbers of 0.77, 1, and 1.5. (c) Focal waveforms containing fully developed shock measured (dashed curves) and theoretically predicted (solid thin curves) for the three transducers. Note the difference in the peak pressures for each waveform. (d) Focal waveforms with the same peak negative pressure of 5 MPa produced by the three transducers. Note the difference in the nonlinear waveform distortion and associated temporal asymmetry of the waveform (difference between the positive and negative phase durations).
Figure 6(b) shows the dependence of the measured and modeled shock amplitude in the focal waveform on the power source voltage. It is seen that shock formation occurs at lower voltages and at lower focal pressure levels for less focused transducers—i.e., transducers with higher F-numbers. In particular, focal waveforms with fully developed shocks are presented in Fig. 6(c). We define the shock as being “fully” developed when the acoustic pressure at the start of the shock is zero. This definition was recently introduced and implies that the shock amplitude is equal to the peak positive pressure in this case (Rosnitskiy et al., 2016). The parameters of the waveforms are listed in Table I. As seen, all waveforms are highly asymmetric, with the rarefaction phase duration being much longer than the compression phase duration, and peak positive pressure much higher than the peak negative pressure.
TABLE I.
Parameters of the developed shocks in the focal waveforms produced by the transducers with different F-numbers. The waveforms are shown in Fig. 6(c). t− and t+ are the durations of the rarefactional and compressional phases of the focal waveform, correspondingly. p+ and p− are peak positive and negative pressures in the waveform.
| F-number | Source voltage, V | p−, MPa | t−/t+ | p+/p− |
|---|---|---|---|---|
| 0.77 | 100 | 17 | 1.33 | 5.6 |
| 1.02 | 70 | 9 | 1.4 | 6.5 |
| 1.52 | 55 | 5 | 1.4 | 5.2 |
If the waveforms produced by the three transducers are plotted at the same peak negative pressure—for example, 5 MPa—the difference in nonlinear distortion can be appreciated [Fig. 6(d)]. For the least focused transducer, this output level corresponds to shock-forming conditions, which is associated with significantly stronger waveform asymmetry. The waveform corresponding to the transducer with F-number 1 exhibits only weak nonlinear distortion, whereas the waveform from the transducer with F-number 0.77 is almost linear.
B. Cavitation activity metrics in the agarose gel phantom
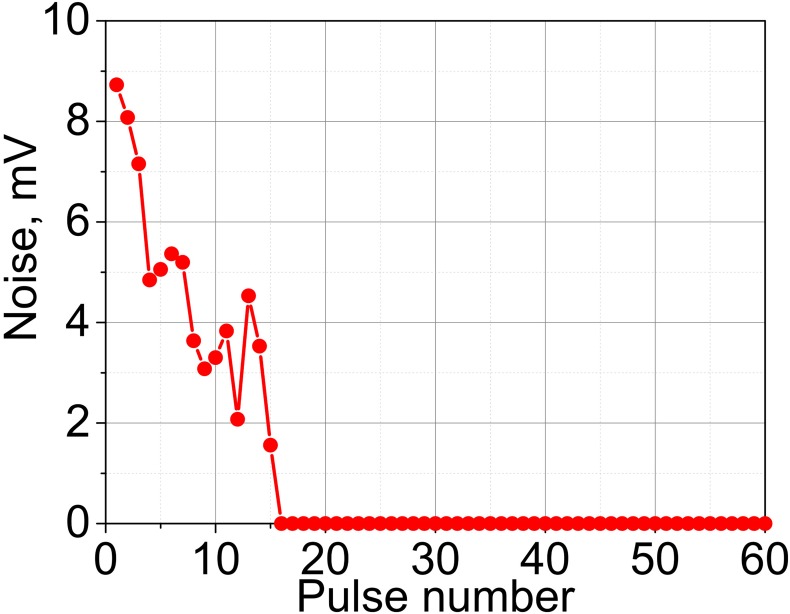
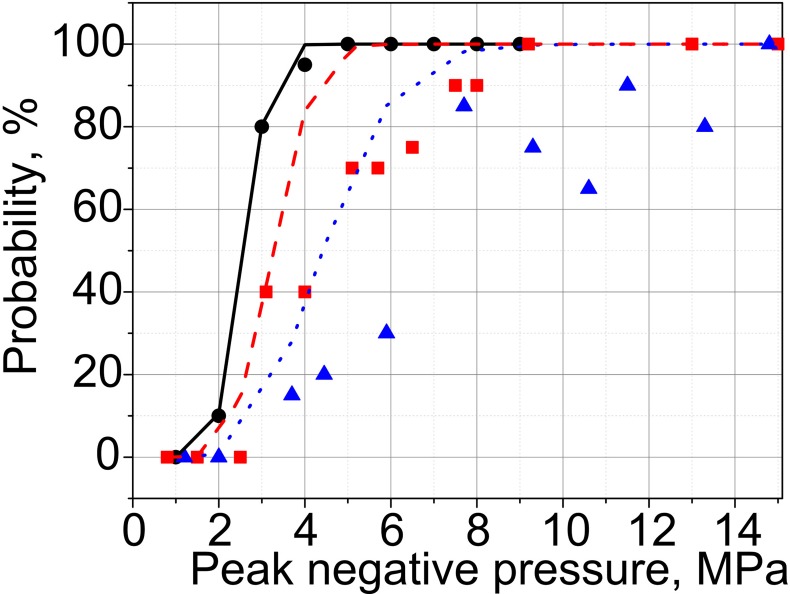
The results of PCD measurements in agarose gel samples are summarized in Fig. 7. As shown, the cavitation probability reaches 100%—the level shown necessary in our prior in vivo investigations for successful drug uptake (Li et al., 2015)—at 5, 9, and 14.8 MPa for the transducers with F-numbers of 1.5, 1, and 0.77, respectively. These levels correspond to the formation of (or approaching, for F-number 0.77) fully developed shocks at the focus. Persistence levels are also considerably different for the three transducers, and are overall higher for the less focused transducers. Notably, persistence does not reach 100% for any of the transducers. Consistent with our prior observations (Li et al., 2014), at each focal spot location the measurable cavitation activity is induced by the first few HIFU pulses, and then reduces and disappears. This means that although the first pulse (or the first few pulses) successfully induces inertial cavitation, probably from pre-existing nuclei, these bubbles dissolve before the next pulse arrives, and subsequent pulses do not encounter appropriate nuclei (Fig. 8). This effect is known as “liquid strengthening” or “nuclei conditioning” already observed in liquids, gels, and tissue (Wang et al., 2011). Although the level of 100% persistence was previously shown necessary to consistently achieve mechanical effects relevant to drug delivery in tissue in vivo, the low persistence values observed here are consistent with our prior measurements in agarose gel, where persistence is generally lower than in both ex vivo and in vivo tissue (Li et al., 2014).
FIG. 7.
(Color online) Metrics of inertial cavitation activity—probability (left), persistence (center), and noise level (right)—measured in the agarose gel phantom for the transducers with the F-numbers of 0.77 (triangles), 1.01 (squares), and 1.52 (circles). The rightmost panel represents broadband noise levels corrected for the difference in the sensitivity of PCD within the focal regions of the three transducers [see Fig. 4(b)]. The arrows indicate the output level corresponding to the formation of fully developed shock at the focus; shocks with smaller amplitudes form within 10% of that output level.
FIG. 8.
(Color online) A representative example of the broadband noise level detected by the PCD throughout the 60-pulse exposure.
Broadband noise levels [Fig. 7(c)] detected for each of the three transducers were very similar at the same p–. However, the distribution of PCD sensitivity at the spatial locations of the foci is very different for the three transducers [see Fig. 4(b)]: the area of the largest PCD sensitivity is co-located with the focal area of the transducer with the F-number 0.77, whereas at the focal locations of the F-number 1 and 1.5 transducers the sensitivity drops down to the relative levels of 0.7 and 0.2, respectively. Thus, if one introduces a simple correction by scaling the broadband noise levels for each transducer by the relative sensitivity of the PCD averaged over the focal areas of the transducers (see Fig. 4—0.9, 0.62, and 0.3 for the transducers with F-numbers 0.77, 1.02, and 1.52, respectively), it is seen that the noise levels are much higher for these transducers given the same p– [Fig. 7(d)]. This difference in PCD sensitivity between the three transducers probably affected probability and persistence as well. Unfortunately, it was not possible to make appropriate corrections to these metrics, given the application of the Rose criterion to each signal. However, since the background noise was electrical and did not scale with PCD sensitivity distribution, unlike the signals from the focal area, it is reasonable to assume that some cavitation events went undetected for the less focused transducers. Therefore, the difference in probability and persistence between the three transducers would be even more pronounced, if the difference in PCD sensitivity was taken into account.
IV. DISCUSSION AND CONCLUSIONS
As widely acknowledged, the onset and dynamics of inertial cavitation activity depend on the peak negative ultrasound pressure and the ultrasound frequency. This understanding is reflected in the definition of mechanical index (MI), which serves as a measure of ultrasound safety for cavitation-induced mechanical effects in tissue (Apfel and Holland, 1991; Nightingale et al., 2015). The reported experiments confirm that p– plays an important role in HIFU-induced cavitation: all inertial cavitation characteristics reported here—cavitation probability, persistence, and broadband noise level—increase with p–. However, the experiments also clearly indicate that p– is not the only parameter that governs cavitation activity: the metrics of cavitation appear to be highly dependent on the transducer F-number. These observations are consistent with recent reports by us and others (Li et al., 2015; Zhou et al., 2016; ter Haar et al., 2014; Maxwell et al., 2011). Several different mechanisms may be contributing to (or solely responsible for) this effect, and we will consider these mechanisms separately below.
First, the size of the focal region increases with F-number, and therefore the probability of encountering a suitable nucleus within that focal volume is also increased for weakly focused transducers (higher F-number). In order to evaluate theoretically how much this effect could contribute to the difference in cavitation probability between the three transducers, it was necessary to assume a model for distribution of the nuclei of different sizes through the medium. We followed the approach of Gateau et al. (2013), where the activation threshold of a nucleus of a certain size corresponds to Blake threshold, and the distribution of nuclei sizes is considered exponential, as reported in Yount et al. (1979) for gelatin,
| (2) |
where n is the concentration of nuclei, is the Blake threshold pressure (negative-valued) for a nucleus of the corresponding size, is the lowest nucleation threshold considered, MPa is atmospheric pressure, and n1 and P1 are medium-dependent fitting parameters. The cavitation probability at the focal peak negative pressure can then be estimated as follows (Gateau et al., 2013):
| (3) |
where is a volume in which the rarefaction pressure is below the threshold P and above the threshold P + dP, assuming that the peak focal rarefactional pressure is . To estimate , the focal volume of the transducer in question was considered as an ellipsoid, with a width and length , and volume . The width corresponded to the lateral size of the focal region, and length—to the axial size thereof, taken at the given pressure level from the measured distribution [Figs. 2(c) and 2(d)], scaled such that the maximum is equal to the peak focal pressure . The volume is then the difference between and .
The cavitation probability was numerically calculated according to the Eq. (3) for the transducer with the F-number of 1.5, and fitted to the experimental nucleation probability [Fig. 7(a)] using non-linear least-squares solver (matlab function lsqcurvefit), with two fitting parameters: n1 and P1. The unknown parameters of the model were thus determined from the best fit to be nucl/mL, MPa, with the coefficient of determination . The resulting theoretical probability distribution is plotted as a solid curve in Fig. 9, along with the experimental data points (circles). These fitting parameters were then used to generate theoretical probability distributions for the two other transducers (with the F-numbers of 0.77, and 1.02), and the results are plotted in Fig. 9 as dotted and dashed curves, respectively. As expected, the predicted probability curves are shifted towards lower pressures for less focused transducers, which is attributable only to the dimensions of the focal area. However, the difference between experimentally observed probability curves is much larger. We therefore speculate that the difference in focal volumes is likely to be a contributing mechanism, but not the only one.
FIG. 9.
(Color online) Theoretically estimated (curves) and experimentally observed (symbols) cavitation probabilities for the transducers with F-numbers of 1.52 (solid line and circles), 1.02 (dashed line and squares), and 0.77 (dotted line and triangles). The theoretical model [Eq. (3)] was meant to account for the effect of the difference in focal volumes on the difference in cavitation probability between the three transducers. The model fit was first performed to the experimental data for the transducer with F-number = 1.52; the model parameters that provided the best data fit in the least-mean-squares sense were then used to calculate the cavitation probability curves for the two other transducers. As seen, the difference between theoretically estimated probability curves is much smaller than that between the experimental data, which indicates that the increase in focal volume may be a contributing factor to enhanced cavitation probability, but unlikely the only one.
Similarly, there is a substantial difference in cavitation persistence between the transducers with different F-numbers, with less focused transducers providing higher persistence. Higher persistence may indicate that a cavitation nucleus excited by the first pulse either grew into a large enough bubble by the end of that pulse to persist until the next pulse arrives or collapsed in such a manner as to provide cavitation nuclei for the subsequent pulse. This, too, may potentially be affected by the difference in focal volumes (the smaller the volume, the lower the chance of encountering suitable nuclei), but again, it is unlikely to be the only mechanism. Cavitation noise level, when not corrected for the difference in the PCD sensitivity, appears similar for the three transducers at the same p–. However, a rough correction to the broadband noise levels encountered by the transducers with F-numbers 1.02 and 1.52, according to the calculated PCD sensitivity map [see Fig. 3(b)], yields a substantial difference in the detected noise level for the three transducers at the same p–. Qualitatively, the difference in focal volumes may be a contributing factor in this effect as a larger number of bubbles could potentially be excited within the focal volume of a less focused transducer. This would be challenging to evaluate quantitatively without direct observation of bubble activity, as it is not known whether higher noise amplitude stems from a more energetic collapse of a single bubble or a cumulative effect of multiple bubble collapses.
A different parameter hypothesized to be responsible for the observed difference in cavitation metrics is the degree of nonlinear distortion of the focal waveform. Given the same peak negative focal pressures, nonlinear distortion is greater for weakly focused transducers, and a shock front forms at the focus at substantially lower p–, as confirmed by measurements and modeling of the acoustic outputs of the three transducers considered here (Fig. 6). There are several ways in which nonlinear distortion of the waveform and shock formation can potentially enhance the cavitation activity and explain the observed differences in cavitation metrics.
First, the nonlinear waveform asymmetry (the difference in duration of the compression and rarefaction phases) can have a rectifying effect on bubble oscillations, whereby the bubble grows on average during each acoustic cycle (Kreider et al., 2013; Bader and Holland, 2016). This rectified growth phenomenon was interpreted as follows: if the bubble reaches a large enough size, the associated inertia makes the bubble more responsive during the longer-duration tensile phase compared to the shorter-duration compressive phase. The influence of nonlinear distortion on bubble radius-time curves and the corresponding impact on gas diffusion are relevant to the likelihood that cavitation nuclei will grow faster during the pulse and persist between consecutive ultrasound pulses. Furthermore, the shock front incident on a bubble can distort its spherical shape and thereby promote asymmetric collapses and jetting (Johnsen and Colonius, 2009). Asymmetric collapses typically involve less dissipation from acoustic radiation, which will lead to larger bubble rebounds that promote bubble growth through diffusion of non-condensable gases. Yet another potential mechanism for promoting inertial cavitation nucleation is the inversion of shock wave polarity during its reflection from bubbles acting as a pressure release interface. This effect was previously demonstrated for histotripsy exposures at very high peak negative pressures (Maxwell et al., 2011). Due to the fact that the shock front has submicron thickness, theoretically any bubble of several microns in size (or larger) could serve as a pressure-release reflector that would invert the waveform. Therefore, the effective p– near such bubbles significantly increases, which may result in nucleation of additional bubbles adjacent to the initial one. The strength of this effect was shown to be dependent on the size of the initial bubble: formation of histotripsy-type dense bubble clouds was only observed in water with initial bubble reaching ∼50–100 μm size.
In addition to the mechanisms described above related to asymmetric pressure waveforms, the presence of shocks is also associated with local, transient temperature elevations. Shock-induced heating during the HIFU pulse may enhance bubble nucleation and growth; moreover, additional heating may occur in the immediate vicinity of any excited bubbles. For the range of shock amplitudes considered here, temperature elevations can be estimated from weak shock theory (Canney et al., 2010) as follows: 0.34 °C–4.6 °C, 8 °C–38 °C, and 32 °C per pulse for the transducers with F-numbers of 1.5, 1.02, and 0.77, respectively. Given the pulse repetition frequency of 1 Hz, corresponding steady-state heat buildups over the duration of a single-site exposure leads to temperature rises [estimated using a Gaussian model of heat diffusion (Parker, 1983)] of 0.1 °C–1.4 °C, 1.2 °C–5 °C, and 3.6 C. Temperature elevation per pulse is largest for the most focused transducer and lowest for the least focused transducer due to the differences in shock amplitude achievable at the focus. This effect of transient local temperature elevation is expected to contribute to bubble nucleation and persistence for all transducers when shock-forming conditions are reached at the focus. Indeed, the levels of cavitation probability and persistence are similar across the three transducers within the shock-forming range of outputs.
In this work, a specific pHIFU protocol designed for drug delivery was considered: pulse duration was kept at 1 ms, and the duty cycle—at 0.1%. It is as yet not entirely clear, how the pulse duration and duty cycle would affect cavitation metrics. Most studies investigating the behavior of cavitation bubbles in response to ultrasound wave bursts have either focused on short pulses of near linear ultrasound waves typical of diagnostic applications (Nightingale et al., 2015), or on single high amplitude shock waves typical of extracorporeal shock wave lithotripsy (Kreider et al., 2011), or on very short (1–20 cycles) ultrasound pulses with very high peak negative pressures (over 20 MPa) used in histotripsy and microtripsy (Maxwell et al., 2011; Maxwell et al., 2013; Gateau et al., 2013; Vlaisavljevich et al., 2017). In particular, in Vlaisavljevich et al. (2017) the dependence of microtripsy efficiency and intrinsic cavitation threshold on transducer F-number within the 0.5–0.89 range was studied in agarose gel phantoms. In that study, the increase in F-number was shown to not affect the intrinsic cavitation threshold, but to negatively affect the ablation efficiency due to the increase in size and decrease in density of the bubble cloud. This difference in conclusion from our study is likely explained by the difference in HIFU excitation as well as potential difference in the populations of nuclei the exposures are exciting. Vlaisavljevich et al., 2017 used a very short HIFU pulse (⩽2 cycles) with a single dominant negative pressure phase to excite cavitation that was hypothesized to originate from ubiquitous nanometer-sized nuclei, also known as homogeneous nucleation (Maxwell et al., 2013). Cavitation observed in the 25–33 MPa range of tensile pressures with these very short pulses is weakly dependent on the ultrasound frequency, but is unable to excite bubbles at lower amplitudes consistently (Vlaisavljevich et al., 2015). Our exposures used sixty 1500-cycle long pulses at lower amplitudes and likely excited a different population of nuclei—randomly distributed sites with gas bodies stabilized by impurities, also known as heterogeneous or incidental nucleation. Such lower-amplitude, longer exposures may be exciting larger nuclei or causing changes in the size of nuclei over the longer pulse duration. The definitions of cavitation threshold in Vlaisavljevich et al. (2017) and in the present work are also notably different and are not directly comparable. The threshold in microtripsy-type exposures (Maxwell et al., 2013; Vlaisavljevich et al., 2015; Vlaisavljevich et al., 2017) termed “intrinsic” was defined to correspond to 50% probability of cavitation within a single acoustic cycle, whereas in our exposures the threshold is defined as corresponding to 100% probability of at least one cavitation event over a large number of acoustic cycles. The two different thresholds have been defined for microtripsy and pHIFU applications because they, respectively, correlate with different bioeffects—namely, disintegration of tissue into subcellular debris using short pulses and facilitation of drug penetration using long pulses to produce scattered, micron-scaled damage to tissue (Li et al., 2014; Li et al., 2015).
In another recent study (Haller and Wilkens, 2018), inertial cavitation induced by a 1 MHz HIFU transducer in 3% agar gel phantoms was investigated at varying pulse durations (10 ms−1 s) and duty cycles (2 × 10−5%–100%). Although the methods for detection and analysis of broadband noise emissions were different from those used here, the results were reported in terms of cavitation probability curves, similarly to our study. The findings confirm the overall consensus in the field that both parameters affect cavitation dynamics, with longer pulses and higher duty cycles leading to the lowering of inertial cavitation threshold.
In conclusion, the results of our study demonstrate that the inertial cavitation metrics, as observed by PCD measurements, depend strongly on the F-number of the ultrasound transducer, given the same source frequency and peak negative pressure at the focus. The hypothesized reason for this effect is enhancement of bubble nucleation, growth, and activity by nonlinear distortion of the focal waveform and shock formation, which are largely determined by the transducer F-number. Although the results presented here empirically support this hypothesis, a more direct investigation of the phenomenon would involve the observation and numerical modeling of shock wave interaction with cavitation nuclei and associated bubble dynamics. This is planned in future work. Nonetheless, we believe that the empirically driven conclusions from this effort have important implications in the field of cavitation-aided drug delivery. Specifically, the use of less focused and therefore smaller-footprint transducers appears to be beneficial in terms of achieving desired cavitation activity levels and bioeffects at lower in situ pressures.
ACKNOWLEDGMENTS
The authors would like to thank Theresa A. Zwaschka for the assembly of the transducers and Petr Yuldashev for providing the database of the multi-parametric solutions to the KZK equation. We gratefully acknowledge funding support from National Institutes of Health R01EB023910, K01DK104854, and R01EB7643 and NIH/RFBR 17-54-33034.
References
- 1. Apfel, R. E. , and Holland, C. K. (1991). “ Gauging the likelihood of cavitation from short-pulse, low-duty cycle diagnostic ultrasound,” Ultrasound Med. Biol. 17, 179–185. 10.1016/0301-5629(91)90125-G [DOI] [PubMed] [Google Scholar]
- 2. Bader, K. B. , and Holland, C. K. (2016). “ Predicting the growth of nanoscale nuclei by histotripsy pulses,” Phys. Med. Biol. 61(7), 2947–2966. 10.1088/0031-9155/61/7/2947 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Bessonova, O. V. , and Wilkens, V. (2013). “ Membrane hydrophone measurement and numerical simulation of HIFU fields up to developed shock regimes,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 60(2), 290–300. 10.1109/TUFFC.2013.2565 [DOI] [PubMed] [Google Scholar]
- 4. Canney, M. , Khokhlova, V. , Bessonova, O. , Bailey, M. , and Crum, L. (2010). “ Shock-induced heating and millisecond boiling in gels and tissue due to high intensity focused ultrasound,” Ultrasound Med. Biol. 36(2), 250–267. 10.1016/j.ultrasmedbio.2009.09.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Canney, M. S. , Bailey, M. R. , Crum, L. A. , Khokhlova, V. A. , and Sapozhnikov, O. A. (2008). “ Acoustic characterization of high intensity focused ultrasound fields: A combined measurement and modeling approach,” J. Acoust. Soc. Am. 124(4), 2406–2420. 10.1121/1.2967836 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Culjat, M. O. , Goldenberg, D. , Tewari, P. , and Singh, R. S. (2010). “ A review of tissue substitutes for ultrasound imaging,” Ultrasound Med. Biol. 36(6), 861–873. 10.1016/j.ultrasmedbio.2010.02.012 [DOI] [PubMed] [Google Scholar]
- 7. Gateau, J. , Taccoen, N. , Tanter, M. , and Aubry, J. F. (2013). “ Statistics of acoustically induced bubble-nucleation events in in vitro blood: A feasibility study,” Ultrasound Med. Biol. 39(10), 1812–1825. 10.1016/j.ultrasmedbio.2013.04.011 [DOI] [PubMed] [Google Scholar]
- 8. Haller, J. , and Wilkens, V. (2018). “ Determination of acoustic cavitation probabilities and thresholds using a single focusing transducer to induce and detect acoustic cavitation events: II. Systematic investigation in an agar material,” Ultrasound Med. Biol. 44(2), 397–415. 10.1016/j.ultrasmedbio.2017.10.007 [DOI] [PubMed] [Google Scholar]
- 9. Johnsen, E. , and Colonius, T. (2009). “ Numerical simulations of non-spherical bubble collapse,” J. Fluid. Mech. 629, 231–262. 10.1017/S0022112009006351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Kreider, W. , Crum, L. A. , Bailey, M. R. , and Sapozhnikov, O. A. (2011). “ Observations of the collapses and rebounds of millimeter-sized lithotripsy bubbles,” J. Acoust. Soc. Am. 130(5), 3531–3540. 10.1121/1.3626157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Kreider, W. , Maxwell, A. D. , Khokhlova, T. , Simon, J. C. , Khokhlova, V. A. , Sapozhnikov, O. , and Bailey, M. R. (2013). “ Rectified growth of histotripsy bubbles,” Proc. Mtgs. Acoust. 19(1), 075035. 10.1121/1.4800326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Lammers, T. , Kiessling, F. , Hennink, W. E. , and Storm, G. (2012). “ Drug targeting to tumors: Principles, pitfalls and (pre-) clinical progress,” J. Control Release 161(2), 175–187. 10.1016/j.jconrel.2011.09.063 [DOI] [PubMed] [Google Scholar]
- 13. Li, T. , Chen, H. , Khokhlova, T. , Wang, Y. N. , Kreider, W. , He, X. , and Hwang, J. H. (2014). “ Passive cavitation detection during pulsed HIFU exposures of ex vivo tissues and in vivo mouse pancreatic tumors,” Ultrasound Med. Biol. 40(7), 1523–1534. 10.1016/j.ultrasmedbio.2014.01.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Li, T. , Wang, Y. N. , Khokhlova, T. D. , D'Andrea, S. , Starr, F. , Chen, H. , McCune, J. S. , Risler, L. J. , Mashadi-Hossein, A. , and Hwang, J. H. (2015). “ Pulsed high-intensity focused ultrasound enhances delivery of doxorubicin in a preclinical model of pancreatic cancer,” Cancer Res. 75(18), 3738–3746. 10.1158/0008-5472.CAN-15-0296 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Maruvada, S. , Harris, G. R. , Herman, B. A. , and King, R. L. (2007). “ Acoustic power calibration of high-intensity focused ultrasound transducers using a radiation force technique,” J. Acoust. Soc. Am. 121(3), 1434–1439. 10.1121/1.2431332 [DOI] [PubMed] [Google Scholar]
- 16. Maxwell, A. D. , Cain, C. A. , Hall, T. L. , Fowlkes, J. B. , and Xu, Z. (2013). “ Probability of cavitation for single ultrasound pulses applied to tissues and tissue-mimicking materials,” Ultrasound Med. Biol. 39(3), 449–465. 10.1016/j.ultrasmedbio.2012.09.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Maxwell, A. D. , Wang, T. Y. , Cain, C. A. , Fowlkes, J. B. , Sapozhnikov, O. A. , Bailey, M. R. , and Xu, Z. (2011). “ Cavitation clouds created by shock scattering from bubbles during histotripsy,” J. Acoust. Soc. Am. 130(4), 1888–1898. 10.1121/1.3625239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Maxwell, A. D. , Wang, T. Y. , Yuan, L. , Duryea, A. P. , Xu, Z. , and Cain, C. A. (2010). “ A tissue phantom for visualization and measurement of ultrasound-induced cavitation damage,” Ultrasound Med. Biol. 36(12), 2132–2143. 10.1016/j.ultrasmedbio.2010.08.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Maxwell, A. D. , Yuldashev, P. V. , Kreider, W. , Khokhlova, T. D. , Schade, G. R. , Hall, T. L. , Sapozhnikov, O. A. , Bailey, M. R. , and Khokhlova, V. A. (2017). “ A prototype therapy system for transcutaneous application of boiling histotripsy,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 64(10), 1542–1557. 10.1109/TUFFC.2017.2739649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Nightingale, K. R. , Church, C. C. , Harris, G. , Wear, K. A. , Bailey, M. R. , Carson, P. L. , Jiang, H. , Sandstrom, K. L. , Szabo, T. L. , and Ziskin, M. C. (2015). “ Conditionally increased acoustic pressures in nonfetal diagnostic ultrasound examinations without contrast agents: A preliminary assessment,” J. Ultrasound Med. 34(7), 1–41. 10.7863/ultra.34.7.15.13.0001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Parker K. J. (1983). “ The thermal pulse decay technique for measuring ultrasonic absorption coefficients,” J. Acoust. Soc. Am. 74, 1356–1361. 10.1121/1.390159 [DOI] [Google Scholar]
- 22. Rapoport, N. , Nam, K. H. , Gupta, R. , Gao, Z. , Mohan, P. , Payne, A. , Todd, N. , Liu, X. , Kim, T. , Shea, J. , Scaife, C. , Parker, D. L. , Jeong, E. K. , and Kennedy, A. M. (2011). “ Ultrasound-mediated tumor imaging and nanotherapy using drug loaded, block copolymer stabilized perfluorocarbon nanoemulsions,” J. Controlled Release 153(1), 4–15. 10.1016/j.jconrel.2011.01.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Rose A. (1974). Vision: Human and Electronic ( Plenum, New York: ). [Google Scholar]
- 24. Rosnitskiy, P. B. , Yuldashev, P. V. , Sapozhnikov, O. A. , Maxwell, A. D. , Kreider, W. , Bailey, M. R. , and Khokhlova, V. A. (2017). “ Design of HIFU transducers for generating specified nonlinear ultrasound fields,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 64(2), 374–390. 10.1109/TUFFC.2016.2619913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Rosnitskiy, P. B. , Yuldashev, P. V. , Vysokanov, B. A. , and Khokhlova, V. A. (2016). “ Setting boundary conditions to the Khokhlov–Zabolotskaya equation for modeling ultrasound fields generated by strongly focused transducers,” Acoust. Phys. 62(2), 151–159. 10.1134/S1063771016020123 [DOI] [Google Scholar]
- 26. Sennoga, C. A. , Kanbar, E. , Auboire, L. , Dujardin, P. A. , Fouan, D. , Escoffre, J. M. , and Bouakaz, A. (2017). “ Microbubble-mediated ultrasound drug-delivery and therapeutic monitoring,” Expert Opin. Drug Deliv. 14(9), 1031–1043. 10.1080/17425247.2017.1266328 [DOI] [PubMed] [Google Scholar]
- 27. ter Haar, G. , Civale, J. , Rivens, I. , and Costa, M. (2014). “ Cavitation threshold determination—Can we do it?,” J. Acoust. Soc. Am. 136(4), 2301. 10.1121/1.4900324 [DOI] [Google Scholar]
- 28. Vlaisavljevich, E. , Gerhardson, T. , Hall, T. , and Xu, Z. (2017). “ Effects of F-number on the histotripsy intrinsic threshold and cavitation bubble cloud behavior,” Phys. Med. Biol. 62(4), 1269–1290. 10.1088/1361-6560/aa54c7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Vlaisavljevich, E. , Lin, K. W. , Maxwell, A. , Warnez, M. T. , Mancia, L. , Singh, R. , Putnam, A. J. , Fowlkes, B. , Johnsen, E. , Cain, C. , and Xu, Z. (2015). “ Effects of ultrasound frequency and tissue stiffness on the histotripsy intrinsic threshold for cavitation,” Ultrasound Med. Biol. 41(6), 1651–1667. 10.1016/j.ultrasmedbio.2015.01.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Wang, T. Y. , Xu, Z. , Hall, T. , Fowlkes, J. , Roberts, W. , and Cain, C. (2011). “ Active focal zone sharpening for high-precision treatment using histotripsy,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58(2), 305–315. 10.1109/TUFFC.2011.1808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Yount, D. E. , Yeung, C. M. , and Ingle, F. W. (1979). “ Determination of the radii of gas cavitation nuclei by filtering gelatin,” J. Acoust. Soc. Am. 65, 1440–1450. 10.1121/1.382905 [DOI] [Google Scholar]
- 32. Zeqiri, B. , Cook, A. , Rétat, L. , Civale, J. , and ter Haar, G. (2015). “ On measurement of the acoustic nonlinearity parameter using the finite amplitude insertion substitution (FAIS) technique,” Metrologia 52(2), 406–422. 10.1088/0026-1394/52/2/406 [DOI] [Google Scholar]
- 33. Zhou, Y. , Wang, Y. N. , Farr, N. , Zia, J. , Chen, H. , Ko, B. M. , Khokhlova, T. , Li, T. , and Hwang, J. H. (2016). “ Enhancement of small molecule delivery by pulsed high-intensity focused ultrasound: A parameter exploration,” Ultrasound Med. Biol. 42(4), 956–963. 10.1016/j.ultrasmedbio.2015.12.009 [DOI] [PMC free article] [PubMed] [Google Scholar]