Dynamic modelling of personal protection control strategies for vector-borne disease limits the role of diversity amplification

Abstract

Personal protection measures, such as bed nets and repellents, are important tools for the suppression of vector-borne diseases like malaria and Zika, and the ability of health agencies to distribute protection and encourage its use plays an important role in the efficacy of community-wide disease management strategies. Recent modelling studies have shown that a counterintuitive diversity-driven amplification in community-wide disease levels can result from a population's partial adoption of personal protection measures, potentially to the detriment of disease management efforts. This finding, however, may overestimate the negative impact of partial personal protection as a result of implicit restrictive model assumptions regarding host compliance, access to and longevity of protection measures. We establish a new modelling methodology for incorporating community-wide personal protection distribution programmes in vector-borne disease systems which flexibly accounts for compliance, access, longevity and control strategies by way of a flow between protected and unprotected populations. Our methodology yields large reductions in the severity and occurrence of amplification effects as compared to existing models.

1. Introduction

The use of epidemiological modelling to study vector-borne diseases has a long history, dating back over 50 years to the classic Ross–MacDonald model [1–3]. Since then, there have been numerous extensions and adaptations [4,5], including spatial dynamics [6], host heterogeneity [7,8], seasonality [9], stochasticity [10] and control [11,12]. There has also been some degree of debate regarding model formulation [13], such as the form of the biting rate and, by extension, disease transmission [14,15]. Unfortunately, different assumptions regarding biting rates can influence predictions for when and where a disease is capable of spreading, as well as estimates of disease controllability.

Model assumptions regarding disease management can also strongly impact estimates of disease controllability. This is particularly true of personal protection. Recently, Miller et al. [16] used a model with two classes of hosts—a protected class and an unprotected class—to show that, in contrast to predictions from simpler models [11,17–21], personal protection use by only sub-portions of the host population can actually worsen an outbreak of a vector-borne disease. This is a result of diversity amplification—an effect in vector-borne disease epidemiology which relates increases in overall disease prevalence to increases in host diversity [22–26]. Amplification is a potential risk whenever vectors preferentially concentrate attacks on sub-populations with high infection susceptibilities [26]. This occurs, for example, when partial personal protection coverage causes mosquitoes to divert from protected individuals and focus bites on unprotected individuals [16,27,28]. Diversion can lead to rapid disease spread within the unprotected sub-population and, consequently, personal protection models which incorporate vector diversion have the potential to display counterintuitive increases in disease severity [16,26,28,29].

Many vector-borne disease models which use multiple host classes and, by extension, potentially exhibit protection-induced diversity amplification (e.g. [16,26,28,29]) suffer from a common shortcoming—assignment of individuals to protected and unprotected classes is assumed static. Some models do allow for hosts who only intermittently apply personal protection (such as hosts who sleep under bed nets only at night), but even in these cases, assignments to sporadically protected and completely unprotected classes typically remain fixed [28,29]. In reality, protection status is dynamic: people forget to apply repellent, run out of repellent, wear down their bed nets, or grow weary of protection efforts and thus falter in compliance [30,31], and non-compliant individuals can potentially re-acquire protection or re-adopt its use. This is particularly true if rigorous campaign initiatives are mounted in support of personal protection use. Consequently, there exists a flux of hosts into and out of the protected class, and this implies that mosquito focusing on unprotected individuals is actually more diffuse than indicated by static protection class models. Furthermore, static protection classes necessitate that control strategies, for example, the supplying protection or partaking in public service announcements by a health agency, be incorporated into models as direct influences over the proportions of the two host populations. More realistically, however, distribution constraints and socioeconomic factors which deter compliance [30,31] severely limit controllability over the actual number of protected individuals, and control efforts will instead have a direct influence over the flux between the protected and unprotected classes. That is, the more health agencies do to make available and encourage the use of personal protection, the more likely people are to adopt and re-adopt personal protection.

In this paper, we present a methodology for modelling personal protection which accounts for flow between the protected and unprotected classes. Specifically, we build a model similar to that in Miller et al. [16], but include movement between classes that we assume to be proportional to control effort. We then study the impact of movement between the protected and unprotected classes assuming frequency-dependent (gonotrophic-limited) transmission, density-dependent (search-limited) transmission and an intermediate scenario that necessitates a functional response approach. Interestingly, we find that movement between classes and indeed, classes in general, do not matter strongly in the density-dependent limit. However, for the other two scenarios, there is strong divergence between our model, an analogous model with static protected and unprotected classes, and a simpler personal protection model with a homogeneous host population. Whereas our model predicts increased disease spread relative to the model with only a single class of hosts, it predicts decreased disease spread relative to the model with fixed protected and unprotected classes. From this model behaviour, we conclude that hosts' propensity to move between protected and unprotected classes can severely hamper a mosquito's ability to focus bites on any one group of individuals, thus mitigating the potential for diversity amplification effects. Consequently, our results indicate that, relative to our model, models with static protection classes generally overestimate parameter ranges over which protection-induced disease amplification will be a practical concern. Our work provides not only a strong theoretical foundation for modelling methodology, but also a partial explanation for the disparity between theoretical prediction of protection-induced diversity amplification and, to the best of our knowledge, its apparent lack of observation in the field.

2. Methods

Here, we outline the basic components of our modelling methodology and the biological facts on which they are based. These details will be used in §§3 and 4 to discern the effects of our methodology on protection-induced amplification and disease controllability in a simple SIR epidemic model, and will also serve as a general schematic for incorporating personal protection control strategies into more complicated vector-borne disease models in future work.

2.1. The biology of mosquito biting rates and personal protection

2.1.1. Mosquito–host interaction

Female mosquitoes require vertebrate blood in order to produce viable eggs. The human disease vectors Aedes aegypti and Anopheles gambiae exhibit a strong preference for human blood [32], and the process of acquiring and handling blood meals can be described in terms of three basic phases of mosquito behaviour. The average amount of time required to complete each phase determines the average rate at which mosquitoes can bite. In Ae. aegypti, for example, the initial phase is a long-range search mode which begins with a mosquito taking flight after detecting a CO₂ plume [33,34]. During this phase, Ae. aegypti mosquitoes investigate visual features and drift through the plume towards its source by surging upwind and casting crosswind [33,34]. The second phase is a short-range identification and landing mode which begins once a mosquito approaches a plume source. In this second phase, Ae. aegypti determine whether and where to land by integrating heat, moisture and olfactory sensory cues [33,34], while gustatory and heat sensory cues govern precisely when and where a mosquito will bite to take a blood meal [32]. Taking a sufficiently large blood meal initiates the third behaviour phase—the typically 3-day-long gonotrophic cycle over which a mosquito processes the blood, finds a nesting site, lays eggs and becomes hungry for the next blood-meal [35]. Although some mosquito species can take multiple blood meals during a single gonotrophic cycle [35], for simplicity, we will consider models which assume one blood meal per gonotrophic cycle.

2.1.2. Mosquito response to bed nets

One method for reducing mosquito contacts with humans is to disrupt the mosquito–host interaction with the use of bed nets. Because CO₂, volatile skin chemicals, heat and moisture plumes readily pass through net meshing, bed nets interfere with neither the initial long-range search phase nor the identification and approach portion of the second short-range phase (spatial repellency effects of insecticide-treated nets are observed to be weak or non-existent) [36,37]. Bed nets do, however, interfere with the landing portion of short-range phase by physically blocking mosquitoes from reaching landing sites, thus preventing biting and the transition to the final gonotrophic phase. Mosquito enter/exit rates at net-occupied dwellings [37] suggest that there is a limit to the amount of time that mosquitoes will attempt to gain access to net-protected human hosts, after which they will abandon the effort and leave to find blood elsewhere.

2.1.3. Mosquito response to personal repellents

A second method for disrupting the mosquito–host interaction is the use of mosquito repellents, most notably DEET. DEET is a broadly effective chemical repellent with volatile and non-volatile odorant [38] and tastant [39] properties, although the precise biological modes of action are still a subject of debate [40]. DEET applied to the skin provides effective protection for many hours, so its efficacy likely results from a low volatile compound, implicating a contact repellent or anti-feedant which cannot interfere with the long-range search phase of the host-seeking process. Both contact repellents and anti-feedants act by inducing taste avoidance mechanisms in mosquitoes [39]; experiments show that mosquitoes do not bite and are repelled within tens of milliseconds after contact with a DEET-treated section of human skin [38]. Thus, like bed nets, DEET interferes with the second short-range phase of host-seeking by preventing biting after a host has been located and identified.

2.2. Biting rate model

Ignoring personal protection for a moment, consider a population of humans of density N_h homogeneously distributed throughout a unit area, Ω. We denote by f the average rate at which the human population is bitten by a single mosquito, also located within Ω. Following Miller et al. [16], Yakob [41] and Antonovics et al. [42], we assume a Holling type-II functional response [43–45] for f:

2.1

where

2.2

In the above two formulae, A denotes the random search rate, where 1/A is defined as the average time taken per unit area by an actively searching mosquito to locate a single human, and β_b denotes the probability for a mosquito to deliver a successful bite to a host once the target has been located and identified. Note that β_b generally differs from unity due to the human ability to spot and avoid approaching mosquitoes, a mosquito's capacity to make mistakes and misidentify targets, and disruption from random environmental factors. The quantity τ_H denotes the handling time and is defined as the average time taken by a mosquito to identify, engage and process the blood meal from a single human after the human has been located. The handling time is written in terms of a pre- and post-bite handling time, denoted by τ₀ and τ, respectively, in equation (2.2).

The parameters A, τ₀ and τ are each associated with a specific phase of mosquito host-seeking and blood processing. The random search rate, A, is associated with the long-range first phase, and 1/A is therefore the average time per unit area a mosquito spends exploring the CO₂ landscape and investigating non-human visual features while attempting to locate a unit density of humans. This term depends on the size of the unit area Ω, the details of the carbon dioxide landscape as determined by both human and non-human sources, and a range of species-specific and environmental factors. The pre-bite handling time, τ₀, is the average time required to complete the short-ranged second phase of the host seeking process. Owing to the short-ranged nature of this interaction mode, we expect τ₀ to be of the order of minutes or, at most, hours. The post-bite handling time, τ, is the gonotrophic cycle time corresponding to the third phase, and is thus of the order of days [35].

The type-II functional response's capacity to account for gonotrophic, density and behavioural limitations on biting rates allows a spectrum of disease transmission assumptions to be modelled [16,41,42]. We will be especially interested in the limits AN_hτ_H ≫ 1 and AN_hτ_H ≪ 1, corresponding to the so-called frequency-dependent and density-dependent limits, respectively [14,15,42]:

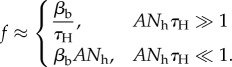2.3

In the frequency-dependent limit, host density is so large that the time spent by mosquitoes in the long-range search phase is negligible compared to the handling time. Mosquitoes bite at a constant rate determined primarily by the gonotrophic cycle time, ultimately resulting in disease transmission assumptions equivalent to those of the Ross–MacDonald model [1–3], which was the first and is arguably the most common framework for modelling vector-borne diseases. In the density-dependent limit, host density is so low that mosquitoes spend the majority of their time in the long-range search phase, and the gonotrophic cycle time is negligible by comparison. Density dependence ultimately leads to mass-action disease transmission, which is another a common framework for vector-borne disease modelling [13,14].

2.3. Personal protection model

2.3.1. Existing personal protection models

Many existing vector-borne disease models that incorporate personal protection can be classified into two categories. The first considers separate protected and unprotected classes (e.g. [16,26,28,46]). We will refer to these types of model as ‘static two-class models’. In these models, differing control strategies correspond to differing fractions of protected and unprotected humans, but there is no notion of control strength and no potential for dynamic control strategies. These models do not allow for movement between protected and unprotected classes, so a person who is protected is always protected and a person who is unprotected is always unprotected. Although one might assume that this distinction is inconsequential, particularly under equilibrium population conditions, we will show (see §3) that, relative to our personal protection model, static two-class models tend to underestimate the beneficial effects of personal protection and overestimate the potential for protection-induced diversity amplification.

Models of the second type assume a single, well-mixed human population as opposed to distinct protected and unprotected classes, and will hereafter be referred to as ‘one-class’ models (e.g. [11,17–21]). In these models, personal protection is usually considered to be control variable which is incorporated as an overall reduction in the mosquito biting rate, with the control strength corresponding to the per cent reduction in biting rate. The virtue of one-class models is their simplicity and compatibility with dynamic and optimal control techniques. However, as we will argue below, the interpretation of control strength as a reduction in f is ecologically unfounded. Indeed, we will show (see §3) doing so results in models that overestimate the beneficial effects of personal protection, and thus the controllability of the disease outbreak, relative to our personal protection model.

2.3.2. Incorporating personal protection into biting rates

We model personal protection's influence on biting rates through modified values of the parameters appearing in equations (2.1) and (2.2). Because bed nets and DEET influence neither the long-range search phase nor the gonotrophic cycle phase, the search rate A and post-bite handling time τ will be unaffected by personal protection use; personal protection's disruption of the short-range, second host-seeking phase affects only the pre-bite handling time τ₀ and the bite probability β_b. Protection measures may extend or shorten the pre-bite handling time depending on if they confuse or induce aversion, respectively. The repellent properties of insecticide-treated nets are uncertain [36], and it is currently unknown whether DEET confuses or induces aversion [40]. Regardless of the protective measure in use, we expect the pre-bite handling time to remain of the order of minutes to at most hours, so personal protection's influence on τ₀ will correspond to relatively small changes in the numerical value for f. Personal protection causes relatively large reductions in f through its effect on the bite probability β_b: mosquitoes are almost instantly repelled and do not bite after making contact with DEET-coated skin, and mosquitoes can only penetrate bed nets and bite when rips or tears are present, so proper bed net and/or DEET use will reduce β_b and, by extension, f, possibly to very small or nearly zero values.

In most real disease control scenarios, even when personal protection is made readily available, complete coverage over an entire population is difficult to achieve. Consequently, blood-seeking mosquitoes will likely encounter and attempt to acquire blood from both protected and unprotected humans. As discussed in Miller et al. [16], this is analogous to a predator–prey system consisting of two distinct prey species whose interactions with the predator species warrant distinct models. Following Miller et al. [16], we define N_u and N_p as distinct unprotected and protected host population densities with associated functional responses

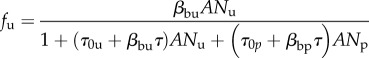2.4

and

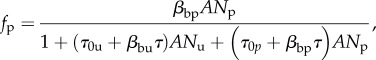2.5

where the subscripts ‘u’ and ‘p’ denote quantities associated with the unprotected and protected groups, respectively.

Throughout this paper, disease models will be constructed under the assumptions that protection strategies have no effect on mosquito health, so they will be unable to account for the killing ability of insecticide treated bed nets. These effects can be modelled by modifying the mosquito death rate to make it an increasing function of f_p [16]. Because we will be primarily interested in the basic behaviour comparisons between simple models, we only consider untreated nets and assume that protection measures have no influence over the mosquito death rate.

2.3.3. Incorporating personal protection into control models

We now turn to modelling personal protection as a disease control strategy operated and implemented by some health agency. Our goal is to construct a model which will allow us to assess the effectiveness of various, possibly time-dependent, control strategies in terms of the ‘control strength’ or ‘control effort’ exerted by the implementing agency. In the case of personal protection, ‘control strength’ corresponds to the number of bed nets or DEET bottles made available and effectively distributed to the public, as well as any public service announcements that encourage their use. Here, we face an immediate obstacle in that there is nowhere in our biting rate expressions (see equations (2.4) and (2.5)) for such a term to appear. Indeed, the search rates, handling times and bite probabilities appearing in f_u and f_p are determined solely by the ecology of the mosquito–human interaction and the biology of personal protection's action on mosquitoes. Consequently, these parameters are unrelated to the amount of personal protection made available to a population or the degree of effort spent encouraging its use.

What control strength does do is to make more protection available or encourage its continued use and thus, at least in theory, allows for a larger protected class relative to the unprotected population. Naively, it might seem that such an effect could be introduced into the functional responses, f_u and f_p, through changes in N_u and N_p. Such a formulation, however, would be unwise, because personal protection use is, ultimately, a dynamical phenomenon; DEET bottles run dry, bed nets wear down, and compliance waivers. Thus, individuals continually lose protection. However, the more DEET and bed nets are made available and the more their use is encouraged, the more people will re-acquire access to personal protection and interest in its use. Incorporation of personal protection control in vector-borne disease modelling thus necessitates a flow between protected and unprotected classes. This observation is central to our work—control strength has a direct influence over the average amount of time individuals remain unprotected while either failing to comply with government suggestions, or else waiting to acquire personal protection that has run out. Said differently, control strength should enter dynamic models as a direct influence over the average flow rates between the protected and unprotected class. Thus, from a control perspective, personal protection acts similar to control schemes used for vaccination [47], albeit with a much faster timescale for return to the unprotected class.

We employ the following minimal ODE system as a personal protection control model:

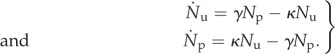2.6

Here, 1/κ is the average time an unprotected individual remains unprotected before acquiring personal protection, and 1/γ is the average time a protected individual remains protected before running out of DEET, having their bed-net fail, or wavering in compliance. Increased control effort may increase κ by making additional resources available to unprotected individuals, or may decrease γ by encouraging continued compliance among protected individuals. For simplicity, we will consider control over resource distribution only and will hereafter refer to κ as the ‘control strength’. For time-independent κ and γ, we find the following equilibrium unprotected and protected population density levels, denoted N^e_u and N^e_p, respectively:

2.7

where N_h is the total density of both protected and unprotected humans. For the remainder of the paper, we will refer to the model in equation (2.6) as the ‘dynamic two-class model’. This simple ODE model implicitly assumes the waiting times within the two classes to be exponentially distributed. Although not entirely realistic, this assumption is consistent with the simple classes of SIR models to be studied in §2.4, and the model's simplicity facilitates derivation of the associated analytic formulae. Deviations from the exponential assumption generally yield intractable delay differential equations [15]. Our mathematical analysis will be focused solely on equilibrium conditions, and we expect the effects of delay dynamics to be most important when systems are driven out of equilibrium, so non-exponential waiting times will not be considered in this paper.

2.4. SIR epidemic model basic reproduction numbers

To assess the impact of host flow on model behaviour, we compare our dynamic two-class model to analogous static two-class and one-class models in a simple SIR epidemic setting. Model predictions for outbreak severity, controllability and protection-induced amplification will be compared by means of the basic reproduction number—an outbreak threshold quantity which quantifies per generation disease growth rates [15]. Basic reproduction numbers are calculated using the next-generation matrix method [48,49].

2.4.1. One-class model

The one-class model does not differentiate between protected and unprotected humans, but instead considers them together as one well-mixed population. For such a model, we cannot use the unprotected and protected biting rate formulas given in equations (2.4) and (2.5), but instead must use the biting rate f given in equation (2.1). For the sake of model comparison, we assume that the host-seeking parameters A, τ₀, τ and β_b appearing in f are numerically equivalent to the corresponding parameters appearing in the unprotected biting rate f_u. We consider the following one-class SIR model:

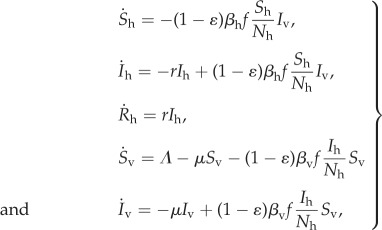2.8

where S_h, I_h and R_h denote the susceptible, infectious and recovered host densities, respectively, while S_v and I_v denote the susceptible and infectious vector densities, respectively. Λ is the mosquito recruitment rate, 1/μ is the average mosquito lifespan, r is the rate of host recovery, β_h is the vector to human transmission probability, β_v is the human to vector transmission probability, and ɛ is the control efficacy, which can vary between zero and one. Following [17–19], we interpret ɛ in terms of protection efficacy and the fraction of the population with access to personal protection:

2.9

where β_bu and β_bp are taken from the biting rate formulae equations (2.4) and (2.5) and are defined as the probability for a mosquito to bite an unprotected or protected host, respectively, after locating and identifying the target. The protected human population level, N_p, is a parameter, so for the sake of model comparison, we will assume that N_p = N^e_p, and thus can be written in terms of κ and γ as in equation (2.7). Our model assumptions yield the following basic reproduction number:

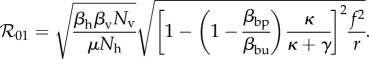2.10

2.4.2. Static two-class model

In the static two-class model, we divide the total host population into protected and unprotected classes. The fraction in each class enters as a fixed parameter, with the two classes summing to N_h. The classes appear both directly in the model and also implicitly through f_p and f_u. The static two-class equivalent to equation (2.8) is as follows:

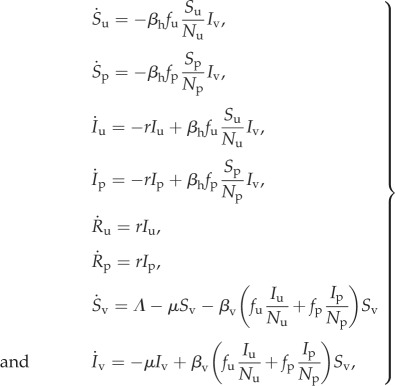2.11

where S_p, I_p and R_p denote densities of protected susceptible, infected and recovered humans, while S_u, I_u and R_u are the equivalent densities of unprotected humans, and all other parameters and state variables are as defined previously. Again, for the sake of model comparison, we assume that N_p = N^e_p and N_u = N^e_u so that the protected and unprotected host densities can be written in terms of the parameters κ and γ as in equation (2.7). This ensures that both the static and dynamic two-class models yield the same protected and unprotected population values at equilibrium. The resultant basic reproduction number for the static two-class model is

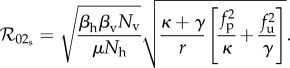2.12

2.4.3. Dynamic two-class model

Using the minimal control model in equation (2.6), we consider the following dynamic two-class SIR model:

2.13

For a constant control strength κ and equilibrium protected and unprotected human population values as given in equation (2.7), the basic reproduction number for the dynamic two-class model is

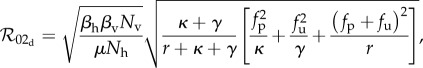2.14

where f_p and f_u are evaluated at the equilibrium protected and unprotected population values.

Note that in the limit of no personal protection, that is 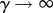with κ finite, all three basic reproduction numbers 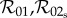and 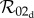reduce to the following expression, which we denote :

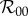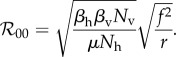2.15

This expression follows by noting that, in the absence of personal protection, N_p and f_p vanish, while N_u goes to N_h and f thus goes to f_u, provided that the parameters in f are taken to be equivalent to those in f_u. Estimated values for 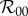have ranged, for example, between 2 and 103 for dengue outbreaks in Brazil and between 1.8 and 14.8 for recent Zika outbreaks throughout the world, although it should be cautioned that numerical estimates for 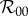calculated from mathematical models depend sensitively on model structure and method of calculation [50].

3. Results

We now present numerical results for the reproduction numbers given in §2.4 as functions of the control strength, κ. Because we are interested in basic model behaviour, we focus on the simplest case of β_bu = 1 and β_bp = 0, meaning that once found and identified, unprotected humans are always bitten while protected humans are never bitten. Although we are uncertain as to whether DEET or bed net use will increase or decrease the pre-bite handling time, we expect this parameter to remain small compared to gonotrophic timescales, so we simply set the protected and unprotected pre-bite handling times to be equal. Based on wind tunnel experiments showing that the source location and landing process take mosquitoes of the order of minutes to complete in laboratory settings (e.g. [33]), as well as the authors' own anecdotal experiences of being bitten after standing outdoors for only a few minutes, we estimate the pre-bite handling time to be 15 min. From Foster & Eischen [35], we estimate the post-bite handling time to be 3 days. We examine a variety of protection measures by considering the cases 1/γ = 15 days, 9 months and 5 years. The 5-year lifetime corresponds to bed net durability estimated from Briet et al. [51], while the 15-day lifetime is an estimate for how long it takes the average person to exhaust a bottle of DEET, assuming frequent use. The nine-month lifetime is simply an intermediate case, though it is likely that, in the absence of a rigorous anti-disease campaign, compliance fails on a months-long timescale. Likewise, to test a variety of commonly modelled infection scenarios, we consider the cases AN_h = 10.0, AN_h = 0.1 and AN_h = 1.0 in units of inverse days. These correspond to limits that are commensurate with frequency-dependent, density-dependent and intermediate infection rates [14,15,42], respectively. With AN_h held fixed, the terms β_h, β_v, N_v, N_h and μ are free parameters which appear only together as an overall multiplicative factor. Because we are interested in relative differences in model predictions within each protection scenario, we adjust this multiplicative factor such that 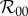scales to unity for each parameter setting, and the resulting basic reproduction numbers will be referred to as ‘scaled 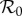’. The only remaining free parameter is the average human recovery time 1/r, which we set to two weeks—somewhere between the long infectious periods of diseases like malaria, and the shorter infectious periods of most viral vector-borne diseases. Human infectious periods of one week and six months yield plots qualitatively similar to those displayed in figures 1–3 and are given as electronic supplementary material.

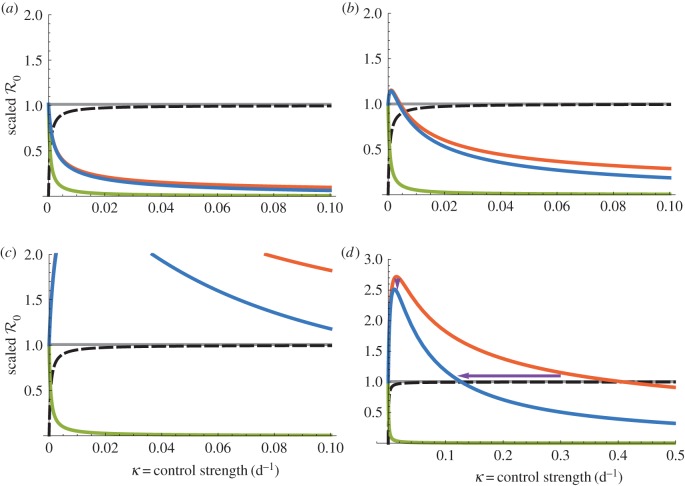
Figure 1.

Dependencies of 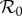on DEET (1/γ = 15 days) control strength for the dynamic two-class model (blue), static two-class model (red) and one-class model (green). Corresponding equilibrium proportions of protected hosts are given by the dashed black curve. Two-host models display diversity amplification at control strengths where respective scaled 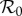curves rise above the grey 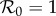line. Large suppressions in amplification severity and occurrence range are indicated by vertical and horizontal purple arrows, respectively, in (d). (a) Density-dependent infection AN_h = 0.1 d⁻¹, (b) moderate infection AN_h = 1.0 d⁻¹, (c) frequency-dependent infection AN_h = 10.0 d⁻¹ and (d) frequency-dependent infection (wide view).

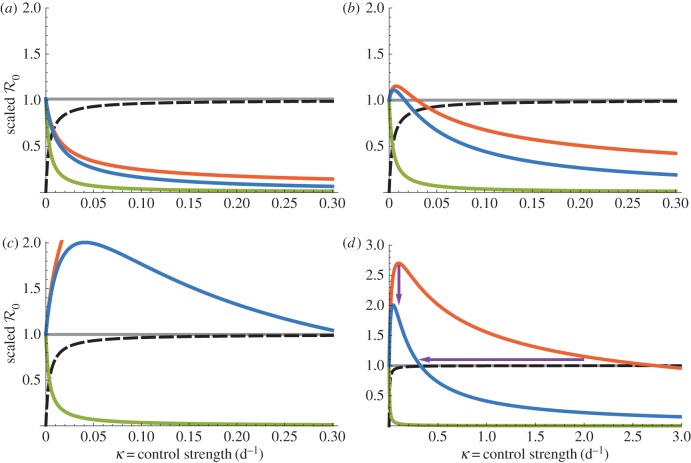
Figure 3.

Dependencies of 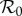on bed net (1/γ = 5 years) control strength for the dynamic two-class model (blue), static two-class model (red) and one-class model (green). Corresponding equilibrium proportions of protected hosts are given by the dashed black curve. Suppressions in amplification severity and occurrence range are indicated by vertical and horizontal purple arrows, respectively, in (d). (a) Density-dependent infection AN_h = 0.1 d⁻¹, (b) moderate infection AN_h = 1.0 d⁻¹, (c) frequency-dependent infection AN_h = 10.0 and (d) frequency-dependent infection (wide view).

4. Discussion

4.1. Model comparison

Figures 1–3 all show that relative to both two-class models, the one-class model overestimates disease controllability. Note, however, that the one-class model does not always give a poor approximation to the two-class models; indeed, all curves are fairly similar in the density-dependent limit in figures 1a, 2a and 3a. It is possible that, by defining the control efficacy, ɛ, in the one-class model as equal to the fraction of protected humans in the two-class models, we have made an unfair comparison, giving an unrealistic overestimate of control efficacy. If this is true, then ɛ would be more properly defined as proportional to the fraction of protected humans, with the proportionality constant less than unity. In this case, the curves for the dynamic two-class model and the one-class model in figures 1a, 2a and 3a would be in even closer agreement. Outside of the density-dependent limit, however, the one-class model tends to severely overestimate controllability relative to either two-class model, and no amount of re-scaling of ɛ can bring the reproduction number curves into agreement. Specifically, the one-class model always predicts a monotonic decrease in the scaled 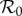as a function of κ, whereas both two-class models become non-monotonic outside of the density-dependent limit. The difference in model behaviour is due to the homogeneous population assumption implicit in the one-class model's formulation—this simplifying assumption prohibits the one-class model from accounting for increases in disease transmission which stem from focused mosquito attacks on unprotected sub-populations [16].

Figure 2.

Dependencies of 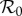on intermediate protection (1/γ = 9 months) control strength for the dynamic two-class model (blue), static two-class model (red) and one-class model (green). Corresponding equilibrium proportions of protected hosts are given by the dashed black curve. Large suppressions in amplification severity and occurrence range are indicated by vertical and horizontal purple arrows, respectively, in (d). (a) Density-dependent infection AN_h = 0.1 d⁻¹, (b) moderate infection AN_h = 1.0 d⁻¹, (c) frequency-dependent infection AN_h = 10.0 d⁻¹ and (d) frequency-dependent infection (wide view).

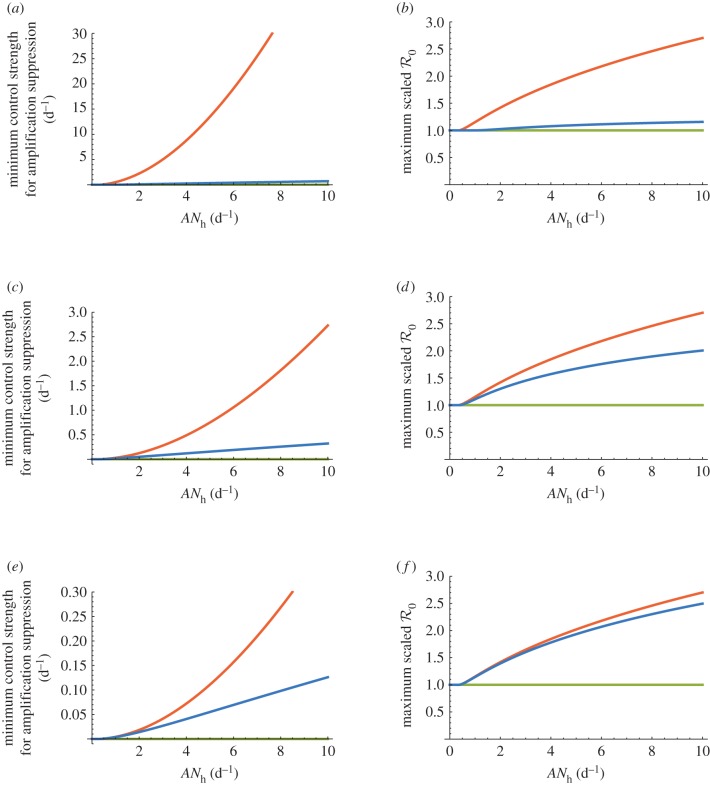
Figures 1–3 also indicate that, relative to our dynamic two-class model, the static two-class model generally underestimates disease controllability and overestimates diversity amplification. More specifically, diversity amplification is indicated whenever scaled 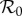curves exceed unity. Whereas strong amplification is apparent in the static two-class model, particularly under the frequency-dependent limit in figures 1d, 2d and 3d, it is much less severe in the dynamic two-class model, and indeed, even disappears in figure 1b. In addition to reduced amplification strength, the dynamic two-class model also predicts large reductions in the parameter ranges over which amplification can occur, particularly under the frequency-dependent limit in figures 1d and 2d. Figure 4 illustrates the reductions in amplification severity and parameter range as explicit functions of AN_h. The decrease in minimum control strength required for amplification suppression in the dynamic two-class model relative to the static two-class model indicates reduction in amplification range, and the decrease in maximum scaled 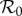in the dynamic two-class model relative to the static two-class model indicates reduction in amplification severity.

Figure 4.

Illustrations of amplification range and strength reduction as functions of AN_h using the dynamic two-class model (blue), static two-class model (red) and one-class model (green). The minimum control strength for amplification suppression is the value of control strength κ* such that scaled 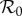exceeds unity for all control strengths κ ∈ [0, κ*]. The maximum scaled 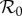is the value of scaled 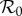at the peak of a model's 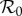versus κ curve for a given value of AN_h. (a) Amplifaction range reduction 1/γ = 15 days, (b) amplifaction severity reduction 1/γ = 15 days, (c) amplifaction range reduction 1/γ = 9 months, (d) amplifaction severity reduction 1/γ = 9 months, (e) amplifaction range reduction 1/γ = 5 years and (f) amplifaction severity reduction 1/γ = 5 years.

Diversity amplification ultimately results from mosquitoes' propensity to focus bites on preferred hosts [16,26], and so our results in figures 1–4 indicate that the movement of people between protected and unprotected classes can severely hinder mosquitoes' tendencies to focus attacks on unprotected human sub-populations, even when host population levels are in equilibrium and the flux between classes is rather small. This observation together with the one-class model's inability to account for diversity amplification indicates that dynamic protection status will generally result in outbreak characteristics lying somewhere between the one-class and static two-class model behaviour.

4.1.1. Density- and frequency-dependent limits

None of the one-class, static two-class or dynamic two-class models exhibit diversity amplification in the density-dependent limit (figures 1a, 2a and 3a), while both two-class models are strongly influenced by diversity amplification effects in the frequency-dependent limit (figures 1d, 2d and 3d). In the density-dependent limit, mosquitoes spend the majority of their time searching for and tracking individual humans through their CO₂ plumes, so the time wasted hunting unbiteable protected targets can significantly reduce the total amount of time a mosquito has to find and attack biteable targets. The resulting overall reduction in bites delivered more than compensates for the extra attacks diverted from the protected to the unprotected class, meaning that diversity amplification effects are suppressed and overall disease levels are reduced. In fact, any mechanism which forces mosquitoes to waste large amounts of time hunting or handling protected hosts has the potential to mitigate diversity amplification. For example, Miller et al. [16] showed that assigning very large pre-bite handling times to protected hosts can completely suppress diversity amplification in the static two-class model. Because diversity amplification is irrelevant in the density-dependent limit, it is less important how protected and unprotected sub-populations are modelled. It should not be surprising then that the differences between the three models are reduced in this limit.

In the frequency-dependent limit, mosquitoes spend very little time searching for and locating any one target, and so the time wasted hunting unbiteable targets is negligible (unless nearly all of the human population is protected). Very nearly all bites which would have originally landed on protected hosts are consequently diverted to the unprotected population, and the result is a strong amplification effect. Because diversity amplification is highly relevant in the frequency-dependent limit, this is where the precise details of how host sub-populations are modelled matters most. Again, then, it should not be surprising that differences between the three models are greatest in this limit. Between the density-dependent and frequency-dependent limits, the role of diversity amplification is intermediate. Thus, depending on the magnitude of host densities and mosquito attack rates, there will be more or less divergence between the one-class, static two-class and dynamic two-class models.

4.1.2. Slow and rapid transition limits

Figures 1–3 differ in their values of 1/γ—that is, the average amount of time that an individual who transitions into the protected class will remain in the protected class. When 1/γ is small (figure 1), our dynamic two-class model is more similar to the one-class model and less similar to the static two-class model. By contrast, when 1/γ is large (figure 3), our dynamic two-class model is more similar to the static two-class model and less similar to the one-class model. Again, the explanation is relatively straightforward. In the limit of rapid transitions between classes, that is, the limit 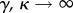with the ratio of unprotected to protected hosts γ/κ held finite, the distinction between protected and unprotected classes disappears, as people ‘instantaneously’ transition from one class to the other, with no dwell time in either class. In this case, our model behaves very much like the one-class model, where mosquitoes see an average level of protection for any given person, rather than two separate classes of people. At the opposite extreme, in the limit of slow class transitions 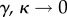with γ/κ finite, the flux between classes becomes insignificant. In this case, an average person remains protected or unprotected for such a long time that, at least on the timescale of disease dynamics, there are, in essence, two distinct host sub-populations, which is the assumption of the static two-class model. To the extent that γ and κ are finite and non-zero, our model is important in providing estimates for disease spread and controllability at intermediate scenarios between the one- and static two-class models. These results indicate that diversity amplification may play a larger role in communities employing only bed nets than in communities employing only DEET. The slow transitions associated with the long life times of bed nets make the class assignments more static than would the fast transitions associated with the short life time of DEET, and amplification is strongest when slow transitions allow mosquitoes to better focus on fixed groups, as occurs in the static two-class model.

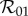The rapid and slow transition limits provide some insight into the suspected overestimate in controllability assumed by the one-class model. If the one-class model and static two-class models are consistent approximations of the dynamic two-class model, then we should be able to recover the expressions for and from 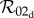by taking appropriate limits. As expected, equations (2.14) and (2.12) show that 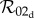reduces to 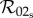in the slow class transition limit. Equations (2.14) and (2.10), however, show that 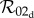reduces to 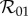in the rapid transition limit only if ɛ is defined as

4.1

This expression is always less than or equal to the expression for ɛ in equation (2.9), with equality holding only in the density-dependent limit AN_hτ_H ≪ 1. Thus, the one-class model defined as in §2.4.1 is a consistent rapid transition approximation of the dynamic two-class model in the density-dependent limit only. Outside of the density-dependent limit, equation (2.9) overestimates the rapid transition level of controllability implied by equation (4.1). These findings suggest that equation (4.1) provides a more biologically sound, albeit more complicated, expression for control efficacy in one-class models than does the more commonly used expression in equation (2.9). Furthermore, these results indicate that a common set-up for one-class control models, one which uses constant density-independent biting rates and a control strength in the form of equation (2.9), makes two implicit mutually inconsistent biological assumptions: the form of control strength assumes density-dependent biting rates, while the constant biting rate is equivalent to assuming frequency-dependent biting rates.

4.2. Diversity amplification in the field

Based on our modelling results, we posit that the mitigation of diversity amplification by class flow is a general feature of vector-borne disease systems. This implies that any model featuring static protected and unprotected classes will overestimate the impact of diversity amplification relative to its dynamic two-class analogue, although the amount of overestimation may be small in certain parameter ranges. No matter how complicated and detailed a static two-class model may be, allowing movement between protection classes will always hamper a vector's ability to focus bites on and amplify disease spread within any one vulnerable host group. Not only can class flow reduce the strength of amplification but, more importantly, it can also restrict the range of parameters where amplification can occur. This observation may at least partially explain the disparity between the theoretically predicted protection-induced amplification effect and its lack of observation in the field. Although there is some field evidence suggesting that mosquitoes divert from individuals using repellent to those that do not [27], protection-induced amplification, to the best of our knowledge, has never actually been observed at the community level. This could be a result of poor compliance, which is hard to assess, or insecticide-treated net use, which is expected to suppress amplification by killing rather than diverting mosquitoes [16,28,29]. Alternatively, given that humans naturally waver in protection status over time, it could be that amplification is simply less important and less likely to occur than suggested by static two-class models. Our dynamic two-class model provides a robust mechanism for the suppression of diversity amplification and thus addresses the contradiction between theoretical prediction and experimental observation.

5. Summary and conclusion

We have introduced a dynamic two-class model to describe vector-borne disease systems incorporating hosts who use personal protection measures. The effects of personal protection usage at the level of individual hosts are captured by functional response biting rates, and the effects of large-scale personal protection campaigns at the community level are captured through flows between protected and unprotected classes. Class flow can severely reduce amplification in both severity and range of occurrence, relative to predictions from existing static two-class models. This, along with the natural propensity of humans to discontinue and re-adopt protection use, offers potential explanation for the lack of observed protection-induced amplification in the field, despite predictions implied by existing models. Static two-class models can fail because they do not acknowledge the fundamental difference between genuinely distinct host species and protected versus unprotected individuals: species type is fixed, while protection status is not. Our dynamic two-class model combines the desirable features of one-class models (dynamic control) and static two-class models (host variability) to provide an ecologically sound methodology for modelling personal protection distribution as a community-wide dynamic control strategy in vector-borne disease systems.

Data accessibility

This article has no additional data.

Authors' contributions

J.D. and S.B. initiated this project, and J.D. prepared the initial draft. S.B. made significant contributions to the second draft, and all authors contributed to subsequent drafts and revisions. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by a University of Maryland–Smithsonian Institution seed grant, and by a DOD SERDP grant.