Machine Learning Methods for X-Ray Scattering Data Analysis from Biomacromolecular Solutions

Abstract

Small-angle x-ray scattering (SAXS) of biological macromolecules in solutions is a widely employed method in structural biology. SAXS patterns include information about the overall shape and low-resolution structure of dissolved particles. Here, we describe how to transform experimental SAXS patterns to feature vectors and how a simple k-nearest neighbor approach is able to retrieve information on overall particle shape and maximal diameter (D_max) as well as molecular mass directly from experimental scattering data. Based on this transformation, we develop a rapid multiclass shape-classification ranging from compact, extended, and flat categories to hollow and random-chain-like objects. This classification may be employed, e.g., as a decision block in automated data analysis pipelines. Further, we map protein structures from the Protein Data Bank into the classification space and, in a second step, use this mapping as a data source to obtain accurate estimates for the structural parameters (D_max, molecular mass) of the macromolecule under study based on the experimental scattering pattern alone, without inverse Fourier transform for D_max. All methods presented are implemented in a Fortran binary DATCLASS, part of the ATSAS data analysis suite, available on Linux, Mac, and Windows and free for academic use.

Introduction

Small-angle x-ray scattering (SAXS) is an increasingly popular method in structural biology that usefully complements high-resolution structural techniques such as x-ray crystallography, nuclear magnetic resonance spectroscopy, and electron microscopy. SAXS does not require crystals, labeling, or isolated particles at cryogenic temperatures, and its applications extend to the determination of structural parameters, e.g., the radius of gyration (R_g), maximal extend (D_max), and the molecular mass (MM), obtaining the low-resolution shapes of macromolecules and rigid body modeling of complexes, quantitative characterization of flexibility, and time-resolved conformational changes (1). The scattering intensity I(q) is recorded as a function of the scattering vector q, with the momentum transfer q = 4π sin θ/λ, where θ corresponds to half of the angle between incoming and scattered photons, and λ corresponds to the wavelength. To determine the scattering of the macromolecule under study, the background scattering, including sample holder and solvent (typically an aqueous buffer), has to be subtracted.

Over time, many methods have been developed to extract relevant information directly from the experimental scattering intensities, exclusively working with the experimentally obtained data. In contrast, in this manuscript, we consider the application of data mining and machine learning (2) to extract structural information from SAXS data. In short, we shall evaluate the idea that, if there were a way to locate similar macromolecules with known structural parameters, the parameter values of these similar structures could be used to approximate the parameter values of the specimen under study. It should be noted that in this context, “similarity” shall refer to similarity in scattering patterns, with the assumption that similar scattering pattern implies similar overall structure and not necessarily similar higher-resolution detail; the latter may not be the case (3).

For each of the major methods in structural biology, curated data banks invite researchers to deposit models as well as raw data, in particular the Protein Data Bank (PDB) (4), the Biological Magnetic Resonance Data Bank (5), the Electron Microscopy Data Bank (6), and the Small Angle Scattering Biological Data Bank (SASBDB) (7), respectively. Here, a large number of records on structural parameters, sequences, shapes, models, and more have been accumulated. Using tools like CRYSOL (8) or FoXS (9), theoretical scattering patterns of atomic models may be readily calculated.

Finally, we bring the initial idea and available data together by describing methods on how to make large amounts of data accessible for Knowledge Discovery. In particular, in the context of data mining and machine learning, any measurable property of the specimen under study may be considered a “feature.” Features describe the input for a machine-learning method and may be concrete values or abstract concepts. In SAXS, the experimental R_g, the calculated forward scattering I(0), and the individual experimental intensities at each q and any function thereof may be considered potential features. In this manuscript, we shall describe how to represent the overall shape of a protein, e.g., compact, flat, extended, or random-chain, with only three shape-related features. Here, random chains are a mixture of conformations ranging from compact to fully extended chains, whereas extended only refers to preferred extended particles in solution. Further, to predict structural parameters, a fourth, size-related feature may be included in the feature vector. The advantage of describing a complex SAXS pattern in a feature vector of only a few components becomes apparent if one assumes a form of distance relationship between feature vectors. If two points in the feature space are close together in the Euclidian sense, then their properties, i.e., shape and/or structural parameters, should be similar. Conversely, if they are far apart, their properties should be significantly different. To predict properties of an unknown entity, one may look up its closest neighbor(s) in the feature space and apply known properties of the neighbor to the unknown entity. However, the larger the number of components in the feature vector—i.e., the more dimensions are considered—the more likely are sparsely populated regions in the underlying data source that could reduce predictive power, a problem also known as the “curse of dimensionality” (10).

Here, we present a framework of data transformation and feature selection for a fast and selective lookup of structural neighbors in the space of SAXS patterns. Based on the proposed feature selection and the source data of the database, different information may be inferred. In the case of geometrical bodies (11), simple shapes may be determined quickly, e.g., for use as a proto-shape for ab initio modeling in the case of the PDB (4), and structural parameters such as D_max and MM of the immediate neighbors as discussed in this work—but also other parameters of interest—may be looked up and used as a starting point for further analysis and refinement.

Materials and methods

Shape classification

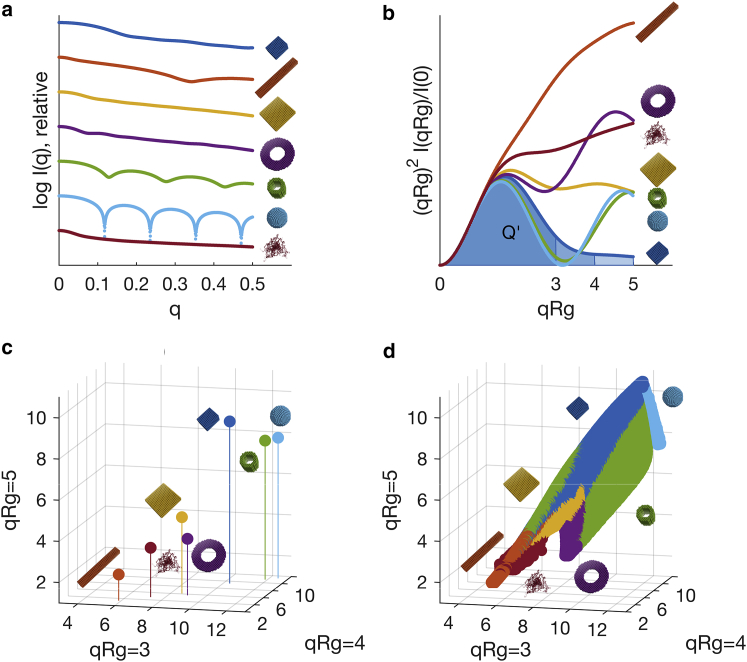
Data simulation. The command-line program BODIES (11) was modified to simplify the automated simulation of large amounts of SAXS patterns derived from geometrical objects with uniform scattering length density of compact spheres, flat discs, extended rods, compact-hollow cylinders, hollow spheres, and flat rings (Fig. 1 a). The corresponding dimensions of the geometric bodies, i.e., inner and outer radius, height, length, and width, etc., were uniformly and independently sampled in ranges from 10 to 500 Å, respectively. Classification labels were generated based on the extent of the object; in short, proportions more or less extreme than 1:4 were considered to define compact, extended, and flat objects, and in addition an inner cavity of more than 25% of the outer radius generally indicates a hollow object. Based on this, 460,000 scattering patterns of various compact, flat, extended, filled, and hollow geometric objects were generated. Although clearly limited, a selection of body types enumerating an exhaustive list of geometrical body shapes would be, at least, very difficult to obtain, especially considering the lack of analytical form factors. As shown later in the text, classification with k-nearest neighbors extends somewhat outside the boundaries of the mapped class volumes, thus smoothing out any gaps between geometric objects (Fig. 1 d). Further, to allow the identification of intrinsically disordered proteins, we employed Ensemble Optimization Method (12) to generate an additional 560,000 simulations of random chains, subsequently averaged in groups of 20 repetitions to simulate mixtures of flexible proteins. The lengths of the random chains were selected to follow the size distribution of amino acid sequences of asymmetric units in the PDB. In total, 488,000 scattering patterns were created across all geometric classes to be used as a training data set for machine-learning classification that encompass basic geometric objects and disordered polymer chains (Fig. 1 d).

Figure 1.

Transformation of scattering patterns of geometric objects and random-chain on arbitrary log scale (a) via integration of the normalized Kratky Plot (b) to V’-space (c and d). (a–c) depict a randomly selected member of each object class, whereas (d) shows the locations of all 488,000 scattering patterns generated. The color assignments are identical in all panels: compact (dark blue), extended (orange), flat (yellow), ring (violet), compact-hollow (green), hollow-sphere (light blue), and random-chain (dark red), also indicated by corresponding pictograms.

Data transformation. To normalize for the varying size of objects, R_g and forward scattering I(0) were required. As the generated data is ideal and free of noise, the R_g was obtained from the slope of the Guinier plot (lnI(q) vs. q²) of the first 10 computed points, and I(0) was directly available from the data due to simulation. With these two parameters, the data was transformed to the dimensionless Kratky scale (13):

$${\left(q{R}_g\right)}^{2}I\left(q{R}_g\right)/I\left(0\right)vs.q{R}_g.$$

After this, the normalized Porod invariant, or integral Q’, of the dimensionless Kratky plot was calculated up to qR_g = 3, qR_g = 4, and qR_g = 5, respectively, and expressed as a normalized apparent volume, or V’ (14), i.e.,

$$V^{\prime }=\frac{2{\pi }^2}{Q^{\prime }}where{Q}^{\prime }=\underset{0}{\overset{q{R}_g}{\int }}{\left(q{R}_g\right)}^{2}I\left(q{R}_g\right)/I\left(0\right)dq{R}_g.$$

Each scattering pattern was therefore reduced to three features and its associated class label (Fig. 1, b and c). The qR_g upper bounds were chosen, as they provide a trade-off between contained shape information and the limitations of the assumption of uniform scattering length density; larger qR_g-values would separate the point clouds in unrealistic ways (data not shown). That said, with the selection presented here, the corresponding three-dimensional scatter plot of the simulated data shows a V’-space with good separation of the different shape classes (Fig. 1, c and d).

Learning, prediction, validation. As Fig. 1 d depicts a well-defined point cloud within the three-dimensional V’-space, we added 25,000 randomized points with unknown class label to the space before learning. This helped to facilitate compactness of the resulting predictions; otherwise, a query point outside this well-defined V’ would still have far-away neighbors and would thus be grouped to a class it does not belong. It should be noted that this random point cloud is not shown in Fig. 1 d, as it would obscure the actual data of interest.

To classify the shape of an unknown entity, its feature vector has to be computed, and the k-nearest-neighbors in the three-dimensional V’-space are determined by k-d-tree search (15) across the whole training set. Here, we chose k = 9, partly to avoid unknown classification of the randomly distributed cases but also to facilitate a majority vote classification in which classes overlap. The classes of the neighbors are then weighted by empirical class weights (Table S3), and the class with the maximal sum of weights is selected as label for the unknown entity.

To evaluate the performance of this approach, we used leave-one-out cross-validation, i.e., we removed each of the 488,000 structures from the source data in turn and used the remaining data points to predict the class of the removed one. Cross-validated performance of this multiclass classifier was evaluated by F1 measure and Matthews correlation coefficient (MCC) (16).

Prediction of structural parameters

Data generation. A snapshot of more than 220,000 asymmetric units and biological assemblies was taken from the PDB (4). From these we discarded duplicates (i.e., biological assemblies identical to asymmetric units), entries with nucleotides, and peptides with less than 50 amino acids. Entries with more than one model were discarded unless the models were very similar, in which case we used the first one listed in the atomic coordinate file. Metals, inorganic molecules, and other posttranslational additions were filtered out from all structures. No filtering was applied with respect to sequence identity, as similarity in sequence does not always imply similarity in structure (17). From the remaining 165,982 unique atomic structures, we calculated scattering patterns with CRYSOL (8) using 30 spherical harmonics and 1001 equidistant points up to a q_max of 0.6 Å⁻¹. Besides the calculated scattering pattern, CRYSOL also reports a variety of structural parameters, in particular R_g, D_max, and MM, which we recorded for later use.

Learning, prediction and validation. Similar to the geometric bodies, the V’-values were computed for the atomic structures. Given that for the estimation of structural parameters not only the shape but also the size of the molecule is important, R_g was included as a size feature in addition to the three V’ shape features; here, R_g was chosen over D_max, as the former can be directly obtained from the experimental data, whereas the latter can usually only indirectly be estimated.

To assess the structural parameters of an unknown entity, the feature vector is computed, and the k-nearest structural neighbors (here k = 5) in a four-dimensional space combining the three dimensions of V’ along with R_g are determined by k-d-tree search (15). Here, the parameter k = 5 was chosen to minimize the relative prediction error. From this, the parameters, i.e., D_max and MM, are estimated as the weighted mean of D_max and MM of the neighbors, where the weights correspond to the normalized inverse Euclidean distance to the unknown entity—i.e., the closer the neighbor, the more important its contribution to the prediction.

To evaluate the performance of this approach, we used leave-one-out cross-validation, i.e., we removed each of the 165,982 structures from the source data in turn and used the remaining structures to predict the D_max and MM of the removed structure.

Application of shape classification and prediction of structural parameters to experimental data

The classifier was further applied to the 401 public experimental SAXS data sets without nucleotides available from SASBDB (7) at the time of writing. As random-chain classifications may potentially indicate modular, flexible, or unfolded proteins, we also collected experimental SAXS data on folded and chemically modified unfolded ribonuclease A and folded and denatured lipase B at the European Molecular Biology Laboratory P12 SAXS beam line at PETRA-III (18), DESY, Hamburg, Germany, to compare the results of the random-chain classification with those from traditional biophysical methods, i.e., circular dichroism spectropolarimetry, and tryptophan fluorescence spectroscopy. See Supporting Materials and Methods for details on their preparation.

To study the effects of experimental noise on shape classification and prediction of structural parameters, we further collected experimental data of 100 repetitions of 50 ms exposures of bovine serum albumin (BSA) in 50 mM HEPES (pH 7.5) buffer. After subtracting 100 buffers from 100 samples, the resulting 100 data sets were identical up to noise as evaluated by CorMap (19).

All experimental data were submitted to SASBDB for reference. The following accession codes were assigned: SASDDK3 (lipase B), SASDDL3 (folded ribonuclease A), SASDDM3 (chemically unfolded ribonuclease A), and SASDDN3 (100 repetitions of BSA; buffers, samples, and subtracted data were deposited).

Results

Shape classification

Appropriate evaluation of multiclass classification systems is itself a topic of ongoing research. In this work, we follow the recommendations of Powers (16) and report the F1 score and MCC for each shape category (Table 1). Here, F1 is a measure that considers precision and recall of the classifier with a range between 0.0 and 1.0, and correspondingly, MCC determines the correlation between expected and predicted classes with a range from −1.0 to 1.0. In both cases, larger (positive) values are associated with better performance. In addition, Fig. S3 details the confusion matrix, i.e., the actual counts of expected and predicted classes of the leave-one-out cross-validation, together with recall and precision percentages in the margins. The overall accuracy of classification across all shapes is reported as 96.5%.

Table 1.

F1 Score and MCC for k-Nearest Neighbors Multiclass Classification Results of the Individual Shape Categories

	F1 score	MCC (%)
Unknown	0.991	99.1
Compact	0.962	95.1
Extended	0.969	95.8
Flat	0.957	94.7
Ring	0.980	97.8
Compact-hollow	0.938	93.3
Hollow-sphere	0.997	99.7
Random-chain	0.964	96.2

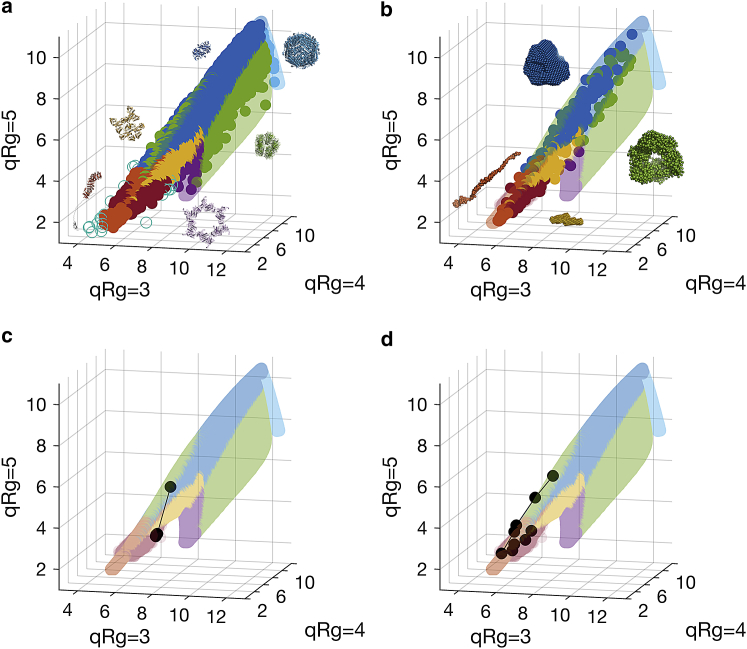
Further, we predicted the shape classification of the 165,982 unique atomic structures of the PDB and visualized the resulting point cloud in V’-space (Fig. 2 a). It is immediately apparent that the overall shape of the distribution of proteins (opaque circles) is very similar to that obtained by geometric objects (transparent background), with only 25 structures considered outside the volume mapped by the geometric objects and thus being assigned an “unknown” class label (open circles). Interestingly, most (∼90%) of the PDB structures are classified as compact/globular, whereas, for example, more extended proteins are much less represented (∼3%). A different picture arises from experimental data deposited in SASBDB (Fig. 2 b). Here, the distribution (Table S4) tends more toward the extended, flat, and random-chain area (>50%), reflecting the fact that solution scattering is often employed for systems that do not easily crystallize. Indeed, the shape classification of experimental SAXS data may also be done to describe protein solution state or solution state transitions when the high-resolution structure is not available or obtainable. For example, Fig. 2, c and d show the V’-space point cloud positions of SAXS data obtained from native ribonuclease A compared to a final-state completely denatured protein, highlighting the shift from compact to random/flexible shape categories. SAXS data collected from lipase B samples that underwent systematic chemical denaturation show the “denaturation trace” through V’-space as the protein populations unfold at ever-increasing concentrations of guanidine hydrochloride.

Figure 2.

Distribution of (a) atomic structures of the PDB and (b) experimental scattering data from SASBDB (opaque) indicating a good agreement of the V’-space mapped out by shapes (transparent) and that covered by atomic structures and experimental data. The open circles in (a) depict classifications with an “unknown” class label; structures and models displayed in (a and b) were randomly chosen and placed for the purpose of illustration (PDB: 12as (compact), 1v18 (extended), 3oei (flat), 3h3w (ring), 4avt (compact hollow), 3a68 (hollow sphere), and 2kzw (unknown); SASBDB: SASDA52 (compact), SASDA57 (extended), SASDAY4 (flat), and SASDBD7 (compact hollow)). (c and d) show the locations of experimental data of chemically unfolded ribonuclease A and lipase B, respectively. The V’-space trace for ribonuclease A shows the position of the native, folded protein (compact) compared to the chemically unfolded final state (random/flexible). The trace for lipase B shows the effect of systematically unfolding the protein population through a denaturation gradient of guanidine hydrochloride from compact to extended until a random-chain conformation is reached (see Supporting Materials and Methods for details). Color assignments are identical to those of Fig. 1.

Prediction of structural parameters

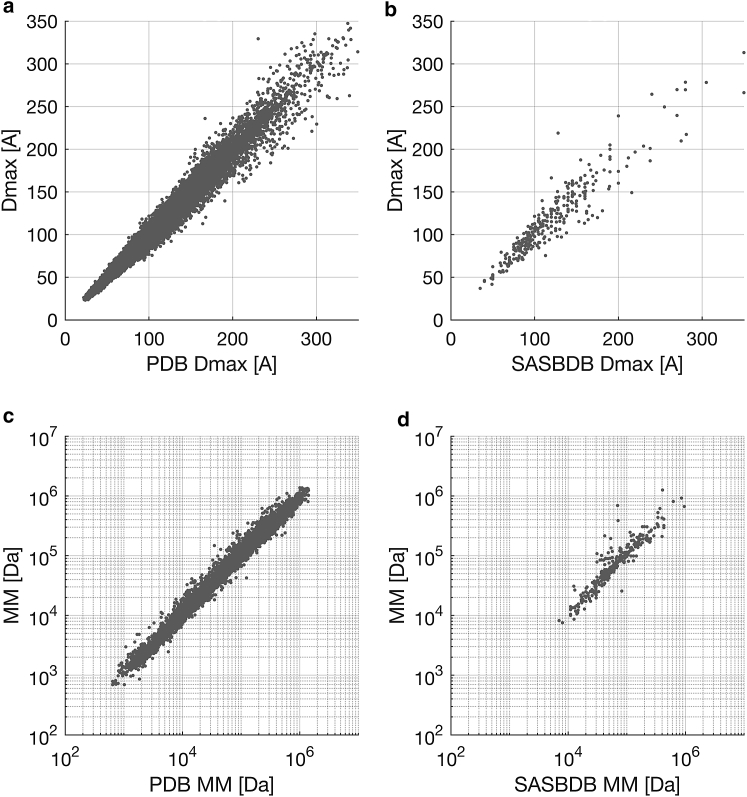
Fig. 3, a and c summarize the results of the leave-one-out cross-validation for the prediction of structural parameters of the PDB. As the values of the parameters are derived from the atomic structures, a good agreement may be expected; in ∼90% of the cases, the estimate is within 10% of the true value. The evaluation of experimental data as deposited in SASBDB (Fig. 3, b and d) is not as straightforward, as the deposited values depend on sample quality, experimental conditions, and the data analysis of the respective researcher. Interestingly, compared to the results of the PDB, there seems to be a tendency to obtain somewhat larger D_max-values in manual analysis (Fig. 3 b), which may, for example, be explained by the influence of the hydration shell.

Figure 3.

Estimates of D_max (a and b) and MM (c and d) for entries of PDB (a and c) and SASBDB (b and d). In the case of the PDB, the expected values are known, and a good agreement can be observed; in ∼90% of the cases, the estimate is within 10% of the expected value (a and c). No such claim can be made in the case of SASBDB, as the expected values obtained depend on the type of the experiment, the sample quality, and the data analysis of the submitter.

Effects of experimental noise

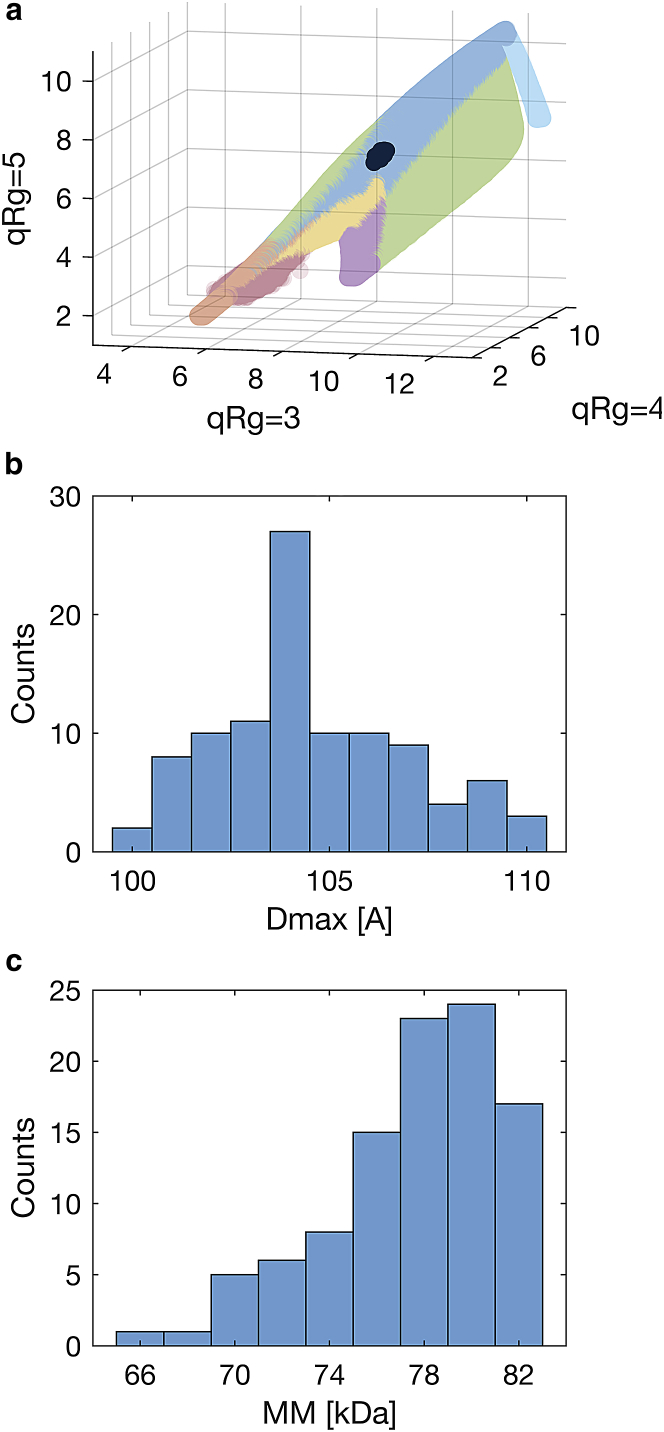
Fig. 4 elucidates the effect of experimental noise on 100 repetitions of BSA; all frames were found similar to each other up to noise as per CorMap test (19). As depicted in Fig. 4 a, the mapped locations of the 100 frames are slightly spread out but still close together. Histograms of the estimated structural parameters D_max and MM are shown in Fig. 4, b and c, respectively. Again, a spread may be observed; however, the width of the distributions most likely correlates strongly with the amount of noise present in the data (not evaluated). Both distributions are centered on values somewhat larger than what one may expect from strictly monomeric BSA (∼100 Å and ∼67 kDa, respectively), but this may be attributed to the presence of a fraction of dimers in solution (20).

Figure 4.

Locations of shape classification in V’-space (a) and histograms of structural parameters (b and c) of 100 repetitions of BSA that are identical up to noise. Although affected by the experimental noise, all frames map closely together in V’-space (a); the estimates of D_max vary from 100 to 110 Å (b), and MM from 66 to 82 kDa (c).

Discussion

Rapid shape classification as presented in this work is a unique approach in the field of biological SAXS. However, it is obvious that accurate estimates of R_g and I(0) are key for appropriate transformation of experimental SAXS data to V’-space. Interestingly, misspecification of these parameters will often result in a data point outside the body of shape space as depicted by Fig. 1 d and consequently lead to an “unknown” classification; therefore, the shape classification may also be used as an initial validation of R_g and I(0). Further, it has applications as a building block for automated data analysis (21, 22, 23), e.g., to decide whether ab initio shape modeling or ensemble optimization should be applied. In addition, shape modeling applications may use the initial classification as a starting point for their models; DAMMIF (24) has already been modified to not only use a start model based on the classification but also to adapt the search and annealing parameters, e.g., by enabling anisometry penalties for extended or flat objects.

Similarly, at present D_max may only be obtained by inverse Fourier transform of the experimental scattering pattern, which may be difficult to determine accurately (25, 26). The presented method provides an independent D_max estimate from similar entries in the PDB based on experimental data alone. Consequently, this approach may be applied to obtain a starting estimate of D_max for the indirect Fourier transform or as a tool for quality assessments during data deposition procedures, e.g., to SASBDB, whereby the automated D_max estimates may be compared to submitted values for validation purposes (Fig. 3 b).

In the past, multiple concentration-independent methods to determine the MM of biological macromolecules from SAXS data have been established (14, 27, 28), each with their own respective strengths and weaknesses. In this manuscript, we report the results of the size-and-shape-based database lookup method (Fig. 3 b) without attempting to directly compare with any of the established methods. The interested reader may find a thorough, comprehensive, and quantitative comparison of all four methods elsewhere (29).

It should be noted that some details of the presented method were empirically determined, e.g., the qR_g integration limits for V’; although the general magnitude is appropriate, e.g., on the lower end, integration to qR_g = 1 corresponds to the Guinier range, and on a normalized scale, the integral is a constant up to rounding errors. Consequently, on the higher end, qR_g = 10 would correspond to wider-angle (i.e., higher-resolution) information that is not easy to rationalize in terms of overall parameters. Thus, the selected qR_g-values of 3, 4, and 5 are reasonable but not necessarily optimal. For example, we chose N = 3 integration limits also for the ease of display. A different selection of limits in number and magnitude might result in an improved predictive performance. Along the same line of argument, one may observe that in many machine-learning applications, it is required to normalize, scale, or transform the training data before learning and prediction to achieve a good predictive result. Here, we used the data “as-is”; however, it is possible that there is a transformation function that minimizes the relative error and/or (root) mean-square error of the prediction. Potential avenues of investigation for the k-nearest neighbors method include the following: 1) selection of k and the applied distance weights; 2) arbitrary linear and nonlinear data scaling and transformation before learning; 3) metric selection and metric learning (30); and, of course, 4) any other learning method such as regression functions, support vector machines, neural networks, deep learning, etc. As in this manuscript we focus on outlining and introducing, to our knowledge, a novel approach, we did not exhaustively investigate all these options; however, the classifier as presented here is already on par with established methods (29).

Conclusions

In this manuscript, we present what is, to our knowledge, a conceptually new approach to rapidly analyze the scattering patterns in biological SAXS, not as an isolated data point but in the context of all known biological macromolecules. We have outlined and described a simple data transformation that combines large amounts of SAXS data into a few numbers that suggest themselves as coordinates in a feature space for machine learning. This space simplifies and improves lookup of similar scattering patterns in a large data set. The presented approach of integrating the intensities has a strong advantage over the methods based on actual (normalized) intensity values. Our method is independent of the spacing of the available data points, obviating the need for interpolation to a common grid, and fluctuations of individual intensities have less of an effect for lookup because of the integration, thus also avoiding the curse of dimensionality.

The techniques described here allow for rapid shape classification and provide estimates of MM and D_max with good accuracy. It should be noted that so far D_max was only available indirectly through inverse Fourier transform, but with the new approach, it is now also accessible from experimental data directly. Further, the general approach as described easily extends to additional parameters of interest extracted from source data, as labels may be assigned arbitrarily.

The method has been implemented in the program DATCLASS, integral part of the ATSAS data processing and analysis suite (31), which is freely available for academic users (https://www.embl-hamburg.de/biosaxs/software.html).

Author Contributions

The initial idea was conceived of and all developments were done by D.F. Experimental data were collected by C.M.J. D.F., C.M.J., and D.I.S. participated in critical discussion and wrote the manuscript.

Editor: Jill Trewhella.

Supporting Citations

References (32, 33, 34) appear in the Supporting Material.