Abstract
Integrin-mediated adhesions between airway smooth muscle (ASM) cells and the extracellular matrix (ECM) regulate how contractile forces generated within the cell are transmitted to its external environment. Environmental cues are known to influence the formation, size, and survival of cell-matrix adhesions, but it is not yet known how they are affected by dynamic fluctuations associated with tidal breathing in the intact airway. Here, we develop two closely related theoretical models to study adhesion dynamics in response to oscillatory loading of the ECM, representing the dynamic environment of ASM cells in vivo. Using a discrete stochastic-elastic model, we simulate individual integrin binding and rupture events and observe two stable regimes in which either bond formation or bond rupture dominate, depending on the amplitude of the oscillatory loading. These regimes have either a high or low fraction of persistent adhesions, which could affect the level of strain transmission between contracted ASM cells and the airway tissue. For intermediate loading, we observe a region of bistability and hysteresis due to shared loading between existing bonds; the level of adhesion depends on the loading history. These findings are replicated in a related continuum model, which we use to investigate the effect of perturbations mimicking deep inspirations (DIs). Because of the bistability, a DI applied to the high adhesion state could either induce a permanent switch to a lower adhesion state or allow a return of the system to the high adhesion state. Transitions between states are further influenced by the frequency of oscillations, cytoskeletal or ECM stiffnesses, and binding affinities, which modify the magnitudes of the stable adhesion states as well as the region of bistability. These findings could explain (in part) the transient bronchodilatory effect of a DI observed in asthmatics compared to a more sustained effect in normal subjects.
Introduction
Contraction of airway smooth muscle (ASM) cells is typically triggered by exposure to irritants or allergens and leads to bronchoconstriction, which is a narrowing of the airways characteristic of asthma (1). Contracted ASM cells transmit strain to the extracellular matrix (ECM) and hence to the airways via focal adhesions (2, 3), of which integrins are a key component. Integrins are transmembrane proteins that provide the necessary mechanical link between the intracellular and extracellular domains by binding to the cytoskeletal network within the cell and to ligands in the ECM (4, 5). Because it is well established that integrins are responsive to mechanical and environmental cues (6, 7, 8), we expect the environment of the in vivo airway, which is inherently dynamic because of tidal breathing, to modulate the integrin-binding dynamics and consequent levels of strain transmission. Several experimental studies have shown that tidal breathing and deep inspirations (DIs) are able to modulate the levels of contractile force in healthy airways (9, 10, 11). In particular, DIs are capable of inducing bronchodilation (reversing airway narrowing) in healthy subjects, but these effects are either transient or diminished in asthmatics. To understand this, a number of studies at the cell level and tissue level have focused on the ASM cell response to oscillatory loading and consequent modulation of contractile force generation (12, 13, 14, 15). Disruption of actin-myosin cross-bridge cycling, which mediates contractile force generation within the cell, reduces the mean contractile force. However, the role of cell-matrix adhesions in understanding how the strain due to contraction is transmitted to the tissue could also be an important factor and has so far been neglected.
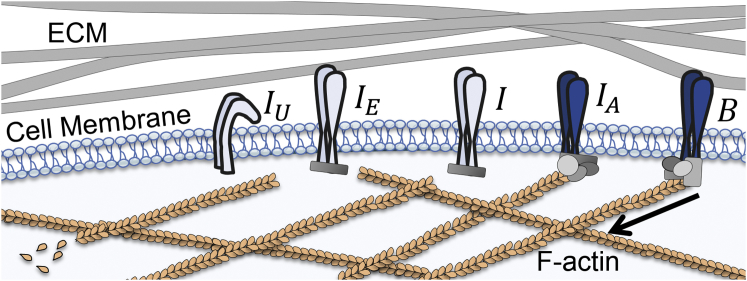
To enable strain transmission between the cell and the ECM, a sequence of molecular events takes place that connect integrins to both the intracellular and extracellular regions of the cell. These events can be thought of as reversible state transitions, in which integrins belong to one of five states (depicted in Fig. 1). Inactive integrins freely diffuse in the plasma membrane in a bent conformation that leaves them close to the membrane and with a low affinity for binding to ligands in the ECM. Integrin activation occurs in stages, with a final stage being recognized as the binding of adaptor proteins—commonly talin—to the integrin cytoplasmic tail (16, 17). At this stage, the active integrin extends into an upright conformation in which it is more readily available for ligand binding. The adaptor proteins additionally form the link to the actin cytoskeleton. Once bound to both the actin cytoskeleton and to ligands in the ECM, the integrins form a physical link between intracellular and extracellular domains, enabling transmission of mechanical strain.
Figure 1.
Representation of the five possible integrin states. Inactive and active (I) integrins diffuse in the membrane. Active integrins may become actin-bound via adaptor proteins, bound to ligands in the ECM , or double-bound to both the actin cytoskeleton and the ECM (B). In our models, we consider actin-bound and double-bound integrins (blue). To see this figure in color, go online.
In previous models, the binding dynamics of individual integrin-ligand bonds have been studied using stochastic simulations. A number of studies (18, 19, 20) investigate the stochastic rupture of parallel bonds under shared loading, and Qian et al. (21) extend this by considering bonds that experience stress nonuniformly because of an inclined loading angle. Of particular relevance to the current work are studies that consider the effect of dynamic loading on adhesion stability (22), measured by the mean change in number of bound integrins when subject to the external load. Kong et al. (22) consider the rupture of adhesion clusters under an oscillatory strain, and starting from a high adhesion state, a threshold strain is observed past which adhesions quickly rupture. In a related modeling framework, although not concerned with external loading, Paszek et al. (23) use lattice spring models together with a stochastic simulation algorithm for modeling integrin-ligand bonds called adhesive dynamics (24, 25) to simulate the formation of integrin clusters. Stochastic models are a common approach for studying the mechanosensitive nature of cell-matrix adhesion. Chan and Odde (26) and Walcott et al. (27) both use stochastic models to investigate the differing adhesion dynamics on stiff and compliant ECM and obtain results in agreement with experimental studies. Walcott et al. (27) show that mechanosensitive adhesion properties emerge naturally with the inclusion of load-dependent reactions.
Studies considering friction generated by discrete bonds in more general contexts are also relevant to modeling cell-matrix adhesions. Filippov et al. (28) consider the stochastic formation and rupture of discrete molecular bonds between two rigid surfaces and simulate macroscopic friction properties with high and low relative velocities of the surfaces. In a closely related study, Srinivasan and Walcott (29) develop a continuum approximation through the use of the Lacker-Peskin model (30) and find that well-known steady-slip and stick-slip friction behaviors are captured. Given the potentially large number of integrins present on the cell surface (densities have been reported to reach 900 in mature adhesions (31)), stochastic models can become prohibitive; continuum models, therefore, have greater utility in such cases, allowing for a more comprehensive exploration of the system behavior. Welf et al. (32) and Block et al. (33) have developed continuum models for integrin binding and for integrin clustering based on biochemical feedback in reaction-diffusion systems. However, these studies do not accommodate the response to local mechanical cues. Integrins are highly mechanosensitive, and Cao et al. (34, 35) have developed continuum models that allow for investigation of the effect of substrate and cell nucleus stiffness on focal adhesion size. The timescale of interest in their studies (focal adhesion growth, occurring over minutes) is relatively large compared to the timescale associated with individual integrin-binding reactions, so a quasi-static approximation for the density of integrins is used. A full review of existing models is not presented here, but other noteworthy examples of models that capture experimentally observed focal adhesion behavior include (36, 37, 38). Further examples of stochastic models have been reviewed by Gao et al (39).
In this article, we develop two closely-related theoretical models to investigate integrin binding and adhesion dynamics between an ASM cell and the surrounding ECM in a dynamic environment. Firstly, we consider a discrete stochastic-elastic model for cell-matrix adhesion and investigate how tidal breathing influences the formation and survival of adhesions. We then develop an analogous multiscale continuum model that couples microscale binding reactions to the mechanical environment and reproduces the qualitative behavior observed in the stochastic simulations. With the more tractable continuum model, we further investigate how material parameters and DIs may affect the adhesion properties of ASM cells in vivo.
Methods
In the models that follow, we consider a simplified reaction scheme in which the previously described integrin activation processes are assumed to have already occurred. We therefore assume that integrins are already attached to the actin cytoskeleton within the cell and undergo reversible reactions to become bound to the ECM and able to transmit force ( binds reversibly to B; see Fig. 1). Similar to Paszek et al. (23), in our discrete model, we represent the cell, ECM, and bound integrins by a network of linear springs but focus on the effect of dynamic loading by introducing an oscillatory shear displacement of the ECM. In our continuum model, we capture microscale binding reactions at the integrin level using an adaptation of the Lacker-Peskin model (30); these integrin dynamics respond to (and generate) ECM and cell deformations at the cell level. Through this multiscale approach, we are able to account for microscale spatial constraints in the binding and unbinding reactions in a similar manner to that of the individual-based approach used in the discrete model.
Discrete model formulation
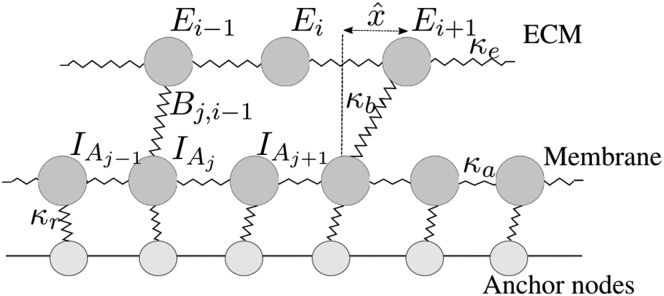
The discrete model comprises an evolving network of nodes and linear springs, the structure of which is governed by stochastic reactions representing transitions between the integrin states and B described above. By modeling individual interactions between integrins, the cell, and the ECM, we aim first to develop an intuitive understanding of cell-matrix adhesion. We assume that the cytoskeleton, integrins, and ECM form a spring network in which actin-bound integrins and “potential binding sites” on the ECM fiber (E) are modeled as individual nodes, indexed by and , respectively (Fig. 2). Hookean springs between the neighboring and E nodes represent the cytoskeleton and ECM, respectively, and are each assigned a spring stiffness ( and ). Reactions between integrins and the ECM are dependent on the proximity and availability of binding sites, and each node is considered to be an individual species so that reaction propensities depend on their pairwise distances. Pairs of compatible nodes may undergo stochastic transitions to form fully bound integrins (B) according to the following reaction:
| (1) |
where is a spatial variable local to each integrin that, following (40), measures the horizontal distance between each pair of and E nodes (see Fig. 2) and is therefore effectively a measure of how far each integrin head is from its unstressed position, . Throughout the article, hats indicate dimensional quantities. In accordance with these stochastic reactions, we add or remove a third spring-type (representing double-bound integrins with stiffness ) between the and E nodes selected to bind. We additionally include springs with stiffness from the nodes to a fixed configuration of “anchor” nodes, as a representation of the restoring forces and attachments to the cytoskeletal network within the cell. Following (40), the vertical movement is constrained, and we only consider horizontal motion, a physical simplification that will be addressed in future work (see Discussion).
Figure 2.
Structure of the discrete spring network. Following (40), the vertical movement is constrained, and we only consider horizontal motion. Actin-bound integrins and ECM binding sites (E) are considered individual nodes connected to their neighbors by linear springs with stiffness constants and , respectively. Bound integrins (B) are represented by removable springs between the two sets of nodes, with spring constant . The local variable measures horizontal distances between pairs of integrin and ECM binding site nodes. We additionally include horizontal restoring forces for the nodes to a fixed configuration of anchor nodes via springs with stiffness .
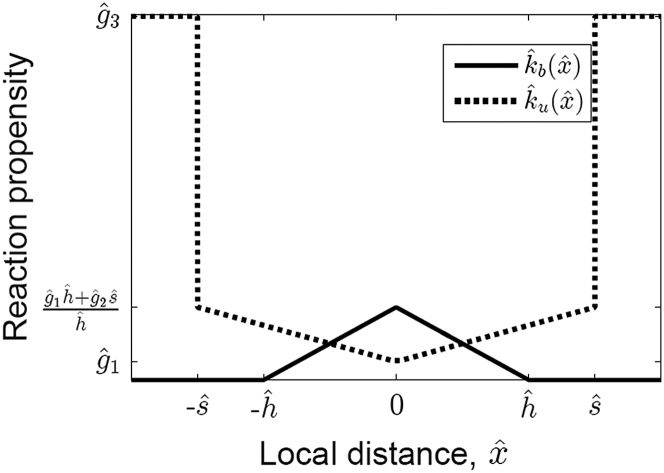
We select the reversible binding events using a stochastic first reaction algorithm (41) and follow the reactions in Eq. 1 for each pair of compatible nodes. In this work, our chosen spatial binding rates are piecewise linear functions (Fig. 3) given by
| (2) |
and
| (3) |
Figure 3.
Sketch of the chosen form of piecewise linear binding (, Eq. 2) and unbinding (, Eq. 3) functions. The local variable measures the local distance between pairs of ECM and actin-bound integrin nodes (see Fig. 2) and is therefore effectively a measure of how far each integrin head is from its unstressed position, .
A maximal binding rate occurs at , after which the binding propensity decreases linearly to zero within a finite binding range, . The unbinding rate when is given by and increases at a rate of as increases. Beyond a maximal horizontal distance of , any remaining bonds rupture quickly with a high rate . We note that these piecewise linear rates approximate those that can be derived using detailed balance (see e.g., Figure 9 c in (42) and Figure 2 in (29)), by which pairs of reaction rates are constrained to ensure thermodynamic reversibility. Within this modeling framework, there is flexibility in the choice of rate functions, and alternative choices can be used (see Discussion).
The stochastic reactions that govern bond formation and rupture are used to update the structure of the mechanical spring network (Fig. 2). To implement a position update of the network, we consider the net force acting on each node, . There are contributions due to neighboring springs, , and forces due to integrin bonds between species, . In this model, electrostatic interactions and inertia are assumed to be negligible. We therefore take and update the positions of the nodes to ensure that at each time step.
To represent fluctuations that occur because of tidal breathing, we impose an external, oscillatory forcing to the ECM via a time-dependent displacement of the boundary node as follows:
| (4) |
where amplitude is , frequency is , and denotes the displacement of the ith ECM node from its rest position. Sinusoidal waveforms are commonly used to represent tidal breathing (43, 44, 45, 46); however, they are a simplification because exhalation is typically longer than inhalation. We include and discuss results for an asymmetric waveform in Supporting Materials and Methods, Section S.3.2. The results and conclusions are consistent with those presented here.
We note that the first reaction algorithm (41) generates an event-based time step. As we are also considering external forcing, we introduce a maximal time step such that, in the case that no reaction occurs within this time step, a position update of the network is induced, and reaction propensities are recalculated. We summarize the computational model in Supporting Materials and Methods, Section S.1.1.
Continuum model formulation
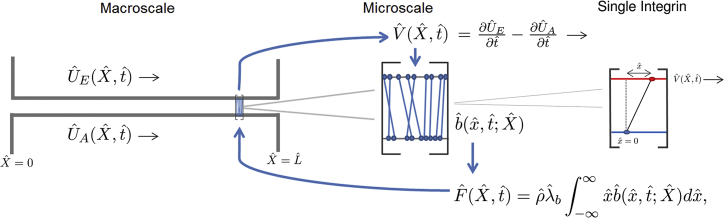
We now introduce an analogous continuum model in which we consider two well-separated scales: a microscale, integrin-level description for bond formation and rupture that is coupled to a macroscale, cell-level model of material deformation (illustrated in Fig. 4). At the macroscale, we consider deformations of the cell, , and of the ECM, , where is a macroscale spatial coordinate and is time. At each point in , a macroscale deformation occurs as a result of the adhesive drag force, , which is generated by integrins cycling between bound and unbound states at the microscale. To model the microscale reactions, we adapt an existing model by Lacker and Peskin (30) (an extension of the Huxley model (40) for actin-myosin cross-bridge dynamics, discussed in detail in (29)).
Figure 4.
Schematic diagram of the multiscale coupling. A relative velocity arising from macroscale deformation influences the binding dynamics and distribution of bonds in a corresponding microscale problem (Eq. 6). As in the discrete model, the variable is local to each integrin and measures the horizontal distance from the cytoskeletal attachment to the binding site on the ECM, as shown. Microscale distributions determine the horizontal drag force, , which is used to update the displacements and and therefore (via Eqs. 7, 8, and 9). To see this figure in color, go online.
Microscale-governing equations
At the microscale, we again consider the binding of active, actin-bound integrins to the ECM to form double-bound integrins (B, Eq. 1). Following the Lacker-Peskin model, the ECM binding sites are assumed to be densely distributed, and there is a characteristic length scale, , associated with the spacing between sites. Each double-bound integrin is associated with a local variable, , measuring the horizontal distance of the bound integrin head from its unstressed (vertical) position at . In the unstressed position, the integrin does not contribute to the horizontal drag force. At each point in the macroscale domain, , bound integrins are collectively expressed by a distribution, , such that the fraction of integrins that are bound with local displacements in a range of ] at time is given by the integral . The total fraction of bound integrins is given by
| (5) |
The evolution of each microscale distribution is governed by the following advection-reaction equation:
| (6) |
where the functional dependencies have been suppressed for brevity. The right-hand side describes binding and unbinding of integrins through the functions and , respectively, for which we employ the same rates as in the discrete model (Eqs. 2 and 3). The scaling of the binding rate by arises in the derivation of the Lacker-Peskin model, which is discussed in detail in (29). Distributions are additionally advected with a macroscale velocity, , which is the velocity of the ECM relative to the velocity of the cell. By treating integrins as Hookean springs, we obtain the drag force per unit length as follows:
| (7) |
where is the integrin spring constant, and is the number of integrins per unit length, acting at a macroscale point . We implicitly assume that there is sufficient scale separation to approximate the microscale distributions to be acting at a macroscale point; a rigorous derivation will be considered in future work.
Macroscale-governing equations
At the macroscale, we assume that the ECM and cell are linear elastic materials that undergo small deformations. The relative macroscale velocity can be written as
| (8) |
which is coupled to the microscale distributions of bound integrins (see Fig. 4) via Eq. 6.
We assume that the drag forces, , due to bound integrins are the only body forces acting on the two materials, and hence, we obtain the following macroscale description by considering the following quasi-static equilibrium conditions:
| (9) |
The constants and are stiffness-like parameters for the cell and ECM, respectively, with units of force per unit strain. The cell and the ECM experience the force in opposite directions.
Boundary conditions
The cell displacement is assumed to be zero at and so that
| (10) |
We apply a time-dependent displacement to the ECM at and zero strain at :
| (11) |
where the oscillatory displacement is chosen to match the discrete model (Eq. 4).
Nondimensionalization
The governing equations and boundary conditions are nondimensionalized with the scalings as follows:
| (12) |
where is the maximal binding rate, and is the integrin-binding range. For simplicity, we assume that is uniform, but an extension to nonuniform is easily incorporated. The dimensionless microscale-governing equations are
| (13) |
where the dimensionless parameters and are the ratios of the integrin-binding range to the macroscale length scale and to the microscale-binding site separation, respectively. The microscale advection-reaction equations are coupled to the macroscale equations via the macroscale velocity .
The dimensionless binding rate functions are
| (14) |
and
| (15) |
where are the ratios of unbinding rates to the maximal binding rate, and . The dimensionless drag force,
| (16) |
features at the macroscale, where the dimensionless governing equations become
| (17) |
with the following boundary conditions:
| (18) |
The remaining dimensionless parameters are
| (19) |
Implementation
To solve the advection-reaction system (Eq. 13), we differentiate the macroscale governing equations (Eq. 17) with respect to time and use Eqs. 8 and 16 to obtain the following second-order partial differential equation for :
| (20) |
where
| (21) |
and
| (22) |
Equations 13 and 20 are solved numerically, as detailed in Supporting Materials and Methods, Section S.1.2, subject to
| (23) |
The macroscale-governing equations (Eq. 17) can be integrated directly to obtain and in terms of . Using Eq. 18, the cell deformation is given by
| (24) |
and the ECM deformation is
| (25) |
Initial conditions
For each amplitude of oscillatory loading, A, we consider two initial conditions: 1) a zero state with no preexisting bound integrins, and 2) a saturated steady state with high integrin binding obtained in the absence of external forcing. In the discrete model, this is found by running the simulation with until the fraction of bound integrins stabilizes; in the continuum model, the steady state, obtained from Eq. 13 when , is given by
| (26) |
Results
Effect of increasing the amplitude of oscillation
We first investigate the effect of varying the amplitude, A, of the oscillatory loading in both the discrete and continuum models. In Fig. 5, we show representative time courses from both models for the fraction of integrins that become fully bound (B) under low-, intermediate-, and high-amplitude oscillatory loading. In the continuum model, the total macroscale bound fraction is found from
| (27) |
where is given by Eq. 21.
Figure 5.
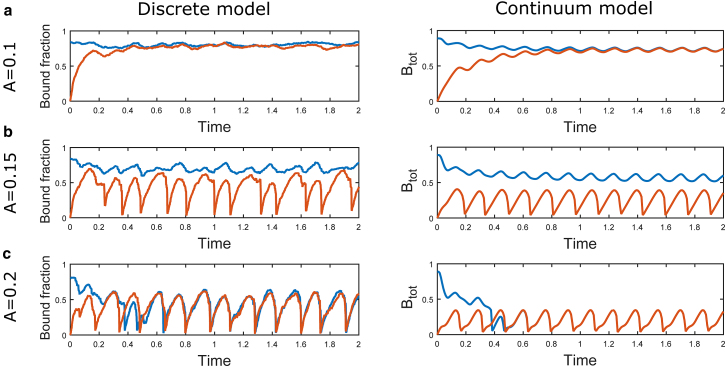
Representative time courses from the discrete stochastic simulation (Discrete Model Formulation) and continuum model (Continuum Model Formulation), shown in the left and right columns, respectively, illustrating the responses of bound integrins (Eq. 27) to (a) low-, (b) intermediate-, and (c) high-amplitude oscillatory loading. This is applied using and amplitudes , , and , respectively, via the boundary conditions in Eq. 4 or Eq. 18 (where Eq. 4 has been nondimensionalized using the scalings in Eqs. 12 and 19). In each case, we consider a zero (orange) and a saturated (blue) initial condition (Eq. 26). See Tables S1 and S2 for a full list of chosen parameter values. To see this figure in color, go online.
For the lowest amplitude oscillation, in both models (Fig. 5 a), we find that both the zero and saturated initial conditions converge to a pattern of high adhesion (with a mean total bound fraction of ∼0.75) subject to small fluctuations as a result of low, sustainable turnover of bound integrins. For the highest amplitude loading (Fig. 5 c), in both models and for both the zero and saturated initial conditions, the result is an oscillatory state in which significant bond rupture leads to a total bound integrin fraction with a lower mean (∼0.2–0.3) and larger amplitude fluctuations. For an intermediate oscillation amplitude (Fig. 5 b), we observe bistability, in which the initial condition determines which of the two adhesion states occur; if adhesions are present when oscillations begin, then shared loading and increased traction prevent high levels of rupture under applied strain. Because of the stochastic nature of the discrete model, under high-amplitude oscillations, we observe small variations in the time of collapse from the high to the low state. Similarly, it is possible to observe stochastic switching (data not shown) between the two adhesion states when the loading parameter is within the bistable range. The high state exhibits persistence of bound integrins, whereas the low state shows cyclic breaking and reattachment of a significant fraction of integrins. These states could be akin to firm and transient adhesions, which are observed to occur in other contexts (see Discussion).
As illustrated in Fig. 5, the discrete and continuum models display strikingly similar qualitative behavior. We exploit the deterministic nature of the continuum model to more reliably investigate the bistability, summarized in Fig. 6, where we present the bound integrin densities obtained for a range of oscillation amplitudes. For each oscillation amplitude, we use both the zero and saturated initial conditions. Because the states under consideration are oscillatory, once the behavior has converged to its periodic steady state, we plot the time-averaged adhesion density given by
| (28) |
where is the oscillation period. There is variation in across the macroscale domain, , and we observe a significantly lower adhesion density near , where the oscillation is applied.
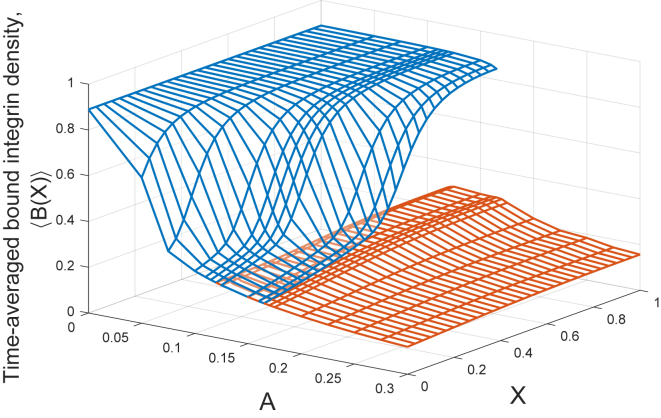
Figure 6.
High (blue) and low (orange) solution surfaces across the macroscale domain, X, indicating stable states of the time-averaged adhesion density (Eq. 28) for a range of oscillation amplitudes, A (Eq. 18), in the continuum model. For intermediate amplitudes, there is bistability. The model parameters are as in Fig. 5 and given in Table S1. To see this figure in color, go online.
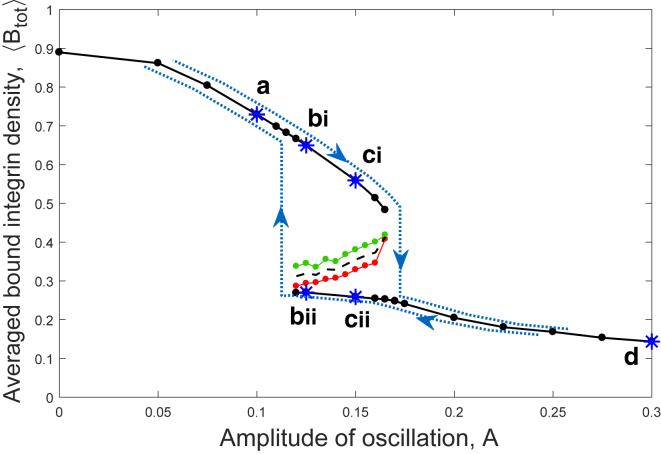
The time-averaged adhesion density plotted in Fig. 6, , is additionally averaged over X to calculate the total time-averaged density (Eq. 27), which is used to generate a bifurcation diagram (Fig. 7). Stable branches indicated by the solid lines confirm, as in Fig. 6, that for low amplitude oscillations, we expect solutions to converge to a high averaged bound integrin state regardless of initial conditions, whereas for high-amplitude oscillations, the solutions converge to a low bound integrin state. For an intermediate range of oscillation amplitudes, we observe a window of bistability in which the initial condition, in relation to an unstable branch (dashed line), determines which of the two stable outcomes occurs. The position of the unstable branch is estimated as the mean of two points that are observed to converge to the upper and lower solutions (green and red markers, respectively). The unstable and stable branches appear to meet in a pair of saddle node bifurcations. As illustrated in Fig. 7, starting on the upper stable branch, an increase in A would lead to a jump from the upper to the lower stable solution at the bifurcation point. The value of A at this point corresponds to a threshold loading at which adhesions quickly rupture. On the other hand, a decrease in A from the lower branch leads to a jump from the lower to upper branch at a different amplitude following a different path, thereby generating a hysteresis loop (blue dotted line).
Figure 7.
Bifurcation diagram indicating steady states of the time-averaged total adhesion density (Eqs. 27 and 28) for a range of oscillation amplitudes, A (Eq. 18). Stable branches are indicated by solid lines separated by the dashed, unstable branch. The position of the unstable branch is bounded by points known to converge to the upper and lower solutions, in green and red, respectively. Blue markers highlight example monostable ((a) , (d) ) and bistable ((b) , (c) ) regimes, and a hysteresis loop is seen (blue dotted line). The path taken as A increases ((a) (b)i (c)i (d)) differs from the path followed as A decreases ((d) (c)ii (b)ii (a)). To see this figure in color, go online.
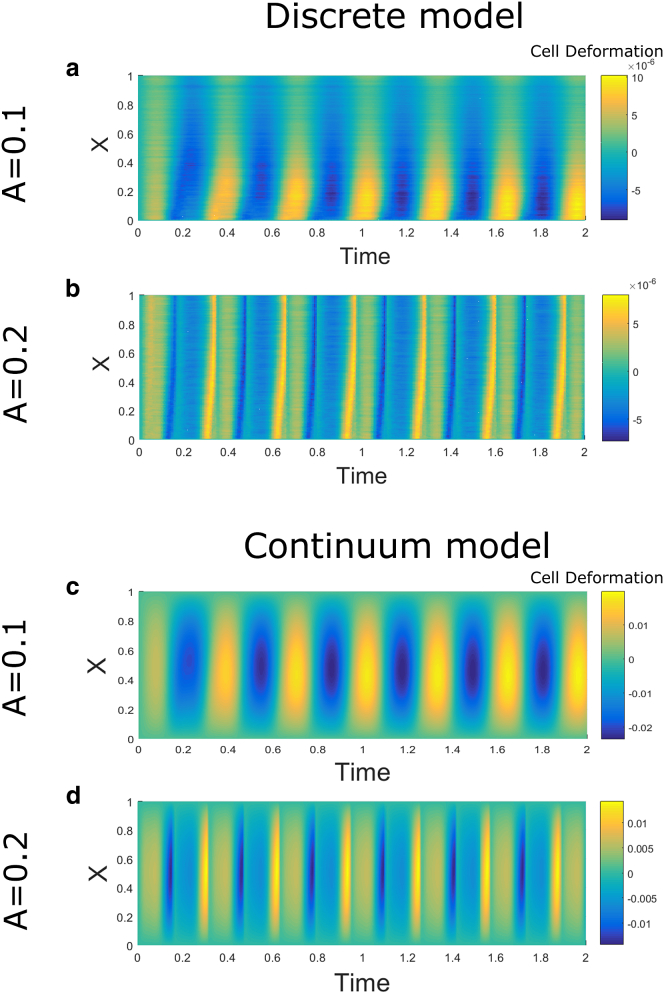
Next, we examine the spatiotemporal cell deformation resulting from oscillatory loading for both the discrete and continuum models in each stable regime (Fig. 8). In the high bound integrin regime (i.e., low amplitude oscillations), adhesions persist, and in both models, there are smooth transitions between positive and negative cell deformations across the domain (Fig. 8, a and c). These appear as wide bands that follow the movement of the ECM. In the low bound integrin regime (high-amplitude oscillations), the bands narrow and exhibit sharp boundaries because of greater numbers of rupture events at each cycle (Fig. 8, b and d). The differences in deformation that result from low and high-amplitude oscillations correspond to differences in the total drag force generated by bound integrins, as shown in Fig. 9. The total drag force in the continuum model, , is defined analogously to (Eq. 27). Note that although the total drag forces are qualitatively similar in both models, there are some significant differences in the spatial propagation of the deformation applied at (Fig. 8) because of the differences between the two modeling approaches. In particular, in the discrete model there are individual springs between each node, but this is simplified in the microscale formulation of the continuum model. Because bond rupture is affected by the level of deformation, the total bound fractions (Fig. 5) also differ slightly in magnitude between the two models; however, there is still striking qualitative agreement for the averaged macroscale quantities of interest (, , in Figs. 5 and 9). Because we are primarily interested in qualitative behavior, we exploit the efficiency of the continuum model in place of discrete stochastic simulations to investigate the effect of perturbations due to DIs. We also investigate the effect of oscillation frequency, material stiffness, and binding affinities on the averaged bound integrin density, (Fig. S1). In each case, bistability is observed, but the positions of the stable branches are shifted.
Figure 8.
Cell deformation, , (indicated by color) plotted as functions of the position in the cell domain, X, and time, t, obtained in the discrete (a and b) and continuum (c and d) models in the cases in which adhesion formation (a and c) and adhesion rupture (b and d) dominate under oscillatory loading. Simulations are carried out from a zero initial condition, and oscillation amplitudes are and in Eqs. 4 and 18. Eq. 4 has been nondimensionalized using the scalings in Eqs. 12 and 19. In (a) and (b), the results have been averaged over 150 simulations, and the spatial positions are presented on a scaled domain . To see this figure in color, go online.
Figure 9.
Total adhesive drag forces, , in the discrete (a and b) and continuum (c and d) models corresponding to the deformations in Fig. 8. (a and c) in Eqs. 4 and 18, and adhesion formation dominates. (b and d) , and there is increased rupture and a constant turnover of bound integrins under oscillatory loading. Eq. 4 has been nondimensionalized using the scalings in Eqs. 12 and 19. As in Fig. 8, simulations are carried out from a zero initial condition. The results in (a) and (b) are from one sample discrete simulation.
Effect of perturbations due to DIs
We now investigate the effect of transient perturbations to the amplitude of oscillatory loading to mimic the strain imposed on ASM cells and the ECM that may result from taking a DI during a period of regular breathing. Starting from the saturated initial condition (Eq. 26), we allow the bound fraction to settle to its periodic high steady state before perturbing the amplitude of the oscillation for one cycle. We therefore impose
| (29) |
for baseline oscillation amplitude , DI amplitude (where ), and oscillation frequency .
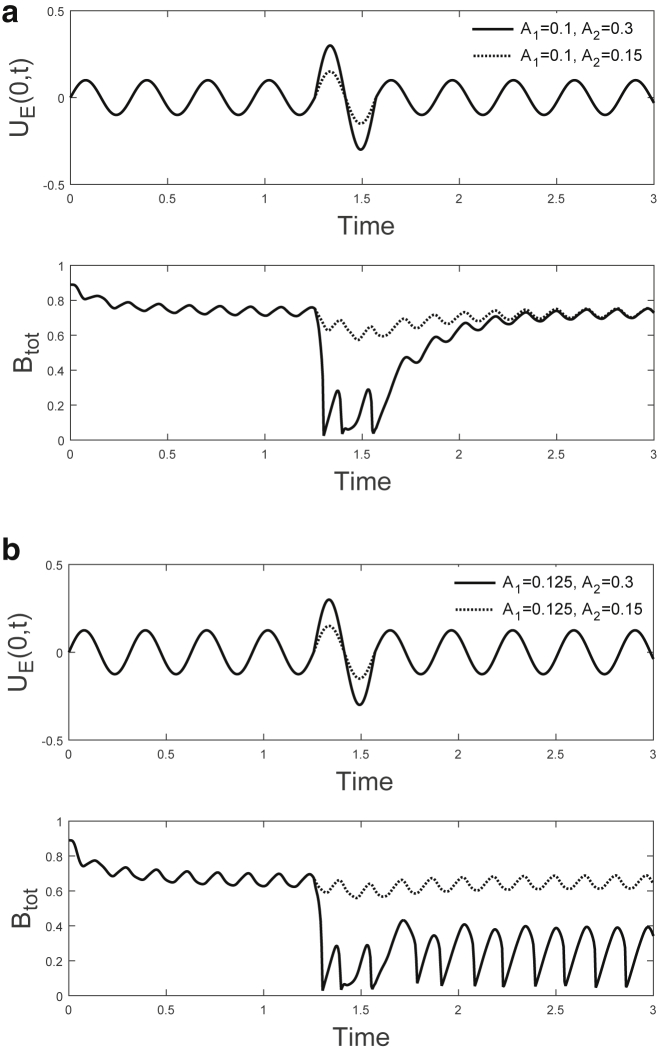
We consider two different baseline oscillation amplitudes ( and , marked by (a) and (b), respectively, in Fig. 7). This choice is motivated by variations in the amplitude of tidal breathing that may arise between individuals; pressure-driven oscillations in vivo lead to smaller strains for greater material stiffnesses (14, 47). The differences in could therefore correspond to asthmatic (stiff) and healthy (compliant) airways. We investigate the response to a small perturbation (, point (c) in Fig. 7) and a DI that is large enough to induce significant rupture of adhesions (, point (d) in Fig. 7) and find that for a starting amplitude , there is recovery to the high adhesion state regardless of the amplitude of the perturbation (Fig. 10 a). For a starting amplitude , there are two possible responses depending on the amplitude of the DI perturbation (Fig. 10 b). As shown by the blue markers in Fig. 7, for , the high adhesion state is the only stable solution, and a high density of bound integrins therefore persists after a perturbation. In contrast, lies within the bistable window, and if the DI perturbation is large enough to drive the system into the basin of attraction of the low adhesion state, there is a transition to a low bound integrin density that persists even after the oscillation returns to its initial amplitude.
Figure 10.
Different amplitude baseline oscillations and DI-like perturbations may lead to a switch in adhesion states. We show the applied oscillatory displacement, , and the total bound fraction of integrins, (see Eqs. 29 and 27), when . (a) For , (solid line) and , (dashed line), the high adhesion state persists after both DI perturbations because for , this is the only steady state. (b) For , (solid line), there is a transition to a low adhesion state because is within the bistable window (see Fig. 7), and the DI is sufficiently large to drive the system into the basin of attraction of the low state. For a smaller amplitude perturbation, (dashed line), the high fraction of bound integrins persists.
These responses demonstrate the possible consequences of bistability as well as the importance of loading history because an event such as a DI perturbation may alter the future state of adhesion when bistability is present. Persistence of the previous state depends on the amplitude of the DI and on where the bistable window (Fig. 7) lies in relation to the baseline oscillation amplitude, . Physiologically, this will be influenced by differences in the amplitude of the baseline oscillatory displacement, representing tidal breathing, and differences in parameters such as the oscillation frequency, material stiffnesses, and binding affinities that shift the location of the bistable window (Fig. S1).
Discussion
We have developed a discrete stochastic-elastic model and a multiscale continuum model to investigate the effect of oscillatory loading on the dynamics of ASM cell-matrix adhesions. We have demonstrated that oscillatory loading, representing deformations due to tidal breathing, can have a significant impact on integrin dynamics and the persistence of adhesions, which we expect to affect the level of force that can be transmitted between intracellular and extracellular domains. In particular, we observe two distinct regimes in which either adhesion formation or adhesion rupture dominates, resulting in differences in the steady-state densities of bound integrins (Fig. 5). Moreover, a window of bistability exists for intermediate loading amplitudes (Fig. 7) because of mechanical cooperativity; shared loading between preexisting adhesions allows the high-density state to persist when rupture would otherwise dominate. This bistability generates a hysteresis loop, and we see that the loading history and events such as perturbations representing DIs can significantly alter the future adhesion dynamics (Fig. 10). In previous studies (23, 48), similar instances of integrin cooperativity have been observed, in which shared loading between integrins aids initial cluster formation. In addition to the differences in bound integrin densities seen in the two regimes, cell deformations and adhesive drag forces also differ significantly in each case, both in terms of magnitude and dynamics (Figs. 8 and 9). The qualitative behaviors seen in the discrete model are also observed in our continuum model, the convenience of which we exploit to investigate the adhesion dynamics further. The existence of a threshold at which bond rupture dominates over adhesion formation is in agreement with the Monte Carlo simulations in a previous study (22), in which an oscillatory strain is applied to an initially fully bound substrate. Our model assumptions differ in some respects from those of Kong et al. (22), but sudden rupture occurs in both when the oscillation amplitude is increased. In our model, we additionally observe bistability and hysteresis. The two adhesion states reported appear to behave similarly to transient and firm adhesions observed in other contexts. Integrin-mediated adhesions can function as either dynamic or stable structures (6), and in the context of cell migration, switching between transient and firm adhesion states (mediated by biochemical signaling) facilitates migration by altering the traction properties between cells and the ECM. Mechanical signals, in addition to biochemical signals, are known to be able to modulate focal adhesion size and dynamics (49), and further studies into how the mechanical environment of ASM affects focal adhesions will be worthwhile.
We propose the following in vitro experiment to investigate whether the mechanical cooperativity of integrins could indeed lead to bistability: using atomic force microscopy, vertical or lateral oscillations could be applied to ECM-coated beads that initially have different but controlled levels of adhesion to the cell. Control over the initial condition can be achieved by varying the contact time between the bead and cell, as previously carried out in (50). In addition, by gradually increasing and then decreasing the amplitude of oscillation, the hysteresis illustrated in Fig. 7 could be tested.
The airway response to DIs is known to be different in asthmatics and nonasthmatics: in healthy subjects, DIs promote bronchodilation, but this effect is either transient or non-existent in asthmatics (9, 10, 11). DI-induced bronchodilation has previously been attributed to disruption of actin-myosin cross-bridges (11), which mediate contractile force generation within the cell. However, because intracellular contractile force transmission to the extracellular domain is reliant on cell-matrix adhesions, the density of adhesions that survive under oscillatory loading in each case could also play an important role; we expect the high and low density adhesion states predicted by the model to produce significantly different levels of strain transmission between contracted ASM cells and the ECM. Our results show either persistence of the high adhesion state or a transition from the high to low adhesion states in response to DI-like perturbations (Fig. 10). The ability of a DI to induce a switch between states is influenced by a difference in 1) the position of the bistable region, which shifts in response to changes in parameters such as oscillation frequency, material stiffnesses, or binding affinities (see Fig. S1); 2) the amplitude of the unperturbed oscillatory displacement, which we use to represent the magnitude of tidal breathing; or 3) the magnitude of the DI. All of these factors could differ between individuals as well as between asthmatics and nonasthmatics. To fully understand the bronchodilatory effect of DIs, it will be crucial to consider the combined dynamics of actin-myosin cross-bridges and integrins; we expect them both to contribute, but their relative importance will only become clear when considered together. Although actin-myosin cross-bridge cycling, which mediates contractile force generation within the cell, undergoes changes during DIs, by considering the possible integrin response to breathing and DIs we have illustrated that strain transmission (via integrins) could also be a highly dynamic process. Integrin-mediated adhesion is therefore an important process to study further in this context.
Further motivation for understanding contractile force transmission between ASM cells and the ECM in the context of asthma is that contractile force is also known to promote the activation of TGFβ, a growth factor that otherwise remains latent in the ECM. TGFβ promotes long-term airway remodeling with consequences such as airway wall thickening and altered material properties (e.g., increased stiffness) of the airway tissue (51, 52, 53, 54, 55). These structural changes are irreversible and over time lead to obstructed airflow and a decline in lung function. To fully understand the effect of cell-matrix adhesion density on levels of contractile force transmission and the consequences that this may have for the activation of TGFβ, future work will involve an extension to higher dimensions at which the constraint on vertical motion will be relaxed. This is an important step toward a full coupling to models of actomyosin dynamics and contractile force generation in ASM cells.
Our results were obtained firstly in a stochastic-elastic computational model and then in a continuum model. We find that our discrete and continuum models produce similar qualitative behavior, and in a future study, we will consider the formal relationship between the two models. This will allow for more rigorous quantitative as well as qualitative comparisons. Although the discrete model is advantageous for incorporating large amounts of individual detail, the continuum model can more easily be coupled to existing models of contractile force generation, for example (56), and is more efficient when the number of integrins is high. In (56), cross-bridge cycling and disruption to actin-myosin contractile units (in response to cell length changes) are considered, which would allow us to more fully investigate the combined dynamics of cross-bridges and integrins during DIs. The continuum model can additionally be extended to address simplifications made during initial model development; in particular, we can consider nonlinear elastic materials to accommodate large deformations, a more complete reaction sequence including integrin diffusion and activation, and different forms for spatial binding and rupture rates. Instead of our simplified piecewise linear rates, a more commonly used description for bond rupture under force is the Bell model (57), in which rupture rates increase exponentially with force. Other rate functions, including a power law relation, have also been presented (58, 59), and obtaining precise measurements for individual integrins using techniques such as atomic force microscopy (60) remains an area of ongoing research. As we explicitly account for binding and unbinding rates that depend on microscale distance, both our discrete and continuum models can accommodate any of these choices.
Here, we have discussed cell-matrix adhesion in the context of tidal breathing and ASM. However, the models presented could be applicable to other contexts in which dynamic environments occur. Interesting examples include the adhesion dynamics that occurs in response to large volume changes in the urinary bladder or in uterine smooth muscle during pregnancy and childbirth. In both of these cases, it is thought that integrins play an important role in the adaptation of smooth muscle to different lengths and functions (61, 62).
In this article, we have shown that cell-matrix adhesion strength can be heavily influenced by dynamic loading (representing tidal breathing and DIs) and by the loading history. To date, consideration of mechanical ASM-ECM interactions via integrins has been neglected in investigations on the effect of tidal breathing and DIs in asthma. Here, we have shown that integrins could play an important role in the level of strain transmission during ASM contraction in vivo because the bound integrin density responds dynamically to oscillatory loading. Furthermore, a simulated DI is shown to induce either transient or permanent changes in the bound integrin density depending on the amplitude of tidal breathing (Fig. 10). This result could help to explain, in part, previous experimental observations on the bronchodilatory effect of DIs, which are transient or absent in asthmatics yet sustained in healthy subjects.
Author Contributions
M.R.O., R.D.O., and B.S.B. designed the research. L.I. performed the research. L.I., M.R.O., R.D.O., and B.S.B. analyzed the data. L.I. prepared the figures. L.I., M.R.O., R.D.O., and B.S.B. drafted the manuscript. L.I., M.R.O., R.D.O., and B.S.B. edited and revised the manuscript.
Acknowledgments
R.D.O. and B.S.B. acknowledge support from the Medical Research Council United Kingdom (MR/M004643/1). We thank Prof. G. A. Meininger (University of Missouri) for helpful discussions and the reviewers for their constructive feedback.
Editor: Jeffrey Fredberg.
Footnotes
Supporting Materials and Methods, five figures, and three tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30520-4.
Supporting Citations
References (63, 64, 65, 66, 67) appear in the Supporting Material.
Supporting Material
References
- 1.Bousquet J., Jeffery P.K., Vignola A.M. Asthma. From bronchoconstriction to airways inflammation and remodeling. Am. J. Respir. Crit. Care Med. 2000;161:1720–1745. doi: 10.1164/ajrccm.161.5.9903102. [DOI] [PubMed] [Google Scholar]
- 2.Gunst S.J., Tang D.D., Opazo Saez A. Cytoskeletal remodeling of the airway smooth muscle cell: a mechanism for adaptation to mechanical forces in the lung. Respir. Physiol. Neurobiol. 2003;137:151–168. doi: 10.1016/s1569-9048(03)00144-7. [DOI] [PubMed] [Google Scholar]
- 3.Zhang W., Gunst S.J. Interactions of airway smooth muscle cells with their tissue matrix: implications for contraction. Proc. Am. Thorac. Soc. 2008;5:32–39. doi: 10.1513/pats.200704-048VS. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hynes R.O. Integrins: bidirectional, allosteric signaling machines. Cell. 2002;110:673–687. doi: 10.1016/s0092-8674(02)00971-6. [DOI] [PubMed] [Google Scholar]
- 5.Schwartz M.A. Integrins and extracellular matrix in mechanotransduction. Cold Spring Harb. Perspect. Biol. 2010;2:a005066. doi: 10.1101/cshperspect.a005066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hoffman B.D., Grashoff C., Schwartz M.A. Dynamic molecular processes mediate cellular mechanotransduction. Nature. 2011;475:316–323. doi: 10.1038/nature10316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sun Z., Guo S.S., Fässler R. Integrin-mediated mechanotransduction. J. Cell Biol. 2016;215:445–456. doi: 10.1083/jcb.201609037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wolfenson H., Lavelin I., Geiger B. Dynamic regulation of the structure and functions of integrin adhesions. Dev. Cell. 2013;24:447–458. doi: 10.1016/j.devcel.2013.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kapsali T., Permutt S., Togias A. Potent bronchoprotective effect of deep inspiration and its absence in asthma. J. Appl. Physiol. 2000;89:711–720. doi: 10.1152/jappl.2000.89.2.711. [DOI] [PubMed] [Google Scholar]
- 10.Crimi E., Pellegrino R., Brusasco V. Deep breaths, methacholine, and airway narrowing in healthy and mild asthmatic subjects. J. Appl. Physiol. 2002;93:1384–1390. doi: 10.1152/japplphysiol.00209.2002. [DOI] [PubMed] [Google Scholar]
- 11.Scichilone N., Kapsali T., Togias A. Deep inspiration-induced bronchoprotection is stronger than bronchodilation. Am. J. Respir. Crit. Care Med. 2000;162:910–916. doi: 10.1164/ajrccm.162.3.9907048. [DOI] [PubMed] [Google Scholar]
- 12.Gunst S.J. Contractile force of canine airway smooth muscle during cyclical length changes. J. Appl. Physiol. 1983;55:759–769. doi: 10.1152/jappl.1983.55.3.759. [DOI] [PubMed] [Google Scholar]
- 13.Latourelle J., Fabry B., Fredberg J.J. Dynamic equilibration of airway smooth muscle contraction during physiological loading. J. Appl. Physiol. 2002;92:771–779. doi: 10.1152/japplphysiol.01090.2000. [DOI] [PubMed] [Google Scholar]
- 14.LaPrad A.S., Szabo T.L., Lutchen K.R. Tidal stretches do not modulate responsiveness of intact airways in vitro. J. Appl. Physiol. 2010;109:295–304. doi: 10.1152/japplphysiol.00107.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bates J.H. Modeling the impairment of airway smooth muscle force by stretch. J. Appl. Physiol. 2015;118:684–691. doi: 10.1152/japplphysiol.00938.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Campbell I.D., Ginsberg M.H. The talin-tail interaction places integrin activation on FERM ground. Trends Biochem. Sci. 2004;29:429–435. doi: 10.1016/j.tibs.2004.06.005. [DOI] [PubMed] [Google Scholar]
- 17.Banno A., Ginsberg M.H. Integrin activation. Biochem. Soc. Trans. 2008;36:229–234. doi: 10.1042/BST0360229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Seifert U. Rupture of multiple parallel molecular bonds under dynamic loading. Phys. Rev. Lett. 2000;84:2750–2753. doi: 10.1103/PhysRevLett.84.2750. [DOI] [PubMed] [Google Scholar]
- 19.Erdmann T., Schwarz U.S. Stability of adhesion clusters under constant force. Phys. Rev. Lett. 2004;92:108102. doi: 10.1103/PhysRevLett.92.108102. [DOI] [PubMed] [Google Scholar]
- 20.Erdmann T., Schwarz U.S. Bistability of cell-matrix adhesions resulting from nonlinear receptor-ligand dynamics. Biophys. J. 2006;91:L60–L62. doi: 10.1529/biophysj.106.090209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Qian J., Wang J., Gao H. Lifetime and strength of periodic bond clusters between elastic media under inclined loading. Biophys. J. 2009;97:2438–2445. doi: 10.1016/j.bpj.2009.08.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kong D., Ji B., Dai L. Stability of adhesion clusters and cell reorientation under lateral cyclic tension. Biophys. J. 2008;95:4034–4044. doi: 10.1529/biophysj.108.131342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Paszek M.J., Boettiger D., Hammer D.A. Integrin clustering is driven by mechanical resistance from the glycocalyx and the substrate. PLoS Comput. Biol. 2009;5:e1000604. doi: 10.1371/journal.pcbi.1000604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hammer D.A., Apte S.M. Simulation of cell rolling and adhesion on surfaces in shear flow: general results and analysis of selectin-mediated neutrophil adhesion. Biophys. J. 1992;63:35–57. doi: 10.1016/S0006-3495(92)81577-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hammer D.A. Adhesive dynamics. J. Biomech. Eng. 2014;136:021006. doi: 10.1115/1.4026402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chan C.E., Odde D.J. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 27.Walcott S., Kim D.H., Sun S.X. Nucleation and decay initiation are the stiffness-sensitive phases of focal adhesion maturation. Biophys. J. 2011;101:2919–2928. doi: 10.1016/j.bpj.2011.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Filippov A.E., Klafter J., Urbakh M. Friction through dynamical formation and rupture of molecular bonds. Phys. Rev. Lett. 2004;92:135503. doi: 10.1103/PhysRevLett.92.135503. [DOI] [PubMed] [Google Scholar]
- 29.Srinivasan M., Walcott S. Binding site models of friction due to the formation and rupture of bonds: state-function formalism, force-velocity relations, response to slip velocity transients, and slip stability. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;80:046124. doi: 10.1103/PhysRevE.80.046124. [DOI] [PubMed] [Google Scholar]
- 30.Lacker, H. M., and C. S. Peskin. 1986. A mathematical method for unique determination of crossbridge properties from steady-state mechanical and energetic experiments on macroscopic muscle. In Some Mathematical Questions in Biology–Muscle Physiology, (The American Mathematical Society), Volume 16, pp. 121–153.
- 31.Wiseman P.W., Brown C.M., Horwitz A.F. Spatial mapping of integrin interactions and dynamics during cell migration by image correlation microscopy. J. Cell Sci. 2004;117:5521–5534. doi: 10.1242/jcs.01416. [DOI] [PubMed] [Google Scholar]
- 32.Welf E.S., Naik U.P., Ogunnaike B.A. A spatial model for integrin clustering as a result of feedback between integrin activation and integrin binding. Biophys. J. 2012;103:1379–1389. doi: 10.1016/j.bpj.2012.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Block M.R., Destaing O., Fourcade B. Integrin-mediated adhesion as self-sustained waves of enzymatic activation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2015;92:042704. doi: 10.1103/PhysRevE.92.042704. [DOI] [PubMed] [Google Scholar]
- 34.Cao X., Lin Y., Shenoy V.B. A chemomechanical model of matrix and nuclear rigidity regulation of focal adhesion size. Biophys. J. 2015;109:1807–1817. doi: 10.1016/j.bpj.2015.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cao X., Ban E., Shenoy V.B. Multiscale model predicts increasing focal adhesion size with decreasing stiffness in fibrous matrices. Proc. Natl. Acad. Sci. USA. 2017;114:E4549–E4555. doi: 10.1073/pnas.1620486114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Maraldi M., Valero C., Garikipati K. A computational study of stress fiber-focal adhesion dynamics governing cell contractility. Biophys. J. 2014;106:1890–1901. doi: 10.1016/j.bpj.2014.03.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Deshpande V.S., Mrksich M., Evans A.G. A bio-mechanical model for coupling cell contractility with focal adhesion formation. J. Mech. Phys. Solids. 2008;56:1484–1510. [Google Scholar]
- 38.Nicolas A., Geiger B., Safran S.A. Cell mechanosensitivity controls the anisotropy of focal adhesions. Proc. Natl. Acad. Sci. USA. 2004;101:12520–12525. doi: 10.1073/pnas.0403539101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gao H., Qian J., Chen B. Probing mechanical principles of focal contacts in cell-matrix adhesion with a coupled stochastic-elastic modelling framework. J. R. Soc. Interface. 2011;8:1217–1232. doi: 10.1098/rsif.2011.0157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Huxley A.F. Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 1957;7:255–318. [PubMed] [Google Scholar]
- 41.Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- 42.Hill T.L. Theoretical formalism for the sliding filament model of contraction of striated muscle. Part I. Prog. Biophys. Mol. Biol. 1974;28:267–340. doi: 10.1016/0079-6107(74)90020-0. [DOI] [PubMed] [Google Scholar]
- 43.Bates J.H., Bullimore S.R., Lauzon A.M. Transient oscillatory force-length behavior of activated airway smooth muscle. Am. J. Physiol. Lung Cell. Mol. Physiol. 2009;297:L362–L372. doi: 10.1152/ajplung.00095.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Harvey B.C., Parameswaran H., Lutchen K.R. Can tidal breathing with deep inspirations of intact airways create sustained bronchoprotection or bronchodilation? J. Appl. Physiol. 2013;115:436–445. doi: 10.1152/japplphysiol.00009.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mailhot-Larouche S., Lortie K., Bossé Y. An in vitro study examining the duration between deep inspirations on the rate of renarrowing. Respir. Physiol. Neurobiol. 2017;243:13–19. doi: 10.1016/j.resp.2017.04.013. [DOI] [PubMed] [Google Scholar]
- 46.Raqeeb A., Solomon D., Seow C.Y. Length oscillation mimicking periodic individual deep inspirations during tidal breathing attenuates force recovery and adaptation in airway smooth muscle. J. Appl. Physiol. 2010;109:1476–1482. doi: 10.1152/japplphysiol.00676.2010. [DOI] [PubMed] [Google Scholar]
- 47.Hiorns J.E., Jensen O.E., Brook B.S. Nonlinear compliance modulates dynamic bronchoconstriction in a multiscale airway model. Biophys. J. 2014;107:3030–3042. doi: 10.1016/j.bpj.2014.10.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Selhuber-Unkel C., López-García M., Spatz J.P. Cooperativity in adhesion cluster formation during initial cell adhesion. Biophys. J. 2008;95:5424–5431. doi: 10.1529/biophysj.108.139584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Na S., Trache A., Humphrey J.D. Time-dependent changes in smooth muscle cell stiffness and focal adhesion area in response to cyclic equibiaxial stretch. Ann. Biomed. Eng. 2008;36:369–380. doi: 10.1007/s10439-008-9438-7. [DOI] [PubMed] [Google Scholar]
- 50.Sun Z., Martinez-Lemus L.A., Meininger G.A. Mechanical properties of the interaction between fibronectin and α5β1-integrin on vascular smooth muscle cells studied using atomic force microscopy. Am. J. Physiol. Heart Circ. Physiol. 2005;289:H2526–H2535. doi: 10.1152/ajpheart.00658.2004. [DOI] [PubMed] [Google Scholar]
- 51.Tatler A.L., John A.E., Jenkins G. Integrin αvβ5-mediated TGF-β activation by airway smooth muscle cells in asthma. J. Immunol. 2011;187:6094–6107. doi: 10.4049/jimmunol.1003507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Oenema T.A., Maarsingh H., Gosens R. Bronchoconstriction induces TGF-β release and airway remodelling in guinea pig lung slices. PLoS One. 2013;8:e65580. doi: 10.1371/journal.pone.0065580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Elias J.A., Zhu Z., Homer R.J. Airway remodeling in asthma. J. Clin. Invest. 1999;104:1001–1006. doi: 10.1172/JCI8124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.James A.L., Wenzel S. Clinical relevance of airway remodelling in airway diseases. Eur. Respir. J. 2007;30:134–155. doi: 10.1183/09031936.00146905. [DOI] [PubMed] [Google Scholar]
- 55.Pascual R.M., Peters S.P. Airway remodeling contributes to the progressive loss of lung function in asthma: an overview. J. Allergy Clin. Immunol. 2005;116:477–486. doi: 10.1016/j.jaci.2005.07.011. quiz 487. [DOI] [PubMed] [Google Scholar]
- 56.Brook B.S. Emergence of airway smooth muscle mechanical behavior through dynamic reorganization of contractile units and force transmission pathways. J. Appl. Physiol. 2014;116:980–997. doi: 10.1152/japplphysiol.01209.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 58.Evans E., Berk D., Leung A. Detachment of agglutinin-bonded red blood cells. I. Forces to rupture molecular-point attachments. Biophys. J. 1991;59:838–848. doi: 10.1016/S0006-3495(91)82296-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Evans E., Ritchie K. Dynamic strength of molecular adhesion bonds. Biophys. J. 1997;72:1541–1555. doi: 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Franz C.M., Taubenberger A., Muller D.J. Studying integrin-mediated cell adhesion at the single-molecule level using AFM force spectroscopy. Sci. STKE. 2007;2007:pl5. doi: 10.1126/stke.4062007pl5. [DOI] [PubMed] [Google Scholar]
- 61.Wilson C.B., Leopard J., Nakamura R.M. Extracellular matrix and integrin composition of the normal bladder wall. World J. Urol. 1996;14(Suppl 1):S30–S37. doi: 10.1007/BF00182062. [DOI] [PubMed] [Google Scholar]
- 62.Williams S.J., White B.G., MacPhee D.J. Expression of α5 integrin (Itga5) is elevated in the rat myometrium during late pregnancy and labor: implications for development of a mechanical syncytium. Biol. Reprod. 2005;72:1114–1124. doi: 10.1095/biolreprod.104.035626. [DOI] [PubMed] [Google Scholar]
- 63.Li F., Redick S.D., Moy V.T. Force measurements of the α5β1 integrin-fibronectin interaction. Biophys. J. 2003;84:1252–1262. doi: 10.1016/S0006-3495(03)74940-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Selhuber-Unkel C., Erdmann T., Spatz J.P. Cell adhesion strength is controlled by intermolecular spacing of adhesion receptors. Biophys. J. 2010;98:543–551. doi: 10.1016/j.bpj.2009.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Nermut M.V., Green N.M., Yamada K.M. Electron microscopy and structural model of human fibronectin receptor. EMBO J. 1988;7:4093–4099. doi: 10.1002/j.1460-2075.1988.tb03303.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Lepzelter D., Bates O., Zaman M. Integrin clustering in two and three dimensions. Langmuir. 2012;28:5379–5386. doi: 10.1021/la203725a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kong D., Ji B., Dai L. Stabilizing to disruptive transition of focal adhesion response to mechanical forces. J. Biomech. 2010;43:2524–2529. doi: 10.1016/j.jbiomech.2010.05.019. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.