Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Aug 7;9(17):4848–4851. doi: 10.1021/acs.jpclett.8b02032

Coherent Light Harvesting through Strong Coupling to Confined Light

Gerrit Groenhof †,*, J Jussi Toppari ‡
PMCID: PMC6129961  PMID: 30085671

Abstract

graphic file with name jz-2018-020328_0004.jpg

When photoactive molecules interact strongly with confined light modes, new hybrid light–matter states may form: the polaritons. These polaritons are coherent superpositions of excitations of the molecules and of the cavity photon. Recently, polaritons were shown to mediate energy transfer between chromophores at distances beyond the Förster limit. Here we explore the potential of strong coupling for light-harvesting applications by means of atomistic molecular dynamics simulations of mixtures of photoreactive and non-photo-reactive molecules strongly coupled to a single confined light mode. These molecules are spatially separated and present at different concentrations. Our simulations suggest that while the excitation is initially fully delocalized over all molecules and the confined light mode, it very rapidly localizes onto one of the photoreactive molecules, which then undergoes the reaction.

Efficient excitation energy transfer, in which a photon is absorbed in one part of the system but utilized in another, is a key process in both natural and artificial light harvesting.1,2 Whereas the transfer usually occurs via the well-established Förster or Dexter mechanisms,3,4 recent experiments5−8 and theories9−12 suggest that strong coupling of donor and acceptor molecules with a single confined light mode in an optical cavity can also mediate the transfer, even at distances beyond which the Förster mechanism can operate.7

Strong coupling between N molecules and confined light leads to formation of N + 1 hybrid light-matter states (so-called polaritons,13−18Figure 1b) that are coherent superpositions of excitations in each of the molecules and of the confined light mode19,20

graphic file with name jz-2018-020328_m001.jpg 1

Here |gi⟩ and |ei⟩ are the ground and excited states of molecule i, while |1⟩ or |0⟩ indicates whether there is a photon in the cavity. The βiK and aK are expansion coefficients, and the index K labels the N + 1 eigenstates of the system. When the excitation energy of the molecules (ℏωi) is resonant with the frequency of the confined light mode (ℏωc), the energy gap (ℏΩRabi) between the lowest (K = 1, i.e., the lower polariton) and highest (K = N + 1, i.e., the upper polariton) hybrid state is proportional to the square root of the number of molecules (N) that are strongly interacting with the confined light mode

graphic file with name jz-2018-020328_m002.jpg 2

where μ⃗m is the transition dipole moment of the molecules, ϵ0 is the vacuum permittivity, and Vc is the volume, in which the photon with (angular) frequency ωc is confined.

Figure 1.

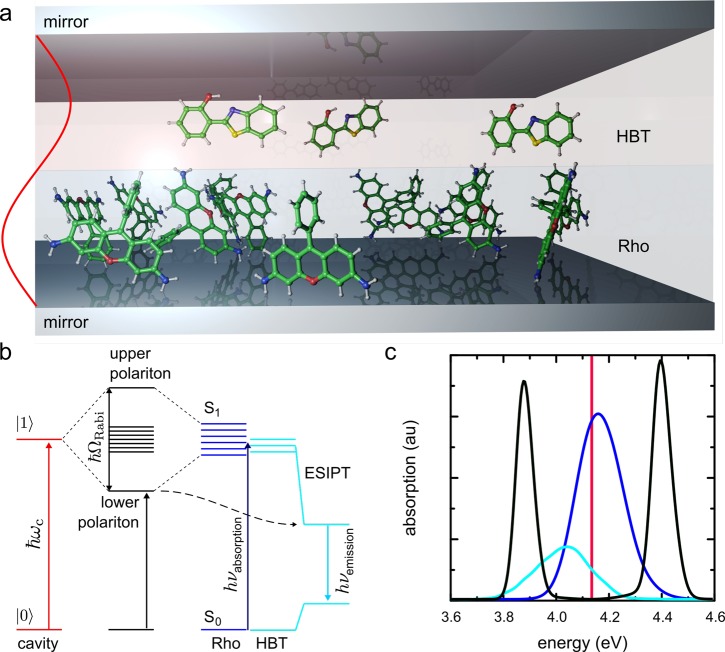
Figure 1

Open in a new tab

(a) Schematic depiction of the cavity–molecule system (not to scale). Inside the cavity there are two spatially separated layers of chromophores: rhodamine (Rho, blue) and hydroxyphenyl-benzothiazole (HBT, cyan). Because the second mode of the cavity (ωc, red) is resonant with the excitations of both chromophores, hybrid light-matter polaritons are formed (b). The dashed arrow in panel b indicates that HBT could potentially undergo ultrafast intramolecular proton transfer (ESIPT) to a configuration with an energy below the lower polariton. Because of the red shift associated with this reaction, the HBT molecule is no longer in resonance with the cavity and can localize the excitation. (c) Polariton absorption spectrum (black) with 1000 Rho (blue) and 10 HBT molecules (cyan) strongly coupled to the confined light mode of the cavity (red).

Because the lower (K = 1) and upper (K = N + 1) polaritons have much higher cross sections for light absorption than the other N – 1 states, the absorption spectrum of the cavity–molecule system has two peaks instead of one, located below and above the absorption maxima of the cavity and the molecules (Figure 1c). In the lower and upper polaritons, the excitation is coherently shared between all molecules and the confined light mode, whereas in the other N – 1 states, the excitation is more localized on subsets of the molecules.

Despite the delocalized character of the excitation into the lower polariton, recent simulations have shown that polaritons follow Kasha’s rule and relax into the lowest energy state available to the cavity–molecule system.21,555 This observation suggests that if there are molecules that can undergo a photochemical reaction to energy levels below the lower polariton, then the coherently shared excitation can collapse and localize the excitation energy onto one of those molecules. Thus polaritonic light harvesting might be achieved if a large number of nonreactive chromophores are combined with a few photoreactive molecules within the volume of a confined light mode that is resonant with both types of molecules. In this situation, all molecules contribute to photon absorption, whereas only one molecule eventually uses that energy for the reaction (Figure 1b).

Light can be efficiently confined between the mirrors of a Fabry-Pérot optical cavity22 or on the surface of metallic nanoparticles supporting a localized surface plasmon resonance (LSPR).23,24 Because in our simulations the details of the actual structure for confining light are irrelevant,21 our results will be valid for both types of light confinement. However, because of the high reflectivity of the mirrors, optical cavities are not very suited for light-harvesting applications. Therefore, practical realizations would more likely have to rely on open nanoparticle-based structures instead.

To test the idea, we constructed atomistic models with both reactive and nonreactive chromophores coupled to a single confined light mode that is resonant with their optical transitions. We assume that our cavity has an infinite quality (Q) factor. Thus a photon can be trapped between the mirrors forever and the cavity excitation never decays. To account for the effect of the light–matter coupling on the dynamics of the N molecules, we followed Galego et al.25 to extend the traditional Jaynes–Cummings model19,20 for molecules inside cavities.21 To obtain the N + 1 polaritonic states (eq 1), the electronic ground and excited states of each molecule were calculated at the QM/MM level26 as well as their transition dipole moments. As explained in the Supporting Information (SI) and in ref (19), we use these energies and dipole moments to construct the light-matter Hamiltonian matrix that we diagonalize at every time step of the simulation to obtain the polaritonic potential energy surfaces and eigenstates. The dynamics of all molecules are propagated simultaneously on a single polaritonic potential energy surface, whereas transitions between the surfaces are modeled with a surface-hopping algorithm.27

The very fast decay rate of cavity photons restricts the choice of photoreactive molecules to those with reaction rates within the polariton lifetime. Here we have selected 2-(2′-hydroxyphenyl) benzothiazole (HBT), which undergoes ultrafast (∼30 fs) excited-state intramolecular proton transfer (ESIPT) upon photoexcitation (Figure 2).28 This reaction is readily observed as a very large red shift in the emission from ultraviolet (UV, 340 nm) to green (525 nm). In line with results from previous simulation studies29 and experiments,28 HBT undergoes proton transfer within tens of femtoseconds after photon absorption in QM/MM simulations (SI).

Figure 2.

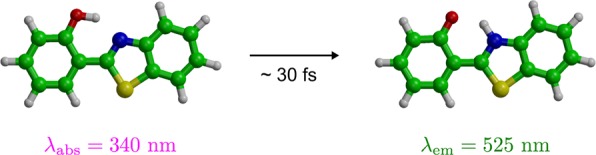
Figure 2

Open in a new tab

Upon excitation with ultraviolet (UV) light at 340 nm, HBT undergoes ultrafast intramolecular proton transfer, which causes the emission to red-shift to 525 nm. Carbon atoms are green, oxygen is red, nitrogen is blue, sulfur is yellow and hydrogens are white.

For the nonreactive molecules, we used the rhodamine model introduced in previous work.21 In this model, the rhodamine has an absorption maximum at 4.15 eV, which is close to the excitation maximum of HBT (4.05 eV) in our simulations (Figure 1c). The simulated cavities contained up to 1000 rhodamines and 10 HBT molecules in spatially separate layers, as in previous experiments.7 Both rhodamine and HBT layers were simultaneously coupled to the second confined light mode of the cavity with energy ℏωc = 4.13 eV (Figure 1a).

After ground-state equilibration, the combined molecule–cavity system is resonantly excited into the optically active lower polariton at 3.9 eV (Figure 1c). Initially, the excitation is fully delocalized over all molecules and the confined light mode of the cavity (Figure 3a). Because there is much more rhodamine than HBT and because rhodamine also has a larger transition dipole moment, the excitation mostly resides in the rhodamine layer (175:1). However, within 20 fs, the excitation localizes onto a single HBT molecule. After the collapse of the initially coherent excitation onto this HBT molecule, its hydroxyl proton transfers rapidly from the oxygen to the nitrogen atom, as shown in Figure 3b.

Figure 3.

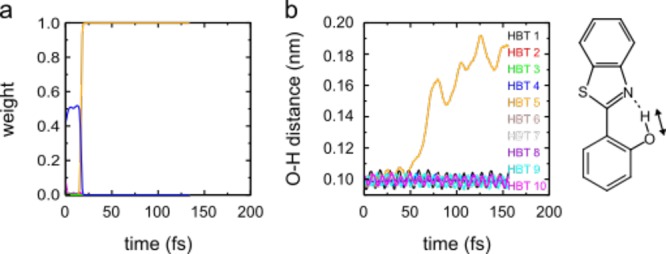
Figure 3

Open in a new tab

(a) Time evolution of the lowest energy polaritonic state during an MD simulation of 10 HBT and 1000 Rho molecules in an optical cavity resonant with the molecular excitations. Plotted in panel a are the weights of the excitations on each molecule (|βiLP|2 in all colors; |β1005|2, with the fifth HBT molecule excited, in orange) and cavity photon (|αLP|2, blue, eq 1). (b) Distance between the donor oxygen (O) and proton (H). About 30 fs after localization of the excitation onto the fifth HBT molecule (orange), proton transfer to the nitrogen (N) occurs, as evidenced by the increase in the O–H distance. In the remaining nine HBT molecules, the O–H distance fluctuates around the ground-state equilibrium bond length.

We repeated the simulations with various combinations of the molecules, keeping the HBT/rhodamine ratio identical. Also, in these simulations, the excitation is initially delocalized over all molecules but rapidly localizes onto one of the HBT molecules. These results, presented in the SI and summarized in Table 1, suggest that the variations have little effect on the efficiency of the excitation energy-transfer process under strong coupling. Because in most simulations the localization of the coherent excitation precedes proton transfer by several tens of femtoseconds, the photonic structures used for confining the light do not require long photon lifetimes or high Q factors. Therefore, if the energy levels, mode volumes and relaxation rates of the photonic structure are sufficient to reach the strong coupling limit for both molecules, then it is not relevant whether these are achieved with Fabry-Pérot cavities or with plasmonic surfaces, arrays or nanoparticles.

Table 1. Number of Trajectories, Time of Excitation Localization, Time of Proton Transfer, and Rabi Splitting with Various Numbers of HBT and Rhodamine Molecules and Vacuum Field Strengths.

HBT/Rho trajectories vacuum field (au)a collapse (fs) ESIPT (fs)b Rabi split (eV)c
10/1000 1 0.00008 19d 65d 0.53
5/500 2 0.00010 26 ± 8 83 ± 25 0.47
1/100 10 0.00020 53 ± 13 145 ± 22 0.42
Open in a new tab
a

Vacuum field is defined as 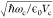Inline graphic (eq 2) in atomic units of energy and dipole moment and was chosen to yield a Rabi splitting of ∼0.5 eV in all simulations.

b

Time at which the O–H distance exceeds 0.125 nm.

c

Rabi splitting at the start of the simulation.

d

No error is estimated when there is only one trajectory.

In summary, our atomistic simulations suggest that strong coupling can be utilized to achieve ultrafast and directional transfer of excitation energy into a single photoreactive molecule. A layer of concentrated chromophores with large transition dipole moments inside a cavity or near a plasmonic nanostructure provides high oscillator strength, while a layer of low-concentration photoreactive molecules collects the energy necessary for their photochemical reactions. Although in this work, the acceptor of the excitation energy undergoes proton transfer, photovoltaic applications would aim for electron transfer instead. Via nanofabrication, such photo-oxidation reactions can be made to occur inside an optimal chemical environment, shielded from the other photoactive molecules, thereby preventing radiation damage or recombination.

Acknowledgments

We thank Professor Thomas Ebbesen for raising our interest in this subject. We also thank CSC-IT Center for Science for generous computational resources as well as PRACE for awarding us access to resource Curie based in France at GENCI. This work was supported by the Academy of Finland (grants 290677 to G.G. and 289947 to J.J.T.).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.8b02032.

  • Full methodological description of the cavity QM/MM simulations, QM/MM models and their validation, and tables and figures with data from all trajectories (PDF)

  • QuickTime animation of excited-state intramolecular proton transfer in an isolated HBT molecule (MOV)

  • QuickTime animation of excited-state intramolecular proton transfer in an HBT molecule that is inside a cavity with four other HBT and 500 Rho molecules (MOV)

The authors declare no competing financial interest.

Supplementary Material

jz8b02032_si_001.pdf (2.8MB, pdf)
jz8b02032_si_002.mov (6.2MB, mov)
jz8b02032_si_003.mov (12.8MB, mov)

References

  1. Croce R.; van Amerongen H. Natural strategies for photosynthetic light harvesting. Nat. Chem. Biol. 2014, 10, 492–501. 10.1038/nchembio.1555. [DOI] [PubMed] [Google Scholar]
  2. Harriman A. Artificial light-harvesting arrays for solar energy conversion. Chem. Commun. 2015, 51, 11745–11756. 10.1039/C5CC03577E. [DOI] [PubMed] [Google Scholar]
  3. Förster T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Ann. Phys. 1948, 437, 55–75. 10.1002/andp.19484370105. [DOI] [Google Scholar]
  4. Dexter D. L. A theory of sensitized luminescence in solids. J. Chem. Phys. 1953, 21, 836–850. 10.1063/1.1699044. [DOI] [Google Scholar]
  5. Coles D. M.; Somaschi N.; Michetti P.; Clark C.; Lagoudakis P. G.; Savvidis P. G.; Lidzey D. G. Polariton-mediated energy transfer between organic dyes in a strongly coupled optical microcavity. Nat. Mater. 2014, 13, 712–719. 10.1038/nmat3950. [DOI] [PubMed] [Google Scholar]
  6. Zhong X.; Chervy T.; Wang S.; George J.; Thomas A.; Hutchison J. A.; Devaux E.; Genet C.; Ebbesen T. W. Non-radiative energy transfer mediated by hybrid light-matter states. Angew. Chem., Int. Ed. 2016, 55, 6202–6206. 10.1002/anie.201600428. [DOI] [PubMed] [Google Scholar]
  7. Zhong X.; Chervy T.; Zhang L.; Thomas A.; George J.; Genet C.; Hutchison J. A.; Ebbesen T. W. Energy transfer between spatially separated entangled molecules. Angew. Chem., Int. Ed. 2017, 56, 9034–9038. 10.1002/anie.201703539. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Akulov K.; Bochman D.; Golombek A.; Schwartz T. Long-distance resonant energy transfer mediated by photonic modes. J. Phys. Chem. C 2018, 122, 15853. 10.1021/acs.jpcc.8b03030. [DOI] [Google Scholar]
  9. Feist J.; Garcia-Vidal F. J. Extraordinary Exciton Conductance Induced by Strong Coupling. Phys. Rev. Lett. 2015, 114, 196402. 10.1103/PhysRevLett.114.196402. [DOI] [PubMed] [Google Scholar]
  10. Schachenmayer J.; Genes C.; Tignone E.; Pupillo G. Cavity-enhanced transport of excitons. Phys. Rev. Lett. 2015, 114, 196403. 10.1103/PhysRevLett.114.196403. [DOI] [PubMed] [Google Scholar]
  11. Reitz M.; Mineo F.; Genes C. Energy transfer and correlations in cavity-embedded donor-acceptor configurations. Sci. Rep. 2018, 8, 9050. 10.1038/s41598-018-27396-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Du M.; Martinez L. A.; Ribeiro R. F.; Hu Z.; Menon V.; Yuen-Zhou J.. Theory for polariton-assisted remote energy transfer. 2018, arXiv:1711.11576. arXiv.org e-Print archive. https://arxiv.org/abs/1711.11576.
  13. Lidzey D. G.; Bradley D. D. C.; Skolnick M. S.; Virgili T.; Walker S.; Whittaker D. M. Strong exciton-photon coupling in an organic semiconductor microcavity. Nature 1998, 395, 53–55. 10.1038/25692. [DOI] [Google Scholar]
  14. Hutchison J. A.; Schwartz T.; Genet C.; Devaux E.; Ebbesen T. W. Modifying chemical energy landscapes by coupling to vacuum fields. Angew. Chem., Int. Ed. 2012, 51, 1592–1596. 10.1002/anie.201107033. [DOI] [PubMed] [Google Scholar]
  15. Ebbesen T. W. Hybrid light-matter states in a molecular and material science perspective. Acc. Chem. Res. 2016, 49, 2403–2412. 10.1021/acs.accounts.6b00295. [DOI] [PubMed] [Google Scholar]
  16. George J.; Wang S.; Chervy T.; Canaguier-Durand A.; Schaeffer G.; Lehn J.-M.; Hutchison J. A.; Genet C.; Ebbesen T. W. Ultra-strong coupling of molecular materials: spectroscopy and dynamics. Faraday Discuss. 2015, 178, 281–294. 10.1039/C4FD00197D. [DOI] [PubMed] [Google Scholar]
  17. Chikkaraddy R.; De Nijs B.; Benz F.; Barrow S. J.; Scherman O. A.; Rosta E.; Demetriadou A.; Fox P.; Hess O.; Baumberg J. J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127–130. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Dovzhenko D. S.; Ryabchuk S. V.; Rakovich Y. P.; Nabiev I. R. Light-matter interaction in the strong coupling regime: configurations, conditions, applications. Nanoscale 2018, 10, 3589–3605. 10.1039/C7NR06917K. [DOI] [PubMed] [Google Scholar]
  19. Jaynes E. T.; Cummings F. W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. 10.1109/PROC.1963.1664. [DOI] [Google Scholar]
  20. Tavis M.; Cummings F. W. Exact solution for an N-molecule-radiation-field Hamiltonian. Phys. Rev. 1969, 188, 692–695. 10.1103/PhysRev.188.692. [DOI] [Google Scholar]
  21. Luk H. L.; Feist J.; Toppari J. J.; Groenhof G. Multi-scale molecular dynamics simulations of polaritonic chemistry. J. Chem. Theory Comput. 2017, 13, 4324–4335. 10.1021/acs.jctc.7b00388. [DOI] [PubMed] [Google Scholar]
  22. Baieva S.; Hakamaa O.; Groenhof G.; Heikkilä T.; Toppari J. J. Dynamics of Strongly Coupled Modes between Surface Plasmon Polaritons and Photoactive Molecules: The Effect of the Stokes Shift. ACS Photonics 2017, 4, 28–37. 10.1021/acsphotonics.6b00482. [DOI] [Google Scholar]
  23. Vahala K. J. Optical microcavities. Nature 2003, 424, 839–846. 10.1038/nature01939. [DOI] [PubMed] [Google Scholar]
  24. Törmä P.; Barnes W. L. Strong coupling between surface plasmon polaritons and emitters: a review. Rep. Prog. Phys. 2015, 78, 013901. 10.1088/0034-4885/78/1/013901. [DOI] [PubMed] [Google Scholar]
  25. Zengin G.; Wersäll M.; Nilsson S.; Antosiewicz T. J.; Käll M.; Shegai T. Realizing strong light-matter interactions between single-nanoparticle plasmons and molecular excitations at ambient conditions. Phys. Rev. Lett. 2015, 114, 157401. 10.1103/PhysRevLett.114.157401. [DOI] [PubMed] [Google Scholar]
  26. Galego J.; Garcia-Vidal F. J.; Feist J. Cavity-induced modifications of molecular structure in the strong coupling limit. Phys. Rev. X 2015, 5, 041022. 10.1103/PhysRevX.5.041022. [DOI] [Google Scholar]
  27. Warshel A.; Levitt M. Theoretical studies of enzymic reactions: dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]
  28. Tully J. C.; Preston R. K. Trajectory surface hopping approach to nonadiabatic molecular collisions: the reaction of H+ with D2. J. Chem. Phys. 1971, 55, 562–572. 10.1063/1.1675788. [DOI] [Google Scholar]
  29. Lochbrunner S.; Wurzer A. J.; Riedle E. Microscopic mechanism of ultrafast excited-state intramolecular proton transfer: a 30-fs study of 2-(2′-hydroxyphenyl) bezothiazole. J. Phys. Chem. A 2003, 107, 10580–10590. 10.1021/jp035203z. [DOI] [Google Scholar]
  30. Pijeau S.; Foster D.; Hohenstein E. G. Excited-state dynamics of 2-(2′-hydroxyphenyl) benzathiazole: ultrafast proton transfer and internal conversion. J. Phys. Chem. A 2017, 121, 4595–4605. 10.1021/acs.jpca.7b01215. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz8b02032_si_001.pdf (2.8MB, pdf)
jz8b02032_si_002.mov (6.2MB, mov)
jz8b02032_si_003.mov (12.8MB, mov)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES