Convolutional neural networks automate detection for tracking of submicron-scale particles in 2D and 3D

Significance

The increasing availability of powerful light microscopes capable of collecting terabytes of high-resolution 2D and 3D videos in a single day has created a great demand for automated image analysis tools. Tracking the movement of nanometer-scale particles (e.g., virus, proteins, and synthetic drug particles) is critical for understanding how pathogens breach mucosal barriers and for the design of new drug therapies. Our advancement is to use an artificial neural network that provides, first and foremost, substantially improved automation. Additionally, our method improves accuracy compared with current methods and reproducibility across users and laboratories.

Abstract

Particle tracking is a powerful biophysical tool that requires conversion of large video files into position time series, i.e., traces of the species of interest for data analysis. Current tracking methods, based on a limited set of input parameters to identify bright objects, are ill-equipped to handle the spectrum of spatiotemporal heterogeneity and poor signal-to-noise ratios typically presented by submicron species in complex biological environments. Extensive user involvement is frequently necessary to optimize and execute tracking methods, which is not only inefficient but introduces user bias. To develop a fully automated tracking method, we developed a convolutional neural network for particle localization from image data, comprising over 6,000 parameters, and used machine learning techniques to train the network on a diverse portfolio of video conditions. The neural network tracker provides unprecedented automation and accuracy, with exceptionally low false positive and false negative rates on both 2D and 3D simulated videos and 2D experimental videos of difficult-to-track species.

In particle tracking experiments, high-fidelity tracking of an ensemble of species recorded by high-resolution video microscopy can reveal critical information about species transport within cells or mechanical and structural properties of the surrounding environment. For instance, particle tracking has been extensively used to measure the real-time penetration of pathogens across physiological barriers (1, 2), to facilitate the development of nanoparticle systems for transmucosal drug delivery (3, 4), to explore dynamics and organization of domains of chromosomal DNA in the nucleus of living cells (5, 6), and to characterize the microscale and mesoscale rheology of complex fluids via engineered probes (7–18).

There has been significant progress toward the goal of fully automated tracking, and dozens of methods are currently available that can automatically process videos, given a predefined set of adjustable parameters (19, 20). The extraction of individual traces from raw videos is generally divided into two steps: (i) identifying the precise locations of particle centers from each frame of the video and (ii) linking these particle centers across sequential frames into tracks or paths. Previous methods for particle tracking have focused more on the linking portion of the particle tracking problem. Much less progress had been made on localization, in part because of the prevailing view that linking is more crucial, having the potential to correctly pick the true positives from a large set of localizations that may contain a sizable fraction of false positives. In this paper, we primarily focus on localization instead of linking. We present a particle tracking algorithm, constructed from a neural network localization algorithm and one of the simplest known linking algorithms, slightly modified from its most common implementation.

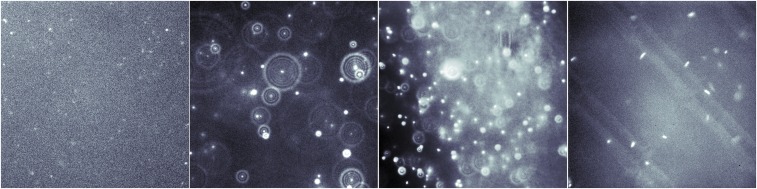
The primary novelty of our method is automation and accuracy. Even though many particle tracking methods have been developed that can automatically process videos, when presented with videos containing spatiotemporal heterogeneity (Fig. 1) such as variable background intensity, photobleaching, or low signal-to-noise ratio (SNR), the set of parameters used by a given method must be optimized for each set of video conditions, or even each video, which is highly subjective in the absence of ground truth. Parameter optimization is time-consuming and requires substantial user guidance. Furthermore, when applied to experimental videos, user input is still frequently needed to remove phantom traces (false positives) or add missing traces (false negatives) (SI Appendix, Fig. S1 A and B) Thus, instead of providing full automation, current software is perhaps better characterized as facilitating supervised particle tracking, requiring substantial human interaction that is time-consuming and costly. More importantly, the results can be highly variable, even for the same input video (see SI Appendix, Fig. S1 C–E).

Fig. 1.

Sample frames from experimental videos, highlighting some of the challenging conditions for particle tracking. (Left to Right) Fifty-nanometer particles captured at low SNR and 200-nm particles with diffraction disc patterns, variable background intensity, and ellipsoid PSF shapes from $1-2\hspace{0.17em}\mathrm{\mu }$m Salmonella.

A major difficulty for optimizing tracking methods for specific experimental conditions is access to “ground truth,” which can be highly subjective and labor intensive to obtain. One approach for applying a tracking method to experimental videos is to tune parameter values by hand, while qualitatively assessing error across a range of videos. This procedure is laborious and subjective. A better approach, using quantitative optimization, is to generate simulated videos—for which ground truth is known—that match, as closely as possible, the observed experimental conditions. Then, a given tracking method suitable for those conditions can be applied to the simulated videos, and the error can be quantitatively assessed. By quantifying the tracking error, the parameters in the tracking method can be systematically optimized to minimize the tracking error over a large number of videos. Finally, once the parameters have been optimized on simulated data, the same parameters can be used (after fine-tuning parameters and adding or removing traces to ensure accuracy) to analyze experimental videos.

To overcome the need to optimize parameters for each video condition, we take the aforementioned methodology to the next logical step: Instead of optimizing for specific microscopy conditions, we compile a large portfolio of simulations that encompasses the wide spectrum of potential variations encountered in particle tracking experiments. Existing methods are designed with as few parameters as possible, to make the software simple to use, and a single set of parameters for specific microscopy conditions (SNR, size, shape, etc.) can usually be found that identifies objects of interest. Nevertheless, a limited parameter space compromises the ability to optimize the method for a large portfolio of conditions. An alternative approach is to construct an algorithm with thousands of parameters, and use machine learning to optimize the algorithm to perform well under all conditions represented in the portfolio. Here, we adapt an existing neural network imaging framework, called a convolutional neural network (CNN), to the challenge of particle identification.

CNNs have become the state of the art for object recognition in computer vision, outperforming other methods for many imaging tasks (21, 22). A CNN is a type of feed-forward artificial neural network designed to process information in a layered network of connections. The linking stage of particle tracking is sometimes viewed as the most critical for accuracy. Here, we develop an approach for particle identification, while using one of the simplest particle linking strategies, namely, adaptive linear assignment (23). We rigorously test the accuracy of our method, and find substantial improvement (in terms of false positives and false negatives) over several existing methods, suggesting that particle identification is the most critical component of a particle tracking algorithm, particularly for automation.

A number of research groups are beginning to apply machine learning to particle tracking (24–26), primarily involving “handcrafted” features that, in essence, serve as a set of filter banks for making statistical measurements of an image, such as mean intensity, SD, and cross-correlation. These features are used as inputs for a support vector machine, which is then trained using machine learning methods. The use of handcrafted features substantially reduces the number of parameters that must be trained.

In contrast, we have developed our network to be trained end to end, or pixels to pixels, so that the input is the raw imaging data, and the output is a probabilistic classification of particle versus background at every pixel. Importantly, we have designed our network to be “recurrent” in time so that past and future observations are used to predict particle locations.

In this paper, we construct a CNN, comprising a three-layer architecture over 6,000 tunable parameters, for particle localization. All of the neural network’s tunable parameters are optimized using machine learning techniques, which means there are never any parameters that the user needs to adjust for particle localization. The result is a highly optimized network that can perform under a wide range of conditions without any user supervision. To demonstrate accuracy, we test the neural network tracker (NN) on a large set of challenging videos that span a wide range of conditions, including variable background, particle motion, particle size, and low SNR.

Materials and Methods

To train the network on a wide range of video conditions, we developed video simulation software that accounts for a large range of conditions found in particle tracking videos (Fig. 1). The primary advance is to include simulations of how particles moving in three dimensions appear in a 2D image slice captured by the camera.

A standard camera produces images that are typically single channel (gray scale), and the image data are collected into 4D (three space and one time dimension) arrays of 16-bit integers. The resolution in the $\left(x,y\right)$ plane is dictated by the camera and can be in the megapixel range. The resolution in the $z$ coordinate is much smaller, since each z-axis slice imaged by the camera requires a piezoelectric motor to move the lense relative to the sample. A good piezoelectric motor is capable of moving between z-axis slices within a few milliseconds, which means that there is a tradeoff between more z slices and the overall frame rate. For particle tracking, a typical video includes 10 to 50 z slices per volume. The length of the video refers to the number of time points, i.e., the number of volumes collected. Video length is often limited by photobleaching, which slowly lowers the SNR as the video progresses.

To simulate a particle tracking video, we must first specify how particles appear in an image. We refer to the pixel intensities captured by a microscope and camera resulting from a particle centered at a given position $\left(x,y,z\right)$ as the observed point spread function (PSF), denoted by ${\psi }_{ijk}\left(x,y,z\right)$, where $i,j,\hspace{0.17em}\mathrm{a}\mathrm{n}\mathrm{d}\hspace{0.17em}k$ are the pixel indices. The PSF becomes dimmer and less focused as the particle moves away from the plane of focus $\left(z=0\right)$. Away from the plane of focus, the PSF also develops disc patterns caused by diffraction, which can be worsened by spherical aberration. While deconvolution can mitigate the disc patterns appearing in the PSF, the precise shape of the PSF must be known or unpredictable artifacts may be introduced into the image.

The shape of the PSF depends on several parameters that vary depending on the microscope and camera, including emitted light wavelength, numerical aperture, pixel size, and the separation between z-axis slices. While physical models based on optical physics that expose these parameters have been developed for colloidal spheres (27), it is not practical for the purpose of automated particle tracking within complex biological environments. In practice, there are many additional factors that affect the PSF, such as the refractive index of the glass slide, of the lens oil (if oil-immersion objective is used), and of the medium containing the particles being imaged. The latter presents the greatest difficulty, since biological specimens are often heterogeneous and their optical properties are difficult to predict. The PSF can also be affected by particle velocity, depending on the duration of the exposure interval used by the camera. This makes machine learning particularly appealing, because we can simply randomize the shape of the PSF to cover a wide range of conditions, and the resulting CNN is capable of automatically “deconvolving” PSFs without the need to know any of the aforementioned parameters.

Low SNR is an additional challenge for tracking of submicron-size particles. High-performance digital cameras are used to record images at a sufficiently high frame rate to resolve statistical features of particle motion. Particles with a hydrodynamic radius in the range of 10 nm to 100 nm move quickly, requiring a small exposure time to minimize dynamic localization error (motion blur) (28). Smaller particles also emit less light for the camera to collect. To train the neural network to perform in these conditions, we add Poisson shot noise with random intensity to the training videos. We also add slowly varying random background patterns (SI Appendix and Fig. 2).

Fig. 2.

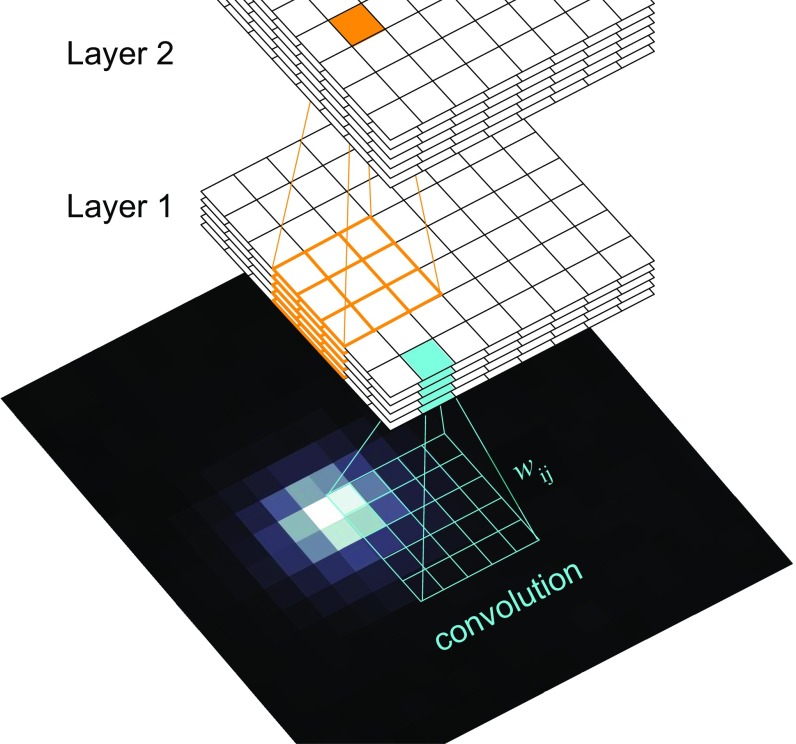
The CNN. Diagram of the layered connectivity of the artificial neural network.

An Artificial Neural Network for Particle Localization.

The “neurons” of the artificial neural network are arranged in layers, which operate on multidimensional arrays of data. Each layer output is 3D, with two spatial dimensions and an additional “feature” dimension (Fig. 2). Each feature within a layer is tuned to respond to specific patterns, and the ensemble of features is sampled as input to the next layer to form features that recognize more-complex patterns. For example, the lowest layer comprises features that detect edges of varying orientation, and the second-layer features are tuned to recognize curved lines and circular shapes.

Each neuron in the network processes information from spatially local inputs (either pixels of the input image or lower-layer neurons). This enables a neuron to see a local patch of the input image. The size of the image patch that affects the input to a given neuron is called its receptive field. The relationship of the input and output, denoted by $I_{ij}$ and $O_{ij}$, for each neuron is given by $O_{ij}=F\left({\sum }_{i\prime ,j^{\prime }}{w}_{i^{\prime },j\prime }{I}_{i+i\prime ,j+j\prime }-b\right)$, where the kernel weights $w_{ij}$ and output bias $b$ are trainable parameters. Each layer has its own set of biases, one for each feature, and each feature has its own set of kernel weights, one for each feature in the layer directly below. The nonlinearity $F\left(\cdot \right)$ is a prespecified function that determines the degree of “activation” or output; we use $F\left(u\right)=\log \left(e^u+1\right)$. Inserting nonlinearity in between each layer of neurons is necessary for CNNs to robustly approximate nonlinear functions. The most common choice is called the rectified linear unit [$F\left(u\ge 0\right)=u$ and $F\left(u<0\right)=0$]. Instead, we use a function with a similar shape that is also continuously differentiable, which helps minimize training iterations where the model is stuck in local minima (29).

The neural network comprises three layers: 12 features in layer one, 32 features in layer two, and the final two output features in layer three. The output of the neural net, denoted by $q_{ijk}$, can be interpreted as the probability of a particle centered at pixel $\left(i,j,k\right)$. We refer to these as detection probabilities.

While it is possible to construct a network that takes 3D image data as input, it is not computationally efficient. Instead, the network is designed to process a single 2D image slice at a time (so that it can also be applied to the large set of existing 2D imaging data) while still maintaining the ability to perform 3D tracking. Constructing 3D output $q_{ijk}$ is achieved by applying the network to each z-axis slice of the input image, the same way a microscope obtains 3D images by sequentially capturing each z-axis slice. Two- or three-dimensional paths can then be reconstructed from the network output as described in Particle Path Linking.

We designed our network to be recurrent in time so that past and future observations are used to predict particle locations. In particular, we use the forward–backward algorithm (30) to improve accuracy. Because detections include information from the past and future, the detection probabilities are reduced when a particle is not detected in the previous frame (the particle just appeared in the current frame) or is not detected in the following frame (the particle is about to leave the plane of focus). In Particle Path Linking, we show how the detection probabilities can be used by the linking algorithm to improve its performance.

Optimizing the Neural Network Parameters.

The values of the trainable parameters in the network, including the kernel weights and biases, are optimized through the process of learning. Using known physical models of particle motion and imaging, we simulate random particle paths and image frames that cover a wide range of conditions, including particle PSF shape, variable background, particle number, particle mobility, and SNR. The ground truth for each image consists of a binary image with pixels values $p_{ijk}=1$ if $\Vert \left(j,i,k\right)-{\mathbf{x}}_n\Vert <2$, and $p_{ijk}=0$ otherwise. Each training image is processed by the neural net, and the corresponding output is compared with the ground truth using the cross-entropy error $H\left[p,q\right]=-\frac{1}{N}{\sum }_{ijk}\left[p_{ijk}\log q_{ijk}+\left(1-p_{ijk}\right)\log \left(1-q_{ijk}\right)\right]$, where $N$ is the total number of pixels in the image. Further details can be found in SI Appendix.

Particle Path Linking.

The dynamics of particle motion can vary depending on the properties of the surrounding fluid and the presence of active forces (e.g., flagellar-mediated swimming of bacteria and molecular motor cargo transport). To reconstruct accurate paths from a wide range of movement characteristics, we develop a minimal model. A minimal assumption for tracking is that the observation sequence approximates continuous motion of an object. To accurately capture continuous motion sampled at discrete time intervals, dictated by the camera frame rate, the particle motion must be sufficiently small between image frames. Hence, we assume only that particles move within a Gaussian range from one frame to the next. Further details can be found in SI Appendix.

Performance Evaluation and Comparison with Existing Software.

We consider the primary goal for a high-fidelity tracker to be accuracy (i.e., minimize false positives and localization error), followed by the secondary goal of maximizing data extraction (i.e., minimize false negatives and maximize path length). To gauge accuracy, particle positions were matched to ground truth using optimal linear assignment. The algorithm finds the closest match between tracked and ground truth particle positions that are within a preset distance of five pixels; this is well above the subpixel error threshold of one pixel, but sufficiently small to ensure one-to-one matching. Tracked particles that did not match any ground truth particles were deemed false positives, and ground truth particles that did not match a tracked particle were deemed false negatives. To assess the performance of the NN, we analyzed the same videos using three different leading tracking software programs that are publicly available: Mosaic (Mos), an ImageJ plug-in capable of automated tracking in two and three dimensions (31); Icy, an open source bioimaging platform with preinstalled plugins capable of automated tracking in two and three dimensions (32, 33); and Video Spot Tracker (VST), a stand-alone application capable of 2D particle tracking, developed by the Center for Computer-Integrated Systems for Microscopy and Manipulation at University of North Carolina at Chapel Hill. VST also has a convenient graphic user interface that allows a user to add or eliminate paths (because human-assisted tracking is time-consuming, 100 2D videos were randomly selected from the 500-video set).

For the sake of visual illustration, we supplement our quantitative testing with a small sample of real and synthetic videos with localization indicators (see Movies S1 and S2). In each video, red diamond centers indicate each localization from the neural network.

Performance on Simulated 2D and 3D Videos.

Because manual tracking by humans is subjective, our first standard for evaluating the performance of the NN and other publicly available software is to test on simulated videos, for which the ground truth particle paths are known. The test included 500 2D videos and 50 3D videos, generated using the video simulation methodology described in Materials and Methods and SI Appendix. Each 2D video contained 100 simulated particle paths for 50 frames at 512 × 512 resolution (see SI Appendix, Fig. S2). Each 3D video contained 20 evenly spaced z-axis image slices of a 512 × 512 × 120 pixel region containing 300 particles. The conditions for each video were randomized, including variable background intensity, PSF radius (called particle radius for convenience), diffusivity, and SNR. Note that SNR is defined as the mean pixel intensity contributed by the particle PSFs divided by the SD of the background pixel intensities.

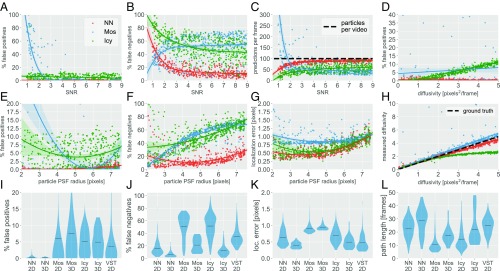
To assess the robustness of each tracking method/software program, we used the same set of tracker parameters for all videos (see SI Appendix for further details). Scatter plots of the 2D test video results for NN, Mosaic, and Icy are shown in Fig. 3. For Mosaic, the false positive rate was generally quite low ($\sim$2%) when $\mathrm{S}\mathrm{N}\mathrm{R}>3$, but showed a marked increase to >20% for $\mathrm{S}\mathrm{N}\mathrm{R}<3$ (Fig. 3A). The average false negative rates were in excess of 50% across most $\mathrm{S}\mathrm{N}\mathrm{R}>3$ (Fig. 3B). In comparison, Icy possessed higher false positive rates than Mosaic at high SNR and lower false positive rates when SNR decreases below 2.5, with a consistent $\sim$5% false positive rate across all SNR values (Fig. 3A). The false negative rates for Icy were greater than for Mosaic at high SNR, and exceeded $\sim$40% for all SNR tested (Fig. 3B).

Fig. 3.

Performance analysis for randomized 2D and 3D synthetic test videos. (A–C) Two-dimensional test results showing the (A) percentage of false positives, (B) percentage of false negatives, and (C) predictions per frame vs. SNR. Mosaic shows a sharp rise in false positives for $\mathrm{S}\mathrm{N}\mathrm{R}<2$ (in A), due to substantially more predictions than actual particles (in C). Conversely, the neural net (NN) and Icy showed no increase in false positives at low SNR. (E–G) Results showing the (E) percentage of false positives, (F) percentage of false negatives, and (G) localization error vs. the PSF radius. (D and H) Results showing the (D) percentage of false positives and (H) measured diffusivity vs. the ground truth particle diffusivity. (I–L) Violin plots showing the performance on 2D and 3D test videos for each of the four methods: the NN, Mos, Icy, and VST. The solid black lines show the mean, and the thickness of the filled regions shows the shape of the histogram obtained from 500 (50) randomized 2D (3D) test videos. Note that the VST results only included 100 test videos.

All three methods showed some minor sensitivity, in the false positive rate and localization error, to the PSF radius (Fig. 3 E and G). (Note that the high sensitivity Mosaic displayed to changes in SNR made the trend for PSF radius difficult to discern.) Mosaic and Icy showed much higher sensitivity, in the false negative rate, to PSF radius, each extracting nearly fourfold more particles as the PSF radius decreased from eight to two pixels (Fig. 3F).

One common method to analyze and compare particle tracking data is the ensemble mean squared displacement (MSD) calculated from particle traces. Since the simulated paths in the 2D and 3D test videos were all Brownian motion (with randomized diffusivity), we have that $⟨|\mathbf{x}\left(t\right){|}^2⟩=4Dt$, where $D$ is the diffusivity. To make a simple MSD comparison for Brownian paths, we computed estimated diffusivities using the MSD at the path duration $1<T\le 50$, with $D\approx ⟨|\mathbf{x}\left(T\right){|}^2⟩/\left(4T\right)$. (See below and SI Appendix, Fig. S4 for an MSD analysis on experimental videos of particle motion in mucus.) When estimating diffusivities, Icy exhibited increased false positive rates with faster-moving particles (Fig. 3D), likely due to the linker compensating for errors made by the detection algorithm. In other words, while the linker was able to correctly connect less-mobile particles without confusing them with nearby false detections, when the diffusivity rose, the particle displacements tended to be larger than the distance to the nearest false detection. Consequently, when $D>2$, the increased false positives along with increased increment displacements caused Icy to underestimate the diffusivity (Fig. 3H), because paths increasingly incorporated false positives.

In contrast to Mosaic and Icy, the NN possessed a far lower mean false positive rate of $\sim$0.5% across all SNR values tested (Fig. 3A). The NN was able to achieve this level of accuracy while extracting a large number of paths, with <20% false negative rate for all $\mathrm{S}\mathrm{N}\mathrm{R}>2.5$ and only a modest increase in the false negative rate at lower SNR (Fig. 3B). Importantly, the NN performed well under low-SNR conditions by making fewer predictions, and the number of predictions made per frame is generally in reasonable agreement with the theoretical maximum (Fig. 3C). Since the neural network was trained to recognize a wide range of PSFs, it also maintained excellent performance (<1% false positive, <20% false negative) across the range of PSF radius (Fig. 3F). The NN possessed localization error that was as good as that of Mosaic and Ivy, less than one pixel on average and never more than two pixels, even though true positives were allowed to be as far as five pixels apart (Fig. 3G).

When analyzing 3D videos, Mosaic and Icy were able to maintain false positive rates ($\sim$5 to 8%) roughly comparable to their rates when analyzing 2D videos (Fig. 3I). Surprisingly, analyzing 3D videos with the NN resulted in an even lower false positive rate than for 2D videos, with $\sim$0.2% false positives. All three methods capable of 3D tracking exhibited substantial improvements in reducing false negatives, reducing localization error, and increasing path duration (Fig. 3 J and L). Strikingly, the neural network was able to correctly identify an average of $\sim$95% of the simulated particles in a 3D video, i.e., <5% false negatives, with the lowest localization error as well as the longest average path duration among the three methods.

Performance on Experimental 2D Videos.

Finally, we sought to evaluate the performance and rigor of the NN on experimentally derived rather than simulated videos, since the former can include spatiotemporal variations and features that might not be captured in simulated videos. Because analysis from the particle traces can directly influence interpretations of important biological phenomenon, the common practice is for the end user to supervise and visually inspect all traces to eliminate false positives and minimize false negatives. Against such rigorously verified tracking, the NN was able to produce particle paths with comparable MSDs across different time scales, alpha values, a low false positive rate, greater number of traces (i.e., decrease in false negatives), and comparable path length (see SI Appendix, Fig. S4). Most importantly, these videos were processed in less than one-20th of the time it took to manually verify them, generally taking 30 s to 60 s to process a video, compared with 10 min to 20 min to verify accuracy.

Discussion

The principal benefit of the trained CNN is robustness to changing conditions. For example, the net tracker was capable, without any modifications, of tracking Salmonella (Fig. 1, Right and Movie S1), which are large enough to resolve and appear as rod-shaped in images. Even though the neural net was trained on rotationally symmetric particle shapes, rod-shaped cells were still recognized with strong confidence sufficient for high-fidelity tracking. Large polydisperse particles are also readily tracked, provided their PSF shape does not deviate too far from the rotationally symmetric training data. Our neural network does not recognize long filaments such as microtubules; such applications will require significant, targeted advances customized to the specific application. Another example of the robustness of the network is its ability to ignore background objects and effectively suppress false positives. The neural network does not recognize large bright objects that sometimes appear in videos (see Movie S1), even though it was trained on images containing slowly varying background intensity.

The particle localization method used the neural network output instead of computing the centroid position from the raw image data (as is typically done), and the resulting localization accuracy was comparable to other methods. However, some applications such as microrheology may require additional accuracy. Several high-quality localization algorithms have been developed that potentially might, given a local region of interest (provided by the neural network) in the raw image, estimate the particle center with more accuracy (34). One alternative to particle tracking microrheology is differential dynamic microscopy, which uses scattering methods to estimate dynamic parameters from microscopy videos (35).

Finally, tools based on machine learning for computer vision are advancing rapidly. Applications of neural network-based segmentation to medical imaging are already under development (36–38). One recent study has used a pixels-to-pixels–type CNN to process raw stochastic optical reconstruction microscopy (STORM) data into superresolution images (39). The potential for this technology to address outstanding bioimaging problems is becoming clear, particularly for image segmentation, which is an active research area in machine learning (22, 40–45).