A Statistical Description of Plant Shoot Architecture

SUMMARY

Plant architectures can be characterized statistically by their spatial density function, which specifies the probability of finding a branch at each location in the territory occupied by a plant. Using high-precision 3D scanning, we analyzed 557 plant shoot architectures, representing three species, grown across three to five environmental conditions, and through 20–30 developmental time points. We found two elegant properties in the spatial density functions of these architectures: all functions could be nearly modified in one direction without affecting the density in orthogonal directions (called “separability”), and all functions shared the same underlying shape, aside from stretching and compression (called “self-similarity”). Surprisingly, despite their striking visual diversity, we discovered that all architectures could be described as variations on a single underlying function: a Gaussian density function truncated at roughly two SDs. We also observed systematic variation in the spatial density functions across species, growth conditions, and time, which suggests functional specialization despite following the same general design form.

In Brief

Conn et al. analyze 557 3D plant shoot architectures and discover that the distribution of branches in space is well approximated by a truncated 3D Gaussian density function. This result highlights a new principle guiding growth and adaptation of plants, and it raises new questions about the molecular mechanisms driving pattern formation.

INTRODUCTION

One central challenge in plant biology is to identify general principles guiding growth and adaptation of plant architectures [1]. Plant architectures are highly complex, developing meticulously over time and constantly adjusting to challenges from the environment [2]. These adjustments include modulation of growth rates, the size and number of branching elements and leaves, and flowering times [3, 4]. Growth strategies also vary across species in terms of the number of seed leaves generated, the presence of secondary growth, and leaf patterning [5].

Over the last several decades, many principles describing plant form have been discovered [6], including phyllotaxis (spatial arrangement of leaves) [7], bifurcation planarity [8], fractal branching [9–11], and allometric scaling of several other plant properties, including plant height, stem diameter, and leaf biomass [12–15]. These insights have led to many models of plant architectures, including Lindenmayer systems [16] and its many variants [17–19], the metabolic theory of ecology [20], and functional-structural models [21–25], used to simulate how different physiological or ecological factors influence plant structure. These models have had wide applications in agriculture [26], plant engineering [27, 28], and computer graphics [16, 29].

Here, we study the spatial density function of plant architectures and ask, for each point in the 3D territory or volumetric space occupied by a plant (defined as the convex hull of the cloud points representing the plant’s architecture), what is the probability of finding a branch at that point? The spatial density function characterizes how plants distribute branches in space and can reveal growth strategies that may not be apparent by eye. Indeed, it is not clear a priori how many different forms of the density function are used. For example, the functional form may be class specific (monocots versus dicots), species specific, or even condition specific; the form may even depend on growth and developmental timing. Understanding which forms are used and in what context may help guide plant biologists studying similarities and differences in the biological mechanisms that produce these structures, including how they may have evolved.

Our goals here are to characterize plant spatial density functions using statistical moments, to test these functions for two mathematical properties (separability and self-similarity), and to determine the form of the density function. “Separability” means that branch density is independent in the X, Y, and Z directions. “Self-similarity” means that architectures of different sizes have the same underlying shape, modulo compression and stretching along one or more directions. The form of the function is not designed to be used to reconstruct an individual plant’s architecture but rather to highlight statistical properties shared by a large collection of architectures.

Compared to prior work, we offer the following contributions:

• (1)Analysis of an extensive dataset of 557 juvenile plant 3D architectures from three species, scanned across various growth conditions for the same species, and several early developmental time points for the same individual plant.
• (2)Quantification of separability and self-similarity of plant spatial density functions. Whereas fractal branching has long been appreciated by mathematical biologists [9–11], there has been little formal analysis of the degree to which this property applies to a population of whole-plant architectures and how it varies across environmental conditions and through development. Moreover, our quantification is done using a statistical test [30], which critically does not rely on template matching or a priori assumptions about the number of functional forms for architectures. Prior work has also quantified the degree of self-nestedness for trees based on measures of graph compression [31, 32], though no claim is made by these works to general validity across all plants.
• (3)Derivation of a single functional form to describe all plant spatial density functions. We applied the methodology developed by Snider et al. [30] and discovered that all density functions can be approximated by a 3D Gaussian truncated at a boundary of roughly two SDs from the center. This means that only four parameters are needed to specify statistically any architecture’s size and shape: its total branch length and the SDs of the Gaussian in the three orthogonal directions. This provides a very simple and compact description of a large diversity of architectures.

We conclude by discussing potential benefits and limitations of these properties, implications for studying their molecular basis, and their analogs in branching dendritic and axonal morphologies in the brain.

RESULTS

Generating a Diverse Dataset of Plant Architectures

We performed 3D laser scanning of plant shoot architectures across three species (tomato, tobacco, and sorghum), three to five growth conditions (ambient light, shade, high heat, high light, and drought), and through 20–30 days of development. Overall, we performed 557 scans (311 tomato, 105 tobacco, and 141 sorghum) summed across species, conditions, and time points (STAR Methods).

From each scan, we extracted the 3D coordinates of each branch point for the dicots (tomato and tobacco) and each leaf point for the monocot (sorghum; Figures 1A–1C). These points were used as input to the analysis described in the next section. We observed a wide range of architectures, with the number of branch points, the number of leaves, and the territory volume occupied by the plants varying by several orders of magnitude (Table 1). Thus, this dataset represents a good benchmark for testing the generality of any property of plant architectures.

Figure 1. 3D Plant Scans and Illustrative Spatial Density Functions.

(A–C) Example scans of three plants on their 20^th developmental day: (A) tomato; (B) sorghum; and (C) tobacco. Grey dots correspond to the mid-points of edges at the shown (x, y, z) location and are used to compute the spatial density function for each plant. Only visible points are shown.

(D) Illustrations of Gaussian spatial density functions in different conditions and time points. Our analysis focuses on the branching architecture above the hypocotyl. The brown cloud denotes the spatial density of the branching architecture. The higher the brown intensity of a point, the higher the probability of finding a branch at that point. The length-to-width ratio of the ellipse reflects differences in density in each direction. The distribution curves on top of the ellipses show examples of the Gaussian density function along one direction.

See also Figure S4.

Table 1.

Architecture Statistics for Our Benchmark Dataset

Species	Environment	Time	No. Branch Points	No. Leaves	Log(Volume) (mm3)
Tomato	ambient	D00	2.00 ± 0.00	2.00 ± 0.00	3.14 ± 0.03
Tomato	ambient	D10	7.00 ± 0.24	9.00 ± 0.37	4.77 ± 0.01
Tomato	ambient	D20	16.20 ± 0.36	17.00 ± 0.35	5.75 ± 0.02
Tomato	shade	D00	2.00 ± 0.00	2.00 ± 0.00	3.21 ± 0.03
Tomato	shade	D10	5.33 ± 0.00	2.00 ± 0.00	4.53 ± 0.05
Tomato	shade	D20	11.50 ± 0.35	13.5 ± 1.06	5.34 ± 0.15
Tomato	high heat	D00	2.00 ± 0.00	2.00 ± 0.00	3.16 ± 0.04
Tomato	high heat	D10	2.00 ± 0.00	4.67 ± 0.38	3.71 ± 0.04
Tomato	high heat	D20	3.00 ± 0.00	6.00 ± 0.00	4.11 ± 0.06
Tomato	high light	D00	2.00 ± 0.00	2.00 ± 0.00	3.15 ± 0.02
Tomato	high light	D10	8.67 ± 0.38	10.33 ± 0.38	4.79 ± 0.02
Tomato	high light	D20	19.33 ± 1.02	20.66 ± 0.84	5.82 ± 0.01
Tomato	drought	D00	2.00 ± 0.00	2.00 ± 0.00	3.07 ± 0.04
Tomato	drought	D10	6.00 ± 0.33	8.00 ± 0.00	4.44 ± 0.03
Tomato	drought	D20	11.67 ± 0.69	12.67 ± 0.69	5.12 ± 0.04
Tobacco	ambient	D00	2.33± 0.19	3.33 ± 0.19	2.79 ± 0.01
Tobacco	ambient	D10	5.67 ± 0.19	6.67 ± 0.19	4.29 ± 0.04
Tobacco	ambient	D20	8.67 ± 0.19	9.67 ± 0.19	5.51 ± 0.07
Tobacco	shade	D00	2.00 ± 0.00	3.00 ± 0.00	2.78 ± 0.02
Tobacco	shade	D10	5.00 ± 0.00	6.00 ± 0.00	4.09 ± 0.03
Tobacco	shade	D20	7.00 ± 0.00	8.00 ± 0.00	4.82 ± 0.01
Tobacco	high heat	D00	2.00 ± 0.00	3.00 ± 0.00	2.81 ± 0.02
Tobacco	high heat	D10	7.00 ± 0.00	8.00 ± 0.00	4.23 ± 0.06
Tobacco	high heat	D20	11.00± 0.00	12.00 ± 0.00	5.27 ± 0.02
Sorghum	ambient	D00	2.00 ± 0.00	1.33 ± 0.19	2.22 ± 0.06
Sorghum	ambient	D10	6.33 ± 0.19	3.33 ± 0.19	5.34 ± 0.03
Sorghum	ambient	D20	10.33 ± 0.38	5.67 ± 0.19	6.04 ± 0.05
Sorghum	shade	D00	2.00 ± 0.00	1.00 ± 0.00	2.18± 0.03
Sorghum	shade	D10	6.00 ± 0.00	3.00 ± 0.00	5.15± 0.02
Sorghum	shade	D20	7.33± 0.51	4.00 ± 0.33	5.62 ± 0.09
Sorghum	high heat	D00	2.00 ± 0.00	1.00 ± 0.00	2.39 ± 0.01
Sorghum	high heat	D10	7.00 ± 0.67	4.00 ± 0.33	5.39 ± 0.01
Sorghum	high heat	D20	10.00 ± 0.58	5.67 ± 0.19	5.56 ± 0.03
Sorghum	high light	D00	2.00 ± 0.00	1.00 ± 0.00	2.42 ± 0.07
Sorghum	high light	D10	8.00 ± 0.00	4.00 ± 0.00	5.38 ± 0.04
Sorghum	high light	D20	11.33 ± 0.38	5.67 ± 0.19	6.03 ± 0.04

For each species and environment, example architectural features are listed for three time points: D00 (the first day of scanning), D10, and D20. For each row, we show the average number of branch points and leaves and the total volume occupied by the plant. The number of leaves includes leaflets and cotyledons. The volume is expressed as the log₁₀ of the convex hull of the cloud points for the scanned plant. All error values represent SE across two to five replicates. See also Figure S6 and Table S1.

Our goal here is to provide a compact, statistical description of the spatial density function of a large collection of plant architectures. We analyze “skeletonized” plant architectures, evaluating their spatial density function based only on length measurements. Overall, we discovered a universal property shared by all plants studied here; their spatial density functions can be described using a single functional form: a truncated 3D Gaussian (Figure 1D). This, as opposed to having several different functional forms for different species, condition, or time points, was an unexpected finding that we substantiate in detail below.

Using Moments to Describe Plant Architectures

To characterize how the branches of a plant are distributed in space, we study the plant’s spatial density function (Figure 1D).

This function describes the density of points in the volumetric territory occupied by the plant, and it determines what architectures can possibly be formed. General properties of architectures can be understood by comparing this function across plants. For tomato and tobacco, we study the spatial density function of only branches (leaves and the hypocotyl are ignored). For sorghum, we study the spatial density function of the leaves, which represent the full architecture, because there are technically no branches.

One conventional approach to compute the spatial density function would be to place a regular k×k×k grid over the plant and to count the density (sum) of points in each 3D voxel. This approach, however, suffers from two limitations. First, grid counting defines density as a local property of the architecture (the total sum of points in each voxel), which can be highly sensitive to noise. Second, grid counting requires an arbitrary selection of the value of k. Large values of k will not provide sufficient spatial resolution, and small values will result in very sparse functions.

To overcome these limitations, we follow the approach developed by Snider et al. [30] and define the spatial density function by its statistical “moments” [33]. Knowing all of the moments of a probability distribution is exactly equal to knowing the function that generates the distribution, with the resolution of the description increasing with the number of moments calculated (ranging from 0 to N; it is impossible in practice to compute all of the moments because of their magnitude; in this study, we could only reasonably compute up to the 20^th moment, which was roughly 10²⁵⁰). For a probability distribution, lower-order moments correspond to common named properties of distributions [34], including the mean (first moment), variance (second moment), skewness (third moment), and kurtosis (fourth moment). Similarly, for a density function, lower-order moments correspond to the total mass (zeroth moment) and the center of mass (first moment divided by the total mass), etc. In general, higher-order moments capture finer details of the architecture, including nonlinearities in branching patterns and the shape of individual branches. Unlike grid counts, moments are global parameters, where each moment calculated depends on the entire structure of the architecture.

To calculate plant moments, we start with the skeletonized architecture, with nodes corresponding to branch points (for the dicots) or leaf points (for the monocot), and with edges between pairs of successive points selected along the manually traced architecture. Each edge is split into ten equal-length segments to increase spatial resolution. For each segment i, we store two quantities: its length w_i and its position p_i = (x_i, y_i, z_i, defined as the mid-point of its two end points. Let n equal the total number of segments over all edges of the plant. Then, the total length of the plant (i.e., its zeroth moment, denoted m₀) is the sum of the lengths of all its segments:

$$m_0={\displaystyle \sum }_{i=1}^n{w}_i.$$

Let k equal the moment order. Following standard probability theory, the k^th “product moment,” m_k, is defined as

$$m_k={\displaystyle \sum }_{i=1}^n{(x_i-\overline{x})}^k{(y_i-\overline{y})}^k{(z_i-\overline{z})}^k{w}_i,$$ (1)

where $\overline{x}$ denotes the center of mass of the plant in the x direction (i.e., the mean of the x coordinates of each segment).

Our first goal is to use these moments to test for the following two properties:

1. Separability: Are all density functions independent in the x, y, and z directions? For example, if a plant is separable, then any growth in the north-south direction would not necessitate a change in growth in the other two orthogonal directions. On the other hand, if the plant is not separable, then any change in the north-south direction would force a corresponding change in at least one other orthogonal direction.

2. Self-similarity: Do all density functions have the same shape, modulo stretching and compression? For example, if both a small plant and a large plant have the same density function, then if they were both scaled to be of the same size, their architectures would exactly overlap. On the other hand, if the two plants have different density functions, they would not well superimpose. The term “self-similarity” is commonly associated with being fractal, i.e., having the property that if a single structure is magnified, then it looks similar at all scales. Our definition of self-similarity considers not a single structure but rather a population of structures and asks whether all of them can be viewed as variations (via stretching or compression) of a single form.

Testing for Separability

Theory

Separability means that the density function can change in one direction without affecting the shape of the function in orthogonal directions. Mathematically, a function of three independent variables is defined to be separable if it can be expressed as a product of three functions, each depending on only one of the variables (STAR Methods).

To test whether a plant spatial density function is separable, we need to determine whether its product moment can be decomposed into the product of individual components for each direction (called “separated moments”). A separated moment is equivalent to projecting the 3D density function onto a chosen direction and calculating moments in that direction. The other two directions do provide information about the total length of the segment (w); however, they do not provide any information about the shape of the function in that direction. In other words, the density function can be translated or rotated in the other two directions without changing the moments in the chosen direction. For each k, the equations for calculating the separated moments m_k,x, m_k,y, m_k,z are described in the STAR Methods.

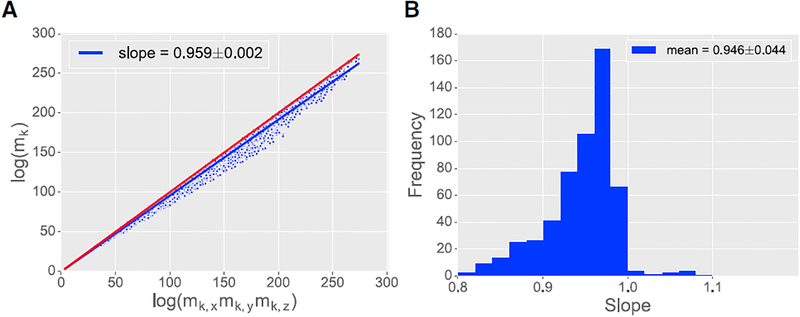
To test separability, we need to test whether m_k = m_k,xm_k,ym_k,z for all moment orders, k. If the function is exactly separable, then the slope of the plot of m_k versus m_k,xm_k,ym_k,z will equal exactly 1. The difference between 1 and the actual slope indicates how far the function is from exact separability. Because higher-order moments can be gigantic (m₂₀ is almost 10²⁵⁰ for the largest plant), we plot all moments on a log-log scale.

Analysis

We used our benchmark dataset to quantify separability for all 557 architectures. All plants analyzed together (i.e., one slope for all plants) achieved near-exact separability, with a slope of 0:959 ± 0:002 (Figure 2A). The observed departure from exact separability (0.959 versus 1.00) is what would be expected by a Gaussian function that is truncated at two SDs (STAR Methods; Figure S1A). That is, the plant spatial density function must be truncated at some boundary. Assuming plants have a spherical boundary, such truncation destroys true separability, and thus, plants cannot be exactly separable. However, the departure from true separability that we observed for plants is consistent with the separability of a truncated Gaussian function. An untruncated Gaussian function is well known to be exactly separable.

Figure 2. Separability of Plant Architectures.

(A) Log-log plot of the product moments (m_k) versus the product of the separated moments (m_k,xm_k,ym_k,z) for even values of k between 0 and 20. There is one dot per moment order per plant scan (557 architectures×11 moment orders = 6127 total dots). The blue line shows the least-squares fit to the data with slope of 0:959 ± 0:002, computed using all values of k plotted together. The red line indicates exact separability with a slope of 1. Plant architectures are nearly, but not exactly, separable.

(B) Frequency histogram of the separability slope calculated for each individual plant over all its moment orders (i.e., 557 slopes; one slope calculated per plant). The average slope was 0.946 with SD of 0.044.

See also Figure S1.

Separability slightly increased when analyzed independently in each pairwise direction: separability in (x, y) was 0:971 ± 0:002; in (x, z) was 0:962 ± 0:002; and in (y, z) was 0:976 ± 0:001. This suggests that the density function is only ≈1% more coupled in three dimensions than in two dimensions.

To test the robustness of this observation, we calculated the separability for each plant separately (i.e., 557 slopes, one per plant). This produced a similar mean slope of 0:946 ± 0:044 (Figure 2B). When slopes were grouped by species (Figures S1B–S1D) and conditions (Figures S1E–S1I), we observed a similar range of separability. For example, tobacco plants across all conditions had a separability of 0:949 ± 0:038, whereas plants grown in shade (across all species) had a separability of 0:946 ± 0:050. Thus, separability does not appear to be a species- or condition-specific property. Separability was also time invariant; the analysis above included both young plants, with only one or two branches and leaves, and more mature plants, with numerous leaves and branches (Table 1).

Overall, this suggests that plant architectures have highly, though not exactly, decoupled density functions and that separability is maintained even in early development.

Testing for Self-Similarity

Theory

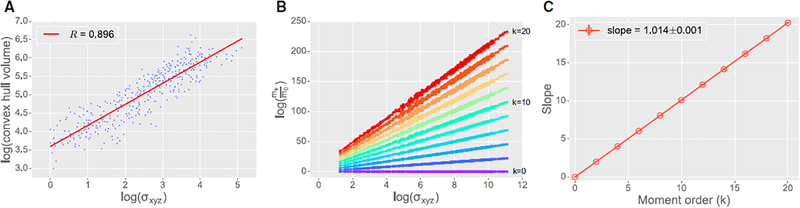
Self-similarity means that different plant spatial density functions can be “morphed” into one another by expansion or contraction along orthogonal spatial dimensions. Mathematically, a function f(x) is defined to be self-similar if the relationship between x and f(x) can be described by a power function [35, 36], such as f(x) = cx^k, where c and k are constants. In our case, the function f(x) represents the spatial density function of a plant (approximated via its moments) with size x. To measure size, we used the SD σ_xyz of the architecture in all directions (STAR Methods; Figure 3A).

Figure 3. Self-Similarity of Plant Architectures.

(A) Log-log plot showing the high correlation of plant architecture size, measured using the convex hull volume (y axis) versus the SDs in the three directions (x axis). Correlation coefficient of the red regression line is shown in the legend.

(B) First step of the self-similarity test, plotting log(m_k=m₀) (y axis) versus log(s_xyz) (x axis) for all 557 plant architectures for k = 0, 2,…, 20. Each architecture contributes one dot per k. Straight lines depict least-squares fit to the data for each k.

(C) Second step of the self-similarity test, plotting the slopes of the regression lines in (B) for each moment order. For each moment order, error bars correspond to 99% confidence intervals, computed using bootstrapping, for each corresponding regression line in (B). Most confidence intervals are less than the diameter of the plotting symbol. Error in the legend indicates the least-squares error of the regression line in (C).

See also Figure S2.

There is a two-step procedure to quantify the degree to which plant spatial density functions are self-similar. The first step is to plot m_k/m₀ versus σ_xyz for each architecture and for various values of k. The term m_k/m₀ corresponds to the function f(x) normalized to unit length, and σ_xyz equals the size of the architecture. If, for each value of k, there is a linear relationship between the two on a log-log plot (with a different slope for each k), then the architectures share the same self-similar function. The second step is to plot the slope of the lines generated in the first step versus the moment order (k). The difference between the slope of this line and 1 denotes the degree of self-similarity. See Snider et al. [30] for a formal derivation of why each moment order k has a slope of k for a self-similar function.

Even if plants are self-similar, however, they may belong to different classes of self-similar functions. Such functions can include a uniform, a Gaussian, or an exponential spatial density. The assignment of architectures to classes may also be species or condition specific. This test can determine the number of classes of self-similar functions required to describe the plant architectures because architectures from one class will fall on one line and architectures for another class will fall on a second line for the same moment order. Thus, this test determines the degree to which architectures are self-similar and the number of classes of architectures. Our dataset includes architectures that vary in size by four orders of magnitude (Table 1), which represents a broad scale to test this theory.

Analysis

Following the first test for self-similarity described above, we plotted log(m_k=m₀)versus log(σ_xyz) for k = 0, 2, …, 20 for all 557 architectures Figure 3B). We computed a least-squares regression line for each moment order, each line closely approximated the data (R² > 0:99 for all 11 regression lines), even as moment values ranged over 250 orders of magnitude. Thus, the first test passes.

For the second test, we plotted the slopes of the lines calculated in the first test versus k, the moment order (Figure 3C). The slope of the line was 1:014 ± 0:001, which is very close to 1, as would be required by true self-similarity.

To again determine the robustness of this observation, we repeated the first and second tests of self-similarity on architectures grouped by each species and environmental condition separately (Figures S2 and S3). All three species exhibited close self-similarity (slopes of 1.013, 1.011, and 1.009, respectively, for tomato, tobacco, and sorghum). When grouped by condition, we observed a similar range of slopes: 1.001 for drought; 1.011 for high light; 1.011 for control; 1.013 for shade; and 1.021 for high heat. We also performed the two tests of self-similarity using both odd and even moments together and observed no change in our conclusions (Figures S3I and S3J).

Together, these tests show that plant shoot architectures deviate only 1% or 2% from true self-similarity. Moreover, these architectures share a single density function because all architectures lie on a single set of lines, one for each moment order.

Deriving a Functional Form of Plant Architectures

The results from the self-similarity test (Figure 3) suggest that a single self-similar function can describe the density of all of the plant architectures. But this does not specify the actual form of the density function. Going from the moments of a function to the exact function itself is a notoriously difficult problem that theoretically requires computing an infinite number of moments [37]. Whereas some methods have been proposed to approximate a function’s form from its moments, these require additional assumptions (e.g., maximum entropy [38], space filling [39], and mass minimization) that may not always hold invariant.

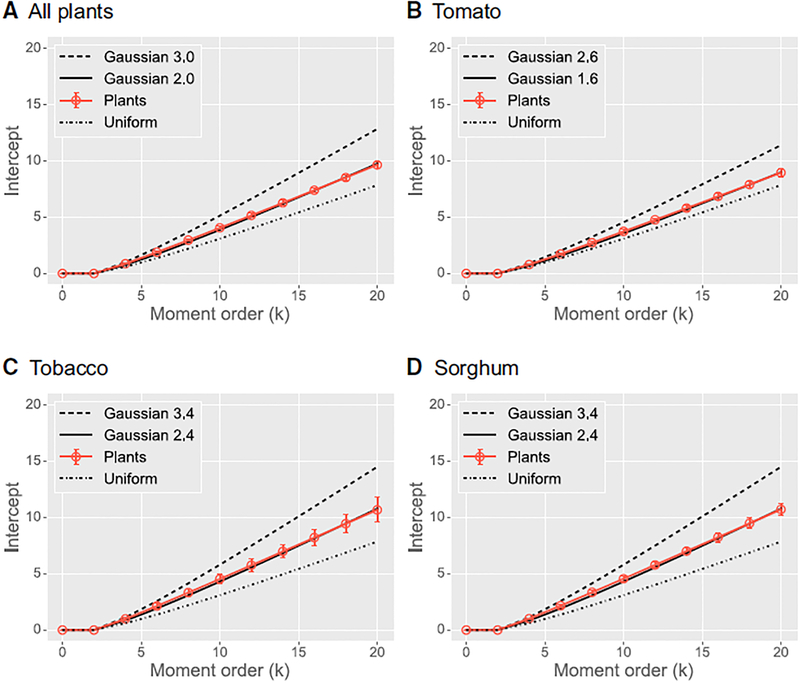
Here, we seek to find a simple function with few parameters that provides an adequate statistical description of plant spatial density functions. There are an infinite number of self-similar functions, and for each, the “slope of the slopes” (Figure 3C) will be 1; the remaining parameter of the line (the intercepts) encodes the functional form of the function because different self-similar functions must have different intercepts. Thus, to determine a functional form from the first 20 moments, we compared the intercepts of the lines in Figure 3B with those intercepts produced by two common density functions: a 3D uniform density (constant density inside a spherical boundary and zero density outside) and a 3D Gaussian density truncated at a spherical boundary. We chose a Gaussian density because it is the only 3D function that is spherically symmetric and separable in Cartesian coordinates [33], and at least some plants have approximately spherically symmetric densities. For both functions, the boundary corresponds to the edge of the territory occupied by the plant in physical space.

Unexpectedly, we found that all architectures can be described by a single density function: a 3D Gaussian truncated at roughly two SDs from the center of mass (Figure 4A). This means that only four parameters are needed to specify how plant architectures distribute branches in space: the center of mass and the SDs in the three orthogonal directions. We can test the goodness of fit of this function by comparing the plant’s intercepts versus the intercepts of a uniform density function and versus a Gaussian density truncated at one additional SD. Both of these result in a poor fit (Figure 4A); for the latter, this suggests that a relatively small change in the density function (one additional SD) is significant. We also observed species-specific differences in the best truncation parameter, but in all cases, the functional form did not change (Figures 4B–4D). Figure 1D illustrates a few example spatial density functions for plants.

Figure 4. Plant Gaussian Spatial Density Functions.

Plots of the intercepts of the self-similarity lines in Figure 3B versus moment order for (A) all plants together, (B) tomato only, (C) tobacco only, and (D) sorghum only. Each panel depicts the intercepts of the plants (solid brown line) with those of a closely matched function (solid black line), as well as a uniform density, and a Gaussian with a larger SD. Error bars denote 99% confidence intervals. Intercepts for the uniform and Gaussian densities for various truncations were computed analytically [30]. Intercepts for k = 0 and k = 2 are both equal to log(1) = 0 due to normalization to unit length and unit variance. See also Figure S3.

Overall, we derived a compact, statistical description of all 557 architectures. The plant moments are consistent with a truncated 3D Gaussian density function. This description is almost as simple as it can possibly be.

Deviation in Growth Strategies across Time, Conditions, and Species

Despite the overall similarity in the shape of the plant spatial density functions, there were architectures scattered above and below the regression lines for each moment order (Figure 3B). Is this noise, or are there systematic differences in this scatter?

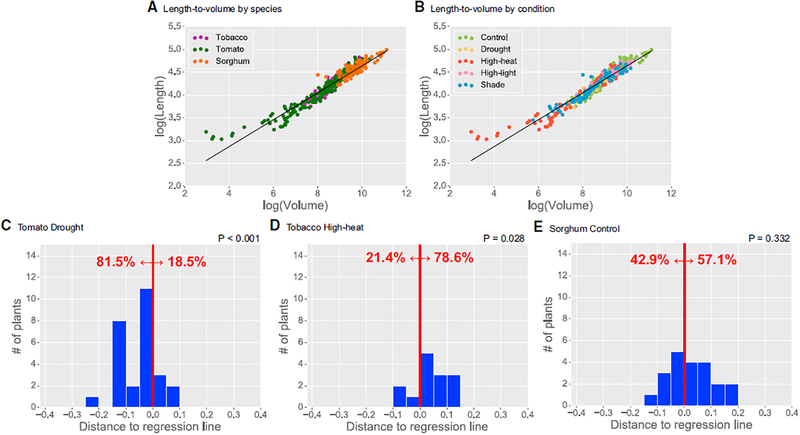
To explore this, we focused on scatter for the total length of the plant (m₀) plotted versus the volume of the plant σ_xyz. Because these showed a linear relationship on a log-log plot (Figures 5A and 5B), these two variables were related as Volume ∝ Length^α, indicating that, as total length increases, the volumetric territory occupied by the plant increases in accordance with a power law [12]. However, plants that lie below the log-log regression line have a shorter total length for the same volume occupied and vice versa. This means that branch density (length per unit volume) is systematically lower for plants below the line versus for those above the line.

Figure 5. Length versus Volume Comparison.

(A and B) Log-log plots of total length (y axis) versus total volume (x axis) of the architecture, grouped by (A) species and (B) condition. Regression line is shown in black. Analysis includes all plants day 8 and higher.

(C–E) Histograms showing the number of plants in three different species-condition pairs—(C) tomato drought, (D) tobacco high-heat, and (E) sorghum control—that lie above or below the regression line, shown as to the right or left, respectively, of the red line. For example, 78.6% of tobacco plants grown in high heat lie significantly above the regression line, i.e., they occupy a smaller volume for the same length compared to the average. Sorghum plants are split evenly above and below the regression line.

See also Figure S5.

First, we sought differences in the length-to-volume relationship across species and conditions. For tomato plants grown in drought conditions, 81.5% of the plants lay below the line, whereas for tobacco in high heat, 78.6% of plants lay above the line (Figures 5C and 5D; p < 0.05 for both). Figure S4 shows visually how much less volume tobacco grown in high heat occupies compared to tobacco grown in control conditions. This difference has a known biological basis [40, 41]: in high heat, tobacco leaves curl upward to reduce moisture loss through evaporation—a classical stress response—and the leaves bunch together, occupying less volume. This strategy increases self-shading and reduces leaf surface area exposed to light, effectively acting as a cooling effect. We also characterized how plant volume scales with a higher-order moment (m₁₀) and found similar differences in the same species-condition pairs (Figure S5), suggesting that these differences extend beyond just simple length-to-volume measurements.

Second, we sought systematic differences in the length-to-volume relationship across time and found that young tomato and tobacco plants occupy more volume than young sorghum plants for the same length (STAR Methods).

Overall, these results further challenge previous hypotheses that branching architectures of plants are always volume filling [39]. Variation in length-to-volume relationships represents one type of “knob” that plants can use to tune their architectures to specific environmental challenges, while still obeying the same general growth rule. Moreover, whereas length-to-volume relationships have long been studied in the literature, characterizing these differences as they vary across environmental conditions for the same species, and across time for the same plant, is to our knowledge novel.

DISCUSSION

We studied the probabilistic shape of plant architectures and found that all architectures share two fundamental properties: their spatial density functions are nearly separable and self-similar. Separability means that spatial density functions are decoupled across the x, y, and z directions. This suggests that the same growth logic can be applied without needing to “rewrite the code” in each direction separately. This may be desirable because the optimal growth direction is highly unpredictable and dependent on light or competition that can come from any direction. Self-similarity means that different plant spatial density functions can be morphed into one another by stretching or compressing along orthogonal directions. Together, these two properties suggest a type of biological modularity [42, 43], where regulating a few parameters may be sufficient to generate a large diversity of architectures. We also found that a single density function, a 3D Gaussian truncated at roughly two SDs, is capable of describing a large diversity of architectures.

There are four ways in which our work may be used in the service of plant biology. First, our finding that all plants considered here are statistically similar raises immediate questions about the molecular mechanisms that give rise to this simplicity in morphology. Gene regulatory networks responsible for pattern formation are often conserved and are capable of producing a broad spectrum of patterns by combinatorially modulating the expression of one or a few core genes [44–46]. Indeed, most mutations lead to changes in gene expression levels, as opposed to the deletion or invention of entirely new genes, and these changes have long been viewed as a primary mechanism of evolutionary adaptation [47–50]. From an evolutionary perspective, some conservation of structure may be expected—it is unlikely that evolution uses growth rules that are unique to every individual species or every different condition. However, only developing the machinery to implement a single functional form is highly economical and was not an expected result. The mechanism driving this form remains a mystery and clearly begs for an explanation by molecular and cell biologists. Second, understanding growth is a grand challenge in plant biology [1]; our finding that the functional form of the density function is similar in both young and adult plants suggests that similar growth strategies may be used throughout development. Whereas the properties studied here are not meant to allow for the reconstruction of individual plant architectures, they do help explain variance in architectures observed at the population level. Third, these properties may provide new evaluation strategies for genome engineering and plant selection that are critical for increasing crop yield [27, 28, 51]. Fourth, we used statistical moments to describe plant architectures; reverse engineering these moments to actual plant traits could provide a new method for understanding and comparing plant forms.

Are there simple models that can generate plant architectures with the described Gaussian functional form? For example, Lindenmayer systems provide a class of recursive growth rules that naturally give rise to fractal branching. One challenge in these models has been in determining the correct branch lengths, which can affect spatial density. We found that the distribution of branch lengths, across all plants, was clearly an exponential (Figure S6). The simplest way to generate such a distribution would be a Poisson process with a single parameter equal to the mean branch length—a constant that is the same across all plants and for all branches within a plant. Similar distributions have been found in leaf venation networks [52]. These observations provide new constraints that realistic generators of plant architectures should satisfy. Generative models may also be useful in quantifying departure from true separability. For example, the model could include a parameter that controls the amount of separability; synthetic architectures generated from these models could then be compared versus actual plant architectures to determine how the observed departure from separability observed here (0.959 versus 1.00) manifests in terms of other plant traits.

All rules have exceptions; where may we find exceptions to the statistical properties studied here? First, gravity imposes physical limitations on both tree height and tree width [53–55], which may alter branching patterns as they approach this physical limitation. Our dataset consisted of plants with sizes below these limits, and it would be important to see how these statistical properties can be refined to address these physical limitations. Second, our analysis studied juvenile plants from three species across multiple conditions. This dataset does not encapsulate the entire plant kingdom and all possible growth climates for plants, for which there may also be exceptions to these rules. Third, some trees, such as giant sequoias, can elongate vertically roughly 100 m before branching. Such architectures would clearly not be separable in the up-down direction. Thus, in our analysis, we removed the part of the plant beneath the first branch point. This part of the plant, called the hypocotyl for di-cots, may be regulated differently, for example, as is well studied in the shade-avoidance response [4]. When analyzing neural branching morphologies, Snider et al. [30] also removed the part of the dendrite before the first branch point, because dendrites of some neurons travel a millimeter in the brain before branching occurs and synapses form; without removing this part, dendrites would also not be separable.

There are also many branching structures in biology where these properties do not hold, indicating that these properties are not “inevitable” and may indeed represent selective optimization by evolution. For example, both cardiovascular networks and sand dune morphologies deviate from strict self-similarity [56, 57]; the former is also better characterized by a uniform density rather than a Gaussian [58]. Self-similarity has also been questioned in some retinal neurons, where they appear to be space filling rather than fractal [59] (though see below); likewise, in the spatial topology of tropical forests, species diversity is not self-similar across all spatial scales [60]. There are also many functions for which we observe curved lines in the moments versus size plot (Figure 3B), also indicating non-self-similarity [30].

On the other hand, there are some branching processes that do display these properties. Snider et al. [30] analyzed thousands of dendritic and axonal arbors in the brain across many cell types and species; they found that all arbors exhibited near separability and self-similarity and could be described by a Gaussian density truncated at roughly 1.7 SDs for 3D arbors. These properties allow complex arbors to be generated by only varying a few parameters, offering a potentially very simple way to form diverse neural circuits [61]. The fact that neural and plant branching structures share similar topological properties offers another correspondence contributing to the field of plant neurobiology [62, 63].

STAR★METHODS

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Plant 3D architecture data		http://plant3d.snl.salk.edu
Plant 3D architecture data		http://dx.doi.org/10.17632/9k7zctdyhs.1
Experimental Models: Organisms/Strains
Tomato (Solanum lycopersicum cv m82D)	Plant Biology Laboratories, Salk Institute	N/A
Tobacco (Nicotiana benthamiana)	Plant Biology Laboratories, Salk Institute	N/A
Sorghum (Sorghum bicolor)	John Mullet, Texas A&M University	N/A
Software and Algorithms
Code to compute plant moments	This paper	http://plant3d.snl.salk.edu
3D scanner (Faro Technologies)		http://www.faro.com/products/metrology/faroarm-measuring-arm/overview
Other
Plant growth chambers	Percival Scientific, IA	https://www.percival-scientific.com/
Plant growth chambers	Conviron model E8	http://www.conviron.com/products/e8-reach-in-plant-growth-chamber

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Saket Navlakha (navlakha@salk.edu).

METHOD DETAILS

Plant growth experiments

Experiments were performed with 3 species of plants (Table S1): tomato (Solanum lycopersicum cv m82D), tobacco (Nicotiana benthamiana), and sorghum (Sorghum bicolor 100m). These species were selected because they encapsulate two well-known classes of flowering plants (monocots and dicots, which produce one and two embryonic leaves, respectively) and because of their overall agricultural importance [64]. Each plant was grown in a medium comprised of 2x soil (SunGro Propagation mix, USA) to 1x medium vermiculite (SunGro, USA). The soil was moistened with water containing 0.12–0.24 oz/gallon fertilizer (Plantex, Canada). All seedlings, except for sorghum, were planted in 12-celled planting trays and then transferred to plastic pots. Tomatoes were transferred to plastic pots (4in. diameter × 3in. tall) on their 9^th day after planting, and scanning began on their 11^th day (which we refer to as scanning day 0, or D0). Tobaccos were transferred to plastic pots (4.5in. diameter × 3.75in. tall) on their 9^th day after planting, and scanning began on their 17^th day. Sorghum were directly planted in plastic pots (4in. diameter x 3in. tall) and scanning began on their 7^th day. All plants were given roughly 50mL of water per day in the greenhouse until they were moved to different environmental conditions in chambers. All plants were placed in their environmental condition 24 hr prior to the first day of scanning (D0).

Experiments for each plant species were performed across 3–5 environmental conditions (with 2–5 replicates per species-condition pair), and through 20–30 days of growth (Table S1). All plants were grown in chambers on a long-day cycle — 8hr dark (1am-9am), 16hr light (9am-1am) — once placed in their environments. All plants received 50mL of water every other day (drought condition excluded). Tomato experiments were performed in ambient conditions (Percival Scientific, IA; 22°C), shade (22°C, R:FR = 0.7), high-heat (35°C), high-light (Conviron model E8; 22°C, PAR = 1140 μmol⁻²m⁻¹), and drought (22°C). Plants in the drought condition were not watered for the entirety of the scanning period. Tobacco experiments were performed in ambient, shade, and high-heat (32°C). Sorghum experiments were performed in ambient, shade, high-heat (35°C), and high-light. These conditions were selected because they represent a range of realistic environments regularly faced by many plant species. Scans were performed every 1–3 days. Each plant was scanned at approximately the same time every scanning day. Each scan took roughly 5–20 min, depending on plant size.

High-resolution 3D plant scanning

A blue-laser scanner (Edge Scan Arm HD, Faro Inc.) was used to non-invasively reconstruct plant architectures in 3D. Scanning requires no contact with the plant. The output of the scanner is a 3D point cloud representation of the plant with unprecedented, micron-level resolution with an error ± 25um. There may be some loss in precision toward the boundary of the plant, but all our input points were selected near the middle of the structure (e.g., each end-point of a branch was selected near the center of its diameter with respect to thickness). Plant moments were all calculated on the order of millimeters (the precision of the scanner is in microns), and thus we do not believe the precision of the scanner unduly affects our skeletonization and conclusions. Spatial encoders in the scanning arm provide automatic 3D registration in X-Y-Z space. This technique avoids common issues in imaging-based approaches that require segmentation, alignment, and thresholding [65, 66] because scanning only captures plant material, without any background. The accuracy of scanning-based measurements have been well-validated compared to reference measurements [67, 68], justifying their use here.

Accompanying software (Polyworks 2016, USA) was used to produce a triangulation mesh of the point cloud. To produce the most accurate representation of the plant, each plant was scanned from two sides — at 0° and after turning the plant 180° — and then automatically aligned.

Selecting input points for moments calculation, and pre-processing

From each scan, input points were selected corresponding to all branch points, including branch terminal points where leaves or leaflets emerge (for dicots). Sorghum do not have branches and instead have long grassy leaves; hence points were selected on the stalk, excluding the coleoptile, and at two locations per leaf: the highest point of the leaf in the up-down (y) direction, and the mid-point between the highest point of the leaf and base of the leaf (where the leaf branches from the stem).

In order to compare many plants, two adjustments to the moments are needed: a scaling of the density function so all plants are of the same size, and an orientation of the axes so all plants are aligned. For the former, we normalize by m₀ to scale each architecture to unit length. For the latter, we rotate the architecture so its co-variance across all pairs of directions is zero. We computed separability without orienting the axes and found that separability was not promoted due to this registration (from 0.959 with orientation to 0.976 without orientation). Thus, we do not believe separability is an artifact induced by registration.

For 2D architectures (e.g., some maize or vine plants), moments must be calculated in 2D, as opposed to 3D; otherwise, all of the moments will be 0.

Definition of separability and separated moments

Formally, a function P(x, y, z) of three variables is separable if it can be rewritten as:

$$P(x,y,z)=p_1(x)p_2(y)p_3(z),$$

for some functions p₁, p₂, p₃ over the domain of P. An example of a function that is separable is P(x, y, z) = xysin(z), which can be written as a product of p₁(x) = x, p₂ (y) = y, p₃(z) = sin(z). On the other hand, P(x, y, z) = sin(xyz) is not separable.

For each k, the separated moments are defined as:

$$\begin{gathered} m_{k,x}={\displaystyle \sum }_{i=1}^n{(x_i-\overline{x})}^k{w}_i \\ {m}_{k,y}={\displaystyle \sum }_{i=1}^n{(y_i-\overline{y})}^k{w}_i \\ {m}_{k,z}={\displaystyle \sum }_{i=1}^n{(z_i-\overline{z})}^k{w}_i. \end{gathered}$$ (2)

For example, m_4,y is the 4^th moment in only the y-direction, and m_2,z is the 2^nd moment (variance) in only the z-direction. If the density function is not separable, then m_4,y would also depend on the values of the function in at least one other direction, x or z.

Each separated moment in Equation 2 is normalized by $m_0^{2/3}$ so that when computing the product of separated moments, the total length w_i is only factored in once, allowing for an equal comparison to the product moment, m_k in Equation 1. We calculate product and separated moments for even values of k and thus leave out the absolute value sign.

Measure of architecture size using moments

To measure size, we used the standard deviation of the architecture in all directions. This denotes the amount the architecture spreads around the center of mass. Recall that the 2^nd moment m₂ corresponds to the variance; thus, the standard deviation equals:

$$\begin{gathered} {\sigma }_{xyz}=\sqrt{\frac{m_2}{m_0}} \\ =\sqrt{\frac{{\displaystyle {\sum }_i{(x_i-\overline{x})}^2{(y_i-\overline{y})}^2{(z_i-\overline{z})}^2{w}_i}}{{\displaystyle {\sum }_i{w}_i}}}, \end{gathered}$$

where we normalize by the total length (m₀) to scale to unit length. This is a typical measure of size that is computable using only the moments themselves, and no other quantity. This measure is also proportional to another common measure of size, the convex hull volume (i.e., the smallest convex polytope that encloses all the scanned cloud points representing the plant), justifying its use as a measure of size (Figure 3A).

Note that the convex hull would not be sufficient to specify the functional form of the architecture: the same convex hull could represent either a uniform or a Gaussian spatial density, and there would be no way to distinguish these from the convex hull alone.

QUANTIFICATION AND STATISTICAL ANALYSIS

The data were quantified using statistical moments as described in Results and Method Details. We used n = 557 architectures. All regression lines were computed using least-squares. Error bars correspond to 99% confidence interval computed using bootstrapping, or least-squares fit error, as noted. Other technical details are described in Results, Figures 2, 3, and 4, and below.

Quantifying departure from true separability

We found that all plants analyzed together achieved a separability of 0.959; however, it is difficult to appreciate how close to true separability this may be without providing some frame of reference. Here, we ask: at how many standard deviations would a true Gaussian density function need to be truncated in order to exhibit the same departure from exact separability that we observed for the actual plant architectures? In the main text, we found that the spatial density function of all plants can be described by a Gaussian density truncated at two standard deviations from the center. Here, we test if a Gaussian truncated at two standard deviations exhibits a similar departure from exact separability as observed by the plants. The key point here is that the amount the function is truncated in one direction depends on the amount of truncation in another direction, which makes the function non-separable. This would occur, for example, when the truncation is spherical for 3D data (circular for 2D).

Snider et al. (2010) provided a test to compute separability using truncated product and separated moments for Gaussian density functions. Figure S1A shows that the observed departure for plants is very similar to that which would be expected by a Gaussian truncated at two standard deviations from the center. Each colored line in Figure S1A corresponds to a true Gaussian function truncated at a different number of standard deviations (as annotated; 1, 2, 3, 4, 6, 8, 10). For a Gaussian truncated very far from the center (8 or 10 standard deviations, the purple and pink lines), the log of the separability is close to 0 = log (1), indicating very little departure from exact separability. Superimposed on this plot are black dots corresponding to the plants’ separability, calculated for each moment order separately (in the main text, we combined all moment orders together).

We find that the separability expected by a Gaussian truncated at two standard deviations closely overlaps with the plant data. Thus, the observed departure from exact separability can be largely attributed to the fact that plant territories are truncated Gaussians.

Quantifying length-to-volume differences across time

We sought systematic differences in the length-to-volume relationship across time. As expected, there was roughly an even split between architectures lying above (280) and below (277) the regression line. However, the 35 architectures lying furthest below the regression line were all tomato or tobacco plants that were less than 6 days into their development. Tomato and tobacco are both dicots, producing two embryonic leaves (cotyledons) that are used to capture resources for initial growth. The cotyledons fan-out opposite from each other, occupying a relatively large volume for its small initial total length. Sorghum, on the other hand, is a monocot which only produces one lengthy, grass-like cotyledon (scutellum); this occupies less volume and thus sorghum plants lie closer to or above the regression line. The scatter observed thus represents a systematic trade-off in length-to-volume ratios employed in early development compared to later time-points.

DATA AND SOFTWARE AVAILABILITY

All data for the 557 3D plant architectures are available to download at Mendeley Data (http://dx.doi.org/10.17632/9k7zctdyhs.1). Code for computing moments, and visualizations of all plant architectures, are available at: http://plant3d.snl.salk.edu.

Highlights.

• We analyzed 557 3D plant architectures to study how branches distribute in space

• Branch density was separable, self-similar, and described by a truncated Gaussian

• These three properties are shared by dendritic and axonal morphologies in the brain