Bend-Induced Twist Waves and the Structure of Nucleosomal DNA

Abstract

Recent work indicates that twist-bend coupling plays an important role in DNA micromechanics. Here we investigate its effect on bent DNA. We provide an analytical solution of the minimum-energy shape of circular DNA, showing that twist-bend coupling induces sinusoidal twist waves. This solution is in excellent agreement with both coarse-grained simulations of minicircles and nucleosomal DNA data, which is bent and wrapped around histone proteins in a superhelical conformation. Our analysis shows that the observed twist oscillation in nucleosomal DNA, so far attributed to the interaction with the histone proteins, is an intrinsic feature of free bent DNA, and should be observable in other protein-DNA complexes.

Introduction –

Elastic models of DNA have been a key tool for understanding the response of the double helix to applied stresses [1]. Such stresses are ubiquitous in cells, where DNA is continuously being bent and twisted. For instance, in eukaryotes about 75% of the DNA is wrapped around cylindrically-shaped octamers of histone proteins [2]. The 147 base pairs (bp) of wrapped DNA sequence and the histone form the nucleosome, which represents the lowest level of chromosomal organization.

At length scales of a few nanometers the behavior of DNA can be modeled by a homogeneous elastic rod, with stiffness constants associated with the different types of mechanical deformations [3–6]. The simplest such model is the twistable wormlike chain (TWLC), which treats bending and twist as independent deformations. However, symmetry analysis of the right-handed, oppositely-directed-backbone double helix indicates that there must be a coupling of bending to twisting [7]. This can be understood as a consequence of the asymmetry between the major and minor grooves of the double helix. Only a few prior works have considered twist-bend coupling [8–15], and its effect on equilibrium and dynamics of DNA remain largely unexplored.

Here we investigate the effect of twist-bend coupling on free DNA minicircles and compare their shapes with X-ray crystallographic structures of nucleosomal DNA (DNA wrapped around histones). We present an analytical solution of the minimal energy configuration of free minicircles which shows that twist-bend coupling induces sinusoidal twist waves coupled to bending waves. The results are in excellent agreement with molecular dynamics simulations of two different coarse-grained DNA models [16]: one with symmetric grooves and one with grooves of unequal widths. Only in the latter twist waves are observed, in agreement with the symmetry argument of Ref. [7]. The nucleosomal DNA shape obtained from averaging 145 available crystal structures displays twist waves quantitatively matching the predictions of our simple theory for free DNA. While several studies in the past analyzed oscillations in twist in nucleosomal DNA, this was usually attributed to interations with the underlying histone proteins [2]. Our work shows that twist waves are a general feature of bent DNA and that similar results should be observable for other protein-DNA complexes.

Theory and Energy Minimization –

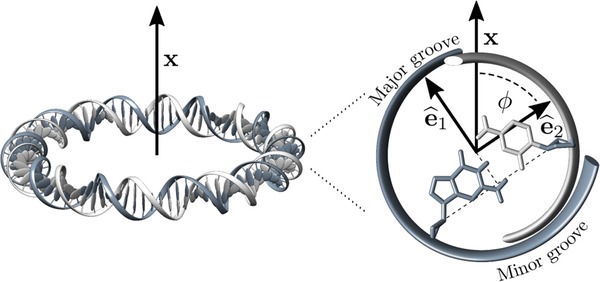
Following prior work [7], we describe the double helix centerline using a space curve in arc-length parameterization, with coordinate s running from 0 to the total DNA length L; we thus treat the double helix as inextensible, which turns out to be appropriate for our purposes. Along the curve we define an orthonormal triad {ê₁(s), ê₂(s), ê₃(s)} where ê₃ is tangent to the curve, while ê₁ and ê₂ lie on the plane of the planar Watson-Crick base pairs [7], with ê₁ directed along the symmetry axis of the two grooves, pointing in the direction of the major groove. Orthogonality then determines ê₂ = ê₃ × ê₁(see Fig. 1).

FIG. 1.

Left: Schematic view of a DNA minicircle lying on a plane orthogonal to a vector x. Right: Zoom-in of a cross-section of the double helix showing the unit vectors ê₁ and ê₂ (the tangent vector ê₃ = ê₁ × ê₂ points inside of the page). In an ideal fully-planar circle x lies on the plane spanned by ê₁ and ê₂. ϕ is the angle between ê₂ and x.

The three-dimensional shape of the space curve fully described by 3-vector unit vectors field Ω that rotates the local unit vectors,

$$\frac{\text{d}{\widehat{e}}_i}{ds}=\left(\Omega +w_0{\widehat{e}}_3\right)\times {\widehat{e}}_i,$$ 1

where the index i runs over the three spatial directions, and where ω₀ is the intrinsic twist-density of the double helix. As is familiar from mechanics, the rotation vector Ω(s) + ω₀ê₃ relates the triad at s + ds to that at s. The three components of Ω(s) along the triad axis are Ω_i(s) ≡ Ω· ê_i(s). Ω₁ and Ω₂ are bending densities (corresponding to the “tilt” and “roll” deformations, respectively, of the DNA literature), with the usual curvature of the backbone given by $k\equiv {\left({\Omega }_1^2+{\Omega }_2^2\right)}^{1/2}.{\Omega }_3$ is the twist density, or, more precisely, the “excess” twist over that of the double helix ground state, ω₀.

Assuming the ground state to be a straight configuration with constant twist density ω₀, one can interpret Ω as a strain-field associated with a free energy density. Taking the symmetries of the double helix into account, the deformation free energy to second order in Ω is [7]

$$\beta E=\frac{1}{2}{\displaystyle {\int }_0^L\left(A_1{\Omega }_1^2+A_2{\Omega }_2^2+C{\Omega }_3^2+2G{\Omega }_2{\Omega }_3\right)}\text{d}s,$$ 2

where β = 1/k_BT is the inverse temperature, and A₁, A₂, C and G are the stiffness parameters. Equation (2) is characterized by a twist-bend coupling term connecting a bending deformation towards the DNA groove (Ω₂) to a twist deformation (Ω₃). G denotes the twist-bend coupling constant, without which (G = 0) one recovers the TWLC.

We investigate the lowest-energy configuration of a circularly-bent DNA molecule, a constraint which can be mathematically imposed by appropriate Lagrange multipliers. This is usually performed by parametrizing Ω_i in a lab frame using Euler angles (see e.g. Refs. [17, 18]), and numerically solving the corresponding Euler-Lagrange equations. We will instead introduce an approximation, which will allow us to work in the material frame using the Ω’s as minimization variables, and perform the minimization analytically.

One might be tempted to fix the curvature $k={\left({\Omega }_1^2+{\Omega }_2^2\right)}^{1/2}$ using a Lagrange multiplier, but this leads to a helical solution, rather than a closed configuration [19]. This is a consequence of the bending anisotropy (A₁ ≠ A₂), together with the fact that the plane on which the bending takes place is not restricted. Instead, we seek to impose bending on a plane, as e.g. illustrated in Fig. 1 (left). The bending component of a local deformation is described by the vector Ω_b ≡ Ω₁ê₁ + Ω₂ê₂. Enforcing bending along a fixed plane, as for instance the plane orthogonal to a vector $\widehat{\text{x}},$ is equivalent to requiring Ω_b to be parallel to $\widehat{\text{x}},$. The term $\mu {\Omega }_b\cdot \widehat{\text{x}}$ provides a constraint, with μ Lagrange multiplier. This can be rewritten in the following form

$$\beta \widehat{E}\equiv \beta E-\mu {\int }_0^L\left[{\Omega }_1\sin \varphi \left(s\right)+{\Omega }_2\cos \varphi \left(s\right)\right]\text{d}s,$$

where we have assumed that $\widehat{\text{x}}$ lies on the plane spanned by ê₁ and ê₂, and that ϕ is the angle formed between ê₁ and ê₂ (see Fig. 1). For a straight DNA lying on the plane orthogonal to $\widehat{\text{x}}$ we have ϕ(s) = ω₀s. If within one helical turn bending is relatively weak (i.e. κ ≪ ω₀), we can approximate $\varphi \left(s\right)\approx w_{0}s,$ with the energy minimization then leading to the simple result

$${\Omega }_1=\frac{\mu \sin \left(w_{0}s\right)}{A_1},{\Omega }_2=\frac{\mu \cos \left(w_{0}s\right)}{A_2-G^2/C},{\Omega }_3=-\frac{G}{C}{\Omega }_2,$$ 4

with μ ≡ l_b/R, where R is the average radius of curvature and l_b the bending persistence length of the model (2)[14]. The Supplemental Material [19] discusses the details of the calculations and alternative approaches [20].

The equations (4) describe a curve with small off-planar periodic fluctuations appearing in the form of standing waves in bending and twist. A non-vanishing G is essential for the emergence of twist waves [21]. Although our minimization is not exact, as it is performed under a fixed “background” ϕ(s), simulations of DNA minicircles of radii ≈ 5 nm (see below, [19]) are in excellent agreement with Eq. (4). In an alternative approach [19] one can obtain twist-waves using a systematic perturbation scheme in powers of κ/ω₀, similar to that of Ref. [7]; this parameter is κ/ω₀ ≈ (1/5)/1.75 ≈ 0.11 for a DNA minicircle radius 5 nm, justifying our approximation [19].

Coarse-grained DNA simulations –

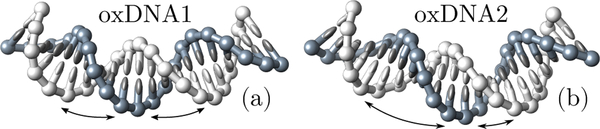
We have performed computer simulations of minicircles with oxDNA, a coarse-grained DNA model in which the double helix is composed of two intertwined strings of rigid nucleotides, held together by non-covalent interactions [16, 23]. Base-pairing together with all other interactions are homogeneous, i.e. sequence-dependent effects are neglected. Various aspects of the mechanics of DNA minicircles, such as kinking, melting and supercoiling, have been discussed in the literature using oxDNA, other coarse-grained models or all-atom simulations [18, 24–27]. Here we focus on the ground-state shape of homogeneous minicircles, and in particular on circular molecules of 85 base pairs (bp), or about 29 nm in length (see Fig. 1). With this choice of length the two ends of the molecule can be joined together without introducing an excess linking number. In addition, the radius of the circles R = 4.6 nm is close to that of nucleosomal DNA (R = 4.2 nm) which will be analyzed later. Two versions of oxDNA were used, see Fig. 2(a,b). In the first version (oxDNA1) the helical grooves have equal width [16], while in the second version (oxDNA2) the grooves are asymmetric, as in real DNA [23]. More details on simulations can be found in Supplemental Material [19].

FIG. 2.

(a,b) Snapshots of minicircles fragments from simulations of oxDNA1 (with symmetric grooves, (a)) and of oxDNA2 (with asymmetric grooves, (b)).

Figure 3(a) shows a comparison between oxDNA1 and oxDNA2 simulations (dashed and solid lines, respectively), in which the Ω_i are plotted as a function of the base-pair phase angle ϕ. The latter was obtained from a Fourier analysis of simulation data: a discrete Fourier transform provides a dominant frequency ω₀ and a global phase $\psi$. From these the local phase of each individual base pair was obtained as ${\varphi }_n=\mathrm{mod}\left(\psi +na{w}_{\text{0}},2\pi \right)$, with the index n = 0, 1 … 84 labeling the base pairs along the circle, and a = 0.34 nm being the base pair separation. The smooth curves of Fig. 3(a) are obtained by binning the data in ϕ and averaging Ω_i within each bin. A key result of Fig. 3(a) is the clear difference in the behavior of Ω₃ between the model with symmetric grooves (oxDNA1, dashed lines) and that with asymmetric grooves (oxDNA2, solid lines). The emergent twist waves are associated with the twist-bend coupling interaction [G ≠ 0 in Eqs. (4)], which arises from the groove asymmetry of DNA [7]. In the unrealistic case of equal major and minor grooves, one expects G = 0, as we indeed observe for oxDNA1. In general, the Ω_i calculated from oxDNA closely follow the predictions of Eqs. (4). For a quantitative comparison see Supplemental Material [19].

FIG. 3.

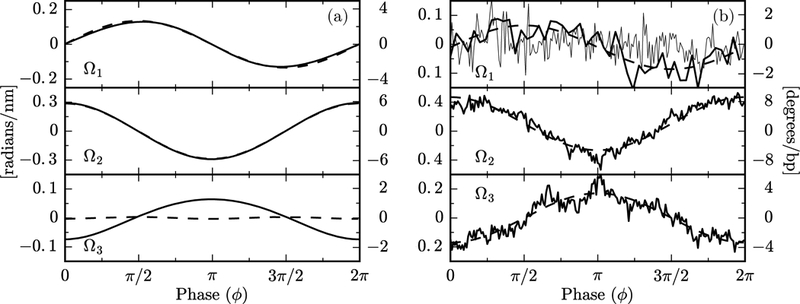
(a) Plot of average values of Ω_i vs. ϕ from oxDNA1 (dashed lines) and oxDNA2 (solid lines) simulations. oxDNA2, but not oxDNA1, has a pronounced twist wave. Overall the data are in good agreement with Eqs. (4). A zoom-in of the Ω₃ for oxDNA1 shows a very weak wave with frequency 2ω₀. This is due to anisotropic bending, as discussed in the Supplemental Material [19]. The Ω_i, as defined in (2), have units of inverse length, which are shown in the left vertical axis. The right axis is in degrees per base pairs, and is obtained by multiplying the left scale by 180a/π, with a = 0.34 nm the base pair separation.(b) Plot of the mean values of Ω_i vs. the phase ϕ (analogously to Fig. 3), obtained from averaging over 145 nucleosome crystal structures. Noisy curves for Ω₂ and Ω₃ are simple averages over all structures; smooth curves show the Fourier component for ω₀, indicating its dominance in the average, as well as the antiphase relation of Ω₂ and Ω₃ expected from the twist-bend coupling. Data for Ω₁ averaged over all structures are extremely noisy (light noisy curve), but when selected structures with large power at ω₀ are analyzed (darker curves) the π/2-phase-shifted signal expected from theory is observed (see text). The output of the software Curves+ [22] is in degree per bp, given in the right vertical axis.

Nucleosomal DNA –

We now turn to the analysis of nucleosomal DNA, which is highly bent around histones, forming a superhelix of radius 4.19 nm and pitch 2.59 nm (for a recent review see e.g. Ref. [2]). The length of the wrapped DNA is 147 bp, corresponding to 1.67 super-helical turns. High-resolution structural crystallographic data for DNA wrapped around histone proteins in nucleosomes is available (we note the seminal work of this type in Ref. [28]). Oscillations in tilt (Ω₁), roll (Ω₂) and twist (Ω₃) were found in early analyses of crystal-lographic data, and were attributed to histone protein-DNA interactions [28]. Since the publication of the first high-resolution nucleosome data [28], many crystal structures have been determined with different wrapping sequences and various DNA or protein modifications (e.g. methylation and phosphorilation). Here we focus on the average shape of nucleosomal DNA, which can be obtained by averaging over different available structures. Nucleosomal DNA forms a superhelix and not a close circle. Nonetheless, Eqs. (4) are expected to approximate well its shape, as the superhelical pitch is small compared to the intrinsic double-helix twist (details in Supplemental Material [19], see also Ref. [12]).

Figure 3(b) shows a plot of average Ω_i vs. ϕ, extracted from the analysis of 145 crystal structures from the Protein Data Bank (PDB [29]), using the conformational analysis software Curves+ [22]. The phase ϕ is calculated from the discrete Fourier analysis, similarly to the oxDNA data of Fig. 3(a). From the analysis of crystal structures we find that in nucleosomal DNA Ω₂ and Ω₃ have a strong oscillatory behavior for all sequences and are in antiphase as predicted by Eqs. (4). The average of Ω₁ over all crystallographic data results in a structureless, highly-noisy signal (thin lines, top of Fig. 3(b)). However, a subset of data (24 PDB entries out of the 145 analyzed) show oscillations in Ω₁, detectable from a dominant peak in the Fourier spectrum corresponding to a frequency ≈ ω₀. The average of this oscillating sub-set is a sinusoidal wave, as expected from Eq. (4). The lack of a clear oscillatory signal may be due to sequence-specific effects and low signal-to-noise ratio, masking the expected behavior.

There is a reasonable quantitative agreement in the wave amplitudes between oxDNA simulations and nucleosome data, as seen by comparing the vertical scales of Fig. 3(a) and (b). According to Eqs. (4) the wave amplitudes depend on the value of the elastic constants, which may be somewhat different between real DNA and oxDNA. Nucleosomal DNA has a larger amplitude in Ω₂ and smaller in Ω₁ than oxDNA. As shown in Supplemental Material [19], from Eqs. (4) it follows that max {Ω₁} + max{Ω₂}= 2/R, a geometric stiffness-independent constant, R being the radius of curvature. Using this relation we find R = 4.7 nm both for oxDNA1 and oxDNA2, which agrees with the expected radius R = 85a/2π = 4.6 nm for a 85-bp minicircle. For the nucleosome, we obtain R = 4.5 nm, which, considering the large uncertainty on Ω₁, is reasonably close to the known nucleosomal-DNA radius R = 4.2 nm. While the sum of the amplitudes Ω₁ and Ω₂ is constrained by the geometry, this is not the case for Ω₃. Its amplitude is larger for the nucleosomal data (Fig. 3(b)) than for oxDNA2 (Fig. 3(a)), suggesting that oxDNA2 has a twist-bend coupling constant lower than that of real DNA, in agreement with a previous analysis [15]. From the ratio between the amplitudes of Ω₃ and Ω₂ in Fig. 3(b) and Eq. (4) we estimate G/C ≈ 0.46. Recent analysis [14] of single-DNA magnetic tweezers experiments on 7.9 kbp DNA molecules estimated G = 40(10) nm and C = 110(5) nm, which would yield G/C = 0.36(09). Although these two ratios are consistent, some caution is required in their comparison. Simulations have shown that elastic constants for deformations at the base-pair level, relevant for the nucleosome, are generally smaller than asymptotic stiffnesses which are obtained for segments of 10–20 base-pairs, relevant for the tweezers data [15].

Elastic rod models have been used in the past to investigate various features of nucleosomes [12, 30–35]. In particular, the structure of nucleosomal DNA has been addressed [12] using a model including, besides twist-bend coupling, a stretching modulus and twist-stretch coupling. The elastic energy was minimized while keeping the twist density fixed to the experimentally determined values of Ref. [28], in order to mimic the interaction of DNA with the histone-proteins. In Ref. [35] minimization of a sequence dependent model was performed, while fixing the base pair orientation in 14 known DNA-histones interaction sites [36]. While partially-constraining the conformation of the nucleosomal DNA along the sequence allows for sharper predictions about its local and sequence-dependent behavior, it may obscure some global features. In particular, our work shows that twist oscillations are an intrinsic feature of bent DNA, rather than an explicit consequence of DNA-protein interactions.

Conclusion –

Summarizing, we have shown that in a coarse-grained model of DNA with asymmetric grooves a bending deformation induces an oscillating excess twist having the form of a standing wave. We devised an approximated energy-minimization scheme, which provides analytical predictions for the shape of bending and twist waves. These are in excellent agreement with the numerical simulations, and show that the induced twist waves have a spatial frequency ω₀, the intrinsic DNA twist-density, and an amplitude which is governed by the radius of curvature and the DNA elastic constants. We also showed that crystallographic X-ray nucleosomal DNA data match our prediction of bend-induced twist waves. In nucleosomes, oscillations in DNA twist and bending are usually attributed to the DNA-protein interactions [28], but our work shows that twist waves are general features of bent DNA. We expect that the same kind of correlation will be observed in other protein-DNA complexes, since twist-bend coupling is a fundamental physical property of the double helix.