Residuals and Diagnostics for Ordinal Regression Models: A Surrogate Approach

Abstract

Ordinal outcomes are common in scientific research and everyday practice, and we often rely on regression models to make inference. A long-standing problem with such regression analyses is the lack of effective diagnostic tools for validating model assumptions. The difficulty arises from the fact that an ordinal variable has discrete values that are labeled with, but not, numerical values. The values merely represent ordered categories. In this paper, we propose a surrogate approach to defining residuals for an ordinal outcome Y. The idea is to define a continuous variable S as a “surrogate” of Y and then obtain residuals based on S. For the general class of cumulative link regression models, we study the residual’s theoretical and graphical properties. We show that the residual has null properties similar to those of the common residuals for continuous outcomes. Our numerical studies demonstrate that the residual has power to detect misspecification with respect to 1) mean structures; 2) link functions; 3) heteroscedasticity; 4) proportionality; and 5) mixed populations. The proposed residual also enables us to develop numeric measures for goodness-of-fit using classical distance notions. Our results suggest that compared to a previously defined residual, our residual can reveal deeper insights into model diagnostics. We stress that this work focuses on residual analysis, rather than hypothesis testing. The latter has limited utility as it only provides a single p-value, whereas our residual can reveal what components of the model are misspecified and advise how to make improvements.

1 Introduction

Ordinal outcomes are prevalent in many research fields, including biological and medical sciences, social and behavioral sciences, and economics and business. For such outcomes, parametric regression models have been widely used to draw conclusions, yielding a large volume of publications. However, the published results, including many of high profile, bear a raised risk of misleading, due to the lack of effective diagnostic tools to check the validity of model assumptions (Zhang, 2011). In fact, any model-based conclusion is questionable if there is no effective way to justify whether or not the assumed model is consistent with the observed data.

Although the importance of checking model assumptions is always stressed in statistical inference, limited attention has been paid to the development of diagnostic tools for ordinal regression models. The challenge arises from the nature of ordinal outcomes. First, due to the discreteness of ordinal outcomes, it is generally difficult to define a residual statistic that has a simple and interpretable reference distribution. Moreover, the label of an ordinal outcome is not a numeric value but an ordered category. To elaborate, for an ordinal variable of four categories, assigning labels {1,2,3,4} is merely for convenience. The equal spacing between the numerals should not be deemed as an indication of the between-category difference being equal numerically. In fact, any order-preserving transformation of the labels (e.g., {1,3,5,7} or {1,2,4,8}) is equally admissible. With these said, the residual defined as the numeric difference between the fitted and observed values, such as Pearson’s residual, is not appropriate for diagnostics of ordinal regression models. Generally, statistical inference should be invariant to the labeling of ordinal outcomes, which makes it even more difficult to appropriately define residuals.

There were very few successful attempts in residual development for ordinal outcomes until recent years. Liu et al. (2009) proposed to collapse ordinal categories into multiple binary outcomes and use the cumulative sums of residuals as considered in Arbogast and Lin (2005). This method results in multiple residuals for a single ordinal outcome, and thus it is not straightforward to interpret. To this end, Li and Shepherd (2012) formally examined the properties of a sign-based statistic (SBS) r^SBS = E{sign(y−Y)} = Pr{y > Y} − Pr{y < Y}, i.e., the difference between two probabilities: the probability of the ordinal variable greater or less than the observed value. This statistic was defined earlier for testing association (Zhang, Wang, and Ye, 2006 and Li and Shepherd, 2010). Li and Shepherd (2012) showed that this statistic can be used as a residual (referred to as the SBS residual hereafter) for model diagnostics. However, the usefulness of this residual heavily relies on its first-moment property (i.e., zero mean under the null hypothesis that the model is specified correctly). This property limits its utility as illustrated below.

Example 1 (Correct specification of the model)

Suppose that the data (x_i, y_i), i = 1, …, n, are generated from the following ordered probit model

$$Pr\{Y\le j\}=\mathrm{\Phi }({\alpha }_j+{\beta }_{1}X+{\beta }_2{X}^2),j=1,2,3,4,$$ (1)

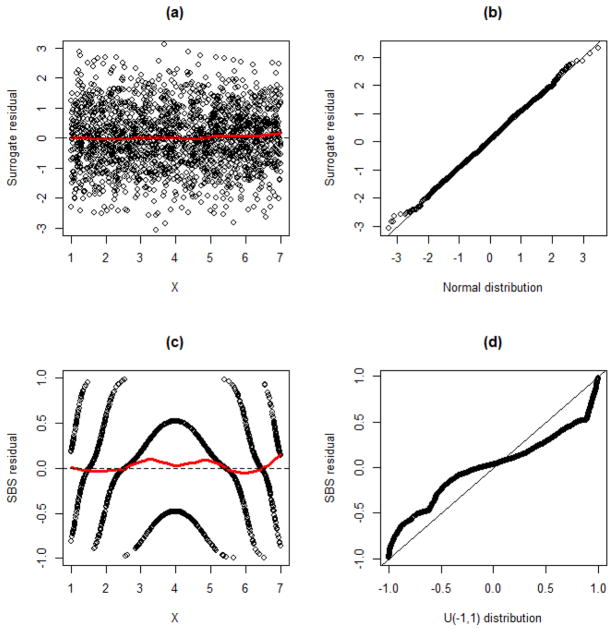
where α₁ = −16, α₂ = −12, α₃ = −8, β₁ = 8, β₂ = −1, and X ~ Uniform(1, 7). We use the true model to fit the simulated data (n = 2000) and obtain the SBS residuals $r_i^{\mathit{SBS}}=\widehat{Pr}\{Y\le y_i-1\}+\widehat{Pr}\{Y\le y_i\}-1=\mathrm{\Phi }({\widehat{\alpha }}_{y_i-1}+{\widehat{\beta }}_1{x}_i+{\widehat{\beta }}_2{x}_i^2)+\mathrm{\Phi }({\widehat{\alpha }}_{y_i}+{\widehat{\beta }}_1{x}_i+{\widehat{\beta }}_2{x}_i^2)-1$. The lower row of Figure 1 presents a residual-by-covariate plot ( $r_i^{\mathit{SBS}}$ versus x_i) and a quantile-by-quantile (QQ) plot (the empirical distribution of $r_i^{\mathit{SBS}}$ versus the uniform distribution on [−1,1]).

Figure 1.

Model diagnostics using our proposed (upper low) and the SBS (lower row) residuals when the model is specified correctly. The figures (a) and (c) are plots of the residuals versus the covariate X (A Loess curve (red solid) is added). The figures (b) and (d) are QQ-plots of the residuals versus the standard normal or the Uniform (−1,1) distribution.

A striking observation is that although the model is specified correctly, diagnostic plots of the SBS residuals display unusual patterns. This property limits the residual’s utility, since diagnostic plots under the null serve as references and thus they are expected not to display any unusual pattern. A fundamental question is: how can we tell whether or not the model is specified correctly, if the reference plots themselves look “abnormal”? This question partially motivates our paper.

We point out that the unusual patterns in Figures 1(c)–(d) may be inevitable if we confine ourselves to the analysis on the discrete space of the data. Specifically, the patterns in Figures 1(c)–(d) stem from the null properties of $r_i^{\mathit{SBS}}$:

• (℘-1)The conditional distribution (e.g., variance/range) of the residual variable $R_i^{\mathit{SBS}}\mid X_i$ varies across the values of X_i (see Figure 1(c)).
• (℘-2)The unconditional distribution of $R_i^{\mathit{SBS}}$ does not have an explicit form (see Figure 1(d)), and it may vary depending on the distribution of X.

The above properties are different from the null properties of the common residuals defined for continuous responses, where

• (℘-0)Both the conditional (on X) and unconditional distributions of the residuals have an explicit form, not depending on X (at least asymptotically).

This property provides a theoretical foundation for model diagnostics. It ensures that if the null hypothesis holds, diagnostic plots should look similar to the upper row of Figure 1, which can then serve as the benchmark in our examination.

Motivated by the problems as seen in Figures 1(c)–(d), we propose a surrogate approach to defining residuals for ordinal outcomes. The idea is to transform the problem of checking the distribution of an ordinal outcome Y to that of checking the distribution of a continuous outcome S, which we call a surrogate variable. The variable S is defined by sampling conditionally on the observed ordinal outcomes (y₁, …, y_n), according to a hypothetical probability model that is coherent with the assumed model for Y. The continuous variable S serves as a “surrogate” of the original ordinal variable Y. A residual variable is defined based on S, i.e., R ≜ S − E₀(S) where the expectation is calculated under the null. In short, the surrogate idea pursues conditional sampling so that we can work on the continuous space of the simulated data, rather than the discrete space of the original data.

We demonstrate in this article that the surrogate approach offers an effective way to perform model diagnostics for ordinal outcomes. For the proposed residual, we study its theoretical and graphical properties. We show that the residual has the property (℘-0), similar to that of the common residuals for continuous outcomes. For a general class of cumulative link regression models, our numerical studies demonstrate that our residual has power to detect misspecification with respect to 1) mean structures; 2) link functions; 3) heteroscedasticity; 4) proportionality; and 5) mixed populations. The key is that, in addition to the first-moment property as seen in the SBS residual, we can make use of the full distributional information of our residual to perform model diagnostics. This property broadens the list of diagnostic tools we can apply and may reveal additional insights into model diagnostics, as illustrated in our analysis of the Study of Addiction: Genetics and Environment (SAGE).

Our residual can also be used to develop new goodness-of-fit tests. But the focus of our work is not on hypothesis testing, which is limited as it only yields a single p-value. A strength of our residual is that it offers insights into what components of the model are misspecified and advises how to improve model fit. A discussion on goodness-of-fit tests versus residual analysis is deferred to the last section.

The surrogate method shares the same spirit as the jittering technique for categorical data analysis (Stevens, 1950; Machado and Silva, 2005; Hong and He, 2010), where an independent noise variable is added to “smooth” the discrete outcome. We show in Section 7 that the jittering is a special case of the surrogate method, and it helps develop residuals for general models.

2 Surrogate approach

2.1 An illustrative example

To illustrate the surrogate idea, we use as a toy example the probit model for binary outcomes. Consider a binary random variable Y following the assumed distribution

$$Pr\{Y=1\}=1-Pr\{Y=0\}=\mathrm{\Phi }(\alpha +X\beta ),$$ (2)

where X is a covariate. The discrete Y can be viewed as sampled from a latent variable Z ~ N(α + Xβ, 1), according to the rule that Y = 0 if Z ≤ 0 and Y = 1 otherwise. In our surrogate framework, the latent variable concept induces a joint distribution f_a(y, z) of the observable Y and a hypothetical continuous variable Z. We can make use of this joint distribution to generate a surrogate variable, denoted by S, to perform model diagnostics.

Specifically, for the assumed model (2), we define a new variable S as following the distribution ∫f_a(z | y)f₀(y)dy. A sample of S can be drawn from the conditional distribution f_a(z | y), i.e.,

$$S~\{\begin{array}{ll}Z\mid Z\le 0\hfill & \text{if}Y=0,\hfill \\ Z\mid Z>0\hfill & \text{if}Y=1,\hfill \end{array}$$

where Z | Z ≤ 0 (or Z | Z ≥ 0) has a left-truncated (or right-truncated) distribution of N(α + X β, 1), truncated at 0. Such a sampling procedure is illustrated in Figure 2 (Supp.Mtl., Part A including all the figures hereafter), where an s value is drawn with the probability proportional to the truncated curve to the right or the left of the vertical dotted line, depending on the observed value of y. Note that the entire curve, piecing together the two truncated curves, depicts the density function of the latent variable Z. A key observation is that if the assumed model (2) agrees with the true model, the entire curve also represents the density function of the unconditional distribution of S. In other words, S is identically distributed as the latent variable Z, i.e., S ~ N(α + X β, 1). This fact suggests that we may use the continuous variable S as a surrogate of the binary variable Y in model diagnostics. In fact, on the continuous scale, we can define a residual variable as R = S − E₀(S) = S − E(Z) = S − (α + Xβ). Under the null, R follows the N(0, 1) distribution, which provides a theoretical foundation of using R for diagnostics.

The concept of latent variables offers a natural way to find surrogate variables for a general class of ordinal regression models (Section 3). The surrogate idea, nevertheless, is broader. It does not necessarily rely on latent variables. For example, the jittering technique can also be used to produce surrogate variables for more general models (Section 7). Broadly speaking, the surrogate idea is to 1) find a new variable S based on the original discrete outcome Y and a hypothetical distribution that is consistent with the assumed model; and 2) conduct inference using a sample of S. We state the general principle of our surrogate approach below.

2.2 General principle

Let f₀(y) denote the true distribution of a categorical outcome Y and f_a(y) the assumed distribution of Y. Our goal is to check whether or not f_a(y) is consistent with f₀(y) which is represented by the observed data {y₁, …, y_n}. The surrogate approach can be generally stated as follows:

1. Find an assumed joint distribution f_a(y, z) for the original outcome Y and a hypothetical continuous random variable Z such that its marginal distribution on Y is f_a(y), i.e., ∫f_a(y, z)dz = f_a(y).

2. Define a variable S following the distribution ∫f_a(z | y)f₀(y)dy/m_c (m_c is a normalizing constant), and draw a random sample {s₁, s₂, …, s_n} of S.

3. Compare the empirical distribution of{s₁, s₂, …, s_n} with the reference distribution of Z, i.e., f_a(z) = ∫f_a(y, z)dy. The discrepancy between the two distributions reflects the inconsistency between f_a(y) and f₀(y).

In Step (I), the only requirement is that the marginal distribution of an assumed joint distribution f_a(y, z) (defined by investigators) should be consistent with f_a(y) (i.e., the model under examination). It does not require that f_a(y, z) be derived by a particular procedure. The hypothetical variable Z is not required to have a practical interpretation. We will show that the techniques of latent variables and jittering can be used to find such a hypothetical distribution f_a(y, z). In Step (II), a sample of S is obtainable, since a sample {y₁, y₂, …, y_n} from the distribution f₀(y) is available and the conditional distribution f_a(z | y) is completely known. Step (III) is justified by a simple but fundamental result as below. We stress that the feasibility of Step (III) depends on the requirement in Step (I) being satisfied.

Theorem 1

If the assumed distribution f_a(y) of Y is the same as the true distribution f₀(y), then the surrogate variable S follows the same distribution as Z, i.e., S ~ ∫f_a(y, z)dy, provided that the requirement in Step (I) is met.

The principle is to transform the problem of checking the discrete distribution of Y to that of checking the continuous distribution of S. This method is useful when it is not convenient to find a reference distribution for Y in ordinal regression models.

3 Residual for ordinal regression models

3.1 Definition

Consider an ordinal variable Y that has J categories {1, 2, …, J}, with order 1 < 2< ⋯ < J. Suppose that the assumed model for Y is in a class of cumulative link regression models

$$G^{-1}(Pr\{Y\le j\})={\alpha }_j+f(\mathit{X},\mathit{\beta }),$$ (3)

where G is a continuous cumulative distribution function, the intercept parameters −∞ = α₀ < α₁ < ⋯ < α_J−1 < α_J = ∞, f (X, β) is a function of the covariates X and the parameter β. Specific but commonly used cases of the model (3) include: logistic (odds) model with the logit link h(γ) = G⁻¹(γ) = log(γ/(1 − γ)); probit model with the normal link h(γ) = Φ(γ); hazards model with the complementary log-log link h(γ) = log(−log(1 − γ)) or the negative log-log link h(γ) = −log(−log(γ)); relative risk model with the log link h(γ) = log(γ). Other less known models in specialized fields, such as economics or political science, include the Pregibon model (Koenker and Yoon, 2009) and the scobit model (Nagler, 1994).

We propose a residual for the ordinal regression model (3) using the surrogate approach. Specifically, the concept of latent variables induces a joint distribution of Y and a hypothetical variable Z = −f(X, β) + ε where ε follows the distribution G. The joint distribution is determined by setting Y ≜ j if α_j−1 < Z ≤ α_j (j = 1, …, J). Then, the marginal distribution of Y is the same as the distribution specified by the assumed model (3) (see Step (I) in Section 2.2). We let S be a random variable following the conditional distribution of Z given Y (see Step (II)). More precisely, S follows a truncated distribution obtained by truncating the distribution of Z = − f(X, β) + ε using the interval (α_y−1, α_y) given Y = y. We define

$$R=S-E_0\{S\mid \mathit{X}\}=S-E\{Z\mid \mathit{X}\}=S+f(\mathit{X},\mathit{\beta })-{\int }_{-\infty }^{\infty }u\mathrm{d}G(u)$$ (4)

as our residual variable (see Step (III)). In practice, given the data (x_i, y_i) and a fitted model, we estimate the conditional distribution Z_i | Y_i = y_i by plugging in the parameter estimates β̂ and α̂_j’s. From the distribution f̂_a(z |y_i), we randomly draw a sample s_i. Then, the i-th residual is ${\widehat{r}}_i=s_i+f({\mathit{x}}_i,\widehat{\mathit{\beta }})-{\int }_{-\infty }^{\infty }u\mathrm{d}G(u)$. Note that r̂_i is not a realization of R ≡ R_α,β, but of the random variable R̂_α̂,β̂. If α̂ → α and β̂ → β in probability, then R̂_α̂,β̂ → R_α,β in distribution and properties of R_α,β apply to R̂_α̂,β̂ asymptotically. For the ease of presentation, we show in Section 3.2 theoretical results for R_α,β and provide parallel results for R̂_α̂,β̂ in Part D of Supplementary Materials.

Remark 1

We assume throughout this paper that the moments of the distribution G exist as needed. If not, we can define R = S + f(X, β) − G⁻¹(1/2) as the residual variable and its properties can be established similarly.

3.2 Theoretical properties

In this subsection, we examine the theoretical properties of the surrogate variable S and the residual variable R. We justify the validity of using R for model checking.

First, we derive the distribution of the surrogate variable S. Suppose the true model for Y is

$$G_0^{-1}(Pr\{Y\le j\})={\stackrel{\sim }{\alpha }}_j+f_0(\mathit{X},\stackrel{\sim }{\mathit{\beta }})$$ (5)

where G₀ is a continuous cumulative distribution function, the intercept parameter −∞ = α̃₀ < α̃₁ < ⋯ < α̃_J−1 < α̃_J = ∞, f₀(X, β̃) is a function of the covariates X and the parameter β̃. Then, the distribution of S in (4) is

$$Pr\{S\le c\}=G_0({\stackrel{\sim }{\alpha }}_{k-1}+f_0(\mathit{X},\stackrel{\sim }{\mathit{\beta }}))+\frac{G_0({\stackrel{\sim }{\alpha }}_k+f_0(\mathit{X},\stackrel{\sim }{\mathit{\beta }}))-G_0({\stackrel{\sim }{\alpha }}_{k-1}+f_0(\mathit{X},\stackrel{\sim }{\mathit{\beta }}))}{G({\alpha }_k+f(\mathit{X},\mathit{\beta }))-G({\alpha }_{k-1}+f(\mathit{X},\mathit{\beta }))}\times \{G(c+f(\mathit{X},\mathit{\beta }))-G({\alpha }_{k-1}+f(\mathit{X},\mathit{\beta }))\},$$ (6)

for any arbitrary but fixed c such that α_k−1 ≤ c < α_k, 1 ≤ k ≤ J. Equivalently,

$$Pr\{S\le c\}=Pr\{Z_0\le {\stackrel{\sim }{\alpha }}_{k-1}\}+\frac{Pr\{{\stackrel{\sim }{\alpha }}_{k-1}<Z_0\le {\stackrel{\sim }{\alpha }}_k\}}{Pr\{{\alpha }_{k-1}<Z\le {\alpha }_k\}}\times Pr\{{\alpha }_{k-1}<Z\le c\},$$ (7)

where the random variable Z₀ = −f₀(X, β̃)+ ε₀ and ε₀ ~ G₀. Equations (6)–(7) show that the distribution of S is determined jointly by the assumed and true models for Y. When the two models agree, we have the result below.

Theorem 2

If the assumed model (3) agrees with the true model (5) (i.e., α = α̃, β = β̃, G = G₀, f = f₀), then the following results hold

1. The surrogate variable S follows the same distribution as Z, i.e., S | X ~ −f(X, β) + ε.

2. The residual variable R, independent of X, follows the distribution G(c+ ∫u dG(u)), i.e., Pr{R ≤ c | X} = Pr{R ≤ c} = G(c + ∫u dG(u)).

Theorem 2 immediately yields the following results useful for model diagnostics.

Theorem 3

If the assumed model (3) agrees with the true model (5) (i.e., α = α̃, β = β̃, G = G₀, f = f₀), then the residual variable R has the following properties:

1. (Symmetry around zero) E{R | X} = 0.

2. (Homogeneous variance) V ar{R | X} is a constant, not depending on X.

3. (Explicit reference distribution) sup_c∈ℝ | Q_n(c; R₁, …, R_n) − G(c+ ∫u dG(u)) |→ 0 almost surely as n → ∞, where $Q_n(c;R_1,\dots ,R_n)=\frac{1}{n}{\sum }_{i=1}^{n}I(R_i\le c)$ is the empirical cumulative distribution function of {R₁, …, R_n}.

Theorem 3 provides a theoretical foundation of using R for diagnostics purposes. Our residual has several advantages over the SBS residual.

• (A1)Our residual is a continuous variable, which allows us to make use of all diagnostic tools developed so far for continuous outcomes. Conditional on X, the SBS residual is still a categorical variable, which can result in “strips” in graphic plots and make visual examination difficult (see Figure 1(c)).
• (A2)The null distribution of our residual is independent of X(Theorems 2(b)). This is a desirable feature for visual check of diagnostic plots (see Figure 1(a)). The null distribution (and variance) of the SBS residual depends on X and it varies across the values of X (see Figure 1(c)), which limits its utility.
• (A3)Under the null, the empirical distribution of our residuals approximates an explicit distribution G(c + ∫u dG(u)), which is related to the link function. The SBS residual does not have an explicit null distribution (see Figure 1(d)).

The advantages (A1)–(A3) will be elaborated in detail in Section 3.4, and demonstrated in the analysis of simulated and real data sets in a variety of settings.

Proposition 1 (Monotonicity)

If we observe x_k = x_j and y_k < y_j, then r_k < r_j almost surely.

Proposition 1 shows that although our residual is randomly drawn from a hypothetical distribution, it is monotonic with respect to the observed y. This property holds no matter whether the model is specified correctly or not. We note that if an ordinal variable were treated as multinomial with the ordering ignored, we would have lost 1) the direction of the data and the order-preserving property as seen in Proposition 1; and 2) the nature interpretation of our residual that its sign and size reflect, respectively, the direction and deviation from the “center” of data.

Remark 2

The properties presented so far concern the residual variable R ≡ R_α,β. In Part D of Supplementary Materials, we state parallel results for R̂_α̂,β̂, where α̂ = α + o_p(1) and β̂ = β + o_p(1) are consistent estimates. The moment and distribution results remain the same except a vanishing term o(1).

3.3 Graphical properties

We use numerical examples to examine graphical properties of our proposed residual, when the model is specified correctly or misspecified with respect to the mean structure or link function. The examples show that our residual yields desirable graphical presentation, similar to diagnostic plots for continuous responses. To be consistent, we use the probit model throughout the examples. The discussions and conclusions, nevertheless, apply to general models in (3).

Example 1 (Continued)

When the model is specified correctly as seen in (1), we obtain our residuals r̂_i. The corresponding residual-by-covariate plot and QQ plot are shown in the upper row of Figure 1. The plots do not exhibit any unusual pattern, which is what we anticipate to see in the absence of model misspecification. This graphical property is desirable, compared to the unusual patterns the SBS residuals display in the lower row of Figure 1.

Example 2 (Misspecification of the mean structure)

Suppose that the data (x_i, y_i) are generated from the ordered probit model (1) in Example 1. To examine diagnostic power of our residual when the mean structure is misspecified, we do not include the quadratic term X² in the assumed model. Instead, we fit the following model with only a linear term of X

$$Pr\{Y\le j\}=\mathrm{\Phi }({\alpha }_j+{\beta }_{1}X),j=1,2,3,4.$$

The residual-by-covariate relationship is plotted in Figure 3(a). This scatter plot exhibits a clear quadratic shape, indicating missing of a quadratic term X² in the mean structure. Figure 3(b) shows that the SBS residuals also captures the quadratic pattern, although they cluster in strips.

Example 3 (Misspecification of the link function)

Suppose that the data (x_i, y_i) are generated from the following model

$$Pr\{Y\le j\}=G({\alpha }_j+{\beta }_{1}X+{\beta }_2{X}^2),j=1,2,3,4,$$

where the link function G(·) is the cumulative distribution function of the log-normal distribution with the location and scale parameters equal to 0 and 1, respectively. Such G is a right-skewed (or positively skewed) distribution. To compare residuals when the link function is misspecified, we use the probit link function Φ(·) instead for model fitting. Both our residual-by-covariate plot and QQ plot in Figures 4(a)–(b) show a heavy tail on the positive side, which indicates that the assumed model fails to capture the skewness of the true link function. For comparison, we present the SBS residuals in Figures 4(c)–(d). Although the plots exhibit specific patterns, we can not conclude with misspecification of the link function, in light of the properties (℘-1) and (℘-2) of the SBS residual as summarized in the introduction.

3.4 Difference between the surrogate and SBS residuals

Unlike the SBS residual defined directly on realizations of Y, our approach pursues conditional sampling based on Y and obtains a new sample set of S. Although such conditional sampling does not bring in “new” information, the resulting residual has properties useful for model diagnostics. In what follows, we provide further insights into the difference between the two residuals.

The key feature of the SBS residual is that its conditional expectation $R_i^{\mathit{SBS}}\mid X_i$ is zero under the null hypothesis, which forms the theoretical foundation for $R_i^{\mathit{SBS}}$ to serve as a tool in model diagnostics. Nevertheless, the SBS residual carries Properties (℘-1), (℘-2) and (℘-3) (below)

(℘-3) The conditional distribution of $R_i^{\mathit{SBS}}\mid X_i$ is discrete with J categories.

These properties (briefly speaking, discreteness and variable variance/range/distribution) limit its utility in model diagnostics. Taking Example 1 (where the null hypothesis is true) for instance, conditional on X_i = 1, the residual $R_i^{\mathit{SBS}}$ takes four possible values ω₁ − 1, 2ω₁ + ω₂ −1, −0.84 and 0.16 (0< ω₁, ω₂ < 10⁻⁶), with a range of (ω₁ − 1, 0.16) and variance of 0.1344; conditional on X_i = 2, $R_i^{\mathit{SBS}}$ takes different values ω₃ −1, 0.5, −0.5 and 1 −ω₄ (0 < ω₃, ω₄ < 10⁻³), with a different range of (ω₃ −1, 1 − ω₄) and variance of 0.25. This example shows that the variance/range/distribution depends on the value of X. This heterogeneity in variance/range/distribution has been observed in Figure 1(c), where the SBS residuals exhibit an up-and-down pattern even when the model is specified correctly. To illustrate its unconditional distribution under the null is also variable, we present in Figure 5(a) a QQ-plot using the same setting as Example 1 except restricting the range of X to [3, 5]. The QQ plot is quite different from that in Figure 1(d) where the range of X is [1, 7]. The variability of its unconditional distribution under the null (Property (℘-2)) prevents us from using QQ-plots. To use the SBS residual, we conclude that we should limit ourselves to the inspection of the zero-(conditional)-mean property. When examining plots of the SBS residuals, we should not take any unusual pattern not related to such a property as an indication of model misspecification.

Unlike the SBS residual, our residual is a continuous variable carrying the property (℘-0). Instead of being restricted to the zero-(conditional)-mean property, we are able to examine its entire conditional or unconditional distribution, including its variance, skewness, mode, quantiles and other distributional properties beyond the first moment. This property allows us to use almost all diagnostic tools developed for continuous responses, including boxplots, QQ-plots, density plots, and existing goodness-of-fit measures, such as the Kolmogorov-Smirnov distance. So we have broadened the scope of diagnostic tools and increased the residual’s utility in model diagnostics. Furthermore, as opposed to the SBS residual whose null (reference) distribution is implicit and variable, the null distribution of our residual has an explicit and invariant form. Due to this property, the deviations observed in our diagnostic plots not only indicate model misspecification, but also advise what components of the model are misspecified and how to make improvements. These advantages have been observed in Examples 1–3 and will be further illustrated in Sections 4–6.

Remark 3

Since the null distribution of the SBS residual is implicit and variable, we can simulate its null distribution from the assumed model and compared it with its empirical distribution in a QQ-plot. However, this QQ-plot is not informative for the behalf of the SBS residual; see an example in Part E of Supplementary Materials. We stress that an advantage of our approach is that to obtain the null distribution, we do not have to simulate from the assumed model to estimate the null distribution of the residual statistic. The reason is that the null distribution of our residual is (asymptotically) invariant, and it has an explicit and known form.

The result below shows that the SBS and the expectation-based residuals can be viewed as “averaged-out” outcomes of our residual.

Proposition 2

If the assumed model is of the form (3), then the following conclusions hold

1. The SBS residual

   $$\begin{array}{l}{r}^{\mathit{SBS}}=Pr\{y>Y\}-Pr\{y<Y\}\\ =G\left(min\{R\mid y\}+\int \mathit{udG}(u)\right)+G\left(max\{R\mid y\}+\int \mathit{udG}(u)\right)-1.\end{array}$$

   The conditional expectation of this residual satisfies that E(R^SBS | X) = 0, and thus the unconditional expectation E(R^SBS) = 0.

2. The expectation-based residual defined as r^E = E(R | y) satisfies that E(R^E |X) = 0, and thus the unconditional expectation E(R^E) = 0.

4 More examples

In this section, we use numerical examples to further demonstrate that our residual is a useful diagnostic tool for checking important aspects of model specification including heteroscedasticity, proportionality, and missing covariates/mixed populations.

Heteroscedasticity

When regression models are used to make inference, such as in economic and social studies, one of the issues that often raise inference concerns is heteroscedasticity, which refers to the situation where the error term is not of a constant variance. The existence of heteroscedasticity can bias the statistical inference, leading to improper confidence intervals and testing results. It is critical to identify heteroscedasticity, if its effect is non-ignorable. Although this issue has been studied extensively for continuous outcomes, it has not been explored for ordinal outcomes.

In the setting of Section 3.1, heteroscedasticity means that instead of model (3), the data follow

$$G^{-1}(Pr\{Y\le j\})=\{{\alpha }_j+f(\mathit{X},\mathit{\beta })\}/{\sigma }_{\mathit{X}},$$ (8)

where the unidentifiable parameter σ_X relies on the value of X. Note if σ_X ≡ σ = 1, then there is no heteroscedasticity and model (8) reduces to model (3). We use the example below to illustrate how our residual can be used to detect heteroscedasticity.

Example 4

Suppose the data (x_i, y_i), i = 1, …, n, are generated from the following ordered probit model with heteroscedasticity

$$Pr\{Y\le j\}=\mathrm{\Phi }\{({\alpha }_j+\beta X)/{\sigma }_X\},j=1,2,3,4,5,$$

where α₁ = −36, α₂ = −6, α₃ = 34, α₄ = 64, β = −4, X ~ U(2, 7) and the heteroscedasticity parameter σ_X = X². We fit a homoscedastic model to the simulated data. The surrogate residuals in Figure 6(a) display an increasing variability as X increases, which is a clear indication of heteroscedasticity. In fact, the varying variance implies that the link function has a varying scale parameter, i.e., $G_0^{-1}(·)\equiv {\sigma }_{\mathit{X}}{G}^{-1}(·)$ as seen in model (8). The SBS residuals in Figure 6(b) may not suggest heteroscedasticity due to the property (℘-2).

Proportionality

The proportional assumption in model (3) requires that the functional form of X, i.e., f(X, β), remains the same for all the categories j, which implies that X has the same effect on the (scaled) cumulative probability G⁻¹ (Pr{Y ≤ j}). Such an assumption is adopted widely in practice to achieve parsimonious models. We show in the example below that our surrogate idea offers a simple way to check this assumption.

Example 5

Suppose the data (x_i, y_i), i = 1, … n, follow the probit model below

$$Pr\{Y\le j\}=\mathrm{\Phi }({\alpha }_j+{\beta }_{1}X),j=1,2,\text{and}Pr\{Y\le j\}=\mathrm{\Phi }({\alpha }_j+{\beta }_{2}X),j=3,4,5.$$

It is of interest to check if it is reasonable to assume β₁ = β₂ (proportionality). Based on Theorem 2, we can generate a surrogate variable S₁ that follows the distribution N(−β₁X, 1) and S₂ that follows N (−β₂X, 1), both conditional on X. We define a difference variable D = S₂− S₁, which then satisfies D | X ~ N ((β₁ − β₂)X, 2). If the proportional assumption β₁ = β₂ holds, D should be independent of X. Thus, it is sensible to check the D-versus-X plot to see if there is any trend. An illustrative plot is shown in Figure 7 for a non-proportional setting where β₁ = 1 and β₂ = 1.5 (α₁ = −1.5, α₂ = 0, α₃ = 1, α₄ = 3). In this case, β₁ −β₂ = −0.5 ≠ 0 and D |X ~ N(−0.5X, 2). This non-proportionality is captured by the D-versus-X plot in Figure 7. The Loess curve is observed far from being flat, which implies that β₁ − β₂ ≠ 0. In fact, the linear descending trend of the Loess curve suggests that the difference of the two functional forms f₁(X, β₁) − f₂(X, β₂) is linear in X and β₁ < β₂.

Missing covariates/Mixed populations

Samples collected for scientific or business studies are often drawn from mixed populations (or multiple subpopulations), and this issue needs to be addressed by including indicator variables, such as sex, race and economic status, in statistical models. Because of possible heterogeneity among the subpopulations, it is crucial or even mandatory to adjust important covariates in genetic, economic, or behavioral studies. The example below shows that our residual can be used to detect missing indicator covariates if the heterogeneity effect is not ignorable.

Example 6

Suppose that the data (x_1i, x_2i, y_i), i = 1, …, n, are generated from the following ordered probit model

$$Pr\{Y\le j\}=\mathrm{\Phi }({\alpha }_j+{\beta }_1{X}_1+{\beta }_2{X}_2),j=1,2,3,4,$$

where α₁ = −2, α₂ = 0, α₃ = 2, β₁ = 1, β₂ =−7, X₁ ~ U(1, 0.3²) and X₂ ~ Bernoulli(0.5). Here, X₂ is an indicator for subpopulations. We ignore X₂ and fit the model Pr{Y ≤ j} = Φ(α_j + β₁X₁) to the simulated data. The density curve for our residuals in Figure 8(a) shows a bimodal distribution, which indicates that there is a residual effect of mixed populations not captured by the assumed model. Note that the null distribution is standard normal and unimodal.

For comparison, we present the density plot of the SBS residuals (black solid) in Figure 8(b). Although the density curve shows multiple modes, there is no ground for interpreting it as an indication of model misspecification, due to the property (℘-2). To see this, we plot the density curve (red dashed) of the SBS residual when the model is specified correctly. Similar to Example 1, the null distribution of the SBS residual exhibits unusual patterns, i.e., multiple modes in this example. The observation here reinforces our statement that we should limit ourselves to examining whether or not the SBS residual has zero mean and avoid interpreting patterns unrelated to the mean property. For instance, when X₂ is not included in the assumed model, we calculate $E(R_i^{\mathit{SBS}})=0.005$ (displayed by a vertical dotted line in Figure 8(b)), which is very close to zero and can hardly be deemed as an indication of model misspecification.

5 Diagnostics based on multiple sampling

The patterns as observed in our diagnostic plots (e.g., Figure 3(a), Figure 4(a)–(b)) result from a combination of two sources of errors: modeling error and simulation error. The modeling error is due to the difference between the assumed model F_a and the true model F₀, which is of our interest. The simulation error is due to the conditional sampling from F_a. If this error is too large, we may observe diagnostic plots vary from one sampling to another, and an unusual pattern may appear.

If the sample size is sufficiently large (e.g., the SAGE study), the simulation error is negligible compared to the modeling error. Thus, any unusual patter observed in diagnostic plots is mostly due to the modeling error. Otherwise, we propose to bootstrap K copies of the empirical distributions of the residual, denoted by $Q_{n,k}^{\ast }(t)\equiv Q_n(t;R_{1,k}^{\ast },\dots ,R_{n,k}^{\ast })$, to account for the variability introduced by the conditional sampling. The task is to examine the discrepancy between the bootstrap empirical distributions { $Q_{n,1}^{\ast }(t),\dots ,Q_{n,K}^{\ast }(t)$} and the reference distribution G(t). This can be achieved by using visualization methods, goodness-of-fit measures and testing procedures. The details can be found in Part B of Supplementary Materials.

6 Analysis of the SAGE data

We apply our residual to model diagnostics in the analysis of the Study of Addiction: Genetics and Environment (SAGE). The main goal is to identify novel genetic factors that contribute to the alcohol and other substances addiction through a large-scale genome-wide association study. The SAGE data set includes 4121 European and African Americans from three sources: the Collaborative Study on the Genetics of Alcoholism (COGA), the Family Study of Cocaine Dependence (FSCD), and the Collaborative Genetic Study of Nicotine Dependence (COGEND). Each subject was genotyped at 1 million markers and diagnosed using a number of DSM-IV symptoms for alcohol and other substances. See Bierut et al. (2010) for more details.

For alcohol addiction, we focused on an ordinal outcome that measures the severity of alcohol symptoms (no, mild, moderate, and severe). We identified a single-nucleotide polymorphism (SNP) rs958331, located on the gene CARD11, as a potential genetic risk factor. Used in our initial analysis is an ordered probit model, which includes environmental covariates such as gender, race (European or African) and study (COGA, FSCD, or COGEND), all in linear terms. In what follows, we illustrate how to use our residual to check, understand, and improve model fitting. We also discuss its utility in comparison with the SBS residual.

Since the covariates are all categorical, scatter plots are not suitable for showing residual-by-covariate association. Instead, we examine boxplots and density plots, as illustrated in Figure 9 for the covariate gender (male=1 and female=2). The boxplot in Figure 9(a) reveals that the median of the SBS residual is close to zero in both male and female groups. Further calculation shows that its means are 0.006 and 0.001 for the two groups. Since the two mean values are very close to zero, we may conclude that the SBS residual does not yield an indication of model misspecification. Again, in view of the property (℘-1), the distinct residual distributions in the two groups, as observed in Figure 9(b), should not be taken as evidence of model misspecification.

For our residual, we have justified the validity of using its full distributional information, including variance and quantiles, to check model assumptions. For example, the boxplot in Figure 9(c) shows that our residual has similar distributions in male and female groups, while the female group has slightly greater variability. Figure 9(d) shows that the residual distributions in both groups (solid and dashed lines) are, in overall, close to the standard normal distribution (dotted line). However, a close look at Figure 9(d) reveals that the residual distribution in each group may be in fact a mixture distribution, although this mixture effect is mild. There may exist some other covariates that need to be adjusted. Our follow-up analysis shows that including the age effect in the model alleviates the mixture effect in the residual distribution. Taking the male group as an example, the Kolmogorov-Smirnov distance between the residual distribution and the standard normal distribution is reduced by 18.8%, and the p-value of the Kolmogorov-Smirnov test increases to 0.13, compared to a p-value of 0.03 for the initial model. Besides statistical evidence, another reason for making this adjustment is that the age effect is likely to influence alcohol dependence and thus is often of interest in addiction studies.

The updated model shows a statistically significant association between the age and alcohol addiction. Given the residue-by-age plots in Figure 10, we see that the points, to the right of the vertical dashed line, have a positive mean shift. These points represent the subjects older than 65. This pattern remains even when higher orders of age are included in the model, which suggests that this elder group may systematically follow a different alcohol addiction mechanism. We therefore exclude them from subsequent analysis. The updated residue-by-age plots are shown in Figure 11.

We use goodness-of-fit tests to see if the revised model better fits the data. For the initial model, our surrogate, Lipsitz et al.’s and Fagerland-Hosmer methods yield p-values of 0, 8.9 × 10⁻⁴⁵ and 8.3 × 10⁻⁷⁷, respectively. The p-values become 0, 0.07 and 1.1 ×10⁻²⁹ after applying model adjustments suggested by our residual analysis. The increase of p-values confirms the model improvement. But the latter p-values may suggest some lack of fit. We note that the face value of a p-value should not be over-interpreted – a small p-value may not necessarily indicate a serious violation of model assumptions, when the sample size is as large as 3380 in the SAGE case.

Our further examination shows that the lack of fit is possibly due to modeling the “study” variable as a covariate in an attempt to build an overarching model for all the three studies. This argument is evidenced by Figure 12. Specifically, to scrutinize the proportionality assumption, we collapse the ordered probit model into separate binary models. The proportionality assumption essentially assumes that the regression coefficients (estimates tabulated in Table 1) are the same across all the binary models. Similar to Example 5, we generate surrogate variables S₁ and S₃ for the models for Pr{Y ≤ 1} and Pr{Y ≤ 3}, respectively. Then, the variable D = S₃ − S₁ satisfies D | X ~ N ((β₃ − β₁)X, 2), and under the null (β₃ = β₁), D is independent of X. Plotted in Figure 12(a) is D versus a study indicator variable “COGEND”. The descending regression line suggests dependence of D on the study, which makes the proportionality assumption questionable. To examine heteroscedasticity among the studies, we plot in Figure 12(b) our residual versus the covariate study. The boxplots show that the residuals from the “COGEND” study have a much smaller variance compared to those from another two studies, which suggests that the “COGEND” study could be different systematically. To summarize, the issues of proportionality and heteroscedasticity are present for the overarching model we build for all the three studies. These issues are resolved if separate models are built for each study and stratified analysis is conducted. The study-specific inference can then be combined by meta-analysis to achieve a synthesized conclusion (Liu, Liu, and Xie, 2015).

7 Residual for general models

The surrogate method is also useful for defining residuals for general models by using the jittering technique. Suppose that the assumed model for an ordinal outcome Y is

$$Y~F_a(y;\mathit{X},\mathit{\beta }),$$ (9)

where F_a(·) is a discrete cumulative distribution function. This model is broad enough to cover virtually all parametric and nonparametric models. For such a general model, we can define a surrogate variable S using either of the following ways:

1. Jittering on the outcome scale. Let S | Y = y ~ U(y, y + 1).

2. Jittering on the probability scale. Let S | Y = y ~ U(F_a(y −1), F_a(y)).

Similar jittering strategies to (A) or (B) can be found in Machado and Silva (2005), Hong and He (2010), and Dunn and Smyth (1996). In both cases of (A) and (B), a residual variable is defined as R = S − E₀{S | X}, where the expectation E₀ is calculated under the null hypothesis F_a ≡ F₀, i.e., the assumed model F_a agrees with the true model F₀(y; X, β). The theorem below summarizes the properties of R.

Theorem 4

If the assumed model is of the form (9), then the residual variable R defined in (A) or (B) has the following properties: (a) For the cases of (A) and (B), the conditional expectation E{R | X} = 0 holds if F_a ≡ F₀. (b) For the case of (B), the conditional distribution R | X ~ U(−1/2, 1/2) holds if F_a ≡ F₀.

Theorem 4(a) shows that the residuals defined in (A) and (B) both have the zero-mean property under the null hypothesis. Therefore, either of them can be used for model diagnostics in a similar way to the SBS residual. Second, Theorem 4(b) shows that the residual in (B) has an additional property; that is, its distribution has an explicit form and it remains homogeneous across all values of X under the null. Such a property ensures the validity of examining the full distributional information of the residual, as demonstrated throughout the paper.

Proposition 3

For the case of (B), the conditional expectation E{R | Y, X} is proportional to the SBS residual R^SBS, i.e., R^SBS = 2E{R | Y, X}.

Proposition 3 reveals that twice the conditional expectation of R in (B) is exactly equal to R^SBS, which basically says that the SBS residual is an averaged-out outcome of our surrogate residual. A similar argument has been made in Proposition 2 for cumulative link regression models.

8 Discussion

In this article, we have proposed a surrogate approach to defining residual for ordinal outcomes. Our theoretical and numerical studies have demonstrated that in addition to the zero-mean property, it is valid and effective to use the entire distributional information of our residual to perform model diagnostics. The examples in a variety of settings show that our residual has power to detect misspecification of many important components of ordinal regression models including mean structures, link functions, heteroscedasticity, proportionality, and mixed populations. Our residual can be used in a similar way to the common residual for ordinary linear regression models. It broadens the set of diagnostic tools in the sense that we can use almost all diagnostic techniques developed for continuous responses. An effective use of the tool set can help us gain deep insights into model fitting as illustrated in the SAGE data modeling. We conclude the paper with a few remarks related to our method.

Choice of surrogate variables

We have shown that the latent variable, implied by the assumed model, offers an approach to defining a surrogate variable for cumulative link regression models, and the jittering approach is feasible for more general models. Based on our theoretical results and numerical studies, we provide guidelines for choosing surrogate variables. When the assumed model has the general form (9), mostly seen in nonparametric fitting, we recommend the jittering method (B). Its advantages over the method (A) have been laid out in the discussion of Theorem 4. When the assumed model has the cumulative link regression form (3), frequently used in parametric fitting, we recommend the latent variable method, naturally implied by the model itself. This method has a desirable property, in addition to all the properties of the jittering method (B); that is, its null distribution has an explicit form of the link function. Due to the lack of a general and well-accepted criterion for evaluating residuals, our recommendations are made solely based on the residual’s properties with regard to its utility in model diagnostics. For a specific model of interest, what surrogate variable “best” suits the diagnostic need warrants further research.

Computational implementation

Our surrogate variable S and residuals can be easily simulated, provided a few common outcomes from a model fitting procedure. For cumulative link regression models (3), we only need 1) the fitted value of the mean structure f(X, β̂); 2) the estimates of the intercepts (cutoff points) α̂_j; and 3) the link function G. For general models (9), we only need the fitted probabilities F_a(y; X, β̂), y = 1, 2, …, J. These outcomes are readily available in common software such as R. For example, in our numerical studies, we extracted the needed outcomes from the R function “vglm”, which is used to fit vector generalized linear models (VGLMs). This is a very large class of models that includes generalized linear models as a special case. Therefore, our method can be easily implanted into a general platform for fitting regression models.

Goodness-of-fit tests versus residual analysis

We have seen continuous efforts to develop goodness-of-fit tests as a way to evaluate model fitting. Nevertheless, far from achieving this goal, statistical tests are known to be quite limited. First, a test can only yield a single p-value. This value merely indicates how strong the evidence (data) is against the null hypothesis. It does not advise how to improve the model, which is often the central goal of diagnostics. Second, a p-value tends to be quite small in practice if the sample size is large, as seen in the SAGE data analysis. As the sample size increases, any misspecification ignorable practically will eventually become significant statistically. With this said, the only hope of not rejecting the null hypothesis is that we do not reach out for large-scale data, which contradicts the principle of searching evidence as much as possible in science and business. These arguments suggest a strong need to develop a valid and effective scheme of residual analysis, which is the focus of this paper. An advantage of our residual analysis over goodness-of-fit tests is that it enables us to examine a given model from different angles, focus on each component one at a time, visualize the practical deviation (rather than merely statistical significance), and advise model improvement.

Conditional sampling for facilitating inference

The surrogate variable S results from conditional sampling given the data. Its usefulness in model diagnostics implies that it captures the information in the discrete variable Y. In fact, the conditional sampling unmasks information that is otherwise hidden in the ordinal data. It has been proven to be a useful inferential tool in other research areas, including general resampling methods (e.g., bootstrap), imputation to missing data (e.g., Little and Rubin, 2014), data augmentation in Bayesian inference (e.g., Tanner and Wong, 2010). It has been well documented that additional sampling may offer a feasible way to circumvent difficulties in directly analyzing the original data. Our work provides another example in the setting of ordinal data.

A challenge in model diagnostics

A challenge to the detection of model misspecification arises from a “compensation effect” in model fitting. Consider a related problem of response misclassification as an example. Suppose the true binary response T (=1 or 2) follows the model Pr{T = 1} = Φ(α_T + Xβ_T) and β_T is the parameter of interest. With a probability of 0.2, T = 1 is misclassified as 2 and T = 2 is misclassified as 1. The observed response with misclassification is denoted by Y. Then, the true model for Y is Pr{Y = 1} = 0.6 · Φ(α_T + Xβ_T) + 0.2, with the true link function being G₀(·) = 0.6 · Φ(·) + 0.2. If we use an assumed model Pr{Y = 1} = Φ(α^* + Xβ^*), then the link function is misspecified. Such a misspecification can be easily detected by our approach if we force α^* = α_T and β^* = β_T. However, in practice, the model fitting process automatically compensates such a misspecification by attenuating regression coefficients, i.e., β^* = cβ_T where 0 < c < 1 (Neuhaus, 1999). Such a compensation effect mitigates the problem caused by the misspecified link function. As a result, the assumed model may provide an adequate approximation to the true Pr{Y = 1} (Neuhaus, 1999), and diagnostics could be very difficult. This example presents a major challenge in model diagnostics and calls for further research. We hope that our current work can stimulate methodological development in this important area.