Fundamental Characteristics of Single-Cell Aging in Diploid Yeast

Summary

Single-cell-level experimentation can elucidate key biological insights about cellular aging that are masked in population-level studies. However, the extensive time requirement of tracking single cells has historically prevented their long-term longitudinal observation. Using a microfluidic device that automates microscopic monitoring of diploid Saccharomyces cerevisiae cells throughout their replicative lifespan, here we report the fundamental characteristics of single-cell aging for diploid yeast. We find that proteins with short versus long half-lives exhibit distinct dynamics as cells age and that the intercellular gene expression noise increases during aging, whereas the intracellular noise stays unchanged. A stochastic model provides quantitative mechanistic insights into the observed noise dynamics and sheds light on the age-dependent intracellular noise differences between diploid and haploid yeast. Our work elucidates how a set of canonical phenotypes dynamically change while the host cells are aging in real time, providing essential insights for a comprehensive understanding on and control of lifespan at the single-cell level.

Graphical Abstract

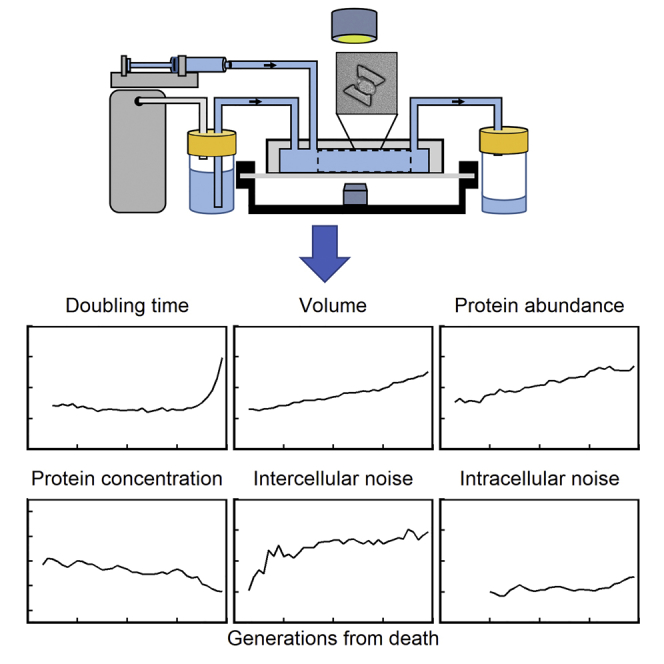
Highlights

• •A microfluidic device facilitates longitudinal observation of aging diploid yeast
• •Proteins with short versus long half-lives exhibit distinct dynamics as cells age
• •Intercellular gene expression noise increases during replicative aging
• •Unlike haploid yeast, intracellular noise is unchanged during aging in diploid yeast

Gene Network; Systems Biology; Biological Science Instrumentation

Introduction

The replicative lifespan (RLS) of Saccharomyces cerevisiae is defined as the number of daughters a mother cell produces before its death. Studies of yeast RLS have played a critical role in elucidating evolutionarily conserved aging pathways (Wasko and Kaeberlein, 2014), including dietary restriction and the mTOR pathway. An important benefit of yeast RLS as an aging model is its rapidity: most cells die within several days of birth. Traditional methods for measuring RLS require manual removal and counting of daughter cells (Steffen et al., 2009). This limitation not only constrains throughput but also requires laboratories to refrigerate the cells overnight to slow division as researchers sleep. Together, these constraints prevent the acquisition of large datasets and compromise reproducibility.

Our laboratory and others have developed devices that permit automated, full-lifespan monitoring of RLS (Chen et al., 2017, Liu et al., 2015). These devices increase throughput and maintain a constant temperature, but they have been designed exclusively for the haploid form of S. cerevisiae. Yeast exist in both haploid and diploid states (Herskowitz, 1988), with significant differences between the two in terms of cell size and morphology: spherical haploids occupy approximately half of the volume occupied by elliptical diploids. Due to these differences, the microfluidic device (termed the Replicator) that we have developed for trapping and tracking haploid yeast cells during their aging cannot be used for diploid cells. A device that works for diploid yeast cells needs to have an elliptical cell-trapping unit that is optimized in size so that the inner area of the unit is just the “right” size; this optimization is necessary as smaller trap sizes would not allow a newborn cell to enter the trapping unit, whereas larger sizes would not be able to keep the cell trapped during the multi-day experiments.

Haploid and diploid yeast are suited to particular research purposes. Haploid S. cerevisiae benefit from facile genetic manipulation and a shorter RLS, making them ideal for screening studies. The longer lived diploid S. cerevisiae, however, are uniquely compatible with experiments that require a chromosomal complement ≥2, such as those investigating loss of heterozygosity (LOH) (McMurray and Gottschling, 2003) or differentiating intrinsic and extrinsic noise (Swain et al., 2002). Furthermore, wild yeasts exist primarily in the diploid state, and studies in diploids may thus be preferable for understanding the evolutionary roots of aging. The quantification of intrinsic and extrinsic noise requires a double reporter system with each reporter integrated at identical loci (Elowitz et al., 2002, Raser and O’Shea, 2004). Intrinsic noise excludes variations due to changes in the intracellular environment that affects all genes in the same cell, which is not possible to measure without a double-reporter system integrated at two identical loci in diploid cells.

Results

A Microfluidic Device to Measure Single-Cell Aging Phenotypes from Diploid Yeast Cells

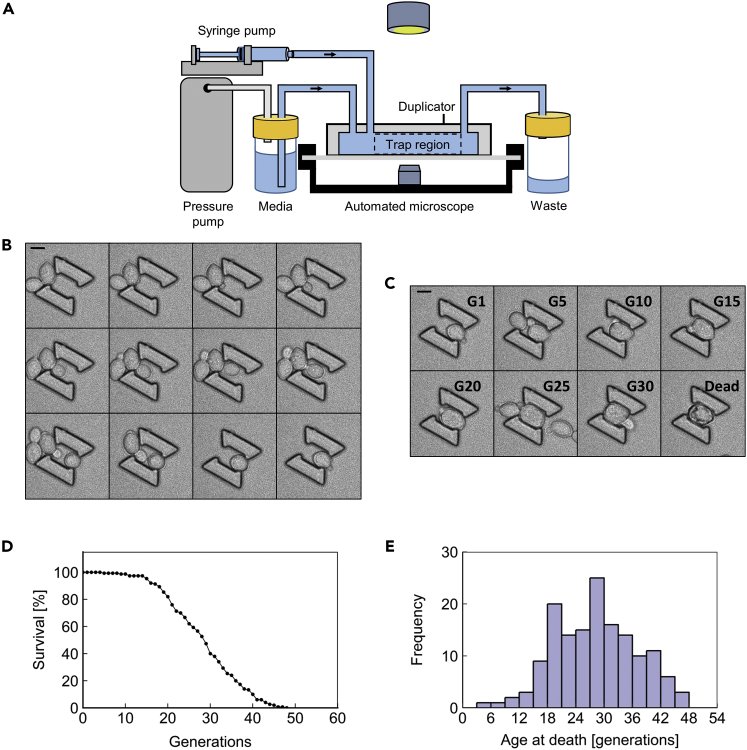
We developed a microfluidic device that enables an automated microscope to image hundreds of diploid S. cerevisiae cells throughout their full RLS (Figures 1A–1E, Table S1, Video S1). We based this device, termed the Duplicator, on our previously published Replicator (Liu et al., 2015) device designed for tracking haploid yeast cells throughout their lifespan.

Figure 1.

The Duplicator

(A) A schematic representation of the Duplicator assembly. Media is supplied via a pressure-driven pump, whereas cells are loaded using a syringe pump. Liquid flows through the Duplicator apparatus into a collection tube. Images are collected using an automated microscope.

(B) Representative time-lapse images at 10-min intervals for a single cell budding into a Duplicator trap. Scale bar, 4.95 μm.

(C) Representative time-lapse images for a single cell at specified generations (G) throughout its lifespan. This cell lived to 33 generations. Scale bar, 4.95 μm.

(D) A viability curve composed of 150 cells from 3 replicate experiments performed in the Duplicator for the BY4743 wild-type background.

(E) The histogram version of the RLS data plotted in (D).

See also Figure S1 and Table S1.

Video S1. Output of the Duplicator at a Single Imaging Location, Related to Figure 1

This video shows a single imaging location within the Duplicator for the duration of an experiment. This experiment was performed with wild-type BY4743.

To evaluate the performance of the microfluidic device, we ran 3 independent Duplicator experiments in which we took time-lapse images of wild-type yeast cells at 10-min intervals for 120 hr, a duration that was sufficient to follow each diploid cell from birth to death. For each experiment, we assessed the lifespan of 50 wild-type cells (Figures 1D, 1E, and S1). The mean lifespan for cells combined from all 3 experiments was 29.0 ± 0.7 generations, with mean values for each individual experiment falling within 5% of the overall mean value (Figure S1A and Table S1). This RLS approximates published values for the diploid BY4743 strain used in our experiments (Delaney et al., 2013, Yang et al., 2011) and exceeds the lifespan of the haploid BY4741 strain (Liu et al., 2015), as expected.

Characterization of Age-Related Changes in Cell-Cycle Durations in Diploid Yeast Cells

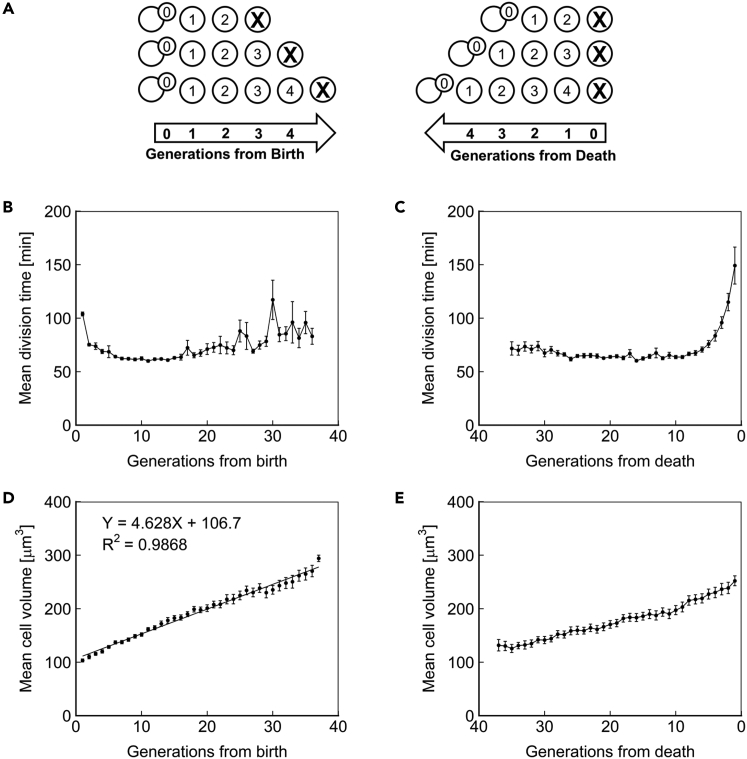
We used the Duplicator platform to investigate the fundamental characteristics of aging diploid yeast. The dynamics of an aging cell can be probed from either a birth-centric or a death-centric perspective; therefore, we aligned single-cell measurements either to the number of generations that had elapsed since the birth of the cell or to the number of generations that remained until the death of the cell (Figure 2A). Aligning measurements to birth relates trends to a cell's distance from the newborn state, whereas alignment to cell death highlights the phenotypes that immediately precede death.

Figure 2.

Fundamental Characteristics of Aging Cells

(A) A schematic demonstrating the principle of cell alignment at birth (left) or to death (right). Individual cells' generational age is displayed within their representation.

(B) Mean division time as a function of age, with cells aligned to birth.

(C) Mean division time as a function of age, with cells aligned at death.

(D) Mean volume of cells as a function of age, with cells aligned to birth. The best-fit line from linear regression is shown.

(E) Mean volume of cells as a function of age, with cells aligned at death. N = 50 cells for all subfigures, with data points where less than 10 cells remained alive omitted. Error bars are SEM.

We first sought to delineate age-related changes in the cell cycle. Previous reports have demonstrated that the first generation of a haploid cell's life is substantially longer than subsequent generations (Ferrezuelo et al., 2012). We observed the same phenotype for diploid cells (Figure 2B). We also observed that cell-cycle duration increases in the last few generations of life (Figure 2C), consistent with our prior observations in haploids (Liu and Acar, 2018, Liu et al., 2017). However, until the last few generations of life, diploid yeast cells displayed steady cell-cycle durations (Figure 2C), whereas haploid yeast had shown increasing cell-cycle durations across their full lifespan (Liu and Acar, 2018). Assuming that longer cell-cycle durations are reflections of the extra time needed for the repair of aging-related damage to cellular components, the difference between diploid and haploid cells in terms of cell-cycle duration dynamics suggests that diploid cells have a greater damage tolerance compared with haploids due to the ploidy-based greater abundance of all cellular components.

Cell Volume Increases Linearly with Replicative Age in Diploid Yeast

We next aimed to measure the cell volume dynamics throughout the lifespan. With each generation, yeast cells grow in volume. This phenotype has been suggested to play a role in mortality, based on the observation that short-lived mutant strains often display the same terminal volume as their wild-type counterparts (Yang et al., 2011, Zadrag-Tecza et al., 2009). We approximated the volume of aging diploid S. cerevisiae by assuming an ellipsoid shape and solving for volume with measured values for area and perimeter. We observed an initial volume of 103 μm³, a linear growth of 4.6 μm³/generation, and a terminal volume of 294 μm³ (Figure 2D). A similar trend was observed when cells were aligned to death (Figure 2E). Interestingly, the 294 μm³ terminal volume of the diploid BY4743 exceeded the ∼190 μm³ observed for haploid BY4741 (Zadrag-Tecza et al., 2009), indicating that either volume does not limit the lifespan or that ploidy determines resistance to the associated cause of death.

Directly Measuring Loss of Heterozygosity in Aging Mother Cells

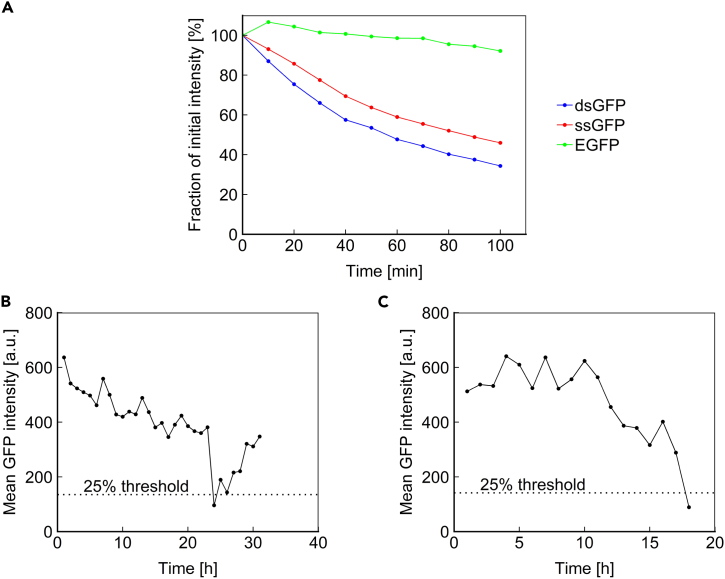
Using population-level and indirect assays, LOH has previously been associated with aging in multiple model organisms (McMurray and Gottschling, 2003, Siudeja et al., 2015, Wiktor-Brown et al., 2006). We sought to directly observe LOH in a longitudinal fashion for single mother cells over their entire lifespan. For this, we chose to use a constitutively expressed fluorescent reporter cassette whose absence would indicate LOH. EGFP and other standard fluorescent proteins have very long lifetimes, with half-lives of multiple days (Natarajan et al., 1998). To increase temporal resolution to identify an LOH event, we performed experiments using a short-lived fluorescent protein. Destabilized GFP (dsGFP), which was generated by fusing EGFP to a degradation sequence from the Cln2 protein (Mateus and Avery, 2000), displayed a half-life of ∼50 min (Figure 3A). Although such a short half-life would enable near-immediate detection of an LOH event, the high degradation rate leads to low steady-state expression of this protein, necessitating bright fluorescent exposure for its measurement, which can be harmful to cells. Therefore, we constructed a semi-stable GFP (ssGFP) by removing part of the destabilization tag from dsGFP (Salama et al., 1994). The resulting protein had a half-life of 84 min (Figure 3A), striking a balance between fluorescence intensity and temporal resolution of LOH detection. Using the half-life measurement method we applied in this study, the median half-life of yeast proteins was shown to be ∼43 min (without dilution by cell division) (Belle et al., 2006). The ssGFP reporter we use in this study exhibits a half-life comparable to many native yeast proteins, whereas EGFP exhibits a half-life on the order of 20+ hours.

Figure 3.

Loss of Heterozygosity Is a Rare Event in the Yeast Lifespan

(A) Fluorescence intensity versus time after blocking translation with cycloheximide for cells expressing EGFP, destabilized GFP (dsGFP), or semi-stable GFP (ssGFP).

(B) ssGFP intensity over time for a representative cell for which fluorescence intensity fell below the 25% threshold, defining the first criteria for LOH.

(C) ssGFP intensity over time for the only cell that exhibited a decline below the 25% threshold and did not subsequently recover.

Using a colony-based assay, a previous study estimated that the rate of LOH at the unstable SAM2 locus is at ∼2% of cell divisions in aged yeast (McMurray and Gottschling, 2003). As diploid mother cells aged, an age-induced switch to a hyper-recombinational state was reported, leading to ∼100-fold increase in LOH, based on assessing the color of the colonies formed from the daughter cells dissected from the aging mother cells. The definition of an “aged” mother cell was based on the first time one of its daughters displayed an LOH event, instead of using a specific generation-number-based cutoff. Here we sought to measure the rate of LOH directly in mother cells aging in real time. For this, we integrated ssGFP driven by the constitutive TEF1 promoter (P_TEF1) at one copy of the SAM2 locus in a diploid yeast strain. Using the Duplicator, we imaged ssGFP intensity at hourly intervals for the duration of the cells' lifespan. Measurements of age-specific ssGFP intensity for 96 mother cells from 20 imaging locations were included in our analyses. We determined that 3 criteria should be met to confirm an LOH event. (1) The ssGFP intensity should drop to <25% of a healthy cell's level, which should occur ∼3 hr after the LOH event based on the half-life of ssGFP; 6 of 96 cells met this criterion (Figure 3B). (2) The ssGFP intensity should not subsequently increase, as this phenotype is not consistent with LOH. Only 1 of 6 cells that met the first criterion did not exhibit a subsequent increase in ssGFP intensity (Figure 3C). (3) The cell should live for at least 3 additional generations, such that we can confirm that the ssGFP has not been temporarily depressed. The cell that passed the second criterion crossed beyond the 25% threshold in only its final measurement. Therefore, none of the tracked cells satisfied the criteria set for observing an LOH event. Counting the total number of cell divisions experienced by the 96 cells tracked, we saw that the cells completed 2,799 divisions across their full lifespans. We report 0% LOH rate (95% confidence interval [CI], 0%–0.13%) at the SAM2 locus based on our direct measurements in aging mother cells, whereas if we counted the experience of the one cell that crossed beyond the 25% threshold in its final measurement as an LOH event, then we would have reported ∼0.04% (=1/2,799; 95% CI, 0%–0.2%) as the single-cell-level LOH rate per cell division. Together, our findings suggest that diploid mother cells experience rare LOH events, if any, across the whole genome.

Aging Yeast Exhibit Distinct Dynamics of Protein Concentration and Abundance

Most studies of gene expression dynamics are performed using stable fluorescent proteins such as EGFP, for which half-life is substantially greater than that of a typical natural protein (Belle et al., 2006). ssGFP's half-life of 84 min approaches the median half-life of S. cerevisiae proteins of ∼43 min measured by a similar technique (Belle et al., 2006). We therefore sought to characterize the expression dynamics of ssGFP on a single-cell level throughout the aging process of diploid yeast as an accurate marker of gene expression.

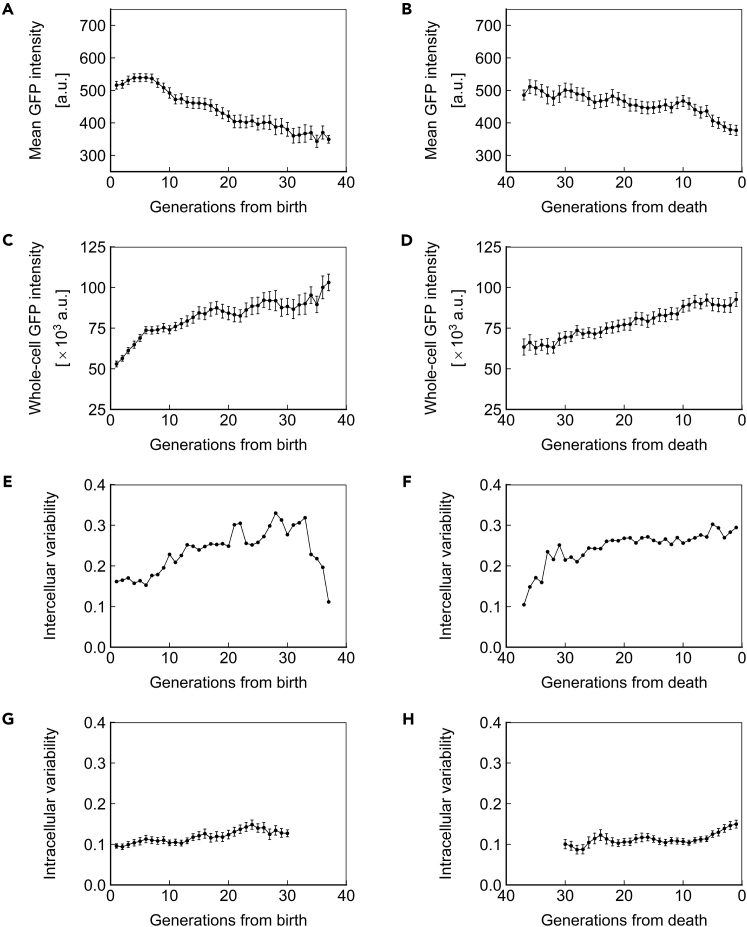
The protein amount in a cell can be conveyed in terms of concentration or total abundance. These 2 variables are closely related through cell volume but have distinct biological meanings. We defined ssGFP concentration as the mean pixel intensity of the cell and ssGFP abundance as the mean pixel intensity multiplied by cell volume. ssGFP concentration declined ∼20% over the lifespan (Figure 4A) and exhibited a more rapid decline immediately before death (Figure 4B). Conversely, we observed an ∼50%–100% increase in ssGFP abundance across the lifespan (Figures 4C and 4D). We note that due to changes in volume as cells age (Figures 2D and 2E), it is impossible that protein concentration and abundance both remain constant during aging.

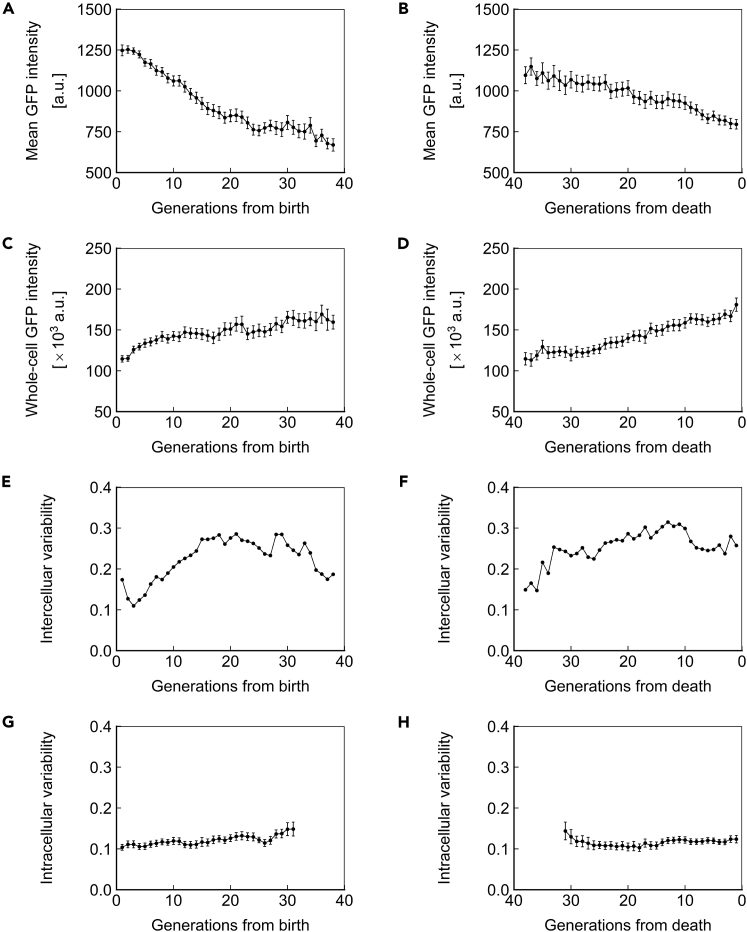
Figure 4.

Short-Lived Reporter Dynamics in Aging Cells

(A and B) Mean ssGFP intensity, a measure of protein concentration, over generations for cells aligned to birth (A) or death (B).

(C and D) Whole-cell ssGFP intensity, a measure of protein abundance, over generations for cells aligned to birth (C) or death (D).

(E and F) Intercellular variability, defined as the SD divided by the mean for mean ssGFP intensity across measurements of all cells in the population at each generation. In (E), cells are aligned at birth, and in (F), cells are aligned at death.

(G and H) Mean intracellular variability, defined as the SD/mean of mean ssGFP intensity for 8 contiguous generations, over generations for cells aligned to birth (G) or death (H). All data represent measurements from a single experiment with ssGFP integrated in a heterozygous fashion at the SAM2 locus under the P_TEF1 promoter. N = 50 cells for all subfigures, with data points where less than 10 cells remained alive omitted. Error bars are SEM.

See also Figures S2 and S7, and Tables S2–S4.

Characterization of Gene Expression Variability during Aging in Diploid Yeast

In addition to mean values, protein expression can be characterized in terms of variability, either longitudinally within a single cell or between cells. We define intercellular variability as the SD(σ) divided by the mean (μ) for the concentrations of all cells within a population. Intracellular variability is defined as σ/μ for measurements of a given cell across a set number of generations, and is expressed as the average intracellular variability for the population of cells of a given age. Therefore, intercellular variability is a measure of the population-level heterogeneity, whereas intracellular variability is a measure of a single cell's inconsistency in expression level.

Cells in a population are expected to be the most similar, and thus exhibit the least intercellular variability, at the point they are aligned to a common trait. Indeed, when cells were aligned at birth, we observed relatively low intercellular variability (coefficient of variation [CV]: ∼0.15) among the young cells (Figure 4E). However, when cells were aligned on the basis of death, we saw high intercellular variability (CV: ∼0.30) among the cells immediately preceding death (Figure 4F), with the intercellular variability staying robust from 20 to 0 generations before death. These observations indicate an approximately 2-fold increase in intercellular gene expression variability between young and old cell populations (Figures 4E and 4F). Interestingly, we saw that intercellular variability declines in the oldest cells aligned at birth (Figure 4E). Although this finding suggests that long-living cells can differentially resist the cause of mortality associated with changes in gene expression, the mechanistic connection between single-cell lifespan and intercellular gene expression variability is not fully understood.

We recently reported that haploid cells expressing YFP under the GAL1 promoter exhibit reduced intracellular variability as they age (Liu et al., 2017). We asked whether the same phenomenon would be seen in diploid cells expressing a short-lived protein under a constitutive promoter. We investigated intracellular variability using a window of 8 generations to minimize the impact of random variation, and for consistency with our prior publication (Liu et al., 2017). Distinct from the intracellular noise reduction trend displayed by haploid cells, we observed that intracellular variability in diploid yeast remains relatively stable as cells age (Figure 4G), but increases shortly before death (Figure 4H), similar to our findings in haploid yeast (Liu et al., 2017). This abrupt increase in intracellular variability suggests that both haploid and diploid cells have diminished control over gene expression shortly before death. We note that the highest levels of intracellular variability observed in diploids approximates the lowest levels observed in haploids. The absence of intracellular noise reduction in diploids may be caused by the combined effect of a variety of factors. For example, because of the difference in ploidy, the abundances of housekeeping proteins and cellular machineries are also different between haploid and diploid cells, and the higher abundance in diploid cells may well provide a buffer that reduces the observed variability. Moreover, the promoters and the integration loci are different in the diploid experiments compared with the haploid, and differences in transcription factor and chromatin dynamics may also contribute to the different intracellular noise dynamics we observed in diploid cells.

Computational Modeling Suggests an Explanation for Intracellular Noise Dynamics

Based on computational simulations, we have previously proposed that the reduced intracellular variability of P_GAL1-YFP expression in haploid yeast cells may be due to increased stochastic promoter state transition rates as the cells age (Liu et al., 2017). To examine the potential impact of such transition rate increases on constitutive promoters in diploid yeast cells, we adapted the stochastic model used in the previous report for this study and fitted the resulting model to the experimentally measured fluorescence distribution to extract the value of model parameters (Tables S2–S4). We then varied the stochastic transition rates between ON and OFF states by up to 10-fold each in both directions and computed the resulting expression level and intracellular variability levels. We found that simultaneous increases in the OFF-to-ON transition rate (r_ON) and the ON-to-OFF transition rate (r_OFF) of the kind we previously postulated (indicated by the dashed line) left the level of intracellular expression variability largely unchanged under the parameter values used for these simulations (Figure S2). This suggests that the P_TEF1 promoter operates at sufficiently high stochastic transition rates and that there is little potential for additional noise reduction. This is borne out by a comparison of the parameter values we extracted for the P_TEF1 promoter (Table S4) with those we previously obtained for the P_GAL1 promoter (Liu et al., 2017). It is also consistent with the fact that the diploid strains showed considerably less variation in expression level than the haploid P_GAL1-YFP strain we used previously (Figure S7), supporting our hypothesis that the diploid strains are at the “noise floor” with little room for further reduction.

Generality of Findings for Age-dependent Gene Expression and Noise Dynamics

The observations of gene expression dynamics described above are limited to a single genomic locus (SAM2), promoter (P_TEF1), and copy number (1, heterozygous). We next asked whether the phenotypes of protein concentration, abundance, and inter/intracellular noise described above were specific to the combination of factors investigated or global. For this purpose, we repeated the measurements made above for strains homozygous for P_TEF1-ssGFP at the SAM2 locus (Figure 5), homozygous for P_TEF1-ssGFP at the HIS3 locus (Figure 6), and homozygous for P_PGK1-ssGFP at the HIS3 locus (Figure 7). Similar trends were found in all cases, indicating that the phenotypes described above are generalizable to constitutively expressed proteins with a half-life that approximates that of a typical, natural protein in yeast. Applying our stochastic model to the experimental data from these strains also yielded similar results (Figures S3, S4, and S6; Tables S5 and S7).

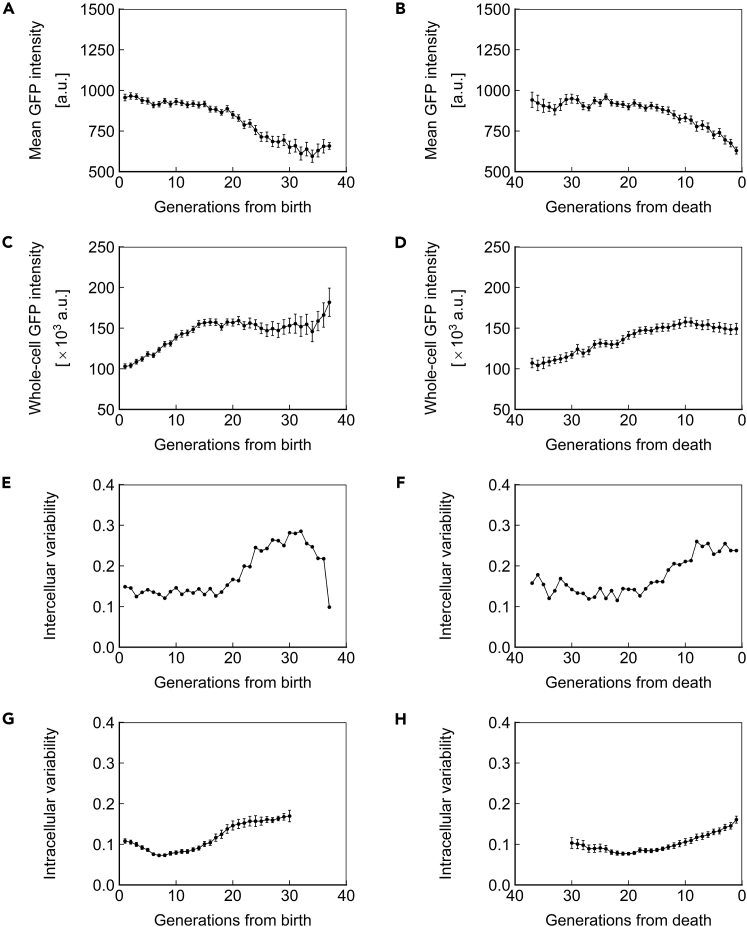
Figure 5.

Dynamics of Homozygous P_TEF1-ssGFP at the SAM2 Locus

(A and B) Mean ssGFP intensity, a measure of protein concentration, over generations for cells aligned to birth (A) or death (B).

(C and D) Whole-cell ssGFP intensity, a measure of protein abundance, over generations for cells aligned to birth (C) or death (D).

(E and F) Intercellular variability, defined as the SD divided by the mean of mean ssGFP intensity across measurements of all cells in the population at each generation. In (E), cells are aligned at birth, and in (F), cells are aligned at death.

(G and H) Mean intracellular variability, defined as the SD/mean of mean ssGFP intensity for 8 contiguous generations, over generations for cells aligned to birth (G) or death (H). All data represent measurements from a single experiment with ssGFP integrated in a homozygous fashion at the SAM2 locus under the P_TEF1 promoter. N = 50 cells for all subfigures, with data points where less than 10 cells remained alive omitted. Error bars are SEM.

See also Figures S3 and S7, and Tables S2–S4.

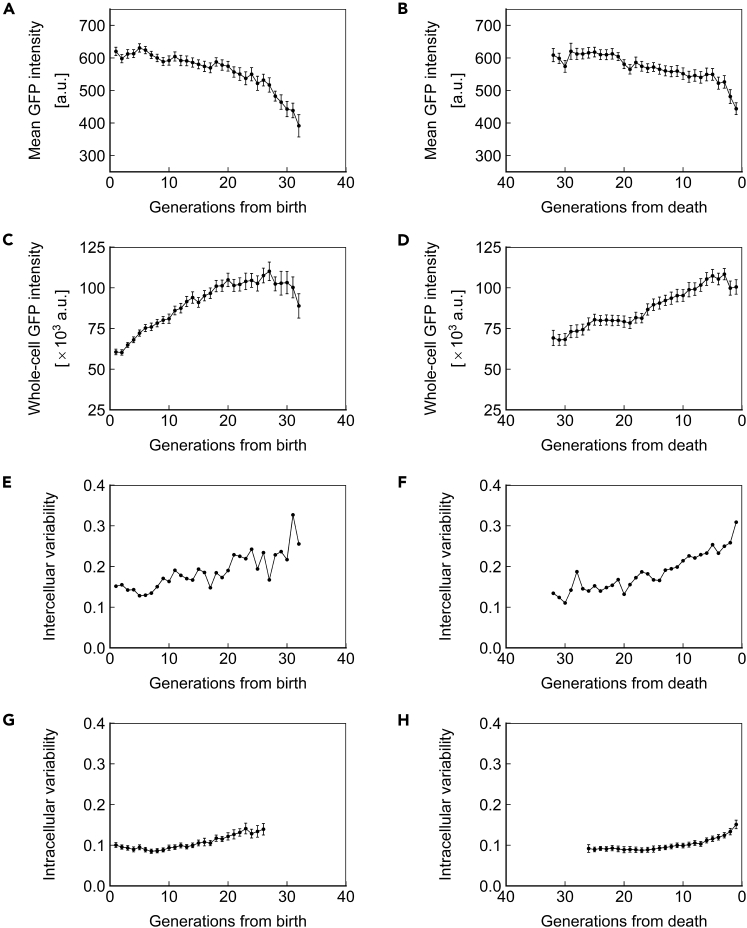
Figure 6.

Dynamics of Homozygous P_TEF1-ssGFP at the HIS3 Locus

(A and B) Mean ssGFP intensity, a measure of protein concentration, over generations for cells aligned to birth (A) or death (B).

(C and D) Whole-cell ssGFP intensity, a measure of protein abundance, over generations for cells aligned to birth (C) or death (D).

(E and F) Intercellular variability, defined as the SD divided by the mean of mean ssGFP intensity across measurements of all cells in the population at each generation. In (E), cells are aligned at birth, and in (F), cells are aligned at death.

(G and H) Mean intracellular variability, defined as the SD/mean of mean ssGFP intensity for 8 contiguous generations, over generations for cells aligned to birth (G) or death (H). All data represent measurements from a single experiment with ssGFP integrated in a homozygous fashion at the HIS3 locus under the P_TEF1 promoter. N = 50 cells for all subfigures, with data points where less than 10 cells remained alive omitted. Error bars are SEM.

See also Figures S4 and S7, and Tables S2, S3, and S5.

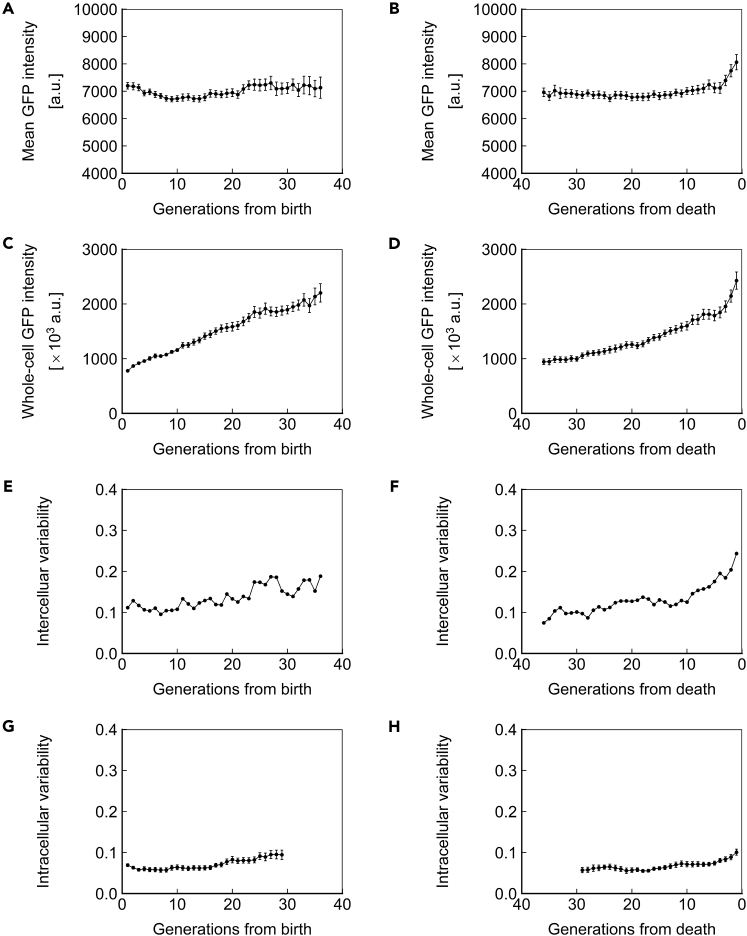
Figure 7.

Dynamics of Homozygous P_PGK1-ssGFP at the HIS3 Locus

(A and B) Mean ssGFP intensity, a measure of protein concentration, over generations for cells aligned to birth (A) or death (B).

(C and D) Whole-cell ssGFP intensity, a measure of protein abundance, over generations for cells aligned to birth (C) or death (D).

(E and F) Intercellular variability, defined as the SD divided by the mean for mean ssGFP intensity across measurements of all cells in the population at each generation. In (E), cells are aligned at birth, and in (F), cells are aligned at death.

(G and H) Mean intracellular variability, defined as the SD/mean of mean ssGFP intensity for 8 contiguous generations, over generations for cells aligned to birth (G) or death (H). All data represent measurements from a single experiment with ssGFP integrated in a homozygous fashion at the HIS3 locus under the P_PGK1 promoter. N = 50 cells for all subfigures, with data points where less than 10 cells remained alive omitted. Error bars are SEM.

See also Figures S6 and S7, and Tables S2, S3, and S7.

Protein Half-Life Drives Distinct Age-Related Expression Dynamics

A previous study in haploid cells demonstrated an age-related increase in long-lived fluorescent proteins expressed under the P_TEF1 promoter (Zhang et al., 2012). We sought to replicate these results in our system using a strain homozygous for P_TEF1-EGFP at the HIS3 locus (Figures 8 and S5; Table S6). No change was detected in EGFP concentration for cells aligned to birth (Figure 8A). This result was surprising, given that a clear decline in ssGFP concentration was detected under identical circumstances (Figures 4A and 6A). Interestingly, a rapid increase in concentration was observed immediately before death (Figure 8B), inversely mirroring the decline observed for ssGFP (Figures 4B and 6B). We note that these results indicating stability of long-living fluorophore concentration during aging are consistent with results we obtained for P_GAL1-YFP in haploid yeast cells, including the observation of a rapid increase in concentration immediately before death.

Figure 8.

Dynamics of Homozygous P_TEF1-EGFP at the HIS3 Locus

(A and B) Mean EGFP intensity, a measure of protein concentration, over generations for cells aligned to birth (A) or death (B).

(C and D) Whole-cell EGFP intensity, a measure of protein abundance, over generations for cells aligned to birth (C) or death (D).

(E and F) Intercellular variability, defined as the SD divided by the mean for mean EGFP intensity across measurements of all cells in the population at each generation. In (E), cells are aligned at birth, and in (F), cells are aligned at death.

(G and H) Mean intracellular variability, defined as the SD/mean of mean EGFP intensity for 8 contiguous generations, over generations for cells aligned to birth (G) or death (H). All data represent measurements from a single experiment with EGFP integrated in a homozygous fashion at the HIS3 locus under the P_TEF1 promoter. N = 50 cells for all subfigures, with data points where less than 10 cells remained alive omitted. Error bars are SEM.

See also Figures S5 and S7, and Tables S2, S3, S5, and S6.

Discussion

In this study, using a microfluidic device design optimized for the longitudinal tracking of diploid yeast cells, we present how a set of canonical cellular phenotypes dynamically change during the replicative aging of diploid yeast. A previous article from our laboratory provided insights into the dynamics of cell-intrinsic noise during the replicative aging of haploid yeast cells; using a stable fluorescent reporter (YFP) driven by the GAL1 promoter integrated in the ho locus, single-cell YFP concentration and cell-intrinsic (intracellular) noise have been measured and reported. In the current study, we introduce a new microfluidic device that can trap and track diploid yeast cells during replicative aging. Then, we directly show in aging mother cells that LOH is a rare event. We next elucidate the single-cell level dynamics of a wide variety of phenotypes during replicative aging: cell volume, cell division times, gene expression (in terms of both protein concentration and abundance), intracellular noise, and intercellular noise, with most of these characterizations performed using both stable and semi-stable reporter proteins driven by multiple promoters integrated at multiple loci. Finally, we use a stochastic model to gather quantitative mechanistic insights into the observed noise dynamics, which sheds light on the age-dependent intracellular noise differences between diploid and haploid yeast.

The Duplicator enables the collection of single-cell microscopy data for hundreds of diploid S. cerevisiae cells throughout their full RLS. We used this technology to measure fundamental phenotypic characteristics associated with single-cell aging that were previously refractory to direct longitudinal investigation in a diploid genetic background. Our observations reveal new insights into the properties of cells during aging and near the end of life.

Consistent with our previous observations in haploids (Liu and Acar, 2018, Liu et al., 2017), the cell division times increased near the end of life in diploid yeast. This differs from observations for some other unicellular organisms (Coelho et al., 2013, Wang et al., 2010). For instance, the fission yeast, Schizosaccharomyces pombe, does not exhibit increased cell division times before death when grown under favorable conditions (Coelho et al., 2013, Spivey et al., 2017). Similarly, the bacteria Escherichia coli, when grown in a microfluidic device, may undergo hundreds of divisions at an approximately constant rate before death (Wang et al., 2010). For both of these symmetrically dividing species, however, age-dependent division time differences have been observed under more stressful conditions (Rang et al., 2011, Stewart et al., 2005). Although information about the full spectrum of aging factors is limited, the difference in the age-dependent division time dynamics under stress-free conditions between these two species and S. cerevisiae may be due to the difference in their cell division styles. In contrast to S. pombe and E. coli, S. cerevisiae mother cell divides asymmetrically and produces a daughter cell that is significantly smaller than the mother. Assuming that certain aging factors are freely diffusible between mother and daughter compartments during cell division, the S. cerevisiae mother cell would be expected to have a diminished capability to dilute away aging factors through cell division compared with S. pombe and E. coli. If the impact of aging factors on S. cerevisiae division times is non-linear, the increased cell division times we observe near death could be interpreted as a reflection of the specific form of the non-linearity.

We also observed distinct age-related concentration dynamics for short-lived and long-lived proteins. A short-lived protein declined in concentration with age, whereas the concentration of a long-lived protein remained relatively stable. Protein concentration is a function of production and elimination. Since production of both proteins was controlled by the same promoter, the observed differences in concentration are the result of elimination. Protein elimination occurs due to both degradation and dilution by cell division. For long-lived proteins, dilution is the primary determinant of elimination, whereas degradation is the greater contributor to elimination for short-lived proteins. Dilution is driven by growth in cell volume, which proceeds at a constant rate until very late in life. Our observations therefore suggest an age-related increase in protein degradation rate. However, this would be unexpected, given that rapid degradation conferred by the CLN2PEST used in ssGFP is thought to be proteasome mediated (Schneider et al., 1998), and proteasome function has been suggested to decline with age (Andersson et al., 2013). One alternative explanation is that protein folding rates are reduced with age, and these effects are more obvious in ssGFP because maturation already takes a substantial portion of its lifetime.

The observation that protein half-life drives distinct age-related dynamics may be important in the context of gene networks. Many subcellular systems rely on a stoichiometric balance between their components (Birchler and Veitia, 2012, Kim and Forger, 2012). If two components experience distinct expression pressures arising from differences in half-life, a negative feedback mechanism would be essential to buffer the impact of the diverging expression pressures and prevent imbalance in the network. More specifically, the negative feedback would act by increasing the expression of the short-living protein in the network in response to age-related decreases in protein level, whereas it would decrease the expression of the long-living protein. We therefore hypothesize that gene networks have evolved to match the half-life of their components or finely control their stoichiometry via negative feedback, or that these age-related dynamics dependent upon protein half-life play a role in the aging process.

We found that protein abundance increased throughout the lifespan for both short- and long-lived proteins. For much of a cell's life, this increase in expression appears to compensate for the growth of cell volume to maintain protein concentration. However, abundance reaches a maximum at 5–10 generations before death, whereas volume continues to linearly increase. This closely matches the point at which the concentration of short-lived protein declines. These results suggest that some physical constraint on expression is reached several generations before cell death. Although there are numerous possibilities, the constraint could, for example, be facilitated by age-related damage experienced by the components of the gene expression machinery. In the case of long-lived proteins, for which concentration does not decline late in life, this leveling off of expression may be matched by a decrease in the rate of dilution, as cell cycle slows down in the last several generations of life.

Since cell volume increases linearly with age, the ratio of the abundance and concentration of a protein cannot remain constant during aging. Therefore, if both of these variables are optimized in young cells, they must necessarily diverge from their optimal values as the cell ages. Both the concentration and abundance of a protein might be relevant to biological function. For example, whereas concentration determines the rate of enzymatic reactions on a cell-wide scale, abundance could actuate compartmentalized activity in response to localization cues. Since both concentration and abundance cannot remain constant, we envision that a protein with activities reliant on both would deviate from optimal function with age. We predict that either cells have evolved mechanisms to avoid this conundrum or that it plays a role in the process of aging.

Limitations of the Study

Our study here is limited to the behavior of an array of constitutive promoters during aging. Thus, it is possible that an inducible promoter may display different expression and noise dynamics during the aging process. The need to avoid phototoxicity during a multi-day aging study also places a limit on the achievable time resolution of expression level observations. Finally, our computational model does not attempt to model the effects of aging directly; instead, we examine the effect of parameter changes in the model to determine which parameters aging could have affected, which is necessarily indirect. Many model parameter values are also nearly impossible to measure directly and are obtained by estimation instead.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: September 28, 2018