Breast Cancer Risk Model Requirements for Counseling, Prevention, and Screening

Abstract

Background

Incorporation of polygenic risk scores and mammographic density into models to predict breast cancer incidence can increase discriminatory accuracy (area under the receiver operating characteristic curve [AUC]) from 0.6 for models based only on epidemiologic factors to 0.7. It is timely to assess what impact these improvements will have on individual counseling and on public health prevention and screening strategies, and to determine what further improvements are needed.

Methods

We studied various clinical and public health applications using a log-normal distribution of risk.

Results

Provided they are well calibrated, even risk models with AUCs of 0.6 to 0.7 provide useful perspective for individual counseling and for weighing the harms and benefits of preventive interventions in the clinic. At the population level, they are helpful for designing preventive intervention trials, for assessing reductions in absolute risk from reducing exposure to modifiable risk factors, and for resource allocation (although a higher AUC would be desirable for risk-based allocation). Other public health applications require higher AUCs that can only be achieved with risk predictors 1.6 to 8.8 times as strong as all those yet discovered combined. Such applications are preventing an appreciable proportion of population disease when employing a high-risk prevention strategy and deciding who should be screened for subclinical disease.

Conclusions

Current and foreseeable risk models are useful for counseling and some prevention activities, but given the daunting challenge of achieving, for example, an AUC of 0.8, considerable effort should be put into finding effective preventive interventions and screening strategies with fewer adverse effects.

Models to predict the risk of developing cancer are used for counseling, clinical management, and developing prevention strategies (1). There has been considerable effort to increase the discriminatory accuracy of models to predict breast cancer incidence by including mammographic density (2–4) and single nucleotide polymorphisms (SNPs) (5–14). It is timely, therefore, to assess what progress has been made in comparison with what is needed in various applications.

Methods

Absolute Risk and Types of Models Available

Absolute risk of invasive breast cancer is the probability that a woman with defined risk factors and free of breast cancer at a given age will be diagnosed with invasive breast cancer during the risk projection interval. This risk is reduced by the chance that the woman may die from other causes. Methods to estimate absolute risk are described, for example, in Chapters 4 and 5 of Pfeiffer and Gail (1). “Pure” risk is the hypothetical risk that would ensue if competing causes of mortality could be eliminated. Some models (eg, Claus [15], BOADICEA [16–18], an option in IBIS [19]) predict the “pure” risk of breast cancer. Pure risk approximates absolute risk over short projection intervals but can be appreciably larger over long intervals. Because competing causes of mortality cannot be eliminated, absolute risk is more relevant in practice.

Several models are available for projecting breast cancer risk (see, eg, [20–22]). Some models are based on genetic theory and extensive family history (15–19,23,24). Of these, some allow for residual genetic familial aggregation in addition to an autosomal dominant component (16–19). Models based on genetic theory are widely used for women in high-risk clinics. Some models, like the National Cancer Institute’s Breast Cancer Risk Assessment Tool (BCRAT) (25–29), are based on empirical regressions. BCRAT includes reproductive history, biopsy history, and family history and is tailored to the general population. Some models include modifiable risk factors, such as body mass index (BMI), hormone replacement therapy, and alcohol intake (7,19,30,31). Others include mammographic density (2–4) and SNPs (7,9,11).

Calibration, Discriminatory Accuracy, and Log-Normal Risk

Various criteria are useful for evaluating risk models (1,32), but calibration and discriminatory accuracy are very important. A model is well calibrated if it accurately predicts the number of breast cancers that arise in an independent validation cohort. If the ratio of the number events predicted by the model to the observed count is near 1.0, both overall and in subgroups, the model is well calibrated. All the applications described below, except ranking individuals for resource allocation, require good calibration.

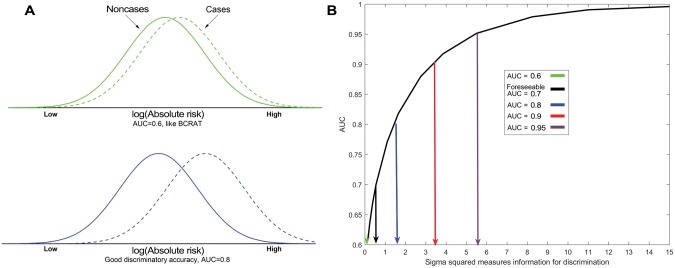
Discriminatory accuracy refers to how well separated the distribution of risk is in case patients (who develop breast cancer) from the distribution in noncase subjects. The AUC is the probability that a randomly selected case patient has a higher projected risk than a randomly selected noncase subject. There is considerable overlap in the risk distributions of case patients and noncase subjects for an AUC of 0.6, and even for an AUC of 0.8 (Figure 1A).

Figure 1.

Illustration of discriminatory accuracy (area under the curve [AUC]) and plot of AUC against the log-normal variance. A) Normal densities of log (absolute risk) for case patients (dashed line) and noncase subjects (solid line) for an AUC of 0.6 (green upper A panel) and an AUC of 0.8 (blue lower A panel). B) AUC is plotted against the variance, ${\sigma }^2$, of lognormally distributed risk in the population. AUC = area under the curve; BCRAT = Breast Cancer Risk Assessment Tool.

Several breast cancer risk models based on standard epidemiologic risk factors have AUCs near 0.6. Tremendous effort to increase the AUC by combining SNPs, mammographic density, and epidemiologic risk factors can increase the AUC to 0.68 (Table 1) (33). Sixty-five recently established SNPs (14) could increase that AUC to 0.69 (Supplementary Materials, available online). The improvement from an AUC of 0.6 to an AUC of 0.69 is still inadequate for some applications.

Table 1.

AUC values for various breast cancer risk models^*

Risk model factors	AUC	Comments with references
7 SNPs	0.574	First proven SNPs; SNP log odds from literature combined theoretically (5)
77 SNPs	0.622	Empirical estimates of SNP log odds and resulting AUC estimated from 33 673 cases and 33 381 controls (12)
92 SNPs	0.623	24 empirical SNP log odds estimates from 17 171 cases and 19 862 controls plus 68 SNP log odds ratios from literature combined by imputation to estimate AUC (7)
BCRAT	0.580	Evaluation in Nurse’s Health Study (34)
	0.603,	Case-weighted average of age-specific AUCs (35)
	0.607	Theoretical calculation based on BCRAT (5)
BCRAT + 7 SNPs	0.632	Theoretical calculation based on BCRAT and SNP literature (5)
Epi + 76 SNPs	0.670	Theoretical combination of log odds ratios from 11 published epidemiologic risk factors and 76 SNPs (33)
Epi + 76 SNPs + MD	0.680	Theoretical combination of log odds ratios from 11 published epidemiologic risk factors, 76 SNPs, and MD (33)

^*AUC = area under the curve; BCRAT = Breast Cancer Risk Assessment Tool; Epi = epidemiologic risk factors in reference (33); MD = mammographic density; SNP = single nucleotide polymorphism.

To understand the challenge, we relate AUC to the variance, ${\sigma }^2$, of a lognormal risk distribution (Supplementary Materials, available online) (36). Pharoah et al. (36) showed that the AUC depends only on ${\sigma }^2$, and not the mean, of the lognormal risk distribution. ${\sigma }^2$ measures the discriminatory information in all the risk factors. An AUC of 0.7 corresponds to a ${\sigma }^2\hspace{0.17em}\text{of}\hspace{0.17em}0.550$ (Figure 1B).AUCs of 0.6, 0.8, 0.9, and 0.95 correspond to ${\sigma }^2$ of 0.128, 1.417, 3.285, and 5.411. The discriminatory information ${\sigma }^2$ that is needed to achieve an AUC of 0.8 is 1.417/0.550, or 2.6 times that needed to achieve an AUC of 0.7, which is the foreseeable goal. To achieve an AUC of 0.9 or 0.95 requires, respectively, 6.0 and 9.8 times the information required to achieve an AUC of 0.7. Thus, only predictors dramatically more informative than all currently foreseeable predictors can push the AUC to 0.8 or higher. We now consider various applications of risk models and their requirements for discriminatory accuracy.

Results

Individual Counseling

Risk models can provide the counselee with a realistic estimate and perspective. Thus, a woman who thought she had a 50% risk of developing breast cancer by age 80 years might be reassured to know her risk was 10%. To provide such perspective, the model must be well calibrated.

Consider a white woman age 40 years whose mother and sister had breast cancer. The 2016 screening mammography recommendation of the US Preventive Task Force (https://www.uspreventiveservicestaskforce.org/Page/Document/RecommendationStatementFinal/breast-cancer-screening1) was: “The decision to start screening mammography in women prior to age 50 years should be an individual one. Women who place a higher value on the potential benefit than the potential harms may choose to begin biennial screening between the ages of 40 and 49 years.” This recommendation makes no reference to breast cancer risk. From BCRAT, the five-year risk of breast cancer for this woman, who has no other BCRAT risk factors, is 2.5%, whereas a white woman age 50 years with no risk factors has a risk of 0.6%. Yet the US Preventive Task Force recommends screening for women age 50 to 74 years. Knowing that her risk is fourfold higher than that of a woman age 50 years for whom screening is recommended, this 40-year-old counselee might well choose to begin screening mammography. Formal comparisons of harms (such as needless biopsies) and benefits from screening in younger women with risks comparable to older women indicate that this would be a wise choice (37,38). In the United States, 74% (11.4 million) of white women age 40 to 49 years had estimated risks as high as a woman age 50 years without BCRAT risk factors (39).

Risk models that include modifiable risk factors, such as alcohol consumption or hormone replacement therapy (7,30,31), may provide perspective on risk reductions from avoiding such exposures.

Knowing one’s breast cancer risk also informs formal assessments of the harms and benefits of an intervention. Both tamoxifen and raloxifene warrant consideration for chemoprevention against breast cancer (40). Yet both have adverse effects that offset the benefit of breast cancer prevention, including increased risk of stroke, pulmonary emboli, and, for tamoxifen, increased risk of endometrial cancer. Because the risks of stroke and endometrial cancer increase with age, higher breast cancer risks are required for the interventions to have a net benefit in older women. For women in their fifties with uteri, the five-year risk threshold for net benefit is 4.5% for tamoxifen but 2.0% for raloxifene, which does not increase endometrial cancer risk (41). Thus, well-calibrated risk estimates, even from models with modest discriminatory accuracy, can aid in deciding whether to have an intervention that has risks and benefits.

The models we have been discussing apply to women in the general population. Genetically oriented models are useful in high-risk clinics both to guide testing for mutations and to project risk based on genetic tests and pedigree data (20). A young woman who carries a BRCA1 mutation has a risk to age 70 years near 50% if she is from the general population and even higher if she is from a family with many breast cancer cases. Because BRCA1 mutations are rare, however, they contribute little to discriminatory accuracy in the general population. In the Supplementary Materials (available online), we show that the addition to ${\sigma }^2$ from BRCA1 is 0.0061, or 1.1% of the information needed for an AUC of 0.7. Recent test versions of BOADICEA have incorporated more common, but less penetrant, truncating mutations (42), such as CHEK2. This mutation adds only 0.0062 to ${\sigma }^2.$ Thus, measuring highly and moderately highly penetrant mutations will not increase the AUC much in the general population (Figure 1B). Such measurements are very useful, however, for advising the rare women carrying such mutations, who might be concentrated in high-risk clinics.

Risk Models for Population-Level Cancer Prevention

Designing Preventive Intervention Trials

Absolute risk models help determine how many subjects are needed and how long they should be followed to achieve the required statistical power. Power depends on the number of incident breast cancers, which is proportional to average absolute risk. For example, among the 5969 women in the control arm of the Breast Cancer Prevention Trial (or P-1 Trial) of tamoxifen (43), BCRAT predicted 159 incident invasive breast cancers, in close agreement with the 155 observed. Thus, BCRAT was well calibrated and provided useful guidance for sample size and trial duration.

Risk models are also used to define eligibility. In designing the P-1 trial, investigators were aware of the adverse effects of tamoxifen. They believed, however, that the five-year risk of invasive breast cancer was high enough (1.66%) in women age 60 years to warrant their inclusion in the trial. Younger women were included in the trial only if their five-year risks were at least 1.66%.

Good calibration overall and in subgroups with varying levels of risk is essential for designing intervention trials; modest discriminatory accuracy (eg, AUC = 0.5–0.7) is adequate.

Estimating Absolute Risk Reduction in the Population From Preventive Interventions

Some models for absolute breast cancer risk include modifiable risk factors (7,30,31). Petracci et al. (30) developed such a model for Italian women and estimated the absolute risk reduction over 20 years that would result from eliminating alcohol consumption, lack of exercise, and BMI of 25 kg/m² or greater in women age 55 years (Table 2). In the entire study population, the 20-year risk is 6.5%, but intervention reduces it by 1.6% to 4.9%. The fractional reduction, 100%(1.6%/6.5%) = 24%, is analogous to attributable risk. For women with risks in the top decile of risk, the 20-year risk is 18.5% before intervention and 18.5%–4.4% = 14.1% after intervention, a fractional reduction of 24%.

Table 2.

Potential reductions in 20-year absolute breast cancer risk from eliminating alcohol consumption, lack of exercise, and body mass index at or above 25 kg/m² in Italian women age 55 years^*

Population	Absolute risk without intervention, %	Reduction in absolute risk from intervention, %	Fractional reduction in risk, %
Entire population	6.5	1.6	24
Women with positive family history	13.7	3.2	23
Women with risk in the top decile (top 10%) of risk	18.5	4.4	24

^*This table presents estimated risk reductions in Petracci et al. (30) for Italian women if all current drinkers had been never drinkers, all women who exercised less than two hours per week exercised at least two hours per week, and all women age 50 years and older maintained a body mass index lower than 25 kg/m². In addition to these modifiable risk factors, the risk model contained nonmodifiable risk factors such as age at first live birth (30).

The high absolute risk reduction of 4.4% in the top decile group (Table 2) results from two sources. The joint relative risks from modifiable and nonmodifiable risk factors are the product of the separate relative risks. Thus, a given reduction in modifiable risk factors causes more reduction in absolute risk in women with high levels of nonmodifiable risk factors, who concentrate in the high-risk group (7). Second, women in the top decile of risk are enriched with elevated modifiable risk factors; thus, intervention induces more risk modification.

Changes in absolute risk give a different perspective than fractional reduction. In 100 000 women age 55 years, intervention potentially prevents 1600 breast cancers over 20 years. If instead the intervention were applied to the 10 000 women in the top decile, then only 4.4%×10 000 = 440 breast cancers would be prevented.

These calculations assume that there is a practical intervention that reduces the exposures, that women will comply with it, and that the risk factor changes will instantaneously have the effects estimated from observational data. Moreover, in the previous example, it is impossible to change a current drinker into a never drinker; one must imagine instead a counterfactual population in which women never drank. Thus, there is considerable potential for systematic error in these calculations, which rely on well-calibrated risk models, but not on highly discriminating ones.

“High-risk Prevention Strategy” for Interventions With Adverse Effects

Rose (44) compared the general population strategy of disease prevention with the high-risk strategy. If an intervention is safe enough to be applied broadly, more disease can be prevented by applying it to the entire population than by intervening only on a high-risk subset.

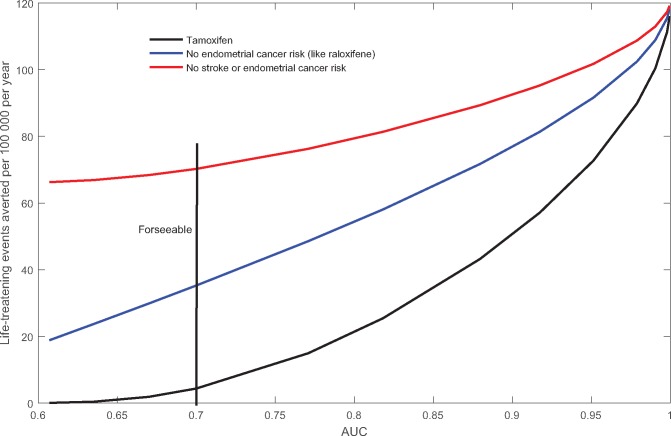
The high-risk strategy prevents less disease because most of the population risk is usually not concentrated in the high-risk subgroup. Nonetheless, one is sometimes forced to restrict interventions to high-risk subsets. If the intervention has adverse effects, it should only be given to those with high enough risk that the benefits of preventing the disease outweigh the adverse effects. Table 3 depicts the expected numbers of life-threatening events in one year in 100 000 white US women with uteri age 50 to 59 years. Absent tamoxifen, 246.6 invasive breast cancers and 589.6 life-threatening events are expected to occur. Giving tamoxifen to the entire population reduces breast cancers and hip fractures, but increases endometrial cancer, strokes, and pulmonary emboli, resulting in 833.5 life-threatening events. Thus, the general population prevention strategy cannot be used. Only the 1% of women with breast cancer risks above 774.3/10⁵ per year have a net benefit (45). Unless most of the breast cancer incidence is concentrated in this 1%, the high-risk strategy cannot prevent much disease. If one uses BCRAT to identify women with yearly risk exceeding 774.3/10⁵, only 1.4 life-threatening events are prevented per year, leading to 589.6–1.4 = 588.2 events. If a perfectly discriminating model was used instead, it would identify the 246.6 women destined to develop breast cancer (Table 3), and tamoxifen could be given to them alone. There would be very few adverse events, while nearly half the breast cancers would be prevented, thus preventing 119.9 life-threatening events (45).

Table 3.

Numbers of life-threatening events in one year in 100 000 white US women age 50–59 years with uteri if none get tamoxifen and if all get tamoxifen^*

Health outcome	Relative risk	Events without tamoxifen	Events if all get tamoxifen
Invasive breast cancer	0.51	246.6	125.8
Hip fracture	0.55	101.6	55.9
Endometrial cancer	4.01	81.4	326.4
Stroke	1.59	110	174.9
Pulmonary embolism	3.01	50	150.5
Total	−	589.6	833.5

^*Relative risk compares tamoxifen with placebo. From Gail (45), based on Fisher et al. and Gail e al. (43,46).

How discriminating must a breast cancer risk model be to prevent a substantial number of life-threatening events with an intervention that has clinically significant adverse effects in white women with uteri, age 50 to 59 years? Very high AUC values are needed (Figure 2). Preventing 20 events requires an AUC of 0.79, well above the foreseeable AUC of 0.7. If the intervention has fewer side effects, it can be given to a larger high-risk subgroup. For example, if tamoxifen did not increase endometrial cancer risk (like raloxifene), nearly 17 events could be prevented each year, even with current models with an AUC of 0.6 (Figure 2). With foreseeable models with an AUC of 0.7, 35 life-threatening events could be prevented. If, in addition, there was no excess stroke risk associated with tamoxifen, 70 events could be prevented with an AUC of 0.7 and 67 with an AUC of 0.6. To prevent 100 life-threatening events with any of these intervention scenarios would require an AUC greater than 0.94, which is not foreseeable.

Figure 2.

Life-threatening events averted each year by breast cancer chemoprevention in 100 000 white women age 50 to 59 years as a function of area under the curve. Only a high-risk subset is given the intervention. Three intervention scenarios are tamoxifen, tamoxifen but with no increased risk of endometrial cancer (like raloxifene), tamoxifen but with no increased stroke or endometrial cancer risk. AUC = area under the curve.

The most effective way to improve the high-risk strategy is to decrease the side effects of the intervention so that it can be applied more widely (Figure 2). Improving the efficacy of the intervention from, say, 50% prevention of breast cancer to 80% could also be beneficial. The value of improving the discriminatory accuracy of risk models for the targeted disease depends on the intervention. Improving AUC from 0.6 to 0.7 (Figure 2) saves few additional lives for an intervention with many side effects, like tamoxifen, or for an intervention with few side effects (eg, tamoxifen but without excess endometrial cancer or stroke risk). However, increasing AUC from 0.6 to 0.7 reduces deaths appreciably for a drug with intermediate side effects, like raloxifene (or tamoxifen but without endometrial cancer risk) (Figure 2). Improvements in AUC above 0.7 avert more life-threatening events, but require new risk factors 1.6 to 8.8 times more informative than all those in foreseeable models (Figure 1B). A fourth approach is to use risk models for the other outcomes affected by the intervention, such as stroke, in addition to the main outcome to be prevented. Previous calculations have assumed that stroke risk depended on age and ethnicity only (41,46), but finer assessment can improve the high-risk strategy modestly (47).

Allocating Preventive Resources Under Monetary or Medical Constraints

The high-risk strategy may also be used when there are insufficient resources to intervene in an entire population (eg, [48]). Suppose that there is only enough money for one-time screening mammograms for half the adult female population. Under random allocation, one expects to prevent half the deaths that could be prevented by screening the entire population. If one first performed a risk assessment on the entire population and then allocated mammograms to those at highest risk, one might prevent more deaths. It costs money to perform the risk assessment, however, which reduces resources for mammography.

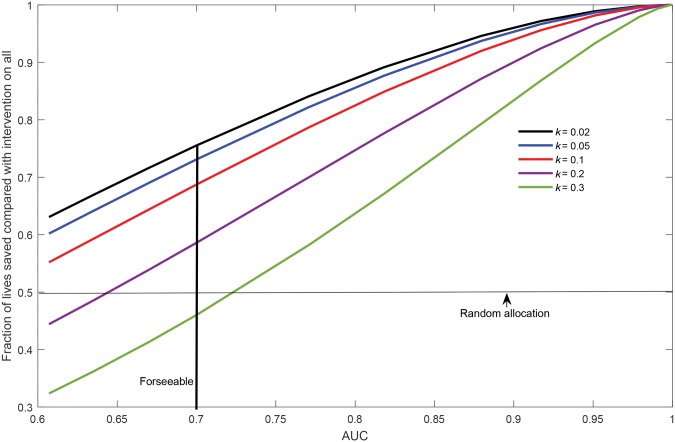
Figure 3 plots the fraction of lives saved, compared with screening the entire population, as a function of AUC for various ratios k of the cost of risk assessment to the cost of a screening mammogram (k = 0.02, 0.05, 0.1, 0.2, 0.3). If mammography costs $100 and contacting a woman and obtaining answers for BCRAT costs $2, then k = 0.02. Calculations in Figure 3 assume the log-normal risk model but otherwise follow Gail (49) (Supplementary Materials, available online). For an AUC near 0.6, there is no benefit from risk assessment with a k of 0.2 or 0.3, but with a k of 0.02, risk assessment improves the fraction of lives saved to 63%, compared with 50% with random allocation. For foreseeable models with an AUC of 0.7, the fraction of lives saved increases to 75%, with a k of 0.02. Thus, foreseeable risk models can improve resource allocation, provided the cost of risk assessment is small enough. Even more lives could be saved with models with nonforeseeably higher AUCs (Figure 3).

Figure 3.

Fraction of lives saved by risk-based allocation of mammograms, compared with giving screening mammograms to all women, as a function of area under the curve when there is only enough money to give mammograms to half the population. Results are shown for various ratios k of the cost of risk assessment to the cost of a mammographic screen. AUC = area under the curve.

These are best-case calculations because they assume that everyone accepts a risk assessment and that those recommended for intervention take it.

Screening for Prevalent Subclinical Disease

Models with high AUCs could identify high-risk women to screen for prevalent breast cancer, thereby sparing other women from needless follow-up exams, anxiety, and biopsies following false-positive screens (50,51), while detecting most disease. Models for breast cancer incidence do not estimate prevalence. However, data from the Breast Cancer Screening Consortium (http://www.bcsc-research.org/statistics/performance/screening/2009/rate_age_time.html) indicate that prevalence is proportional to incidence in previously unscreened women. Assuming prevalence is proportional to incidence, one can use incidence models to determine who should receive screening. Here we consider a single screen to detect prevalent disease.

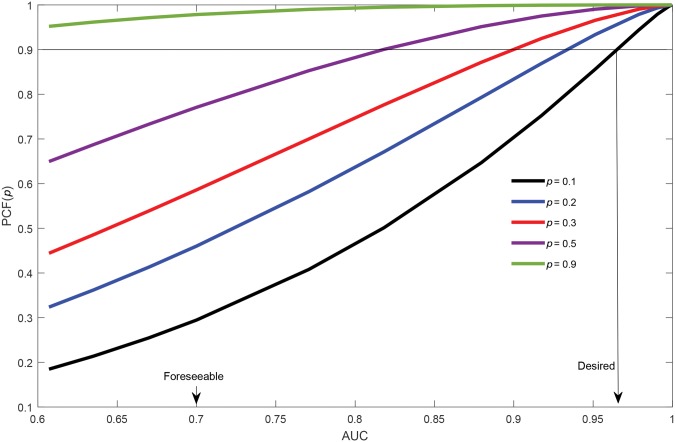
Suppose one performs a risk assessment on all members of the population and screens only individuals in the 100p% of the population at highest prevalence risk, namely those with risks above the ${(1-p)}^{th}$ quantile of risk. Pfeiffer and Gail (52) call the proportion of all prevalent cases contained in this high-risk group the “proportion of cases followed,” $PCF(p)$. Assuming an AUC of 0.67, Park et al. (8) calculated the $PCF(p)$ for breast cancer in women age 50 to 54 years as .255 for a p of .1 and .539 for a p of .3. In other words, even with a risk model more discriminating than those in current use, 74.5% of the prevalent cases would be missed if one only screened the top 10% of the population, and 46.1% would be missed if one screened the top 30%.

$PCF(p)$ increases with AUC for ps of .1, .2, .3, .5, and .9 for lognormally distributed risk (Figure 4). With a p of .1, the AUC would need to be 0.97 to capture 90% of the cases. With a p of .3, the AUC would need to be 0.90. Even screening the half of the population with risk above the median risk (p = .5) would require an AUC of 0.82 to capture 90% of the cases, and nearly 23% of prevalent cases will be missed with an AUC of 0.7 (Figure 4). Thus, foreseeable models will miss many prevalent cases in screening only a high-risk group. If the 10% of the population at lowest risk were not screened (p = .9), with an AUC of 0.7, only 2% of cases would be missed.

Figure 4.

Proportion of cases followed, $PCF(p),$ plotted as a function of AUC for p values of .1, .2, .3, .5, and .9. AUC = area under the curve.

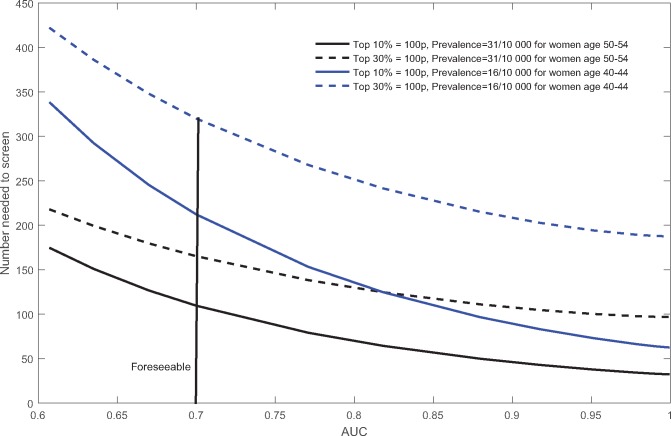
The proportion of cases followed, PCF(p), is related to the positive predictive value, PPV(p) = πPCF(p)/p, where π is the prevalence of screen-detectable disease. $PPV(p)$ is the proportion of the high-risk group with prevalent screen-detectable disease. Assuming an AUC of 0.67, PCF(.1) = 0.255, and $\pi$= 0.0031 for women age 50 to 54 years (8), PPV(.1) = πPCF(.1)/.1 = 0.00791. The number needed to screen to detect one case is $NNS=1+(1-PPV)/PPV$= 126.5. Choosing an acceptable number needed to screen (NNS) below which screening is recommended is tantamount to assigning relative costs to false-positive and false-negative screening results.

Figure 5 plots NNS against AUC for women age 50 to 54 or 40 to 44 years and for screening the top 10% (p = .1) or top 30% (p = .3) at highest risk. NNS is higher for the younger women (blue loci), who have a lower prevalence ($\pi$= 0.0016). Among women age 50 to 54 years, NNS is 227 for a p of .3 and 184 for a p of .1 with an AUC of 0.6. With an AUC of 0.7, NNS decreases to 165 and 108, respectively. Among women age 40 to 44 years, NNS is 435 for a p of .3 and 350 for a p of .1 with an AUC of 0.6. With an AUC of 0.7, these NNS values decrease to 319 and 223, respectively, and with an AUC of 0.8, to 250 and 127. Even though these higher AUC values can lower the NNS, particularly for a p of .1, many prevalent cases would be missed with a p of .1 (Figure 4).

Figure 5.

Number needed to screen to detect one prevalent breast cancer plotted against area under the curve. Four loci are shown for women age 40 to 44 or 50 to 54 years and based on screening either the top 10% or top 30% at highest risk. AUC = area under the curve.

Discussion

Considerable progress has been made or is foreseeable for increasing AUC from 0.6 to 0.7 for breast cancer risk models. Provided the models are well calibrated, they provide useful perspective in individual counseling and for weighing the risks and benefits of preventive interventions. They are helpful for designing preventive intervention trials and estimating decreases in absolute risk from reducing exposure to modifiable risk factors. For allocating limited preventive resources, such models are potentially useful, but higher AUC would be desirable.

Other public health applications require higher discriminatory accuracy that can only be achieved with predictors much stronger than those yet discovered. Such applications include employing the high-risk prevention strategy and deciding who should not be screened for disease.

The usefulness of a risk model for disease prevention depends on the specific intervention. An intervention with few side effects benefits a larger portion of the population, thereby requiring less discriminatory accuracy (Figure 2). An intervention with more side effects requires high discriminatory accuracy to concentrate population risk into a small high-risk subset.

If one can only offer an intervention like screening mammography to half the population, low-cost (k < 0.1) risk-based allocation is preferable to random allocation (Figure 3) or to age-based allocation (53), even with an AUC of 0.6. However, nearly 23% of prevalent cases will be missed even with an AUC of 0.9 (Figure 4 with p = 0.5).

Our study has limitations. These calculations are based on the previously used log-normal distribution of risk (36) and are justified in the Supplementary Materials (available online), but our conclusions likely hold for other reasonable risk distributions. Our analysis treated only a single prevalence screen; current risk models may be adequate to address related questions, for example, when to start screening, frequency, and use of supplemental modalities (54). The ratio k of risk assessment to intervention costs may be lower if a single risk assessment (eg, genetic test) serves for multiple screenings or health outcomes. We did not consider the harms from false-positive screening explicitly, but these are implicit in choosing an acceptable number needed to screen.

Improving disease prevention by developing more discriminating risk models is daunting. Achieving an AUC of 0.8 will require risk factors 1.6 times as powerful as all those currently at hand. Thus, considerable effort should be put into finding preventive interventions and screening strategies with fewer adverse effects.

Funding

This work was supported by the Intramural Research Program of the Division of Cancer Epidemiology and Genetics, National Cancer Institute, National Institutes of Health.

Notes

Affiliations of authors: Biostatistics Branch, Division of Cancer Epidemiology and Genetics, National Cancer Institute, Rockville, MD.

The funder had no role in the design of the study; the collection, analysis, or interpretation of the data; the writing of the manuscript; or the decision to submit the manuscript for publication.

Organizers of a 2016 American Association for Cancer Research “Special Conference on Improving Cancer Risk Prediction for Prevention and Early Detection” in Orlando, Florida, asked MHG to speak on “Risk Model Requirements for Counseling, Prevention and Early Detection.” This paper is in response to that challenge. The authors have no conflicts of interest to disclose.