A neoantigen fitness model predicts tumor response to checkpoint blockade immunotherapy

Abstract

Checkpoint blockade immunotherapies enable the host immune system to recognize and destroy tumor cells¹. Their clinical activity has been correlated with activated T-cell recognition of neoantigens, which are tumor-specific, mutated peptides presented on the surface of cancer cells^2,3. Here, we present a fitness model for tumors based on immune interactions of neoantigens that predicts response to immunotherapy. Two main factors determine neoantigen fitness: its likelihood of presentation by the major histocompatibility complex (MHC) and its subsequent T-cell recognition. We estimate these two components using a neoantigen’s relative MHC binding affinity and a non-linear dependence on its sequence similarity to known antigens. To describe the evolution of a heterogeneous tumor, we evaluate its fitness as a weighted effect of dominant neoantigens in the tumor’s subclones. Our model predicts survival in anti- CTLA-4 treated melanoma patients^4,5 and anti-PD-1 treated lung cancer patients⁶. Importantly, low-fitness neoantigens identified by our method may be leveraged for developing novel immunotherapies. By using an immune fitness model to study immunotherapy, we reveal broad similarities between the evolution of tumors and rapidly evolving pathogens^7–9.

Although T-cell receptors are capable of recognizing and eliminating tumors, cancers evolve resistance mechanisms by utilizing checkpoint blockade molecules to disrupt the processes of immune recognition and attack. Clinical trials using immune checkpoint blocking antibodies, such as anti-cytotoxic T-lymphocyte-associated protein 4 (anti-CTLA-4) or anti-programmed cell death protein-1 (anti-PD-1), have improved overall survival in many malignancies by inhibiting these checkpoints¹. Though only a minority of patients achieve durable clinical benefit, multiple studies have shown genetic determinants of response. Nonsynonymous de novo somatic mutations can create neoantigens - novel protein epitopes specific to tumors which may be presented by MHC molecules and recognized by T-cells as non-self^2,3. An elevated number of mutations or putative neoantigens has been linked to improved response to checkpoint blockade therapy in multiple malignancies^4–6,10. Hence, inferred neoantigen load is a coarse-grained proxy for whether a tumor is likely to respond. Other implicated biomarkers of response include T-cell receptor (TCR) repertoire profiles¹¹, assays of checkpoint status^12,13, immune microenvironment landscape^4,14,15 and tumor heterogeneity¹⁶. Despite high overall neoantigen load, a heterogeneous tumor may have immunogenic neoantigens present only in certain subclones. Therapies targeting a fraction of the tumor could disrupt clonal competitive balance and inadvertently stimulate growth of untargeted clones¹⁷. Worldwide efforts are being undertaken to model neoantigens and quantify their features from genomic data. A predictive neoantigen-based model for immunotherapy response, complementing mass spectrometry-based neoantigen validation¹⁸, is therefore a highly sought-after goal.

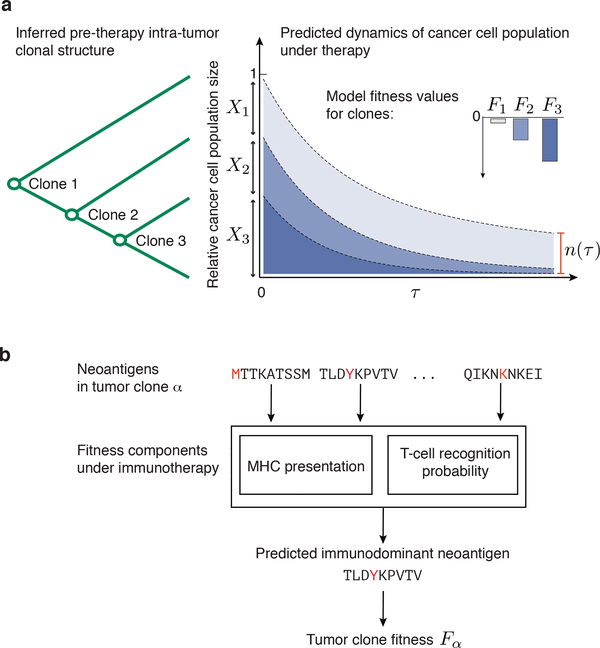
We propose a fitness model of tumor-immune interactions as a general mathematical framework to describe the evolutionary dynamics of cancer cell populations under checkpoint-blockade immunotherapy and provide a proof of concept regarding its utility (Fig. 1). Analogous fitness models based on immune interactions have been successfully applied to human influenza⁷, HIV⁸ and chronic viral infections⁹. Checkpoint blockade exposes cancer cells to strong immune pressure on their neoantigens, reducing their reproductive success. Our model predicts the evolutionary dynamics of a cancer cell population after a finite time under such pressure. We compute (𝜏), the predicted future effective size of a cancer cell population in a tumor relative to its effective size at the start of therapy. The size is a weighted sum over tumor’s genetic clones (Fig. 1a, Methods),

$$n(\tau )={\displaystyle \sum _{\alpha }{X}_{\alpha }}\exp \left(F_{\alpha }\tau \right)$$ (1)

where F_α is the fitness, X_α is the initial frequency of clone α and 𝜏 is a characteristic time scale when predictions are evaluated. As tumors may include other cell types, it is not to be interpreted as a direct measure of physical tumor size. Patients with less immunologically fit tumors will have more significant effective size reductions and, presumably, improved overall survival after therapy. The ancestral dependencies between clones determine the mutations and neoantigens inherited by clones from their ancestors (Fig. 1a). Our fitness model assigns to subclones the same or lower fitness than their ancestral clones, depending on whether they acquired new dominant neoantigens.

Figure 1 |. Evolutionary tumor dynamics under strong immune selection and a neoantigen fitness model based on immune interactions.

a, Clones are inferred from a tumor’s genealogical tree. We predict (𝜏), the future effective size of the cancer cell population, relative to its size at the start of therapy (equation (1)) by evolving clones under the model over a fixed time-scale, 𝜏. Application of therapy can decrease fitness of clones depending on their neoantigens. Clones with strongly negative fitness have greater loss of population size than more fit ones. b, Our model accounts for the presence of dominant neoantigens within a clone, α, by modeling presentation and recognition of inferred neoantigens, assigning fitness to a clone, F_α.

Our approach quantifies essential factors in determining immunogenicity of a neoantigen: an amplitude, A, determined by mutant and wildtype class I MHC-presentation and an intrinsic TCR-recognition probability, R (both are defined below). We call the product of these two factors, A×R, a neoantigen’s recognition potential. We quantify total fitness for cancer cells in a clone by aggregating over the fitness effects due to immune recognition of its neoantigens (Fig 1b, Methods). Here, we model the fitness of a given clone α by the recognition potential of its dominant neoantigen,

$$F_{\alpha }=-\underset{i\in \text{ Clone }\alpha }{\max }\left(A_i\times R_i\right)$$ (2)

where index 𝑖 runs over all neoantigens in clone α (we discuss other choices for aggregating neoantigen fitness effects in Methods).

We utilize nonamer neoantigens inferred by a consistent identification pipeline with affinities, standing in for dissociation constants, for both mutant and wildtype peptides for a patient’s HLA type¹⁹ (SI); we define the amplitude A using the relative MHC affinity between the wildtype and the mutant peptide (Methods). Despite their differing only by a single mutation, inferred binding affinities for these peptides can be substantially different (Extended Data Fig. 1). Unlike considering solely mutant or wildtype affinities, the amplitude has consistent predictive value within our model (Extended Data Table 1). A simple interpretation of this observation is that the amplitude is related to the quantity of TCRs available to recognize the neoantigen. A neoantigen needs to have low dissociation constant (i.e. high binding affinity) to be presented and generate a TCR response. However, if the wildtype peptide also has a low dissociation constant, tolerance mechanisms could have removed wildtype peptide specific TCRs. Due to cross-reactivity, the quantity of mutant specific TCRs could be reduced (see discussion in Methods).

We also estimate the intrinsic probability of TCR-recognition of a neoantigen. Here we utilize the strength of neoantigen’s alignments to positively recognized, class-I restricted T-cell antigens from the Immune Epitope Database²⁰ (IEDB).

This approach does not assume preexisting host immunity due to this epitope set. Rather, we posit high-scoring neoantigens are more “non-self”. As TCRs have intrinsic biases in their generation probability and can recognize large classes of peptides via cross reactivity^21,22, such neoantigens would be more likely recognized. We use a consistent thermodynamic model to estimate this probability (Methods): for a neoantigen with peptide sequence 𝐬 and IEDB epitope with sequence 𝐞, the alignment score between 𝐬 and 𝐞 estimates the binding free energy between 𝐬 and a TCR that recognizes 𝐞. Importantly, the probability a neoantigen is bound by a TCR is given by a nonlinear logistic dependence on sequence alignment scores to the epitope set (Methods).

We apply our model to three datasets: two melanoma cohorts treated with anti- CTLA-4^4,5, and a non-small-cell lung cancer cohort treated with anti-PD-1⁶. Efficacy is assessed using overall survival of patients from the beginning of immunotherapy (Methods). Neoantigen anchor positions 2 and 9, for the majority of HLA types, are constrained by hydrophobic bias, as reflected by decreased amino-acid diversity at these positions²³ (Extended Data Fig. 2). We observe computational predictions of MHC affinities for wildtype peptides with non-hydrophobic anchor residues led to non-informative amplitudes. Hence, neoantigens with mutations generated from non-hydrophobic wildtype residues at positions 2 and 9 are excluded. The parameter 𝜏 in equation (1) sets the characteristic time scale of response to therapy. At this time, clones with dominant neoantigens having amplitudes larger than 1/𝜏 will have been suppressed. The model has two other free parameters: the midpoint and steepness defining R (Methods). For each cohort, we infer parameters by maximizing the survival log-rank test score on independent training data.

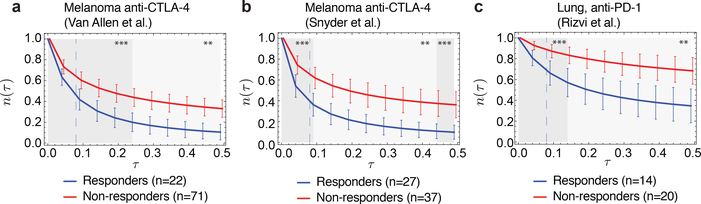
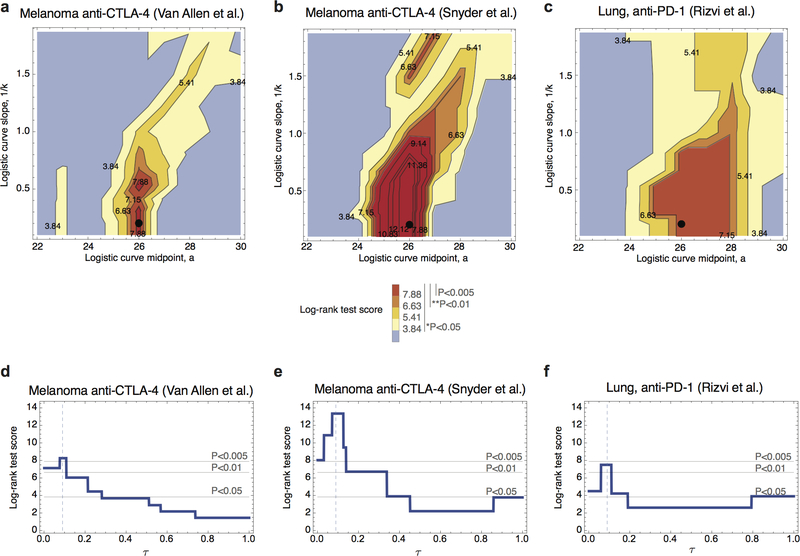
We use the Snyder melanoma cohort with 64 patients to train parameters for the 103 metastatic patients in the Van Allen cohort and vice versa; we use the total score of both melanoma cohorts to train parameters for the smaller lung cancer cohort from Rizvi et al. with 34 patients (Methods). For each cohort, we obtain significant stratification of patients: log-rank test p-values are p=0.0049 for the Van Allen et al., p=0.0026 for Snyder et al., and p=0.0062 for Rizvi et al. (Extended Data Table 1). The parameters thereby obtained are consistent between datasets and mutually included within each other’s error bars (Extended Data Table 1, Methods). We further performed a joint optimization of the cumulative log-rank test score of the three cohorts, obtaining a single set of parameters with predictions highly stable around these values (Extended Data Fig. 3). The alignment threshold parameter is consistently set to 26 (Extended Data Table 1), which in our datasets is obtained by alignments of average length of 6.8 amino-acids, just above the length of peptide motifs one would expect the TCR repertoire to discriminate (SI). The slope parameter is set to 4.87 defining a strongly nonlinear dependence on alignment score, with the recognition probability dropping below 0.01 for score 25 and reaching above 0.99 at score 27 (Extended Data Fig. 4). The 𝜏 parameter is set to 0.09, meaning clones with amplitudes larger than 11.1 are, on average, suppressed at prediction time. At these consistent parameters, separation of patients does not change for Van Allen et al. and Rizvi et al. (log-rank score increases by less than 1 unit, p=0.004 for Van Allen et al. and p=0.0062 for Rizvi et al.), and it improves to p=0.00026 for Snyder et al. (Fig. 2). Patient segregation by (𝜏) evaluated at infinitesimally small 𝜏 (equivalent to average tumor fitness over clones, Methods) is also significant (Extended Data Fig. 3, Extended Data Table 1), suggesting predictive power depends more on the model’s ability to capture immune interactions than the duration of evolutionary projections. Finally, the predicted evolutionary dynamics of tumors separate therapy responders and non-responders, using patient classifications defined in the original studies^4,5,6. In all datasets responders are predicted to have significantly faster decreasing relative sizes (𝜏) across a broad interval of 𝜏 values (Fig. 3). The performance of the model deteriorates when we disrupt the biological relevance of input data. When using the IEDB epitopes not supported by positive T-cell assays, the model loses predictive ability in both melanoma cohorts (Methods, Extended Data Table 1, and Extended Data Fig. 5). Similarly, the model generally does not give significant patient separations when using neoantigens derived with randomized patient HLA types (Extended Data Fig. 6, SI).

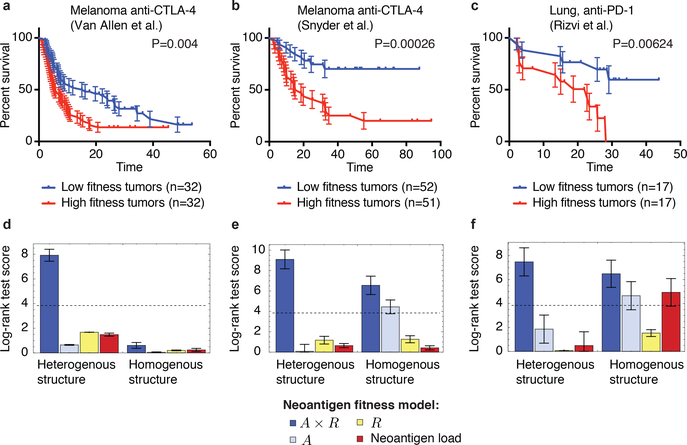
Figure 2 |. Neoantigen fitness model is predictive of survival after checkpoint blockade immunotherapy.

a-c, Tumor fitness is calculated across two melanoma cohorts treated with anti-CTLA-4^4,5 and one lung cancer cohort treated with anti-PD-1⁶. Kaplan-Meier curves of overall survival are displayed for each, with samples split by the median value of their tumor’s relative population size (𝜏) (equation (1)). Error bars represent standard error due to sample size (SI). The p-values from log-rank tests comparing the two KM curves are shown above each plot. d-f, Log-rank test score for the full neoantigen fitness model (navy blue), for partial models accounting for a single feature of the full model (light blue and yellow) and for the neoantigen load model (red). All models are evaluated both over a tumor’s clonal structure (heterogenous, left) and without clonality (homogenous, right). All model scores are presented for parameters obtained on independent training data (Methods). Error bars are the standard deviation of the log-rank test score acquired from survival analysis with one sample removed at a time (d, n=64, e, n=103, f, n=34). Dashed lines correspond to 5% significance.

Figure 3 |. Predicted evolutionary dynamics in cohorts.

a, Distribution of predicted relative population size 𝑛(𝜏) for responders and non-responders at consistent parameters across a, Van Allen et al.⁴ b, Snyder et al.⁵; and c, Rizvi et al.⁶ cohorts. Responders and non-responders were defined within those studies; samples not classified as either are excluded. Error bars are 95% confidence intervals around the population average. The dashed line indicates the consistent time-scale, 𝜏 = 0.09, used across all three datasets for survival predictions (Methods and Extended Data Fig. 3). The significance of separation of the two groups was computed with Kolmogorov-Smirnov test, p-values at 𝜏 = 0.09 are 0.0016 (Van Allen et al.), 0.00084 (Snyder et al.) and 0.00071 (Rizvi et al.). Background shading represents significance of separation of the two groups as a continuous function of 𝜏 (**p<0.01, ***p<0.001).

The success of our model strongly depends on the joint contribution of 𝐴 and 𝑅 in equation (2). We construct partial models with only one component and repeat the same training and validation procedure, with survival analysis separating patients into equal size groups as in the full model (Fig. 2, and Extended Data Table 1). In all datasets, partial models have lower log-rank scores than the full model and neither 𝐴 nor 𝑅-only models result in significant segregation for any cohort. We also compare our full model with a neoantigen load model, which assigns a uniform fitness cost to each neoantigen. This model does not significantly separate patients by median in either cohort (Fig. 2, Extended Data Table 1). Finally, we assess the importance of tumor clonal structure in our identification of dominant neoantigens. In all data sets, our full clonal model performs significantly better than an alternative model assuming homogenous tumor structure (Fig. 2). Clonality appears less crucial in partial models, which have either marginal or no statistical significance (Fig. 2, Extended Data Table 2). Moreover, our model is predictive independent of other clinical correlates (Proportional Hazard model, Extended Data Table 3).

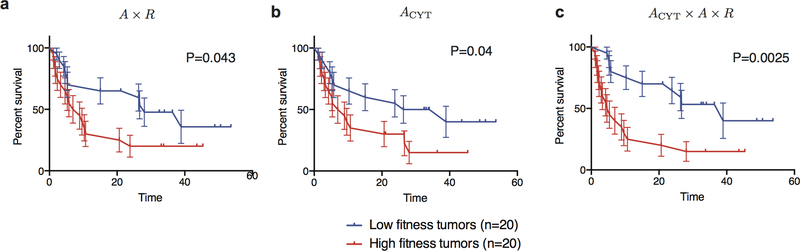
Our framework allows for straightforward incorporation of information about the tumor’s microenvironment. For the cohort from Van Allen et al., gene expression data is available on 40 patients and local cytolytic activity is significantly associated with benefit (p=0.04, Methods), as also observed in the original study by Van Allen et al⁵. As a proof of principle, we incorporated cytolytic score²⁴ as an amplitude multiplying the T-cell recognition probability. Its inclusion improves predictions on these 40 patients, as assessed with survival analysis, (p=0.043 and p=0.0025 respectively, Extended Data Fig. 7).

Immune interactions govern the evolutionary dynamics of cancers under checkpoint blockade immunotherapy and many rapidly evolving pathogens; fitness models can predict such dynamics over limited periods into the future, as recently shown for seasonal human influenza⁷. However, influenza evolution is determined by antigenic similarity with previous strains in the same lineage, whereas cancer cells acquire somatic mutations in a large set of proteins. Hence, the cancer immune interactions are distributed in a larger and less homogenous antigenic space. The fitness effects of these interactions have a specific interpretation: they capture neoantigen “non-selfness”. Our model formalizes what makes a tumor immunologically different from its host, analogously to models for innate recognition of non-self nucleic acids²⁵.

The approach can be naturally extended to other fitness effects, such as positive selection due to acquisition of driver mutations, the impact of additional components in the microenvironment or the hypothesized role of the microbiome^26,27. Further advances in predicting proteosomal processing¹⁸ and stability²⁸ of neoantigen-MHC binding could improve predictions. Our framework should be useful in studies of acquired resistance to therapy and may be crucial for understanding when cross-reactivity with self-peptides may result in side effects^29,30. Because our fitness model is based on specific interactions underlying presentation and recognition of neoantigens, it may also inform the choice of therapeutic targets for tumor vaccine design.

Methods

1. Evolutionary dynamics of a cancer cell population in a tumor

The fitness of a cancer cell in a genetic clone α is its expected replication rate, i.e.

$$\frac{d{N}_{\alpha }}{d\tau }=F_{\alpha }{N}_{\alpha }$$ (3)

where N_α is the population size of clone α and F_α is that clone’s fitness. Checkpoint-blockade immunotherapy introduces a strong selection challenge, which we anticipate overshadows pre-therapy fitness effects in a productive response. For a given clone α the dynamics of its absolute size are therefore given by N(𝜏) = N_α (0)exp(F_α𝜏), and the total cancer cell population size is computed as a sum over its clones

$$N(\tau )={\displaystyle \sum }_{\alpha }{N}_{\alpha }(\tau )={\displaystyle \sum }_{\alpha }{N}_{\alpha }(0)\exp \left(F_{\alpha }\tau \right).$$ (4)

The absolute size N(𝜏) is an effective population size, the number of cells estimated to have generated the observed clonal diversity.

As our measure of survival, we use the evolved relative effective population size 𝑛(𝜏) = N (𝜏) /N (0), which compares the predicted future population size after a characteristic dimensionless time scale of evolution 𝜏 to the initial pretreatment effective size N(0), the assumption being that successful responders to therapy will have their future effective cancer cell population size more strongly suppressed. We denote the initial frequency of clone α as X_α = N(0)/N(0), these frequencies are inferred from bulk exome reads from a tumor sample, as described in the Supplementary Information. Hence, to compute (𝜏) we only require estimates of the initial frequencies and fitness values for each clone, as shown in equation (1); the absolute population size estimates are not needed. We model the hypothesis that due to the unleashing of a T-cell mediated immune response by checkpoint-blockade immunotherapy, the deleterious effects due to recognition of neoantigens are a dominant fitness effect, and tumors with the greatest degree of selective immune challenge are better responders to therapy.

Clonal structure of a tumor and clone frequencies.

To reconstruct the clonal tree structure of a tumor from exome sequencing data, we use a likelihood scheme based on the allele frequencies of its mutations³¹ (SI). The trees estimate the nested clonal structure of the tumor and the frequency of each clone, X_α. The differences between the high scoring trees are marginal on our data, concerning only peripheral clones and small differences in frequency estimates. We compute the predicted relative size of a cancer population, (𝜏), as an averaged prediction over the 5 trees with the highest likelihood score, weighting their contribution proportionally to their likelihood.

2. Fitness model based on neoantigen recognition potential

Neoantigen recognition based fitness cost for a tumor clone.

Our model associates each neoantigen with a fitness cost, which we term the recognition potential of a neoantigen. The recognition potential of a neoantigen is the likelihood it is productively recognized by the TCR repertoire. It is defined by two components. The first is the amplitude A which is given by the relative probability that a neoantigen will be presented on class I MHC and the relative probability that its wildtype counterpart will not be presented. The second is the probability R that a presented neoantigen will be recognized by the TCR repertoire. For a given neoantigen their product defines its recognition potential, AxR. Both components are described in detail below.

To assess the total fitness effect for a clone α with multiple neoantigens, we aggregate individual neoantigen fitness effects as F_α = - max_i∈Cloneα(A_i×R_i), where i is an index iterating over neoantigens in the clone. Therefore, the full form of the predicted relative cancer cell population size is given by

$$n(\tau )={\displaystyle \sum }_{\alpha }{X}_{\alpha }\exp \left[-\underset{i\in \text{Clone}\alpha }{\max }\left(A_i\times R_i\right)\tau \right].$$ (5)

One could use a more general model for aggregating neoantigen fitness effects within a clone,

$$n(\tau ,\beta )={\displaystyle \sum }_{\alpha }{X}_{\alpha }\exp \left[{\displaystyle \sum }_{i\in \text{Clone}\alpha }\frac{\exp \left(-\beta f_i\right)}{Z(\beta )}{f}_i\tau \right],$$ (6)

where f_i = − A_i×R_i and Z(β) = Σ_{iϵ Clone α} exp(−βf_i)In addition to equation (5), which corresponds to the limit β→∞, we show the case where β = 0 (uniform summation over all neoantigens, Extended Data Table 1). In that sense equation (6) represents a general mathematical framework for weighing neoantigen contributions, with weights reflecting the probability of their productive recognition. The choice of β could be informed by additional data sources or defined in a clone specific manner, and it would then become an additional model parameter (or parameters). Taking the highest score within a clone as in equation (5) is consistent with notions of immunodominance - that a relatively small set of antigens drive the immune response.

MHC-amplitude.

The amplitude, A, is the ratio of the relative probability that a neoantigen is bound on class I MHC times the relative probability that a neoantigen’s wildtype counterpart is not bound. The amplitude is defined as$A=\left(P_U^{WT}/P_B^{WT}\right)\times \left(P_B^{MT}/P_U^{MT}\right)$, where $P_B^{MT}$ is binding probability of a neoantigen, $P_B^{WT}$is the binding probability of its wildtype counterpart, and $P_U^{WT}=1-P_B^{WT}$ and$P_U^{MT}=1-P_B^{MT}$. As a result, the amplitude rewards cases where the discrimination energy between a mutant and wildtype peptide by the same class I MHC molecule (i.e. the same HLA allele) is large³², while the mutant binding energy is kept low. The 𝜏 parameter effectively sets this energy scale for dominant neoantigens in a clone when R = 1. Assuming similar concentrations for mutant and wildtype peptides, the amplitude is the ratio of wildtype to mutant dissociation constants,

$$A=K_d^{WT}/K_d^{MT}.$$ (6)

Negative thymic selection on TCRs is not absolute, but rather “prunes” the repertoire recognizing the self proteome^33,34 We therefore use A as a proxy for the availability of TCRs in the repertoire to recognize a neoantigen. Neoantigens differ from their wildtype peptides by only a single mutation. Given the uniqueness of nonamer sequences in the self-proteome due to finite genome size (SI) it is highly improbable that the mutant peptide would have another 8-mer match in the human proteome, so we only account for the comparison with the respective wildtype peptides. We verified that the above is the case for 92% of all neoantigens, with the remainder largely emanating from gene families with many paralogs (SI). The amplitude can be interpreted as a multiplicity of receptors available to cross-reactively recognize a neoantigen.

MHC-binding probabilities are derived from the dissociation constants, which are themselves estimated from computationally predicted binding affinities, as justified below. Affinities are inferred for each peptide sequence and patient HLA type¹⁹; all mutant peptide sequences considered as neoantigens meet a standard 500 nM cutoff for their affinities (SI). NetMHC 3.4 occasionally predicts affinities with very high values where training may be limited, and creating small denominators that can inflate the amplitude. In melanoma and lung cancer a high mutational burden inflates the frequency of such events. As a remedy, a pseudocount, 𝜀, is introduced so that, for both mutant and wildtype peptides P_u/P_b →(P_u + 𝜀)/(P_b + 𝜀). In this case the new dissociation constant divided by peptide concentration becomes

$$\frac{K_d/[L]+\epsilon \left(1+K_d/[L]\right)}{1+\epsilon \left(1+K_d/[L]\right)}\approx \frac{K_d/[L]}{1+\epsilon K_d/[L]}$$ (7)

for small 𝜀, where K_d was the original dissociation constant and [L] is the peptide concentration. Consequently 1/𝜀 sets a scale at which dissociation constants are not reliable for large K_d at a given concentration. To fix these scales, we note that assays to determine dissociation constants for peptide-MHC binding are typically performed at 0.1–1 nM where the ligand concentration is typically small compared to the dissociation constant³⁵. In this regime, affinities can be interpreted as dissociation constants and 3687 nM is the outer range of predictability for the assays upon which NetMHC 3.4 is trained at no more that unit peptide concentrations. 𝜀/[L] is therefore chosen to be 0.0003≈1/3687 across datasets.

As the affinity is always less than 500 nM for the mutant peptide this correction is only relevant for the wildtype peptides. The corrected amplitude then becomes

$$A\approx \frac{K_d^{WT}}{K_d^{MT}}\cdot \frac{1}{1+(\epsilon /[L])\cdot K_d^{WT}}.$$ (8)

The amplitude in this form, combined with the TCR-recognition term discussed below, has a high predictive value for patient survival predictions (Fig. 3), consistently over the three patient cohorts, which is not the case of either the mutant or wildtype dissociation constants on their own (Extended Data Table 1).

TCR-recognition.

We estimate R, the probability that a neoantigen will be recognized by the T-cell receptor repertoire by alignment with a set of epitopes given by the Immune Epitope Database and Analysis Resource²⁰ (IEDB, described in the Supplementary Information). We restrict ourselves to linear epitopes from human infectious diseases that are positively recognized by T-cells after class I MHC presentation. In this approach, we assume that a neoantigen predicted to cross-react with a TCR from this pool of immunogenic epitopes is a neoantigen more likely to be immunogenic itself, as members of the T-cell receptor repertoire both recognize a high number of presented antigens^36,37 and have intrinsic biases in their generation probabilities²¹.

We use a multistate thermodynamic model to define R. In this model, we treat sequence similarities as a proxy for binding energies. To assess sequence similarity between a neoantigen with peptide sequence 𝐬 and an IEDB epitope 𝐞, we compute a gapless alignment between the two sequences with a BLOSUM62 amino-acid similarity matrix³⁸ and we denote their alignment scores as |𝐬, 𝐞|, Given these sequence similarities, for a given neoantigen with peptide sequence 𝐬, we compute the probability that it is bound by a TCR specific to some epitope e from the IEDB pool as

$$R=Z{(k)}^{-1}{\displaystyle \sum }_{\text{e}\in \text{IEDB}}\exp [-k(a-\left|s,e\right|)],$$ (9)

where a represents the horizontal displacement of the binding curve, k sets the steepness of the curve at a, and

$$Z(k)=1+{\displaystyle \sum _{\text{e}\in \text{IEDB}}\exp }[-k(a-\left|s,e\right|)]$$ (10)

is the partition function over the unbound state and all bound states. In the model, k functions as an inverse temperature and a - |𝐬, 𝐞| functions as a binding energy. These parameters define the shape of the sigmoid function (Extended Data Fig. 4) and, along with the characteristic time scale 𝜏, are free parameters to be fit in our model (see below).

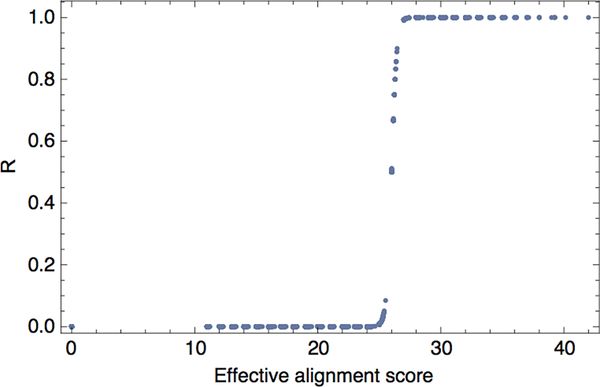
The parameters which give consistently informative predictions across all three datasets are a = 26 and k = 4.87. The logistic function is therefore a strongly nonlinear function of the effective alignment score, log(∑_e∈IEDB exp[− k(a − |s,e|)]). The average alignment length corresponding to score 26 is 6.8 for neoantigens in our datasets, but the effective alignment score is occasionally increased by multiple contributions of shorter alignments. Under the interpretation where, for a sufficiently presented neoantigen, A represents the multiplicity of available TCRs and R represents an intrinsic probability of recognition, A×R represents the effective size of the overall TCR response. We present it as a core quantity that can be modulated by additional environmental factors such as the T- cell infiltration (discussed below).

IEDB sequences.

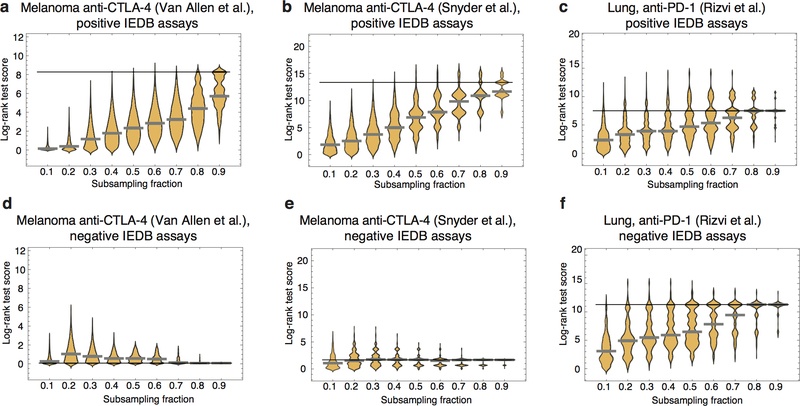
The predictive value of R depends on the input set of IEDB sequences. The set we used in our analysis contained 2552 unique epitopes (SI). We tested how the predictions depend on the content and size of the dataset by performing iterative subsampling of IEDB sequences at frequencies varying from 10% to 90% of the total set size. We repeated the survival analysis and log-rank test score evaluation (Extended Data Figure 5). For all three datasets removal of sequences has on average a negative impact on their predictive power, which monotonically decreases with the subsampling rate. In the Van Allen et al. cohort median performance was below significance already at 70% subsampling and lower, and for Snyder et al. and Rizvi et al. at 20% and lower. To investigate the biological input associated with the set of curated IEDB sequences that we use, we also evaluated the R component using an alternative set of IEDB sequences, coming from T-cell assays that did not have a positive validation. This is a larger set of 4657 sequences. In the two melanoma datasets, the predictions have gotten worse, not giving significant separation of patients in the survival analysis. This effect was also not due to the different sequence set size - subsampling of sequences did not improve the outcome. While in the Rizvi et al. dataset the predictions were still significant, this significance was not supported by consistency between all three datasets which is observed on the IEDB sequence set with positive assays.

Inclusion of microenvironment and proteosomal processing in fitness model.

The role of the microenvironment in the likelihood of productive T-cell recognition of tumor neoantigens can be incorporated in a natural manner into our modeling framework. We utilize the cytolytic score (CYT), the geometric mean of the transcript per kilobase million of perforin and granzyme²⁴. We do so for the 40 patients from the Van Allen, et al, anti-CTLA4 melanoma dataset, which have matched genome and transcriptome sequencing and where CYT had shown predictive value. For this set we also derive the CD8 T-cell fraction using CIBERSORT³⁹. The two values have a Pearson correlation coefficient of 0.938. Given their encapsulation of similar information we used CYT as it had previously been show to give significant segregation of patient benefit⁵. The score provides an additional amplitude A_CYT and the recognition potential becomes A_CYT×A×R. Therefore, the cytolytic score amplifies the recognition potential by the degree of cytolytic activity. We attempted to include proteosomal processing into our model as an additional criterion, as evaluated with NetCHOP⁴⁰ We tested this procedure on the Rizvi et al. cohort; however, the imposed stronger filtering of neoantigens leads to the loss of predictive power of the model.

3. Model parameters

Parameter training.

To choose model parameters a and k in equation (9) and the characteristic time 𝜏 at which the prediction is evaluated (equations (2) and (5)), we select the parameters that maximize log-rank-test scores of survival analysis on patient cohorts. The survival analysis is performed by splitting patient cohort by the median value of (𝜏) into high and low fitness groups. For each cohort, we perform parameter training on independent data: we use the melanoma cohorts to train parameters for each other by using the maximal score of one to define parameters for the other, and we use both melanoma cohorts and maximization of their total log-rank test score to train parameters for the lung cohort. To infer consistent parameters between all datasets, we maximize the total log-rank test score over the three cohorts.

For a given training set we compute the optimal parameters$\widehat{\Theta }=[a,k,\tau ]$, as an average $\widehat{\Theta }={\langle \Theta \rangle }_w$ over a distribution w(Θ) defined by the log-rank test score landscape on this set

$$w(\Theta )=Z^{-1}(\lambda )\exp [\lambda \left(S_{\text{max}}-S(\Theta )\right],$$ (11)

where Z(𝜆) is the probability distribution normalization constant, S(Θ) is the value of the log-rank test score with parameters Θ and S_max is the maximal score value obtained over all possible parameters. The weight parameter 𝜆 is chosen such that the total statistical weight of the suboptimal parameter region is less than 0.01, the suboptimal scores are those less than max(3.841, S_max - 2) (where 3.841 is the score value corresponding to 5% significance level of the log-rank test score). Using a smooth local neighborhood of parameters around the optimal values prevents over-fitting on a potentially rugged score landscape. For each individual parameter, the error bars reported in Extended Data Tables 1 and 2 are computed as standard deviation using marginalized probability distribution w (Θ) for this parameter.

The survival score landscapes (Extended Data Fig. 3) are consistent between the datasets. The optimal value of parameter a, the midpoint of the logistic binding function, is around 26 and parameter k, the steepness of the logistic function, lives on a trivial axis above value 4, suggesting strong nonlinear fitness dependence on the sequence alignment score.

4. Model selection

Alternative fitness models.

We compare our full model in equation (5) to alternative models. We perform simple model decompositions, where only one component is used

$$F_{\alpha }=-\underset{i\in \text{Clone}\alpha }{\max }{A}_i,$$ (12)

$$F_{\alpha }=-\underset{i\in \text{Clone}\alpha }{\max }{R}_i.$$ (13)

Further, we decompose the amplitude $A=K_d^{WT}\times \frac{1}{K_d^{MT}}$ and test various variants of the model, with and without the R component,

$$F_{\alpha }=-\underset{i\in \text{Clone }\alpha }{\max }{K}_d^{WT}{}_i\left[\times R_i\right],$$ (14)

$$F_{\alpha }=-\underset{i\in \text{Clone }\alpha }{\max }\frac{1}{K_d^{MT}{}_i}\left[\times R_i\right].$$ (15)

We investigate how informative the alignments contributing to the R_i components are and we test a model where alignments are restricted to the 6 residues in- between anchor positions, on positions 3–8. We also demonstrate the loss of predictive power of a model that does not implement any filtering of neoantigens mutated on position 2&9 (see discussion in section 2 of Methods and Extended Data Fig. 2).

We reduce the problem of choosing the neoantigen aggregating function to that of model selection. We test a model where fitness is defined by the total effect of all neoantigens in the clone (which is the limit case of β = 0 in equation (6)),

$$F_{\alpha }=-{\displaystyle {\sum }_{i\in \text{Clone}\alpha }}{A}_i\times R_i.$$ (16)

Finally, we formulate a simple fitness model that associates a constant fitness cost with each neoantigen,

$$F_{\alpha }=-L_{\alpha },$$ (17)

where L_α is the number of neoantigens in clone α, referred to as the neoantigen load of clone α.

Homogenous structure models.

For each fitness model, we can define its homogenous structure equivalent, which assumes a tumor is strictly clonal with all neoantigens in the same clone at frequency 1. In a homogenous model the population size is thus modeled by a simple exponential,

$$n(\tau )=\exp [F\tau ],$$ (18)

where F is the fitness of the homogenous tumor. Since in this model tumors show a constant decay over time, ranking of (𝜏) values for patients is defined only by fitness and does not depend on 𝜏. Therefore, 𝜏 is not a free parameter in these models when optimizing log-rank test score in survival analysis.

Average fitness.

We also investigate the average fitness of clones,

$$\langle F\rangle ={\displaystyle \sum _{\alpha }{X}_{\alpha }}{F}_{\alpha },$$ (19)

as a predictive marker for patients and an alternative to 𝑛(𝜏). The average fitness reflects the rate at which the tumor cell population is decreasing in size at the beginning of therapy. For the purpose of patient ranking, it is equivalent to (𝜏) at infinitesimally small values of the time parameter 𝜏. This is a lower complexity model because 𝜏 is not a free parameter. However, this measure is less robust to outliers - small clones with very low fitness can dominate the average fitness, while the evolutionary projection in (𝜏) removes such effects.

Predictive power.

We assess the predictive power of all models with survival analysis, separating patients into equal size groups by the median value of (𝜏) or the median value of the average fitness ⟨F⟩ within the cohort. We use a log- rank test, the results of this comparison are reported in Extended Data Table 1 and in Extended Data Table 2 for models that disregard tumor subclonal composition. To assign error bars to fluctuations of the log-rank test score we perform a leave-one-out analysis. That is, we repeat the survival analysis for each dataset after leaving out one sample in a cohort and compute standard deviation of the test statistic over all leave-one-out iterations. We claim a fitness model is predictive if it gives patient segregation of highly significant scores in all datasets with the same consistent set of parameters. Only the full neoantigen fitness model meets these criteria. The results are highly significant when patient segregation is based on (𝜏) values. The average fitness criterion from (equation 19) marginally meets the above requirements for predictiveness, but with smaller significance (Extended Data Table 1).

Comparison with thresholded neoantigen load.

In our survival analysis, we use a standard, non-optimized partitioning of patients into two equally sized groups by the median value of (𝜏). This approach allows for unbiased comparison of models, and assigns a stringent predictive value. Our results do not contradict the earlier reported predictive quality of neoantigen load. Consistent with Snyder et al.⁴, we observe a significant split at a threshold value of 100 neoantigens or less. This threshold classifies more than 70% of the patients in a long-term surviving group; separation by total neoantigen load is not significant at lower fractional partitions, including the median. In Van Allen et al., survival analysis was not originally presented and we did not see a significant separation of patients at any possible splitting by a neoantigen load threshold. Finally, the significant separation for the Rizvi et al. cohort is observed for the range a 32–50% range of partitions, including by the median (Fig. 2, Extended Data Table 1). It is worth noting that for this cohort we use previously unpublished overall survival data, which differs from the progression free survival data used by the original study⁶. In all cohorts, our neoantigen fitness model and partitioning based on (𝜏) measure give significant separations at a larger range of partitions: 40–60% for the Van Allen et al. cohort, above 40% for the Snyder et al. cohort and 47–80% for the Rizvi et al. cohort.

Data availability

Sequencing data from the three cohorts are publicly available and deposited in dbGap (Van Allen et al. - accession number phs000452.v2.p1, Snyder et al. - accession number phs001041.v1.p1 and Rizvi et al. - accession number phs000980.v1.p1). Mutations, inferred neoantigen peptides, survival data for each dataset are submitted as supplementary data. We also submit neoantigen fitness predictions for clones and neoantigens of all cohorts, and the sets of IEDB sequences used in this analysis.

Code availability

Custom script examples for computation of neoantigen fitness cost are included as Supplementary Data 7. Additional custom code will be made available upon reasonable request.

Extended Data

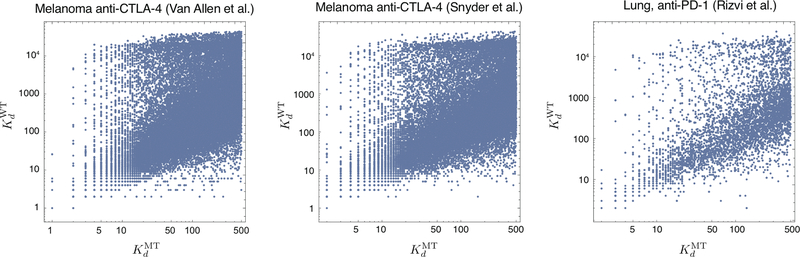
Extended Data Figure 1 |. Inferred MHC binding affinities of mutant versus wildtype peptides.

Neoantigens used in this study are 9-residue long peptides affinities predicted to be less than 500nM by NetMHC3.4¹⁹ (SI). We plot predicted affinities of mutant peptides, designated$K_d^{MT}$, versus the predicted dissociation affinities of the wildtype peptides, which generated them, designated$K_d^{WT}$. A single point mutation can lead to predicted dissociation constant difference of up to 4 orders of magnitude.

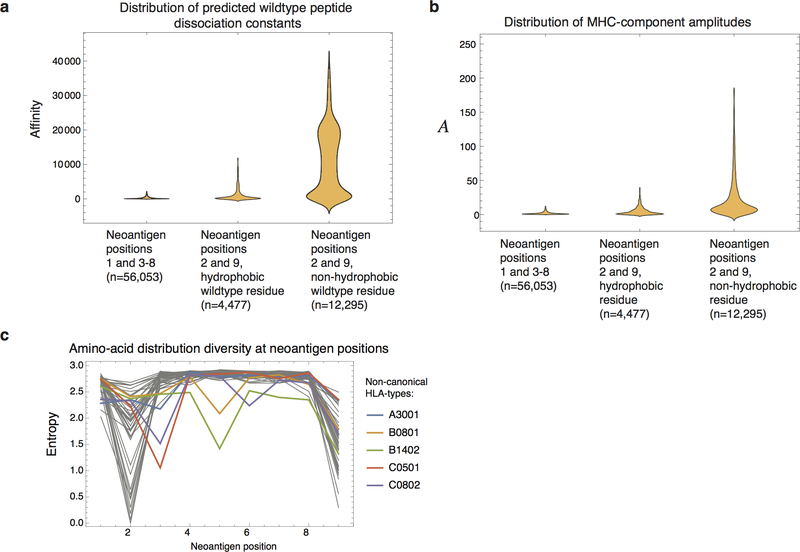
Extended Data Figure 2 |. Positions 2 and 9 have a subset of neoantigens with less predictive value.

The violin plots represent data density at a given value on a vertical axis. a, Neoantigens coming from mutations at position 2 or 9 tend to have wildtype peptides with larger predicted affinities. In particular, this is magnified if the corresponding wildtype residue is non-hydrophobic. b, Those biases are reflected in a wider distribution of amplitudes (Methods, equation (6)) for wildtype peptides with non-hydrophobic residues at positions 2 and 9. c, Shannon entropy of amino acid diversity by position in neoantigens, shown for all distinct HLA-types and computed based on neoantigens across all datasets. Positions 2 and 9 have lower entropy than other residues. Other sites have the same entropy as the overall proteome²³ and are therefore unconstrained. Five HLA with non-canonical entropy profiles are singled out in the plot. These HLA- types contributed only 5 informative neoantigens across all datasets and therefore are not treated differentially in our model.

Extended Data Figure 3 |. Survival analysis score landscape as a function of model parameters.

a-c, The landscape of log-rank test scores as the function of the parameters of the TCR binding model (a and 1/k), shown for the consistent choice of 𝜏 = 0.09, colors represent the significance level of the long-rank test. The regions of high scores are similar across all three datasets. The point corresponding to consistent parameters (a = 26 and k = 4.87) is marked by a black dot in each plot. d-f, Log-rank score for fitness model at consistent binding function parameters, plotted as a function of 𝜏. Dashed vertical lines are at 𝜏 = 0.09, thin solid lines mark the score values corresponding to significance of 0.05, 0.01 and 0.005. (n=103 (a, d), n=64 (b, e), n=34 (c, f)).

Extended Data Figure 4 |. Alignments to IEDB epitopes.

The TCR recognition probability for a neoantigen is a sigmoidal function of the neoantigen’s alignment scores with IEDB epitopes, here shown as evaluated for the set of neoantigens from Van Allen et al. cohort patients, using the consistent set of parameters.

Extended Data Figure 5 |. Effect of IEDB sequence content on predictive power of neoantigen fitness model.

Predictions were performed using subsampled IEDB epitope sequences, with subsampling rate varying between 0.1 and 0.9. For each rate, 10,000 iterations were performed to obtain a distribution of log-rank test scores. The violin plots represent data density at a given value on a vertical axis (n=10,000). Solid black lines mark the log-rank test score of the prediction on the full set of epitope sequences and gray thick lines mark the median scores on subsampled data. a-c, Subsampling of the original set of IEDB sequences, supported by positive T-cell assays, shows that quality of predictions decreases with subsampling rate. Prediction quality is more robust in the Snyder et al. and Rizvi et al. datasets. d-f, Analogous subsampling procedure was repeated on IEDB sequences not supported by positive T-cell assays. For Van Allen et al. and Snyder et al. model performance is substantially lowered.

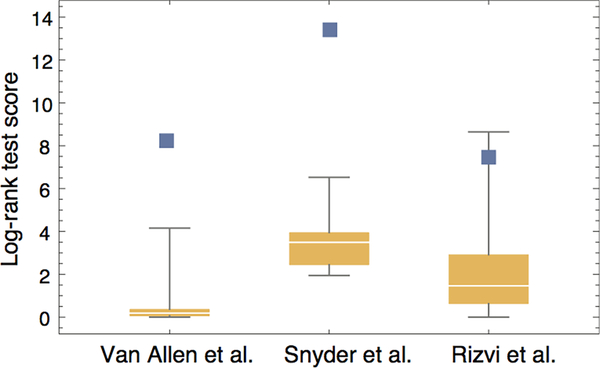
Extended Data Figure 6 |. Reshuffling patient HLA-types reduces predictive power of neoantigen fitness model.

In each cohort, we performed 10 iterations of reshuffling patient HLA-types, followed by computational neoantigen prediction, fitness model calculation and survival analysis. We report the distribution of log-rank test scores over these iterations: boxes mark 75% confidence intervals and whiskers mark the range of scores (n=10). The score values for the model on original data are marked with blue squares.

Extended Data Figure 7 |. Cytolytic score improves prediction quality.

a, Kaplan-Meier curves of overall survival shown for our model applied to Van Allen et al. for n=40 patient subset with transcriptional data. Samples are split by the median value of their tumor’s relative population size (𝜏) (equation (1)). Error bars represent standard error due to sample size. b, Model optimized for cytolytic score significantly separates patients (Methods). c, Inclusion of cytolytic score in our model improves prediction on 40 patient subset. The p-values from log-rank tests comparing the two KM curves re shown above each plot. In a and c, we use consistent parameters trained on the three cohorts (Extended Data Fig. 2); in b parameter 𝜏 is optimized.

Extended Data Table 1 |. Ranking of fitness models when accounting for tumor subclonal composition.

We present ranking of fitness models evaluated for the three cohorts, Van Allen et al. (n=103), Snyder et al. (n=64) and Rizvi et al. (n=34). We compare survival prediction of full fitness model (Methods, equation (9)) with alternative models described in Methods: (1) models that eliminate one of the features of the full model, namely A-only model (Methods, equation (12)) and R -only model (Methods, (equation 13)); models without wildtype dissociation constant (Methods, equation (14)) and without mutant dissociation constant (Methods, equation (15)); neoantigen load model (Methods, equation (17)); an additive neoantigen fitness model (Methods, equation (15)) which uniformly summates fitness contributions of neoantigens in a clone. Additionally, we compare the model in which alignments to IEDB epitopes are evaluated only on position 3–8, a model that does not implement any filtering of neoantigens on position 2&9, and a model where the R component is evaluated on IEDB assays without positive validation. Finally, we test an alternative predictive criterion by using the average fitness over tumor clones instead of η(τ) (Methods, (equation 18)) to separate patients in survival analysis. For each model, we report parameters used for predictions and error bars for these parameters (Methods). We report log-rank test scores for all models and the log- rank test p-value for models with significant patient segregation (p<0.05). The significant models are highlighted: yellow for models significant in a single cohort, orange for models significant across two cohorts, and red for models significant in all three cohorts.

Van Allen et al., Melanoma anti-CTLA-4	Parameters trained on Snyder						Log-rank test
Models	τ		a		k		Score		Significance		Equation
	Mean	Std	Mean	Std	Mean	Std	Mean	Std
AxR	0.09003	±0.077	26	±2.988	4.19761	±0.01	7.92	±0.49	0.00489	***	(2)
Partial models:
A	0.00131	±0.0001	-	-	-	-	0.65	±0.03			(12)
R	12.33338	±1.827	12.5	±1.074	1.89795	±24.161	1.68	±0.01			(13)
1/kdM xR	0.03851	±1.711	21.3	±0.353	1.50243	±0.02	2.01	±0.45			(14)
1/kdM	0.3386	±0.0001	-	-	-	-	1.46	±0.23			(14)
kdWxR	0.00048	±0.0001	31	±2.911	6.26907	±0.001	0.09	±0.25			(15)
kdW	0.00307	±0.0001	-	-	-	-	0.04	±0.2			(15)
Alternative models:
Neoantigen load	16.39039	±0.0001	-	-	-	-	1.48	±0.12			(17)
AxR, sum over neoantigens	18.3366	±0.471	38.3	±0.001	10.1531	±29.105	0.21	±0.08			(16)
AxR, alignments at positions 3–8	0.0716	±1.011	22.3	±0.273	0.46591	±0.022	0.94	±0.13			(2)
AxR, negative IEDB assays	0.00091	±0.58	15.8	±0.056	0.45236	±0.001	0.98	±0.03			(2)
AxR, all neoantigens	0.01602	±0.559	34.9	±0.051	0.53933	±0.834	0.13	±0.03			(2)
AxR, average fitness	-	-	26.3	±0.252	1.06061	±0.001	4.03	±0.84	0.04476	*	(2) and (19)
Snyder et al., Melanoma anti-CTLA-4	Parameters trained on Van Allen						Log-rank test
Models	τ		a		k		Score		Significance		Equation
	Mean	Std	Mean	Std	Mean	Std	Mean	Std
Ax R	0.02326	±0.479	26	±3.835	3.44101	±0.088	9.1	±0.92	0.00256	***	(2)
Partial models:
A	0.1007	±0.0001	-	-	-	-	0.09	±0.68			(12)
R	1.3483	±17.017	21.2	±5.133	5.57735	±27.093	1.17	±0.38			(13)
1/kdM xR	0.0786	±5.21	22	±0.445	1.4779	±0.065	0.41	±0.65			(14)
1/kdM	0.06196	±0.0001	-	-	-	-	0.63	±0.61			(14)
kdWxR	0.00096	±15.302	27	±4.14	5.53499	±0.001	0.53	±0.22			(15)
kdW	13.33274	±0.0001	-	-	-	-	1.21	±0.75			(15)
Alternative models:
Neoantigen load	0.10065	±0.0001	-	-	-	-	0.64	±0.21			(17)
AxR, sum over neoantigens	0.08928	±27.215	27	±8.827	5.01647	±34.399	0.09	±0.53			(16)
AxR, alignments at positions 3–8	1.82771	±11.104	24.9	±8.066	8.08455	±1.826	5.33	±1.05	0.021	*	(2)
AxR, negative IEDB assays	0.16414	±10.716	11.7	±0.768	0.89312	±0.164	1.83	±0.97			(2)
AxR, all neoantigens	0.00772	±23.665	25.7	±7.145	7.16555	±0.834	2.63	±0.92			(2)
AxR, average fitness	-	-	26	±3.158	3.34043	±0.001	8.03	±0.92	0.00459	***	(2) and (19)
Rizvi et al., Lung anti-PD-1	Parameters trained on Van Allen and Snyder						Log-rank test
Models	τ		a		k		Score		Significance		Equation
	Mean	Std	Mean	Std	Mean	Std	Mean	Std
A x R	0.08958	±0.458	26	±1.679	4.8714	±0.014	7.48	±1.17	0.00624	***	(2)
Partial models:
A	0.09278	±0.0001	-	-	-	-	1.86	±1.17			(12)
R	1.9744	±13.288	18.4	±4.897	5.36039	±27.055	0.07	±0.01			(13)
1/kdM x R	1.50385	±6.017	22.2	±0.74	1.71159	±1.503	0.1	±0.16			(14)
1/kdM	3.42166	±0.0001	-	-	-	-	0.52	±0.13			(14)
kdWxR	0.78791	±5.582	30.5	±4.853	4.92212	±0.788	1.62	±0.54			(15)
kdW	7.31748	±0.0001	-	-	-	-	0.62	±0.75			(15)
Alternative models:
Neoantigen load	3.89326	±0.0001	-	-	-	-	0.49	±1.15			(17)
A x R, sum over neoantigens	22.06719	±1.493	38.4	±0.004	10.1531	±26.389	0	±0.11			(16)
A x R, alignments at positions 3–8	0.06281	±6.254	21.4	±0.34	0.63805	±0.041	2.55	±0.59			(2)
Ax R, negative IEDB assays	0.01993	±5.485	16.8	±0.485	0.66568	±0.02	3.39	±0.51			(2)
A x R, all neoantigens	0.44272	±9.226	33.7	±0.464	0.71345	±0.707	0.88	±0.84			(2)
A x R, average fitness	-	-	26	±1.502	1.85617	±0.001	4.49	±1.17	0.03402	*	(2) and (19)

Extended Data Table 2 |. Ranking of fitness models disregarding subclonal composition of tumors.

Fitness models from Extended Data Table 1 evaluated without accounting for subclonal composition of tumors on the same three cohorts, Van Allen et al. (n=103), Snyder et al. (n=64) and Rizvi et al. (n=34). As in Extended Data Table 1, we report parameters used for predictions and error bars for these parameters (Methods). Parameter 𝜏 is not a free parameter when disregarding subclonal composition of tumors (Methods) and is not reported. We report log-rank test scores for all models and the log-rank test p-value for models with significant patient segregation (p<0.05). The significant models are highlighted: yellow for models significant in a single cohort, orange for models significant across two cohorts, and red for models significant in all three cohorts.

Van Allen et al., Melanoma anti-CTLA-4	Parameters trained on Snyder et al. dataset				Log-rank test
Models	a		k		Score		Significance		Equation
	Mean	Std	Mean	Std	Mean	Std
Ax R	18.5	±0.152	0.59845	±0.001	0.61	±0.24			(2)
Partial models:
A	-	-	-	-	0.05	±0.03			(12)
R	18.2	±2.995	4.54981	±0.001	0.2	±0.03			(13)
1/kdMxR	26.6	±1.609	1.34421	±0.001	1.41	±0.61			(14)
1/kdM	-	-	-	-	0.69	±0.23			(14)
kdWxR	23.7	±2.593	3.83397	±0.001	1.35	±0.34			(15)
kdW	_	_	_	_	0.46	±0.2			(15)
Alternative models:
Neoantigen load	_	_	_	_	0.24	±0.12			(17)
A x R, sum over neoantigens	25.1	±3.308	4.89176	±0.001	1.57	±0.39			(16)
Ax R, alignments at positions 3–8	21.9	±2.871	3.1276	±0.001	0.35	±0.36			(2)
Ax R, negative IED3 assays	14.4	±2.58	2.20223	±0.001	0.04	±0.03			(2)
A x R, all neoantigens	29.2	±2.892	3.88642	±0.001	0.24	±0.19			(2)
Snyder et al., Melanoma anti-CTLA-4	Parameters trained on Van Allen et al. dataset				Log-rank test
Models	a		k		Score		Significance		Equation
	Mean	Std	Mean	Std	Mean	Std
Ax R	26.4	±0.892	1.0851	±0.001	6.55	±0.9	0.01047	*	(2)
Partial models:
A	-	-	-	-	4.44	±0.68	0.03507	*	(12)
R	29.7	±4.829	2.51962	±0.001	1.26	±0.34			(13)
1/kdM x R	26	±1.929	0.82074	±0.001	3.65	±0.81			(14)
1/kdM	_	_	_	_	3.44	±0.61			(14)
kdWxR	26.9	±2.735	3.73387	±0.001	1.67	±0.22			(15)
kdW	-	-	-	-	3.11	±0.75			(15)
Alternative models:
Neoantigen load	-	-	-	-	0.42	±0.21			(17)
A x R, sum over neoantigens	27	±3.005	5.08369	±0.001	1.63	±0.53			(16)
Ax R, alignments at positions 3–8	30	±4.023	1.35553	±0.001	2.73	±0.65			(2)
Ax R, negative IED3 assays	36	±9.57	10.1531	±0.001	0.23	±0.65			(2)
Ax R, all neoantigens	26	±1.95	5.22216	±0.001	0.59	±0.92			(2)
Rizvi et al., Lung anti-PD-1	Parameters trained on Van Allen et al. and Snyder et al. datasets				Log-rank test
Models	a		k		Score		Significance		Equation
	Mean	Std	Mean	Std	Mean	Std
Ax R	27	±0.787	1.00032	±0.001	6.48	±1.14	0.01088	*	(2)
Partial models:
A	-	-	-	-	4.65	±1.17	0.03099	*	(12)
R	19.6	±3.355	4.29127	±0.001	1.53	±0.29			(13)
1/kdM x R	21	±2.027	0.53498	±0.001	0.02	±0.07			(14)
1/kdM	-	-	-	-	0.17	±0.13			(14)
kdWxR	23	±2.737	5.37707	±0.001	10.48	±1.71	0.00121	***	(15)
kdW	-	-	-	-	4.49	±0.75	0.03416	*	(15)
Alternative models:
Neoantigen load	-	-	-	-	4.93	±1.15	0.02639	*	(17)
A x R, sum over neoantigens	25	±4.316	4.03113	±0.001	3.09	±1.09			(16)
Ax R, alignments at positions 3–8	22	±3.042	5.2228	±0.001	2.3	±0.82			(2)
Ax R, negative IED3 assays	14.5	±2.806	1.90577	±0.001	1	±0.45			(2)
Ax R, all neoantigens	29	±4.469	1.87092	±0.001	0.75	±0.62			(2)

Extended Data Table 3 |. Multivariate analysis with a Cox proportional hazards model.

A multivariate analysis with a Cox proportional hazards model, was performed to adjust for important clinical covariates, while assessing for the predictive value of (𝜏) values. In melanoma cohorts (Van Allen et al., n=103 and Snyder et. al, n=64), we controlled for stage, gender, and age. Stage IIIC and IVa are combined together, as both of these stages had limited number of patients in either cohort. Stage IIIc/IVa serve as the reference in the table. In both the Van Allen et al. and Snyder et al. cohorts, (𝜏) predictions are independently associated with overall survival after anti-CTLA4 therapy. In the lung cancer cohort (Rizvi et al., n=34), all patients are Stage IV, so we correct for age, gender, and number of pack years smoked, and continued to find that 𝑛(𝜏) predictions are independently associated with overall survival after anti-PD1 therapy.

Variable	Snyder			Van Allen
	HR	95% Cl	p-value	HR	95% Cl	p-value
n(τ)> Median	3.88	1.72 –8.75	0.001	1.99	1.25 – 3.15	0.004
Stage M1b	1.36	0.3 –6.15	0.69	0.8	0.27 – 2.40	0.703
Stage M1c	2.41	0.69 – 8.40	0.168	1.52	0.60 – 3.88	0.372
Age	1	0.98 –1.03	0.802	1	0.99 – 1.02	0.43
Gender (Male)	0.82	0.40 –1.69	0.59	0.72	0.43 – 1.21	0.218
Variable	Rizvi
	HR	95% Cl	p-value
n(τ)> Median	4.85	1.34 – 17.45	0.016
Age	1	0.95 –1.05	0.962
Gender (Male)	1.61	0.61 –4.25	0.339
Pack-Years Smoked	1	0.98–1.03	0.534