Empirical Optimization of Interactions between Proteins and Chemical Denaturants in Molecular Simulations

Abstract

Chemical denaturants are the most commonly used perturbation applied to study protein stability and folding kinetics, as well as the properties of unfolded polypeptides. We build on recent work balancing the interactions of proteins and water, and accurate models for the solution properties of urea and guanidinium chloride, to develop a combined force field which is able to capture the strength of interactions between proteins and denaturants. We use solubility data for a model tetraglycine peptide in each denaturant to tune the protein-denaturant interaction by a novel simulation methodology. We validate the results against data for more complex sequences: single molecule Förster resonance energy transfer data for a 34-residue fragment of the globular protein CspTm, and photoinduced electron transfer quenching data for the disordered peptides C(AGQ)_nW in denaturant solution, as well as the chemical denaturation of the mini-protein Trp cage. The combined force field model should aid our understanding of denaturation mechanisms and the interpretation of experiment.

Graphical TOC Entry

1. Introduction

Determining the stability or folding rate of a protein from ensemble data requires sufficient perturbation to cause a detectable change in the relative populations of folded and unfolded molecules. Adding chemical denaturants such as urea or guanidinium chloride (GdmCl) is the most straightforward way of doing this, since chemical denaturation is usually reversible and does not lead to aggregation, as often occurs with thermal denaturation. The molecular mechanism of denaturation has been the subject of some debate, but recent experimental and simulation studies have tended to favour a mechanism involving weak binding of denaturant molecules to the protein.^1–11 There is less consensus, however, on the details, such as the relative contributions to destabilization from interactions of denaturant molecules with the protein backbone versus the side-chains. Molecular simulations can clearly play a role in helping to understand this mechanism, and to interpret experiment. However, there has been some difficulty in obtaining reliable force fields to represent this process. Even for describing the properties of the denaturant solution alone, standard protocols for generating force field parameters, based on the principle of parameter transferability, have been shown to give poor results.^9,12,13 The most encouraging development has been the parametrization of force fields based on the Kirkwood-Buff (KB) theory of solutions,¹⁴ which associates a number of thermodynamic observables with integrals over pair distribution functions for the components in a solution. KB-derived force fields (KBFF) have been shown to reproduce the experimental solution properties of both urea and GdmCl.^12,13 We have therefore adopted these models here.

Beyond the properties of the denaturant solution itself, the model should be able to capture correctly the effect of denaturants on proteins, which does not necessarily follow from the quality of the force fields for proteins or denaturants separately. A number of computational studies have shown dramatic effects of chemical denaturants on protein stability,^2,4 as well as on the dimensions of unfolded proteins.¹⁵ However, relatively little work has been done to evaluate the accuracy of these protein-denaturant interactions.^9,10 Recently, Netz and co-workers calculated transfer free energies for amino acids from water to urea solutions using different force field combinations.¹⁰ They found a wide variation of binding strength of urea to protein, with most force field models for urea binding much more strongly than in experiment. The best urea/protein force field combination in that study (KBFF urea with SPC water¹⁶ and the GROMOS 53a6 protein force field¹⁷) reproduced well the variations in transfer free energy from water to urea across different amino acids, but resulted in net transfer free energies that were typically too favourable by ~ 0.5 kJ mol⁻¹ M⁻¹ per residue. Such apparently small differences can clearly sum to a very large error over a typical single-domain protein of 50–150 residues, in a high concentration of denaturant.

A partial explanation for the urea binding being apparently too strong lies in the solubility of proteins in water in simulation models. Several recent studies have noted that proteinwater interactions are too weak in most current force fields, and have proposed various remedies to the problem.^18–21 Thus, the excessively strong binding of urea to the polypeptide could clearly arise indirectly from competition with water being too weak. Because of our interest in the properties of unfolded proteins in both water and chemical denaturant, we have sought to combine the improvements in protein-water interactions described in our recent work¹⁹ with accurate denaturant force fields for urea and GdmCl.

Our starting point is the recently developed Amber ff03ws force-field,¹⁹ which is a version of Amber ff03.r1,²² with TIP4P/2005 water²³ and a modified mixing rule for the proteinwater Lennard-Jones terms.¹⁹ Specifically, the Lennard-Jones 𝜖 for all protein-water atom pairs is scaled by a factor of 1.10 relative to the standard force field value (obtained from mixing rules)¹⁹ and an additional backbone torsion term has been applied to the 𝜓 torsion angle to match experimental helix propensities at 300 K.^24,25 Amber ff03ws has been shown to yield promising results for protein-protein interaction strengths, as well as for the radius of gyration of unfolded and disordered proteins.¹⁹ For the denaturant model, we use the KBFF force field for both urea¹² and GdmCl.¹³ We have tested and optimized the protein-denaturant binding using solubility data for a model tetraglycine peptide in different denaturant concentrations,²⁶ using a novel simulation methodology. We then test the optimized denaturant force fields, denoted KBFFs, on larger and more complex systems, finding very promising agreement.

2. Methods

2.1. Molecular Simulation Methods

Langevin dynamics was performed in GROMACS (version 4.6.5²⁷), using a time step of 2 fs and a friction coefficient of 1 ps⁻¹. Except for the transfer free energy calculation, Parrinello-Rahman pressure coupling²⁸ was used for production simulations and Berendsen pressure coupling²⁹ for equilibration. Lennard-Jones (LJ) pair interactions were cut off at 1.4 nm. Electrostatic energies were computed using particle-mesh Ewald³⁰ with a grid spacing of 0.12 nm and a real-space cutoff of 0.9 nm. The protein force field in all cases is a derivative of Amber ff03.r1:²² either Amber ff03w³¹ or Amber ff03ws.¹⁹ For simplicity, we will use ff03w and ff03ws in the text below.

The force field for denaturant was KBFF,^12,13 except that for urea the OPLS³² and Amber urea models were also tested. The Amber urea model (noted as Amber_D to distinguish from the protein force field) is the one provided with the Amber simulation package³³ and included in the port of Amber force fields to GROMACS,³⁴ with RESP charges derived by Jim Caldwell, and other parameters taken from the Amber ff94 family of force fields.³⁵ The combination rule for between denaturant and water is geometric (σ_ij = (σ_i𝜎_j)^0.5) for KBFF and OPLS and Lorenz-Berthelot (σ_ij = (σ_i +σ_j)/2) for Amber, and the combination rule of 𝜖 is always geometric. For the combination of the Amber protein force field with KBFF, the combination rule is undefined. Here we follow the Amber standard and use Lorenz-Berthelot for protein-urea atom pairs.

All protein and denaturant force fields used are listed in Table 1 for reference. The water model was always TIP4P/2005²³ except when comparing results with the original denaturant KBFF¹² in section 3.1, where SPC/E³⁶ and TIP3P³⁷ were used. Therefore we describe each simulation only in terms of the protein and denaturant force fields, separated by a dot, e.g. ff03ws·KBFFs refers to the ff03ws protein force field and KBFFs denaturant force field.

Table 1:

Description of force field variants used in this paper.

Protein
ff03w31	Amber ff03.r122 with fixed helical propensity
ff03ws19	Amber03w with scaled protein-water interaction
Denaturant
AmberD33	Amber urea model provided with Amber simulation package
OPLS32	OPLS urea model
KBFF12,13	KBFF urea and GdmCl models
KBFFs	KBFF model with scaled protein-denaturant interaction

For comparing KB integrals in different denaturant models, we ran 30 ns simulations at constant temperature and pressure after 200 ps equilibration. A cubic box with edge ~ 4 nm is used for both urea and GdmCl cases. The simulation is recorded every 1 ps to allow sufficient data for the calculation of radial distribution function.

For checking the denaturing effect of urea on Trp cage mini protein, we ran 100 ns replica exchange simulations at constant temperature and pressure, spanning a temperature of 300–495K with 32 replicas. The box size was about 4.5 nm with a dodecahedron shape. The first 50 ns of simulation was discarded for equilibration. The errors were estimated from a box average with 5 boxes.

2.2. Calculation of transfer free energy

The experimental transfer free energy ΔF_tr from denaturant solution to water was obtained from the solubility S of the peptide in different denaturant conditions as

$$\beta \Delta F_{\text{tr}}=-\ln \left(S/S_0\right)$$ (1)

where S₀ is the solubility of the peptide in pure water solvent, and β = 1/k_BT where k_B is the Boltzmann constant and T the temperature. To compute the transfer free energy, we have introduced a gradient of denaturant concentration on the z-axis of the simulation box by applying the biasing potential U_d shown below to the C atom of the denaturant molecules:

$$U_d(z)=k\left[\cos \frac{2\pi \left(z-z_c\right)}{z_{\max }}+1\right]$$ (2)

where z_c is the box center, z_max is the length of the box in the z-dimension, and k equals 2.5 kJ/mol. For equilibration of denaturant concentration gradient, the simulation was set up in a 4×4×12nm box (12nm along z-axis) with Berendsen pressure coupling and semi-isotropic scaling only along the z-axis, and the biasing potential shown in Eq. 2 with z_max=12nm. The equilibration was run for 500 ns to get a smooth denaturant concentration gradient. For different strengths of protein-denaturant interaction, we saw negligible deviation from this concentration gradient (provided the same denaturant model was used). This method is inspired by the work of Luo and Roux to calculate the osmotic pressure of sodium chloride.³⁸ They used a similar rectangle box with longer z-axis than the other two dimensions, and virtual wall restraints to confine sodium chloride in the middle of the box. The osmotic pressure was then calculated from the wall force applied onto the sodium chloride.

Starting from a denaturant-water equilibrated configuration, we ran a 200 ps equilibration for different protein-denaturant models with the same Berendsen pressure coupling and semiisotropic scaling along the z-axis. We note that semi-isotropic scaling was only used for historical reasons and is not needed. Since it is only used for equilibration, it should not affect our results. In order that the z-dependent periodic external bias potential does not change during the production runs, these were performed at constant volume and temperature and z_max was set to be the same as the z-axis box size for periodicity. To compare with the experiment,²⁶ the simulations were run at 298 K. The free energy of the peptide projected onto the z-axis is therefore directly proportional to the transfer free energy of the peptide at different denaturant concentrations.

To achieve convergence of the peptide z-position, we applied an umbrella sampling scheme to the peptide. In each simulation window, a harmonic bias was applied onto the z-coordinate of the C_α atom of the third Gly residue:

$$U_p(z)=\frac{1}{2}k{\left(z-z_0\right)}^2$$ (3)

where z₀ is 0,2,4,6,8,10 nm for the 6 simulation windows and k equals 6 kJ/mol. We have achieved sufficiently small errors for the transfer free energy with 500 ns long simulations in each simulation window (the first 10 ns is discarded for equilibration). The weighted histogram analysis method³⁹ (specifically its implementation in MBAR package⁴⁰) was used to merge the simulations and calculate the free energy profile. The errors were estimated from a box average with 3 boxes.

2.3. FRET experiments on Csp-M34

Single-molecule instrumentation.

Observations of single-molecule fluorescence were made using a custom-built confocal microscope equipped with a continuous-wave 488 nm solid-state laser (FCD488–010, JDSU, Milpitas, CA, USA) and an Olympus UplanApo 60×/1.20W objective. After a dichroic mirror that separates excitation and emission light (500DCXR, Chroma Technology, Rockingham, VT, USA), fluorescence emission passed through a 100 𝜇m pinhole and was split by a second dichroic mirror (585DCXR, Chroma Technology) into donor and acceptor fluorescence. Donor fluorescence then passed a filter (ET525/50M, Chroma Technology) before being focused onto a single-photon avalanche diode (MPD 100ct, Micro Photon Devices, Bolzano, Italy) while acceptor fluorescence passed a filter (QT 650/100) before being focused onto a single-photon avalanche diode (SPCM-AQR-13, PerkinElmer Optoelectronics, Vaudreuil, QC, Canada). The arrival time of every photon was recorded with a two-channel time-correlated single-photon counting module (PicoHarp300, PicoQuant, Berlin, Germany). All measurements were performed with a laser power of 100 𝜇W, measured at the back aperture of the objective (beam waist: 8 mm).

Single-molecule equilibrium measurements.

We used the short M34 variant of CspTm prepared by proteolytic cleavage of full length CspTm and labelled with Alexa 488 and Alexa 594 as described previously.⁴¹ The sequence of the peptide is CEGFKTLKEGQVVE-FEIQEGKKGGQAAHVKVVEC, with the labels attached to the cysteine residues using maleimide chemistry. All experiments were performed at 295 K, at a protein concentrations of 30 pM, in the same solution conditions: 50 mM sodium phosphate pH 7, 0.001 % Tween 20, 140mM β-mercaptoethanol. Tween 20 (Pierce) was used to prevent surface adhesion of the proteins,⁴² and the photoprotective agent β-mercaptoethanol (Sigma) was used to minimize chromophore damage.⁴³ Data were collected for 15 minutes; bursts of fluorescence photons were identified by combining photons detected within 150 𝜇s from each other, and events comprising 50 or more photons were used for the subsequent analysis. Transfer efficiencies were corrected for quantum yields, cross-talk and direct excitation as described previously.⁴⁴ Populations of unfolded molecules in the transfer efficiency histograms were fitted using a Gaussian distribution; donor-only population (i.e. molecules lacking an active acceptor fluorophore) was fitted with a log-normal distribution. GdmCl and urea concentrations were measured with an Abbe refractometer (Krüss, Germany).

2.4. Simulations of Csp-M34

Csp-M34 is not a large peptide considering the size of the dyes used in the FRET experiment. To avoid making assumptions about the effect of the dyes on the peptide dimensions, we built the protein fragment with the chromophores Alexa 488 and Alexa 594 explicitly represented in the simulation, so that the exact same conjugate is used to compare with the experiment. The force field for the chromophores Alexa 488 and Alexa 594 was described in a recent publication⁴⁵ and was extensively verified against experimental data. The FRET efficiency can be directly calculated using the distance R between the chromophores as

$$E=\langle {\left(1+{\left(R/R_0\right)}^6\right)}^{-1}\rangle$$ (4)

where the Förster distance R₀ is 5.4 nm,⁴² assuming that chromophore reorientation is fast relative to the donor lifetime and that the orientation factor κ² = 2/3. The ensemble-averaged orientation factors in different solvent conditions in simulations are close to the expected value (Supporting Figure S1).

Replica exchange simulation at constant temperature and pressure is used to achieve a converged distribution of chromophore distances, with 42 replicas spanning a temperature of 275–423 K. We used a 6.5 nm truncated octahedron periodic box for the case without denaturant and 7 nm with denaturant, because of the larger radius of gyration at high denaturant concentration. In the case without denaturant using ff03ws and the case with 8M urea using ff03ws·KBFF, 50 ns simulation was used to calculate the FRET efficiency after discarding the first 50 ns of REMD as equilibration. In the case with 8M urea and 6M GdmCl using ff03ws·KBFFs, we started the simulation from the final configurations of the case without denaturants using ff03ws. 200 ns equilibration was discarded before collecting the 250 ns data to allow sufficient expansion of the peptide with the scaling factor of interactions between denaturants and protein. The choice of equilibration time for each simulation was based on computing a window average of the radius of gyration with a window of 50 ns; the equilibrated region of the simulation was that in which there was no net drift in the window average (Supporting Figure S2). κ² was also calculated from the corresponding equilibrated region of the trajectories. The errors were estimated from a box average with 5 boxes.

In simulations when calculating chromophore distances, we discarded the configurations where the distances of the protein to its periodic image are smaller than 0.3 nm, which are unavoidable due to the limited size of the box. A Gaussian chain model could be used to calculate the upper bound of the underestimation of radius of gyration assuming all structures with end-end distance larger than the box size are discarded. This will be discussed in the Results section.

2.5. Theoretical calculation of PET quenching

In order to compare our results directly with photoinduced electron transfer (PET) quenching experiment on C(AGQ)_nW peptide (n = 1 – 6), we compute the quenching rates q using a step function dependence of q on the Trp-Cys separation r_cw, that is q(r_cw) = q_cH(r_c – r_cw), where q_c = 8 × 10⁸ s⁻¹ is the constant quenching rate in contact, H(x) is the Heaviside step function and r_c = 0.4 nm is the contact distance. The distance r_cw is taken as the minimum distance between the sulfur in the cysteine side-chain and the heavy atoms of the tryptophan indole ring system.^46,47 Assuming a step function for the distance dependence is clearly an approximation. However, we have recently shown (see supporting manuscript for review⁴⁸) that very similar results are obtained using a more realistic exponential distance dependence, whose parameters are determined from experiment. The step function is a good approximation due to the very steep distance dependence of the quenching rate.

The observed rate is then determined from the decay of the triplet survival probability $S(t)={\langle \exp \left[-{\displaystyle {\int }_{t_0}^{t_0+t}q}\left(r_{\text{cw}}\left(t^{\prime }\right)\right)d{t}^{\prime }\right]\rangle }_{t_0},$ where the average is over equilibrium initial conditions t₀, obtained by taking every saved frame of the simulation as a valid starting point.

For all force fields tested, simulations of the C(AGQ)_nW peptides with n = 1 −6 AGQ repeated units were run. For ff03w with KBFF, two independent 2 𝜇s simulations at each repeated length were run at constant temperature and pressure after 500 ps equilibration. For ff03ws with KBFF or KBFFs, four independent 2 𝜇s simulations at each repeated peptide length were run at constant temperature and pressure after 500 ps equilibration. The temperature of the simulations is 293K to compare with the experiment.⁴⁹

3. Results

3.1. Properties of KBFF urea and GdmCl in combination with TIP4P/2005

Denaturants using the parameters from the Kirkwood-Buff force field (KBFF) for urea and GdmCl have been shown to fit a number of experimental observables including densities, activity coefficients, and partial molar volumes.^12,13 However, the KBFF models were originally developed in conjunction with SPC/E water, although they have been found to give reasonable results in conjunction with other water models, such as TIP3P. Since our protein force field ff03ws is specifically parametrized with respect to TIP4P/2005 water, we first check that the thermodynamic quantities that were captured by the original KBFF can also be reproduced with TIP4P/2005.

For a binary solution of water and denaturant, many solution thermodynamic properties may be computed from the KB integrals G_ij, defined as lim_r→∞ G_ij(r) for

$$G_{ij}(r)=4\pi {\displaystyle {\int }_0^r\left|g_{ij}\left(r^{\prime }\right)-1\right|}{r}^{\text{'}2}d{r}^{\prime }$$ (5)

where ij refers to water-water, water-denaturant and denaturant-denaturant combinations and g_ij is the corresponding radial distribution function.

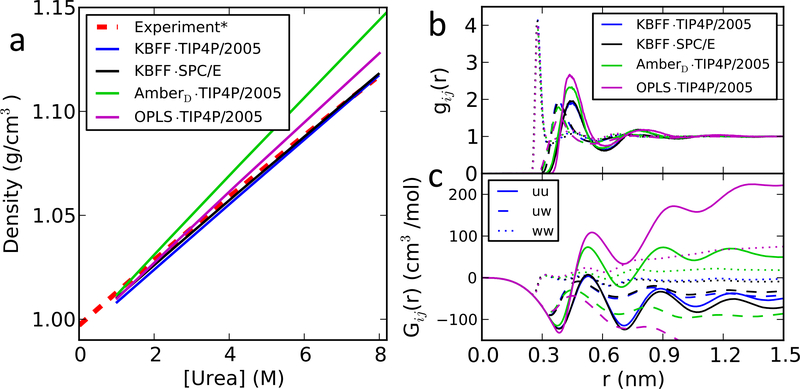
In Figure 1, we show the densities and G_ij(r) in different urea concentrations. The results using KBFF urea with the water model TIP4P/2005 are in good agreement with those from SPC/E, suggesting that the solution of KBFF urea in TIP4P/2005 water should reproduce the same experimental observables as the original version using SPC/E water. We also considered for reference a couple of other urea models, namely the published OPLS urea model³² and the model for urea included with the Amber simulation package³³ (notated as Amber_D). It has previously been shown that OPLS urea when used with TIP3P water gives poor estimates of Kirkwood-buff integrals and activity coefficients.¹² Here, we investigated the combination of the OPLS and Amber_D models with TIP4P/2005 water model, by also computing the densities and KB integrals (Figure 1). Both introduce larger deviations from the experimental densities, pair distribution functions and KB integrals compared to the reference simulation of KBFF with SPC/E water.

Figure 1:

Properties of urea solutions. (a) Density as a function of denaturant concentration; (b) radial distribution functions g(r) and (c) Kirkwood-Buff integrals G_ij(r) (bottom) for 8M urea solution. Radial distribution functions g_uu and Kirkwood-Buff integrals G_uu between urea and urea are shown with solid lines; g_uw and G_uw between urea and water with dashed lines; and g_ww and G_ww between water and water with dotted lines.

Since the KB integrals are not a physical observable, in Table 2 we show a set of observables at ~ 8 M urea concentration: density, activity coefficient derivative and partial molar volumes. We find in all cases that the combination of KBFF urea with TIP4P/2005 shows comparable agreement with experimental data and with the values obtained in the original KBFF paper.^12,13

Table 2:

Comparison of different denaturant models for 8 M urea and 6 M GdmCl. The water model if not specifically mentioned is TIP4P/2005. a_uu is derivative of the activity coefficient and ${\overline{V}}_x$ the partial molar volume of species x. The methods for obtaining activity coefficients and partial molar volumes from KB integrals are shown in the Supporting Information.

8 M urea	KBFF·SPC/E	KBFF	AmberD	OPLS	Expt (8 M)
concentration (M)	7.98	7.97	8.00	8.01
density (g/cm3)	1.119	1.118	1.145	1.129	1.11750
auu	1.32	1.09	0.46	0.27	1.1951/1.1752/1.1653
${\overline{V}}_u$(cm3/mol)	45.7	45.4	42.0	43.8	45.750
${\overline{V}}_w$(cm3/mol)	17.9	18.0	18.0	18.0	18.050
6 M GdmCl	KBFF·SPC/E	KBFF	Expt (6 M)
concentration (M)	6.02	6.02
density (g/cm3)	1.125	1.132	1.14154
auu	1.20	1.33	1.1155
${\overline{V}}_u$(cm3/mol)	43.5	37.1	36.355
${\overline{V}}_w$(cm3/mol)	24.1	25.1	17.955

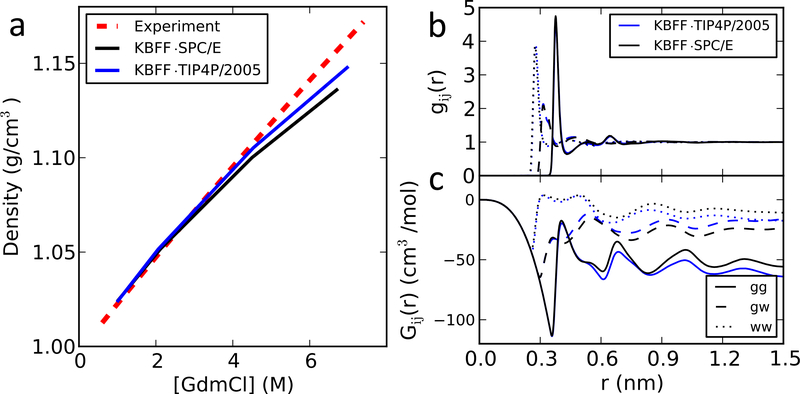
We apply the same test to GdmCl-water mixture and find that again KBFF performs similarly when using TIP4P/2005 or SPC/E water (Figure 2), though in both cases, a slight deviation from the experimental densities is seen at high GdmCl concentrations. The details are summarized in Table 2.

Figure 2:

Properties of GdmCl soluitons. (a) Density as a function of denaturant concentration; (b) radial distribution functions gij and (c) Kirkwood-Buff intergrals Gij of a 6M GdmCl solution. g and G between GdmCl and GdmCl are shown with solid lines; between GdmCl and water with dash lines; and between water and water with dotted lines. The values of KB integrals are the average between 0.95 and 1.3 nm for urea and between 1.10 and 1.45 nm for GdmCl, which were used in the KBFF work.^12,13

3.2. Parameters for protein-denaturant interactions from transfer free energies

Since we have a reasonable force field capturing interactions between denaturant and water,^12,13 and between protein and water,¹⁹ the only interactions that remain to be determined are those between denaturant and protein. A computationally feasible system with experimental data available is acetyltetraglycine ethyl ester (Ace-(Gly)₄-OEt, hereafter abbreviated as Gly₄), which is a compound that could be considered to be representative of the protein backbone. Robinson and Jencks²⁶ have studied the solubility of Gly₄ in different denaturant concentrations. This can be directly used to calculate the transfer free energy of Gly₄ from water to denaturant solutions. Here we use these experimental data to assess the denaturant-protein interactions in the combined force field of ff03ws and KBFF.

To determine the transfer free energy computationally, the standard method would be to compute the solvation free energy for the peptide in water and in denaturant solution via alchemical pertubation,⁵⁶ and take the difference. However, the transfer free energy varies by only ~ 1 k_BT from the smallest to the largest denaturant concentration in experiment for the model peptide Gly₄,²⁶ whereas the total solvation free energy for the same peptide in simulation (results not shown) is about 50 times larger. Therefore accurately determining the transfer free energy with alchemical pertubation is challenging because the error of the difference of the solvation free energies in water and different denaturant conditions is almost comparable to the transfer free energy itself. Instead, we use an alternative method where an external z-dependent potential is used to vary the concentration of denaturant across the simulation box. The transfer free energy can then be determined from the distributions of peptide and of denaturant along z.

Using umbrella sampling along z, it is straightforward to obtain the distribution of the protein on z, which essentially parametrizes the denaturant concentration (assuming the effect of the probe peptide to be negligible). Here, the transfer free energy equals the free energy of the model compound projected onto z-axis (plus an offset).

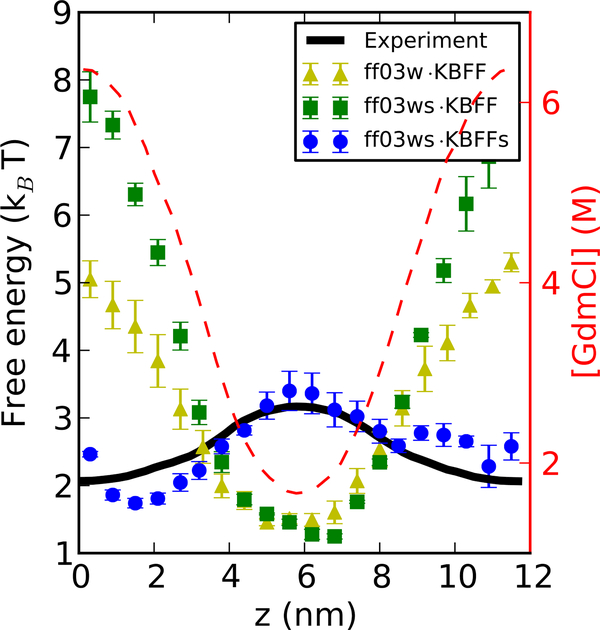
In Figure 3, we show the free energy F(z) of Gly₄ with the z-dependent profile of urea concentration, using different force fields. In the corresponding Table 3, we show the value of transfer free energy of Gly₄ from small to high denaturant concentrations in our simulations in different models. Note that a different denaturant-water model would result in a different denaturant concentration gradient even with the same biasing potential on the denaturants, therefore we show the results of KBFF·TIP4P/2005(s) models in Figure 3, and the results of KBFF·TIP3P and Amber_D·TIP4P/2005 with urea in two other figures (Supporting Figure S3).

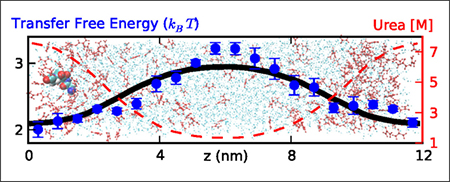
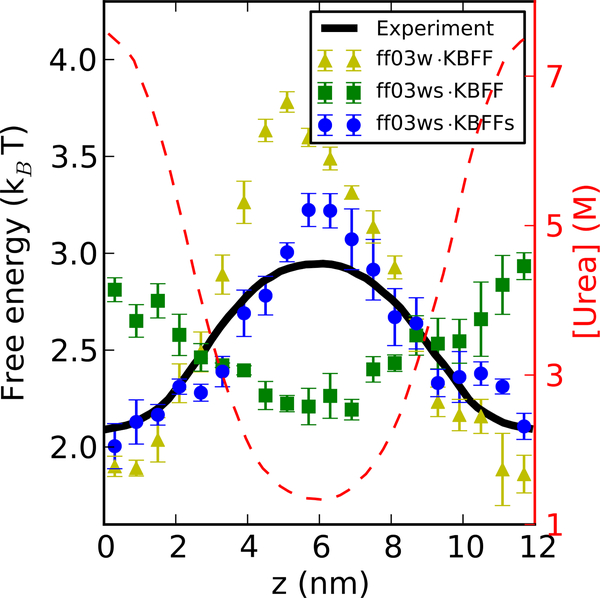
Figure 3:

Computing transfer free energy of Gly₄ from water to urea solutions. A z-dependent concentration profile of urea (broken red lines, right axis) has been built up by applying a constant external potential to the urea molecules. The symbols indicate the corresponding free energies F(z) for individual Gly₄ molecules determined from the population density, as indicated in the legend. The black line is interpolated from the experimental data.²⁶

Table 3:

Transfer free energy of Gly₄ within different denaturant conditions. We show for illustration the difference between 7 M and 1.5 M for urea, and between 6 M and 2 M for GdmCl, which are close to the lowest and highest denaturant concentrations in the current simulations. Water model if not specified is TIP4P/2005. Errors are shown in brackets.

Denaturant Model	Force Field	Transfer Free Energy (kBT)
Urea
KBFF	ff03ww·TIP3P	−1.99 (0.11)
AmberD	ff03w	−3.03 (0.27)
KBFF	ff03w	−1.83 (0.08)
KBFF	ff03ws	0.43 (0.10)
KBFFs	ff03ws	−0.81 (0.12)
Experiment		−0.7726
GdmCl
KBFF	ff03w	2.92 (0.38)
KBFF	ff03ws	5.14 (0.19)
KBFFs	ff03ws	−1.23 (0.16)
Experiment		−0.9226

Amber ff03w (without scaled protein-water interactions) combined with KBFF, and either TIP4P/2005 or TIP3P water model overestimates the free energy difference between lowest and highest urea concentrations by more than 1 k_BT, consistent with the work from Horinek and Netz.¹⁰ By using a periodic homopolypeptide, they found that the transfer free energy of the amino acids they tested were larger by ~ 0.5 kJ mol⁻¹ per molar denaturant per residue, using KBFF urea with the GROMOS 53a6¹⁷ protein force field and SPC water,¹⁶ qualitatively consistent with our results. When combining our protein force field with rescaled water-protein interactions (ff03ws) with KBFF, the transfer free energy of Gly₄ from water to urea solution becomes positive, which means the transfer free energy of Gly₄ from water to urea is in fact slightly unfavorable. This is probably due to the competition from the stronger protein-water interactions. To remedy this problem, we have chosen to rescale the protein-urea Lennard-Jones terms in the same fashion as protein-water interaction so as to balance the three-component mixtures.

Our motivation for rescaling these interactions is that the original parametrization of the denaturant models does not explicitly consider interactions between protein and denaturant, with the Lennard-Jones parameters for protein-denaturant interactions being automatically determined by combination rules. We therefore choose to modify these interactions with a tuning parameter, in a similar manner in which we successfully modified protein-water interactions.¹⁹ The scaling factor for interactions between denaturant and protein was always applied on the Lennard-Jones (LJ) 𝜖 as

$${ϵ}_{dp}^{*}=\gamma {\left({ϵ}_d{ϵ}_p\right)}^{1/2}$$ (6)

where 𝜖_d and 𝜖_p are the LJ 𝜖 on the denaturant and protein atoms, and γ is the adjustable scaling parameter. While in principle the adjustment needed may vary according to atom type, we have taken a pragmatic approach which avoids a complete, simultaneous, refitting of the many parameters in both protein and denaturant force fields, which would not be justified given the limited experimental data set we are considering. Operationally, we are effectively doing a global parameter fit in which the solution is very strongly constrained to be similar to the original parameters.

For urea, we find that rescaling protein-urea interactions by a modest factor of 1.04 approximately reproduces the experimental transfer free energy.

Similarly, we have tested the transfer free energy of Gly₄ in different GdmCl concentrations with different force fields. Amber ff03w combined with KBFF underestimates the transfer free energy substantially, contrasting with the urea case. With ff03ws, the transfer free energy becomes even more unfavourable, as expected, with a positive change of about 5 k_BT for a 4 M increase of GdmCl concentration (Table 3). As a consequence, we required a larger scaling factor of 1.30 to match the experimental results for the protein-Gdm interaction. It is worth noting that we do not rescale the protein-Cl interaction. This is partially motivated by the Hofmeister series which suggests the effect of chloride ions on protein solubility to be weak, whilst guanidinium has a strong “salting in” effect. This choice was also motivated by consistency, since one otherwise would have to scale all protein-Cl interactions, even in simulations where guanidinium ions were not present. The transfer free energy can be well-reproduced for most GdmCl concentrations and only starts to deviate at very high concentration (> 6 M). This is probably due to the excluded volume effect in high GdmCl concentration; it is also the point at which the density of pure GdmCl solutions with KBFF deviates from the experimental data. Since 6 M is already close to the solubility limit of GdmCl in water, the scaling factor of 1.30 covers the majority of the experimentally relevant concentration range.

To understand the transfer free energy trends observed with different scaling factors for urea and GdmCl, we can use a highly simplified model where the effective energy ΔU for forming a contact between protein and denaturant in solution contains four terms

$$\Delta U=U_{PD}+U_{WW}-U_{PW}-U_{DW}.$$ (7)

in which U_PD, U_WW, U_PW and U_DW are respectively the energies to form a protein-denaturant, water-water, protein-water and denaturant-water contact in isolation. The difference between urea and GdmCl then essentially comes down to the strength of the initial ΔU for contact formation in ff03w: i.e. slightly favourable for urea, but rather unfavourable for GdmCl. Introducing scaled protein-water interactions (U_PW ) naturally weakens the effective interaction with denaturant molecules in both cases if the other terms remain the same. In the case of GdmCl this makes little difference because the original protein-denaturant interaction ΔU is already unfavourable and its sign is not altered by increasing protein-water scaling, while in urea the slightly favourable ΔU can be easily made unfavourable by the change in U_PW, consequently introducing a different trend of transfer free energy before and after protein-water scaling.

For simplicity, we will refer to the new urea force field with the scaling factor of 1.04 and GdmCl force field with the scaling factor of 1.30 as KBFFs in the discussion below.

3.3. Distance distributions in an unfolded protein fragment

Since Gly₄ is a rather small model compound containing essentially only glycine, it was necessary to test whether the new denaturant force field can be applied to larger and more complex sequences. We therefore chose a 34-residue peptide, Csp-M34, corresponding to the C-terminal half of the globular cold shock protein CspTm.⁴¹ In contrast to the full-length protein, this fragment simplifies extensive sampling in simulations while at the same time representing a well-mixed natural protein sequence whose chain dimensions can be investigated by single-molecule FRET. Another important distinction of this system is the presence of non-glycine residues, compared to Gly₄. The size of Csp-M34 in water from FRET experiments has been shown to be correctly captured by ff03ws in our previous work.¹⁹ Here we have revisited this protein fragment in different urea and GdmCl conditions instead of pure water using new FRET measurements reported here to verify the denaturant force field.

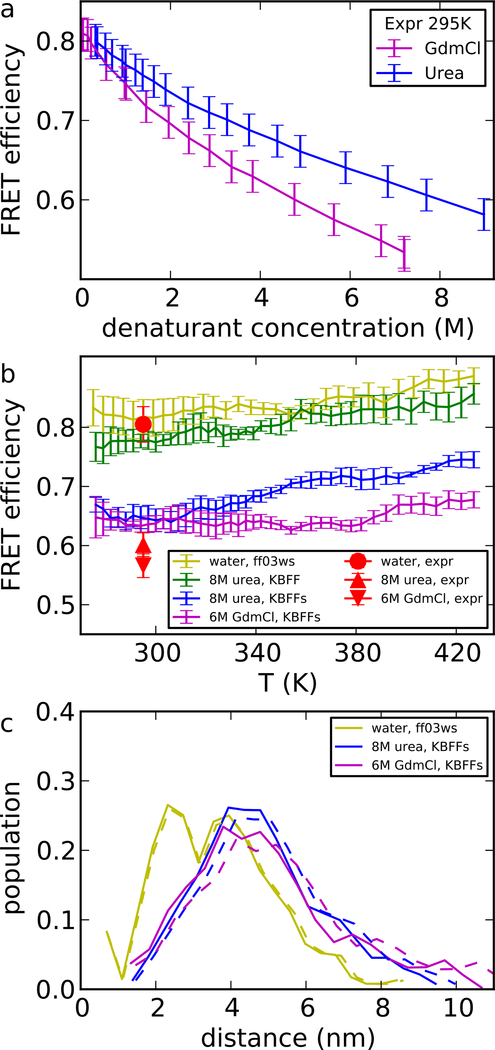
We have run a series of REMD simulations of Csp-M34, with FRET chromophores explicitly present in the simulation, in 8 M urea or 6 M GdmCl solutions. The calculation of FRET efficiency is therefore straightforward from the distance between the two dye molecules. In Figure 5, we show the FRET efficiency in different denaturant solutions and the experimental data. As was shown in the previous work,¹⁹ the simulation matches nicely the experimental FRET efficiency of Csp-M34 without denaturants at room temperature. When going to high denaturant concentration, Csp-M34 expands as expected in both simulation and experiment.⁴¹

Figure 5:

FRET efficiency and radius of gyration of a Csp-M34 protein fragment (experimental data in Supporting Table S1 and S2). (a) FRET efficiency in experiment, as a function of denaturant concentration. The values came from the average of the two independent measurements and the errors shown here took into account our estimate of the variability of measurements due to instrument calibration. (b) FRET efficiency E in simulations and experiment. (c) Population density of distance between chromophores from simulation. Dashed lines show the shift of distribution to exactly match the experimental average FRET efficiency Ē_exp. Shifting is accomplished by applying a transformation P_ζ(R) = ζP(ζR), where P(R) is the initial distribution and ζ is obtained from ${\displaystyle {\int }_0^{\infty }E}(R)P_{\zeta }(R)dR={\overline{E}}_{exp},$, with E(R) = (1+(R/R₀)⁶)⁻¹. ζ equals 0.95 for urea and 0.92 for GdmCl. The protein force field is ff03ws.

In 8 M urea, Csp-M34 only experiences slight expansion with the non-scaled ff03ws·KBFF force field. This suggests urea has very weak interactions with Csp-M34. In the same force field, we observe a positive transfer free energy of Gly₄, which means peptides prefer to stay in water instead of urea. Therefore, despite having different types of amino acids and chain lengths, Csp-M34 and Gly₄ both interact weakly with urea in ff03ws·KBFF. After scaling the KBFF force field, the agreement with the experimental FRET efficiency is much improved in 8M urea.

In 6 M GdmCl, we saw a clear expansion of Csp-M34, and the effect is comparable to 8 M urea. However there is a weaker temperature dependence of FRET efficiency in GdmCl. While determining the actual reason for the difference in temperature dependence may not be straightforward, one possible explanation involves the temperature-dependence of the denaturant solvation: the solvation free energy of the ionic denaturant GdmCl is expected to decrease sharply with temperature, due to the large, unfavourable, entropic contribution to ion solvation. As a result, higher temperatures would increasingly favour interactions between denaturant and protein. The solvation free energy of the protein and of urea also decreases with temperature, but the absolute change is much smaller.⁵⁷

In both the urea and GdmCl cases, the simulated FRET efficiencies are slightly larger than the experimental ones. This discrepancy can probably be reduced by using a larger simulation box to avoid the excluded volume effects due to the periodic image; the box size is limited by the computational resources needed for running replica exchange simulations. The same slight compaction due to excluded volume has been seen in replica exchange simulation of ACTR compared with experiment in our previous work.¹⁹ As mentioned in the method section, we discard the configurations where the distance of the protein to its periodic image is smaller than 0.3 nm. An estimate from a Gaussian chain model would suggest about 10% underestimation of radius of gyration in simulations assuming structures with end-end distance larger than the box size are discarded. It is also worth noting that the FRET efficiency is most sensitive when the distance between chromophores is close to the Förster radius R₀ (5.4 nm).^58,59 To illustrate this effect, we show in Figure 5c (dash lines) how much we would need to scale the distribution of radius of gyration to match the experimental FRET efficiency (such a scaling is justified by the scale invariance of common polymer end-end distribution functions). As expected, only a small scaling is sufficient.

3.4. Dynamics of a disordered polypeptide

In addition to testing equilibrium properties, we investigated contact quenching experiments, which served as a sensitive measurement of both distance distributions and dynamics of unfolded proteins. Our recent work has shown that the PET quenching data for peptides C(AGQ)_nW in water can be well reproduced by ff03ws⁴⁸ (the manuscript is attached for review). The same sets of experimental measurements have been made in both urea and GdmCl solutions.⁴⁹

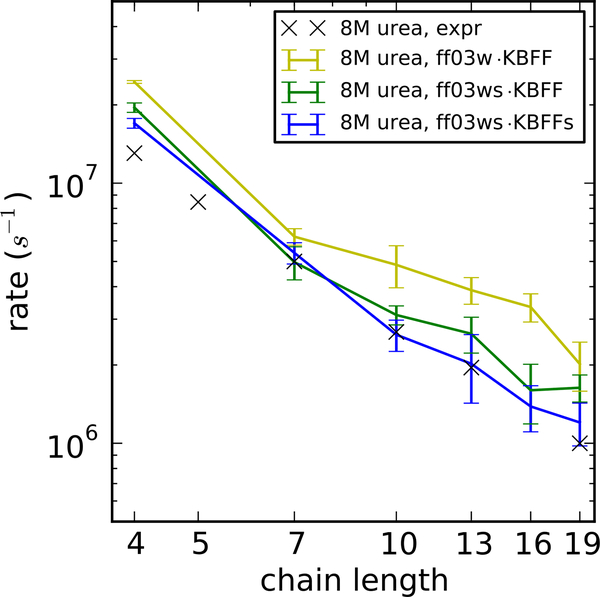
In Figure 6, we show the quenching rate on the Trp-Cys separation in 8 M urea for three different force fields. This rate is related to the rate of forming contacts between Trp and Cys, as well as to how long they spend in contact. The rate is much larger in ff03w with KBFF than in the other two rescaled force fields, consistent with previous observations that peptides are much more collapsed in the current force field,^18–21 and therefore the contacts are present more frequently. After rescaling the protein-water interaction in ff03ws with KBFF, the peptide becomes much more expanded and therefore the quenching rate becomes much smaller. With a second scaling of protein-urea interactions in KBFFs, the peptide is even more expanded and the simulation matches the experimental quenching rate reasonably well for almost all peptide lengths. There is a slight deviation from experiment at the smallest peptide length (n=1), similar to what we have seen without denaturants,⁴⁸ and at the largest peptide length (n=6) albeit within the error bars, probably due to the sampling difficulty when the peptide becomes longer.

Figure 6:

Quenching rates of the tryptophan triplet state by cysteine in the disordered peptides C(AGQ)_nW using different denaturant models. The black crosses represent the experimental data.⁴⁹

We have also applied the same test to GdmCl solutions. However, we observed very limited contact formation between Trp and Cys residues and therefore we were not able to calculate the quenching rate from simulations. We suspected that the reason for this was the association of Gdm⁺ ions with the tryptophan side-chain, which we confirmed by computing the radial distribution function between the side chain of Trp and Gdm⁺ ions. This distribution has a larger contact peak than that between the side chain of Trp and urea (Supporting Figure S4), suggesting a stable contact between Trp side-chain and guanidinium. Such stacking may be related to the larger scaling which was needed between the guanidinium and protein. Nonetheless, we have also found that the distribution of the minimum distance between the sulfur in the cysteine side-chain and the heavy atoms of the tryptophan indole ring system are very similar in 6 M GdmCl and 8 M urea, except at the very small values related to contact formation (Supporting Figure S5). This indicates that the effect of 6 M GdmCl on the dimensions of the peptide is very similar to 8 M urea as also implied by the similarity in the raw quenching rates in the experiment,⁴⁹ suggesting that the KBFFs GdmCl is capturing the overall dimensions of the peptide correctly, but not specific interactions with the Trp. A non-uniform scaling to different residue types would be one solution to this problem. However, since the KBFFs GdmCl force field captures the major denaturing effect on the dimensions of the peptide as well as its effect on Csp-M34, we will not address this discrepancy here.

3.5. Denaturation of the Trp cage miniprotein

As a last test of the denaturant force field, we check the denaturing effect of urea on a folded protein. We choose a mini protein, Trp cage, with both helical secondary structure as well as a small hydrophobic core in the folded state.⁶⁰ It is an ultrafast folder⁶¹ and has been studied with available experimental denaturation data.⁶²

We run replica exchange simulations in both water and 3 M urea solvent. In both cases we assume Trp cage is a two-state folder as observed in the experiment and define the folded and unfolded states by using the fraction of native contacts Q. Q is defined as

$$Q(x)=\frac{1}{N_{ij}}{\displaystyle \sum _{(i,j)\in \text{native}}\frac{1}{1+e^{\beta \left(d_{ij}(x)-\gamma d_{ij}^0\right)}}},$$ (8)

where d_ij(x) is the distance between atoms i and j in configuration x, $d_{ij}^0$ is the corresponding distance in the native state, the factor γ = 1.8 allows for fluctuations of distance within the native state, and β = 50 nm⁻¹. The native contacts were defined as when the distance between pair of atoms is smaller than 0.45 nm, except that the contacts within the nearest two residues were excluded from Q. The free energy projected onto Q, F(Q), is shown in Supporting Figure S6. The barrier position on Q (Q = 0.63) is used to separate the folded and unfolded states.

To compare with experiment over the full temperature range, we fit a thermodynamic model including a heat capacity term, as used in interpreting the experimental data⁶²

$$\Delta G(T)=\Delta H\left(T_m\right)+\left(T-T_m\right)\Delta C_p-T\left[\Delta H\left(T_m\right)/T_m+\ln \left(T/T_m\right)\Delta C_p\right]$$ (9)

in which ΔG is the free energy difference between the folded and unfolded states, T_m the melting temperature, ΔH(T_m) the enthalpy difference at melting temperature, and ΔC_p the heat capacity change. In the experiments,⁶² ΔC_p was determined from the average dependence on the urea concentration for several proteins⁶³ and therefore T_m and ΔH(T_m) were the only free parameters when fitting experimental data to Eq. 9. Here we also fit ΔC_p at the same time.

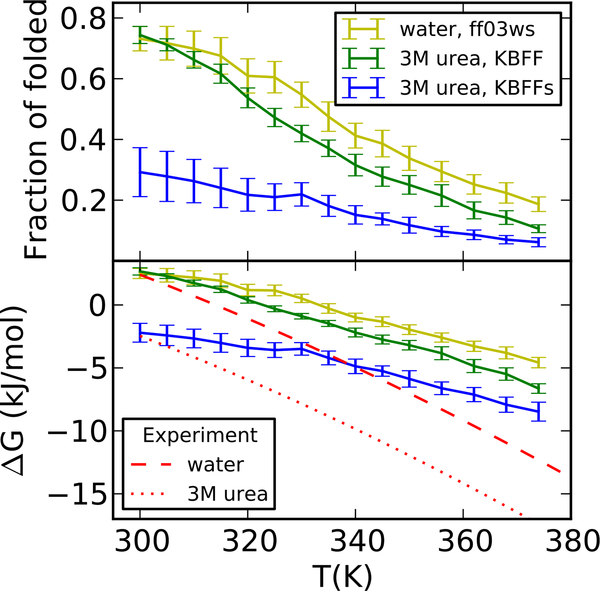
As shown in Table 4 and Figure 7, Trp cage has similar stability in water and ~3 M urea with non-scaled KBFF, consistent with the transfer free energy results. After scaling the protein-urea interaction in KBFFs, we see a clear decrease of folded state stability from water to 3 M urea, and the changes (gap between blue and yellow lines in Figure 7) in our simulation are in good agreement with those from the experiment over a wide range of temperatures (gap between red dash and dotted lines in Figure 7). Note that the slight discontinuity of the fraction of folded state and ΔG at 330K using KBFFs is probably the result of statistical error, being within the error bars and therefore not a significant overall feature of the data.

Table 4:

Thermodynamic parameters of unfolding of the Trp cage mini protein. Errors are shown in the bracket.

[Urea] (M)	model	Tm (K)	ΔH(Tm) kJ/mol	Cp (kJ/mol/K)	ΔG (298K) kJ/mol
0	ff03ws	328 (5)	32 (4)	0.12 (0.04)	2.6 (0.4)
0	Experiment	314 (2)	56 (2)	0.3 (0.1)	2.6 (0.3)
3.13	ff03ws·KBFF	323 (2)	41 (2)	−0.03 (0.02)	3.0 (0.3)
3.13	ff03ws·KBFFs	280 (12)	19 (7)	0.13 (0.04)	−1.5 (0.7)
3.13	Experiment	284 (3)	34 (5)	0.34 (0.10)	−1.7 (0.4)

Figure 7:

Stability of the Trp cage miniprotein in water and 3M urea solution. Top: temperature-dependence of the folded fraction; Bottom: free energy difference between unfolded and folded states (i.e. positive values indicate that the folded protein is more stable). Protein force field is ff03ws.

However, even though ΔG matches the experiment reasonably well with ff03ws and KBFFs at 298K, the fitted values of enthalpies and heat capacities are only about half of the experimental values in both water and 3M urea solution, which means ΔG decreases much slower when increasing the temperature in the simulation and suggests a less cooperative folding in the current force field. This lack of cooperativity is a well-known feature of current additive protein force fields.^24,31,64

4. Discussion

We have shown here by appropriately balancing protein-water and protein-denaturant interactions in simulations, together with denaturant models which accurately represent the solution thermodynamics of pure denaturant solutions, we are able to reproduce additional data relating to the degree of expansion of unfolded chains, the dynamics of contact formation, as well as the effect of denaturants on protein stability.

Going beyond what we have presented, an obvious concern would be that introducing multiple scaling factors for Lennard-Jones parameters between different parts of the system may be hard to scale to multicomponent systems with many more types of molecules. Clearly, parameterizing all the combinations of molecule pairs would rapidly become very difficult to manage. That may seem a limitation, but it should not be necessary to perform this exercise for all components of a simulation: while obtaining very accurate free energies of association is essential for modeling weak binding, such as that of denaturant molecules to proteins, there are many situations where obtaining an accuracy of < k_BT is not needed. For example, when describing very tight binding, such as of drug molecules to their targets, errors of this magnitude are much less than the overall affinity and would not change the qualitative or even (significantly) the quantitative results.

In future force field development, the aim is clearly to produce models such that the parameters are closer to being truly “transferable” from one molecule to another. This might be achieved by using modern computational power to refit Lennard-Jones parameters for all atom types using larger experimental data sets than previously done (together with possibly a larger number of atom types).⁶⁵ This might also require a more specialized mixing rule⁶⁶ or additional terms in the force field such as polarizability^67–69 or charge penetration.⁷⁰ With the use of such features, the need for additional empirical corrections ought to be reduced. Even so, transferability of empirical parameters is an assumption which needs to be validated wherever very accurate free energies of intermolecular association are needed. If it is found that specific intermolecular interactions are not captured with sufficient accuracy for the problem at hand, the method we have used provides a straightforward means of tuning the force field.

The fact that the correction factor for protein-urea interactions (1.04) is close to unity gives us some confidence in the accuracy of the resulting force field: since we are using a very simple uniform scaling for correcting the interactions, we do not want the scaling to be too large or we risk obtaining the correct overall balance between the solution components, but at the expense of the detailed interactions being unphysical. The small correction also suggests that the original force field model was already rather accurate.

On the other hand, we do require a larger correction factor of 1.30 for GdmCl, for which there is no evident explanation. It may relate to the ionic nature of this denaturant vis-à-vis urea, such that a polarizable force field may be required to capture the protein-denaturant interactions in a more transferable manner. The consequence of using a larger scaling factor for GdmCl is that while we should still obtain good global properties (e.g. average affinity of denaturant molecules for the chain, distribution of radius of gyration), the detailed proteindenaturant interactions (e.g. whether the denaturant binds more to the backbone or to the side-chains) are likely to be less trustworthy than in the case of the urea model. Therefore, while the optimized GdmCl force field is expected to capture the overall dimensions of proteins, specific effects on folding dynamics and pathways should not be over-interpreted.

In conclusion, we have parameterized a combination of protein, water and denaturant models in order to obtain solution properties which are consistent with a range of experimental data. We anticipate that such a combination will be very useful for the quantitative treatment of the effects of denaturant on the properties of unfolded or disordered proteins, the mechanism of chemical denaturation of proteins, and protein folding.

Figure 4:

Computing transfer free energy of Gly₄ from water to GdmCl solutions. A z-dependent concentration profile of GdmCl (broken red lines, right axis) has been built up by applying a constant external potential to the Gdm+ molecules. The symbols indicate the corresponding free energies F(z) for individual Gly₄ molecules, as determined from the population density, as indicated in the legend. The black line is interpolated from the experimental data.²⁶