Inferring dynamic topology for decoding spatiotemporal structures in complex heterogeneous networks

Significance

Inferring connections forms a critical step toward understanding large and diverse complex networks. To date, reliable and efficient methods for the reconstruction of network topology from measurement data remain a challenge due to the high complexity and nonlinearity of the system dynamics. These obstacles also form a bottleneck for analyzing and controlling the dynamic structures (e.g., synchrony) and collective behavior in such complex networks. The novel contribution of this work is to develop a unified data-driven approach to reliably and efficiently reveal the dynamic topology of complex networks in different scales—from cells to societies. The developed technique provides guidelines for the refinement of experimental designs toward a comprehensive understanding of complex heterogeneous networks.

Abstract

Extracting complex interactions (i.e., dynamic topologies) has been an essential, but difficult, step toward understanding large, complex, and diverse systems including biological, financial, and electrical networks. However, reliable and efficient methods for the recovery or estimation of network topology remain a challenge due to the tremendous scale of emerging systems (e.g., brain and social networks) and the inherent nonlinearity within and between individual units. We develop a unified, data-driven approach to efficiently infer connections of networks (ICON). We apply ICON to determine topology of networks of oscillators with different periodicities, degree nodes, coupling functions, and time scales, arising in silico, and in electrochemistry, neuronal networks, and groups of mice. This method enables the formulation of these large-scale, nonlinear estimation problems as a linear inverse problem that can be solved using parallel computing. Working with data from networks, ICON is robust and versatile enough to reliably reveal full and partial resonance among fast chemical oscillators, coherent circadian rhythms among hundreds of cells, and functional connectivity mediating social synchronization of circadian rhythmicity among mice over weeks.

Complex systems in which multiple agents affect each other dynamically are prevalent in nature and human society in different scales (1–3). Undesirable behavior of such systems, in the form of disease, epidemics, economic collapse, and social unrest, has generated considerable interest in understanding the dynamic structures of and devising ways to control complex dynamic networks. Thanks to the advances in data science and digital technology, data are abundant and easy to access; however, models often remain elusive. Extracting dynamic interactions of a large complex network from noisy data is becoming a central challenge in diverse areas of science and engineering (4–6). For instance, the topology of networks of biological oscillators could indicate their ability to achieve stable synchrony, and abnormality in brain networks may predict the imminence or occurrence of disease, such as seizures.

Data-driven research on dynamical systems has been extensively conducted in recent years. Various studies based on Bayesian statistics, information theory, and spectral analysis have been proposed to extract the dynamics of systems using their measured data (7, 8). The developed methods were mostly aimed toward discovering governing equations of a single nonlinear dynamical system (9) or reconstructing biological networks, such as gene regulatory networks or oscillator networks, from data. In these studies, the reconstructions were realized in the cases for which the topology of networks is known and the connection strength is estimated (10) or the topology is simply logic-based, i.e., the interactions between nodes are binary values (11, 12), and the developed techniques are robust when the network is sparse and small (8, 13).

In this report, we establish a unified framework for robust determination of dynamic topology of complex networks constituted by a population of nonlinear dynamical units. In particular, we develop a reliable and efficient, data-driven approach for inferring connections of networks (ICON), which requires no assumptions on the network topology and structure, e.g., sparsity, and prior statistics of the interactions. We apply the ICON technique to reveal topology and analyze dynamic structures (e.g., the nodes and functions that mediate synchrony) of complex networks with different spatial and temporal scales—from in silico circuits to cells to societies. Specifically, we reveal features of the functional connectivity of interacting chemical oscillators, circadian cells, and cohoused mice.

Theory and Algorithms

With ICON, we study any broadly defined complex network that consists of a population of $N$ units (agents), $x_1,\dots ,x_N$, following the dynamical law governed by the agent’s self-dynamics and the influence from other agents,

$${\dot{x}}_i\left(t\right)=f\left(x_i\right)+{\displaystyle \sum _{j\ne i}}{K}_{ij}\left(x_i,x_j\right),\hspace{1em}i=1,\mathrm{...},N,$$ [1]

where the vector $x_i\left(t\right)\in {\mathrm{ℝ}}^n$ denotes the state of agent $i$ at time $t$, the function $f$ represents the baseline dynamics, e.g., frequency, of each agent, and $K_{ij}$, where $i,j=1,\dots ,N$, is the coupling function between agent $i$ and $j$ ($K_{ij}$ can be different from $K_{ji}$). The dynamics, i.e., $f$ and $K_{ij}$, and thus the topology of such a directed network are problematic to infer from data, because the inherent nonlinearity within and between individual agents as well as the large-scale nature of these systems deteriorate the computational efficiency and accuracy for estimation (10); moreover, state observations may be incomplete or only partially available in practice and contaminated by intrinsic and external noise (14).

The central idea of our approach is to approximate the agent’s self-dynamics and coupling dynamics, $f$ and $K_{ij}$, respectively, by using complete orthogonal bases, e.g., the Legendre or Chebyshev polynomials, or the Fourier basis. Specifically, we represent each of these functions as a truncated series, i.e., $f\left(x_i\right)\approx {\displaystyle \sum _k}{a}_k{Q}_k\left(x_i\right)$ and $K_{ij}\left(x_i,x_j\right)\approx {\displaystyle \sum _k}{\displaystyle \sum _{\ell }}{b}_{ij}^{k\ell }{P}_k\left(x_i\right)P_{\ell }\left(x_j\right)$, where ${\left\{Q_k\right\}}_{k=1}^{\infty }$ and ${\left\{P_k\right\}}_{k=1}^{\infty }$ constitute orthonormal bases of the respective function space containing $f$ and $K_{ij}$. Then, the dynamical law in ref. 1 can be expressed as (for $n=1$)

$${\dot{x}}_i\left(t\right)={\displaystyle \sum _k}{a}_k{Q}_k\left(x_i\right)+{\displaystyle \sum _{j\ne i}}{\displaystyle \sum _k}{\displaystyle \sum _{\ell }}{b}_{ij}^{k\ell }{P}_k\left(x_i\right)P_{\ell }\left(x_j\right),$$ [2]

where $a_k$ and $b_{ij}^{k\ell }$ are the scalar coefficients, and the coupling strength ${\alpha }_{ij}$ is defined by ${\alpha }_{ij}=\sqrt{{\displaystyle \sum _k}{\displaystyle \sum _{\ell }}{\left(b_{ij}^{k\ell }\right)}^2}.$ Following this strategy based on the orthonormal basis representation, given the measurement data (time series) of each agent $i$ in the network, the topology estimation can be formulated as a simple linear inverse problem for each agent $i$, given by

$$\underset{z^{\left(i\right)}}{\min }{\Vert y^{\left(i\right)}-A^{\left(i\right)}{z}^{\left(i\right)}\Vert }_2,$$ [3]

where $y^{\left(i\right)}$ is the data vector; $A^{\left(i\right)}\in {\mathrm{ℝ}}^{M\times (r^{2}N+m)}$ is a matrix composed of the orthonormal bases, in which $M$ is the number of data points in the time series for agent $i$ and $r$ and $m$ are the numbers of expansion terms in the truncated series $\left\{P_k\right\}$ and $\left\{Q_k\right\}$, respectively; and $z^{\left(i\right)}$ is the coefficient vector that is being determined (see SI Appendix, sections 1 and 2 for detailed formulation and examples for the case of $n>1$).

Most importantly, this formulation enables independent estimation of the coupling dynamics for each individual agent in the network, so that estimating topology of very large networks becomes possible via a parallel computation architecture. Note that there exists a variety of techniques for solving the large-scale least squares (linear inverse) problem as in Eq. 3 (15), for example, the truncated singular value decomposition (TSVD) for regularization of ill-conditioned matrix $A^{\left(i\right)}$ (15, 16), compressive sensing for very large-scale networks with sparse topology (17), and iterative methods, such as the iterative recursive thresholding and iterative shrinkage-thresholding algorithms for large-scale inverse problems with dense matrix data (18, 19). One may employ a specific method depending on the size and structure of the network. The optimized coefficient vectors $z^{\left(i\right)}$ for $i=1,\cdots ,N$ define the time-varying functions $f$ and $K_{ij}$ in Eq. 1, and thus identify the dynamic network topology from data.

Results

Complex systems constituted by a network of rhythmic components appear in many engineered and living systems at different scales, such as circadian neurons, chemical oscillators, power grids, and animal societies (20–24), in which the network emerging properties are functionally significant, such as sleep−wake cycles and jet lag, battery pack charge−discharge cycles, and short-term memory and communication through social behaviors (25). Revealing topology and connectivity is essential to characterize the dynamical structures and functions of such networks, which, in turn, leads to the fundamental understanding of many real-world complex systems, such as functional connections in the brain, synergy of circadian clocks, and social synchronization in groups of animals. We apply the ICON technique to determine topology of networks of oscillators with different periodicities, degree nodes, coupling functions, and time scales, arising in silico, and in electrochemistry, neuronal networks, and groups of mice. The excellent agreement of the estimation with the experiments over such an extremely diverse set of systems validates our strategy and suggests that our data-driven methodology provides a general framework that can be applied to numerous additional systems of interacting dynamic units.

Synthetic Networks.

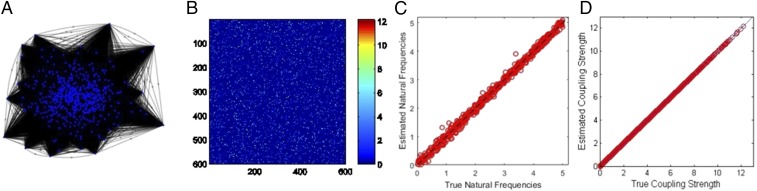
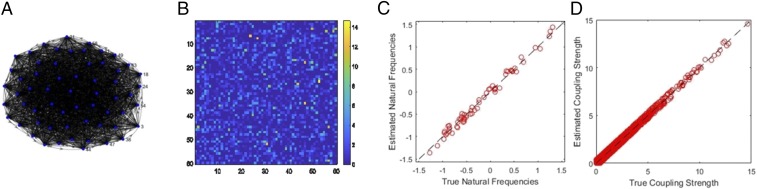
We first tested the accuracy of ICON to estimate the topology of a synthetic network with oscillatory system dynamics. The techniques of phase model reduction have been widely used to describe the dynamics of coupled nonlinear oscillatory systems (22, 26–28), e.g., circadian clock networks. Here, we consider topology estimation of a network of slightly heterogeneous, weakly coupled, generalized Kuramoto-type nonlinear oscillators (26), whose dynamics are described by ${\dot{\varphi }}_i\left(t\right)={\omega }_i+{\displaystyle \sum _{j\ne i}}{K}_{ij}\left({\varphi }_i-{\varphi }_j\right),$ where ${\varphi }_i\in \left[\mathrm{0,2}\pi \right)$ and ${\omega }_i>0$ denote the phase and the natural oscillation frequency of oscillator $i$, respectively, and the coupling function $K_{ij}$, $i,j=1,\dots ,N$, is $2\pi$-periodic. Fig. 1 shows the estimation of a representative network consisting of 600 oscillatory units in the presence of white noise. This synthetic network (Fig. 1A) was created using the above Kuramoto model, with ${\omega }_i$ randomly sampled over $(0,\pi )$ and the coupling functions $K_{ij}$, $i,j=1,\dots ,600,$ randomly synthesized, and following the procedure presented in SI Appendix, section 2. The reconstructed network (represented using ${\alpha }_{ij}$ over the sampling time interval) is shown in Fig. 1 A and B. The estimation, using the TSVD with $A^{\left(i\right)}\in {\mathrm{ℝ}}^{\mathrm{12,000}\times \mathrm{6,001}}$, showed excellent agreement with the true network (Fig. 1 A and B) with precise recovery in the natural oscillation frequency (Fig. 1C) and the coupling strength (Fig. 1D), where $K_{ij}$ was approximated using a Fourier series of 10 terms. The computational time for estimating the entire network simultaneously was 381.3 min (65.3 s for estimating an agent) on a standard desktop computer (time was averaged over estimating 10 such randomly synthesized networks of 600 nodes).

Fig. 1.

Demonstration of inferring the connections, and their strengths, of a synthetic network. (A) The graph representation of a synthetic noisy random network of 600 oscillators created using Eq. 2 with additive white noise (1% intensity with respect to the maximum coupling strength) over the time horizon $t\in \left[\mathrm{0,20}\right]$, where the frequencies of the oscillators ${\omega }_i$ were randomly sampled over (0,$5$), the coupling strength of the functions $K_{ij}$ were randomly selected over [0,12] (each colored dot represents the coupling strength ${\alpha }_{ij}$ of the time-varying coupling $K_{ij}$), and the matrix $A^{\left(i\right)}$ in Eq. 3 is of the dimension $\mathrm{12,000}\times \mathrm{6,001}$. (B) The heat map of the coupling topology. (C) The accuracy of the estimated natural oscillation frequencies. (D) The accuracy of the estimated coupling strength. In this estimation, ICON accurately recovered 95.1% of connections (26,561/27,930) with 93.1% accuracy rate on recovering the coupling strength in this representative network.

Electrochemical Oscillators.

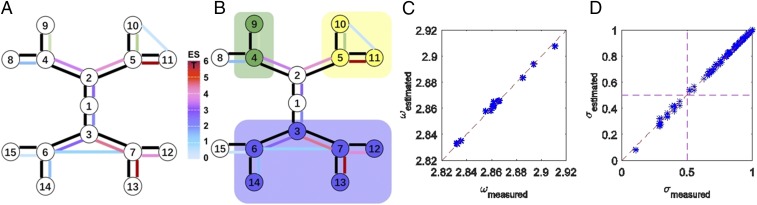
We chose a network of oscillatory chemical reactions to validate the ICON method in an experimental system where a complex coupling topology can be experimentally designed with a relatively large number of nodes. In this experiment, 15 corroding nickel wires immersed in sulfuric acid represent the nodes of the network; the reactions are coupled by resistors to produce the network structure (Fig. 2A) (29). Because of inherent heterogeneities in the uncoupled network, the oscillatory reactions have slightly different frequencies on each node. When electrical coupling occurs through the resistors with sufficiently strong coupling, the network can exhibit synchronized oscillations. We applied a synchronization engineering technique with a global linear feedback (22) to desynchronize the oscillations, and recorded the relaxation of the system to the synchronized behavior (about 33 cycles of data collection, 37,600 sample points) and applied the ICON technique to reconstruct the dynamics of the system.

Fig. 2.

ICON-derived estimation of interactions between chemical oscillators. (A) Experimentally designed (black connections) and estimated (colored connections) oscillator networks. (B) Experimentally observed (colored nodes) and predicted (colored shades) synchronization subgroups of the respective networks in A with reduced coupling strength. (C) Experimentally measured and estimated oscillation frequencies of the oscillators. (D) Pairwise synchronization parameters of experimental designed and estimated networks.

The estimated natural frequencies (Fig. 2C) precisely matched (with 0.05% relative SD) the values measured in independent experiments. Fig. 2A shows that the ICON technique identified all of the 14 existing network connections properly out of the 105 possible links. The technique also found two connections between nodes that were not coupled (6–7 and 10–11). Because these two predicted links were weak and between nodes that were coupled indirectly through another node, the impact of such mismatches on the overall network behavior was small. We validated the reliability of the frequency and topology estimation by looking at the synchronization pattern at a 44% weakened coupling strength. At this coupling strength, the network splits into three frequency clusters with two, three, and six elements, respectively; the rest of the nodes were phase-drifting (Fig. 2B). As shown in Fig. 2D, the phase model extracted from the ICON technique (adjusted for the weakened coupling strength) properly predicted all of the pairwise synchronization indices ${\sigma }_{ij}$ between the elements, and thus properly predicts the synchronization pattern of the system. Such high-fidelity prediction of the spatiotemporal pattern was not previously possible, e.g., with methods based on kinetic models (29), because of the inability to extract theoretical and experimental information on the origin of heterogeneities and the timing of the interactions between the regulated chemical reactions.

Circadian Neurons.

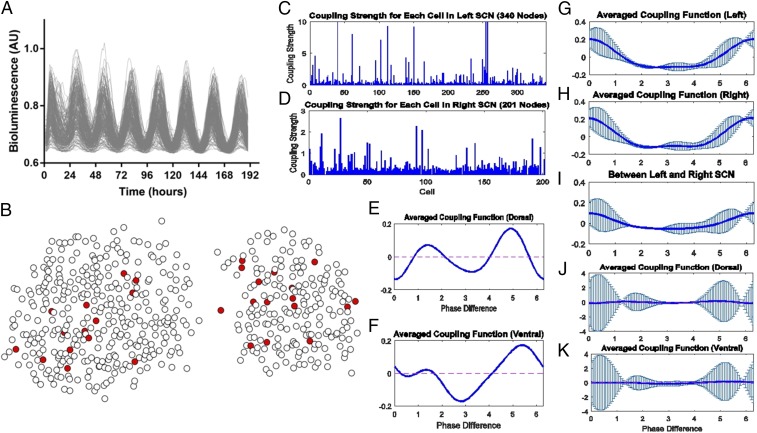
The suprachiasmatic nucleus (SCN) of the mammalian hypothalamus has been referred to as the master circadian pacemaker that drives daily rhythms in behavior and physiology (4). When isolated from their network, SCN neurons can express sustained or damped circadian oscillations, or even arrhythmic patterns. The SCN network can be pharmacologically perturbed while monitoring the component cells for desynchronization and resynchronization of their circadian gene expression (4, 30–32). We tested the ability of ICON to estimate the connections and coupling functions that underlie circadian resynchronization by analyzing PERIOD2 (PER2) protein levels during and after SCN explants were treated with the voltage-gated Na⁺ channel blocker, tetrodotoxin (TTX). Using recordings of PER2-driven bioluminescence (2,850 sample points) from 541 SCN cells (Fig. 3A), ICON recovered a time-dependent network. We found that the influence of individual cells on the network resynchronization (i.e., the sum of the coupling strengths of all of its outgoing connections) varied ∼10-fold, depending on the cell and its location within the SCN (Fig. 3 B–D). The 14 and 16 hub cells (the cells with strong outgoing connections) identified in the left and right SCN, respectively, could indicate the presence of supercells with greater impact on circadian synchrony in the SCN. The coupling dynamics can be further analyzed by comparing the shape of the averaged coupling functions between different SCN regions. Specifically, we found similar numbers and kinds of connections within left and right SCN (Fig. 3 G and H), but weaker connections between than within the two SCN (Fig. 3 G–I). Coupling functions within the bilateral dorsal SCN (Fig. 3 E and J) were more similar to each other than to those in the bilateral ventral SCN (Fig. 3 F and K), consistent with prior predictions based on anatomy and physiology (33–36). We note that the averaged interaction functions often have large cosine harmonics, which results in nearly zero slope at zero phase difference. Such large nonisochronicity is an important oscillatory property, which was computationally predicted by a biomolecular model of the SCN (33) and supported in Fig. 3 E and F.

Fig. 3.

ICON-derived intercellular communication in a circadian tissue. (A) Bioluminescence shows PER2 expression in over 500 SCN cells used for connectivity estimation. TTX was washed out at day 0 to allow the cells to resynchronize their daily rhythms. (B) ICON identified hub cells (red dots) as 5% of the recorded cells and localized throughout the SCN. The estimated total outgoing coupling strength for each cell revealed similar distributions of strongly coupled cells (14 and 16 hub cells, respectively) in the (C) left and (D) right SCN. The corresponding averaged coupling functions between cells were similar within (G) left and (H) right SCN, but different between (I) left and right SCN, and (E and J) dorsal and (F and K) ventral SCN (error bars show SD).

Social Synchronization in Groups of Mice.

Social synchronization of animal and human activities is a central phenomenon that characterizes the temporal order and structures in both social and biological systems (14, 30, 37). We utilized ICON to reconstruct the topology of social networks of groups of cohoused laboratory mice, and to analyze and predict synchronization of their circadian rhythms within each group. Using previously reported recordings of body temperature of inbred female mice housed in groups of five (38) (15-min resolution over 10 d before they were grouped, 68 d of cohabitation, and 7 d after separation), we convolved the data (8,192 sample points) with the complex-valued Morlet continuous wavelet functions to measure period and amplitude over time (39). Daily phases of the circadian peak were determined for each mouse and then interpolated with a peak-finding approach.

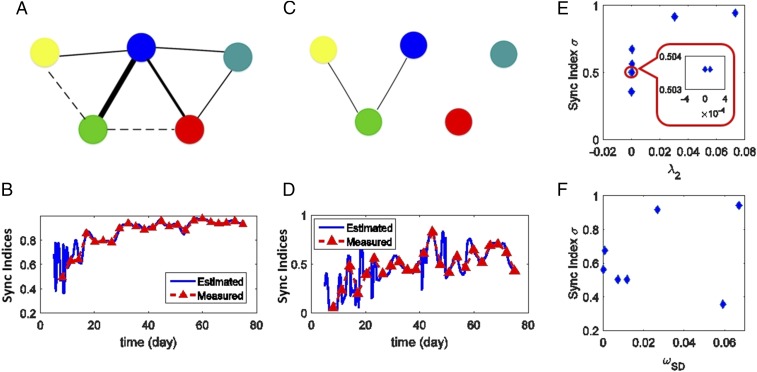
The network estimations using ICON differed depending on the synchronization behavior of the seven recorded quintets of mice (Fig. 4 and SI Appendix, section 4). The recorded synchronization behavior of each group of mice and predicted coordination of the inferred network, i.e., the sync indices calculated based on the experimental data (measured sync indices, red triangles in Fig. 4) and the estimated phase data (estimated sync indices, blue curves in Fig. 4), reliably and quantifiably identified mutual entrainment in the same cohabitating groups as demonstrated by the positive correlation between the sync index, σ, and the dominant eigenvalue, λ₂, of the Laplacian matrix of each of the seven estimated networks. [A relationship between sync index and ${\lambda }_2$ could be expected based on the Wu−Chua conjecture (40), which was experimentally confirmed by electrochemical oscillators (29).] Moreover, our results suggest that the synchrony of such social networks was not induced by the distribution of the natural frequencies of the mice (Fig. 4F), but by the interactions among mice within each quintet (Fig. 4E).

Fig. 4.

ICON-derived social interactions that synchronized circadian rhythms of cohabitating mice. (A and C) The estimated network topologies for two quintets of laboratory mice using ICON, based on the measurement of body temperature data (seven quintets, in total, listed in SI Appendix). (B) The estimated (blue curve) and measured (red triangle) sync index trajectories for the network in A, which is connected and synchronized over the cohabitation period. (D) The estimated (blue curve) and measured (red triangle) sync index trajectories for the network in C, which is partially connected and not synchronized over the cohabitation period. (E) The illustration of positive correlation between the sync index $\sigma$ and the dominant eigenvalue ${\lambda }_2$ of the Laplacian matrix of each quintet network. (Inset) Results from the two experiments with ${\lambda }_2$ near 0 and $\sigma$ near 0.5 are expanded to illustrate their nearly overlapping values. The Spearman correlation coefficient was 0.9727 (SI Appendix, section 4). (F) The illustration of noncorrelation between the natural frequency distribution and synchrony, which shows that synchrony is not induced by the similarity of the frequencies, where ${\omega }_{SD}$ is the SD of the natural frequencies ${\omega }_i$, $i=1,\dots ,7,$ of the seven quintets.

Nonoscillatory Networks.

The ICON technique is not restricted to the inference of the topology of networks with oscillatory coupling dynamics. Fig. 5 shows the estimation of a network with nonperiodic coupling dynamics consisting of 60 nonlinear dynamical units. This synthetic network was created using Eq. 1, with constant self-dynamics, $f\left(x_i\right)={\omega }_i$, randomly sampled over $(-\pi /2,\pi /2)$, and the coupling functions $K_{ij}\left(x_i,x_j\right)$, $i,j=1,\dots ,60,$ randomly synthesized using the procedure presented in SI Appendix, section 2, where $x_i\left(t\right)\in \mathrm{ℝ}$. The reconstructed network (Fig. 5 A and B), using TSVD, showed excellent agreement with the true network with precise recovery in both the natural oscillation frequency (Fig. 5C) and the coupling strength (Fig. 5D), where $K_{ij}$ was approximated using a 2D Fourier series of 10 terms. More analysis of the ICON estimation on multidimensional ($n=2$) nonoscillatory and larger networks (up to 30,000 agents) with respect to different network properties (e.g., sparsity and noise intensity) is provided in SI Appendix (SI Appendix, section 2 for numerical examples and SI Appendix, section 3 for robustness, reliability, and efficiency of the ICON technique).

Fig. 5.

Demonstration of inferring the connections, and their strengths, of a synthetic nonoscillatory network. (A) The graph representation of a synthetic noisy random network of 60 nonoscillatory oscillators created using Eq. 2 with additive white noise (1% intensity with respect to the maximum coupling strength) over the time horizon t ∈ [0,20], where the frequencies of the oscillators ${\omega }_i$ were randomly sampled over $(-\text{π}/2,\text{π}/2)$ and the coupling strength of the functions $K_{ij}$ were randomly selected over [0,15] (each colored dot represents the coupling strength ${\alpha }_{ij}$ of the time-varying coupling $K_{ij}$). (B) The heat map of the coupling topology. (C) The accuracy of the estimated natural oscillation frequencies. (D) The accuracy of the estimated coupling strength. In this estimation, ICON accurately recovered 96.0% of connections (7,230/7,532) in this representative network.

Discussion

In summary, we developed a unified data-driven methodology for revealing the dynamic topology of complex networks and demonstrated its validity for diverse scientific fields and scales by analyzing networks of in silico circuits, artificial chemical oscillators, cells in a tissue, and animals in a group. The robustness and versatility of the ICON technique applied to these four distinct systems suggests its broad applicability to determine network topology and dynamics in diverse natural and engineered systems. For example, prior efforts using mutual information (4) or cross-correlated activity (41) estimated the direction or strength of connectivity among cells in the SCN, but not the coupling functions. Most recently, a theoretical framework for how SCN cells might behave under different levels of coupling was used to support the prediction that TTX weakens coupling in the SCN (42). Here, ICON goes beyond categorizing coupling as either undercritical or overcritical by providing testable predictions for the direction, strength, and dynamics of all cell−cell interactions in the SCN. The notion of the orthonormal basis representation introduced in this paper enables the linear and parallel formulation of the nonlinear topology estimation problem, which lays the foundation for analyzing real-world complex networks of tremendous size, such as brain, transportation, internet, power grids, and social networks (14, 24). Importantly, the ICON technique provides guidelines for the refinement of experimental designs toward a comprehensive understanding of complex heterogeneous networks. We note that, in this work, we assumed that the network dynamics are additive between the self-dynamics and the coupling dynamics and within the coupling dynamics, and considered the networks in the presence of white noise. Although these are valid assumptions in many practical scenarios, future studies should test ICON on networks that reorganize (e.g., add or lose nodes or change coupling) or have multiplicative and colored noise in their self-dynamics or coupling dynamics. Here, ICON was used on networks where we have some prior knowledge of the agent’s self-dynamics [i.e., the functional form of $f\left(x_i\right)$] and with data recorded from nodes while the network relaxed from desynchronized to synchronized states. These expectations also need further evaluation. Ultimately, constructing reliable network topology is the essential next step for the control of collective behavior of networked systems, such as the design of entrainment waveforms for asymptotic synchronization of a nonsynchronous network, pinning controls for stabilization of an oscillatory network, or desynchronization stimulus for suppression of unwanted synchrony in brain networks.

Materials and Methods

See SI Appendix for detailed materials and methods. Detailed formulation and implementation of the ICON technique can be found in SI Appendix, sections 1 and 2. Especially, the detailed method for weakly coupled oscillatory networks is provided in SI Appendix, section 1. The robustness, reliability and efficiency of the ICON technique can be numerically validated by numerous synthetic networks, and the results are included in SI Appendix, section 3. The phase definition of the experimental data and the detailed analysis of the mouse and SCN data are also provided in SI Appendix, sections 2, 4, and 5, respectively. All SCN and mouse data came from previous publications (4, 38).