Size and topology modulate the effects of frustration in protein folding

Significance

Frustration is a central concept in the study of protein folding kinetics. While it has been proposed that most proteins are minimally frustrated, recent experiments have found systems with surprisingly slow reconfiguration dynamics, suggesting an underlying landscape that is frustrated or “rough.” Our results suggest that protein size and topology play a role in determining how sensitive a protein is to frustration.

Abstract

The presence of conflicting interactions, or frustration, determines how fast biomolecules can explore their configurational landscapes. Recent experiments have provided cases of systems with slow reconfiguration dynamics, perhaps arising from frustration. While it is well known that protein folding speed and mechanism are strongly affected by the protein native structure, it is still unknown how the response to frustration is modulated by the protein topology. We explore the effects of nonnative interactions in the reconfigurational and folding dynamics of proteins with different sizes and topologies. We find that structural correlations related to the folded state size and topology play an important role in determining the folding kinetics of proteins that otherwise have the same amount of nonnative interactions. In particular, we find that the reconfiguration dynamics of α-helical proteins are more susceptible to frustration than β-sheet proteins of the same size. Our results may explain recent experimental findings and suggest that attempts to measure the degree of frustration due to nonnative interactions might be more successful with α-helical proteins.

Protein folding has become an exemplar problem for the study of conformational changes in biomolecules. During the past couple of decades, significant theoretical (1) and computational (2) advances have shown that, even though the folding of a protein involves the complex and coordinated motion of many atoms, it can often be described by relatively simple models (3, 4). In general, the number of collective variables needed to describe large macromolecular rearrangements depends on the separation between fast and slow relaxation timescales, and the complexity of these systems often requires the use of computational methods to extract the relaxation timescales from simulation and understand their corresponding structural processes (5). However, energy landscape theory has shown that, under general physical assumptions (6), protein folding can be described as the slow equilibration between the folded and unfolded free energy basins while neglecting the fast relaxations.

The principle of minimal frustration, a central tenet of energy landscape theory, posits that evolution has crafted protein interactions to stabilize the native state while destabilizing competing misfolded states (6). This picture has inspired “structure-based” coarse-grain models where the energy landscape is funneled toward the native state by design, by including the native structural geometry in the construction of the model and by discarding potentially conflicting “nonnative” interactions (7). These models have had success illuminating how folding rates, folding mechanisms, and functional motions depend on native topology (8, 9). However, proteins with the same native structure can still have starkly different folding behavior (10), suggesting that sequence-specific effects are necessary for a more complete picture.

While the principle of minimal frustration has become a central paradigm for molecular biophysics, recent single-molecule experiments on several aggregation-prone proteins, such as the prion protein (PrP) (11) and the intrinsically disordered protein $\alpha$-synuclein (12), have provided examples where frustration may be significant. In particular, a careful analysis of the extension statistics from force spectroscopy has revealed multiple “off-pathway” misfolded states in monomeric PrP (11) and several marginally stable states in monomeric $\alpha$-synuclein (12). These proteins provide concrete examples where nonnative interactions may be an important source of frustration. While some progress has been made in understanding the role of nonnative interactions in specific cases (e.g., ref. 13), it has been unclear if there are more general conclusions to be made. Experimental evidence has shown that the effect of nonnative interactions varies between different proteins and experimental conditions. For example, studies have found that the unfolded state tends to collapse in a protein-specific manner at low concentrations of denaturant (14) or high concentrations of salt (15), with more collapsed states showing slower rates of folding or reconfiguration.

As an attempt to garner general principles, we investigate the effect of nonnative interactions on the (mis)folding of proteins with different topologies. We show that rates of folding and reconfiguration depend on the strength of nonnative interactions in a protein-specific way. In particular, we find that $\alpha$-helical proteins have more compact misfolded ensembles than $\beta$-sheet proteins of a comparable size and, consequently, have slower reconfiguration dynamics. We further connect these differences to the underlying energy landscape. Our results provide some general insight into the role of frustration in protein (mis)folding and why some proteins appear more frustrated than others.

Results

Nonnative Heterogeneity and Folding Dynamics.

The role of nonnative interactions can be quantified in terms of a simple diffusional model of folding. If folding is much slower than forming nonnative structure, the dynamics can be modeled as diffusion along a one-dimensional reaction coordinate (16, 17) with the folding rate given by Kramers theory (18):

$$k_f=k_0{e}^{-\frac{\mathrm{\Delta }{G}^{†}}{k_{B}T}},$$ [1]

where $k_{B}T$ is the thermal energy, $\mathrm{\Delta }{G}^{†}$ is free energy barrier to folding, and $k_0$ is the rate prefactor. The prefactor describes the elementary rate of conformational change (19), and it is sensitive to the structure of the energy landscape. According to the diffusion model, the prefactor $k_0$ in Eq. 1 is given by ref. 18:

$$k_0=\frac{\beta D\sqrt{{\kappa }_u{\kappa }_b}}{2\pi },$$ [2]

where ${\kappa }_u$ (${\kappa }_b$) is the curvature of the unfolded well (transition barrier) along the free energy profile, $\beta =\frac{1}{k_{B}T}$, and $D$ is the diffusion coefficient. Theory predicts that frustration increases energy fluctuations on the folding landscape, $\mathrm{\Delta }E$, and that averaging over these fluctuations gives the diffusion coefficient $D$ a strong temperature dependence, $D\propto \exp \left(-{\left(\mathrm{\Delta }E/k_{B}T\right)}^2\right)$ (16). The diffusion model has been fruitfully applied to simulations (20) and to extract $D$ from experiments (21, 22). Interestingly, experiments on several aggregation-prone proteins, such as the PrP (11, 23), the intrinsically disordered protein $\alpha$-synuclein (12), and the engineered protein ${\alpha }_3$D (21), have found diffusion coefficients much smaller than other globular proteins, indicating that these proteins may have frustrated landscapes. Connecting measurements of $D$ to properties of the energy landscape ($\mathrm{\Delta }E$) can help illuminate the degree of frustration for real proteins.

Here we take a statistical approach to modeling the effects of nonnative interactions. Starting with a structure-based model (7), we add nonnative interactions whose strengths are assigned from a zero-mean Gaussian distribution with standard deviation b (24). As such, each nonnative interaction is equally likely to be attractive or repulsive (see Materials and Methods and SI Appendix for details). The parameter $b$ increases the nonnative heterogeneity and, as a result, increases the potential for competing misfolded states (i.e., frustration). For example, $15\%$ of nonnative interactions are stronger than native interactions when $b=1$ (see SI Appendix, Fig. S1).

We simulate many independently sampled nonnative parameter sets for each value of $b$ and average the resulting observables (e.g., folding time) across the different parameter sets. Data points and error bars (see Figs. 1, 3, and 5) show the average and SD, respectively, over all parameter sets at each $b$ (unless otherwise indicated). Averaging over parameter sets reveals that many important structural and kinetic properties depend generically on the level of nonnative heterogeneity, through $b$. In addition, the SD across parameter sets shows that some observables are more sensitive than others to the specific set of nonnative interactions and that the differences parameter sets increases at higher degrees of frustration (see SI Appendix, Fig. S4).

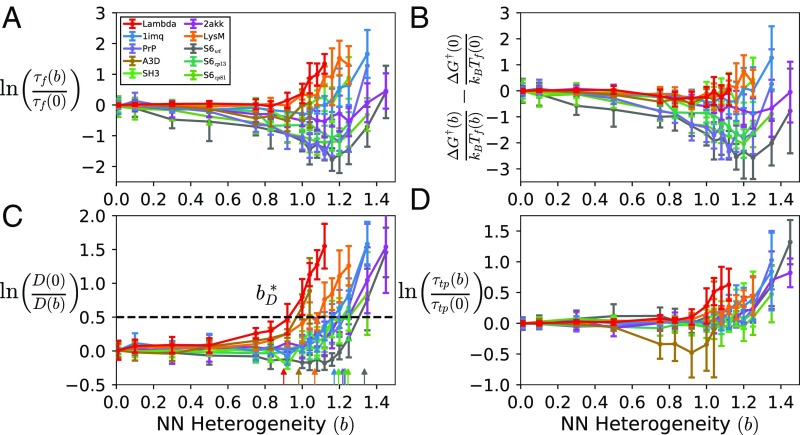
Fig. 1.

The dependence of the following as a function of nonnative heterogeneity: (A) folding time, (B) free energy barrier height, (C) diffusion coefficient in the unfolded state, and (D) transition path time. Observables in B–D are normalized by their pure structure-based ($b=0$) values for ease of comparison. Arrows in C indicate the nonnative heterogeneity $b_D*$ needed to slow diffusion by the same amount for each protein. Error bars indicate the SD across parameter sets.

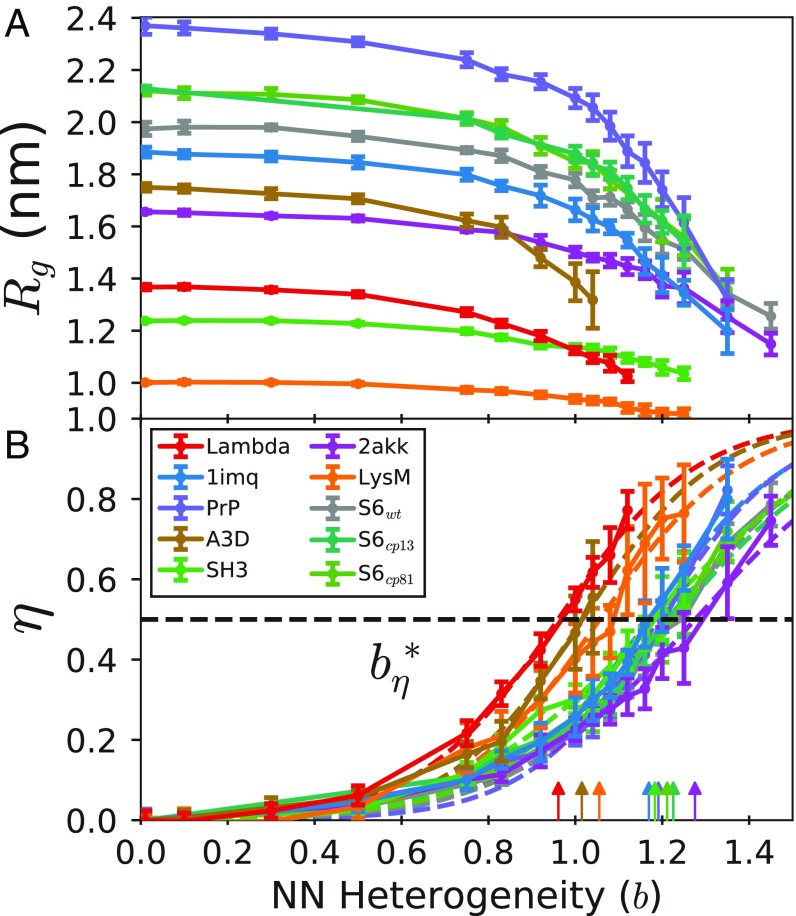
Fig. 3.

Unfolded state dimensions. (A) Radius of gyration $R_g$ and (B) degree of collapse $\eta$ versus $b$. The nonnative heterogeneity needed to collapse the unfolded state of each protein to $\eta =0.5$ is labeled $b_{\eta }*$ and indicated by arrows.

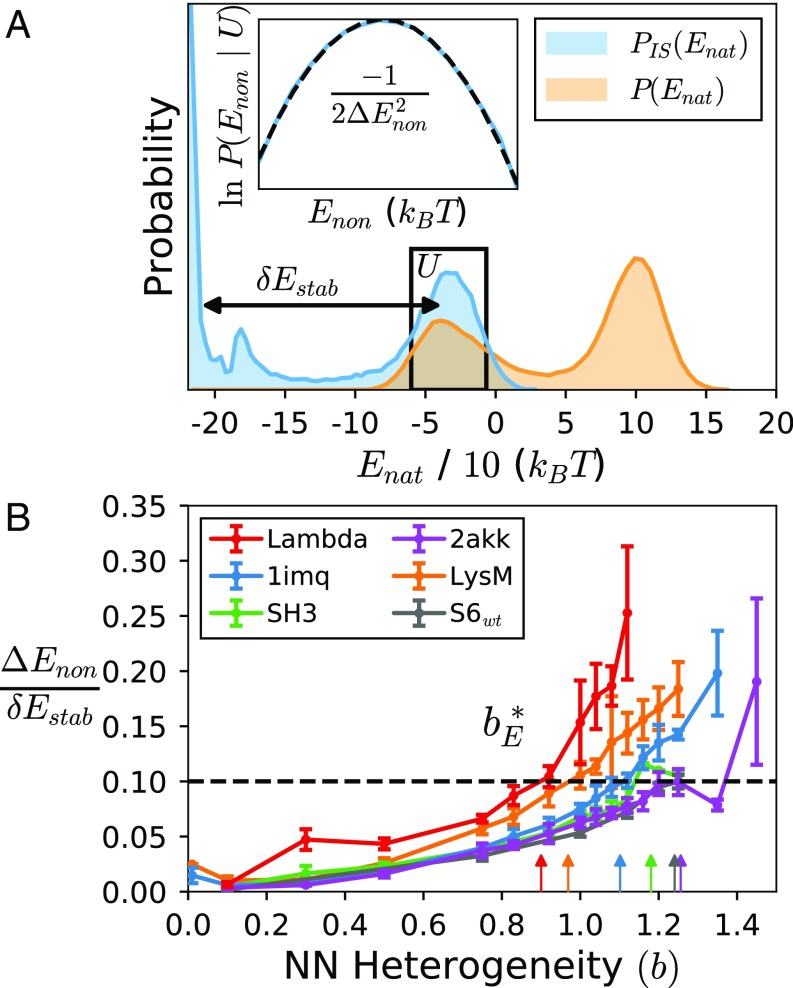
Fig. 5.

Results from inherent structure analysis. (A) Distribution of native energy $E_{\text{nat}}$ before (orange) and after (blue) minimization. The depth of the folding minimum is denoted $\delta E_{stab}$. Inset shows how fitting the distribution of nonnative energies $E_{\text{non}}$ in the unfolded state (U) yields the depth of typical misfolded minima, $\mathrm{\Delta }{E}_{non}$ (see SI Appendix, Eq. S20). (B) The degree of frustration $\frac{\mathrm{\Delta }{E}_{non}}{\delta E_{stab}}$. Arrows indicate the heterogeneity needed to observe a given degree of frustration on the energy landscape, $b_E*$.

A statistical approach is motivated by the fact that, at the level of our coarse-grained representation (one bead per residue), nonnative interactions could have different physical and chemical origins, and they could be modulated by denaturant, salt, mutations, etc. While this level of coarse-graining does not allow us to comment on proteins with a specific sequence of amino acids, we can investigate the general principles underlying the differences in the level of frustration observed between different protein topologies and between different sequences for the same topology.

To determine how the effects of nonnative interactions depend on native structure, we have selected 10 proteins with different sizes and topologies (Table 1). Several of our proteins were chosen because they have exhibited signs of frustration in other studies, such as the aggregation-prone PrP (23) and the engineered protein ${\alpha }_3$D (A3D) (21) [the topology of protein A3D is also similar to one of the Spectrin proteins (25), on which frustration has been experimentally observed]. Our set also includes the ribosomal protein S6 and two of its circular permutants [${\mathrm{S}\mathrm{6}}_{cp13}$ and ${\mathrm{S}\mathrm{6}}_{cp81}$ (26)]. S6 and its circular permutants are included because they have the same native structure but different contact order, which we found to be a useful metric in understanding our findings.

Table 1.

Proteins in this study

Name	PDB	N	M	ACO	$\alpha$, %	$\beta$, %
Lambda	1R69	63	155	17.14	54	0
A3D	2A3D	73	151	18.68	75	0
LysM	1E0G	48	117	18.69	38	17
1imq	1IMQ	85	219	22.39	64	0
SH3	1FMK	58	164	22.67	5	41
2akk	2AKK	74	213	24.41	0	46
${\mathrm{S}\mathrm{6}}_{\text{cp}13}$	1RIS	95	263	27.53	30	47
PrP	1QLX	104	266	27.61	58	4
${\mathrm{S}\mathrm{6}}_{\text{cp}81}$	1RIS	95	264	31.57	30	47
${\mathrm{S}\mathrm{6}}_{\text{wt}}$	1RIS	95	263	37.37	30	47

ACO, absolute contact order; M, number of native contacts; N, number of residues; PDB codes, Protein Data Bank codes.

Absolute Contact Order (ACO) characterizes differences in native structure (27) and is defined as the average sequence separation between native contacts: $\text{ACO}=\frac{1}{N_{\text{nat}}}\sum _{ij}^{N_{\text{nat}}}{l}_{ij}$, where $l_{ij}=|i-j|$ is the sequence separation between residues that make a native contact and $N_{\text{nat}}$ is the number of native contacts. ACO captures aspects of both size and topology; ACO increases with size, and $\beta$ proteins have larger ACO than $\alpha$ proteins of the same size.

We seek to characterize the folding and reconfiguration dynamics as a function of nonnative heterogeneity $b$. To do so, we project the dynamics onto the fraction of native contacts $Q$. By combining Eqs. 1 and 2, we can recast the folding time ${\tau }_f=1/k_f$ in the diffusion model as

$$\ln \left(\frac{{\tau }_f\left(b\right)}{{\tau }_f\left(0\right)}\right)\hspace{0.17em}=C+\ln \left(\frac{D\left(0\right)}{D\left(b\right)}\right)\hspace{0.17em}+\hspace{0.17em}\frac{\mathrm{\Delta }{G}^{†}\left(b\right)}{k_B{T}_f\left(b\right)}-\frac{\mathrm{\Delta }{G}^{†}\left(0\right)}{k_B{T}_f\left(0\right)},$$ [3]

where remaining factors have been grouped into $C$. Eq. 3 shows that the folding time as a function of nonnative heterogeneity, ${\tau }_f\left(b\right)$, normalized by its value in the pure structure-based model at $b=0$, ${\tau }_f\left(0\right)$, depends on the change in free energy barrier and diffusion coefficient.

We compare the terms of Eq. 3 estimated from simulation. The folding time ${\tau }_f$ is calculated as the average dwell time in the unfolded state (SI Appendix, Fig. S1, Left), and the free energy barrier $\mathrm{\Delta }{G}^{†}$ is estimated from the free energy profile (SI Appendix, Fig. S1, Right). While Kramers’ theory technically requires the diffusion coefficient at the barrier top $D\left(Q=Q^{†}\right)$ in Eq. 2, here we report the diffusion coefficient in the unfolded state: $D=D\left(Q=Q_U\right)=\frac{{⟨\mathrm{\Delta }{Q}^2⟩}_U}{{\tau }_r}$, where $\mathrm{\Delta }Q=Q-{⟨Q⟩}_U$ and ${\tau }_r$ is the reconfigurational timescale in the unfolded state, which can be estimated as the decay time of the autocorrelation function (28), ${\tau }_r=\underset{0}{\overset{\infty }{\int }}\frac{{⟨\mathrm{\Delta }Q\left(t+\tau \prime \right)\mathrm{\Delta }Q\left(t\right)⟩}_U}{{⟨\mathrm{\Delta }Q{\left(t\right)}^2⟩}_U}d\tau \prime$. We report $D\left(Q=Q_U\right)$ because it may be more relevant for comparing with energy landscape theory (29) and experiments that probe transient misfolding (30). If $D$ has a weak dependence on $Q$, as some previous studies have found for structure-based models (31), then $D\left(Q=Q_U\right)$ is an acceptable approximation for $D$ in Eq. 2.

We find that folding time decreases for some range of nonnative heterogeneity for all proteins except Lambda and LysM (Fig. 1A), which have two of the three lowest ACO values. Previous work suggests that the impact of nonnative interactions on the free energy barrier and diffusion coefficient can have potentially competing effects on the folding time (24, 32). Consistent with previous studies, we find that, for all proteins studied, there is a range of nonnative heterogeneity that lowers the barrier to fold (Fig. 1B). The protein-specific behavior of ${\tau }_f$ indicates that the folding time is not solely determined by the free energy barrier height but depends significantly on the diffusion coefficient $D$, and changes in $D$ are strongly protein-dependent.

The unfolded state diffusion coefficient displays two regimes for all proteins (Fig. 1C): a regime where $D$ is relatively insensitive to $b$, and a regime where $D$ decreases dramatically with $b$. We can empirically define the crossover between these regimes as the amount of nonnative heterogeneity, $b_D^{*}$, needed to decrease the diffusion coefficient such that $\ln \left(\frac{D\left(0\right)}{D\left(b_D^{*}\right)}\right)=0.5$ (see Fig. 1C). We find that $b_D^{*}$ correlates strongly with ACO (Fig. 2 red points) but is less correlated with the number of residues $N$ and uncorrelated with relative contact order $\text{RCO}=\text{ACO}/N$ (see SI Appendix, Table S1 and Fig. S3). Interestingly, Fig. 2 shows that the behavior of $b_D^{*}$ versus ACO is linear at small values and then appears to saturate at high values of ACO. The saturation can be explained by considering that ACO increases with the protein size, while $b_D^{*}$ is an intensive variable and is expected to converge to a finite value in the thermodynamic limit (32).

Fig. 2.

Value of crossover nonnative heterogeneity $b*$ versus ACO. The values of $b*$ are obtained from the decrease of the diffusion coefficient as a function of frustration ($b_D*$, red points), the increase of the degree of collapse ($b_{\eta }*$, blue points), and the increase of the depth of nonnative minima in the folding landscape ($b_E*$, green points).

This result implies that size and topology both play a role in setting the reconfiguration rate in proteins with frustration. In particular, for proteins with the same number of residues, the ones with lower ACO (i.e., $\alpha$-helical proteins) are more sensitive to frustration. This has important implications for how we understand the connection between intermolecular interactions and molecular motion.

Recent single-molecule experiments have been interested in the transition path time ${\tau }_{tp}$ (SI Appendix, Fig. S1, Middle) as a way to measure the diffusion coefficient, because ${\tau }_{tp}$ only depends weakly on the free energy barrier in the diffusion model (33), ${\tau }_{tp}\approx \frac{\ln \left(2e^{\gamma }\beta \mathrm{\Delta }{G}^{†}\right)}{\beta D{\kappa }_b}$, where $\gamma$ is Euler’s constant and the equation is exact only in the large barrier limit $\mathrm{\Delta }{G}^{†}\gg k_{B}T$. We find that ${\tau }_{tp}$ calculated from simulation (Fig. 1D) increases at large $b$ and qualitatively resembles the behavior of $D$ for all proteins, except A3D. It is worth noting that A3D has the smallest folding barrier of all proteins studied ($\mathrm{\Delta }G<1k_{B}T$), and the assumptions of the diffusion model underlying the equation above may not apply.

We expect that our findings can be tested by experiments that measure ${\tau }_{tp}$ to determine the reconfigurational diffusion coefficient $D$. In particular, we expect that proteins with larger contact order require more frustration (i.e., a higher fraction of strongly attractive nonnative interactions) to slow their diffusion compared with proteins with lower contact order.

Collapse and Nonnative Structural Motifs.

We investigate the structural properties of the unfolded state to understand how nonnative interactions can have a protein-specific effect on the reconfiguration dynamics. We find several interesting differences between how proteins with different topologies respond to frustration. The first difference arises in the collapse of the unfolded state. The second difference arises in the patterns of nonnative contacts, with $\alpha$-helical and $\beta$-sheet topologies displaying different “motifs” in nonnative contact formation.

The central feature of disordered polymer states, such as the unfolded state in protein folding, is their overall size, which is given by their radius of gyration $R_g$ or their degree of collapse $\eta$. The radius of gyration $R_g$ of the unfolded state (Fig. 3A) scales with protein size $R_g\propto N^{\gamma }$ at $b=0$ and decreases monotonically with increasing nonnative heterogeneity. To compare $R_g$ from different proteins on the same scale, we define the degree of collapse as $\eta =\frac{R_g-R_g^{\text{max}}}{R_g^{\text{min}}-R_g^{\text{max}}}\in \left(\mathrm{0,1}\right)$, where $R_g^{\text{max}}=R_g^{b=0}$ is the radius of gyration of the unfrustrated coil and $R_g^{\text{min}}\propto N^{\frac{1}{3}}$ is the radius of gyration of the completely collapsed chain (details in SI Appendix). The degree of collapse (Fig. 3B) depends on frustration in a similar way to the diffusion coefficient discussed above (Fig. 1C). For example, $\alpha$ proteins become more compact than $\beta$ proteins of a similar size. The degree of collapse $\eta$ has a sigmoidal dependence on nonnative heterogeneity, and the midpoints of the sigmoid functions for each protein $b_{\eta }^{*}$ also strongly correlate with ACO (Fig. 2 blue points). The same saturation behavior at high values of ACO observed for $b_D^{*}$ above is also present for $b_{\eta }^{*}$.

Contact maps show that, even when a significant amount of nonnative heterogeneity is present, the unfolded state is largely unstructured on average (Fig. 4, Upper Triangles), with some partially formed native contacts (blue) but very little nonnative structure (red). However, even if the unfolded state has very little average structure, it is not featureless. Patterns emerge in how structure forms transiently, and these patterns are revealed by the fluctuations in contact formation. Contact fluctuations, given by the mean-squared variation of contacts ${⟨\mathrm{\Delta }{q}_{ij}^2⟩}_U$ where $\mathrm{\Delta }{q}_{ij}=q_{ij}-{⟨q_{ij}⟩}_U$, are largest for contacts that form and break most often and, therefore, reveal preferences in how structure forms transiently.

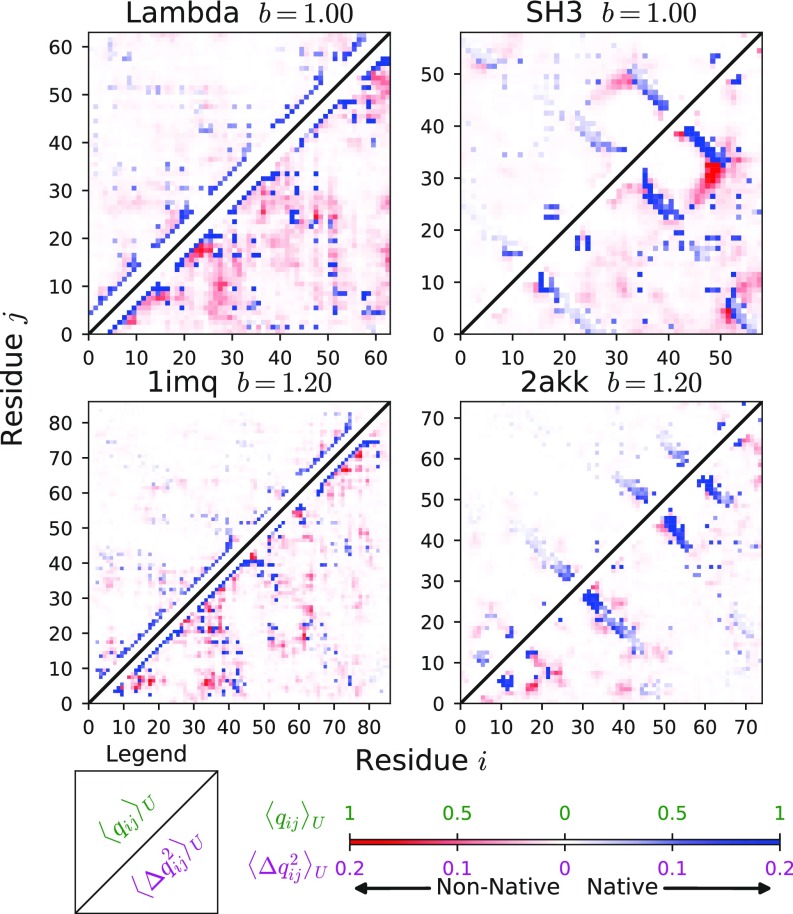
Fig. 4.

Nonnative structure in the unfolded state. Unfolded state contact formation ${⟨q_{ij}⟩}_U$ (upper triangles) and contact fluctuations ${⟨\mathrm{\Delta }{q}_{ij}^2⟩}_U$ (lower triangles) for selected proteins.

Contact fluctuations in the unfolded state (Fig. 4, Lower Triangles) show that native topology qualitatively changes how proteins form transient nonnative structure. In particular, contact fluctuations show that $\alpha$ proteins (Fig. 4, Left) form more nonnative contacts close to each other in sequence than $\beta$ proteins (Fig. 4, Right). In addition, the $\alpha$ proteins form more nonnative contacts in between secondary structural elements, while $\beta$ proteins form nonnative contacts that are more localized near native $\beta$-sheets. This suggests that the coupling of secondary structure formation with nonnative interactions may lead to different motifs in the misfolded ensembles of $\alpha$ and $\beta$ proteins.

Probing the Underlying Energy Landscape.

Energy landscape theory links protein folding kinetics to the statistical properties of the energy landscape (6). At the folding temperature, the distribution of energies is bimodal (Fig. 5A orange), with the lower (higher) energy peak corresponding to the folded (unfolded) state. At a constant temperature, these peaks are significantly broadened from vibrations around the minima on the landscape. By performing energy minimization of configurations sampled along the trajectory, we get a clearer picture of the “inherent structure” of the energy landscape (Fig. 5A blue) (34) (details in SI Appendix).

We perform inherent structure analysis on a subset of our proteins and calculate two important properties of their landscapes: the depth of the folded state minimum relative to the unfolded ensemble, $\delta E_{\text{stab}}={\overline{E}}_{\text{folded}}-{\overline{E}}_{\text{unfolded}}$, and the breadth of the energy distribution within the unfolded state, $\mathrm{\Delta }{E}_{\text{non}}$ (Fig. 5A). The ratio of these energy scales $\mathrm{\Delta }{E}_{\text{non}}/\delta E_{\text{stab}}$ describes the degree of frustration on the landscape: When $\mathrm{\Delta }{E}_{\text{non}}/\delta E_{\text{stab}}$ approaches 1, misfolded minima are just as deep as the native minimum (35).

Interestingly, we find that $\mathrm{\Delta }{E}_{\text{non}}/\delta E_{\text{stab}}$ (Fig. 5B) has protein-specific dependence on the amount of frustration $b$ similar to what was noted above for the diffusion coefficient and degree of collapse: The amount of nonnative heterogeneity needed to increase the degree of frustration on the landscape by a given amount $b_E^{*}$ also strongly correlates with ACO (Fig. 2, green points). Again, the saturation behavior at high values of ACO noted above is observed. This means that for the same amount of nonnative heterogeneity, size and topology modulate the depth of the unfolded state minima. This result provides an energy landscape basis for interpreting the results of previous sections.

The degree of frustration on the energy landscape can alternatively be quantified by comparing the folding temperature $T_f$ to the glass temperature $T_g$, where $T_g$ is the temperature where the system would get stuck in a single misfolded state. The glass temperature can be calculated by the distribution of inherent structures $T_g=\frac{\mathrm{\Delta }{E}_{\text{non}}}{\sqrt{2S_0}}$, where $S_0$ is the entropy of the unfolded state minima (6, 35). The ratio of temperatures $T_g/T_f$ displays qualitative similar dependence on size and topology (SI Appendix, Fig. S5). Theoretical estimates of $T_g/T_f$ for proteins span a range, from $T_g/T_f\approx 0.2$ (36) to $T_g/T_f\approx 0.6$ (35). Our findings suggest there is a range of nonnative heterogeneity allowable for proteins to be within the theoretical range (gray rectangle in SI Appendix, Fig. S5). Notably, proteins with larger ACO appear to have a wider range of nonnative heterogeneity permissible.

It must be noted that our estimates appear to increase beyond the theoretical bound of $T_g/T_f<1$. This is most likely an artifact of approximations made in the inherent structure analysis that underestimate the magnitude of $S_0$.

Discussion

We have found that the impact of nonnative interactions on protein folding and reconfiguration dynamics depends systematically on native state size and topology. In particular, we have found that the amount of nonnative heterogeneity required to produce signs of a frustrated landscape (e.g., slower reconfiguration, collapse, etc.), which we have called $b^{*}$, has a simple dependence on the ACO (Fig. 2). In particular, $b^{*}$ is linear at low ACO and then saturates when ACO $\ge$ 25. This saturation is expected because $b^{*}$ is an intensive variable that should converge to a finite value in the thermodynamic limit (and ACO increases with size) (32). This means that protein topologies in the finite-size regime (ACO < 25) are more sensitive to nonnative interactions. It interesting to note that the PrP protein, which appears frustrated in the experiment (11), has a large enough ACO ($\simeq 28$) to fall in the plateau region of Fig. 2, which would suggest that this topology is generally less sensitive to nonnative interactions. However, it should be noted that the PrP structure has several long stretches lacking secondary structure. As our model considers the effect of nonnative interactions on the tendency to form native secondary structure, we expect the results may differ for proteins that are partially intrinsically unstructured.

Our model suggests that the coupling between nonnative interactions and protein topology could result in different misfolding behavior for $\alpha$ and $\beta$ proteins. In particular, $\alpha$ proteins have slower reconfiguration times because nonnative interactions induce the unfolded state to become more collapsed, creating deeper misfolded minima on the folding landscape. Coupling between secondary structure and nonnative interactions might explain why the latter have been posited to be important in $\alpha$-helical proteins, such as Im9 (15), the Spectrin proteins R16/R17 (25), and protein A3D (21). Indeed, A3D is one of the protein topologies that was found to be most sensitive to the effect of frustration in our study, in agreement with experimental observation. A study of the salt-induced collapse of S6 also found native-like secondary structure content (37), indicating a general link between secondary structure and the effect of nonnative interactions.

Interestingly, a recent study using a native-centric polymer model found that, in the absence of nonnative interactions, the native contact map of $\beta$ proteins promotes collapse while folding (38). As our study focuses on the coupling of secondary structure with nonnative interactions, such results do not conflict with our findings.

We also find that the variation between parameter sets tends to increase with the onset of the frustrated regime. For example, some quantities, such as the folding time, show large variations between parameter sets at large levels of nonnative heterogeneity (SI Appendix, Fig. S4). This means that particularly attractive or repulsive nonnative interactions, or clusters of such interactions, could have a large influence on these quantities. This could explain, for example, why a small number of mutations in the Spectrin proteins can result in large differences in folding time (25). Interestingly, the radius of gyration of the unfolded state is relatively insensitive to the parameter set, as shown by the small error bars in Fig. 3A.

Although there is no experimental equivalent to our parameter $b$, experiments can modulate nonnative interactions by varying solution conditions and measure the degree of collapse, secondary structure formation, and reconfiguration rate to connect with our results. Our results could be tested by studying circular permutations of the same protein under solution conditions that modulate collapse (e.g., salt, denaturant). If, for example, salt concentration is analogous to our parameter $b$, then the different circular permutants may show a turnover in their folding rate at different concentrations of salt (e.g., see figure 3 of ref. 39). Alternatively, our findings could be tested by measuring the transition path time under different pH conditions, as was done for the protein ${\alpha }_3$D (21).

Materials and Methods

Simulation Model.

We simulate a set of 10 proteins that span a range of sizes and topologies, described in Table 1. Our $C_{\alpha }$ structure-based simulation model with nonnative interactions is similar to what was used in previous work (24) and is described in SI Appendix.

Inherent Structure Analysis.

Performing energy minimization of configurations sampled in a constant temperature simulation maps each frame to its inherent structure minimum on the landscape (34). Following previous applications, we perform inherent structure analysis on a subsample of frames from trajectories at the folding temperature. Details are provided in SI Appendix.