Ab initio spectroscopy and ionic conductivity of water under Earth mantle conditions

Significance

Despite more than a century of study, the properties of water at high pressure and temperature remain difficult to measure. First-principles computations are ideal tools to study matter under extreme conditions, as they require neither assumptions about chemical bonds nor experimental data for fitting interatomic potentials. Here we carry out first-principles simulations to study the diffusivity, vibrational properties, and conductivity of water in a controversial region of its phase diagram (1,000 K, 10–20 GPa). Our results provide insight into water’s dissociation mechanism, the origin of its large ionic conductivity, and the spectroscopic signatures of ionic species. We predict Raman and infrared spectra at several conditions, which will serve as a guide for future experiments.

Abstract

The phase diagram of water at extreme conditions plays a critical role in Earth and planetary science, yet remains poorly understood. Here we report a first-principles investigation of the liquid at high temperature, between 11 GPa and 20 GPa—a region where numerous controversial results have been reported over the past three decades. Our results are consistent with the recent estimates of the water melting line below 1,000 K and show that on the 1,000-K isotherm the liquid is rapidly dissociating and recombining through a bimolecular mechanism. We found that short-lived ionic species act as charge carriers, giving rise to an ionic conductivity that at 11 GPa and 20 GPa is six and seven orders of magnitude larger, respectively, than at ambient conditions. Conductivity calculations were performed entirely from first principles, with no a priori assumptions on the nature of charge carriers. Despite frequent dissociative events, we observed that hydrogen bonding persists at high pressure, up to at least 20 GPa. Our computed Raman spectra, which are in excellent agreement with experiment, show no distinctive signatures of the hydronium and hydroxide ions present in our simulations. Instead, we found that infrared spectra are sensitive probes of molecular dissociation, exhibiting a broad band below the OH stretching mode ascribable to vibrations of complex ions.

Water at extreme conditions plays a critical role in Earth and planetary science. For example, ice has been proposed to exist in cold, subducting tectonic slabs at 10–20 GPa, bearing large reservoirs of water with immense impact on terrestrial geochemistry (1). In addition, recent studies supported the existence of stable hydrous silicate minerals in the deep Earth (2) and of local aqueous pockets in the upper mantle (3) where water is an important medium to transport oxidized carbon (4, 5). At the fundamental level, high pressure and temperature create complex changes in the bonding and structural properties of water, eventually leading to dissociation, and many of these changes remain poorly characterized. One of the reasons stems from experimental difficulties in probing the liquid at extreme conditions, including water’s reaction with metals present in the experimental apparatus, high corrosiveness of the liquid, and other limitations of current high-pressure experimental techniques. Available measurements of water at extreme conditions are mostly limited to vibrational spectroscopy and conductivity, obtained in static and shock-wave high-pressure experiments. On the theoretical side, spectroscopic signatures and ionic transport may not be studied with simple classical simulations, due to the presence of complex dissociation processes. Hence, their investigation calls for the use of quantum mechanical calculations, which are usually rather demanding from a computational standpoint. To this date there have been few ab initio simulations of high-pressure water encompassing structural, vibrational, and transport properties (e.g., ionic conduction); for example, no vibrational spectra have been computed for the fluid close to the ice VII melting line, and water conductivity has been investigated primarily at conditions well above 20 GPa (6–9).

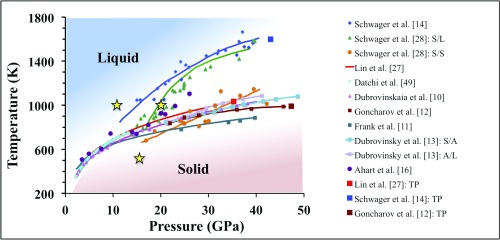
Overall the water phase diagram at high pressure is still poorly known, with many controversial results present in the literature, e.g., regarding the location of the melting line in the region of 10–50 GPa (Fig. 1). A number of experimental studies (10–13) indicate the presence of a melting line near 700 K at 20 GPa, almost 400 K lower than previously reported (14, 15); however, the most recent measurements proved to be inconclusive in fully resolving the discrepancy (16). In addition, three markedly different locations for the triple point of the liquid, ice VII, and ice X have been proposed in the literature (17), differing by 500 K and 10 GPa. The structural and dynamical properties of the fluid close to melting are also not well established, with ongoing debates on many fronts, including the existence of plastic ice phases close to the ice VII melting line (18, 19), the molecular or dissociative nature of water (20), and the primary mechanism of ionic conduction (9, 21). Some studies suggested a unimolecular dissociation process (7, 22–25), ${\text{H}}_2\text{O}\to {\text{H}}^{+}+{\text{OH}}^{-}$ occurring above 10 GPa and 1,000 K, while others pointed at the existence of bimolecular dissociation (8, 12, 26), i.e., $2{\text{H}}_2\text{O}\to {\text{H}}_3{\text{O}}^{+}+{\text{OH}}^{-}$ similar to low pressure, with some experiments being unable to corroborate either mechanism (27). Likewise the interpretation of vibrational spectra (12, 22) of high-pressure water remains controversial.

Fig. 1.

The phase diagram of water at high pressure (P) and temperature (T). All points are experimental data, marking the ice VII/liquid transition unless otherwise specified. Other points mark the proposed ice VII/solid (S/S), solid/liquid (S/L), solid/amorphous (S/A), and amorphous/liquid (A/L) transitions. Proposed triple points (TP) of ice VII, liquid, and ice X phase are marked as squares. The (P, T) conditions investigated in this work are marked with yellow stars.

To shed light on the water phase diagram between 10 GPa and 20 GPa, we carried out a series of ab initio simulations aimed at characterizing the structure of the fluid, its vibrational spectra, and the mechanism of ionic conduction. We focused on three specific [pressure, temperature (P, T)] conditions, including one (11 GPa and 1,000 K) where the system is believed to be a fluid according to all experiments and for which measured Raman spectra are available and another condition (20 GPa and 1,000 K) characterized as either solid or liquid by different measurements. We also considered an amorphous phase, quenched from the liquid (16 GPa, 500 K), to compare vibrational signatures of fluid and disordered solid water in a similar pressure range. We computed ab initio molecular dynamics trajectories of length $\sim$240 ps at each of the (P, T) conditions.

Our results are consistent with the most recent estimates (12, 13) of the location of the water melting line between 11 GPa and 20 GPa; our simulations provide a detailed microscopic picture of the fluid, including dissociation mechanisms, and the origin of its high conductivity above 10 GPa.

Results and Discussion

Structure and Diffusion.

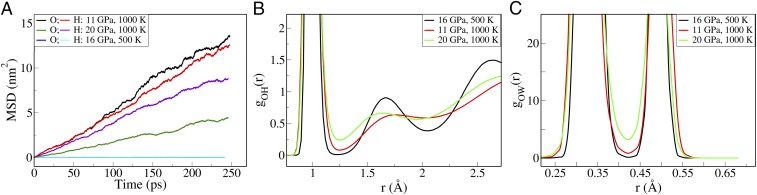
We first determined whether water is solid or liquid at the conditions chosen in our study by computing diffusion coefficients from the mean-squared displacement of oxygen and hydrogen (Fig. 2A and SI Appendix, Table S1). We found that at 1,000 K, both at 11 GPa and 20 GPa, water is a liquid. Hence our results are consistent with the melting line reported by Lin et al. (27) but not with studies which classified water as solid at these conditions, where the system was suggested either to be in the ice VII (14) structure or to adopt a new, unspecified crystalline phase (28). We found that the quenched phase at 16 GPa/500 K is instead nondiffusive and we classified it as solid-like. A summary of the thermodynamic conditions and computed diffusion coefficients is given in SI Appendix, Table S1.

Fig. 2.

(A) The mean-squared displacement of oxygen/hydrogen at 11 GPa/1,000 K, 20 GPa/1,000 K, and 16 GPa/500 K. (B) The oxygen–hydrogen RDFs. (C) The oxygen–MLWF RDFs.

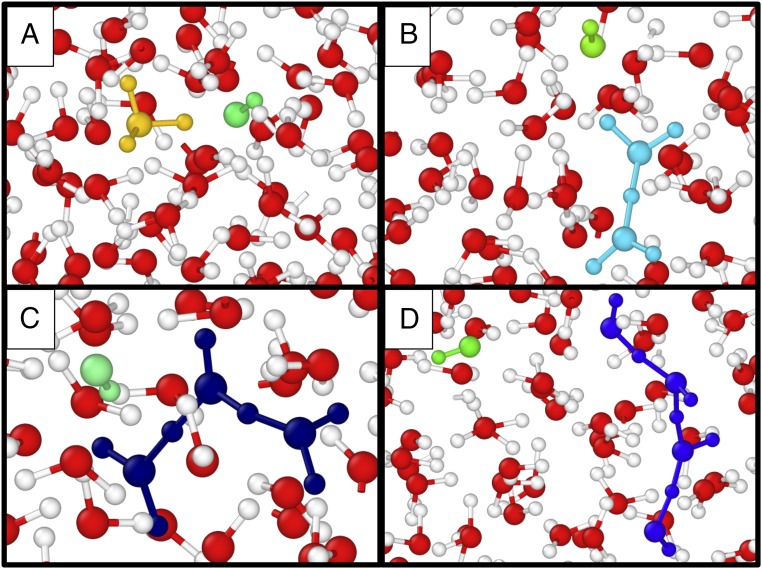
At 20 GPa/1,000 K, we found that hydrogen diffuses twice as fast as oxygen. Clear evidence of the dissociation processes occurring in the liquid emerges from the analysis of radial distribution functions (RDFs), e.g., a significant intensity of the O-H RDF (Fig. 2B) near its first minimum. Further evidence of molecular dissociation is in the RDF between oxygen atoms and maximally localized Wannier function centers (Fig. 2C). The latter represent centers of charge in the system. There are four centers associated to an intact water molecule, with two lone pairs and two bond pairs located within O-H covalent bonds. The nonnegligible intensity in correspondence of the minimum between lone and bond pair distributions is a signature of proton transfer. We directly observed dissociation and proton transfer events in our simulation, with frequent creation of short-lived (<10 fs) ionic products of bimolecular dissociation events, consistent with earlier studies (26, 29). While the most commonly observed ionic species are simple hydronium and hydroxide (Fig 3A), we also detected the formation of larger transient ionic species, as defined by simple distance cutoffs. Many of them are “Zundel” (${\text{H}}_5{{\text{O}}_2}^{+}$) ions (Fig. 3B). Our observations of transient multimolecular ionic species differ from the hypothesis of unimolecular dissociation, which would imply the existence of free protons (7, 22–24).

Fig. 3.

Snapshots of configurations extracted from molecular dynamics trajectories at 20 GPa and 1,000 K, showing short-lived ionic species. Color coding of ionic species is based on a distance cutoff corresponding to the first minimum of the O-H RDF. Hydroxide ions are shown in green. (A) A hydronium (yellow)/hydroxide pair, formed after a bimolecular dissociation event. (B) A Zundel-like ${\text{H}}_5{{\text{O}}_2}^{+}$ species (cyan) with a nearby hydroxide. (C) A ${\text{H}}_7{{\text{O}}_3}^{+}$ species (dark blue) with a nearby hydroxide. (D) A ${\text{H}}_7{{\text{O}}_4}^{-}$ species (blue) and a hydroxide ion.

We explicitly monitored the formation of ionic species as a function of time, using the hydrogen bond definition of ref. 30; we found that hydronium and hydroxide ions are formed in a highly correlated fashion (see SI Appendix, Ionic Species and Ionic Lifetimes for details). The maximum free proton lifetime is very short, of the order of 0.3 fs. Despite its simplicity, the method adopted here to define free protons (using a cutoff distance; SI Appendix, Ionic Species and Ionic Lifetimes) clearly indicates that isolated hydrogen ions are transient species, consistent with a bimolecular dissociation mechanism. These rapid dissociation events occur in the liquid at both 11 GPa and 20 GPa, with frequency increasing with pressure (SI Appendix, Fig. S1), consistent with the trend observed in RDFs.

Interestingly, at both 11 GPa and 20 GPa the fluid exhibits a distinct second coordination shell in the O-H RDF. This indicates that intermolecular hydrogen bonding persists at these conditions, despite molecular dissociation and proton transfer events. The location of the second peak of the O-H distribution is sensitive to pressure, varying from 1.75 Å at 11 GPa to 1.62 Å at 20 GPa. In contrast, the maxima of the first coordination shell are in similar locations at both pressures, confirming the insensitivity of water’s first coordination shell to compression, as noted by other authors (31).

Ionic Conductivity.

To understand whether the short-lived hydronium, hydroxide, and more complex ions found in our simulation act as charge carriers, we computed the ionic conductivity of the fluid. Along the shock Hugoniot, the conductivity of water has been shown to rapidly increase by several orders of magnitude under pressure, before reaching a plateau on the order of 10 ${\left(\mathrm{\Omega }\text{cm}\right)}^{-1}$ above 30 GPa (32). This increase has been interpreted as the result of increasing dissociation of water molecules (8), although the nature of the ionic species responsible for conduction was not determined and the ability of ionic species present in the fluid to effectively carry charge has been questioned in the literature (21, 22).

We computed ionic conductivities directly from first principles, without resorting to a priori definitions of ionic charges, e.g., geometric partitioning, (8, 33) or Mulliken (7) or Born effective charges (9). Avoiding approximate definitions of charges is key for obtaining unbiased and predictive results for ionic conductivities. Using the Green–Kubo relation, we express the conductivity, $\sigma$, as

$$\sigma =\frac{1}{3k_{b}TV}{\int }_0^{\infty }⟨\dot{\overrightarrow{M}}\left(0\right)\dot{\overrightarrow{M}}\left(t\right)⟩dt,$$ [1]

where $k_b$ is Boltzmann’s constant, T is the temperature, V is the cell volume, and $\dot{\overrightarrow{M}}$ is the time derivative of the sample dipole moment $\overrightarrow{M}$, defined as

$$\begin{array}{c}\hfill \overrightarrow{M}\left(t\right)=e\cdot \sum _{i=1}^{N_H}{\overrightarrow{R}}_i^H\left(t\right)+6e\cdot \sum _{i=1}^{N_O}{\overrightarrow{R}}_i^O\left(t\right)-2e\cdot \sum _{i=1}^{N_{\mathit{\text{MLWF}}}}{\overrightarrow{R}}_i^{\mathit{\text{MLWF}}}\left(t\right).\end{array}$$ [2]

Here $e$ is the elementary charge, ${\overrightarrow{R}}^O\left(t\right)$ and ${\overrightarrow{R}}^H\left(t\right)$ are the coordinates of oxygen and hydrogen atoms, respectively, and ${\overrightarrow{R}}^{MLWF}\left(t\right)$ are the coordinates of the center of a maximally localized Wannier function (MLWF) (34). The summations run over all species of the simulation cell. The conductivity is computed using the Einstein relation (SI Appendix, Ionic Conductivity).

This study computes the ionic conductivity of water entirely from first principles, using MLWFs. An equivalent approach used by Cavazzoni et al. (6) used the Berry phase method at 30–300 GPa and 300–7,000 K.

To minimize error arising from statistical noise (35), we obtained estimates of $\sigma$ by partitioning the total trajectory over which $\overrightarrow{M}\left(t\right)$ was computed into shorter portions (of 10 ps each) and computing the ionic conductivity as an average (SI Appendix, Ionic Conductivity and SI Appendix, Figs. S3 and S4). We obtain an estimate of $\sigma$ $\sim$ 1 ${\left(\mathrm{\Omega }\text{cm}\right)}^{-1}$ at 11 $\pm$ 1 GPa, 1,000 K and $\sigma$ $\sim$ 10 ${\left(\mathrm{\Omega }\text{cm}\right)}^{-1}$ at 20 $\pm$ 1 GPa, 1,000 K. We report these values emphasizing their orders of magnitude, as multiple additional trajectories would be required for a more precise determination.

The values of $\sigma$ obtained at 11 GPa and 20 GPa along the 1,000-K isotherm are six and seven orders of magnitude higher than at ambient conditions, respectively (36). SI Appendix, Fig. S5 shows how these estimates compare with previous experimental and computational reports of water’s ionic conductivity along the principle Hugoniot. We note that our data are on the 1,000-K isotherm, while the Hugoniot includes temperatures such as 990 K at 12 GPa and 1,710 K at 22 GPa (37); a full comparison of data from SI Appendix, Fig. S5, including temperatures, is presented in SI Appendix, Table S2. Our finding of an order of magnitude increase in conductivity between 11 GPa and 20 GPa is consistent with experimental reports of orders of magnitude increases in conductivity along the Hugoniot, which were attributed to autoionization of water (32, 37). Our estimates of $\sigma$ are also consistent with computational results obtained using approximations based on Mulliken charges [$\sigma$ = 6 $\pm$ 2 ${\left(\mathrm{\Omega }\text{cm}\right)}^{-1}$ at 18.2 $\pm$ 0.2 GPa, 790 K] (7). They are also consistent with other computational results, which computed $\sigma$ using a generalized Einstein formulation for diffusion coefficients of unbound protons [$\sigma$ = 2 $\pm$ 1 ${\left(\mathrm{\Omega }\text{cm}\right)}^{-1}$ at $\sim$15 GPa, 1,010 K and $\sigma$ = 11 $\pm$ 4 ${\left(\mathrm{\Omega }\text{cm}\right)}^{-1}$ at $\sim$24 GPa, 1,550 K] (8). Unlike both of these computational studies, we emphasize that our estimates required no a priori assumptions about the effective charge transported. Our findings indicate that the large increase in conductivity near the melting line is related to the existence of the short-lived and fast-recombining hydroxide/hydronium and more complex ionic species that are effective charge carriers.

A strong argument against bimolecular dissociation at high pressure, originally raised in ref. 22, is the lack of a spectroscopic signature of hydronium in measured Raman spectra, near the O-H stretching peak at 2,900 cm⁻¹. It was later suggested that the missing signature could be due to the short lifetime of hydronium ions, leading to a broad peak, difficult to identify (26). To address this controversy, we computed the Raman spectra of water at 11 GPa and 20 GPa, explicitly searching for vibrational signatures of the short-lived ionic species identified from the analysis of our molecular dynamics (MD) trajectories.

Raman Spectra.

Raman spectra were computed as the Fourier transforms of the time correlation function of the system’s polarizabilities, obtained from density functional perturbation theory (38), as implemented in the Qbox code (39, 40). Here we focus on unpolarized Raman spectra, for which measurements are available (12, 22, 27, 41) (see SI Appendix, Raman Spectra for additional details).

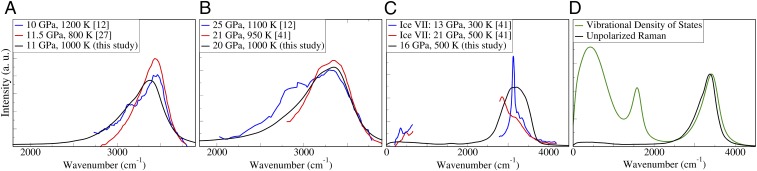
Our results in the O-H stretching region are compared with experiment in Fig. 4 and show good agreement. The low-frequency part of the spectrum was omitted since the measured one is featureless. Our simulations reproduce two key trends observed under pressure: the considerable decrease in the O-H mode intensity (Fig. 5 A and B) and a redshift of 70 cm⁻¹ between 11 GPa and 20 GPa at 1,000 K. This comparison represents a crucial validation of the model of the fluid derived in our ab initio simulations. We note that the computed spectra reported in Figs. 4 and 5 A and B represent available Raman spectra of high-pressure water over the full 0- to 3,000-cm⁻¹ range, as experimental limitations prevent the measurement of frequencies between 800 cm⁻¹ and 2,200 cm⁻¹.

Fig. 4.

(A) Computed unpolarized Raman spectrum at 11 GPa, 1,000 K compared with experiment (12, 27). (B) The unpolarized Raman spectrum at 20 GPa, 1,000 K compared with experiment (12, 41). (C) Computed unpolarized Raman spectrum of amorphous water at 16 GPa, 500 K compared with the experimental spectrum of ice VII (41). (D) Computed unpolarized Raman spectra at 11 GPa, 1,000 K compared with the vibrational density of states.

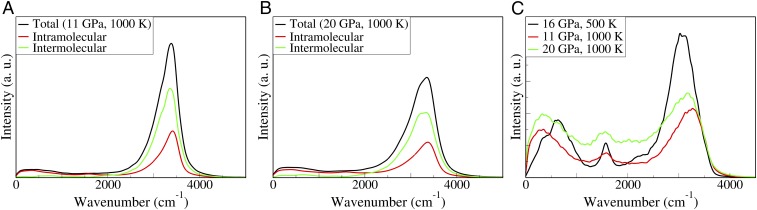
Fig. 5.

(A) Computed unpolarized Raman spectrum at 11 GPa, 1,000 K with inter- and intramolecular components. (B) Unpolarized Raman spectrum at 20 GPa, 1,000 K with decomposition into intramolecular (red) and intermolecular (green) spectra. Both A and B are normalized for intensity comparison. (C) Computed IR spectra under different P, T conditions. Note the broad continuum intensity in the mid-IR region.

Previous computational studies have simply used the vibrational density of states (VDOS) as an approximation of the Raman spectrum (12). Fig. 4D shows that the VDOS reproduces the qualitative shape of the O-H vibrational stretching mode. However, it differs from the Raman spectrum in the position of the maximum—the Raman peak is redshifted by about 50 cm⁻¹ relative to the VDOS. In addition, the VDOS spectrum exhibits a peak near 1,600 cm⁻¹, as well as prominent low-frequency collective modes. Neither of these modes is Raman active and they do not appear in the unpolarized spectrum.

Having validated our results with experiments, we proceeded to analyze them in detail. In agreement with the report of ref. 22, we found no specific signature associated to hydronium ions, indicating that Raman spectra are not a good probe for these species in the liquid, where, however, they are present, as discussed above. We also observed the same asymmetry in the O-H stretching peak as reported experimentally (22); by using a simple decomposition of the signal into two Gaussians, Holmes et al. (22) attributed the lower- and higher-frequency shoulders of the stretching peak to hydrogen- and non–hydrogen-bonded water molecules, respectively. To analyze the nature of this asymmetry, we decomposed the total spectrum into inter- and intramolecular components; we followed the procedure of Wan et al. (39) and used MLWFs to define effective molecular polarizabilities in the fluid (SI Appendix, Raman Spectra). We found that the lower- and higher-frequency shoulders of the asymmetric peak correspond to inter- and intramolecular contributions, respectively; this finding is consistent with experimental reports. However, we found that the intensity of the low-frequency shoulder relative to the total peak at 11 GPa and 20 GPa is similar; this finding is contrary to the experimental claim that the lower-frequency contribution (from hydrogen bonding) is substantially weakened between 11 GPa and 20 GPa along the Hugoniot. The persistence of hydrogen bonding at high pressure was also observed in the analysis of the pair correlation functions (Fig. 2).

The described asymmetry in the O-H stretching Raman peak has been used as a crucial fingerprint of melting. For example, large changes in such asymmetry combined with the absence of a low-frequency translational mode have been used to identify melting of ice VII (27, 41). The computed spectra at 11 GPa and 20 GPa confirm these qualitative properties of the liquid phase. However, the absence of low-frequency modes should not be interpreted as a sufficient indication that the system is liquid. Fig. 4C presents a spectrum of the nondiffusive quenched phase at 16 GPa and 500 K, together with the experimental ice VII Raman spectra from Lin et al. (41). Although both the simulated and experimental samples are nondiffusive, they display markedly different spectra. The quenched phase exhibits neither a low-frequency lattice mode nor a heavy asymmetry of the O-H stretching peak. We present this case as a cautionary example that amorphous phases may display Raman features usually assigned to liquid.

IR Spectroscopy.

We showed above that computed Raman spectra, similar to experimental ones, present no clear signatures of the short-lived dissociating species effectively present in our simulations. Instead we found that such signatures are present in IR spectra shown in Fig. 5C. The computed IR spectra display clear OH stretching modes centered near 3,100 cm⁻¹, but unlike the Raman spectra, they also display a considerable intensity below the OH mode.

Such intensity is enhanced with pressure: We observed a roughly twofold increase in the background IR intensity in the mid-IR region (400–2,500 cm⁻¹) with increasing pressure from 11 GPa to 20 GPa along the isotherm. From an analysis of our MD trajectories, we could detect the presence of transient Zundel ions in the high-pressure fluids, which are expected to be responsible, at least in part, for the broad IR band below the OH stretching peak, consistent with the hypothesis of ref. 42. We note that a broad, mid-IR continuum absorbance was also observed in a number of aqueous systems at ambient conditions, from protonated clusters (43) to bulk acidic solutions (44–46). An ultrafast 2D IR study of the excess protons in aqueous hydrochloric solutions (44) ascribed the broad-band intensity to vibrational modes of the Zundel and Eigen ions. This view is consistent with that of a recent study using femtosecond spectroscopy to precisely probe the vibrational signatures of the Zundel ions in a HClO⁴ solution (47).

Conclusions

In summary, we have investigated water under pressure at 11 GPa and 20 GPa, along the 1,000-K isotherm, using ab initio MD. We have characterized the properties of the fluid by computing structural properties, ionic conductivities, and Raman and IR vibrational spectra, and we have identified dissociation mechanisms from a detailed analysis of computed trajectories. Our results are consistent with the estimate of the ice VII melting line proposed by Lin et al. (27), with a melting temperature below 1,000 K at 20 GPa. We found that along the 1,000-K isotherm, liquid water is a rather complex fluid, exhibiting rapid molecular dissociation events occurring via a bimolecular mechanism. The short-lived hydroxide, hydronium, and more complex ions present in the fluid are responsible for a conductivity which, at 11 GPa and 20 GPa, is six and seven orders of magnitude larger than at ambient conditions, respectively. We emphasize that the conductivity calculations reported in our work were conducted fully from first principles, without any a priori assumption on charge carriers or ad hoc definition of charges. Despite frequent dissociation and reassociation events occurring under pressure, hydrogen bonds persists in the fluid at least up to 20 GPa. Interestingly, while vibrational signatures of hydroxide and hydronium ions are not present in unpolarized Raman spectra, as observed experimentally, they can be identified in IR spectra at frequencies lower than those of the OH stretching band. The absence of Raman signatures of hydronium ions led to past suggestions of unimolecular dissociation in water at high P, at variance with what we observed in our simulations where free protons are transient species with lifetimes below 0.3 fs. Finally, the interpretation of the depth dependence of the electrical conductivity in the mantle transition zone as measured by magnetotellurics is still controversial and linked to the effect of water on mantle minerals (48). Our findings on the high conductivity of water and the dissociation mechanism found in the liquid at (P, T) conditions relevant to the mantle transition zone may guide future models of water in mantle geochemistry. We expect that our computed Raman and IR spectra, reported also for a quenched amorphous phase, will serve as guidance for future experiments.

Materials and Methods

We performed ab initio MD simulations in the Born–Oppenheimer approximation with the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional (50) and the Qbox code (40). The choice of the PBE functional was motivated by the good agreement with experiment found for the fluid equation of state at high pressure (5, 51, 52).

We used norm-conserving pseudopotentials (53) (fpmd.ucdavis.edu/potentials/), with a plane wave basis set and kinetic energy cutoff of 85 Ry, which was increased to 220 Ry for pressure calculations. The densities of water were 1.57 g/cm⁻¹ and 1.86 g/cm³, computed at 1,000 K to correspond to pressures of 11 GPa and 20 GPa, respectively. Our simulation supercell was cubic, with 64 water molecules. Molecular dipole moments were calculated using MLWF centers (34, 54). Temperature was controlled with the stochastic velocity rescaling method (55). Simulation time steps were 5 a.u. (0.121 fs), while the thermostat time was 121 fs. In the interest of computational time, the full computation of DFPT-based polarizabilities was performed every 25 MD steps. Trajectories were collected for $\sim$240 ps at each pressure, after initial equilibration of $\sim$10 ps.