Characterizing the 3D structure and dynamics of chromosomes and proteins in a common contact matrix framework

Abstract

Conformational ensembles of biopolymers, whether proteins or chromosomes, can be described using contact matrices. Principal component analysis (PCA) on the contact data has been used to interrogate both protein and chromosome structures and/or dynamics. However, as these fields have developed separately, variants of PCA have emerged. Previously, a variant we hereby term Implicit-PCA (I-PCA) has been applied to chromosome contact matrices and revealed the spatial segregation of active and inactive chromatin. Separately, Explicit-PCA (E-PCA) has previously been applied to proteins and characterized their correlated structure fluctuations. Here, we swapped analysis methods (I-PCA and E-PCA), applying each to a different biopolymer type (chromosome or protein) than the one for which they were initially developed. We find that applying E-PCA to chromosome distance matrices derived from microscopy data can reveal the dominant motion (concerted fluctuation) of these chromosomes. Further, by applying E-PCA to Hi-C data across the human blood cell lineage, we isolated the aspects of chromosome structure that most strongly differentiate cell types. Conversely, when we applied I-PCA to simulation snapshots of proteins, the major component reported the consensus features of the structure, making this a promising approach for future analysis of semi-structured proteins.

INTRODUCTION

The functions of large classes of biopolymers are related to their structural stability and conformational dynamics, from small scale conformational changes of proteins responding to chemical and physical stimuli to large scale genome structure reorganization. While the 3D structure of biopolymers is often represented by the Cartesian coordinates of each point along the polymer, other structure representations, such as contact matrices, can facilitate analyses of the configuration and motion of biopolymers in desirable situations. The structural features of a folded polymer can be captured by recording the contacts formed between different regions of the molecule. This information can then be organized in a contact matrix form in which the linear constituents (e.g. amino acid residues or genomic positions) of the polymer are labeled along the rows and columns of the matrix.

In protein studies, such contact information is typically derived from a 3D structure (obtained from either experiments and/or computer simulations), defining a ‘contact’ formed when one region of the amino acid chain is within a certain distance of another region (1,2). For chromosomes, a similar distance threshold approach can be employed when high resolution microscopy data (showing the path of a chromosome in 3D space) are available (3). Even more commonly, chromosome contact matrices are measured directly using chromosome conformation capture experiments (4,5). This approach chemically captures contacts between chromosome regions using formaldehyde crosslinking followed by DNA digestion and proximity ligation. Then, in the genome-wide version of the technique, Hi-C, contacts are identified by high throughput sequencing of ligated DNA pairs (6). In most Hi-C experiments, the resulting chromosome contact matrices report the frequency of contacts between pairs of chromosome loci within a population of cells. Single-cell Hi-C techniques are also emerging (7–9), resulting in contact maps at the single-cell resolution, which are directly analogous to the contact maps of protein snapshots described above. Even Genome Architecture Mapping, which uses sequencing of cryosectioned nuclei to identify colocalized chromosomal regions, results in linkage matrices, which are then treated as chromosome contact matrices (10).

Contact matrix descriptions of polymer configurations, and the ensuing statistical analyses of the matrices, have proven to be tremendously useful for the study of protein and chromosome structures. The first chromosome contact matrices generated by Hi-C immediately revealed major principles of chromosome folding. In particular, a ‘plaid’ pattern on the contact map was found to represent the spatial compartmentalization of active and inactive regions (also termed the A and B compartment) along the chromosome (6). This pattern has been mathematically isolated and quantified using a version of Principal Component Analysis (PCA) (11) in which each row of the contact matrix is treated as a set of stochastic variables (details described below) (6). As increasing numbers of contact matrices are published in different cell types and conditions, PCA has continued to be frequently used to analyze the chromosome spatial compartmentalization from Hi-C data (12,13) and linkage matrices from Genome Architecture Mapping (10). Meanwhile, PCA has been extensively used to characterize protein conformational dynamics, especially directly using the Cartesian coordinates of the system (14–16). In recent years, PCA has also been applied for the statistical analysis of other degrees of freedom (DOFs), such as torsion angles (17) and residue-residue contacts (18) in the protein system. Particularly, treating each individual contact as a degree of freedom, PCA assisted researchers in identifying regions of protein with concerted dynamics of contact forming and breaking (18–24).

Even though the underpinning data structure of contact matrices is identical, because protein and chromosome structure analyses have largely been developed in separate communities of researchers thus far, there has been little comparison of the analysis methods used to study these contact matrices. Particularly, no comparison between different approaches to similar analyses (such as PCA) has been made. A unified viewpoint and comparison of the analyses performed using contact matrices in these different biological systems will facilitate the further development of these research areas. Here, we formally describe the differences between the divergent contact correlation analyses that have been used to date almost exclusively on either proteins or chromosomes. By swapping approaches and applying both versions of PCA to both chromosome and protein systems, we elucidate the advantages, disadvantages, and biological insights about protein and chromosome structure that can be determined by each method. We term the PCA method previously developed for chromosome contact matrices ‘implicit contact correlation analysis’ (I-PCA) and the method previously developed for proteins ‘explicit contact correlation analysis’ (E-PCA). Analysis details and an in-depth comparison between I-PCA and E-PCA are provided in the Materials and Methods section.

In this study, we first apply E-PCA (previously developed for proteins) to chromosome contact matrices. We begin by analyzing chromosome structure data that more closely mimics protein structure snapshots: 3D coordinates of chromosome structures within individual cells traced by microscopy (3). Using detailed snapshots of individual chromosome structures as input to E-PCA may reveal molecular fluctuation at a single cell level, parallel to previous analysis of dynamics using E-PCA on protein snapshots. Notably, however, the only PCA analysis performed in the original analysis of this chromosome snapshot data was MI-PCA (a variant of I-PCA, defined below, as usually performed on Hi-C maps) on the mean spatial distance matrix to show that spatial compartments revealed by imaging matched previous reports from Hi-C data. Our E-PCA results reveal the primary correlated fluctuation modes of chromosome structure across individual cells. We further explore the utility of the E-PCA method for chromosome structure analysis by applying it to chromosome contact matrices from ensemble Hi-C data collected across a group of related blood cell types (25). Our results show that E-PCA can highlight dominant modes of chromosome structure changes between cell types. We demonstrate the results of applying I-PCA and MI-PCA contact analyses to protein conformations using two nuclear hormone receptor complexes as examples. Swapping methods (applying E-PCA to chromosomes and I-PCA to proteins) allows us to find analogies and contrasts between methods and to reveal new aspects of these biopolymer systems.

MATERIALS AND METHODS

Our statistical analysis has two stages: acquisition of contact matrices and statistical analysis of these matrices. Thus, we first describe how one can obtain the contact matrix ensemble 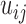from three main resources studied here (i. TAD imagining of chromosome, ii. Hi-C method of chromosome, iii. simulation of protein) for downstream covariance analyses. We then compare covariance analysis approaches (E-PCA versus I-PCA) on these ensembles of contact matrices obtained.

Distance matrices from TAD imaging data

The first type of contact matrices we studied is derived from microscopic detection of labeled TAD positions along chromosomes (chr21 and chr22), obtained directly from (3). In the experiment of Wang et al. (3), Topologically Associating Domains (TADs) identified by previous ensemble Hi-C experiments (26) were used as structural subunits along chromosomes and were labeled with fluorescent probes in IMR-90 fetal lung fibroblast cells. After imaging fluorescent probes specific to certain loci along chromosomes, the authors of this study reported Cartesian coordinates of 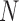TAD labels along chromosomes from a set of T individual cells. From this data, we constructed a symmetric matrix of 3D distances between each pair of TADs, 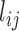, resulting in 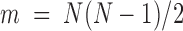independent nonzero distance variables, whereas the 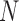diagonal variables 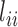are always 0. If needed, one could further convert into a discrete contact matrix 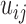by defining a minimum distance cutoff that should be called a ‘contact’. Here, instead of converting distances into discrete values via a cutoff, we directly used the set of T distance matrices 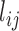as input to the E-PCA covariance analysis.

Hi-C contact matrices across the blood cell lineage

The second type of contact matrices we studied here is from Hi-C experiments performed on nine blood cell-types, obtained from (25) and Hi-C data on GM12878 cells (27). Specifically, the nine different cell types selected from the blood cell lineage were: (i) neutrophil, (ii) monocyte, (iii) M0 macrophage, (iv) naïve B-lymphocyte, (v) naïve CD4⁺ T-lymphocyte, (vi) naïve CD8⁺ T-lymphocyte, (vii) erythroblast, (viii) megakaryocyte (25) and (ix) lymphoblast cell line GM12878 (27). Using a proximity ligation approach, Hi-C directly measures the frequency of contacts made between any two regions in the genome within a population of cells. Thus, for population ensemble Hi-C chromosome structure data, the value of 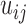is the number of cross-links between two genomic loci detected in the population (6). For the blood cell types, approximately 80 million formaldehyde crosslinked cells of each cell type were used to probe interacting regions of chromosomes. Restriction enzyme digestion followed by ligation between interacting pieces of DNA created a library of chimeric DNA molecules representing all contacting chromosomal regions. By high-throughput paired end DNA sequencing, the number of contacts between each pair of chromosomal locations was measured. With permission from the PCHI-C Consortium that generated this data and the European Genome-phenome Archive, we downloaded the raw pairs of interacting DNA sequences and mapped them to their genomic positions, resulting in one contact matrix for each cell type containing raw counts of pairwise contacts between all chromosomal positions. Before using this contact matrix for E-PCA and I-PCA analyses, we selected bin sizes to coarse-grain the contact data and performed normalization and filtering to remove known experimental biases as previously described (12). To analyze a 17 Mb section of chr10, we binned the contacts into 250 kb bins. We normalized these matrices by the expected number of random contacts at each genomic distance, as described previously (28). To make a direct comparison to the TAD imaging matrices, we also summed Hi-C contacts within the same genomic positions measured in the TAD imaging study, further normalizing the number of contacts to account for the varying sizes of regions used for imaging.

Protein contact matrices from computational simulations or NMR data

The third type of contact matrices 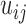that we studied here is from protein conformations, mostly from atomistic molecular dynamics simulations of nuclear receptor complexes. The detailed system setup and simulation protocol was reported previously (23). The simulation was performed at constant temperature (300 K) and pressure (1 atm) for 200 ns using NAMD (29), where we recorded conformations every 1 ps. In the current protein study, system size N is the number of amino acid residues and T is the number of simulated conformations. For a given conformation, we construct a contact matrix 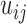of size 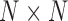. We deemed a particular contact formed (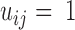) if any atoms belonging to residues 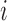and 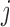are closer than the cutoff 4.2 Å ( 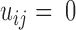otherwise). Other more elaborate improvements of contact matrix definition include using continuous contact energy (22) and coarse-graining the contacts (23). Additionally, we constructed contact matrices using an NMR ensemble (T = the number of NMR models) from hen lysozyme (PDB ID 1E8L). As with the simulated conformations, a contact was recorded between two amino acid residues if the distance between them fell below the 4.2 Å cutoff.

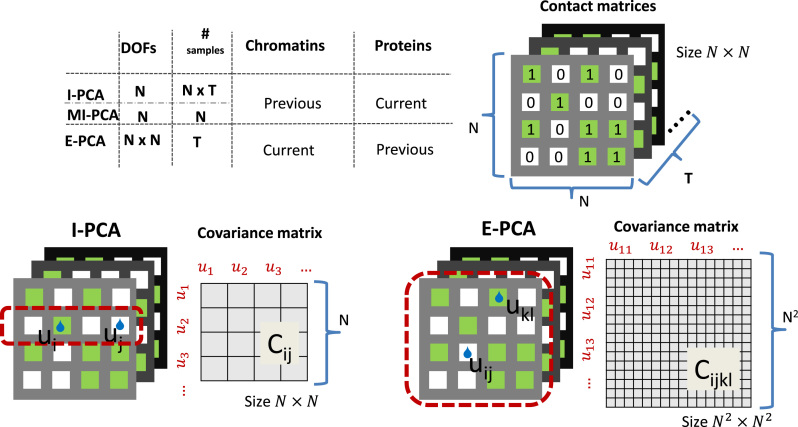
A comparison between I-PCA and E-PCA approaches

Both I-PCA and E-PCA begin with contact matrices of size (for a polymer comprised of 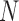constituents: amino acids or genomic bins, for example). Once contact matrices are obtained, a covariance matrix of the contact variables can be calculated. Then, PCA of the covariance matrix reveals major properties of the contact pattern. The essential difference between E-PCA and I-PCA is how the stochastic contact variables are defined. In E-PCA analysis, explicit contacts (contacts between two explicitly labeled regions of the biopolymer, 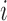and 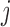) are treated as independent variables 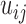. E-PCA tracks the correlation between these 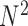contact elements 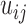(as shown in the dashed red square in Figure 1) across T snapshots or samples, and the size of covariance matrix is 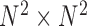in principle, as illustrated in Figure 1. Practically, due to symmetry, only the 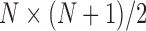unique contacts are used. Thus, the covariance matrix for E-PCA explicitly provides correlation information among four regions (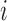, , 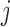, 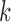and 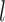) of the biopolymer, 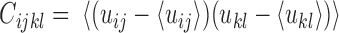, that is, when 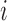and 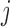form a contact, whether 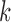and 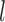are likely to form a contact (Figure 1). Here <> indicates an ensemble average.

Figure 1.

An illustration of contact correlation analysis methods. Here, identical input information, an ensemble of contact matrices, is being digested two different ways. In explicit contact correlation analysis (E-PCA), specific contacts are treated as independent variables and their covariance matrix is calculated using the whole contact matrix as one sample (dotted red line). On the other hand, implicit contact correlation analysis (I-PCA) treats rows of the contact matrix (a contact pattern between one constituent of the polymer and the rest of the polymer) as independent variables and calculates the covariance matrix using each row as one sample (dotted red line).

On the other hand, I-PCA has less stochastic contact variables, labeled as 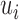, as shown in the red rectangle (one row or column) of Figure 1. For a polymer with 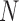units, one has only total 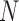stochastic variables. The contact variable 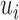registers whether a contact between a labeled region 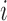and another untagged region of the polymer is made. Each contact matrix has 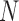rows and thus contributes 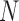sample points, while in E-PCA, by contrast, each entire contact matrix contributes to 1 sampling point. The covariance matrix of I-PCA, 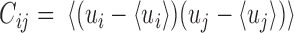, reveals the correlation between the interaction pattern between 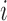and the rest of the polymer vs. the interaction pattern of j with the rest of the polymer (Figure 1).

A notable difference between E-PCA and I-PCA is the number of contact degrees of freedom. As shown in the cartoon illustration shown in Figure 1, in a 4 × 4 matrix, I-PCA examines the correlation between four contact variables, each representing the contact pattern of one biopolymer element (e.g. genomic bin) with the rest of the polymer. E-PCA, on the other hand, examines the correlation between sixteen contact variables across many related contact matrices, where each variable is an explicit contact between two sites along the biopolymer. In general, for a total 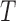contact matrices of size 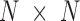, E-PCA identifies N² contact variables (more precisely, 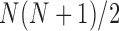) and total 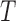sampling data points while I-PCA identifies total N contact variables and total 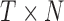data points. When I-PCA is applied to a system with only one population-averaged contact map (T = 1; as in a population Hi-C experiment), we term the approach ‘mean implicit contact correlation analysis’ (MI-PCA). MI-PCA can be applied to systems with many contact matrix snapshots by first obtaining the mean contact matrix of matrices and then performing I-PCA on this mean matrix. Thus, MI-PCA has 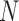contact variables and only 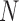data points. Since the computational complexity of obtaining 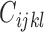is in the order of 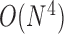, and the computation time increases in proportion to the quartic power of the system size 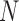, we also term E-PCA a four-point correlation analysis. Thus, E-PCA is more computationally demanding than I-PCA. On the other hand, I-PCA is beyond a two-point correlation analysis, since the correlation examined using I-PCA is not about the direct contacts formed between 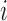and 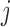. Although the size covariance matrix of I-PCA is 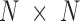, the computational complexity of I-PCA is rather 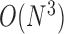, since each matrix contributes 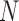sampling points (rows). These technical differences of choosing stochastic variables dictate the natures of the analyses. As we demonstrated below, both methods have drastically different results, despite having identical data as the entry point.

RESULTS

Explicit contact correlation analysis reveals correlated variations in chromosome structure between individual cells

E-PCA has previously been used to examine correlated fluctuations across many snapshots of protein structures. In the early days of 3D chromosome conformation studies, there were not enough sets of data available on different individual chromosome structures to make this analysis possible for chromosomes. Now, with increasing numbers of Hi-C datasets, single-cell Hi-C, and high-resolution microscopy data, we can apply E-PCA to chromosome structure data.

For our first application of E-PCA, we examined an ensemble of structural data on human chromosome 21 (chr21) obtained by high resolution microscopy (3). These microscopy data provide the 3D spatial coordinates of each TAD along chr21 in 120 cells (only 47 cells having full data and are being used here, i.e. 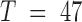). The original analysis of this data used MI-PCA on the average chromosome structure to define the ‘A’ and ‘B’ compartments (positive and negative elements of eigenvector PC1) and to demonstrate that active and inactive chromatin compartmentalization is detected with microscopic chromosome tracing just as it is found with ensemble average Hi-C data. One compartment (‘A’) turns out to contain the relatively active, gene rich regions of the chromosome while, the other (‘B’) is generally inactive and gene poor (6,30). We applied E-PCA to this data to study correlated structural fluctuations across the snapshots of chromosomes from single cells.

For chr21, 34 TAD positions were measured for each cell (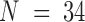). We first constructed a matrix of pairwise distances between each combination of TADs along the chromosome, giving 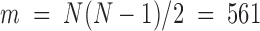pairwise distance variables (Methods). We then constructed the covariance matrix of distances across all 47 cells 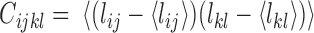, where 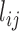is the distance between TA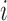D and 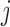, and <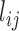> its ensemble average. We performed E-PCA on this covariance matrix of distances. For comparison, we also displayed in Supplemental Information (SI) the results of I-PCA for the same data set (SI Figure S1).

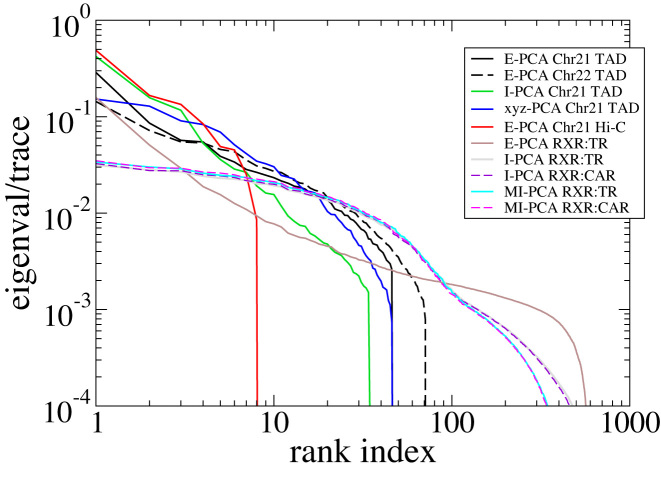
How quickly the top eigenvalues of the covariance matrix decrease with the ranking index provides an overall idea of how degenerate the dataset is. When a conformational ensemble has only a few major modes of fluctuation, the first few eigenvalues will dominate the distribution and on the other hand, if many eigenvalues are nearly equally high, we can conclude that there are many different motions in the ensemble of structures. The eigenvalues of this and other systems we examined are shown in Figure 2. To facilitate an effective comparison across different types of matrices, we normalized these eigenvalues by their trace (the sum of the eigenvalues). Specifically, for this chr21 microscopy data (3), we have examined the eigensystems of E-PCA, I-PCA, and Cartesian covariance matrices. Regardless of the method used, all eigenvalues drop to zero after the 46th eigenvector, reflecting that we have only 47 conformations (cells). Although we focus on reporting the results of chr21 below, our study of chr22 TAD imaging data revealed similar features which demonstrated the robustness of our conclusions.

Figure 2.

The eigenvalue distribution for various covariance matrices studied in this work. The main systems we consider (TAD imaging for chromosome 21, Hi-C from chromosome 10, and the protein complex RXR:TR) are shown in solid lines and comparison systems (TAD imaging from chr22 and the protein complex RXR:CAR) are shown in dashes.

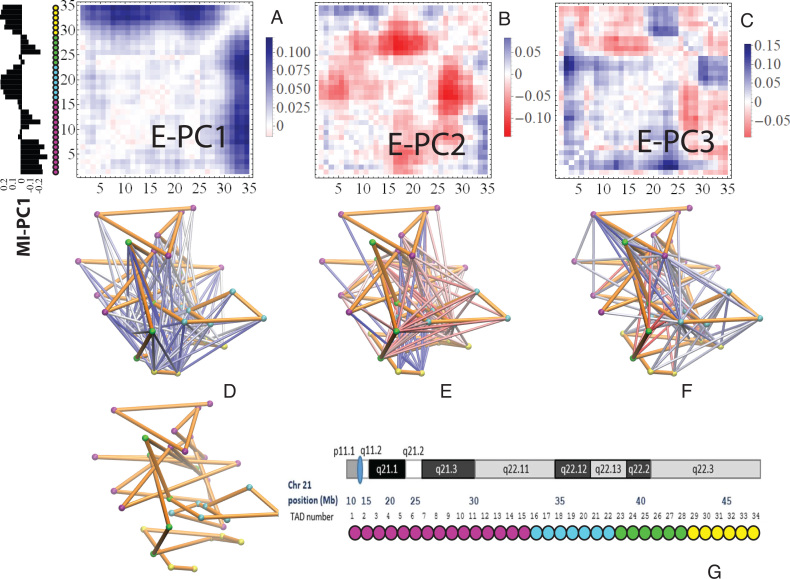
The top three principal components (PCs, eigenvectors of the covariance matrix) of E-PCA are displayed in a two-dimensional symmetric matrix known as displacement matrix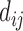, as shown in Figure 3A–C. Each displacement matrix represents a specific mode of fluctuation around the mean, d_ij ∼ δu_ij = u_ij − <u_ij>. Each conformational ensemble only has one mean contact matrix <u_ij> but displays many orthonormal modes of fluctuation. The displacement matrix shows how each explicitly expressed contact contributes to the given mode of fluctuation. When a particular contact, say one between 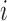and, shows strong blue (a highly positive value of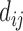), the dynamics of that contact are highly significant for this mode of fluctuation. Additionally, the contact dynamics of blue regions are correlated, i.e. the contacts form and break in sync with each other. Similarly, the strongest red (negative) regions are also highly correlated with each other in their fluctuations, but opposite (anti-sync) from the blue regions. When one red contact is formed, other red contacts are likely to be formed as well, while blue contacts are likely to be broken. The corresponding three-dimensional rendition of eigenvectors is shown in Figure 3D–F where strong fluctuation relationships between different parts of chromatin are rendered as colored cylinders. Note that we choose to use the 3D coordinates of the first cell to display TAD positions instead of an average (see Supplemental Information for further explanation). Both the 2D displacement matrix plot and 3D rendering of the E-PCA eigenvectors provide essential information on the biopolymer's structural changes as concerted modes of contact forming and breaking, or in the current case using a distance matrix, positions moving toward and away from each other.

Figure 3.

E-PCA applied to chr21 TAD imaging data reveals modes of chromosome fluctuation across individual IMR90 cells. The displacement matrix view of PC1, PC2, PC3 of E-PCA are shown in (A–C). PC1 from MI-PCA on the same system is shown as a bar-graph at left and TAD elements are colored according to general domains detected by E-PCA. The corresponding 3D representations are shown in (D–F), where the values of displacement matrix elements 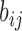are used to color cylinders that connect TADs 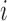and 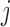. Less significant relationships (cutoff is 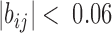) are not shown. The reference 3D path of the 34 TADs (the configuration detected for a chosen cell, cell #1) is shown in (G) along with a reference for the genomic position of each TAD probe. Explanation was made in SI for the selection of cell #1 as the reference.

The dominant eigenvector from E-PCA analysis of chr21 TAD imaging, E-PC1, shows a prominent and simple inter-domain motion (association and dissociation) between two large-scale domains (TAD 1–28 and TAD 29–34), indicated by the strong blue region formed in Figure 3A. The intradomain motions are primarily absent with small anticorrelated features (subtle red regions), i.e. when each domain is slightly more packed (indicated by the shortening of the distances between intradomain TADs, subtle red), the two domains dissociate (indicated by the lengthening of the distances between interdomain TADs, strong blue), and vice versa. The matrix for eigenvector PC2 in Figure 3B, on the other hand, shows intricate interactions between four independent regions (Domain 1: TAD 1–15, which belongs to the ‘B’ compartment, colored by magenta; Domain 2: 16–22, ‘A’, cyan; Domain 3: 23–28, ‘B’, green; and Domain 4: 29–34, ‘A’, yellow) defined by their correlated dynamics. Interestingly, these domains with correlated interaction dynamics generally correspond well with the average domain compartmentalization identified by the top PC of MI-PCA (shown as a bar graph label in Figure 3A). Indeed, the interactions contributing most strongly to PC2 (darkest red) are between neighboring domains, 2 and 3, that are, on average, spatially separated from each other in the ‘A’ and ‘B’ compartments respectively. When these two domains (2,3) move closer together, so does another pair of domains (1,2). This might be thought of as a concerted ‘stretch and compress’ motion within the first three regions of TADs. When the three domains stretch further away from each other, an anti-correlated interaction tends to be formed between the telomeric domain (TAD 29–34) and small local segments of the three domains (blue regions of the heatmap). Conversely, when the first three domains become aggregated, the last domain wants to break away. The first two PCs suggest that dynamic changes in chr21 structure largely occur within inter-compartment contacts (‘A’-‘B’ type of contacts, such as 1–2, 2–3, and 1–4) with relatively little fluctuation contribution from intra-compartment contacts (‘A’-‘A’ or ‘B’-‘B’ type, such as 1–3). In Figure 3C, the mode of motion reported by eigenvector PC3 is much more localized. Similar to the interpretation of PC2, the classification of four regional domains (TAD 1–15, 16–22, 23–28, 29–34) can be utilized to describe these interactions.

Overall, this E-PCA method reveals information about the dynamics of chromosome compartmentalization within individual cells, rather than just reporting an average spatial segregation. It allows us to begin to address persistent questions within the chromosome conformation field, such as how certain interactions or folding patterns relate to one another dynamically. These correlated movements could be related to the fact that different genes can be regulated in sync. To alleviate the concern that our results could be affected by the small sample size of chromosome conformations, we split the 47 sampling points (individual cells) into two halves (first 23 and last 24) and performed E-PCA analyses on each half. We found a covariance between the normalized top eigenvectors of 0.834, which indicates the motions detected are genuine, and are not resulting from random noise of a small sampling size (SI Figure S2).

Key differences in 3D chromosome structure between cell types are captured by explicit contact correlation analysis

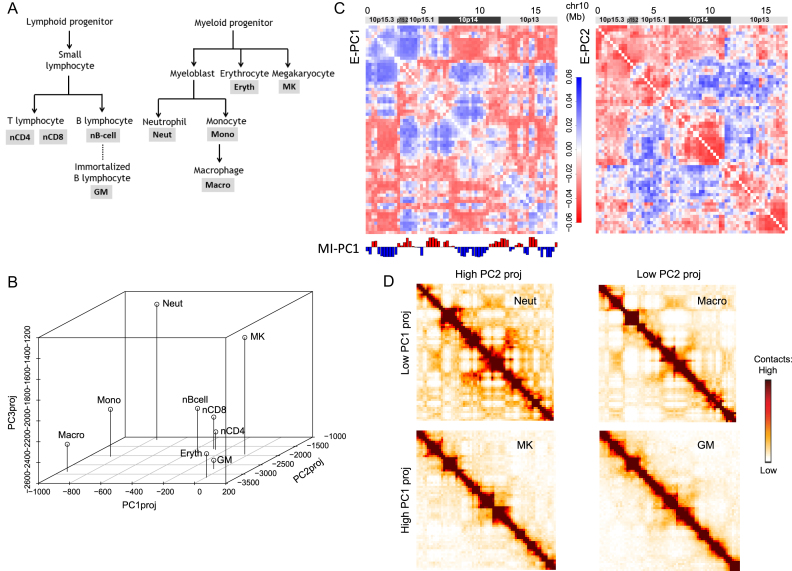
The above analysis shows that E-PCA is useful to analyze a set of chromosome contact or distance matrices from single-cell data. However, population-averaged Hi-C data is the only available structural information in many situations. Can contact PCA help us detect chromosome conformation changes using a set of average contact maps from different cell types or conditions? MI-PCA has been used toward this goal, and, by comparing vectors of PC1 values from MI-PCA, previous work has identified regions of chromosomes that, for example, switch their association from the ‘A’ compartment to the ‘B’ compartment on average in different cell types (13,25,31–34). A previous study has applied an E-PCA approach to single cell Hi-C data from different cell types and found that the resulting PC projections do tend to distinguish between cell types (9). Here, we investigate whether E-PCA can differentiate cell types based on population average Hi-C maps and, beyond simple classification, what the structural fluctuations defining these differences are. We applied E-PCA to chr21 (as studied in the TAD imaging data) and the first 17 Mb of chr10 across Hi-C data from nine related human blood cell types (25,27) (Figure 4A). We chose this chr10 region as a representative example from a mid-size chromosome with no major repetitive regions and strong A/B compartmentalization. Hi-C data was binned at 250 kb, to emphasize the compartment level of genome structure, and processed and normalized as previously described ((12,28), Materials and Methods Section and SI). Other regions or levels of resolution could be chosen based on the particular biological focus or genes of interest.

Figure 4.

E-PCA applied to Hi-C data from 9 different blood cell types provides insight about chromosome structure differences between cell types. (A) The blood cell lineage from which the Hi-C data are derived, showing developmental relationships. Abbreviations used in subsequent panels are defined. (B) The projection of each cell type's Hi-C contact map onto E-PC1, 2 and 3. Cell types segregate in this space according to lineage relationships. (C) The displacement matrix for E-PC1 and E-PC2, showing the 17 Mb region of chromosome 10 from which the sample Hi-C data was drawn. (D) Representative original input Hi-C contact matrices for this same region of chr10 for cell types with high and low E-PC1 or PC2 projections, visibly showing the contact pattern differences between these categories of cell types.

For this blood cell lineage data, the eigenvectors show the dominant chromosome conformational differences across cell types, whereas in the TAD imaging data, the conformational differences occur within an ensemble of cells of the same type. Since there are only 9 cell types, thus the number of contact matrices 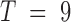, only the top 8 eigenvectors and corresponding eigenvalues are nontrivial (Figure 2). Still, the statistics for this eigensystem is robust, since each Hi-C data point is not obtained from a single instant snapshot of the chromosome, but rather from an ensemble of millions of cells.

Here, PC projection is used distinguish chromosome conformations of one cell type from another. PC projections cast each conformation onto the PCs and render the conformations using the new coordinates spanned by the eigenvectors of the covariance matrices. The PC projection of each cell type onto E-PC1, 2 and 3 clearly reflects known relationships and differences between cell types (Figure 4A and B). From this projection alone, we can see that E-PC1 tends to segregate the myeloid lineage cells (macrophage, monocyte and neutrophil; all have low values of E-PC1 projections) from the lymphoid lineage cells (which have higher values of E-PC1 projections). E-PC2 and E-PC3 further segregate within these major classes, distinguishing, for example, macrophages from neutrophils. Meanwhile, highly related cell types like nCD8 and nCD4 cluster near each other on all three PC axes. The displacement matrices for E-PC1 and E-PC2 (shown in Figure 4C, analogous to Figure 3A–C) show the interaction patterns that most distinguish these sets of cell types. Similar to the observations from the TAD imaging data above, the major features of E-PC1 relate to the A and B compartment segregation identified by MI-PCA (depicted under the displacement matrix in Figure 4C). However, unlike MI-PCA, which focuses on the average associations of a genomic region with A or B and how that mean association changes between cell types, E-PCA reports on the correlated changes in the A/B compartmentalization of regions across the cell types. For E-PC1, the strongest positive values represent interactions between A and B compartment bins while the strongest negative values often represent interactions between regions of the same compartment identity. This result suggests that the strongest differentiator between cell types is the strength of compartment segregation. Indeed, representative raw Hi-C contact matrices from cell types with high and low values of E-PC1 projections (Figure 4D) show that cells like neutrophils and macrophages have a stronger segregation of A and B compartment regions (seen as a plaid pattern in the contact map) compared to cells like megakaryocytes and GM12878 lymphoblasts. E-PC2 shows that beyond strength of compartmentalization overall, there are more specific patterns of interaction within these broader domains that further distinguish between cell types. For example, across cell types, higher local interactions within 10p14 correspond to lower distant interactions between this region and neighboring regions, and vice versa. We find that these major fluctuation modes are similar, whether or not the Hi-C data is first normalized to remove the generic decay of interactions over increasing genomic distance, as is often done before performing MI-PCA on Hi-C data (6) (SI Figures S3 and S4).

E-PCA analysis of chr21 Hi-C data (SI Figure S5) identified dominant modes of fluctuation between blood cell types that were similar to the fluctuations across individual IMR90 cells from the TAD imaging results of the previous subsection. As with IMR90 imaging data, E-PC1 for these blood cell types shows the separation of chr21 into two large-scale domains. The higher resolution ‘sub-compartment’ classifications (A1, A2, B1 and B2) available for GM12878 (35) show that one of these domains belongs to A1 while the other is more interspersed with B1 and B2. Future comparisons of E-PCA results with mean structure results such as compartment, sub-compartment, and TAD structures may reveal how the basic structure of a chromosome relates to its dynamics.

Implicit contact correlation analysis reveals consensus features of protein conformational ensembles

Besides using contact analysis for characterizing chromosome conformations, this type of analysis has been prominent for studying protein folding and structures. As noted above, E-PCA was developed for studying protein conformation dynamics and I-PCA (particularly, MI-PCA) for chromatin structural analysis. Here, we demonstrate what I-PCA can reveal about protein structure and/or dynamics. I-PCA considers two types of deviations between samples: (i) a static one that emphasizes the difference between different rows of either of the same matrix or different matrices (snapshots), and (ii) a truly dynamic one, the variance of the same row in different matrices. The former term dominates over the latter, linearly increasing with the matrix size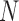. MI-PCA, on the other hand, only captures features of the static structure.

Two sets of molecular dynamics simulations of protein complexes were used in this study. The system setup details have been reported previously for E-PCA analysis (20,21) and are described in the Materials and Methods section. Here, we focused on conformations from a long-time simulation of the wild-type complex (23). Both protein systems we considered contain a dimer of the ligand binding domains of nuclear hormone receptors. One system is a dimer complex between retinoid receptor (RXR) and thyroid receptor (TR), whereas the second system is a complex between the same RXR and another nuclear receptor, constitutive androstane receptor (CAR). Including associated ligands, the RXR(9c):TR(t3) system has total 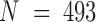residues with the internal indices as the following: RXR = 1–232; TR = 233–491; 9c = 492; t3 = 493 (unless specified otherwise). Here ligands 9c (9-cis retinoic acid) and t3 (triiodothyronine) are the corresponding ligands for RXR and TR respectively. Similarly, the complex RXR(9c):CAR(tcp) has 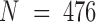with the following breakdown: RXR = 1–232; CAR = 233–474; 9c = 475; tcp = 476. A total of T = 200 000 conformations for each of the two complexes were converted into contact matrices for the I-PCA and E-PCA methods.

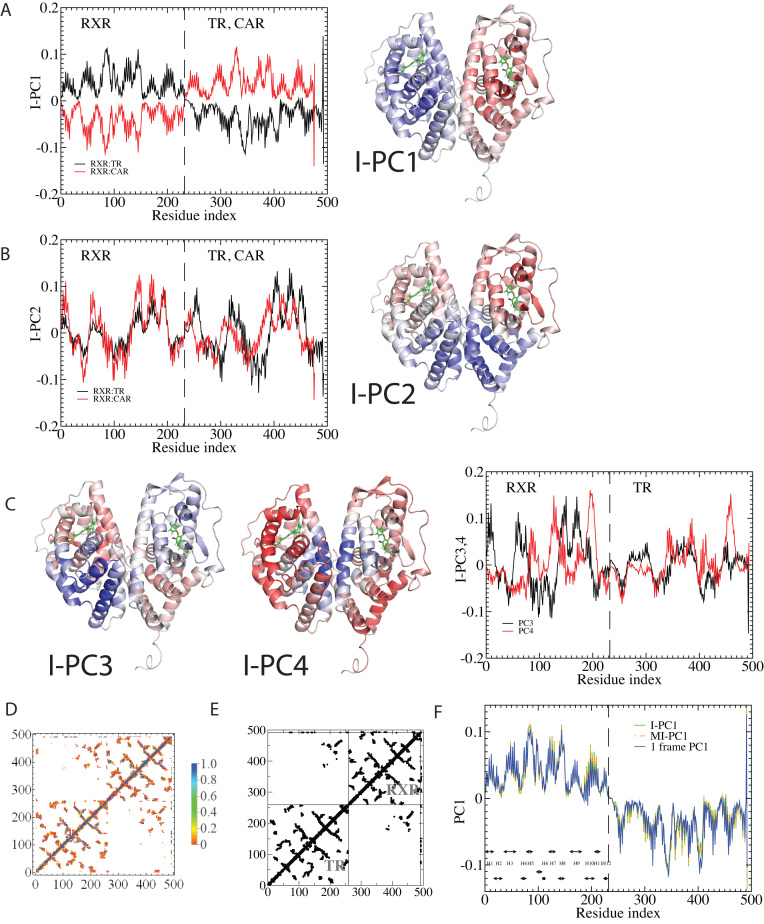
Figure 5 shows the top four eigenvectors of I-PCA for the protein complex RXR:TR, both in the line representation and in a 3D cartoon representation. The top eigenvector (Figure 5A) shows a concerted anticorrelation between two monomers of the complex and naturally separates the complex as two halves (domains). One can also observe a certain level of symmetry between the monomers from I-PC1 of Figure 5. This is expected, given that the ligand binding domains of the nuclear hormone receptors share the same fold. The second eigenvector, I-PC2 also largely splits the complex into two halves, though the splitting planes are different. I-PC2 separates the bottom half (N-terminus, H1, H8, H9, half of H10, indicated by blue) and the top half (C-terminus, H6, H7, half of H10, indicated by red). Similarly, as shown in Figure 5C, I-PC3 is yet another two-domain split while this time the front vs and the back. I-PC4 separates an interior core of the complex (center of H10 and H7) and the outside surface (the rest). Note that the top four eigenvectors are all large scale, global modes of fluctuation. To evaluate how robust our I-PCA results are, we also examined a second complex, RXR:CAR. One can see the corresponding top two eigenvectors show overall similarities, which indicates, at the large scale, the observed feature is robust. There are subtle differences observed: in I-PC2, for example, the absolute values of the eigenvector are larger for TR than RXR in the RXR:TR complex, while in complex RXR:CAR, CAR is more subdued than RXR. This would suggest that there is a more spatially extended RXR structure and a more compact CAR structure.

Figure 5.

The I-PCA and MI-PCA results for protein conformations. (A) The top eigenvector, I-PC1 for RXR:TR and RXR:CAR are shown in the left panel, while the 3D view of the same information (for the RXR:TR case) is shown on the right panel. Here the values of the elements of eigenvector I-PC1 are displayed by color on a cartoon representation of the protein complex. (B) The corresponding information for eigenvector I-PC2. (C) The eigenvectors I-PC3 and I-PC4 for RXR:TR complex. (D) The mean contact matrix of RXR:TR. (E) The contact matrix of one frame. (F) The comparison of I-PCA, MI-PCA and 1-frame PCA.

MI-PCA only considers a single contact matrix and does not study the dynamic correlations between any contact events. As mentioned in the introduction, it has been the best-known analysis method to determine the spatial separation of chromosome compartments. It is interesting to see what MI-PCA can reveal about protein conformations. Here, we applied MI-PCA to protein systems using the mean contact map (shown in Figure 5D). For a comparison, we also tested the MI-PCA analysis using a single frame, replacing the mean contact matrix with one instant contact map (Figure 5E). Surprisingly, the MI-PCA and, to a lesser extent, 1-frame PCA result in a very similar PC1 and PC2 as were obtained using I-PCA on the full set of individual snapshots for the RXR:TR system (Figure 5F, SI Figure S6). Larger differences between I-PCA and the corresponding MI-PCA results were apparent for subsequent eigenvectors; in particular, differences between MI- and I-PCA results were observed in the CAR part of PC2 for the RXR:CAR system (SI Figure S7). These results echo the similarities between I-PCA and MI-PCA across the Hi-C data of nine cell types (SI Figure S3). Similarity between I-PCA and MI-PCA, especially for the top eigenvectors, indicates the I-PCA analysis largely reveals the consensus features of the conformational ensemble, despite being a method analyzing of covariance fluctuation and the inclusion of individual snapshots. This focus on consensus features arises from the fact that each row (or column) of the contact matrix is treated as an independent entity in this method. The total variation between rows of the same contact matrix is far more significant than the difference between the same rows of different contact matrices. One can expect a high similarity between MI-PCA and I-PCA for a highly structured biopolymer, especially when is large, but we expect that the level of similarity would decrease for semi-structured biopolymers such as chromosomes and intrinsically disordered proteins. Besides protein ensembles generated from simulations, an NMR conformational ensemble of lysozyme was used to support our conclusion that I-PCA and its variants are largely consistent and reveal the consensus features of the ensemble (SI Figure S8).

Traditionally, E-PCA and Cartesian PCA include a PC projection analysis, rendering the original conformation sampling points using the newly found top PCs (for the ^th PC in E-PCA, the projection is 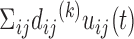). Each conformation of the biomolecule (snapshot) is displayed on the new coordinates spanned by the PCs, as previously demonstrated in Ref. (18–20,36) and in the previous section of this current work for chromosomes. One can observe the fluctuation of individual conformations and the amplitude of fluctuation, where PCs themselves are normalized eigenvectors and do not provide overall amplitude. We tested PC projections for I-PCA (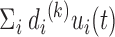) and found that a direct application of PC projection for I-PCA leads to a largely ‘spreading-out’ pattern (SI Figure S9A). One reason is that in I-PCA, each conformation (contact matrix) contributes 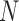sampling points. For total 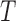conformations, there are 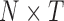points with two types of variance: ‘static’ (variance between different rows) and ‘dynamic’ (variance of the same row in different matrices) types. When we further averaged the PC projections from these N points, we obtained a largely random distribution with few recognized features. Perhaps, a more meaningful way to display the variance is by focusing on the ‘static’ component, i.e., focusing on PC projections obtained from MI-PCA (SI Figure S9)

DISCUSSION

With the results we have obtained, we can make a more detailed comparison between the two methods being used. Based on how fast eigenvalues decay with increasing rank, we observe that I-PCA contains fewer modes of fluctuation whereas E-PCA typically has a slower decay and thus many fluctuation modes. This makes sense since E-PCA focuses on the explicit details of contacts being made. However, E-PCA has a faster initial decay at the top eigenvalues which means it contains fewer dominant modes, as shown in Figure 2. From a statistical analysis perspective, both methods study the same amount of information. E-PCA has more independent variables and less sampling points, while I-PCA has more sampling points (by dividing one contact matrix to 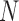‘pieces’) but fewer stochastic variables.

The fact that I-PCA has previously been associated with chromosome structure analysis reflects the fact that initially, Hi-C data were scarce, and little was known about the basic domains of the genome structure. Thus, it was useful in this system to first focus on the consensus features of an ensemble. However, our results here suggest that E-PCA is also useful to study the correlated dynamics of chromosome structures, particularly as increasing numbers of both ensemble and single cell Hi-C datasets become available. I-PCA (PC1) provides a simple dichotomy, separating two types of domains: those with local contacts increasing (folding) and local contacts decreasing (unfolding). In contrast, as was seen in E-PC2 of the TAD imaging data, E-PCA can provide a detailed description of more complicated motions involving multiple domains.

Conversely, as I-PCA mainly reveals consensus structural features, it had not previously been applied within the protein field, in which structures are often already known and dynamic fluctuation is often the focus. However, our results suggest that I-PCA would have useful applications for semi-structured polymers where the ground state is less defined. For example, I-PCA is suitable for identifying protein domains and self-interacting regions from simulation data of intrinsically disordered proteins (37).

E-PCA explicitly tracks the correlated dynamics of polymer contacts, thus revealing detailed correlated motions of the biopolymer and/or structure variation in the ensemble. However, E-PCA requires more data points than I-PCA, and thus a main drawback of E-PCA is the fast rise of the size of the covariance matrix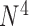. Such higher order correlation analysis requires more computational resources for the PCA data reduction task. For this reason, previous work has involved selecting dynamic contacts or coarse-graining contacts in the protein system to make the matrix size manageable. The reduced dimensionality of I-PCA, therefore, may be another feature which gives it value for studying protein structures, especially for large protein complexes which contain thousands of amino acid residues.

Regardless of the types of the covariance matrix being considered, it is always interesting to ask whether these eigenvectors represent true dynamic motions of the biopolymers under investigation, or whether these are simply a way of illustrating the difference between different conformations in the ensemble. The answer has nothing to do with a particular analysis procedure but rather depends on how the ensemble data has been generated. In the current work, the example using protein simulation is clearly an example of dynamic motions, because the underlying data are time-related snapshots of one protein complex. In contrast, the second example of chromosomes involving different blood cell types is clearly not reporting ‘dynamics’ but instead the conformational differences between different biological states. The first example with TAD imaging data is more ambiguous, as chromosome conformation differences between cells could reflect either heterogeneous stable conformations or conformations that interconvert within cells at a physiologically relevant timescale.

An attempt at directly comparing the dynamic motions of proteins and chromosomes is hampered by the inequivalent sampling data. Simply judging from the eigenvalue distribution, it would be tempting to conclude that the motion of chromosomes is largely ‘frozen’ while proteins show a larger variety of modes of dynamics. However, several factors make this an unfair comparison: the amount of data (<100 snapshots in chromatin systems versus 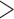100 000 in protein systems) used for the current work is highly discordant, the chromosome structure is likely much more hierarchical than the protein structure, and the results can be resolution-dependent.

As demonstrated from three distinct types of structural information (TAD imaging, Hi-C and computer simulation) of biopolymers across scales, PCA of contact information can provide a powerful description of structural consensus and fluctuation of proteins and chromosomes. Different types of contact analyses appear to have a preferred scale: I-PCA is suitable to identify the overall consensus picture (ground state) such as domains, using large scale, low resolution data with fewer conformations in hand; whereas E-PCA highlights the major differences of an ensemble (the dominant fluctuations around the ground state) when sufficient data is available.

DATA AVAILABILITY

This study makes use of data generated by the PCHI-C Consortium. A full list of the investigators who contributed to the generation of the data is available in (25). The software package CAMERRA is used to perform the I-PCA and E-PCA analyses of protein data (38). MI-PCA, I-PCA, and E-PCA analyses of chromosome contact matrices were performed using custom R scripts which are available upon request.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

PCHI-C project was provided by the National Institute for Health Research of England, UK Medical Research Council [MR/L007150/1]; UK Biotechnology and Biological Research Council [BB/J004480/1]. Funding for open access charge: University of Tennessee.

Conflict of interest statement. None declared.