High-throughput inference of pairwise coalescence times identifies signals of selection and enriched disease heritability

Abstract

Interest in reconstructing demographic histories has motivated the development of methods to estimate locus-specific pairwise coalescence times from whole-genome sequence data. Here we introduce a powerful new method, ASMC, that can estimate coalescence times using only SNP array data, and is orders of magnitude faster than previous approaches. We applied ASMC to detect recent positive selection in 113,851 phased British samples from the UK Biobank, and detected 12 genome-wide significant signals, including 6 novel loci. We also applied ASMC to sequencing data from 498 Dutch individuals to detect background selection at deeper time scales. We detected strong heritability enrichment in regions of high background selection in an analysis of 20 independent diseases and complex traits using stratified LD score regression, conditioned on a broad set of functional annotations (including other background selection annotations). These results underscore the widespread effects of background selection on the genetic architecture of complex traits.

Introduction

Recently developed methods such as the Pairwise Sequentially Markovian Coalescent (PSMC)¹ utilize Hidden Markov Models (HMM) to estimate the coalescence time of two homologous chromosomes at each position in the genome^1–6, leveraging previous advances in coalescent theory^7–11. These methods have been broadly applied to reconstructing demographic histories of human populations^12–20. More generally, methods for inferring ancestral relationships among individuals have potential applications to detecting signatures of natural selection²¹, genome-wide association studies^22–24, and genotype calling and imputation^25–28. However, all currently available methods for inferring pairwise coalescence times require whole genome sequencing (WGS) data, and can only be applied to small data sets due to their computational requirements.

Here, we introduce a new method, the Ascertained Sequentially Markovian Coalescent (ASMC), that can efficiently estimate locus-specific coalescence times for pairs of chromosomes using only ascertained SNP array data, which are widely available for hundreds of thousands of samples²⁹. We verified ASMC’s accuracy using coalescent simulations, and determined that it is orders of magnitude faster than other methods when WGS data are available. Leveraging ASMC’s speed, we analyzed SNP array and WGS data sets with the goal of detecting signatures of recent positive selection and background selection using pairwise coalescence times along the human genome. We first analyzed 113,851 British individuals from the UK Biobank data set²⁹, detecting 12 loci with unusually high density of very recent coalescence times as a result of recent positive selection at these sites. These include 6 known loci linked to nutrition, immune response, and pigmentation, as well as 6 novel loci involved in immunity, taste reception, and other aspects of human physiology. We then analyzed 498 unrelated WGS samples from the Genome of the Netherlands data set³⁰ to search for signals of background selection at deeper time scales and finer genomic resolution. We determined that SNPs in regions with low values of average coalescence time are strongly enriched for heritability across 20 independent diseases and complex traits (average N=86k), even when conditioning on a broad set of functional annotations (including other background selection annotations).

Results

Overview of ASMC method

We developed a new method, ASMC, that estimates the coalescence time (which we also refer to as time to most recent common ancestor, TMRCA) for a pair of chromosomes at each site along the genome. ASMC utilizes a Hidden Markov Model (HMM), which is built using the coalescent with recombination process^7–11; the hidden states of the HMM correspond to a discretized set of TMRCA intervals, the emissions of the HMM are the observed genotypes, and transitions between states correspond to changes in TMRCA along the genome due to historical recombination events. ASMC shares several key modeling components with previous coalescent-based HMM methods, such as the PSMC¹, the MSMC², and, in particular, the recently developed SMC++³. In contrast with these methods, however, ASMC’s main objective is not to reconstruct the demographic history of a set of analyzed samples. Instead, ASMC is optimized to efficiently compute coalescence times along the genome of pairs of individuals in modern data sets. To this end, the ASMC improves over current coalescent HMM approaches in two key ways. First, by modeling non-random ascertainment of genotyped variants, ASMC enables accurate processing of SNP array data, in addition to WGS data. Second, by introducing a new dynamic programming algorithm, it is orders of magnitude faster than other coalescent HMM approaches, which enables it to process large volumes of data. Details of the method are described in the Online Methods section; we have released open-source software implementing the method (see URLs).

URLs.

• The ASMC software is available at http://www.palamaralab.org/software/ and https://github.com/pierpal/ASMC

• UK Biobank website: http://www.ukbiobank.ac.uk/

• Genome of the Netherlands website: www.nlgenome.nl

• UK Biobank Genotyping and QC: http://www.ukbiobank.ac.uk/wp-content/uploads/2014/04/UKBiobank_genotyping_QC_documentation-web.pdf

• Human genetic maps: https://mathgen.stats.ox.ac.uk/impute/genetic_maps_b37.tgz

• The dbPSHP database of positive selection: ftp://jjwanglab.org/dbPSHP/curation/dbPSHP_20131001.tab

• Python’s Scipy library: http://www.scipy.org/

• 1000 Genomes Project Phase 3 data: ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/release/20130502

• SMC++ program: https://github.com/popgenmethods/smcpp

• ARGON simulator: https://github.com/pierpal/ARGON

• Simupop software: http://simupop.sourceforge.net/

• Selscan software: https://github.com/szpiech/selscan

• SLiM simulator: https://messerlab.org/slim/

Simulations

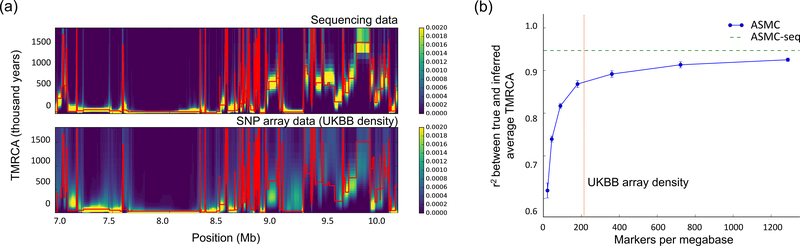
We assessed ASMC’s accuracy in inferring locus-specific pairwise TMRCA from SNP array and WGS data via coalescent simulations using the ARGON software³¹. Briefly, we measured the correlation between true and inferred average TMRCA for all pairs of 300 individuals simulated using a European demographic model³, for a 30 Mb region with SNP density and allele frequencies matching those of the UK Biobank data set (Figure 1; see Online Methods). As expected, ASMC achieved high accuracy when applied to WGS data (r²=0.95). When sparser SNP array data were analyzed, the correlation remained high (e.g. r²=0.87 at UK Biobank SNP array density), and increased with genotyping density. Similar relative results were obtained when comparing the root mean squared error (RMSE) between true and inferred TMRCA at each site, and the posterior mean estimate of TMRCA attained higher accuracy than the maximum-a-posteriori (MAP) estimate (Supplementary Figure 1). Inferring locus-specific TMRCA is closely related to the task of detecting genomic regions that are identical-by-descent (IBD), which we define as regions for which the true TMRCA is lower than a specified cut-off (other, related definitions have been proposed³²). ASMC attained higher IBD detection accuracy (area under the precision-recall curve) than the widely used Beagle IBD detection method³³ (Supplementary Table 1).

Figure 1. ASMC accuracy in coalescent simulations.

(a) Sample posterior decoding of TMRCA along a 3 Mb segment for a pair of simulated individuals with ASMC run on WGS data (top) and on SNP array data (bottom). Red lines represent the true TMRCA, while the heat map represents the inferred posterior distribution. Posterior density tends to concentrate more tightly around the true TMRCA when WGS data are analyzed, due to the higher density of polymorphic variants. Posterior estimates using SNP array data are more dispersed for distant TMRCA, but remain highly concentrated for recent TMRCA. (b) Accuracy (r² between true and inferred average TMRCA) as a function of marker density. TMRCA are inferred using the posterior mean obtained by ASMC at each site. ASMC-seq represents the accuracy obtained using ASMC on WGS data. The red vertical line indicates marker density in the UK Biobank data set. Errors bars represent standard errors. Dots and error bars represent the average and its SE from 10 independent simulations. Numerical results are reported in Supplementary Table 11.

We evaluated the robustness of ASMC to various types of model misspecification, including an inaccurate demographic model, inaccurate recombination rate map, and violations of assumptions on allele frequencies in SNP ascertainment. To evaluate the impact of using an inaccurate demographic model, we simulated data under a European demographic history, but assumed a constant effective population size when inferring TMRCA (see Online Methods). As expected, this introduced biases, decreasing the accuracy of inferred TMRCA as measured by the RMSE, but had a negligible effect on the correlation between true and inferred TMRCA (Supplementary Table 2). An inaccurate demographic model is thus likely to result in biased TMRCA estimates, but has little effect on the relative ranking of TMRCA along the genome. Consistent with this observation, IBD detection remained accurate when an incorrect demographic model was used (Supplementary Table 3). We used a similar approach to evaluate the impact of using an inaccurate recombination rate map (see Online Methods), observing only negligible effects on the accuracy of inferred TMRCA (Supplementary Table 4). We next tested the robustness of ASMC to violations of the assumption that observed polymorphisms are ascertained solely based on their frequency, by instead ascertaining more rare variants in certain regions (mimicking genic regions; see Online Methods). We found that the distribution of inferred TMRCA in these “genic” regions did not deviate substantially from other regions (Supplementary Figure 2). Next, we evaluated the impact of varying the number s of discrete TMRCA intervals (i.e. states of the HMM); we observed that increasing s had only a minor impact on posterior mean estimates of TMRCA, although the higher resolution led to noisier MAP estimates (Supplementary Table 5). Finally, we evaluated the effects of ancestry-specific ascertainment of SNPs, mimicking an analysis where ASMC is used to infer coalescence times in individuals that have been genotyped using an array designed for a different, highly diverged population (see Online Methods). Ascertainment of SNPs in a highly diverged population leads to a depletion of informative (high frequency) markers. Consistent with previous simulations with low SNP density (Figure 1B), this leads to reduced accuracy and creates an upward bias in the inferred TMRCAs (Supplementary Figure 3). ASMC should thus be utilized with particular care in the analysis of multi-ethnic cohorts.

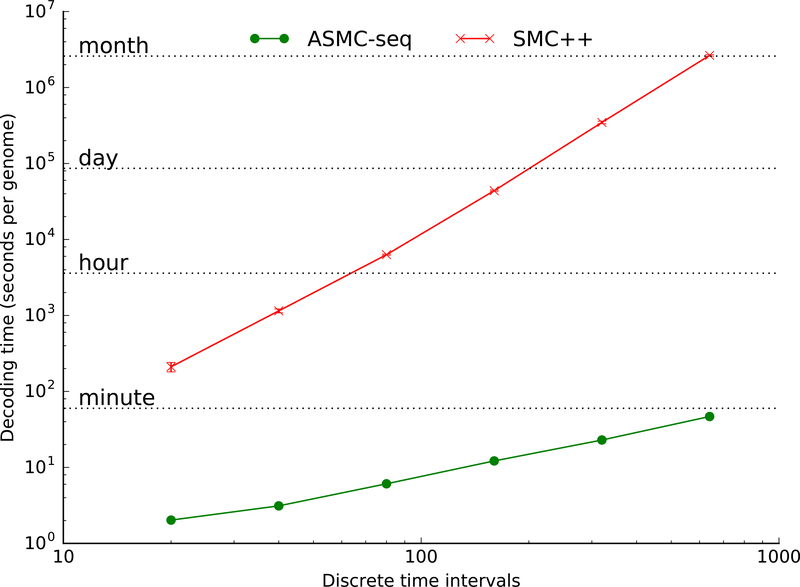
We next evaluated the running time and memory cost of ASMC. ASMC can be run on both SNP array and WGS data. When used to infer coalescence times in WGS data, ASMC is equivalent to the SMC++ method, although it runs considerably faster, making approximations that have only a small impact on accuracy (Figure 1). Letting s be the number of discrete TMRCA intervals (i.e. states of the HMM) and m be the number of observed polymorphic sites, ASMC has asymptotic running time O(sm). In comparison, the SMC++ method, which was shown to be more computationally efficient than other coalescent-based methods³, has asymptotic running time O(s³m). Accordingly, we observed that the running time of ASMC was 2 to 4 orders of magnitude faster than SMC++ when applied to simulated WGS data, depending on the number of discrete TMRCA intervals (Figure 2). For example, analysis of a pair of simulated genomes using 100 discrete time intervals required 7.4 seconds on a single processor for ASMC, compared to 3.3 hours for SMC++. This speedup in the analysis of WGS data leverages approximations that do not result in a significant loss of accuracy (Supplementary Figure 4). The memory cost of ASMC was also efficient compared to SMC++, scaling linearly with s (Supplementary Figure 5).

Figure 2. Running time of ASMC.

We report the running time required to analyze a pair of simulated haploid genomes (extrapolated from running times in 5Mb regions) as a function of the number of discrete TMRCA intervals. Both SMC++ and ASMC-seq were run on WGS data. Numerical results are reported in Supplementary Table 12.

Signals of recent positive selection in the UK Biobank

ASMC’s computational efficiency enables its application to analyses of TMRCA in large data sets. We thus used ASMC to infer locus-specific TMRCA in 113,732 unrelated individuals of British ancestry from the UK Biobank, typed at 678,956 SNPs after QC and phased using Eagle³⁴ (see Online Methods); we note that phasing accuracy in this data set is very high, with average switch error rate on the order of 0.3% (one switch error every ∼10 cM³⁴). We partitioned the data into batches of approximately 10,000 samples each and inferred locus-specific TMRCA for all haploid pairs within each batch, analyzing a total of 2.2 billion pairs of haploid genomes.

We sought to identify genomic regions with an unusually high density of very recent inferred TMRCA events (i.e. within the past several thousand years). Such signals are expected at sites undergoing recent positive selection, since a rapid rise in frequency of a beneficial allele causes all individuals with the beneficial allele to coalesce to a more recent common ancestor than under neutral expectation³⁵; approaches to detect selection based on distortions in inferred coalescence times have been recently applied at different time scales²¹. We thus computed a statistic, DRC_T, reflecting the Density of Recent Coalescence (within the past T generations), averaged within 0.05 cM windows. To compute approximate p-values, we noted that the DRC_T statistic under the null is approximately Gamma-distributed. We thus obtained approximate p-values for the DRC_T statistic by fitting a Gamma distribution to the null 18% of the genome obtained by conservatively excluding 500Kb windows around regions previously implicated in scans for positive selection (see Online Methods). Using coalescent simulations, we determined that DRC₁₅₀ is highly sensitive in detecting signals of positive selection within the past ~20,000 years, as compared to other methods^36,37 (see Online Methods, Supplementary Figure 6).

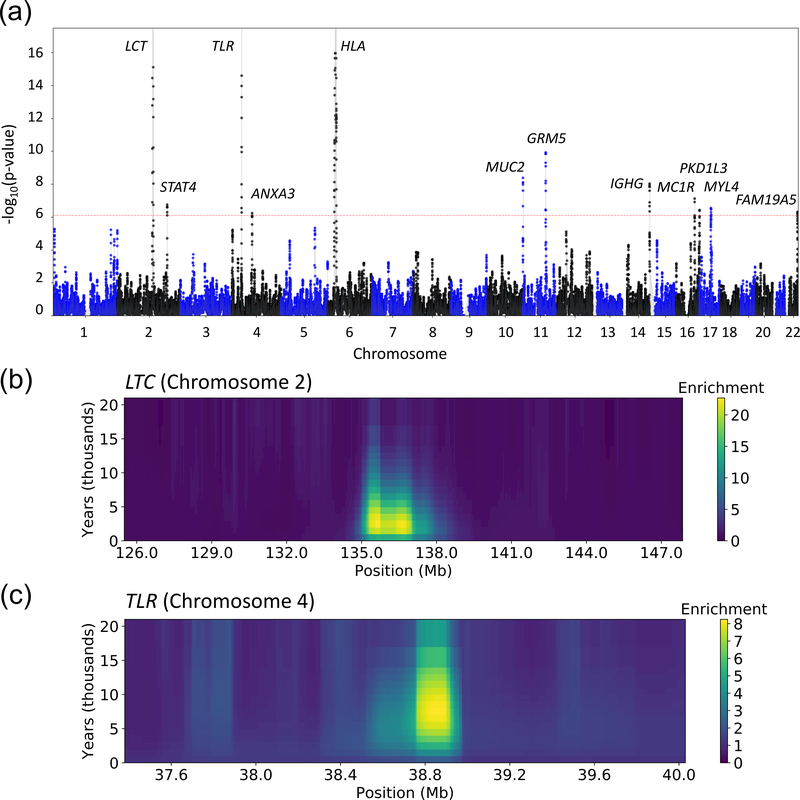
Analyzing 63,103 windows of length 0.05cM in the UK Biobank data set, we detected 12 genome-wide significant loci (p < 0.05 / 63,103 = 7.9 × 10⁻⁷; see Figure 3A and Table 1). The loci that we detected exhibited strong enrichment of recent coalescence events spanning up to the past 20,000 years (Figure 3B, 3C and Supplementary Figure 7), consistent with our simulations (Supplementary Figure 6). Of the 12 loci, 6 are loci known to be under recent positive selection, harboring genes linked to nutrition (LCT³⁸), immune response (HLA³⁹, TLR⁴⁰, IGHG⁴¹), eye color (GRM5⁴¹), and skin pigmentation (MC1R⁴¹). We also detected 6 novel loci, harboring genes involved in immune response (STAT4⁴², associated with autoimmune disease^43–45); mucus production (MUC5B⁴⁶ within cluster of mucin genes, involved in protection against infectious disease⁴³, associated with several types of cancer⁴⁷ and lung disease⁴⁸); taste reception (PKD1L3⁴⁹, associated with kidney disease^50,51); cardiac and fetal muscle (MYL4, associated with atrial fibrillation⁵²); blood coagulation (ANXA3⁵³, associated with cancer⁵⁴ and immune disease⁵⁵); and brain-specific expression and immune response (FAM19A5⁵⁶). We note that suggestive loci implicated by the DRC₁₅₀ statistic (p < 10⁻⁴; Supplementary Table 6) include known targets of selection linked to eye color (HERC2^57,58), retinal and cochlear function (PCDH15⁴¹), celiac disease (SLC22A4^58,59) and skin pigmentation (SLC45A2⁵⁸).

Figure 3. Genome-wide scan for recent positive selection in the UK Biobank data set.

(a) Manhattan plot with candidate gene labels for 12 loci detected at genome-wide significance (adjusting for multiple testing, p < 0.05 / 63,103 = 7.9 × 10⁻⁷; dashed red line). The DRC₁₅₀ statistic of recent positive selection was computed using all individuals of British ancestry from the UK Biobank (n=113,851, divided in batches of ~10,000 samples; see Online Methods for details on how p-values were computed). Numerical results for top loci are reported in Table 1; additional suggestive loci are reported in Supplementary Table 6. (b) Enrichment for recent coalescence events at the LCT locus (Chromosome 2). (c) Enrichment for recent coalescence events at the TLR locus (Chromosome 4). y-axis labels assume a 30-year generation time. Analogous plots for other top loci are provided in Supplementary Figure 7.

Table 1. Genome-wide significant signals of recent positive selection.

We report genomic locations, minimum p-value across 0.05cM windows (not adjusted for multiple testing and capped at 10⁻¹⁶), SNP corresponding to signal peak, and candidate gene for the 12 genome-wide significant signals of recent positive selection (adjusting for multiple testing, p < 0.05 / 63,103 = 7.9 × 10⁻⁷). Novel loci are denoted in bold font. The The DRC₁₅₀ statistic of recent positive selection was computed using all individuals of British ancestry from the UK Biobank (n=113,851, divided in batches of ~10,000 samples; see Online Methods for details on how p-values were computed).

Chromosome	From (Mb)	To (Mb)	Min. p-value	SNP	Candidate gene(s)
2	134.44	139.01	<10−16	rs10206673	LCT38
2	191.73	192.07	1.81×10−7	rs7556924	STAT4
4	38.44	38.97	<10−16	rs7660745	TLR gene gamily40
4	79.11	79.51	5.90×10−7	rs2867461	ANXA3
6	25.18	33.82	<10−16	rs2104362	HLA39
11	1.08	1.23	4.21×10−9	rs11019228	GRM541
11	88.21	90.55	1.20×10−10	rs72636988	MUC gene family
14	106.35	107.12	9.49×10−9	rs10142951	IGHG41
16	70.89	71.80	7.73×10−8	rs141399030	PKD1L3
16	89.12	90.14	3.78×10−7	rs62052682	MC1R41
17	42.64	45.18	2.87×10−7	rs75229873	MYL4
22	48.98	49.08	4.94×10−7	rs78014641	FAM19A5

Heritability enrichment in regions under background selection

We next sought to detect signals of natural selection at deeper time scales. To accomplish this, we used ASMC to estimate locus-specific TMRCA for all ~0.5 million pairs of haploid genomes from unrelated individuals in the Genome of the Netherlands (GoNL) WGS data set (498 samples and 19,730,834 variants after QC; see Online Methods); we note that WGS data are required to achieve accurate resolution at deeper time scales (Figure 1A). Motivated by the fact that natural selection modulates the effective population size along the genome^35,60, we set out to estimate its strength by measuring average pairwise TMRCA at each site, which is proportional to effective population size⁶¹. We refer to this annotation as ASMC_avg. Forward-in-time simulations confirmed that the ASMCavg annotation captures the presence of unusual TMRCA variation due to background and positive selection, which leads to lower values of ASMCavg (see Online Methods, Supplementary Figure 8). We expect much or most of the variation in the ASMC_avg annotation to be driven by deleterious effects, as supported by several recent studies^60,62–66, and thus interpret ASMC_avg as an annotation of background selection. We note, however, that in general ASMC_avg can be affected by several types of selection that have an impact on effective population size^35,60, including background, positive, and balancing selection, and that some authors suggested that positive selection plays an important role in shaping genomic diversity^37,67. The genome-wide average of ASMC_avg in the GoNL data was 17,399 generations (s.d. = 9,957 generations), consistent with several recent analyses of human effective population size variation^1–3,19 , and with an effective size of ~10k commonly assumed in the literature^68,69 (we note, however, that our analysis is limited to obtaining posterior TMRCA estimates, which are driven by the demographic model provided in input). We thus expect the ASMC_avg annotation to capture background selection occurring within the past several hundred thousand years. As expected, ASMC_avg was highly correlated with other measures of background selection, including nucleotide diversity (r=0.50), the McVicker B-statistic⁶⁰ (r=−0.28), and allele age predicted by ARGWeaver⁶, quantile-normalized within 10 minor allele frequency bins⁷⁰ (r=0.26, see Supplementary Table 7).

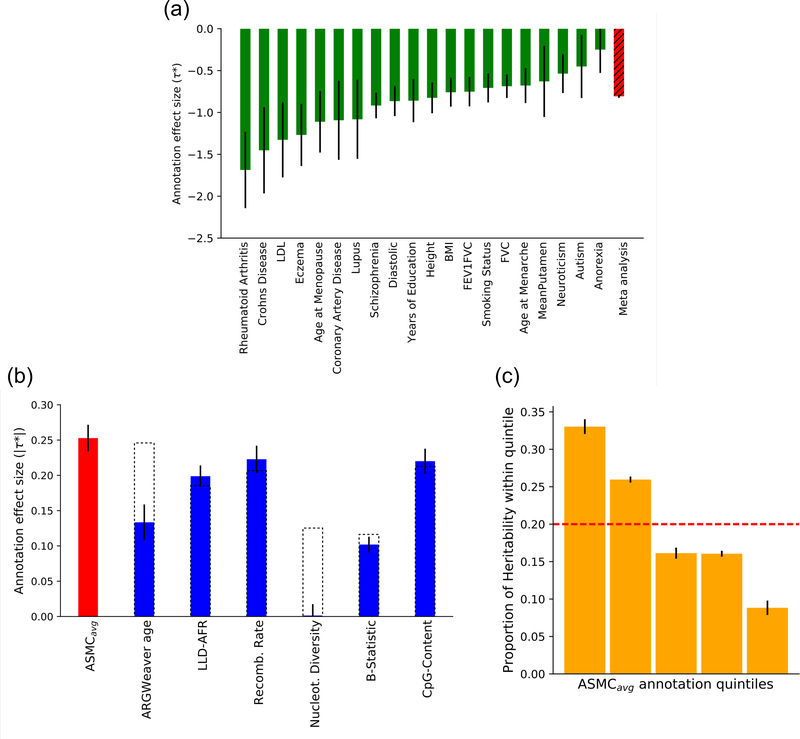
Analyses using stratified LD score regression (S-LDSC)⁷¹ have shown that regions under background selection are enriched for disease and complex trait heritability⁷⁰; enrichment was observed for the nucleotide diversity, McVicker B-statistic, and ARGWeaver predicted allele age annotations, as well as three other annotations linked to LD and recombination. We evaluated the ASMC_avg background selection annotation for heritability enrichment by applying S-LDSC to summary association statistics from 20 independent diseases and complex traits (Supplementary Table 8, average N=86k). We performed both an unconditioned analysis using only the ASMC_avg annotation, and a joint analysis conditioned on the 75 annotations from the baselineLD model⁷⁰ (which includes a broad set of functional annotations, in addition to the six annotations linked to background selection and LD), in order to specifically assess whether our annotation provides additional signal. Focusing on the ASMC_avg annotation, we computed the τ* metric⁷⁰, defined as the proportionate change in per-SNP heritability resulting from a 1 standard deviation increase in the value of the annotation, conditional on other annotations included in the model.

In the unconditioned analysis, lower ASMC_avg was associated with higher per-SNP heritability for all 20 traits analyzed (Figure 4A), confirming that regions under background selection are enriched for disease heritability. Meta-analyzed across the 20 traits, the τ* for ASMC_avg had a value of −0.81 (s.e. = 0.01; Z-test p < 10⁻³⁰⁰). After conditioning on the baselineLD model, the τ* for ASMC_avg remained strongly significant at −0.25 (s.e. = 0.01; Z-test p = 7×10⁻¹⁵³), implying that ASMC_avg remains informative for disease heritability after conditioning on other annotations linked to background selection as well as a broad set of functional annotations. Furthermore, ASMC_avg attained a larger value of τ* than each of the other six annotations linked to background selection (Figure 4B), implying that it was the most disease-informative background selection annotation in this analysis; we note that adding ASMC_avg to the baselineLD model reduced the |τ*| of the nucleotide diversity annotation from 0.13 to 0.00 and reduced the |τ*| of the ARGWeaver⁶ predicted allele age annotation from 0.25 to 0.13, indicating that ASMC_avg subsumes signals from these annotations. We computed the proportion of heritability explained by each quintile of the ASMC_avg annotation, which provides a more intuitive interpretation of the strength of the annotation’s effect (Figure 4C). We observed that SNPs in the smallest quintile of the annotation explained 33.1% (s.e. 0.5%) of heritability, 3.8x more than SNPs in the highest quintile (8.7%, s.e. 0.5%), the largest ratio among annotations linked to background selection (Supplementary Table 9) (tied with the nucleotide diversity annotation, whose effect was however subsumed by the ASMC_avg annotation; Figure 4B). Annotations constructed based on average pairwise TMRCA conditional on the allele present on each chromosome were further informative for disease heritability (Supplementary Figure 9 and Supplementary Figure 10; see Online Methods).

Figure 4. S-LDSC analysis of ASMC_avg background selection annotation and disease heritability.

(a) τ* value of the ASMC_avg annotation for 20 independent diseases and complex traits (sample sizes in Supplementary Table 8). Error bars represent SE of the τ* estimate. (b) Absolute values of τ* estimates (meta-analyzed across 20 independent diseases and complex traits, sample sizes in Supplementary Table 8) in joint analysis conditioned on baselineLD annotations. Error bars represent SE of the meta-analyzed τ* estimate. Dashed bars reflect values for six baselineLD annotations linked to background selection before the introduction of the ASMC_avg annotation. (c) Proportion of heritability explained by SNPs within different quintiles of ASMC_avg annotation (in joint analysis conditioned on baselineLD annotations). Error bars represent SE of the estimated proportions. Numerical results are reported in Supplementary Table 13.

Discussion

We have introduced a new method for inferring pairwise coalescence times, ASMC, that can be applied to either SNP array or WGS data and is highly computationally efficient. Exploiting ASMC’s speed, we analyzed ~2.2 billion pairs of haploid chromosomes from 113,851 British samples within the UK Biobank data set, and detected strong evidence of recent positive selection at 6 known loci and 6 novel loci linked to immune response and other biological functions. We further used ASMC to detect background selection at deeper time scales, estimating the average TMRCA at each position along the genome of 498 WGS phased samples from the Netherlands. Using this annotation in a stratified LD score regression analysis of 20 diseases and complex traits, we detected a strong enrichment for heritability in regions predicted to be under background selection; our annotation had the largest effect among available annotations quantifying background selection.

High-throughput inference of ancestral relationships has a number of applications beyond those related to recent positive selection and disease heritability that we have pursued in this work. Genotype calling and imputation methods^25–28, for instance, infer unobserved genotypes relying on ancestral relationships, which are usually estimated using computationally efficient approximations of the coalescent model (e.g. the copying model⁷²). Related ideas have been applied to detect phenotypic associations^22–24. The processing speed achieved by the ASMC approach, on the other hand, enables making minimal simplifications to the full coalescent process, while retaining high computational scalability. In addition, accurate detection of very recent common ancestors (IBD regions) across samples is a key component of several other types of analysis, including long-range phasing^34,73,74, estimation of recombination rates using haplotype boundaries^75–77, haplotype-based association studies⁷⁸, estimation of mutation and gene conversion rates⁷⁹. In addition, ASMC’s linear-time forward-backward algorithm can be leveraged to scale up demographic inference in both WGS and SNP array data. The use of this approach in large SNP data sets, in particular, will allow to accurately infer fine-scale demographic history within the past tens of generations, improving on methods that focus on summary statistics of shared long-range haplotypes^80–82, rather than directly estimating recent coalescence rates.

Although the ASMC offers new opportunities for inference of pairwise coalescence times, we note several limitations. First, the ASMC can operate either on pairs of unphased chromosomes within a single diploid individual, or on pairs of phased chromosomes across individuals. To prevent biases³, the latter application requires haplotypes phased with extremely high accuracy, which may be difficult to obtain. In this work, extremely accurate phasing was possible in the UK Biobank data set due to the very large sample size paired with the Eagle phasing algorithm³⁴ (on the order of one switch error every ~10cM; also see ref. ^72,82), and also possible in the GoNL data set due to leveraging trio information. Second, ASMC assumes a demographic model that includes a single panmictic population, and does not allow for the presence of samples from multiple ethnic backgrounds. Analyses of multi-ethnic samples will require extending the current approach so that it can accommodate demographic models involving multiple populations. Furthermore, ancestry-specific SNP ascertainment may lead to a depletion of high-frequency markers, creating an upward bias (Supplementary Figure 3). Third, ASMC is not currently applicable to imputed data. We have shown that higher genotyping density leads to higher accuracy in the inference of coalescence times. However, our preliminary tests involving the use of ASMC on imputed data where only markers with high-quality imputation accuracy are retained (e.g. imputation r²>0.99) resulted in substantial upward biases of the inferred coalescence times, which are due to spurious genotype calls. Effectively extending the ASMC to handle imputed data will thus require additional modeling of imputation accuracy. Fourth, our approach to assess the statistical significance of loci under recent positive selection is based on approximate p-value calculations. The use of approximate p-values has previously been adopted in detecting signals of positive selection³⁷, and is more conservative than the widespread approach of simply ranking top loci³⁶; nonetheless, the construction of an improved null model is a desirable direction of future development⁸³. Finally, we note that although ASMC’s speed enables the analysis of large data sets, the computational costs of inferring pairwise coalescence times scale quadratically with the number of analyzed individuals. It may be possible to improve on this quadratic scaling given that at each location in the genome the ancestral relationships of a set of n samples can be efficiently represented using a tree-shaped genealogy containing n-1 nodes. The task of efficiently reconstructing a samples’ ancestral recombination graph (ARG)^6,24,84, however, is substantially more complex than that of estimating pairwise TMRCA, and remains an exciting direction of future research. Despite these limitations and avenues for further improvement, we expect that ASMC will be a valuable tool for computationally efficient inference of pairwise coalescence times using SNP array or WGS data.

Online Methods

We provide an overview of the main components of the ASMC approach. An extended description can be found in the Supplementary Note.

ASMC model overview.

The ASMC is a coalescent-based HMM^1-4 (see Supplementary Note for background on related methods). At each site along the genome, hidden states represent the time at which a pair of analyzed haploid individuals coalesce, which we also refer to as their time to most recent common ancestor (TMRCA). In this model, time is discretized using a set of s user-specified time intervals, each representing a possible hidden state. The TMRCA may change between adjacent sites whenever a recombination event occurs along the lineages connecting the two individuals to their MRCA. The transition probability between states is modeled using a Markovian approximation⁵ of the full coalescent process. Observations are obtained using genotypes of the pair of analyzed samples, as well as a set of additional samples, as detailed below, and emission probabilities reflect the chance of observing a specific genotypic configuration, conditional on the pair’s TMRCA at a site. Calculations of the initial state distribution, the transition, and the emission probabilities consider the demographic history of the analyzed sample, which is separately estimated (e.g. using other coalescent HMMs run on available WGS data for the analyzed population) and provided as input. The main goal of the ASMC is to perform high-throughput inference of posterior TMRCA probabilities along the genome for many pairs of haploid individuals genotyped using either WGS or SNP array platforms.

Emission model.

ASMC’s emission probability calculations rely on the recently developed Conditioned Sample Frequency Spectrum (CSFS)⁴, which is extended to handle non-randomly ascertained genotype observations (e.g. SNP array data). Consider a sample of n individuals, and define 2 of them as distinguished, (n-2) of them as undistinguished. We are interested in estimating posterior TMRCA probabilities at a set of observed sites in the genome of the 2 distinguished samples. At each site, the CSFS model⁴ allows computing the HMM emission probability P(d,u|τ), i.e. the probability that d ∈{0,1,2} derived alleles are carried by the distinguished pair of samples, while u ∈[0, n-2] derived alleles are observed in the (n-2) undistinguished samples, conditioned on the fact that the distinguished pair’s TMRCA (the HMM’s hidden state) is τ. Intuitively, this approach enables exploiting the relationship between an allele’s frequency and its age, which is modeled using the set of undistinguished samples and used to improve the inference of TMRCA for the distinguished pairs⁴. Because the set of undistinguished samples is solely used to obtain allele frequencies, their ancestral relationships need not be tracked, leading to a substantially simplified and tractable model. In the ASMC, this approach is extended to accommodate the fact that the observed sites may not be a randomly ascertained subset of polymorphic variants in the sample. To this end, we write the emission probability as P(obs|d+u)×P(d,u|τ), where the additional term P(obs|d+u) represents the probability that a site with (d+u)∈[0, n] carriers of the derived allele is observed in the ascertained data. In the ASMC, this probability is estimated using the ratio between the empirical allele frequency spectrum obtained from the analyzed data and the allele frequency spectrum that is expected under neutrality for the demographic model provided in input. Details are provided in the Supplementary Note. The emission model enables handling both major/minor and ancestral/derived genotype data encoding. We verified using coalescent simulation (see Simulations), that the number of individuals used when computing the CSFS model does not have a substantial impact on accuracy (Supplementary Table 10).

Transition model.

The transition model describes the probability of transitioning along the genome between any pair of the s possible time intervals for the TMRCA of the two analyzed samples (which we referred to as distinguished individuals in the emission model). These transition probabilities are computed using the conditional Simonsen-Churchill model (CSC)^5,6. In contrast to previously proposed Markovian approximations of the coalescent process, such as the SMC⁷ and the SMC’⁸, the CSC model remains accurate even if the observed genotypes are distant from one another⁵. This is an important requirement in the analysis of SNP array data, as markers in this type of data are separated by substantially larger genetic distances than in the case of WGS data. Details on the calculation of transition probabilities can be found in the Supplementary Note. ASMC supports variable recombination rates along the genome through a genetic map provided in input.

Inference.

The standard HMM forward-backward algorithm to perform posterior inference has computational cost O(s²m) for analysis using s hidden states in a sequence of length m⁹. Current analyses making use of coalescent HMMs to infer demographic histories utilize a number of hidden states in the order of 10². When human WGS data is analyzed, the number of observed sites is in the order of 10⁹. Thus, the computational cost of applying the standard HMM approach is very high, and a number of solutions to speed up the inference have been proposed (see Supplementary Note for an overview). Here, we devise a new approach that uses dynamic programming to reduce the computational dependence on the number s of hidden states from quadratic to linear, resulting in a gain of 2 orders of magnitude for the average analysis compared to the standard algorithm. A related procedure exists for the SMC transition model¹⁰, but cannot be applied to the more accurate and more complex CSC approach used in this work. The speed-up in the HMM forward algorithm is obtained by simplifying the key operation of computing an updated α′ vector of forward probabilities using the current forward vector, α, and the transition matrix, T, which is obtained from the CDC model. Computing the i-th entry of this vector normally requires performing the summation ${\alpha }_i^{\text{'}}={\sum }_{k=1}^s{\alpha }_k{T}_{k,i}$, which has computational cost O(s). This operation, however, can be rewritten as a linear combination of three terms, each of which can be recursively computed in time O(1), reducing the cost of computing the entire forward vector from O(s²) to O(s) (see the Supplementary Note for a detailed derivation). An equivalent speed-up can be obtained for the backward algorithm. Furthermore, to reduce the dependence of ASMC’s running time on sequence length when WGS data are analyzed, we make the following approximation. Consider two polymorphic sites separated by a stretch of n monomorphic sites. Computing an updated forward probability vector α′ using the standard approach would require performing the operation α′ = α(TE₀)ⁿTE_p, where E₀ is a diagonal matrix with emission probabilities for a monomorphic site in its diagonal entries and E_p is the equivalent matrix for the emission at the next polymorphic site in the sequence. For short genetic distances that are observed between polymorphic sites, the matrix T is close to diagonal, and we can thus effectively approximate this product as αTⁿEⁿ₀TE_p (see Supplementary Figure 4). Using the previously described dynamic programming approach, this operation can be computed in time O(s), and only needs to be performed at a subset of polymorphic sites, resulting in a further speedup of 2-3 orders of magnitude compared to the standard forward/backward approach operating on all sites. This approximation is not needed when SNP array data are analyzed, as we need not integrate over large stretches of monomorphic sites, treating instead all sites between a pair of genotyped SNPs as unobserved. In addition to this, most quantities involved in the O(ms) forward/backward operations can be precomputed and stored in a cache, substantially reducing constant terms in the computation.

ASMC simulations.

We performed extensive coalescent simulations to assess the accuracy of the ASMC method. Unless otherwise specified, all simulations use the setup described in this section (standard setup). We used the ARGON simulator¹¹ (v0.1.160415), incorporating a human recombination rate map (see URLs) and a recent demographic model for European individuals⁴. We simulated 300 haploid individuals and a region of 30Mb. To simulate SNP array data, we subsampled polymorphic variants to match the genotype density and allele frequency spectrum observed in the UK Biobank data set (described below). We used recombination rates from the first 30Mb of Chromosome 2, whose average rate of 1.66 cM/Mb well represents the recombination rates observed along the genome (mean 1.45 cM/Mb, s.d. 0.33 cM/Mb across autosomes). The demographic model and genetic map used to simulate the data were used when running ASMC, unless otherwise specified.

Time discretization.

We ran ASMC using different numbers of discrete time intervals, which were chosen to correspond to quantiles of the pairwise coalescence distribution induced by the demographic model. To achieve increased resolution into the recent past, some simulations utilized 160 discretization intervals chosen as follows: 40 intervals of length 10 between generations 0 and 400, 80 intervals of length 20 between generations 400 and 2,000, and 40 intervals corresponding to quantiles of the coalescence distribution, starting at generation 2,000. While using a larger number of time intervals provides increased resolution, the choice of time discretization should take into account that a larger number of time intervals typically results in noisier MAP estimates of TMRCA (see Supplementary Table 5).

Accuracy evaluation.

ASMC’s inference accuracy was evaluated using two metrics. For a given region, and for all pairs of samples in a simulated data set, we computed the squared correlation (r²) between the true and inferred sum of TMRCA at each site within the region. This metric captures the accuracy of inferred genetic kinship, but is unchanged by potential scaling factors and possible systematic biases in the TMRCA estimates. We thus also measured the root mean square error (RMSE) between true and inferred TMRCA at individuals sites, which we usually report as a percent difference compared to analysis of WGS data for improved readability. For our analysis of IBD detection accuracy, we defined as true IBD regions all sites for which pairwise TMRCA were lower than a specified time threshold (note that several definitions exist for IBD sharing among unrelated individuals¹², and that IBD is also sometimes defined as the set of sufficiently long genomic regions where two chromosomes share a common ancestor uninterrupted by recombination^13,14). We ran Beagle¹⁵ (v4.1) providing the true genetic map and using default parameters, and used threshold values for the output LOD score (ibdlod) to select the set of inferred IBD sites. To detect IBD using ASMC, we obtained MAP estimates of TMRCA at all sites using 160 discretization intervals (see Time discretization), and used thresholds on the inferred TMRCA values to select the set of inferred IBD sites. For both methods, we computed accuracy using the precision-recall curve. Neither Beagle nor ASMC enable obtaining recall values in the full [0,1] range, due to the presence of a lower bound for Beagle’s admissible LOD threshold values, and ASMC’s time discretization. To compare the two methods’ accuracies in each simulation, we computed the area under the precision-recall curve (auPRC) only within the range in which the accuracy of both methods could be measured, and reported the percent difference between the two methods’ auPRC (see Supplementary Figure 11 for an illustration). The PRC curve between observed points was interpolated using the method of ref ¹⁶.

Model misspecifications.

To mimic inaccuracies in the genetic map we simulated data using a human recombination map for the simulated region, but run ASMC using a map with added noise. To introduce noise, the recombination rate between each pair of contiguous markers in the map was altered by randomly adding or subtracting a fraction of its true value (see Supplementary Table 4). To test whether deviations from the assumption of frequency-based ascertainment introduce significant biases, we mimicked over-ascertainment of rare variants in genic regions of the genome. To this end, we randomly sampled ~25% of the markers from 10Kb-long genes placed every 200Kb, while the remaining variants were sampled to match the UK Biobank frequency spectrum as in standard simulations, and compared the distribution of coalescent times within over-ascertained regions and the rest of the genome (Supplementary Figure 2). To test ASMC’s robustness to an accurate demographic model we simulated data under a European demographic history, but ran ASMC assuming a constant population size of 10,000 diploid individuals (see Supplementary Table 2). To test the effects of ancestry-specific SNP ascertainment, we simulated an analysis where a group of individuals is genotyped using an array that has been designed using a different, highly diverged population. To this end, we simulated two populations that split 2,000 generations (or ~60,000 years) in the past. The two populations have identical, European-like effective population size histories after the split, and a symmetric migration rate of 0.0, 3×10⁻⁵ or 1×10⁻² per generation. We simulated ancestry-specific marker ascertainment by selecting SNPs based on frequencies from only one of the two populations, matching the spectrum observed in the UK Biobank. We then inferred coalescence times in both populations independently as described in previous experiments involving a single population. Results are reported in Supplementary Figure 3.

UK Biobank (UKBB) data set.

The UK Biobank interim release data comprise 152,729 samples, from which we extracted 113,851 individuals of British ancestry (as described in ref. ¹⁷). 95 trio parents were excluded and used to assess phasing quality with the Eagle¹⁸ software, leaving a total of 113,756 samples. From these, we created 11 batches with 10,000 samples and 1 batch with the remaining 3,756 samples, which we analyzed using ASMC. Out of the original ~800k variants (for basic quality control details see URLs: UK Biobank Genotyping and QC), we analyzed a total of 678,956 SNPs that were autosomal, polymorphic in the set of analyzed samples, biallelic, with missingness ≤10%, and not included in a set of 65 variants with significantly different allele frequencies between the UK BiLEVE array and the UK Biobank array. We divided the genome in 39 autosomal regions from different chromosomes or separated by centromeres.

Detection of recent positive selection.

To detect the occurrence of recent positive selection, we computed a statistic related to the Density of Recent Coalescence events within the past T generations (DRC_T statistic). The DRC_T statistic was measured as follows. At a given site along the genome, we first averaged all posterior TMRCA estimates obtained from all analyzed pairs of samples and renormalized these averages to obtain an average pairwise coalescence distribution at the site. The DRC_T statistic was then obtained by integrating this distribution between generations 0 and T. The statistic was measured in windows of 0.05 cM, reporting an average of all SNPs within each window. We tested the sensitivity of the DRC_T statistic in detecting recent positive selection using extensive simulation. Details for these simulations can be found in the Supplementary Note.

Null model calibration.

Given n samples from a population of recent effective size N, the DRC_T statistic is approximately Gamma-distributed under the null for sufficiently small values of T and n⟨⟨N. The rationale of this approximation is that for n⟨⟨N, a small number of coalescence events will have occurred within the short time span of T generations. In this regime, the coalescence time of each pair of lineages may be modeled as independent and exponentially distributed, which allows approximating the total number of early coalescence events as a Gamma-distributed random variable. Similar approximations have been recently used elsewhere^19,20. We thus computed approximate p-values for our selection scan in the UKBB data set using the following approach. We first extracted a subset of “neutral” genomic regions, spanning a total of 18% of the genome, and defined as any genotyped site at a distance greater than 500Kb from regions contained in a recent database of positive selection²¹ (see URLs: database of positive selection). We then built an empirical null model by fitting a Gamma distribution (using Python’s Scipy library, see URLs) to these putatively neutral regions, and used this model to obtain approximate p-values throughout the genome. We analyzed 63,103 windows, using a Bonferroni significance threshold of 0.05 / 63,103 = 7.9 x 10^-7. One of the genome-wide significant signals that we detected (PKD1L3 locus, chr16:70.89-71.80Mb) fell within the putatively neutral portion of the genome. We thus iterated this procedure, excluding this locus from the set of putatively neutral loci.

Genome of the Netherlands (GoNL) data set.

The data set consists of 748 individuals who passed quality control and were sequenced at an average of ~13x (quality control details for the Release 4 data are described elsewhere²²). We analyzed 19,730,834 sequenced variants for 498 trio-phased unrelated parents, excluding centromeres and dividing the genome in the same 39 autosomal regions used for analysis of the UKBB data set.

ASMC_avg annotation.

We set out to estimate the strength of background selection by measuring variation in local effective population size along the genome²³. We used ASMC to estimate the posterior mean TMRCA at all sites and for all pairs of haploid individuals in the GoNL data set. We averaged these estimates at each site to obtain an annotation of background selection, which we refer to as ASMC_avg. We similarly computed other annotations, conditioning on whether either or both individuals at a site carried a mutated allele. The ASMC_het annotation (Supplementary Figure 9), was obtained by averaging at each site the posterior mean TMRCA estimates for all pairs of individuals that were found to be heterozygous at each site. Other annotations were similarly computed using only pairs carrying e.g. minor/major alleles at each site (see Supplementary Figure 10). We verified that the ASMC_het annotation captures the effects of natural selection using forward simulation. Details for these simulations can be found in the Supplementary Note.

Stratified LD Score (S-LDSC) analysis

We investigated whether large values of our annotations related to background selection corresponded to an enrichment in heritability for 20 complex traits and diseases listed in Supplementary Table 8. The S-LDSC analysis was run on data sets containing European individuals using standard guidelines²⁴. The sets of LD-score, regression, and heritability SNPs were defined as follows. LD score SNPs were set to be 9,997,231 biallelic SNPs with at least 5 minor alleles observed in 489 European samples from the 1000 Genomes Phase 3 data set²⁵ (see URLs); regression SNPs were set as 1,217,312 HapMap Project Phase 3 SNPs; and Heritability SNPs, used to compute trait heritability, were chosen as the 5,961,159 reference SNPs with MAF ≥ 0.05. The MHC region (2Mb 25-34 on Chromosome 6) and SNPs with χ²>80 or 0.0001N were excluded from the analysis. Annotations contained in the baselineLD model, which we included in our joint analyses, can be found in Supplementary Table S9 of ref. ²⁶. To avoid minor allele frequency (MAF)-mediated effects, all ASMC-related annotations used in the S-LDSC analysis were quantile-normalized with respect to MAF of regression SNPs. Specifically, we used 10 MAF ranges specified in the baselineLD model, corresponding to 10 frequency quantiles for the regression SNPs. For each range, we ranked values of an annotation for the corresponding SNPs, and mapped them to quantiles of a Standard Normal distribution. Annotation effects, τ*, were obtained from the output of S-LDSC, as described in ref. ²⁶. Independent traits were selected on the basis of low genetic correlation, as previously described²⁴. Meta-analysis of τ* values across independent traits was performed computing a weighted average of individual estimates of τ*, weighted using 1/(h_i²ε_i²), where h_i² represents heritability for the i-th trait, and ε_i represents the standard error of the trait’s τ* estimate.

Data and code availability

The ASMC program and source code, as well as genomic annotations of positive and background selection can be downloaded at http://www.palamaralab.org/software/ and https://github.com/pierpal/ASMC.