A fluid-to-solid jamming transition underlies vertebrate body axis elongation

Abstract

Just as in clay molding or glass blowing, sculpting biological structures requires the constituent material to locally flow like a fluid while maintaining overall mechanical integrity like a solid. Disordered soft materials, such as foams, emulsions and colloidal suspensions, switch from fluid-like to solid-like behaviors at a jamming transition^1–4. Similarly, cell collectives have been shown to display glassy dynamics in 2D and 3D^5,6 and jamming in cultured epithelial monolayers^7,8, behaviors recently predicted theoretically^9–11 and proposed to influence asthma pathobiology⁸ and tumor progression¹². However, it is unknown if these seemingly universal behaviors occur in vivo and, specifically, if they play any functional role during embryonic morphogenesis. By combining direct in vivo measurements of tissue mechanics with analysis of cellular dynamics, we show that during vertebrate body axis elongation, posterior tissues undergo a jamming transition from a fluid-like behavior at the extending end, the mesodermal progenitor zone (MPZ), to a solid-like behavior in the presomitic mesoderm (PSM). We uncover an anteroposterior, N-cadherin-dependent gradient in yield stress that provides increasing mechanical integrity to the PSM, consistent with the tissue transiting from a wetter to a dryer foam-like architecture. Our results show that cell-scale stresses fluctuate rapidly (~1 min), enabling cell rearrangements and effectively ‘melting’ the tissue at the growing end. Persistent (>0.5 h) stresses at supracellular scales, rather than cell-scale stresses, guide morphogenetic flows in fluid-like tissue regions. Unidirectional axis extension is sustained by the reported PSM rigidification, which mechanically supports posterior, fluid-like tissues during remodeling prior to their maturation. The spatiotemporal control of fluid-like and solid-like tissue states may represent a generic physical mechanism of embryonic morphogenesis.

One of the hallmarks of animal development is the formation of the anteroposterior (AP) body axis, which occurs by nearly unidirectional elongation of tissues at the anterior and posterior body ends¹³. During posterior elongation, which does not depend on cell proliferation at early stages¹⁴, descendants of neuromesodermal progenitors move ventrally from the dorsal medial (DM) region to the paraxial MPZ as mesodermal progenitors^15,16 (Fig. 1a,b). These progenitor cells progressively differentiate into mature mesodermal cells that are incorporated in the PSM as body elongation proceeds. Both in amniotes and fish, cells display a graded reduction of their movements as they progress from the MPZ (referred to as posterior PSM in amniotes) to the PSM^15,17, where they arrest and undergo a mesenchymal-to-epithelial transition that anticipates somite formation¹⁸. The observed patterns of cell motion in these kinematic studies^15,17 could potentially be caused by a gradient in cell or tissue mechanics along the AP axis. However, the physical mechanism causing such cellular movements and, more generally, sculpting the body axis, remains unknown.

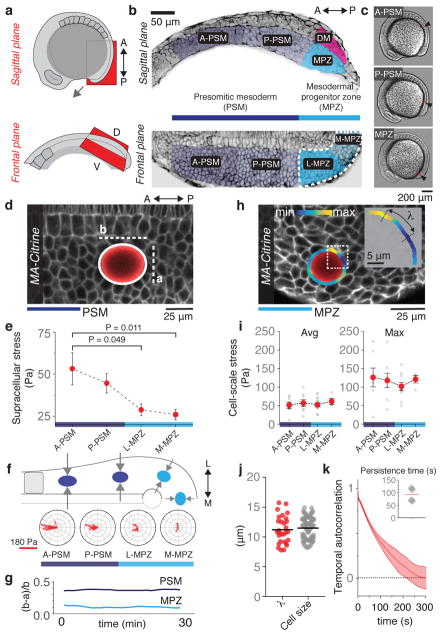
Figure 1. Supracellular and cell-scale mechanical stresses during body axis elongation.

a, Sketch showing lateral views of a 10-somite stage and sagittal and frontal anatomical planes. b, Confocal sections along sagittal and frontal planes of posterior extending tissues in Tg(actb2:MA-Citrine) embryos (inverted). The PSM and MPZ are divided into anterior (A-PSM) and posterior (P-PSM) regions, and lateral (L-MPZ) and medial (M-MPZ) regions, respectively. The dorsal medial (DM) zone is dorsal to the MPZ. c, Embryos with droplets (red; arrows) located in the different regions. d, Elliptical fit (white; b and a being the long and short semi-axes) of a ferrofluid oil droplet (red) in the PSM of a Tg(actb2:MA-Citrine) zebrafish embryo (no magnetic actuation). e, Magnitude of supracellular stresses along the AP axis (n= 9, 24, 25, 27; mean ± SEM). Mann-Whitney test. f, Orientation of the droplets’ long axis with respect to the AP axis (n=15, 12, 11, 13). Sketch showing the average droplet orientations along AP axis (top) and the posterior-to-anterior increase in mediolateral constriction (arrows) in the PSM. g, Time evolution of the ellipsoidal droplet deformation, (b − a)/a. h, Ferrofluid droplet (red) in the MPZ of a Tg(actb2:MA-Citrine) embryo. Curvature values along the detected droplet contour (color coded), with λ being the distance between consecutive curvature maxima and minima (inset). i, Measured average and maximal cell-scale stresses along the AP axis (n=7, 8, 10, 4; mean ± SEM). j, Measured values of λ (n = 29) and cell size (n = 100 cells). Line indicates mean. k, Temporal autocorrelation of droplet shape deviations from the ellipsoidal mode (n=2062 curvature time traces obtained from 4 embryos). Average half-life is approximately 1 min (inset; n=4; line indicates mean). Unless stated otherwise, n represents number of embryos, given for each tissue region as shown in each panel.

Mechanical forces are generally believed to guide morphogenetic movements¹⁹. To establish the role of mechanical forces in vertebrate body elongation, we measured the endogenous mechanical stresses along the zebrafish AP axis using magnetically-responsive oil microdroplets²⁰ (Fig. 1a–c; Methods). In the absence of applied magnetic field, the deformations of droplets inserted between cells in the tissue provide a readout of the local mechanical stresses²¹. To detect potential spatial variations in mechanical stresses at supracellular scales we analyzed the droplets’ ellipsoidal deformation (Fig. 1d; Methods). Our analysis shows a posterior-to-anterior increase in the magnitude of supracellular stresses (Fig. 1e), with the axis of droplet elongation oriented mediolaterally in the medial MPZ (M-MPZ) and progressively reorienting along the AP axis in the PSM (Fig. 1f), consistent with the previously reported directions of morphogenetic flows^15,17. Monitoring the ellipsoidal droplet deformation over time shows that supracellular stresses persist over more than 30 min (Fig. 1g), compatible with developmental timescales (~0.5–1h). These data indicate that supracellular stresses guide morphogenetic flows and reveal an increase in mediolateral constriction during PSM maturation, consistent with mediolateral thinning of the body axis¹⁵ and anisotropy of nuclear deformation and cell shape (Extended Data Fig. 1).

Beyond supracellular stresses, the deviations of the droplets’ shapes from ellipsoidal deformations display cell-sized stress inhomogeneities (Fig. 1h,j; Extended Data Fig. 2; Methods). Both the average and maximal values of these cell-scale stresses are uniform along the AP axis (Fig. 1i). Temporal autocorrelation analysis of these higher order droplet deformations shows that cell-scale stresses are short-lived, with a persistence time of approximately 1 min (Fig. 1k; Methods). These data show that cell-scale stresses are non-persistent at developmental timescales (~0.5–1h) and uniform throughout the tissue, suggesting that their role may be to introduce active stress fluctuations (causing cell ‘jiggling’; Supplementary Video 1), as previously proposed for 3D multicellular aggregates²².

Since morphogenetic flows also depend on the tissue material properties^23,24 and involve large tissue rearrangements, it is important to probe the tissue mechanical response to large deformations. To do so, we applied a controlled, uniform magnetic field for a defined time period (15 min) to droplets previously inserted in the tissue²⁰ (Fig. 2a; Methods). Magnetic actuation caused large droplet deformations of more than one cell size, corresponding to applied strains in the 50–150% range (Fig. 2a,b). Upon removal of the magnetic field, droplets progressively relaxed toward a spherical shape due to the restoring force of interfacial tension (capillary stress, σ_c), but arrested before reaching that state, displaying a residual deformation and revealing the presence of a yield stress σ_y in the tissue (Fig. 2a–c; Methods). The yield stress, which corresponds to the maximal mechanical stress that a material can sustain in a solid-like state before starting to flow³, provides a direct measure of the tissue’s ability to withstand sustained mechanical loads, i.e., its mechanical integrity. Performing these experiments along the body axis shows that the yield stress is spatially graded and minimal in the MPZ (Fig. 2d; Methods), revealing a posterior-to-anterior gradient of increasing tissue mechanical integrity that parallels PSM maturation.

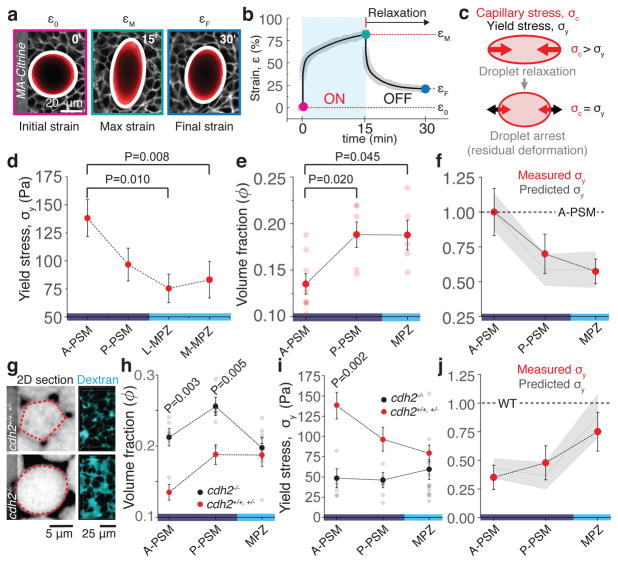
Figure 2. Mechanical integrity of the extending body axis.

a, Example of droplet dynamics during magnetic actuation. White lines indicate ellipse segmentation. Droplet actuation is characterized by an initial deformation or strain, ε₀, a maximal strain, ε_M, and a final residual strain, ε_F (Methods). b, Temporal evolution of the droplet strain during magnetic actuation. Experimental data points (gray) and fit (black line) are shown (Methods). c, The residual droplet deformation is set by the balance between the capillary stress σ_c and the tissue yield stress σ_y. d–e, Measured yield stress (d; n=12, 12, 13, 13) and volume fraction of extracellular space ϕ (e; n=8, 6, 5) along the AP axis. Mean ± SEM; Mann-Whitney test. f, Comparison between measured (red dots) and predicted (gray line and band representing mean ± SEM) yield stress along the AP axis, relative to the A-PSM. g, Confocal sections (inverted) and 3D reconstructions (Methods) of Dextran-labeled extracellular space for WT (cdh2^+/+, cdh2^+/−) and cdh2^−/− embryos. h–i, Measured volume fraction of extracellular space (h; n=6, 8, 7) and yield stress (i; n=5, 5, 12) along the AP axis in cdh2^−/− embryos (black dots) compared to WT (red dots). Mean ± SEM; Mann-Whitney test. k, Measured (red dots) and predicted (gray line and band representing mean ± SEM) yield stress values in cdh2^−/− embryos normalized to WT values in each region. In all cases, n represents number of embryos, given for each tissue region as shown in each panel.

As pointed out by D’Arcy Thompson²⁵ and others more recently^9,22, the disordered cellular structure of tissues strongly resembles that of aqueous foams, which display a finite yield stress when the volume fraction ϕ of fluid between bubbles becomes lower than a critical value ϕ_c at the jamming transition^1,2 (Supplementary Figure 1). Following the analogy to foams, we explored the potential role of the extracellular spaces in controlling tissue yield stress. We measured the volume fraction of extracellular spaces along the AP axis using fluorescent Dextran (Methods) and observed decreasing spaces between cells away from the posterior end (Fig. 2e). Since cohesion between cells depends on their adhesion strength and N-cadherin (Cdh2) has been shown to be essential for body axis elongation^15,26 and PSM maturation²⁷ in zebrafish, we measured the volume fraction of extracellular space and yield stress along the AP axis of cdh2 loss-of-function mutants²⁶. Disruption of N-cadherin-mediated adhesion resulted in larger extracellular spaces in the PSM, but not in the MPZ (Fig. 2g,h; Extended Data Fig. 3). Accordingly, the yield stress in cdh2 mutants is altered in the PSM but not in the MPZ (Fig. 2i). No significant spatial variation in yield stress was observed in cdh2 mutants, indicating that N-cadherin-mediated adhesion is necessary to maintain the AP gradient in extracellular spaces and tissue mechanical integrity (yield stress). In addition, the reported AP gradients in supracellular stresses (Fig. 1e) and nuclear anisotropy observed in wild type (WT) are lost in cdh2 mutants (Extended Data Fig. 1), indicating that mediolateral constriction in the PSM is N-cadherin-dependent. Further supporting the analogy to foams, both the measured values of yield stress along the AP axis in WT, and the changes in yield stress between WT and cdh2 mutants, can be accounted for (with no adjustable parameters) by assuming such changes to result solely from the observed variations in extracellular volume fraction in a tissue that behaves like a 3D disordered monodispersed foam (Fig. 2f,j; Methods). Cell rearrangements induced by droplet actuation (Extended Data Fig. 4) further indicate that the yield stress arises from the jammed cellular environment, as in 3D disordered foams¹. While jamming transitions have recently been predicted by 2D vertex models of multicellular systems with no extracellular spaces^10,11 and observed in epithelial cell culture⁸, our measurements indicate that jamming in 3D embryonic tissues is consistent with classical jamming scenarios in foams, where the volume fraction of extracellular spaces plays a prominent role^1,2.

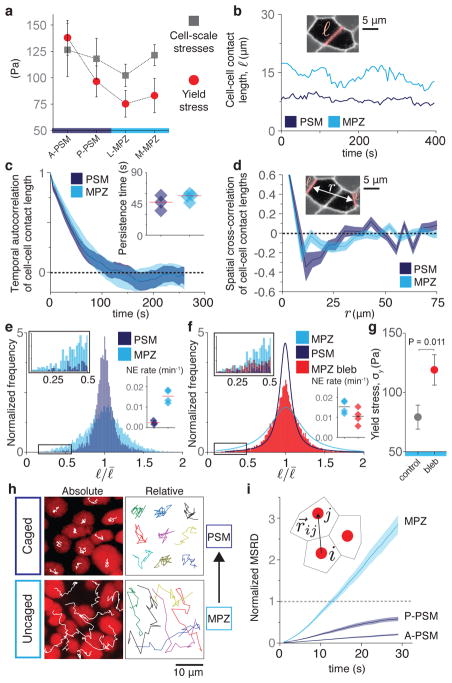
Unlike aqueous foams though, living tissues are characterized by active cellular stresses that could locally unjam the system and fluidize the tissue, as known for systems in which thermal fluctuations are relevant^2,4,9. Comparison of the yield stress and the magnitude of cell-scale stresses indicates that the maximal stress fluctuations are well above the yield stress in the MPZ, but below it in the anterior PSM (A-PSM; Fig. 3a), suggesting that actively-generated stress fluctuations may help fluidize the tissue at its posterior end. Since neighbor exchanges are necessary to fluidize foam-like tissues^1,9 and actomyosin-driven fluctuations in cell-cell contact length cause cellular rearrangements¹⁹, we characterized the dynamics of cell-cell contacts both in the PSM and MPZ (Fig. 3b–f; Methods). Autocorrelation analysis shows that cell-cell contact lengths become temporally uncorrelated within less than 1 min and spatially uncorrelated beyond 2–3 cell sizes (Fig. 3c,d), consistent with our measurements of cell-scale stresses (Fig. 1i,k) and indicating that, at developmental timescales (~0.5–1h), cell-cell contact dynamics can be seen as short-lived, active fluctuations uniform in the tissue. As only large fluctuations can induce neighbor exchanges and fluidize the tissue, we measured the distribution of cell-cell contact lengths both in the PSM and MPZ tissues (Methods). Our results show a broader distribution in the MPZ, with large fluctuations being considerably more frequent in this region than in the PSM (Fig. 3e), both in WT and in cdh2 mutants (Extended Data Fig. 5). Accordingly, we found that the neighbor exchange rate is 6 times higher in the MPZ than in the PSM (Fig. 3e, inset), consistent with the MPZ being in a fluid-like state and the PSM in a solid-like state. No systematic alignment of neighbor exchanges along a single spatial direction was observed (Extended Data Fig. 6), indicating that cell intercalation in these tissues does not contribute to posterior elongation. Interpreting active fluctuations as an effective temperature^9,17,22, a key parameter in the control of jamming transitions^2,4, it is possible to obtain the energy landscape of neighbor exchanges in both MPZ and PSM (Extended Data Fig. 7; Methods). In this framework, reducing fluctuations in cell-cell contact length (lower effective temperature) by impairing myosin II-dependent force generation at the cell cortex should render the MPZ more solid-like. Partial inhibition of myosin activity with blebbistatin led to smaller cell-cell contact length fluctuations (narrower distribution; Fig. 3f), decreased neighbor exchange rate (Fig. 3f, inset) and increased yield stress in the MPZ (Fig. 3g), thereby rigidifying the tissue and leading to a reduction in both cell movements and body elongation speed (Extended Data Fig. 8). These results indicate that while the PSM is jammed in a solid-like state, with weak cell-cell contact length fluctuations (low effective temperature) unable to fluidize the tissue, the stronger cell-cell contact length fluctuations (high effective temperature) in the MPZ cause substantial cell rearrangements that effectively ‘melt’ the tissue into a fluid-like state.

Figure 3. Cell-cell contact length fluctuations and cellular movements along the AP axis.

a, Comparison of yield stress (Fig. 2d) and maximal cell-scale stresses (Fig. 1i) along the AP axis. b, Examples of time traces of cell-cell contact length ℓ in the PSM and MPZ. c–d, Temporal autocorrelation of cell-cell contact length (c) and spatial cross-correlation of cell-cell contact lengths separated by a distance r (d) both in the PSM and MPZ (n=186, 54 cell-cell contacts). Correlation (persistence) timescale (c, inset; line indicates mean). e, Normalized frequency of cell-cell contact lengths in the PSM and MPZ (n=6969, 7896 cell-cell contacts). Zoomed in distribution tail (box, left inset). Neighbor exchange (NE) rates (per cell) in PSM and MPZ (right inset; n=14, 49 NE; line indicates mean). For c–e, n is given for PSM, MPZ and obtained from 3, 4 embryos, respectively. f, Normalized frequency of cell-cell contact lengths in the MPZ of embryos treated with blebbistatin 100 μM (n=13813 cell-cell contacts from 4 embryos). Zoomed in distribution tail (box, left inset). NE rate in the MPZ region of treated embryos compared to WT (right inset; n=20 NE from 3 embryos). g, Measured yield stress in the MPZ of embryos treated with blebbistatin (red; n=12 embryos) compared to WT (gray, n=26 embryos). Mean ± SEM; Mann-Whitney test. h–i, Tracks (h; absolute and relative; nuclear tracking) and normalized mean square relative displacement (MSRD, i; n=1937, 1776, 2523 analyzed cell pairs for A-PSM, P-PSM and MPZ, obtained from 5, 5, 6 embryos) of cellular movements during a 30 min time window.

Since cellular movements result from the combined effect of active stresses and mechanical constraints (tissue material properties), their analysis informs about the mechanical state of the tissue^6,8. Both direct observation (Fig. 3h) and analysis (Fig. 3i; Mean Squared Relative Displacement, MSRD; Methods) of cellular movements in the tissue showed caged behavior in the PSM, consistent with cells being trapped in a solid-like material, and uncaged cell mixing in the MPZ, consistent with this region being fluid-like. Our measurements indicate that the posterior-to-anterior transition between uncaged to caged cellular movements, consistent with previous observations in chicken¹⁷, results from an increase in physical constraints on cells, rather than a decrease in cellular stresses, as the spaces between cells are reduced anteriorly while maintaining a constant cell density (Extended Data Fig. 9; Methods).

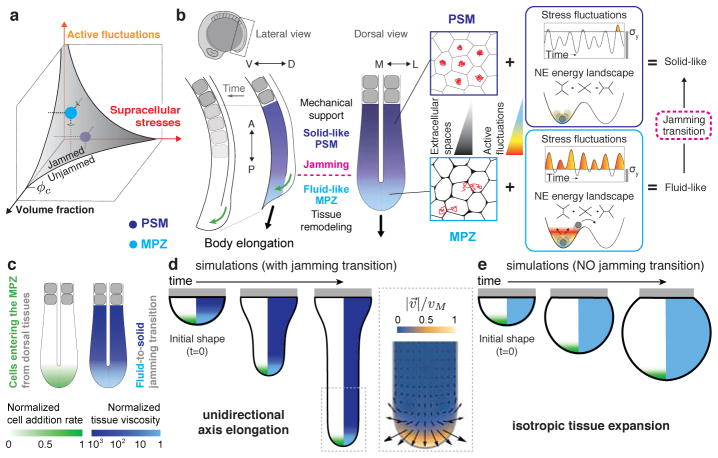
Taken together, our direct in vivo measurements of tissue mechanics and analysis of cell rearrangements and movements are all consistent with the tissue behaving as a disordered, glassy material undergoing a jamming transition as the MPZ progressively rigidifies into the PSM (Fig. 4a,b). The solid-like state of the PSM helps maintain tissue architecture and mechanically supports the extending, fluid-like end of the posterior body, as cells from the DM region are added to the MPZ and progressively elongate the body axis (Fig. 4b). Indeed, simulations of tissue morphogenesis based solely on first principles (Fig. 4c–e; Methods; Supplementary Note 1) show that unidirectional body axis elongation naturally occurs in the presence of the observed fluid-to-solid jamming transition (Fig. 4d; Supplementary Video 2). In absence of jamming transition, the tissue expands isotropically like a growing spherical blob and no unidirectional axis elongation occurs (Fig. 4e; Supplementary Video 3). The predicted tissue morphogenetic flows in the presence of the reported jamming transition display high posterior-directed velocities at the posterior end, no tissue flow in the A-PSM, and the existence of two counter-rotating vortices as the tissue transits from fluid-like to solid-like states (Fig. 4d, inset). Remarkably, all these predicted features in tissue flows have been observed experimentally¹⁵, indicating that the fluid-to-solid jamming transition is essential for proper unidirectional axis elongation. Phenotypes like curved tails and the reduced elongation speed in cdh2 mutants (Extended Data Fig. 8) can be explained by the reported loss of mechanical integrity in the PSM (Fig. 2i) during body axis elongation.

Figure 4. Physical mechanism of vertebrate body axis elongation.

a, The MPZ (fluid-like) and PSM (solid-like) tissue states are represented in the jamming phase diagram^2,4, which organizes jammed (solid-like) and unjammed (fluid-like) phases as the volume fraction of extracellular spaces, supracellular stresses and active fluctuations (effective temperature) change. b, The higher cell-cell contact length fluctuations (high effective temperature) in the less constrained environment (more extracellular spaces) of the MPZ (light blue) drive cell rearrangements and cell mixing, effectively ‘melting’ the tissue in this region. As the paraxial mesoderm matures, the smaller extracellular spaces and low cell-cell contact fluctuations (low effective temperature) in the PSM (violet) rigidify the tissue via a jamming transition. Cells entering the MPZ from the DM region (green arrows; lateral view) cause the expansion of the fluid-like MPZ tissue, with the solid-like PSM acting as a rigid support that biases tissue expansion towards the posterior direction, thereby elongating the body axis. While persistent mediolateral supracellular stresses restrict lateral tissue expansion, the main role of non-persistent cell-scale stresses is to ‘melt’ the MPZ tissue, enabling its expansion and posterior elongation upon addition of new cells from the DM. c, Sketch of the posterior body showing the input physical fields in the simulation. d–e, Time evolution of simulated tissue shapes (black outline) in the presence (d) and absence (e) of a jamming transition along the AP axis. The color code in the right half of each shape corresponds to the spatial profile of the tissue viscosity (diverging in solid-like tissue regions), whereas the left half shows the AP profile of cell ingression rate into the MPZ from DM tissues. Gray rectangles represent a rigid boundary. (d, inset) Simulated morphogenetic flows (velocity field: direction, arrows; magnitude, color coded) in the presence of a jamming transition leading to unidirectional body elongation.

More generally, the spatiotemporal control of fluid-like and solid-like tissue states, enabling or restricting morphogenetic flows, represents a novel mechanism of tissue morphogenesis. The previously observed oscillations in actomyosin contractility during apical constriction²⁸ in Drosophila epithelia may be necessary to overcome a yield stress and fluidize an otherwise jammed tissue²⁹. Beyond cellular jamming, transitions between fluid-like and solid-like states in tissues containing extracellular matrix between cells are likely to occur via the control of the extracellular matrix physical-chemical state. As suggested by D’Arcy Thompson a century ago²⁵, the shaping of living tissues shares fundamental physical principles with the sculpting of many inert materials, where fluid-to-solid transitions are necessary to mold them into functional shapes.

Methods

Zebrafish husbandry, fish lines, and experimental manipulations

Zebrafish (Danio rerio) were maintained as previously described³⁰. Animals were raised and experiments were performed following all ethical regulations and according to protocols approved by the Institutional Animal Care and Use Committee (IACUC) at the University of California, Santa Barbara. For ubiquitous labeling of cell membranes we used Tg(actb2:MA-Citrine) embryos^26,31 or embryos at 1-cell stage were injected with membrane-GFP mRNA. For experiments to perturb the amount of extracellular spaces we used cdh2^tm101/tm101 embryos (parachute (pac) mutants²⁶), which feature a truncated N-cadherin (CDH2) extracellular domain and have been shown to display cell-cell adhesion defects²⁶. For tracking of cell movements, 1-cell stage embryos were injected with H2B-RFP mRNA.

Generation and injection of ferrofluid droplets

The composition and preparation of ferrofluid droplets was identical as previously described²⁰. Briefly, we prepared biocompatible fluorocarbon-based ferrofluids by diluting DFF1 (Ferrotec) in Novec 7300 (3M) at varying concentrations to achieve the necessary magnetic stresses to generate the desired droplet deformations (applied strains). To prevent non-specific adhesion between the cells and the ferrofluid droplets, a fluorinated Krytox-PEG(600) surfactant (008-fluorosurfactant, RAN Biotechnologies³²) was diluted in the ferrofluid at a 2.5% (w/w) concentration. The ferrofluid used in each experiment was calibrated as previously described²⁰, so that the stresses applied by the ferrofluid droplet on the surrounding material in the presence of a uniform magnetic field are quantitatively known. Ferrofluid droplets were generated inside embryos, by direct injection of the ferrofluid in the tissue of interest, as previously described²⁰. Control of droplet size was achieved by controlling the injection pressure and time of the injection pulse. Droplets were injected in the MPZ tissue at the 4- and 6-somite stages for measurements in the PSM and MPZ, respectively. Droplets were imaged at least 2 hours after injection to allow enough time for the tissue to recover from the injection. The mechanical relaxation timescales in the MPZ and PSM are short (~1 min; Supplementary Figure 2b) and cell rearrangements are observed in timescales shorter than 10 min (Fig. 3e, inset). Therefore, our experiments, performed 2 hours after injection, allow enough time for the tissue to remodel. Indeed, no trace of the injection is observed in the tissue when imaged. Importantly, we have previously shown that injection and actuation of magnetic droplets located in the MPZ and PSM tissues do not affect normal developmental processes and, especially, body axis elongation²⁰.

Imaging

Embryos were mounted for imaging in 0.8% low-melting agarose and imaged at 25 °C using a laser scanning confocal (LSM 710, Carl Zeiss Inc.). Images were taken every at 2.5 – 5 s (0.3 – 0.5 s) temporal resolution using a 40x water immersion objective (LD C-Apochromat 1.1W, Carl Zeiss Inc.) or a 10x air objective (EC Epiplan-Neofluar 10x 0.25, Carl Zeiss Inc.). Imaging of ferrofluid droplets in the embryo was done as previously reported²⁰. Ferrofluid droplets were fluorescently labelled using a custom-synthesized fluorinated Rhodamine dye³³, which was dissolved in the fluorocarbon-based ferrofluid oil at a final concentration of 37 μM.

Measurement of supracellular (tissue-level) stresses

To quantify supracellular stresses we measured the droplet ellipsoidal deformation, as this deformation mode reveals mechanical stresses occurring at the length scale of the droplet diameter (and slightly larger scales), which we purposely made larger than the cell size (Fig. 1d; droplet diameter: 44 ± 6 μm; cell diameter: 11 ± 5 μm; mean ± SEM). We used ferrofluid droplets because their interfacial tension can be calibrated in vivo²⁰. No magnetic field was applied on the droplet before or during the measurement of supracellular stresses. Moreover, we prevented cell adhesion to the droplets to reveal the stresses associated solely with (supracellular) morphogenetic flows, mirroring previous studies in inert fluids³⁴. Two hours after injection, the droplet mid-plane was imaged using confocal microscopy (Zeiss LSM 710, Zeiss Inc.). To quantify the ellipsoidal deformation of the droplet (and neglect high order deformations), we fitted an ellipse to the measured droplet shape, as previously described²⁰. The value of anisotropic stresses for the ellipsoidal droplet deformation is given by ${\sigma }_T^A=2\gamma (H_b-H_a)$, where H_b and H_a are the mean curvatures of the droplet at the intersection of the two principal axis with the ellipsoid and γ is the droplet’s interfacial tension (Fig. 1d), as previously established for droplet with arbitrary deformations^21,35. The mean curvatures H_b and H_a are given by H_b = b/a² and H_a = 1/2a + a/(2b²), with b and a being the long and short semi-axis of the fitted ellipse (Fig. 1d). At the end of each experiment, i.e. after recording the shape of each droplet, we measured its interfacial tension γ in situ, within the developing embryo, as previously described²⁰.

To obtain the direction of droplet deformation, we measured the angle between the direction defined by the long axis of elliptical droplet deformation and the AP axis of the embryo using ImageJ.

While droplets cannot measure isotropic stresses because of droplet incompressibility²¹, the ellipsoidal droplet deformation provides a quantitative measure of the difference in stresses along the direction of droplet elongation and the perpendicular direction in the observation plane (the principal directions of the deformation). Ellipsoidal droplet deformations can, in general, be caused both by shear stresses or by stress differences along principal axes of droplet deformation (stress anisotropy).

Droplet shape segmentation and measurement of in-plane curvature

Confocal sections through the middle of a ferrofluid droplet were obtained by confocal microscopy, as described above. We then used a custom-made MATLAB code (adapted from a previously published code³⁵) to obtain the coordinates of the droplet contour (segmentation) and measure the in-plane curvature κ(s) along the droplet contour, with s being the arclength along the contour. We first applied a gaussian lowpass filter on the original raw image. The drop shape was identified from the filtered image using active contour segmentation to generate a mask. The edge was located by convolving the mask with the sobel operator. The locations of edge pixels were then converted to ordered polar coordinates, which were smoothed using a moving average filter with a span of 5 pixels. We resampled the coordinates at even spacing using shape-preserving piecewise cubic interpolation. The curvature κ(s) along the droplet contour was obtained by cubic fitting of edge coordinates over a small neighborhood of each point along the contour.

Measurement of stresses associated with deviations from the ellipsoidal droplet deformations

To measure the value of stresses associated with deformation modes of higher order than the ellipsoidal deformation mode (droplet deformations at length scales smaller than the droplet size), we used a similar procedure as that described in²¹ to obtain cellular stresses from 2D confocal sections. Maximal and minimal values of the curvature along the droplet contour were spaced on average by the measured cell size (Fig. 1h,j), confirming that these deformations are associated with spatial variations in stresses occurring at the cell scale. Briefly, we first segmented the 2D droplet shape and obtained the in-plane curvature κ(s) along the droplet contour, as described above. We then calculated the deviations δκ(s) ≡ κ(s) − κ_e(s) of the curvature along the contour from the curvature κ_e of the elliptical deformation mode. We fitted an ellipse to the contour coordinates using the Matlab function EllipseDirectFit (written by Nikolai Chernov based on previous algorithm) to determine the elliptical curvature κ_e, and then calculated directly δκ(s) along the droplet contour. We then detected the maxima and minima of δκ along the contour and defined the amplitude of curvature deviations from the elliptical mode as the difference between a consecutive maximum and minimum of curvature, δκ^MAX and δκ^MIN respectively, along the droplet contour, namely Δκ_C ≡ δκ^MAX − δκ^MIN. We also defined the maximum amplitude of curvature deviations from the elliptical deformation mode, $\mathrm{\Delta }{\kappa }_C^{\mathit{MAX}}\equiv \delta {\kappa }^{\mathit{MAX},A}-\delta {\kappa }^{\mathit{MIN},A}$, where δκ^MAX,A and δκ^MIN,A correspond to the absolute maximum and absolute minimum in δκ along the droplet contour. The average and maximal values of the stresses associated to cell-sized deviations from the ellipsoidal mode, ${\sigma }_C^{\mathit{avg}}$ and ${\sigma }_C^{\mathit{max}}$ respectively, are given by ${\sigma }_C^{\mathit{avg}}=2\gamma \langle \mathrm{\Delta }{\kappa }_C\rangle$ (average 〈·〉 was done over multiple consecutive maxima and minima for a single droplet and also over multiple droplets in the same region of the tissue in different embryos) and ${\sigma }_C^{\mathit{avg}}=2\gamma \langle \mathrm{\Delta }{\kappa }_C^{\mathit{MAX}}\rangle$ (average 〈·〉 was done over multiple droplets in the same region of the tissue in different embryos). As previously noted²¹, this calculation assumes no major structural anisotropies in the tissue.

To measure the length scale associated with shape deviations from the elliptical deformation mode, we obtained the locations of maxima and minima of δκ(s) along a droplet’s contour, and calculated the contour distance λ between consecutive maxima and minima (Fig. 1h).

Measurement of persistence in supra-cellular (tissue-level) stresses

To quantify the persistence timescale of tissue-level stresses, we imaged equatorial sections of magnetic droplets (no applied magnetic fields, as described above) at time intervals of one second for up to 30 minutes. We fitted ellipses to droplet sections at each timepoint and reported the droplet aspect ratio as a function of time. We observed no substantial change in the average droplet aspect ratio over the course of 30 minutes, indicating that tissue-level stress anisotropies persist in the tissue for longer than at least 30 minutes.

Measurement of persistence in cell-scale stresses

To obtain the persistence of cell-scale stresses, we performed time-lapses of ferrofluid droplets (no magnetic actuation) inserted in the MPZ tissue at 2.5 s time intervals, for 10 to 16 minutes. We segmented those droplets at each timepoint and obtained the in-plane curvature κ(s, t) along the contour (parameterized with the contour length s), as well as the curvature deviations from the elliptical droplet deformation, κ(s, t), as described above. For each time-lapse, we resampled κ(s, t) at equal angular (θ ) spacing, to obtain κ(θ, t). We then calculated the temporal autocorrelation C_δκ(τ) at each value of θ, namely

$$C_{\delta \kappa }(\tau )\equiv \frac{{\langle \left(\delta \kappa (\theta ,t+\tau )-{\langle \delta \kappa (\theta ,t+\tau )\rangle }_{\theta ,t}\right)\left(\delta \kappa (\theta ,t)-{\langle \delta \kappa (\theta ,t)\rangle }_{\theta ,t}\right)\rangle }_{\theta ,t}}{\sqrt{{\langle {\left(\delta \kappa (\theta ,t+\tau )-{\langle \delta \kappa (\theta ,t+\tau )\rangle }_{\theta ,t}\right)}^2\rangle }_{\theta ,t}}\sqrt{{\langle {\left(\delta \kappa (\theta ,t)-{\langle \delta \kappa (\theta ,t)\rangle }_{\theta ,t}\right)}^2\rangle }_{\theta ,t}}}$$

We reported the value of the timescale τ_1/2 for which C_δκ(τ) drops below 0.5 (or C_δκ(τ_1/2) = 0.5), which corresponds to its half-life and provides a measure of the timescale of correlation loss or, equivalently, the persistence timescale of cell-scale droplet deformations.

Measurement of average cell size

Cell size was calculated using the polygonal drawing tool of ImageJ to outline the cells of each region and calculate the area of each selection. The average cell diameter was obtained by the diameter of a circle with the same area as the measured from the polygonal cell shape. The average cell size in a given region of the tissue was obtained from the ensemble average of 100 cells (approximately 35 in each region, A-PSM, P-PSM and MPZ).

Measurement of cell shape and nuclear anisotropy

Maximum intensity projections of 3 consecutive planes of a confocal stack, spanning in total 6 μm in z, were subjected to thresholding and converted to binary images using ImageJ. Subsequently, the ImageJ plug-in ‘Fill Holes’ was applied and ellipses were fitted to the H2B-labeled nuclei. Nuclear anisotropy was given by the aspect ratio of the fitted ellipse. To quantify the orientation of nuclear elongation, we used ImageJ to measure the angle between the axis of nuclear elongation (given by the long axis of the fitted ellipse) and the AP axis. The direction of the AP axis was revealed by the notochord in the images. To obtain cell shape anisotropy, we first measured the length of cell-cell contacts oriented within 18 degrees of the AP and mediolateral (ML) axis. To do so, we used Tissue Analyzer (see methods section ‘Spatial and temporal autocorrelation of cell-cell contact length’) to obtain the cell-cell contact lengths versus their orientation in 2D confocal sections of different regions. Each image contained roughly 200 cells and 1000 cell-cell contacts. We analyzed 11 images for PSM and 8 images for MPZ.

Magnetic actuation of ferrofluid microdroplets

Actuation of ferrofluid droplets was done with the same equipment and methods as described in²⁰. Briefly, we deformed a ferrofluid droplet previously injected in the tissue using an applied, uniform and constant magnetic field (as previously described²⁰), thereby generating a controlled local strain in the tissue. We applied a uniform and constant magnetic field for 15 minutes, as this time is considerably longer than all measured stress relaxation timescales in the tissue²⁰ (Supplementary Figure 2b). Ferrofluid droplets deform into ellipsoids when a uniform, constant magnetic field is applied^20,36. We monitored the time evolution of the droplet deformation and measured the initial (b₀), maximal (b_M) and final (b_F ) droplet semi-axis in the direction of the applied magnetic field (Fig. 2a,b). The final droplet semi-axis (b_F ) was determined from the asymptotic deformation of the droplet after relaxation following the removal of the applied magnetic field. We defined the droplet strain as ε ≡ (b − R/R) ²⁰. With this definition, the initial strain ε₀, the maximum applied strain ε_M and the final strain ε_F are given by ε₀ = (b₀ − R)/R, ε_M = (b_M − R)/R and ε_F = (b_F − R)/R, respectively. We applied maximal mechanical strains in the 50–150% range, depending on the droplet’s interfacial tension and the magnitude of the applied magnetic field.

Measurement of local yield stress with ferrofluid microdroplets

To measure yield stress, we applied strong magnetic fields to generate ellipsoidal droplet deformations larger than at least one cell size, as in these conditions the tissue flows irreversibly. Upon removal of the magnetic field, the capillary stress of the droplet pulls the droplet back towards the undeformed, spherical droplet shape (Fig. 2c). The capillary stress, σ_c, is the mechanical normal stress that tries to restore the spherical droplet shape because of the presence of an interfacial tension and depends on how deformed the droplet is: the larger the droplet deformation, the larger the capillary stress, as its value at a given point of the droplet’s surface is proportional to the mean curvature H of the droplet at that point. Starting from the maximal droplet deformation induced by the applied magnetic field (maximal strain, ε_M), the capillary stresses driving droplet relaxation are large and become smaller as the droplet shape relaxes towards the sphere. In the absence of a yield stress in the tissue, the droplet would relax to the spherical shape. However, the presence of a yield stress halts the relaxation of the droplet at the aspect ratio for which the capillary stress is equal to the yield stress (Fig. 2c), preventing further droplet relaxation. At this point, the yield stress balances the droplet’s capillary stresses (Fig. 2c). Since the interfacial tension of the droplet is measured in situ, the final aspect ratio of the arrested droplet serves as a direct read out of the yield stress. Importantly, we applied the magnetic field in the perpendicular direction to the droplet pre-deformation, so that the final aspect ratio in the direction of the magnetic field could not be attributed to the supracellular tissue anisotropy in mechanical stress that deformed the droplet initially. Moreover, to allow accurate comparisons between the measured anisotropic stresses and yield stress measurements, we defined the anisotropic yield stress as the anisotropic stress that results from the residual droplet deformation that remains after droplet relaxation is halted by the yield stress (Fig. 2c). The anisotropic yield stress is given by σ_y = 2γ(H_b,r − H_a,r), where H_b,r and H_a,r are the mean curvatures of the residual droplet shape (deformation) at the intersection of the principal axis with the ellipsoid. Since the residual droplet shape is a prolate spheroid with long and short semi-axes b_r and a_r, respectively, H_b,r and H_a,r read $H_{b,r}=b_r/a_r^2$ and $H_a=1/2a_r+a_r/(2b_r^2)$. The interfacial tension of each droplet was measured directly in situ, within the developing embryo, as previously described²⁰. Using the measured value of the interfacial tension for each droplet and the mean curvatures of the residual droplet deformation, we obtained the value of the yield stress, σ_y.

The measured values of the yield stress did not depend on the extent of droplet deformation before starting the relaxation process (maximal droplet deformation or strain, ε_M; Fig. 2a,b), ruling out potential memory effects that could occur in hysteretic plastic materials (Extended Data Fig. 10).

Measurement of volume fraction of extracellular space

To obtain the volume fraction of the extracellular space we injected Dextran, Alexa Fluor^™ 488 (10000 MW) in the MPZ of 9-somite stage embryos. After 30–45 minutes embryos were mounted and imaged. 3D reconstructions of different regions of the paraxial mesoderm were analyzed in Imaris (Bitplane), using the surface reconstruction algorithm. The volumes encapsulated by the Alexa Fluor^™ 488⁺ segmented surfaces were then divided by the total volume analyzed. Injection of Dextran, Alexa Fluor^™ 488 in the PSM of 9-somite stage embryos led to consistent results. The extracellular spaces are also visible by fluorescently labeling cell membranes (Extended Data Fig. 4), but the quantification of extracellular spaces was considerably more difficult and less accurate in this case.

Theoretical predictions of yield stress from volume fraction of extracellular space

To obtain the predicted values of yield stress (gradient in WT, Fig. 2f, and change between cdh2 mutants and WT, Fig. 2j) from the measured values of the volume fraction ϕ of extracellular space, we assumed the tissue to behave as a 3D disordered monodispersed foam¹ for which the yield stress is given by ${\sigma }_y={\sigma }_y^2{({\varphi }_C-\varphi )}^2$, where ϕ_C is the critical volume fraction (ϕ_C = 0.36 for 3D disordered monodispersed foams¹) and ${\sigma }_y^0$ is a stress scale that depends on the interfacial tension of bubbles and their size. We assumed the magnitude of cell-cell contact tensions (playing the role of the bubble interfacial tension in an aqueous foam) to be constant along the AP axis, as our measurements indicated that cell-scale stresses are largely uniform in the tissue. The cell size was also assumed to be constant because our measurements indicate no significant changes along the AP axis (Extended Data Figure 9). The comparison between the experimental values of the yield stress and the predicted ones has no adjustable parameters (Fig. 2f,j).

Measurement and analysis of 3D cellular movements

To track cellular movements in 3D, both in WT and cdh2 embryos, we first fluorescently labeled cellular nuclei by injecting H2BmRFP mRNA into one-cell stage embryos. At the 10-somite stage, embryos were manually dechorionated and mounted in 0.8% low melting point agarose in a 35mm glass-bottom dish (MatTek Corporation). Each region (A-PSM, P-PSM and MPZ) was imaged at 25°C using a 40x water immersion objective (LD C-Apochromat 1.1W, Carl Zeiss Inc.), with z-stacks acquired at one minute intervals for 30 minutes total. Z-stacks were cropped to include only cells corresponding to the region of interest. Loss of signal intensity over time was corrected with the EMBL Bleach Correction plugin for ImageJ using the Histogram Matching Method. The 3D nuclei positions r⃗_i (with i specifying the nuclei) at each time point were determined using the Imaris (Bitplane) automated spot detection. We then used the Imaris (Bitplane) tracking algorithm to obtain the nuclei trajectories r⃗_i(t). For subsequent analysis, the results were filtered by track duration to include only those tracks that were maintained over the full course of the time lapse. We then used the nuclei 3D trajectories r⃗_i(t) as a proxy for the trajectories of the cells. To eliminate the effect of translational and rotational motions of the whole tissue/embryo, we analyzed the relative cell distances r⃗_ij ≡ r⃗_i − r⃗_j. We evaluated the mean-square displacement of the relative distances, or mean-square relative displacements (MSRD), from their initial values, i.e. MSRD (t) ≡ 〈(r⃗_ij(t) − r⃗_ij(0))²〉, for (i,j) pairs which were nearest neighbors at t = 0. We evaluated the normalized MSRD(t), namely (MSRD(t) − MSRD(t = 0))/d² (with d being the average cell size), for every (i,j) nearest pair in each region (A-PSM, P-PSM, and MPZ) of a given embryo, and averaged the results over all the pairs in the same region for each embryo.

Spatial and temporal autocorrelation of cell-cell contact length

To determine the characteristic timescale of changes in cell-cell contact lengths, we acquired a single confocal section of embryos injected with memGFP mRNA for 30 minutes with time resolution of 5 seconds. We detected the location of cells’ vertices and cell-cell contact lengths in the images using Tissue Analyzer³⁷ (TA, formerly known as Packing Analyzer), a Fiji plugin capable of segmenting 2D tissue images and quantifying cell-cell contact lengths and position of vertices over time. For each embryo, we segmented a region of interest (ROI) in the PSM or Tailbud (MPZ) for which cell-cell contacts were trackable over a 400s time period. We then used the TA package to obtain the contour length of cell-cell contacts and the (x,y) positions of the vertices. Using the time-series of the contour length of cell-cell contacts and the (x,y) positions of the vertices, we calculated the temporal autocorrelation function, namely

$$C_{xx}(\tau )\equiv \frac{{\langle (\ell (t+\tau )-{\langle \ell (t+\tau )\rangle }_t)·(\ell (t)-{\langle \ell (t)\rangle }_t)\rangle }_t}{\sqrt{{\langle {(\ell (t+\tau )-{\langle \ell (t+\tau )\rangle }_t)}^2\rangle }_t}\sqrt{{\langle {(\ell (t)-{\langle \ell (t)\rangle }_t)}^2\rangle }_t}}$$

where ℓ is the cell-cell contact length. To reduce numerical errors, each average 〈·〉_t was evaluated with the data in a time interval (0,T − τ), with T being the duration of the experiment, and 〈·〉_t+τ was evaluated with the data in the time interval (τ, T). We analyzed each ROI and obtained the correlation function for each embryo separately. The obtained autocorrelation functions were nearly exponential in all cases (Fig. 3c). We therefore obtained the characteristic timescale of the decay of the correlation function by fitting an exponential function. The reported characteristic timescale was obtained from a weighted average of the timescales measured in different embryos, with the weights being the inverse of the variance. To obtain the spatial cross-correlation, a similar analysis was done, but correlating instead every two pair of cell-cell contact lengths in the region of the tissue analyzed. The distance between cell-cell contact pairs was given by the norm of the vector connecting the midpoints of the two cell-cell contacts (Fig. 3d).

Normalized frequency (distribution) of cell-cell contact length fluctuations and energy landscape of neighbor exchanges

We obtained the distribution of normalized cell-cell contact lengths, and the corresponding dimensionless energy landscape, which characterizes neighbor exchanges. For the ROIs described above (in ‘Spatial and temporal autocorrelation of cell-cell contact length’), we selected all cell-cell contacts that persist for at least 100s, and obtained their time-dependent normalized lengths ℓ/ℓ̄, where ℓ is the cell-cell contact length at a given time point and ℓ̄ is the average length of each individual cell-cell contact over time. We then combined all the values of ℓ/ℓ̄ for all times and cell-cell contacts into a single, normalized frequency distribution p(ℓ/ℓ̄) which peaks around 1 (Fig. 3e). Assuming that the cell-cell contact length fluctuations are probing an energy landscape that varies much more slowly (equilibrium approximation) before they undergo neighbor exchanges, we obtained the dimensionless energy landscape of neighbor exchanges by calculating -ln[p(ℓ/ℓ̄)] (Extended Data Figure 7). Since the statistics of cell-cell contact length fluctuations is small for values close to 0 (i.e., close to a neighbor exchange event), this method provides the dimensionless energy landscape close to the bottom of the energy landscape but does not allow to obtain the size of the energy barrier.

Measurement of neighbor exchange rates and orientation

To quantify the neighbor exchange rate in the tissue, we analyzed 2D confocal sections of WT and blebbistatin-treated embryos, both in the PSM and MPZ. We counted the number of cell-cell contacts that underwent a neighbor exchange in the plane of observation. We obtained the neighbor exchange rate per cell by normalizing the number of measured neighbor exchanges in the observed region with the average cell area and observation time (30 min). To obtain their orientation we measured the angle between the cell-cell contact and the direction of the AP axis before neighbor exchange. The direction of the AP axis was revealed by the notochord in the images.

Inhibition of myosin activity

Myosin activity was inhibited by adding in the embryo medium blebbistatin (Tocris) at the final concentration of 100 μM. Treatments were started at the 4-somite stage.

Measurement of cell density

To measure cell number density (number of cells per unit volume), we performed confocal 3D scans of the different regions (MPZ, P-PSM and A-PSM) in embryos with fluorescently labeled nuclei (same procedure as described above in ‘Measurement and analysis of 3D cellular movements’). We then used Imaris software to detect the location of the nuclei in the tissue (approximately 300 cells per imaged volume). After obtaining the 3D coordinates of each nuclei in a volume, we defined a box of smaller size than the full scanned volume and measured the number of nuclei in the box. Moving the small box inside the originally scanned volume, we obtained statistics for the density measurement. This procedure was repeated with varying box sizes to ensure that the measured value of the density did not depend on the box size.

Actin staining

10-somite stage embryos were dechorionated and fixed in 4% PFA for 1.5 hours at RT. Embryos were then washed 2–3 times with PBS. One drop of ActinRed^™ was added to the PBS solution (500 μL) containing the embryos. After 30 minutes the embryos were washed with new PBS for 3 times and prepared for imaging as described above.

Simulations

We simulated the physical expansion of a 2D dorsal-ventral projection of the PSM and MPZ tissues at supracellular length scales and developmental time scales using Finite Element Methods, accounting for the fluid-to-solid jamming transition (or its absence, depending on the simulation) and the entrance of cells to the MPZ from DM tissues (see Supplementary Note 1 for details). The fluid-to-solid jamming transition was simulated by a sharp increase in the tissue viscosity along the AP axis, with a diverging (very large) viscosity simulating the solid-like tissue state. The dynamics of the tissue is governed by fundamental physical laws, namely momentum conservation (which reduces here to local force balance because inertial terms are negligible for embryonic tissues) and mass balance. We solved the equations using COMSOL Multiphysics 5.3 software, starting from a semi-circular tissue shape and with a fixed rigid boundary at the most anterior end. The solutions provided the time evolution of the tissue shape and velocity field.

Statistics

In experiments involving zebrafish embryos, the sample size was chosen so that new data points would not change significantly the standard deviation. No samples were excluded from the analysis and the analysis of all the data was done by automated software to ensure full blinding and avoid biases in the analysis. No randomization of the data was used.

Code availability

A previously published version of the custom-made Matlab code to analyze droplet deformations³⁵ is available on GitHub at https://github.com/ElijahShelton/drop-recon. A modified version of that code to analyze 2D confocal sections of the droplet is available upon request.

Extended Data

Extended Data Figure 1.

Loss of AP gradients of supracellular stresses and cell and nuclear shape anisotropy in N-cadherin mutants. a, ActinRed^™ staining of F-actin in the PSM of control (cdh2^{+/+, +/−}) and mutant (cdh2^−/−) embryos at the 10-somite stage. Cell shapes are visibly elongated along the mediolateral (ML) direction in control (cdh2^{+/+, +/−}) embryos. Cell shape anisotropy is largely lost in cdh2^−/− embryos. b, DAPI staining showing higher nuclear ML elongation in the PSM of control embryos compared to cdh2 mutants. c, Frequency of nuclear major axis orientations in the MPZ and PSM (A-PSM and P-PSM). In control embryos (cdh2^{+/+, +/−}), nuclei in the PSM are elongated along the mediolateral direction, whereas nuclei are oriented randomly in the MPZ. The observed nuclear anisotropy along the ML direction in the PSM of control embryos is decreased in cdh2 mutants (cdh2^−/−). For cdh2^{+/+, +/−}: n=695 (A-PSM), n=752 (P-PSM) and n=732 (MPZ), obtained in 6 embryos per region. For cdh2^−/−: n=833 in 5 embryos (A-PSM), n=538 in 6 embryos (P-PSM), n=336 in 4 embryos (MPZ). d, A posterior-to-anterior increase in the extent of nuclear elongation (quantified by the nuclear aspect ratio; see inset and Methods) is observed in control embryos (cdh2^{+/+, +/−}). No AP gradient in the extent of nuclear elongation (aspect ratio) is observed in cdh2 mutants (cdh2^−/−). For cdh2^{+/+, +/−}: n=695 (A-PSM), n=752 (P-PSM) and n=732 (MPZ), obtained in 6 embryos per region. For cdh2^−/−: n=833 in 5 embryos (A-PSM), n=538 in 6 embryos (P-PSM), n=336 in 4 embryos (MPZ). Mean ± SEM. e, Relative change of cell-cell contact length along the anterior-posterior (AP) axis and the medial-lateral (ML) axis (n=6427 and 4319 cell-cell contacts for PSM and MPZ from 5 embryos, respectively). Cell junctions are longer along the ML axis compared to the AP axis, both in the PSM and MPZ. Mean ± SEM. f, Supracellular stresses are uniform along the AP axis in cdh2 mutant embryos (n=5 for A-PSM, n=5 for P-PSM, and n=12 for MPZ). Mean ± SEM; Mann-Whitney test. The observed posterior-to-anterior increase in both supracellular stresses and nuclear elongation in control embryos (Fig. 1e and panel d), and the loss of both such gradients in cdh2 mutants (panels d and e), indicate the existence of a N-cadherin-dependent, posterior-to-anterior increase in supracellular stresses, consistent with a posterior-to-anterior increase in mediolateral constriction. Importantly, if the observed thinning of the body axis was caused by pulling forces from the MPZ on the PSM, as previously proposed¹⁷, both cells and nuclei would be elongated along the AP axis.

Extended Data Figure 2.

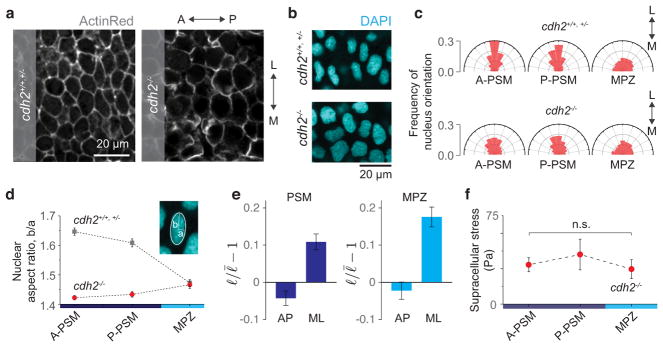
Curvature changes along the droplet contour correlate with the locations of cell-cell contacts surrounding the droplet. Confocal section of a ferrofluid droplet (red) in the MPZ of a Tg(actb2:MA-Citrine) embryo. The measured curvature values along the detected droplet contour are shown (color coded as in Fig. 1h) overlaid with the confocal image (left) and without it (right). White arrows point to locations of cell-cell contacts of cells surrounding the droplet, which correlate with maxima and minima of droplet curvature, consistent with the distance between maxima and minima being approximately the cell size (Fig. 1j).

Extended Data Figure 3.

Increase of extracellular spaces and cell rounding in cdh2 mutants. 2D confocal sections (inverted) of WT and cdh2^−/− Tg(actb2:MA-Citrine) embryos showing an increase in extracellular space (cyan), as well as more cell rounding, in the PSM tissue of the mutant embryos.

Extended Data Figure 4.

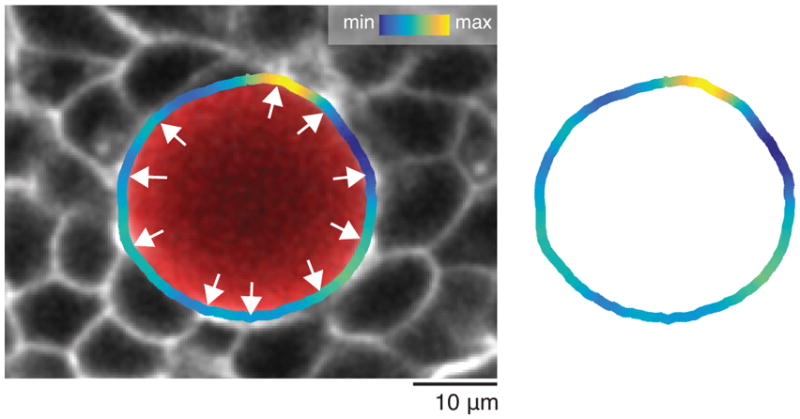
Example of neighbor exchanges induced in the tissue upon droplet actuation with a magnetic field. Confocal section showing the spatial arrangements of cells in the neighborhood of a magnetically-responsive droplet both in the absence of magnetic field (OFF) and after applying a magnetic field (ON) for 15 minutes (left). Several cell rearrangements are observed to be induced by droplet actuation (right). Some of the cells undergoing neighbor exchanges are colored and numbered to highlight the rearrangements. Tg(actb2:MA-Citrine) embryos were used to visualize cell membranes.

Extended Data Figure 5.

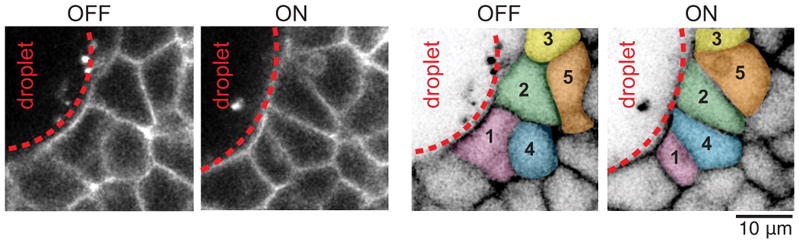
Distribution of cell-cell contact length fluctuations in cdh2 mutants. Normalized frequency (distribution) of cell-cell contact length fluctuations in the PSM and MPZ of cdh2 mutants (red bars) compared to the control (blue and light blue lines). For PSM and MPZ, n=13212 and 13634 cell-cell contacts obtained from 5 and 4 embryos, respectively.

Extended Data Figure 6.

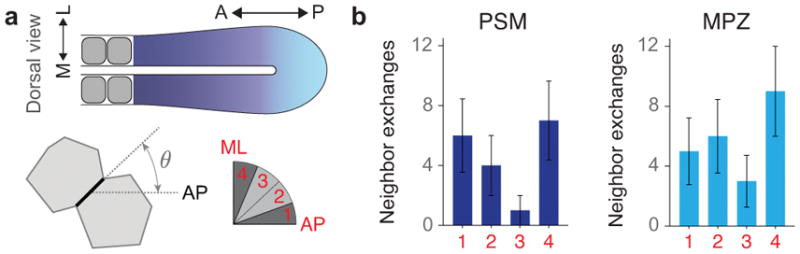
Orientation of neighbor exchanges in the MPZ and PSM. a, Sketch of a dorsal view of the elongating body axis, with the AP and ML directions defined (top). Sketch showing the orientation of a cell-cell contact (black thick line) before undergoing a neighbor exchange (bottom left). The angle θ corresponds to the angle between the cell-cell contact before undergoing the neighbor exchange and the AP axis (bottom). Four equal bins are defined (bin 1: 0 < θ < 22.5°; bin 2: 22.5° < θ < 45°; bin 3: 45° < θ < 67.5°; bin 4: 67.5° < θ < 90°) between the AP and ML orthogonal directions (bottom right). b, Frequency of neighbor exchanges along different angular regions (n=18 in 4 embryos for PSM and n=23 in 3 embryos for MPZ, with n being the number neighbor exchanges analyzed). Mean ± SD. Neighbor exchanges are largely randomly oriented in the MPZ. In the PSM, neighbor exchanges occur predominantly along either the mediolateral (ML) direction or along the AP axis, with neighbor exchanges occurring slightly less frequently for angles in between these orthogonal orientations. The more frequent occurrence of neighbor exchanges along the AP and ML axes in the PSM is consistent with the measured directions and extent of ellipsoidal droplet deformation (Fig. 1f), as the persistent and larger supracellular stresses in the PSM may bias neighbor exchanges in these directions. Since neighbor exchanges occur equally frequently along the ML and AP directions in the PSM, and are uniformly oriented in the MPZ, our results indicate no systematic alignment of neighbor exchanges along a single spatial direction that could potentially contribute to the elongation of the body axis.

Extended Data Figure 7.

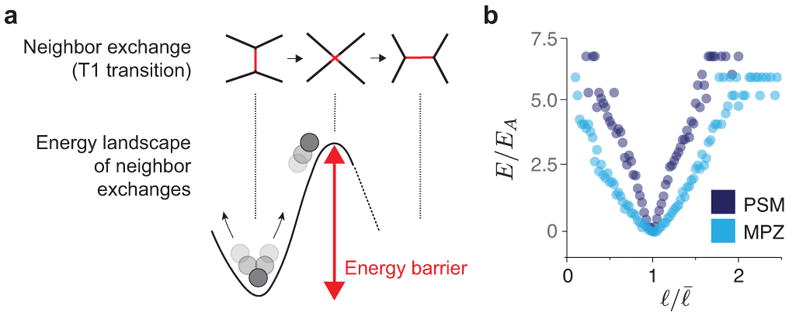
Energy landscape of neighbor exchanges. a, Schematic of key cellular configurations throughout a neighbor exchange and associated energy landscape. Changing neighbors requires overcoming an energy barrier. Large enough, active cell-cell contact length fluctuations enable neighbor exchanges. b, Measured energy landscape, E, for PSM and MPZ regions, normalized energy scale E_A associated with cell-cell contact activity or effective temperature energy scale, namely E_A = k_BT_Eff, where k_B is the Boltzmann constant and T_Eff is the effective temperature. n = 6969, 7896 cell-cell contacts obtained from 3, 4 embryos for PSM, MPZ, respectively.

Extended Data Figure 8.

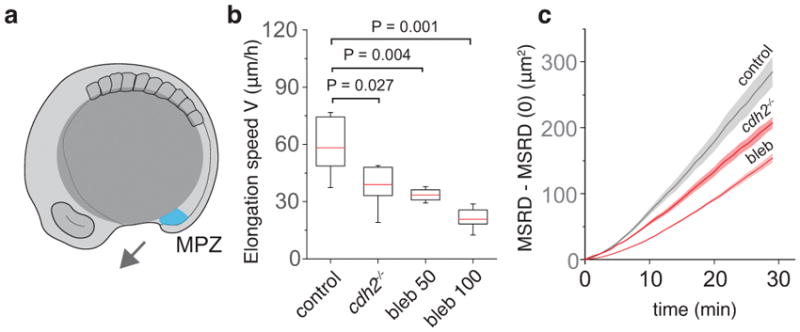
Dependence of posterior axis elongation speed and relative cellular movements in the MPZ on N-cadherin and non-muscle myosin-II activity. a, Sketch of a 10-somite stage embryo highlighting the mesodermal progenitor zone (MPZ, cyan) and the direction of posterior elongation (arrow). b, Comparison of posterior body elongation speeds between WT (n=6), cdh2 mutants (n=7), and blebbistatin-treated embryos (n=6 for 50 μM and n=7 for 100 μM). Box plots representing median (red line) and second and third quartiles. Error bars indicate 95% CI. Mann-Whitney test. c, Mean square relative displacement (MRSD; Methods) of cells in the MPZ region of WT (n = 2523 analyzed cell pairs from 6 embryos), cdh2^−/− (n = 1154 analyzed cell pairs from 4 embryos) and blebbistatin-treated embryos (n = 2026 analyzed cell pairs from 4 embryos).

Extended Data Figure 9.

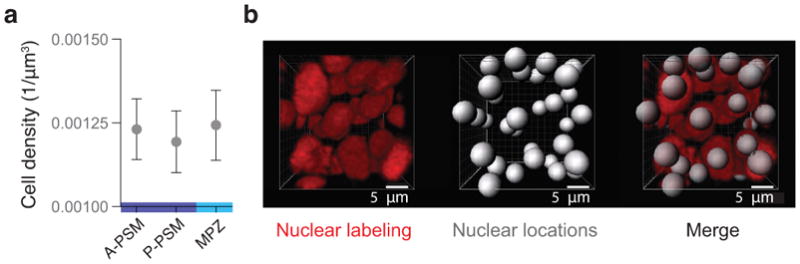
Cell density is uniform along the AP axis. a, Measured cell number density (cells per unit volume) in the MPZ, P-PSM and A-PSM. Mean ± SEM. Cell density does not vary significantly along the AP axis (within the 10% accuracy of our 3D measurements; Methods). b, 3D reconstructions of confocal stacks showing nuclei labeled with H2B::RFP, detected nuclei positions, and composition of both. Cell density was measured using 3D data of nuclear positions in the different regions (n = 7866, 7214, 11537 detected cells in 694, 694, 833 defined boxes in 5, 5, 6 embryos, respectively; Methods).

Extended Data Figure 10.

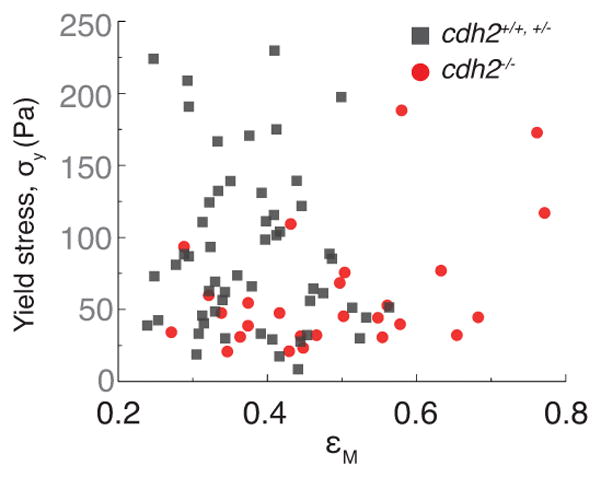
Yield stress values do not depend on the extent of droplet deformation before droplet relaxation. Measured values of the yield stress plotted against the maximal droplet deformation (maximal applied strain, ε_M; Fig. 2a,b) before starting droplet relaxation. The measured yield stress values do not correlate with the maximal strain applied, neither in control (cdh2^+/+,+/−, gray dots, n=53 embryos) or mutant embryos (cdh2^−/−, red dots, n=27 embryos). Correlation coefficient, r: r = ⁻0.34 (cdh2^+/+,+/−), r = ⁻0.04 (cdh2^−/−).