Permeability Mapping of Gelatin Methacryloyl Hydrogels

Abstract

We report the development of an efficient, customized spherical indentation-based testing method to systematically estimate the hydraulic permeability of gelatin methacryloyl (GelMA) hydrogels fabricated in a wide range of mass concentrations and photocrosslinking conditions. Numerical simulations and Biot’s theory of poroelasticity were implemented to calibrate our experimental data. We correlated elastic moduli and permeability coefficients with different GelMA concentrations and crosslinking densities. It was revealed that the permeability values of GelMA followed a negative power-law function of the crosslinking time. Our model could also predict drug release rates from the GelMA hydrogels and diffusion efficiency of nutrients into the three-dimensional GelMA hydrogels. The results potentially provide a design map for choosing desired GelMA-based hydrogels for use in drug delivery, tissue engineering, and regenerative medicine, which may be further expanded to predict the permeability behaviors of various other hydrogel types.

Introduction

Naturally derived hydrogels are among the most popular choices as scaffolds for tissue regeneration due to their hydrophilic nature as well as biophysicochemical properties that resemble the native extracellular matrix (ECM) [1]. A biocompatible hydrogel is basically a fluid-saturated solid network of selected materials that ideally provides proper cell-binding sites [2]. Fluid movements within the hydrogel regulate delivery of nutrients to encapsulated cells while they proliferate and migrate within the interconnected space (see Fig. 1). The design of a porous microstructure is indeed the key criterion for many scaffold fabrication techniques, such as particulate leaching [3], gas-foaming [4], emulsion-templating [5], and freeze-drying [6]. These techniques have been employed to regulate ECM microstructure in terms of the void volume, geometry, homogeneity, and interconnectivity. These microstructural characteristics can be represented by hydraulic permeability, i.e., the hydrogel resistance to diffusion or movement of fluid content and immersed particles (Fig. 1) [7].

Figure 1.

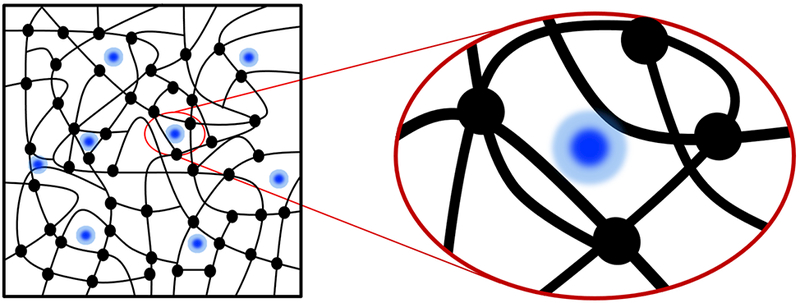
Schematic representing a hydrogel embedded with particles (black circles indicate crosslinking points within the hydrogel network).

Among the hydrogels, those made from gelatin methacryloyl (GelMA) have attracted increasing interest in recent years as artificial ECM materials [8]. This inexpensive polymer consists of gelatin, denatured collagen, functionalized with methacryloyl groups that can be crosslinked by photoinitiated chemical reactions [9]. Due to the presence of the integrin-binding motif, Arg-Gly-Asp (RGD), GelMA hydrogel exhibits intrinsic cell-binding characteristics [8]. In addition, photocrosslinking takes place only in the presence of a photoinitiator upon light illumination, resulting in hydrogels that are formed on demand, facilitating the fabrication of desired structures [9]. Polymer mass concentration (or volume fraction), the degree of functionalization (methacryloyl substitution), photoinitiator concentration, ultraviolet (UV) light intensity, and exposure time can all be controlled to generate a range of stiffness and crosslinking density for GelMA-based hydrogels [10]. The role of physical gelation is less dominant than chemical crosslinking in GelMA hydrogel compared to unmodified gelatin, which can practically enhance the reproducibility of GelMA preparations for biomedical applications [11].

Different properties, such as physical interaction, chemical modification, and hydrophobic interactions are exploited in different hydrogel systems to affect the permeability, and hence the drug release [12–14]. In this study, we have focused only on the physical diffusion of molecules as simplification. The porous microstructure of GelMA hydrogel affects the macroscale and microscopic diffusion of biological molecules through the hydrogel, such as the diffusion of anti-cancer drugs [15]. Using this concept, the GelMA hydrogel was used as a three-dimensional (3D) model to mimic the natural, local microenvironment of a growing tumor to investigate the interactions between cancer cells and the surrounding ECM [11]. In such a case, the interconnected pores within the hydrogel provide the passage of various agents (Fig. 1). Growth factors and biological agents with low molecular weights (e.g., 1 to 200 kDa) are commonly used to formulate the release response of hydrogels [16]; for example, it was shown that the particle size can affect the release rate from gelatin hydrogels [11].

Mechanical properties of hydrogels can be measured by compression tests [11]. Unconfined compression tests show the quasi-static elastic properties of GelMA hydrogel and its compression strength [10], while shear rheological measurements yield dynamic viscoelastic properties of GelMA hydrogel [17]. These methods require specific shapes of the sample and provide bulk properties of the sample. In a related study, atomic force microscopy (AFM)-based indentation test was used to measure the elasticity of GelMA hydrogel constructs under static conditions [18]. This method allows the quantification of elastic modulus at localized regions although it requires a smooth surface and can be used to estimate other physical characteristics such as hydraulic permeability [19]. The permeability parameter can be employed to predict the release response of such hydrogels [20].

While implementing AFM-based indentation tests requires extensive sample preparation and are undesirable for cell-laden hydrogel applications, here we developed an experimental protocol to perform spherical indentation-based relaxation test for the measurement of hydraulic permeability of GelMA hydrogel, across different weight concentrations and UV crosslinking times [19, 21]. The poroelastic theory of Biot [22], when used together with numerical simulation, was employed to analyze the relaxation data and to estimate the permeability of GelMA hydrogel. Phenomenological functions were used to formulate how hydrogel permeability varied versus UV crosslinking time. Our results potentially provide a design map for choosing desired GelMA-based hydrogels for a wide range of applications in tissue engineering and drug delivery. The developed protocol for measuring the permeability may also be extended to other types of fluid-saturated hydrogels for real-time monitoring of their dynamic mechanical response and property selection for specific applications. This work has promising outlooks for various tissue engineering applications, such as designing drug-delivery carriers.

Methods & Materials

Sample preparation

GelMA precursor was synthesized following our well-established protocol [9]. Powdered gelatin from cold water fish skin was obtained from Sigma-Aldrich (St. Louis, MO). The low melting temperature of fish skin-derived gelatin hydrogels (< 22°C) excluded the role of physical gelation in the current study, which was conducted at room temperature. Gelatin was added to phosphate-buffered saline (PBS; Fisher Scientific, Hampton, NH) at a concentration of 10% w/v and heated at 40 °C while stirring until gelatin was dissolved. Methacrylic anhydride (94% grade; Sigma-Aldrich) was gradually added to the stirring mixture at three different ratios: 3%, 5%, and 8% v/v, representing low, medium, and high methacryloyl (MA) degrees, respectively [23]. The reaction was allowed to proceed for 3 h at 40 °C. It was then stopped by adding PBS at three times its original volume and dialyzed with dialysis tubes (12–14 kDa cutoff; Fisher Scientific) against deionized water. Following 1 week of dialysis, the solution was then filtered and frozen before lyophilizing at −50 °C and 90 mbar. Freeze-dried GelMA in the form of a white porous foam was mixed into PBS containing 0.5% (w/v) 2-hydroxy-1-(4-(hydroxyethoxy)-phenyl)-2-methyl-1-propanone (Irgacure 2959, Sigma-Aldrich) as the photoinitiator. A volume of 12 ml was poured into a petri-dish (60-mm diameter and 15-mm height; Fisher Scientific) and exposed to UV light (Omnicure S1000, Lumen Dynamics, Mississauga, ON) at a power of 3.95 W/cm² and a source-sample distance of 8 cm for the selected time periods. The cylindrical hydrogel construct was then mounted on a mechanical tester as shown in Fig. 2a.

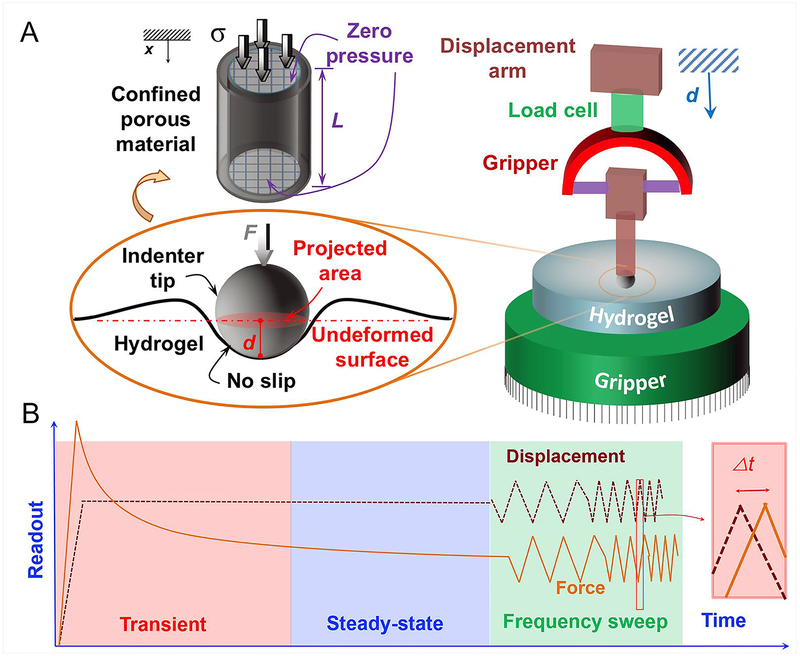
Figure 2.

A) Schematic of the mechanical test design using an axial tester and stainless-steel tip (cartoon on the right; the indentation point was selected far from the edges), and the geometry of hydrogel around the indentation point, i.e., spherical head (cartoon on the left). In 1D consolidation test, the parameter “L” denotes the sample thickness under axial compression, “d” denotes the movement of the spherical head in the vertical direction, “F” demonstrates the contact force on the tip, and “σ” represent the normal stress. B) The viscoelastic force and displacement histories from two loading regimes: i) relaxation (including transient and steady-state responses) and ii) zig-zag displacements, where Δt denotes time difference between the applied displacement and the sensed force vectors.

Mechanical testing

The mechanical test design is shown in Fig. 2. We designed and fabricated a spherical head of 6 mm in diameter made by stainless-steel ball assembled to a plastic gripper and attached it to the tensile displacement arm in a mechanical tester (Instron, Norwood, MA), equipped with a 10-N load cell. We defined a customized program to perform our indentation tests at three subsequent loading regimes: indentation (or ramp), relaxation, and oscillation tests. The input displacement included a straight ramp at a rate of 5 mm/s, a relaxation region where the tip contacted the surface for 300 s (which was longer than the relaxation time of the samples observed in the preliminary experiments), the frequency-dependent zig-zag region, and the unloading curve. To have genuine data [19], four different points at randomly selected locations and far from the sample edges were subjected to indentation tests to achieve the typical loading profile shown in Fig. 2b. This way, the effects of boundary conditions were eliminated in the test results. An area of approximately 3 mm × 3 mm was indented by our customized stainless-steel tip, and the force–time histories, similar to those shown in Fig. 2b, were saved for the postprocessing described below.

Theoretical modeling

Similar to spring-mass models [24], one-dimensional (1D) consolidation problem can be used to simplify poroelastic systems (see Fig. 2a). The consolidation problem consists of a cube of fluid-filled hydrogel, having a defined length of L, under confined compression (i.e., no lateral displacement) and vanishing fluid pressure at both boundaries (i.e., x=0, L). The unloaded hydrogel (i.e., t = 0) is assumed to be homogenous and after compression, the displacement vector of this 1D problem denotes u = u₁(x,t) and the associated strain (ε_ij) and stress (σ_ij) tensors are given by:

$${\epsilon }_{ij}=\left(\partial u_i/\partial x_j+\partial u_j/\partial x_i\right)/2$$ (1a)

$${\sigma }_{ij}=2G[{\epsilon }_{ij}+{\epsilon }_{kk}{\delta }_{ij}v/(1-2v)]$$ (1b)

, where (u₂ = u₃ = 0), G is the shear modulus and v is the Poisson’s ratio. According to Darcy’s law [22]:

$$\dot{\mathit{u}}=-\kappa \mathit{\nabla }p$$ (2)

, where k is the hydraulic permeability of the material model, p is hydrostatic fluid pressure and over-dot indicates partial differentiation with respect to time. A combination of the continuity and constitutive relations with the equation of equilibrium (for the saturating fluid) leads to the diffusion equation:

$$\raisebox{1ex}{$\partial \epsilon $}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.=D{\mathit{\nabla }}^{\text{2}}\epsilon$$ (3)

The symbol ε indicates the axial strain and the constant D denotes diffusivity constant of the hydrogel. For 1D consolidation problem, it reads [19]:

$$D={[\frac{d\sigma }{d\epsilon }\kappa (1-\epsilon )]}_{eq}={[E\kappa (1-\epsilon )]}_{eq}$$ (4)

, where:

$$(1-\epsilon )(1-\varphi )=1-{\varphi }_0$$ (5)

, in which E denotes the elastic modulus, and ϕ represents the fluid volume fraction and ϕ₀ is the initial fraction (i.e., mass concentration of the GelMA hydrogel subtracted by 1.0). The governing equation of a poroelastic construct under relaxation will not have an exact solution unless we simplify the consolidation problem (see Fig. 2a). A few attempts have been tried to formulate such problems using numerical simulations, for example generating master curves and mathematical regression functions [25]. We used the approach introduced earlier [19], which relies on a direct calibration by a numerical solution. The solution of Eq. (3) for 1D diffusion equation gives:

$$\epsilon (x,t)={\epsilon }_{\infty }+{\displaystyle {\sum }_{i=1}^{\infty }{C}_i}\text{cos}\left(i\frac{\pi x}{L}\right)\exp \left(-\frac{t}{{\tau }_i}\right)$$ (6)

, where ε_∞ represents the equilibrium strain, C_i denotes unknown constants, and τ_i indicates the time constant, which is defined by the following relation [19]:

$${\tau }_i=\frac{L^2}{i^2{\pi }^{2}D}$$ (7)

In general, C_i is negligible for i > 1 compared to C₁ The measured force in the experiment, F, is proportional to the stress at the region below the tip (x = 0; Fig. 2):

$$F(t)=F_{eq}+{\displaystyle {\sum }_{i=1}^{\infty }{F}_i}\exp \left(-\frac{t}{{\tau }_i}\right)$$ (8)

Regression of Eq. (8) with the force function gives the time constant and consequently the diffusivity. The characteristic length, L, was obtained by numerical simulation of the geometry, as described in the next section. We found this parameter by fitting our model (the force history in Eq. (8)) to numerical simulations data through the inverse problem approach, and then used the length parameter to find permeability values, while the force-indentation history was already used to estimate the indentation elastic modulus in Eq. (4). It was obtained from the application of Hertz contact theory to the equilibrium response (Eq. (8)) [26]:

$$F_{eq}=\frac{4}{3}Ed\sqrt{Rd}$$ (9)

, in which d is the indentation depth (our test input) and R is the radius of indenter tip (~3 mm).

Mathematical models of mass transport can provide reliable predictions of drug release rates as a function of drug system composition or its physical properties. To this aim, we assumed the hydrogel as a point source in the bath solution with M solute particles at x=0 and t=0. The solute particles can be any biological components with a density similar to or higher than the saturating fluid and a size smaller than the average distance between the crosslinking nodes (i.e., interchain distance) within the hydrogel network. It can be shown that the solution for the diffusion equation in Eq. (3) with a singular point source yields:

$$S(x,t)=\frac{M}{\varphi .A}\frac{\exp (-x^2/4Dt)}{\sqrt{4\pi Dt}}$$ (10)

, which allows us to simulate diffusion in unbounded (infinite) media by adding together the contributions from several point sources distributed along the x-axis at t = 0. Then we can use the diffusivity equation similar to Eq. (3), based on solute concentration, to best fit any release data.

The above formulation describes the physical diffusion of drug particles or molecules within the network of the fluid-saturated hydrogel system. It is pertinent to mention here that our model ignores the special conditions where physical interactions or chemical affinity between the drug and the hydrogel is used to dictate drug release kinetics. These approaches are used for sustained release where the transport of drug is mediated by different factors, such as electrostatic interactions, or hydrophobic association [14]. Since our study primarily focuses on permeability of GelMA hydrogels without any further physical or chemical modification, as such any drug release kinetics is presumed to be driven purely by diffusion, which in turn is considered to be dependent on the porous microstructure of the hydrogel [23]. As a model biomolecule to study diffusion-driven release kinetics, we chose bovine serum albumin (BSA). It is one of the most widely used model biomolecules in drug-release characterizations for different drug delivery platforms, including various hydrogel-based systems [27–29]. In this study, we used BSA without any modifications to reflect on the pore-size dependent diffusion process. The BSA molecules are much smaller than the interchain distances in GelMA hydrogels; thus the effects of friction forces and surface tensions are further eliminated in our release profiles, as in the diffusivity constant in Eq. (4). Assuming a homogeneous distribution of BSA molecules throughout the hydrogel along with zero concentration of BSA at the gel-fluid interface at all times, one may derive the relevant equation for the solute concentration in the medium, S [30]. It is anticipated that BSA must dissolve from the GelMA hydrogel network into the void (or pore) volumes prior to transport via diffusive mechanisms. The solute concentration profile is:

$$S(x,t)=S_0\mathrm{erf}\left(\frac{x}{\sqrt{4Dt}}\right)$$ (11)

It is assumed that BSA is dissolved homogenously in the medium and the initial concentration in the hydrogel is S₀ (i.e., S (t = ∞) = S₀). The BSA molecules in the medium will be released and can be measured at a specific distance with respect to the source (assuming x). To properly use Eq. (10), the released mass (normalized to the total mass) is defined by the following equation:

$$\mathrm{Re}\text{lease}=1-\mathrm{erf}\left(\frac{x}{\sqrt{4Dt}}\right)$$ (12)

Release tests

To validate the release formula (Eq. (12)), and to assess the accuracy of our model in predicting GelMA hydrogel properties, we measured the rate of release of BSA from the microstructure of GelMA hydrogel blocks into a PBS bath. We fabricated disk-shape GelMA samples with a BSA concentration of 70 mg/mL. GelMA samples were then submerged in a bath of PBS (10:1 volume). To measure the release rates, small aliquots were read by a plate reader at a 280-nm wavelength in different time intervals until 48 h. Different concentrations (from low to high) of BSA in PBS were used to calibrate our readout and conclude BSA concentrations. The overall results were final BSA concentrations with respect to the initial concentration, i.e. the release of the molecules.

Numerical simulation

Numerical simulations were carried out using the ABAQUS™ software (Providence, RI) to simulate two-step indentation tests. In the first step, Static General solver was used to indent a rigid spherical probe of 3-mm radius into the hydrogel surface down to 1.5-mm penetration depth. In the next step, the Transient Soils Mechanics solver was used to simulate the relaxation response in the continuum hydrogel system till steady-state was achieved. Hard-contact interaction type was used in the normal direction and frictionless condition was utilized in the tangential direction to define the contact between the spherical probe and the hydrogel surface. Four-node axisymmetric quadrilateral elements (CAX4P) that are based on bilinear displacement and fluid pressure were selected from the standard element library in the software (ABAQUS™). Mesh was almost 100 times finer beneath the probe tip and close to the surface (see Fig. S1a) to facilitate the solution convergence. The applied boundary conditions and the used mesh system were illustrated in Fig. S1a. The used material properties are shown in Table 1. The elastic modulus as well as the hydraulic permeability of the hydrogel were varied in a range, according to Table 1, to elucidate the role of elastic modulus and permeability parameter on the dynamics of stress relaxation.

Table 1.

Material properties for the model used in numerical simulations.

Density [kg/m3]	Elastic Modulus [kPa]	Poisson’s ratio	Permeability [μm2/Pa·s]	Porosity
1200	0.1–20	0.45	10−3–103	85–95%

Biological study

The biological study was dedicated to measuring the distance through which nutrients could diffuse into the hydrogel when a constant flow of cell culture medium was perfused within the pre-fabricated channels [31]. Breast cancer cells (MCF-7, American Type Culture Collection, Manassas, VA)-laden GelMA hydrogels of a cylindrical-shape, crosslinked in predefined cylindrical molds and different concentrations (5%, 10%, 15% w/v; medium-MA), were placed into a polydimethylsiloxane (PDMS) mold (having a cylindrical hole). Cell culture medium (Dulbecco’s Modified Eagle Medium, Sigma-Aldrich) was perfused within the straight channels of 500-μm diameter at a continuous rate of 20 μL/min for 3 days by a syringe pump (Harvard Apparatus, Holliston, MA). The culture medium contained 25 μM blebbistatin (ab120425, Abcam, Cambridge, MA) to ensure that the cells would not proliferate in the first part of the biological study [32]. A cytotoxicity kit (Fisher Scientific) was used to assess the cell viability within the transverse cross sections of hydrogels (i.e., perpendicular to the channel axis). This way we measured the distance that cell death occurred due to the lack of nutrients and oxygen.

Scanning electron microscopy (SEM)

For SEM sample preparation, the hydrogel templates were serially transferred from deionized water to 20, 40, 60, 80, and 100% ethanol solutions with 30 min of incubation each to dehydrate. Then, the samples were placed into the chamber of a freeze-dryer at −50 °C for 3 h. The dehydrated specimens were sputter-coated with 80/20 mix of Pt/Pd (JFC-1600, JEOL), and the specimens were examined using an Ultra55 field-emission SEM (FESEM; Zeiss, Oberkochen, Germany) [16].

Results and Discussions

Permeability and viscoelasticity map of GelMA hydrogel

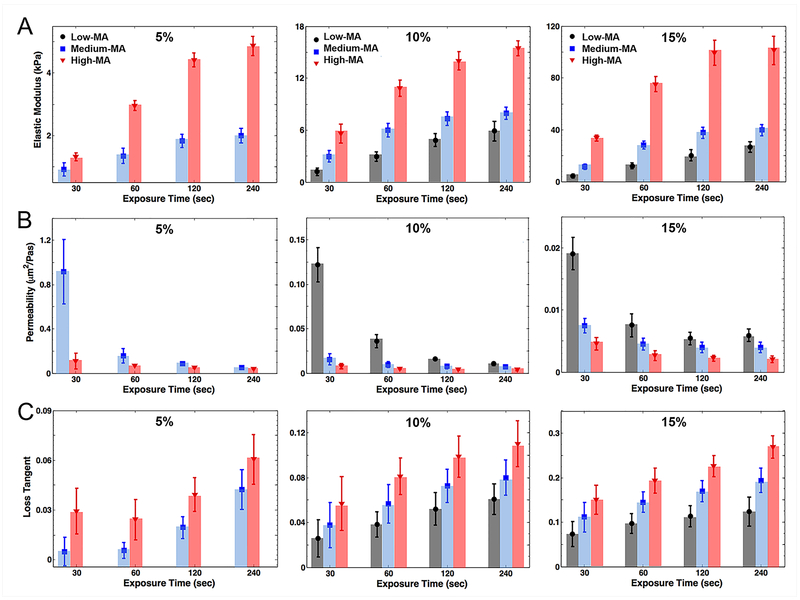
GelMA hydrogel with three different degrees of MA was synthesized by altering the volume of methacrylate anhydride during the reaction, at 3 mL, 5 mL, and 8 mL per 10 g gelatin, resulting in MA degrees of ~25%, ~50%, and ~90%, respectively [23], termed as low-, medium-, and high-MA samples throughout this article. The chemical characterization of GelMA samples with different degrees of MA were thoroughly analyzed using NMR spectroscopy and Fourier Transform Infrared (FTIR) spectroscopy recently by us [23]. A higher degree of MA for crosslinking the molecules and macromeres in GelMA hydrogel is anticipated to lead to a higher density of crosslinking sites that affects the elasticity of the resulting GelMA network. Indeed, from low to high degrees of MA, the elastic modulus increased from ~ 1 kPa to ~ 6 kPa for 10% GelMA hydrogel at 30 s of UV exposure (Fig. 3a), and longer UV exposures for 60 s and 120 s further enhanced the elasticity of 10% GelMA hydrogel up to ~11 kPa and ~14 kPa, respectively. The same trend was observed for 5% GelMA hydrogel (e.g., ~ 2 kPa to ~ 5 kPa for 120 s of crosslinking and medium-to-high degrees of MA) and 15% GelMA hydrogel (e.g., ~ 25 kPa to ~ 100 kPa for 120 s of crosslinking and low-to-high degrees of MA). Increasing the crosslinking time led to raised elastic modulus, although differences between those of 120 s and 240 s were not significant, regardless of hydrogel concentration or MA degree (Fig. 3a). The variation of bulk elastic modulus versus UV exposure time was nearly logarithmic with a sharp rise within the first 2 min.

Figure 3.

A) Indentation elastic modulus of GelMA hydrogel versus concentrations and UV exposure times. B) Hydraulic permeability of GelMA hydrogel versus concentra-tions and UV exposure times. C) Loss tangent of GelMA hydrogel versus concentrations and UV exposure times at a low frequency rate of indentation, 0.1 Hz.

GelMA hydrogels with concentrations of higher than 15% are rarely used for biomedical applications because of very slow degradation rate and reduced compatibility with cell encapsulation [33]. In this view, the results in Fig. 3a provided a design guidance for the fabrication of biomimetic constructs, ranging from nearly 0.5 kPa to 100 kPa, through variations of the hydrogel concentration, MA degree, and the UV crosslinking time. To further analyze the behavior of our data, the variations of elastic moduli in Fig. 3a were curve-fit by X.log(t)−Y, with X and Y being regression (or curve-fitting) coefficients. The correlation coefficients, which ranges between 0 and 1, were higher than 0.90 when fitting the mean values in Fig. 3a. The slope constant, X, increased significantly from the case of low-MA (e.g., X = 2.54 in 10%) to that of medium-MA (e.g., X = 3.13 in 10%) and high-MA (e.g., X = 4.89 in 10%). Surprisingly, the interception points for all time histories, where elastic moduli eliminate, ranged within 9.8 ± 1.7 s mean values in all concentrations and MA levels. This time point might indicate the minimum time required to reach the threshold of photo-crosslinking in the hydrogel network. This threshold that depends on the UV energy introduced into the hydrogel can be varied by changing UV input parameters such as power.

Simplifying the hydrogel microstructure as a polymer-like chain network, we could interpret the elasticity of GelMA hydrogel based on the entropy of building blocks, the polymer-like chains shown in Fig. 1 [24, 34]. Following the formulation derived by Heris et al. [35] for spherical indentation of an eight-chain material, the elastic modulus of GelMA hydrogels reads:

$$E=4.71n(1-v^2)(0.53N^{-4}+0.50N^{-3}+0.48N^{-2}+0.51N^{-1}+0.85)$$ (13)

, where n is the number of chain segments or crosslinking nodes per unit volume, ν is the Poisson’s ratio, and dimensionless N is the number of segments in each chain or interchain distance of polymer chains [35]. Hence, the indentation modulus has a direct correlation with network crosslinking density, while it follows a negative-power function of the average chain length, N. The increase in MA degree raises the density of network crosslinks (see Fig. 1), as represented by n, and shortens the length of the building blocks, as represented by N. These parameters define how the microstructure resists against deformation under external loading.

The role of fluid-solid interactions in mechanics of GelMA hydrogel was quantified through analyzing creep spectra. As plotted in Fig. S1, fluid pressure diffused down under the indentation tip. This diffusion-like behavior of GelMA hydrogel was summarized in the bulk hydraulic permeability of hydrogels, ranged from nearly 0.002 μm²/Pa·s to 1 μm²/Pa·s for different hydrogel concentrations and crosslinking conditions. The bulk hydraulic permeability in a range of 0.7–1.2 μm²/Pa·s relating to medium-MA and 5% concentration decreased over crosslinking time by one order of magnitude in 120 s. This may show that the vast majority of crosslinking chains inside the GelMA network were formed within this time frame. The differences in permeability values became less prominent for higher hydrogel concentrations, e.g., from 0.10–0.14 μm²/Pa·s to 0.01–0.02 μm²/Pa·s for low-MA and 10% concentration and from 0.016–0.022 μm²/Pa·s to 0.005–0.007 μm²/Pa·s for low-MA and 15% concentration (Fig. 3b). The permeability values followed a negative-power-law function, i.e., X.t^−Y in which X is the coefficient constant and Y denotes the power constant. The correlation coefficients between data and fit curves were higher than 0.85 for the mean values in Fig. 3b. The power constant became similar for both medium- and high-MA (e.g., Y ~ 0.22 in 10%) while it was increased in the case of low-MA (e.g., Y = 1.07 in 10%). This power-law behavior of permeability values with respect to the UV crosslinking time also indicate how fast the microstructure evolves during the photo-crosslinking process.

The polymer chain densities of GelMA hydrogels at low- and high-MA degrees are suggested by SEM images in Fig. S2a-b. The SEM images do not directly reveal the interchain distances due to the possible packing of polymer chains during the freeze-drying process, but the pore sizes observed in the images should be indicative of void fractions in the different groups. For comparison, we analyzed the pore size distributions of the samples using ImageJ. Pores in the SEM images were traced, and the enclosed areas and perimeters of voids were determined by the software. The diameters of the pores are summarized in Fig. S2c, where they ranged from a few micrometers to more than a hundred micrometers in all groups. The 5% hydrogel showed the largest pore diameter distribution ranging from ~30 to ~150 μm, for different MA degrees, while the smallest pore diameter distribution was observed in the 15% hydrogel in the range of ~5 to ~60 μm. The correlations between the pore size and the mesh size (directly indicative of interchain distance) were further established. We estimated the mesh sizes of medium- and high-MA GelMA hydrogels using the data presented by Yoon et al. [36] and by adapting the model derived by Zhou et al. [37], as shown in Fig. S4 (also see calculations in Supporting Information). A positive correlation was observed between the mesh size and the pore size despite the fact that the two phenomena belonged to different length scales. While this numerical approach indirectly calculates the mesh size values, there exist several experimental techniques as well to directly characterize the mesh size such as confocal microscopy (combined with measurements of the transport of molecular probes), electron microscopy, and small-angle X-ray scattering [38, 39]. These different methods may be supplemented as needed, to more precisely characterize the mesh size of a given hydrogel system. It should be noted that, neither the pore sizes measured from SEM images nor the calculated mesh sizes were needed in our formulas to derive the permeability.

The pore/mesh sizes negatively correlated with the trend of elastic modulus variations (Fig. 3), where the lower elasticity was associated with a lower level of polymerization and network crosslink density. In case of transport-associated design, Fig. 3b provides a wide range of hydraulic permeability from ~0.001 to ~1 μm²/Pa·s. This range spans across various tissue engineering applications from highly permeable tissues such as the articular cartilage [40, 41] and connective tissues [42] to tissues of low permeability such as the bone (not considering the mechanics) [43]. We also investigated the effects of hydrogel fabrication parameters on the dynamic mechanical properties of GelMA hydrogel (Fig. 3c). The ratio of loss (or viscous) modulus and storage (or elastic) modulus is represented by the loss tangent [44]. It ranges from zero (representing elastic solids or incompressible non-viscous fluids) to large numbers (representing highly-viscous materials). The loss tangent of GelMA hydrogels was significantly increased with the crosslinking time, which indicates how increasing the network crosslink density improved the viscoelasticity of the GelMA hydrogels. The values of all the 30-s crosslinked GelMA hydrogels were much lower than those of the 60-s samples, indicating that the crosslink network density and the subsequent viscous behavior of the GelMA network was lower in the beginning of UV exposure. This crosslinking rate was enhanced in higher hydrogel concentrations such as 15% GelMA hydrogel since practically the higher content of MA could raise the probability of crosslinking, which could enhance the viscoelasticity of GelMA hydrogel. The augmented viscoelasticity associated with higher crosslinking of GelMA solid network could come from the fact that oscillation tests were performed following the steady state (Fig. 2b), thus eliminating the effects of the fluid content [45]. In addition, the large standard deviations observed in Fig. 3c were associated with high noise-to-signal ratios of our measurements (or low sensitivity of our machine) as well as higher contributions of surface adhesion effects.

Drug release properties of GelMA hydrogel

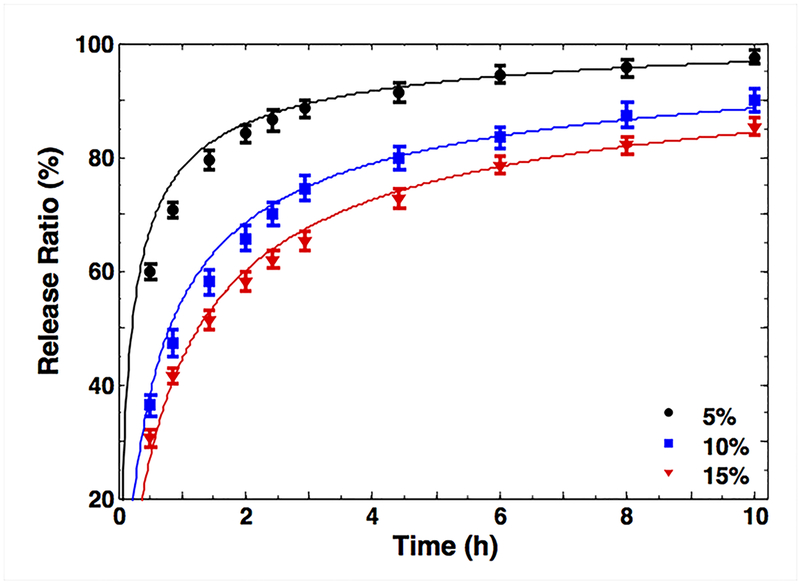
It is pertinent to mention here that this study focuses on diffusion-driven drug release. The kinetics described in this section will be affected when the drug release is dictated by drug-hydrogel physical, covalent, or hydrophobic interactions in the special cases where the hydrogels are used for controlled drug release. In our case, where the diffusion is determined by the hydrogel mesh size, we used methods to control the void fraction in the mesh to study the effect on permeability, and hence the diffusion. GelMA molecules with three different degrees of MA were synthesized as described earlier [18] and were used to prepare various hydrogel samples encapsulating BSA [46]. It was shown that 5%, 10%, and 15% hydrogels exhibited similar trends but different release rates (Fig. 4). Compared to the 10% and 15% hydrogels, the 5% samples had significantly enhanced release rates. We used regression of the simple model in Eq. (10) with that of the release profile in Fig. 4 to estimate the diffusivity constant D and attempted to find the correlation coefficient between the diffusivity constant (D) and hydraulic permeability (κ) in one condition (15%) for prediction of the other two cases. The good agreement between theoretical and experimental curves validated our assumption of poroelastic modeling for GelMA hydrogels. This coefficient and the permeability values in Fig. 3b were used to predict release profiles for 5% and 10% hydrogel groups (Fig. S3a) and the different degrees of MA (Fig. S3b). As the UV exposure time increased, the release rate of BSA from the hydrogels steadily decreased (i.e., longer release rates). The same trend was observed for the different degrees of MA in Fig. S3b. It is expected that the denser network caused by the higher crosslinking made the encapsulated BSA molecules more difficult to disperse out of the hydrogels. Even when the network is not sufficiently dense to influence BSA diffusion, fluid pressure may still affect the osmotic potential that drives the diffusion [47].

Figure 4.

Release ratio of BSA in medium-MA GelMA hydrogel versus concentration for a selected UV crosslinking time (240 s) for experiments (symbols) and simulations (solid lines).

This validation study would reveal the importance of our permeability map in depicting transport characteristics of GelMA hydrogels. GelMA hydrogels with tunable permeability are indeed suitable for controlled release. As mentioned earlier, it is to be noted that the release rate of solutes from hydrogels may also depend on the chemical properties of the macromolecules forming the hydrogels and solute molecules affecting their interactions. The present model was derived for a simplified case of physical diffusion through the hydrogel system. Thus, any considerations of molecular interactions should be implemented on top of the present model to predict the permeability behavior of other occasions where such a process is not solely dependent on diffusion. Examples could include affinity-based drug delivery systems (e.g., fibrin-based systems [48, 49] and heparin-functionalized systems [50]), degradation-controlled polymeric systems [51], and various environment-sensitive hydrogel systems [52].

Cell behavior: role of poroelasticity

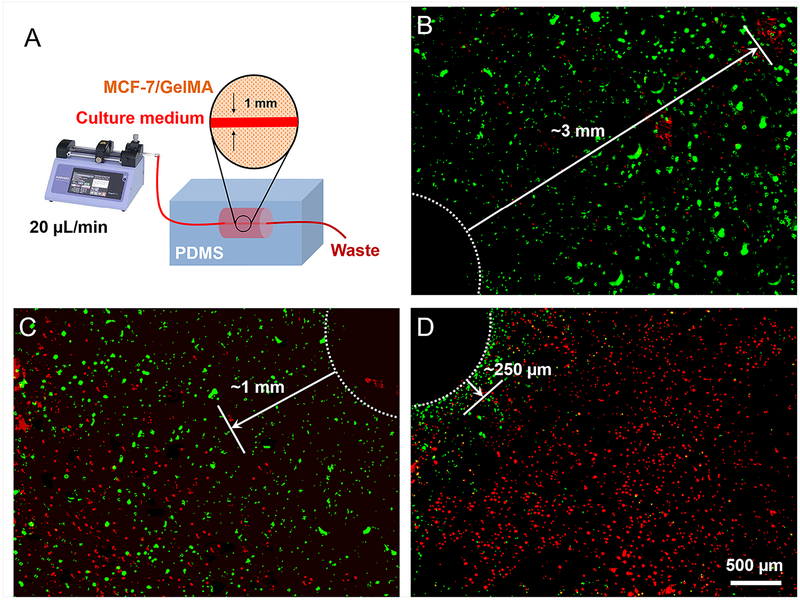
By varying the parameters of crosslinking, we created GelMA hydrogels with tunable stiffness (Fig. 3a), hydraulic permeability (Fig. 3b), and interchain distance (Fig. S2). In our biological assay, we exposed the three concentrations of cell-laden GelMA hydrogels to a constant flow of culture medium though a microchannel with a size of 500 μm in each hydrogel construct. The diffusion of nutrients through the microchannel to the surrounding hydrogel matrix depends on the geometry, size, and interconnectivity of the voids [53]. While the void volume fraction is dictated by the concentration of GelMA molecules in the hydrogel [54] (i.e., fluid volume is dictated by GelMA hydrogel mass concentration), interconnectivity is controlled by the density of crosslinking (Fig. S2). To this end, diffusion of nutrients from the medium into the hydrogel volume until a specific distance was noted after 3 days of culture (Fig. 5a). Several factors affect cell viability including the diffusivity through the GelMA hydrogel and the microstructural properties of the hydrogel construct. In order for delivery of nutrients and oxygen to occur, the solute must be able to diffuse into the hydrogel network and overcome capillary forces that resist the fluid flow [22]. The oxygen can reach further distance compared to nutrients due to a lower gas resistance [55]; however, the current model has not been made to capture the diffusion of gas molecules such as oxygen through the GelMA hydrogels. For a variety of biomedical applications, the results derived from this example can be used to rationalize the generation of microchannels with specific distances that ensure cell viability throughout the network [56].

Figure 5.

Bioreactor study: GelMA channels under continuous medium perfusion (20 μL/min) where the white dotted circles denote the channels and solid arrows denote the distances that the MCF-7 cells showed consistently good viability: A) Schematic of the setup. B-D) Cross-sectional viability mappings of the cells in (B) GelMA ~5% medium-MA, (C) GelMA 10% medium-MA, and (D) GelMA 15% medium-MA.

To quantify the differences in Fig. 5, the reader is referred to the time constant of the material system in Eq. (6). This time constant is an intrinsic property of material systems [19]. The characteristic length parameter, L, denotes the distance that liquid phase can diffuse into the material, and bulk diffusivity, D, is directly linked to the permeability constant. The discussions after Fig. 3a,b showed that the following phenomenological equations govern to define the relationship between the permeability and modulus values versus the exposure time, t:

$$\kappa (t)=\tilde{X}{t}^{-\tilde{Y}}andE(t)=\overline{X}Log(t)-\overline{Y}$$ (14)

, in which X̃, Ỹ, X̅, and Y̅ (i.e. the regression constants) are positive integers obtained from our measurements. Based on Eq. (7), the characteristic length has a direct relation to square root of the diffusion constant (for a fixed time constant). A manipulation Eq. (7) and Eq. (14) reads (new constants are used for brevity):

$$L\propto \sqrt{D}\propto \sqrt{t^{-\tilde{Y}}(\check{X}Log(t)-\check{Y})}$$ (15)

This relation depicts how the UV crosslinking time (or energy) controls the distance of nutrient (or any solute particles immersed in the hydrogel fluid) diffusion into the hydrogel construct. From Fig. 3b, one may conclude that the 5% GelMA hydrogel (medium-MA; 30 s) had a diffusivity 11 times higher than that of the 10% GelMA hydrogel (medium-MA; 30 s). Using Eq. (15), their diffusion length ratio should be approximately 3.3. Similarly, the 10% GelMA hydrogel had a diffusivity 12 times higher than that of the 15% GelMA hydrogel, leading to a diffusion length ratio of nearly 3.5. These ratios were in good agreement with the lengths from the channels to the locations where the cell viability started to consistently drop, when MCF-7 cells were cultured in the different GelMA hydrogels (Fig. 5). In other words, the proportions obtained from the proposed indentation test (Fig. 3b) were validated by the proportions of nutrient diffusion through cell studies in the hydrogel-based bioreactor system.

Adjusting GelMA hydrogel permeability might be used to regulate cell migration for applications in tissue engineering. As a complex and dynamic phenomenon, cell migration is regulated by many biological, chemical, and physical factors, such as microstructure of the ECM. In particular, interconnectivity and geometry of the voids have been shown to display a significant effect on cell migration [53]. The microstructural properties direct chemo-attractant and nutrient diffusion that affect cell proliferation and migration.

Conclusions

We presented a systematic study of the mechanical properties of GelMA hydrogel, a widespread scaffold material in tissue engineering. An efficient approach that involved spherical indentation and numerical simulation was used to estimate the bulk hydraulic permeability of GelMA hydrogel for different crosslinking conditions and weight concentrations. Our results may provide a road map to estimate the applications of GelMA hydrogels in biomedicine, from cell viability prediction and to design of drug release systems [57]. For example, we can possibly derive the correlation between crosslinking conditions and release rates of biomolecules from the hydrogels. A combination of Eq. (4) and Eq. (14), and inserting into Eq. (12), yields the time-dependent release profile as (material constants, geometry constant in Eq. (12), and strain value in Eq. (4) are mixed to introduce X̂ and Ŷ):

$$\mathrm{Re}\mathrm{lease}=1-\text{erf}\left[\frac{t^{\tilde{Y}/2}}{(\widehat{X}Log(t)-\widehat{Y})t}\right]$$ (16)

, in which t denotes UV exposure time, Ỹ represents the power constant from the permeability data (Fig. 3b), and X̂ and Ŷ are regression coefficients of the elastic moduli (Fig. 3a). Equation (16) shows how the release profile explicitly varies based on UV exposure time, depicting how particles could be released in a slower rate by increasing time.

With only one parameter (such as UV exposure time), one may easily control the release behavior of biological agents and therapeutic molecules in the hydrogel systems. In addition, adjusting the hydrogel permeability might be used to regulate cell migration for in vitro applications in tissue engineering [41]. Future studies will involve the investigation of how permeability affects dynamic cell migration in a controlled experiment (i.e., similar elasticity and cell densities). Of note, the characterization method was developed using the time-dependent relaxation response of fluid-saturated gels; thus, it is applicable to any fluid-saturated hydrogel systems, in which void volumes allow the easy passage of fluids. This may include most of existing the hydrogel systems that have been designed for cell encapsulations. This method further allows testing cell-encapsulated hydrogels when a sterile indenter tip, attached to a loading head, is used in a closed environment. The experimental parameters such as the tip size and testing time should be adjusted to the range of stiffness and permeability of the desired hydrogel system to calibrate model constants. We selected GelMA hydrogel system here due to its wide range of applications in tissue engineering [23], and this work may be further expanded to predict the permeability behaviors of various other hydrogel types besides GelMA. It is important to note that this study ignores the special conditions where hydrogels are made from materials that are specifically chosen to mediate controlled drug release through physical interactions, chemical modifications, and hydrophobic forces [14]. The study on permeability discussed here should be adapted accordingly for those special cases where the release is controlled through different interactions of the drug and the polymers making up the hydrogels.