Abstract
Electroporation is the process by which applied electric fields generate nanoscale defects in biological membranes to more efficiently deliver drugs and other small molecules into the cells. Due to the complexity of the process, computational models of cellular electroporation are difficult to validate against quantitative molecular uptake data. In part I of this two-part report, we describe a novel method for quantitatively determining cell membrane permeability and molecular membrane transport using fluorescence microscopy. Here, in part II, we use the data from part I to develop a two-stage ordinary differential equation model of cellular electroporation. We fit our model using experimental data from cells immersed in three buffer solutions and exposed to electric field strengths of 170 to 400 kV/m and pulse durations of 1 to 1000 μs. We report that a low-conductivity 4-(2-hydroxyethyl)-1 piperazineethanesulfonic acid buffer enables molecular transport into the cell to increase more rapidly than with phosphate-buffered saline or culture medium-based buffer. For multipulse schemes, our model suggests that the interpulse delay between two opposite polarity electric field pulses does not play an appreciable role in the resultant molecular uptake for delays up to 100 μs. Our model also predicts the per-pulse permeability enhancement decreases as a function of the pulse number. This is the first report of an ordinary differential equation model of electroporation to be validated with quantitative molecular uptake data and consider both membrane permeability and charging.
Keywords: permeability, pulsed electric fields, porosity, differential equation, solute, diffusion
Introduction
An intact cell membrane normally provides a barrier to most molecular transport into and out of a cell. Electroporation (EP) is a biophysical process in which brief, yet intense, electrical pulses disrupt bilayer membranes to enhance the flow of molecules. The electrically motivated buildup of charged molecules at the water–lipid interface raises the electric potential difference between the inside of the membrane and the outside, known as the transmembrane potential (TMP).1–4 When the TMP reaches threshold values of 0.2 to 1.0 V, EP spontaneously occurs, as polar molecules are inserted through the membrane.5 Simulations of molecular systems including phospholipids, water, and other small-molecule solutes have shown that nanoscale defects formation occurs on the order of picoseconds to nanoseconds.6,7
When applied to cell membranes, EP-mediated defects render the cell membrane porous and enable solutes to better flow into and out of the cell. In the minutes to hours following EP, a porous membrane can reseal to again inhibit molecular transport.8,9 The generation of these defects is typically modeled using the asymptotic Smoluchowski model (ASM), which considers the nucleation of trapezoidal defect structures approximately 0.8 nm in radius.10 The ASM enables the calculation of the dynamic density of these defects on a membrane and includes considerations for the surface tension, tension of the defect, electrical energy, and steric hindrance of the membrane, as lipid molecules are reoriented.11 The ASM has been widely implemented in spatiotemporal EP models,12–16 although direct comparisons to quantitative experimental data are yet to be made. This model also relies on the exponential of the squared TMP and therefore requires small time steps to resolve in numerical simulations. Simulations of even an idealized cell with sufficient resolution to capture the spatiotemporal dynamics of EP are computationally expensive. These resource requirements functionally limit the validation of such simulations against experimental data over the longer time scales (minutes to hours) relevant to the applications of EP-based technologies, including electrochemotherapy or irreversible EP.
The translation of the presence of conductive membrane defects to an effective permeability has been used to couple the generation of membrane defects with the electric flux continuity17 and drift–diffusion equations.18 Measurements of the electric current through the cell membrane decreases from 30 to 260 - 0 pA over 10 to 500 milliseconds following in vitro EP treatment.19,20 Experimental data have also shown the rate at which exclusion dyes enter a cell after EP decreases over 190 to 289 seconds21 from initial permeabilities of 8.57 × 10−12 m/s for a 20-microsecond pulse at 300 kV/m.9 In part I of this 2-part report, we describe a novel method for measuring molecular transport across the cell membrane and quantitatively characterizing membrane permeability following EP. These permeability measurements are more readily compared to computational models through the abstraction of aggregate membrane defects to a net membrane porosity.22–25
Here, in part II of our report, we detail the development of such a model and fit it to the experimental data generated in part I from adherent cells in a microfluidic chamber. Previous models of membrane defect formation have included three to four stages in which an electroporated membrane can exist.16,21,26 In these schemes, an intact membrane is modeled as having a minimal permeability. When the TMP reaches the EP threshold, the membrane becomes sufficiently permeable to conduct small ionic currents. At this stage, the membrane still inhibits the transport of larger molecules, such as exclusion dyes. As its porosity increases, especially during EP schemes comprised of longer pulses (0.1-1.0 milliseconds), larger polyions and other small-molecule solutes are able to cross the cell membrane.9,21 The net porosity of the cell membrane is modeled as a linear combination of these porosity stages weighted by the fraction of the membrane in each stage, with an ordinary differential equation system representing the flow of the membrane through each available stage.
Once porous, membranes shunt ionic currents along the charge gradient, decreasing the TMP.11,12,27 This charging to the EP threshold, followed by the rapid formation of membrane defects, results in a characteristic sharp peak in the evolution of the TMP over time.19 Lumped parameter resistive–capacitive circuit models have been used to model the ionic currents through each defect stage.11,28–31 The parallel flow of ionic currents, modeled as parallel conductances, through the fraction of the membrane in each porosity stage is driven by an applied electric field, modeled as a source voltage in series with a Thevenin equivalent conductance that models the conductance of the buffer surrounding the cell. Lumped parameter models are particularly interesting, as they provide a means of connecting quantitative cell-level data with tissue-level phenomena.32 While these models have the potential to simplify comparisons with experimental data, no computational model of EP to date has been fit to quantitative experimental data.
The goal of part II of our work was to investigate EP-facilitated membrane permeability within a theoretical framework and avoid the computational expense of spatial models. To this end, we have developed a lumped parameter model that includes a cell membrane circuit model coupled with a novel phenomenological dual-porosity model and simple diffusion. Our model treats the cell using parameters that are representative of the whole cell rather than varying spatially.30,32 We fit our model using experimental data reported in part I of this report, including pulse durations of 1 to 1000 microseconds, electric field strengths of 170 to 400 kV/m, and 3 buffer compositions: phosphate-buffered saline (PBS), serum-free Dulbecco Modified Eagle Medium/F-12 cell culture medium (SFDF), and a low-conductivity 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid buffer (HEPES). Analysis of this model indicates that it is asymptotically stable following the removal of the applied electric field (ie, during defect resealing). Model parameters and variables were normalized, which reduced the parameter space to 6 parameters. Of these, 5 parameters were fixed based on existing literature, and the sixth, the forward transition rate between the low-porosity stage and the high-porosity stage, was fit to quantitative experimental data. Our results indicate that buffer composition plays a critical role in EP-mediated membrane porosity.
We extend our model to examine its implications for multipulse EP schemes. These results indicate that the relaxation of the high- to low-porosity stage is slow and results in a relatively long-lived membrane fraction in the high-porosity stage, compared to the fraction in the low-porosity stage. We show that the difference in relaxation time scales gives rise to a membrane permeability increase proportional to the pulse number raised to the power of 0.7. Finally, we demonstrate that the difference in relaxation times between the high- and low-conductivity stages, which explains the negligible impact of delays of less than 100 milliseconds between consecutive pulses. The small parameter space and conclusions of our model are consistent with existing literature and serve as a robust link between experimental observations and theoretical models. While the scope of the present work focuses on the biophysical mechanisms governing EP, we acknowledge that it has direct applications to optimizing clinical techniques using EP processes that rely on membrane transport, including electrochemotherapy. Robust linkages between theoretical and experimental results are critical to improving clinical EP technology. Our model provides a simple, concise methodology exploring these connections in greater depth.
Materials and Methods
We develop the following system of equations to describe EP and subsequent molecular transport into a single idealized, spherical cell immersed in an aqueous buffer (Figure 1). Our model comprises equations that describe EP as a reversible primary process coupled with an irreversible secondary process.33 In the reversible primary process, a source current proportional to the applied electric field drives an increase in the TMP (U). As the TMP increases, the formation of reversible membrane defects begins to occur and more readily allow ions to flow across the membrane. These ionic currents slow the TMP increase until either a dynamic equilibrium between the formation and relaxation of conducting defects is reached or the source current is removed. When a defect is initially formed (N), it does not initially allow for the transport for molecules larger than small ions. However, these initial defects can be expanded radially to accommodate the transport of larger ions, such as propidium, in a secondary defect stage (M). In the irreversible process, the transport of a small-molecule solute (X), such as propidium, is considered from a high extracellular concentration into a cell initially containing no solute. Our model consists of the system:
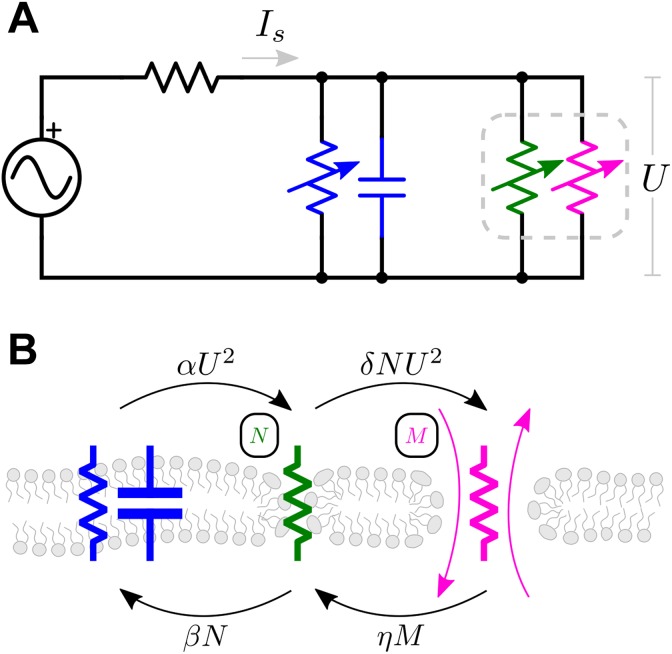
Figure 1.
EP model diagram. A, Electrical schematic representation of the cell membrane charging including the extracellular conductivity to model the electric current incident to the cell membrane. The conductivity of the cell membrane is given by the parallel conductances of the naive membrane (blue) and porous membrane weighted by the membrane fraction in each of 2 stages (green and magenta). B, The naive membrane contributes a conductivity and permittivity to the electrical model (blue). The N membrane fraction contributes to the permeabilized conductivity of ionic currents but does not permit the transport of larger solutes (green). The M membrane fraction contributes to and permits diffusive transport of solute with relative intracellular concentration X (magenta). Note that the membrane dielectric constant was considered constant across each membrane fraction and in time.
| 1 |
| 2 |
| 3 |
| 4 |
where , , , and U and time τ are the result of normalization. N is fraction of the membrane area that is conductive of small ions yet restricts the entry of larger molecules and M is the fraction of the membrane area permissive of the entry of larger solutes. X is the intracellular concentration of a solute such as propidium normalized to the extracellular concentration of the same. is the source transmembrane current and is proportional to the applied electric field. is the normalized TMP, where is the TMP and is the EP threshold voltage. is the normalized simulation time to the electrical time constant associated with a naive cell membrane, where , and and are the conductivity and permittivity of a naive cell membrane, respectively.
To maintain the utility of the present modeling scheme model for describing experimental results, the parameters are meant to describe the combined effects of all phenomena affecting membrane defects. We conceive of the transition from N defects to M defects occurring according to a mechanism that begins with an N-stage defect forming in an intact membrane as the result of an applied electric field.10 Provided the electric field is sufficiently strong and prolonged, the porosity of the cell membrane is increased as the size of the defects increases.12 The total porosity of the cell membrane is modeled as a linear combination of the N and M pore stages. Equation 1 is derived from a circuit model of an electroporated cell membrane30 (Appendix A). In this model, the membrane conductance dominates the circuit response and other components, such as the cytoplasm, have little effect. The value of time constant is well known for single cells ( s). γ is also well defined, as conductivities of both a naive membrane and a completely porous membrane have been experimentally measured19 and estimated to be . The term translates the applied electric field to the source voltage across the membrane, where is the electric field strength of the homogenous electric field if it were undisrupted by the immersed spherical cell.
Equation 2 describes the fractional porosity of the cell membrane generated by normalized TMP U at rate α and is quadratic in U, consistent with the dominant term in a first-order Taylor expansion of the ASM. The second term describes the transition from the N porosity stage to the M porosity stage that occurs at rate δ and is motivated by the presence of the TMP U. The third term in Equation 2 describes the transition from the N stage back to a naive membrane stage with rate constant β. The fourth term describes the M to N transition that occurs at rate η. Within this scheme, the membrane fraction in the M stage cannot exist without passing through the N stage during generation and relaxation. Additionally, this scheme does not specifically address whether the mechanism by which N-stage defects transition to M-stage defects is through coalescence of the existing N-stage defects34 or the radial expansion of M-stage pores35 but instead considers the total contribution of each defect population to the membrane conductance and permeability.
With the duration of the applied electric field 1000-fold shorter than the interval between the control measurement and the first posttreatment measurement in the experimental data, we assume that the molecular flux into the cell interior is purely diffusive.36,37 A Hagen–Poiseuille model of mass transport through a porous membrane was used to develop Equation 4, where ξ is the normalized permeability coefficient of the M porosity stage. Flow through a porous membrane is given according to Equation 4, where ,25,38 is the free diffusion coefficient of solute of interest with concentration X in an aqueous environment, h is the membrane thickness, r is the cell radius, and is the hindrance factor. This approximation assumes that and , where is the ratio of the solute radius () to the defect radius (). This formulation is solute dependent implying that λ will change based on the solute. However, in the present case, the solute is propidium as described in part I. It also assumes that the porosity of the cell membrane is uniformly distributed across the cell membrane and that flow into the cell occurs in the radial direction only. Modeling defects as cylinders, the hindrance factor is evaluated using a formula corrected for small porosities.25,39,40 Assuming and , ξ is calculated to be . With a priori knowledge of the molecular radius of the solute, ξ can be estimated from these calculations as well as from experimental measurements.9,21
Results
Parameter Fitting
Equations 1 to 4 were implemented in Python 3.6.5 using the Livermore Solver for Ordinary Differential Equations (LSODA) algorithm41 with the odeint() function in the Scipy (1.0.1) module.42 The solver was initialized with the initial conditions: , , , and . A stability analysis revealed that the model is asymptotically stable following the removal of the applied electric field (Appendix B). Experimental time-series data from single adherent cells within a microfluidic chamber were used to calibrate the model (part I). Within this dataset, the observed average molecular uptake was calculated from experimental data prior to electric field exposure and each minute for 30 minutes following treatment to obtain 31 total observations for each electric field strength and pulse duration combination. The mean and variance were calculated for each measurement. In order to estimate δ for all treatments for each buffer composition, the Nelder–Mead method was implemented using the minimize() function in the LmFit (0.9.7) module to minimize the sum of square residuals (SSR) given by:
| 5 |
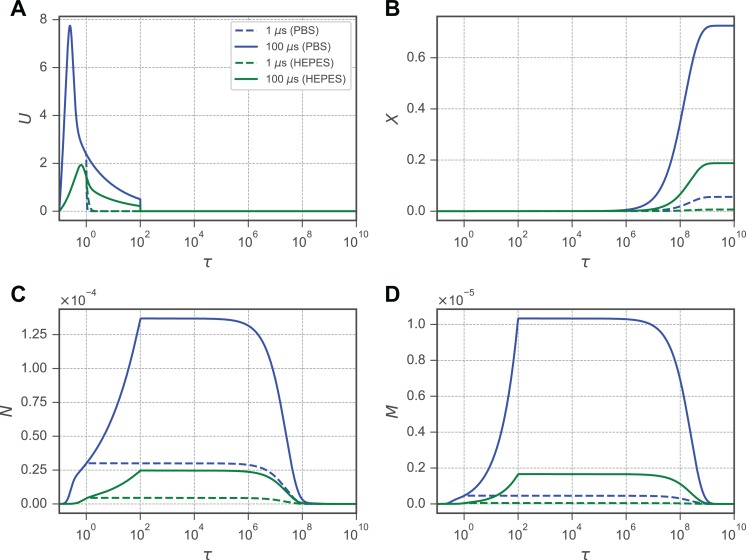
where X model(ti) and X data(ti) are the model and data points for X, respectively, at time ti ∈ . Simulations were plotted over the experimental data and show good agreement visually, with the maximum max(SSRPBS) = 0.025, max(SSRSFDF) = 0.0070, and max(SSRHEPES) = 0.0066 Figure 2. Notably, the to generation rates δ were similar for cells immersed in PBS and SFDF but were consistently 3- to 5-fold larger for cells immersed in HEPES buffer.
Figure 2.
The 2-stage model recapitulates experimental averages of molecular uptake. Representative parameter fits are shown for X for cells exposed to a pulse at 320 kV/m to pulse widths of 1, 10, 100, and 1000 microseconds in (A) phosphate buffered saline (PBS), (B) serum-free DMEM/F12 medium (SFDF), and (C) 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid buffer (HEPES). Equations 1 to 4 were fit to time series datasets from cells in 3 buffer compositions (PBS, SFDF, and HEPES), 4 pulse durations (1, 10, 100, and 1000 microseconds), and 4 electric field strengths (170, 250, 320, and 400 kV/m). Fitting was performed using the Nelder–Mead method to minimize Equation 6 by varying δ. (d) The best fit δ is shown as a product of the source term and the pulse duration normalized to the time constant for all 48 treatment combinations.
HEPES Buffer Increases Membrane Permeability
Experimental data (part I) from 3 different buffer compositions reveal that cells immersed in the HEPES buffer during EP experienced a larger molecular uptake following the application of the 100-microsecond pulse than the cells immersed in PBS or SFDF. With a 1000-microsecond pulse, the ultimate molecular uptake was similar for each of the electric field strengths experimentally examined, but the time-to-saturation decreased with increasing field strength. Although the HEPES buffer has a lower conductivity than the PBS or SFDF by an order of magnitude, δ for the cells in the HEPES buffer is 2 orders of magnitude larger than for the cells in PBS and SFDF buffers, which are themselves similar (Table 1). This is counterintuitive to previous data from studies, where the ionic strength of the buffer was manipulated for otherwise similar buffers.31 In our model, this observation is driven by a more rapid transition rate from the N membrane stage to the M membrane stage that results in a larger accumulation M that contributes to a rapid increase in X over the responses evoked by the other buffers (Figure 2). Our data show that although the HEPES buffer slows the rise in U (Figure 3), X increases similar to the cells in PBS and SFDF. This observation suggests that electroporating cells in a HEPES buffer may result in increased permeability over similar cells treated in PBS and SFDF, despite the lower induced TMP (U).
Table 1.
Model Parameters.
| Parameter | Value | Description (Units) | References |
|---|---|---|---|
| α | 2.0×10−6 | N formation rate | 43 |
| β | 4.0×10−6 | N relaxation rate | 8,10,19,44 |
| γ | 1.0×106 | Relative permeabilized conductance | 19,44,45 |
| η | 4.0×10−9 | M relaxation rate | 9,21 |
| ξ | 5.0×10−4 | Permeability coefficient | 9,21,25 |
| 0.63 | Solute radius/defect radius | 25 | |
| 0.5 | Solute radius (nm) | 46 | |
| 0.8 | Defect radius (nm) | 10,47 | |
| 250 | EP threshold voltage (mV) | 19 | |
| 1.0 | Membrane time constant (microseconds) | 19,20,48,49 | |
| 0.5×10−9 | Solute diffusivity (m2/s) | 46 | |
| h | 5.0 | Membrane thickness (nm) | 50,51 |
| r | 7.5 | Cell radiusa (μm) | |
| 1.01 | PBS conductivitya (S/m) | ||
| 0.93 | SFDF conductivitya (S/m) | ||
| 0.08 | HEPES conductivitya (S/m) |
a Denotes values found in the accompanying manuscript.
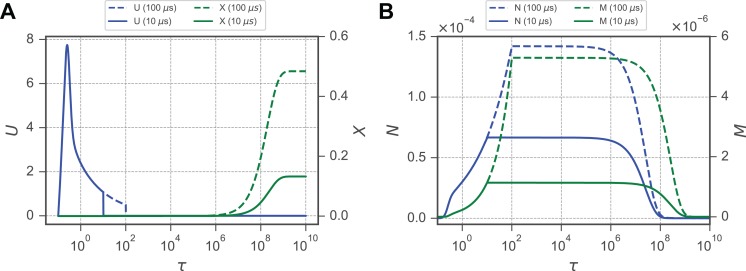
Figure 3.
Evolution of membrane porosities N and M and the resultant molecular uptake X following an increase in the normalized transmembrane potential U. In each plot, solid lines indicate an applied electric field microseconds, and dashed lines indicate microseconds. Blue lines indicate a phosphate buffered saline buffer solution, and green lines indicate a 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid buffer. A, The TMP U, driven by a large external electric field, reaches an initial maximum until the membrane begins to shunt ionic currents as N and M increase. B, The intracellular concentration of solute X increases as it enters the cell through the membrane porosity stage. C, An intact membrane enters a stage conductive of small ions N driven by a TMP. D, M develops from N, dependent on U, and allows larger molecules to pass through the cell membrane. For all simulations, kV/m.
Generally, in each of the primary variables (N, M, X, and U), several characteristic features emerge. Immediately following application of the electric field, the TMP U experiences a characteristic spike within to (Figure 3A). This spike is followed by a sharp decline as N and M increase and begin conducting ionic currents through the cell membrane. For N, the initiation of the waveform appears biphasic: An initial rapid increase is followed by a more gradual increase until a plateau is reached (Figure 3C). The first phase is where U is the largest. The second phase occurs when the membrane begins to shunt small ionic currents that rapidly decrease U and slows the increase in N. This progression occurs for cells in each buffer examined in this study, but the cells in HEPES experience a larger for both the 1- and 10-microsecond pulses than the cells in PBS experienced at 10 microseconds. For (Figure 3D), a similar biphasic response exists but is more stratified between the 1- and 10-microsecond pulse durations for the cells in the HEPES buffer. Interestingly, the 1-microsecond pulse generated an M for cells in the HEPES buffer similar to that generated by the 10-microsecond pulse for the cells in PBS. The result of this stratification is apparent in (Figure 3B). The membrane permeability (Pm = ξMh) is directly impacted by the M membrane stage, and consequently, depends on both the extracellular–intracellular concentration gradient (1 − X) and M. However, while the concentration gradient could limit the molecular uptake as it decreases, (1 − X) > 0.30 for even the largest pulse strengths and durations examined here. Therefore, it is assumed that the changes in M are largely responsible for the molecular uptake observed.
The High-Conductivity Membrane Fraction Is Slow to Relax
Prior experimental data have shown that U is highly dynamic during the application of an electric field but quickly returns to its ground state following the removal of Is (Figure 3A). However, it is clear that molecular transport across the membrane continues for minutes to hours afterward (Figure 2A–C). This discrepancy between the electrical and transport time scales is motivation to explore the mechanism producing a long-lived M stage membrane fraction (Figure 4A). As a large U generates an initial increase in N, a small M begins to develop (Figure 4B). M increases until the removal of Is, at which point the plateau of M coincides with the return of U to its ground state. Both M and N persist near their plateau for approximately 106τ, at which point N begins to relax to the ground state it reaches at 108τ. However, while the N stage decays, the M stage persists until 109. Because the membrane fraction in the M stage is approximately 2 orders of magnitude smaller than in the N stage, the transition of an M-stage porosity to an N-stage porosity results in a large decrease in the low conductivity, yet larger, portion of the membrane while the membrane overall continues to be permeable to solutes. This slow relaxation in the M stage is responsible for the difference in time scales between the rapid electrical charging and the relatively slow uptake of solutes in the minutes following EP.
Figure 4.
The transmembrane potential and molecular uptake occur on dramatically different timescales. A, Pulses with durations of 10 and 100 microseconds are shown simulated using . B, A lag exists between when the N stage is fully relaxed to 0 as the M stage persists. M and N reach plateaus upon removal of the source current with the applied electric field of kV/m.
Consecutive Pulses Diminish Permeabilization Efficiency
While multipulse experiments can confound observations of membrane dynamics due to the complex cellular response, EP schemes often rely on a series of pulses, rather than a single continuous pulse, to limit Joule heating.52,53 δ = 1.0 × 10−3 was fixed within the range for the PBS buffer, which is commonly used experimentally. Alternating polarity pulses are becoming increasingly relevant to EP technology.54–56 To investigate the implications of our model within such schemes, bipolar pulse trains were simulated as ideal square waveforms from 1 to 1000 microseconds (Figure 5). The interpulse delay td between the start of the falling edge of 1 pulse and the start of the initiation of the following pulse has been implicated in governing cell permeability and death induced by EP protocols.57–61 To determine the role of td in the induced permeability Pm, simulations were performed using two consecutive, alternating polarity pulses at 400 kV/m with a variable delay between them, shown, for example, by 10-microsecond pulses (Figure 5A). The induced permeability was evaluated at the beginning of the falling edge of the second pulse for td ∈ [10−6 s, 10−1 s], and it was found that td within this range does not appreciably affect membrane permeability for 1-, 10-, 100-, and 1000-microsecond pulses (Figure 5B). These results corroborate experiment reports of nanosecond pulses that show a relatively small difference between pulses delivered at intervals from 2 to 1000 milliseconds62 and that the impedance change in cells is relatively small yet similar between consecutive pulses for interpulse delays less than 100 milliseconds.59
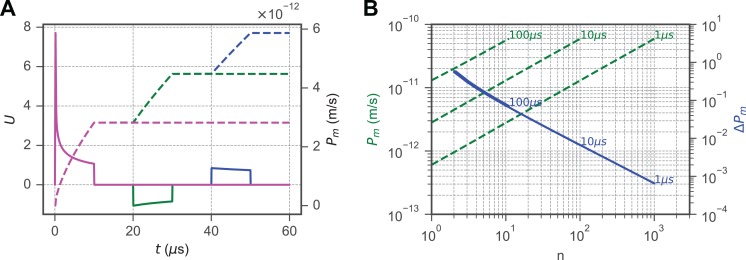
Figure 5.
Interpulse delays of less than 1 millisecond negligibly impact membrane permeability, while increasing pulse number n and duration () increases membrane permeability. A, The normalized transmembrane potential (U) response to consecutive, a delay () of 1-, 100-, and 500-microsecond pulses between opposite polarity pulses 10 microseconds are shown as solid magenta, green, and blue lines, respectively. The membrane permeability () given in m/s is shown as a dotted line corresponding to each waveform. In each case, the membrane permeability increases to approximately the same value at 1000 microseconds following the initiation of the first pulse in the applied electric field. Pulses are shown with an external electric field of kV/m. B, Two consecutive, opposite polarity pulses interpulse delays of 1 to 105 microseconds for pulses with durations of 1, 10, 100, and 1000 microseconds retain a constant permeability at 1 millisecond following application of the stimulating electric field. was fixed for both figures.
The impact of the number of consecutive pulses n has been reported as an important factor in membrane conductance changes resulting from EP.4,29,63 We refer to the measurement of the effect of the number of pulses on the cell’s permeability, as the permeabilization efficiency is defined as:
| 6 |
where is the time at the initiation of the pulse and is the initiation of the subsequent pulse in a series containing n alternating polarity pulses of duration . Simulations were performed using pulses generated by an external electric field with an amplitude of 400 kV/m and varying the pulse number from 1 to 1000 pulses with durations of 1 to 100 microseconds. The relation between pulse number and permeability is given by
| 7 |
where is the membrane permeability generated by the first pulse (Figure 6), as these lines are parallel and have a slope of using propidium and under the conditions described in part I. The central implication of this relationship is that knowing the permeability generated by a single electrical pulse in a series of alternating polarity pulses, the number of pulses required to generate and equivalent permeability induced by a second treatment with an equivalent applied electric field strength may be estimated through the relation:
Figure 6.
Permeabilization efficiency decreases for each consecutive pulse delivered in a given series. A, Alternating polarity pulses increase the normalized transmembrane potential (U) and generate increasing membrane permeabilities . U is driven by an electric field of kV/m comprising 1, 2, or 3 pulses, shown in magenta, green, and blue, respectively. Pm increases with each consecutive pulse, denoted by the magenta, green, and blue dotted lines identifying the corresponding TMP. B, The increase in upon removal of the last pulse in a train of n alternating polarity pulses is shown as green dotted lines for 1-, 10-, and 100-microsecond long pulse durations () with a 1-microsecond delay () between consecutive pulses. The fractional increase in membrane permeability () between the falling edge of 2 such pulses decreases linearly with , where shown as a blue solid line. was fixed for both figures.
| 8 |
where na and nb are the numbers of alternating polarity pulses in treatment a and b, respectively, Pa and Pb are the permeabilities after the first pulse of each treatment using constant duration pulses (Figure 6B). This equation takes a similar form to previous models describing equivalent pulse parameters.33,64 Although more quantitative measurements of membrane permeability are needed to validate this result, it could provide a guide to designing future in vitro EP protocols.
Discussion
In the proposed model, normalization of the governing equations results in only 6 parameters: (Table 1). γ, ξ, and η are the most readily measurable parameters in the present model and have been well characterized and estimated in previous literature.9,19,63 We emphasize that these parameters describe the net rates of defect formation and relaxation as an aggregate of the underlying mechanism that contribute to membrane EP. α and β were fixed based on previous estimates8,9,65,66 and do not correspond to physical parameters but to net transition rates between porosity stages. We varied δ, which is also an aggregate simulation parameter, to fit our model to the experimental data set. Fitting our model in this way indicated a 3- to 5-fold difference in the δ for cells treated in the HEPES buffer over the cells treated in SFDF or PBS (Figure 2). These data indicate that the composition of the HEPES buffer impacts the rate at which M is generated following EP, which is counterintuitive when considering the model in terms of circuit theory. The HEPES buffer has an electrical conductivity 10-fold lower than PBS and SFDF and should result in a smaller . Biochemically, there are 2 components in the HEPES buffer—HEPES (10 mmol/L) and sucrose (250 mmol/L)—that differentiate this buffer from PBS and SFDF. HEPES buffers are commonly used for in vitro EP studies, as they maintain cellular viability without the presence of calcium,67–69 and the common use of HEPES buffers may suggest that this buffer does not affect cellular EP. Additionally, cells immersed in isosmotic sucrose-containing buffers, even in the absence of HEPES, have been shown to uptake more propidium than cells in buffers without sucrose.70
While the impact of HEPES buffers on EP appears to be negligible, there is evidence that the inclusion of sucrose affects cells as they are permeabilized. Sucrose is excluded from electroporated membranes65 and has been shown to result in the formation of blebs.71 Within the context of these results, the large δ our model predicts for the sucrose-containing HEPES buffer may assist in expanding or stabilizing membrane defects. The membrane fraction in the low-conductivity N stage could widen into the M stage to more rapidly shunt the flow of water along the osmotic pressure gradient and into the cell. In addition to the expansion and stabilization of defects, the osmotic pressure gradient could also deliver solutes, such as propidium, into the cell more rapidly. Both of these effects may explain the increased δ for cells in HEPES. More investigation is required to further characterize this mechanism, although explaining the specific effects of the HEPES buffer on cellular permeabilization is beyond the scope of the present work. This is an important consideration for future studies and would be valuable to the field of EP in general, but the focus of this work is developing a phenomenological model that can be directly fit using experimental data.
The flow of propidium and other small-molecule solutes into the cell through the cell membrane following EP is the result of both electrophoretic drift and diffusion along concentration gradients. However, the flow of propidium into an electroporated cell following the removal of the applied electric field is largely due to diffusion through defects in the cell membrane.72,73 Here, the defect population is divided into 2 subpopulations, N and M, which are treated in aggregate based upon whether the defects permit propidium transport. Previous reports have suggested subdividing the induced membrane porosity into diffusive and electrically conductive portions,16,23,74,75 but these models have typically relied on the incorporation of interface conditions in continuum models. In our model, the dimensionality of the problem is collapsed to yield average porosities for the whole membrane, rather than addressing the generation, relaxation, and interconversion of individual defects (Figure 1). Furthermore, removing this spatial dependence allows our model to be solved using standard ordinary differential equation solvers, enabling the simplified spatial system to be readily incorporated as a material property into larger systems.32 In the present model, this reduced dimensionality was achieved through the use of dynamic porosities N and M 16,23,75,76 rather than more conventional defect numbers.77–80 The transport through the M stage then facilitates hindered diffusion of propidium into the cell and is represented as an average over the whole cell, rather than at each individual defect, giving rise to a dual-porosity model of the cell membrane.25
While our 2-stage model is fit using single-pulse propidium uptake data, further data sets should be considered in future work, although our model is qualitatively consistent with previous reports. The electrical waveforms used to generate our experimental data set comprised a single pulse with significant ringing on the initiation and termination of each pulse. Due to the ringing, the cells in the microdevice were exposed to a much larger electric field strength during the first 100 nanoseconds than during the remainder of the pulse. Furthermore, in many experimental investigations, a voltage overshoot may exist on the rising edge of each pulse, depending on the generator topology and experimental apparatus,55 which differs from the idealized square pulses simulated in the present model. Experimental investigations of pulse modulation have found that a square pulse with 10% sinusoidal modulation varied only slightly from an idealized square pulse,81 although a 90%-modulated pulse increased the permeabilized cell fraction. By analogy, we expect that for the 10-, 100-, and 1000-microsecond pulses, our experimental data would closely approximate a square pulse. Experimental data from the 1-microsecond pulses could overpredict the EP threshold, as the ringing in the applied pulse is of the order of the pulse duration. Ultimately, little permeabilization occurred for pulses <10 microseconds, and our model is able to phenomenologically reflect this observation.
Our 2-stage model can also be easily extended from a single pulse to a series of alternating polarity pulses (Figure 6). Due to the slow relaxation rate (η) of the M stage (Figure 4), 2 consecutive pulses separated by milliseconds allow a negligible M to N relaxation prior to the start of a second pulse. The membrane conductance, which most significantly depends on N, is highly dynamic compared to the membrane permeability to solutes, which depends on M (Figure 6A). This is consistent with the relatively rapid recovery of the naive membrane conductance observed in patch-clamp experiments.19. However, the long-lived M stage results in a appear to be independent of (Figure 6B).
At the removal of each consecutive pulse, increases with , where for up to one thousand 1- to 10-microsecond pulses, regardless of the pulse duration (). In our simulations, the electric field strength and duration of each pulse remains constant and the pulse number is varied. Our model suggests that 2 disparate series with different pulse durations and interpulse delays generate equivalent permeabilities if the number of pulses in each series satisfies Equation 8, suggesting that permeability increases with increasing applied energy.82 These data are consistent with previous reports that relate the electric field intensity required to electroporate 50% of a population of cells with the requisite pulse duration , where k is constant.33,64 From Equation 8, our data suggest a modification of this relationship , where the energy density generated by a single pulse is combined with the diminishing permeabilization efficiency for multiple pulses in a train. Together, these observations are consistent with previous experimental reports using series of long pulses of alternating polarity pulses,63 although it is the first time membrane permeability has been quantitatively related to the energy applied through electrical pulses.
The repetition rate () has been observed to impact the uptake of propidium. Repetition rates of 1 to 10 Hz induce greater permeabilization than pulses delivered more rapidly.58,59 Delays of 1 and 4 microseconds have also been shown to produce relatively similar permeabilities with longer pulses of equivalent total duration producing even larger permeabilities.63 In our model, the permeability is dependent only on the membrane fraction in the M stage, which is a small fraction of the total porous area (). The N stage is formed more quickly and relaxes more rapidly than the M stage. At longer interpulse durations (on the order of several seconds), the membrane fraction in the M stage begins to relax. If the cell membrane in the M stage is allowed to partially relax between pulses, a lower average permeability is obtained over the course of the EP treatment. To design optimal EP protocols, pulse durations must be long enough to induce the largest membrane fraction in the M stage while preventing its relaxation.
Our 2-stage lumped parameter model is presently limited in scope by the data with which it has been validated, namely, adherent cells cultured in vitro in a dispersed fashion using the methods described in part I. For cells cultured in a 3-dimensional environment, we expect the parameter values in our model would necessarily reflect changes in cell morphology and physiology. For example, if a solute with a larger molecular radius or charge was used, the parameters in our model would necessarily change to reflect the ability of each solute to travel through the membrane; the transport of differently sized molecules with different charges will inherently be different. Especially, with regard to the M to N porosity stages, we expect that the parameters describing these kinetics would vary greatly.83 Our present model is only validated in vitro using propidium for cells that exist far from the electrodes, which is consistent with the experimental setup in the accompanying article. For cells near the electrode contacts, other mechanisms of cell membrane damage may dominate, and our model may not recapitulate experimental observations.
Conclusion
Here, we present the second part of a 2-part report on in vitro EP. In part I, we developed a method of quantitatively determining molecular uptake and measuring membrane permeability for cells in a microdevice using fluorescence microscopy. Here, in part II, we develop and fit a computational model of small-molecule transport into cells using only 6 parameters. We fit our model using experimental data of propidium uptake following EP gathered in part I. When extended to multiple bipolar pulses, our model corroborates previous experimental reports and suggests a relationship that defines the pulse number required to obtain equivalent molecular uptake between disparate EP schemes.
Abbreviations
- ASM
asymptotic Smoluchowski model
- EP
electroporation
- HEPES
4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid
- PBS
phosphate-buffered saline
- SFDF
serum-free DMEM/F12 medium
- TMP
transmembrane potential
Appendix A
Derivation of Circuit Model
Enforcing current continuity across the membrane gives:
| 9 |
where E is the electric field in the source-free membrane interior, is the permittivity of the cell membrane Γ. The radial component of the electric field has the form , where is the electric field strength of the homogenous electric field, if it were undisrupted by the immersed spherical cell.73 Let be the membrane conductivity, be the conductivity of the cell interior, and be the extracellular conductivity. The electric current I through the membrane surface of a spherical cell with outer radius r, membrane thickness h, and permittivity is given by
| 10 |
where , for , , and . By definition, the radially defined electric field is . This allows the electric current between the inside of the cell and the outside of the cell to be integrated to yield
| 11 |
where , and for a spherical conductor, , where . Two paths were considered for the transmembrane conduction current: through the naive membrane fraction and through porous fraction such that, , where is the effective ionic conductance of the cell membrane, is the conductance of the naive membrane fraction, and is the conductance of the porous fraction. Splitting the conductance in this manner yields,
| 12 |
where , is the non-normalized TMP and is the electrostatic potential threshold voltage, , the source term relating applied electric field to the induced transmembrane voltage is , , and is the conductivity of the external buffer.
Appendix B
Steady State Analysis
In order to determine the model’s steady states, the time derivatives in Equations 1 to 4 were set to 0. Furthermore, because is delivered as a pulse, conditions at the time after its removal are considered as the initial conditions for a source-free system. This yields the linear system
| 13 |
| 14 |
| 15 |
| 16 |
Six possible steady states arise from this system, but the domain constraints and only permit 2 steady states that reflect the reality:
| 17 |
| 18 |
To determine the stability of these steady states, all the eigenvalues of the Jacobian must have negative real parts. The Jacobian of Equations 1 to 4 with is
| 19 |
The eigenvalues are given at steady states by , where are the eigenvalues and I is the identity matrix. This yields the same characteristic equations for both steady states with eigenvalues of . arises from Equation 15, which contains the only appearance of X and its first derivative and has no bearing on any of the other equations in the model. Because this coupling of M to X is unidirectional, Equation 15 and derivatives with respect to X were removed from J. was recalculated and yielded . In this case, all of the real parts of the eigenvalues are negative and therefore the postpulse system coupling N, M, and U is asymptotically stable.
Footnotes
Declaration of Conflicting Interests: The author(s) declared the following potential conflicts of interest with respect to the research, authorship, and/or publication of this article: Daniel C. Sweeney and Rafael V. Davalos have patents pending related to cellular electroporation.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: Funding for this work was graciously provided by the NSF CAREER Award CBET-1055913, the NSF IGERT DGE-09661, and the NIH R01-CA213423.
ORCID iD: Daniel C. Sweeney  http://orcid.org/0000-0002-1289-1627
http://orcid.org/0000-0002-1289-1627
References
- 1. Leontiadou H, Mark AE, Marrink SJ. Molecular dynamics simulations of hydrophilic pores in lipid bilayers. Biophys J. 2004;86(4):2156–2164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ziegler MJ, Vernier PT. Interface water dynamics and porating electric fields for phospholipid bilayers. J Phys Chem B. 2008;112(43):13588–13596. [DOI] [PubMed] [Google Scholar]
- 3. Delemotte L, Tarek M. Molecular dynamics simulations of lipid membrane electroporation. J Membr Biol. 2012;245(9):531–543. [DOI] [PubMed] [Google Scholar]
- 4. Murovec T, Sweeney DC, Latouche E, Davalos RV, Brosseau C. Modeling of transmembrane potential in realistic multicellular structures before electroporation. Biophys J. 2016;111(10):2286–2295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Tarek M. Membrane electroporation: a molecular dynamics simulation. Biophys J. 2005;88(6):4045–4053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Tieleman DP, Marrink SJ, Berendsen HJC. A computer perspective of membranes: molecular dynamics studies of lipid bilayer systems. Biochim Biophys Acta. 1997;1331(3):235–270. [DOI] [PubMed] [Google Scholar]
- 7. Kramar P, Delemotte L, Maček Lebar A, Kotulska M, Tarek M, Miklavčič D. Molecular-level characterization of lipid membrane electroporation using linearly rising current. J Membr Biol. 2012;245(10):651–659. [DOI] [PubMed] [Google Scholar]
- 8. Saulis G, Venslauskas MS, Naktinis J. Kinetics of pore resealing in cell membranes after electroporation. Bioelectrochemistry Bioenerg. 1991;321(1):1–13. [Google Scholar]
- 9. Shirakashi R, Sukhorukov VL, Tanasawa I, Zimmermann U. Measurement of the permeability and resealing time constant of the electroporated mammalian cell membranes. Int J Heat Mass Transf. 2004;47(21):4517–4524. [Google Scholar]
- 10. Neu J, Krassowska W. Asymptotic model of electroporation. Phys Rev E. 1999;59(3):3471–3482. [Google Scholar]
- 11. DeBruin KA, Krassowska W. Modeling electroporation in a single cell. I. Effects of field strength and rest potential. Biophys J. 1999;77(3):1213–1224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Son RS, Smith KC, Gowrishankar TR, Vernier PT, Weaver JC. Basic features of a cell electroporation model: illustrative behavior for two very different pulses. J Membr Biol. 2014;247(12):1209–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Leguèbe M, Poignard C, Weynans L. A second-order Cartesian method for the simulation of electropermeabilization cell models. J Comput Phys. 2015;292(1):114–140. [Google Scholar]
- 14. Yu M, Lin H. Quantification of propidium iodide delivery with millisecond electric pulses: a model study. arXiv. 2014;1401(6954):1–23. [Google Scholar]
- 15. Li J, Lin H. The current-voltage relation for electropores with conductivity gradients. Biomicrofluidics. 2010;4(1):013206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Miklavcic D, Towhidi L. Numerical study of the electroporation pulse shape effect on molecular uptake of biological cells. Radiol Oncol. 2010;44(1):34–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Li J, Tan W, Yu M, Lin H. The effect of extracellular conductivity on electroporation-mediated molecular delivery. Biochim Biophys Acta. 2013;1828(2):461–470. [DOI] [PubMed] [Google Scholar]
- 18. Moran JL, Dingari NN, Garcia PA, Buie CR. Numerical study of the effect of soft layer properties on bacterial electroporation. Bioelectrochemistry. 2017;123:261–272. [DOI] [PubMed] [Google Scholar]
- 19. Ryttsén F, Farre C, Brennan C, et al. Characterization of single-cell electroporation by using patch-clamp and fluorescence microscopy. Biophys J. 2000;79(4):1993–2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Hibino M, Itoh H, Kinosita K. Time courses of cell electroporation as revealed by submicrosecond imaging of transmembrane potential. Biophys J. 1993;64(6):1789–1800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Rols M-P, Teissié J. Electropermeabilization of mammalian cells: quantitative analysis of the phenomenon. Biophys J. 1990;58(5):1089–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Saulis G. Pore disappearance in a cell after electroporation: theoretical simulation and comparison with experiments. Biophys J. 1997;73(3):1299–1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Neumann E, Toensing K, Kakorin S, Budde P, Frey J. Mechanism of electroporative dye uptake by mouse B cells. Biophys J. 1998;74(1):98–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Kakorin S, Neumann E. Ionic conductivity of electroporated lipid bilayer membranes. Bioelectrochemistry. 2002;56(1-2):163–166. [DOI] [PubMed] [Google Scholar]
- 25. Mahnič-Kalamiza S, Miklavčič D, Vorobiev E. Dual-porosity model of solute diffusion in biological tissue modified by electroporation. Biochim Biophys Acta. 2014;1838(7):1950–1966. [DOI] [PubMed] [Google Scholar]
- 26. Abidor IG, Arakelyan VB, Chernomordik LV, Chizmadzhev YA, Pastushenko VF, Tarasevich MR. Electric breakdown of bilayer lipid membranes I. The main experimental facts and their qualitative discussion. J Electroanal Chem Interfacial Electrochem. 1979;104:37–52. [Google Scholar]
- 27. Li J, Lin H. Numerical simulation of molecular uptake via electroporation. Bioelectrochemistry. 2011;82(1):10–21. [DOI] [PubMed] [Google Scholar]
- 28. Hu Q, Joshi R, Beskok A. Model study of electroporation effects on the dielectrophoretic response of spheroidal cells. J Appl Phys. 2009;106(2):024701. [Google Scholar]
- 29. Bhonsle SP, Arena CB, Sweeney DC, Davalos RV. Mitigation of impedance changes due to electroporation therapy using bursts of high-frequency bipolar pulses. Biomed Eng Online. 2015;14(S3):1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Moen EK, Ibey BL, Beier HT, Armani AM. Quantifying pulsed electric field-induced membrane nanoporation in single cells. Biochim Biophys Acta. 2016;1858(11):2795–2803. [DOI] [PubMed] [Google Scholar]
- 31. Rols M-P, Teissie J. Ionic-strength modulation of electrically induced permeabilization and associated fusion of mammalian cells. Eur J Biochem. 1989;179(1):109–115. [DOI] [PubMed] [Google Scholar]
- 32. Voyer D, Silve A, Mir LM, Scorretti R, Poignard C. Dynamical modeling of tissue electroporation. Bioelectrochemistry. 2017;119:98–110. [DOI] [PubMed] [Google Scholar]
- 33. Neumann E. Membrane electroporation and direct gene transfer. J Electroanal Chem. 1992;343(1-2):247–267. [Google Scholar]
- 34. Neamtu S, Morariu V, Turcu I, Popescu AH, Copaescu LI. Pore resealing inactivation in electroporated erythrocyte membrane irradiated with electrons. Biochem Bioenerg. 1999;48(2):441–445. [DOI] [PubMed] [Google Scholar]
- 35. Neu JC, Krassowska W. Modeling postshock evolution of large electropores. Phys Rev E. 2003;67(2):021915. [DOI] [PubMed] [Google Scholar]
- 36. Sadik MM, Li J, Shan JW, Shreiber DI, Lin H. Quantification of propidium iodide delivery using millisecond electric pulses: experiments. Biochim Biophys Acta. 2013;1828(4):1322–1328. [DOI] [PubMed] [Google Scholar]
- 37. Pucihar G, Kotnik T, Miklavcic D, Teissié J. Kinetics of transmembrane transport of small molecules into electropermeabilized cells. Biophys J. 2008;95(6):2837–2848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Subczynski WK, Hopwood LE. Is the mammalian cell plasma membrane a barrier to oxygen transport?. J Gen Physiol. 1992;100(1):69–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Higdon JJL, Muldowney GP. Resistance functions for spherical particles, droplets and bubbles in cylindrical tubes. J Fluid Mech. 1995;298(-1):193–210. [Google Scholar]
- 40. Dechadilok P, Deen WM. Hindrance factors for diffusion and convection in pores. Ind Eingineering Chem Res. 2006;45(21):6953–6959. [Google Scholar]
- 41. Petzold L, Hindmarsh A. LSODA. Livermore, CA: Lawrence Livermore National Laboratory; 1997. [Google Scholar]
- 42. Jones E, Oliphant T, Peterson P. SciPy: Open Source Scientific Tools for Python. 2001. http://www.scipy.org/. Accessed August 8, 2018.
- 43. Krassowska W, Filev PD. Modeling electroporation in a single cell. Biophys J. 2007;92(2):404–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Hai A, Spira ME. On-chip electroporation, membrane repair dynamics and transient in-cell recordings by arrays of gold mushroom-shaped microelectrodes. Lab Chip. 2012;12(16):2865–2873. [DOI] [PubMed] [Google Scholar]
- 45. Chernomordik LV, Sukharev SI, Popov SV, et al. The electrical breakdown of cell and lipid membranes: the similarity of phenomenologies. Biochim Biophys Acta. 1987;902(3):360–373. [DOI] [PubMed] [Google Scholar]
- 46. Smith KC. A Unified Model of Electroporation and Molecular Transport. Cambridge, Massachusetts: Massachusetts Institute of Technology; 2011. [Google Scholar]
- 47. Glaser RW, Leikin SL, Chernomordik LV, Pastushenko VF, Sokirko AI. Reversible electrical breakdown of lipid bilayers: formation and evolution of pores. Biochim Biophys Acta. 1988;940(2):275–287. [DOI] [PubMed] [Google Scholar]
- 48. Flickinger B, Berghöfer T, Hohenberger P, Eing C, Frey W. Transmembrane potential measurements on plant cells using the voltage-sensitive dye ANNINE-6. Protoplasma. 2010;247(1-2):3–12. [DOI] [PubMed] [Google Scholar]
- 49. White JA, Pliquett U, Blackmore PF, Joshi RP, Schoenbach KH, Kolb JF. Plasma membrane charging of Jurkat cells by nanosecond pulsed electric fields. Eur Biophys J. 2011;40(8):947–957. [DOI] [PubMed] [Google Scholar]
- 50. Paula S, Volkov AG, Van Hoek AN, Haines TH, Deamer DW. Permeation of protons, potassium ions, and small polar molecules through phospholipid bilayers as a function of membrane thickness. Biophys J. 1996;70(1):339–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Heinrich V, Ritchie K, Mohandas N, Evans E. Elastic thickness compressibilty of the red cell membrane. Biophys J. 2001;81(3):1452–1463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Davalos RV, Mir LM, Rubinsky B. Tissue ablation with irreversible electroporation. Ann Biomed Eng. 2005;33(2):223–231. [DOI] [PubMed] [Google Scholar]
- 53. Davalos RV, Bhonsle S, Neal RE. Implications and considerations of thermal effects when applying irreversible electroporation tissue ablation therapy. Prostate. 2015;75(10):1114–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Gianulis EC, Casciola M, Xiao S, Pakhomova ON, Pakhomov AG. Electropermeabilization by uni- or bipolar nanosecond electric pulses: the impact of extracellular conductivity. Bioelectrochemistry. 2018;119:10–19. [DOI] [PubMed] [Google Scholar]
- 55. Yao C, Dong S, Zhao Y, Mi Y, Li C. A Novel configuration of modular bipolar pulse generator topology based on marx generator with double power charging. IEEE Trans Plasma Sci. 2016;44(10):1872–1878. [Google Scholar]
- 56. Arena CB, Sano MB, Rylander MN, Davalos RV. Theoretical considerations of tissue electroporation with high-frequency bipolar pulses. IEEE Trans Biomed Eng. 2011;58(5):1474–1482. [DOI] [PubMed] [Google Scholar]
- 57. Zupanic A, Ribaric S, Miklavcic D. Increasing the repetition frequency of electric pulse delivery reduces unpleasant sensations that occur in electrochemotherapy. Neoplasma. 2007;54(3):246–250. [PubMed] [Google Scholar]
- 58. Pucihar G, Mir LM, Miklavčič D. The effect of pulse repetition frequency on the uptake into electropermeabilized cells in vitro with possible applications in electrochemotherapy. Bioelectrochemistry. 2002;57(2):167–172. [DOI] [PubMed] [Google Scholar]
- 59. Silve A, Brunet AG, Al-Sakere B, Ivorra A, Mir LM. Comparison of the effects of the repetition rate between microsecond and nanosecond pulses: Electropermeabilization-induced electro-desensitization? Biochim Biophys Acta. 2014;1840(7):2139–2151. [DOI] [PubMed] [Google Scholar]
- 60. Novickij V, Ruzgys P, Grainys A, Saulius Š. High frequency electroporation efficiency is under control of membrane capacitive charging and voltage potential relaxation. Bioelectrochemistry. 2018;119:92–97. [DOI] [PubMed] [Google Scholar]
- 61. Lebar AM, Troiano GC, Tung L, Miklavcic D. Inter-pulse interval between rectangular voltage pulses affects electroporation threshold of artificial lipid bilayers. IEEE Trans Nanobioscience. 2002;1(3):116–120. [DOI] [PubMed] [Google Scholar]
- 62. Steelman ZA, Tolstykh GP, Beier HT, Ibey BL. Cellular response to high pulse repetition rate nanosecond pulses varies with fluorescent marker identity. Biochem Biophys Res Commun. 2016;478(3):1261–1267. [DOI] [PubMed] [Google Scholar]
- 63. Sweeney DC, Reberšek M, Dermol J, Rems L, Miklavčič D, Davalos RV. Quantification of cell membrane permeability induced by monopolar and high frequency bipolar bursts of electrical pulses. Biochim Biophys Acta. 2016;1858(11):2689–2698. [DOI] [PubMed] [Google Scholar]
- 64. Pucihar G, Krmelj J, Reberšek M, Napotnik TB, Miklavčič D. Equivalent pulse parameters for electroporation. IEEE Trans Biomed Eng. 2011;58(11):3279–3288. [DOI] [PubMed] [Google Scholar]
- 65. Kinosita KJ, Tsong TY. Formation and resealing of pores of controlled sizes in human erythrocyte membrane. Nature. 1977;268(4):438–441. [DOI] [PubMed] [Google Scholar]
- 66. Demiryurek Y, Nickaeen M, Zheng M, et al. Transport, resealing, and re-poration dynamics of two-pulse electroporation-mediated molecular delivery. Biochim Biophys Acta. 2015;1848(8):1706–1714. [DOI] [PubMed] [Google Scholar]
- 67. Frandsen SK, Gissel H, Hojman P, Eriksen J, Gehl J. Calcium electroporation in three cell lines: a comparison of bleomycin and calcium, calcium compounds, and pulsing conditions. Biochim Biophys Acta. 2014;1840(3):1204–1208. [DOI] [PubMed] [Google Scholar]
- 68. Cantu JC, Tarango M, Beier HT, Ibey BL. The biological response of cells to nanosecond pulsed electric fields is dependent on plasma membrane cholesterol. Biochim Biophys Acta. 2016;1858(11):2636–2646. [DOI] [PubMed] [Google Scholar]
- 69. Wasson EM, Ivey JW, Verbridge S, Davalos RV. The feasibility of enhancing susceptibility of glioblastoma cells to IRE using a calcium adjuvant. Ann Biomed Eng. 2017;45(11):2535–2547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Dermol J, Pakhomova ON, Pakhomov AG, Miklavčič D. Cell electrosensitization exists only in certain electroporation buffers. PLoS One. 2016;11(7):1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Rassokhin MA, Pakhomov AG. Electric field exposure triggers and guides formation of pseudopod-like blebs in U937 monocytes. J Membr Biol. 2012;245(9):521–529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Bartoletti DC, Harrison GI, Weaver JC. The number of molecules taken up by electroporated cells: quantitative determination. FEBS Lett. 1989;256(1-2):4–10. [DOI] [PubMed] [Google Scholar]
- 73. Kotnik T, Pucihar G, Miklavčič D. Induced transmembrane voltage and its correlation with electroporation-mediated molecular transport. J Membr Biol. 2010;236(1):3–13. [DOI] [PubMed] [Google Scholar]
- 74. Kakorin S, Neumann E. Kinetics of the electroporative deformation of lipid vesicles and biological cells in an electric field. Berichte der Bunsengesellschaft für Phys Chemie. 1998;102(4):670–675. [Google Scholar]
- 75. Tsong TY. On electroporation of cell membranes and some related phenomena. J Electroanal Chem. 1990;299(3):271–295. [Google Scholar]
- 76. Pavlin M, Miklavčič D. Theoretical and experimental analysis of conductivity, ion diffusion and molecular transport during cell electroporation—relation between short-lived and long-lived pores. Bioelectrochemistry. 2008;74(1):38–46. [DOI] [PubMed] [Google Scholar]
- 77. Danesi PR, Horwitz EP, Vandegrift GF, et al. Mass transfer rate through liquid membranes: interfacial chemical reactions and diffusion as simultaneous permeability controlling factors. Sep Sci Technol. 1981;16(2):201–2011. [Google Scholar]
- 78. Sugar IP, Neumann E. Stochastic model for electric field-induced membrane Pores. Biophys Chem. 1984;19(3):211–225. [DOI] [PubMed] [Google Scholar]
- 79. Neu JC, Smith KC, Krassowska W. Electrical energy required to form large conducting pores. Bioelectrochemistry. 2003;60(1-2):107–114. [DOI] [PubMed] [Google Scholar]
- 80. Casciola M, Kasimova MA, Rems L, Zullino S, Apollonio F, Tarek M. Properties of lipid electropores I: molecular dynamics simulations of stabilized pores by constant charge imbalance. Bioelectrochemistry. 2016;109:108–116. [DOI] [PubMed] [Google Scholar]
- 81. Kotnik T, Pucihar G, Reberšek M, Miklavčič D, Mir LM. Role of pulse shape in cell membrane electropermeabilization. Biochim Biophys Acta. 2003;1614(2):193–200. [DOI] [PubMed] [Google Scholar]
- 82. Ibey BL, Xiao S, Schoenbach KH, Murphy MR, Pakhomov AG, Andrei G. Plasma membrane permeabilization by 60- and 600-ns electric pulses is determined by the absorbed dose. Bioelectromagnetics. 2009;30(2):92–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Bowman AM, Nesin OM, Pakhomova ON, Pakhomov AG. Analysis of plasma membrane integrity by fluorescent detection of Tl(+) uptake. J Membr Biol. 2010;236(1):15–26. [DOI] [PMC free article] [PubMed] [Google Scholar]