Abstract.
Tumor volume has been a topic of interest in the staging, prognostic evaluation, and treatment response assessment of malignant pleural mesothelioma (MPM). Deep convolutional neural networks (CNNs) were trained separately for the left and right hemithoraces on the task of differentiating between pleural thickening and normal thoracic tissue on computed tomography (CT) scans. A total of 4259 and 6192 axial sections containing segmented tumor were used to train the left-hemithorax CNN and the right-hemithorax CNN, respectively. Two distinct test sets of 131 sections from the CT scans of 43 patients were used to evaluate segmentation performance by calculating the Dice similarity coefficient (DSC) between deep CNN-generated tumor segmentations and reference tumor segmentations provided by a total of eight observers. Median DSC values ranged from 0.662 to 0.800 over the two test sets when comparing deep CNN-generated segmentations with observer reference segmentations. The deep CNN-based method achieved significantly higher DSC values for all three observers on the test set that allowed direct comparisons with a previously published automated segmentation method of MPM tumor on CT scans (). A deep CNN was implemented for the automated segmentation of MPM tumor on CT scans, showing superior performance to a previously published method.
Keywords: image segmentation, deep learning, computed tomography, malignant pleural mesothelioma, convolutional neural networks
1. Introduction
Malignant pleural mesothelioma (MPM) is a cancer of the pleura primarily caused by exposure to asbestos, with an average of about 1 case per 100,000 people diagnosed annually in the US.1 This malignancy has a poor prognosis; median patient survival is year.2,3 Computed tomography (CT) is the primary imaging modality used for the assessment and follow-up of MPM during treatment.4
The standard clinical evaluation of MPM treatment response involves image-based linear thickness measurements made at up to six tumor locations; however, the nonspherical presentation and nonuniform growth patterns of MPM complicate the acquisition of reproducible linear measurements.5,6 Tumor volume has been found to be associated with patient outcomes in MPM, and it has been suggested that image-based tumor volume could be a more representative measure of tumor bulk for the staging of MPM, assessment of tumor response to treatment, and as a predictor of patient survival.7–13 The time-consuming nature of manual (or even semiautomated) volumetric segmentation of measurable MPM tumor throughout the entire hemithorax currently precludes the use of image-based volume in clinical practice; an accurate, automated, computerized volumetric segmentation of MPM tumor could streamline the acquisition of such measurements.
Deep convolutional neural networks (CNNs) are a type of machine learning classifier that can be readily applied to image classification. Such networks have recently gained attention for a variety of visual recognition tasks, including those with biomedical applications.14,15 Deep CNNs consist of multiple layers of convolutional filters that can be trained to recognize image features that correlate with a given classification of images or image regions. The training of such classifiers requires optimizing a large number of parameters at different layers of the network. Recent advances in the design and applications of such networks have coincided with the increased availability of large annotated image datasets and advancements in computing and processing power.16
The application of deep CNNs to the automated segmentation of medical images involves producing a pixel-wise classification of the input image rather than a global classification of the imaged anatomy. The U-Net architecture presented by Ronneberger et al.17 is among the deep CNN models that have been successfully applied to this class of problem.18 This network architecture allows for the input of full-resolution images of arbitrary size, and the network learns to detect both small- and large-scale features of images in the training set through a downsampling and an upsampling path within the network. Other approaches to deep CNN-based segmentation include the three-dimensional (3-D) U-Net and V-Net architectures, and the application of advanced postprocessing methods to deep CNN-acquired segmentations.19–21
One previously published study presented a method on the automated segmentation of MPM tumor on CT scans; this study employed a step-wise method to identify the pleural space by segmenting the lung parenchyma (a task that has been addressed by others)22–24 and the hemithoracic cavities before attempting to identify MPM tumor within the pleural space.25 Traditional step-wise segmentation methods carry the inherent vulnerability that if one stage of the process fails, the tumor segmentation will be unsuccessful. On the other hand, given a network architecture that is applicable to the segmentation task, a deep CNN trained on a sufficiently extensive and varied set of reference segmentations has the potential to bypass this limitation of traditional approaches.
In this study, we investigated the application of deep CNNs based on the U-Net deep CNN architecture to the automated segmentation of MPM tumor on CT scans. This task is challenging due to case-to-case variability in the presentation and the low contrast of MPM tumor relative to surrounding soft tissue structures.26,27 The ability of deep CNN architectures to effectively learn and combine local and global image features in their classification model could provide a key to the robust volumetric segmentation of MPM tumor.
2. Materials and Methods
MPM patients often present with pleural effusion and atelectatic lung adjacent to the pleural space, both of which have considerable overlap in Hounsfield unit (HU) values with MPM tumor.26,27 Early-stage MPM patients exhibit unilateral disease, although in later stages of the disease the tumor may extend to the contralateral pleura or invade nearby structures, such as the mediastinum, peritoneum, and chest wall.28 As an initial effort at implementing a deep CNN-based method for the segmentation of MPM tumor, this study focused on identifying pleural thickening (which predominantly includes tumor, along with potential pleural effusion and pleural plaques) in patients with unilateral disease in which the tumor had not invaded other organs or structures.
Two deep CNNs were trained separately in the left and right hemithoraces on the two-class problem of differentiating between pleural thickening and “background” pixels on axial CT sections. Results of the present deep CNN-based segmentation method were compared with (1) the output of a previously published automated MPM tumor segmentation method and (2) manual tumor outlines constructed on two sets of CT sections not included in the training dataset: one set of scans had tumor outlines constructed by a group of three observers (two attending thoracic radiologists and one radiology resident) and the other set of scans had tumor outlines constructed by five attending thoracic radiologists.25
2.1. Data Preprocessing
All CT scans used for training, validation, and testing underwent an in-house thoracic segmentation method developed in MATLAB (MathWorks Inc., Natick, Massachusetts) to segment out the patient couch and surrounding air. All CT sections used for training, validation, and testing were converted to unsigned 8-bit integer images with a linear scaling such that pixels lying outside the thorax and pixels of value equal to or below HU were given a value of 0 and pixels of value equal to or greater than 400 HU were given a value of 255. This rescaling of pixel values was used, as preliminary investigations on a subset of the training set showed that capturing the structure of the lungs could be advantageous with respect to distinguishing between tumor pixels lying in the pleural space and soft tissue pixels lying along the outside of the thorax.
2.2. Training Set
234 CT scans from 87 MPM patients were retrospectively collected for training the networks of this study. These images were a subset of those analyzed in a previously published method on the use of disease volumes as a marker for patient response in MPM.11 Pleural thickening was outlined on the scans of the training set by an imaging scientist trained in thoracic anatomy using a semiautomated segmentation method. Of the 87 patients, 39 patients (103 scans) had disease in the left hemithorax and 48 patients (131 scans) had disease in the right hemithorax. Slice thickness varied across scans (see Table 1); to reduce the probability that scans containing a relatively large number of axial sections would overly influence the training process, only every other section was included in the training set for scans of slice thickness , and only every third section was included for scans of slice thickness .
Table 1.
Characteristics of patient scans available for training of the deep CNNs.
| Characteristic | Value |
|---|---|
| Disease laterality | |
| Left hemithorax | 39 (103 scans) |
| Right hemithorax | 48 (131 scans) |
| Median no. of segmented sections per scan | |
| Scans with left-sided disease | 61 (range: 28 to 167) sections |
| Scans with right-sided disease | 69 (range: 35 to 153) sections |
| Median slice thickness | |
| Scans with left-sided disease | 5 (range: 0.625 to 10) mm |
| Scans with right-sided disease | 2.5 (range: 0.625 to 7) mm |
| Median pixel spacing | |
| Scans with left-sided disease | 0.703 (range: 0.582 to 0.871) mm |
| Scans with right-sided disease | 0.703 (range: 0.543 to 0.836) mm |
2.3. Test Sets
Two test sets of MPM patient scans with radiologist-provided reference tumor segmentations were used for testing the deep CNNs trained in this study.
Test set 1 consisted of 61 axial CT sections from 16 patients with pathologically confirmed MPM, with reference segmentations provided independently by two attending radiologists and one radiology resident (observers A, B, and C). These images were used in the analysis of a previously published method on the automated segmentation of MPM tumor on CT scans (the “2011 Method”)25 and provided a direct comparison with that method. Scans containing prominent calcifications or surgical intervention were excluded from the original study, as were CT sections for which no disease was present or the mean Dice similarity coefficient (DSC) value across all observers was (thus reflecting complex disease with low observer agreement). Furthermore, sections for which all three observers did not agree on the laterality of disease were excluded from the analysis of this study due to the hemithorax-specific nature of the present deep CNN-based segmentation method. Of the 61 axial sections, 42 had right-hemithorax disease and 19 had left-hemithorax disease (see Table 2).
Table 2.
Characteristics of CT sections used for testing the deep CNN-based segmentation method.
| Characteristic | Value |
|---|---|
| Test set 1 | |
| Sections with right-sided disease | 42 sections (69%) |
| Sections with left-sided disease | 19 sections (31%) |
| Median slice thickness | 1 (range: 1 to 2) mm |
| Median pixel spacing | 0.709 (range: 0.629 to 0.861) mm |
| Test set 2 | |
| Sections with right-sided disease | 49 sections (70%) |
| Sections with left-sided disease | 21 sections (30%) |
| Median slice thickness | 3 (range: 3 to 5) mm |
| Median pixel spacing | 0.734 (range: 0.535 to 0.883) mm |
Test set 2 consisted of 70 axial CT sections from the baseline scans of 27 patients with pathologically confirmed MPM, with reference segmentations provided independently by five attending thoracic radiologists (observers 1, 2, 3, 4, and 5). These images were used in a previously published study on observer variability in MPM tumor area measurements.29 Sections for which all observers did not agree on the presence or laterality of disease, and for which the mean DSC value across all observers was , were excluded from the present analysis. Of the 70 axial sections, 49 had right-hemithorax disease and 21 had left-hemithorax disease (see Table 2).
2.4. Deep CNN Architecture
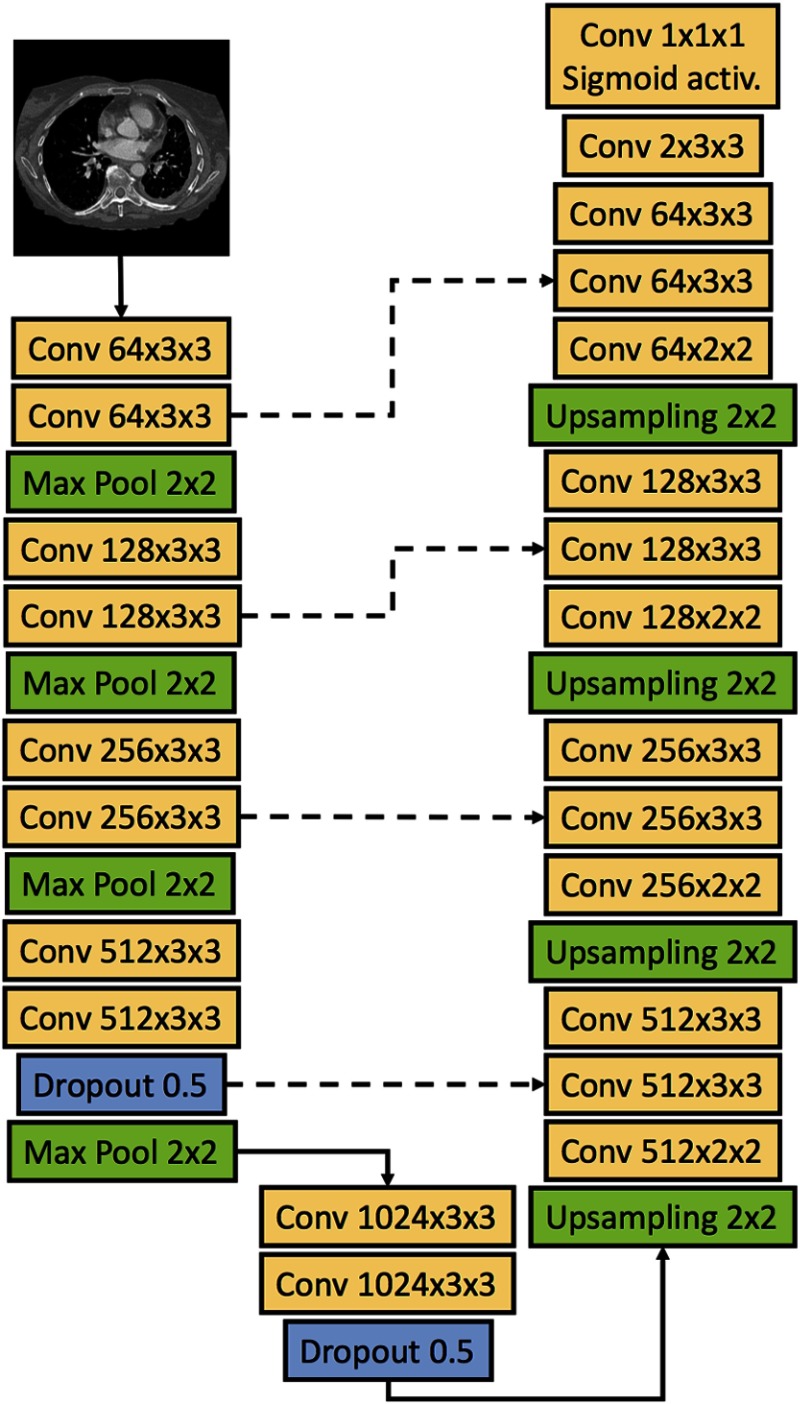
The U-Net deep CNN architecture presented by Ronneberger et al.17 was used for the classification of pixels as pleural thickening or background on axial CT sections. Figure 1 shows the architecture of the deep CNN used in this study. The network accepted as input a image matrix, consisted of a contracting path and an expansive path, and produced a tumor segmentation mask of the same size as the input. At each level of the contracting path, two convolutional layers were applied to the input matrix or the matrix output by the previous level. Convolutional layers in the down- and upsampling paths of the network were followed by a rectified linear unit (ReLU) activation function.30 Following the convolutional layers at each level, the downsampling of the matrix was achieved through a max pooling operation with stride 2. As described in the original U-Net paper, the number of feature channels was doubled at each downsampling step, starting with 64 channels at the input level of the network. At levels for which the downsampled matrix had reached a size of pixels or smaller, the second ReLU was additionally followed by a randomized “dropout” procedure where individual neurons were ignored, or “dropped”, with a probability of 0.5 to prevent overfitting.31
Fig. 1.
Architecture of the U-Net deep CNN of this study. The deep CNN takes as input a image matrix. Solid arrows indicate the flow of the input matrix through the network, and dashed lines indicate merging of information through concatenation of feature maps. Convolutional layers are labeled as “Conv” followed by a triplet of numbers; the first number represents the number of feature channels of the layer, and the second and third number represent the height and width of the convolution window, respectively. Individual neurons were “dropped” at a probability of 0.5 in the two dropout layers of the network. All convolutional layers used the ReLU activation function, except where noted. Upsampling was acquired through nearest-neighbor interpolation.
The upsampling path of the network was initiated once the downsampled matrix reached a size of , with 1024 feature channels at that level. At each level of the upsampling path, a two-dimensional upsampling operation using nearest-neighbor interpolation was applied to the feature matrix followed by a convolutional layer, and the resulting feature map was concatenated with the feature map from the corresponding level of the downsampling path. Two convolutional layers were applied to the resulting input feature matrix at each level of the upsampling path. When the feature matrix had reached a size of , the max pool operation was replaced by a convolution with two feature channels. Finally, a pixel-wise probability matrix of size was acquired using a convolutional layer followed by a sigmoid activation function.
Network loss during training was calculated as the cross-entropy averaged over all pixels of each deep CNN-predicted segmentation and the corresponding reference segmentation:
| (1) |
where is an indicator variable taking the value 1 if the reference classification of pixel is tumor and 0 otherwise, and is the (continuous) deep CNN-predicted probability that pixel is tumor () or background (). The Adam method was used to optimize the network during training using a learning rate of , chosen a priori.32 The deep CNN architecture was implemented using the Keras and Tensorflow deep learning frameworks.33 Experiments were run using online learning (i.e., a batch size of 1) on a scientific computing cluster at the University of Chicago using Nvidia GeForce GTX Titan and Nvidia Tesla K20c Kepler-class graphics processing units (GPUs; Nvidia, Santa Clara, California).
2.5. Experiments
Deep CNNs were trained separately on the sections and reference segmentations of MPM patients with visible disease in the left and right hemithoraces. In cases for which more than two scans were available for a single patient, only the earliest and last available CT scans were used for training of the networks to reduce the influence of individual patients. To evaluate the level of overfitting of the deep CNNs to the training sets during the training process, eight patients were randomly excluded from the training set of each hemithorax classifier and used as a validation set during training. A single scan was randomly selected out of all available scans for each of these eight patients for use in the validation set. During training, the CNNs were applied to these validation sets after each training epoch (i.e., iteration over the training set). To evaluate the variance of the segmentation method, this process of validation set extraction was repeated two more times for each hemithorax, without replacement. Each of these pairs of training and validation sets was used to train a deep CNN. Only the deep CNN trained using the first such selected validation set for each hemithorax was subsequently applied to the test sets; the corresponding training sets consisted of 4259 and 6192 axial sections in the left and right hemithoraces, respectively.
Data augmentation is a technique in which random deformations are applied to the images of the training set to improve CNN generalizability to other datasets and to increase the amount of data available for training.16 The use of data augmentation was investigated in this study for the task of MPM segmentation on axial CT sections. Only minimal augmentation was applied to the set of axial sections used for training due to the inherent asymmetry of the imaged patient anatomy. For this purpose, before each training iteration of the network, a random rotation in the range [, ] and a random scaling in the range [0.95, 1.05] were applied to each of the sections used for training. The ranges of the rotation and scaling were determined by visualizing different rotation angles and scaling values on example CT sections from the training set.
The average binary cross-entropy and the average DSC computed from the validation sets were used in each hemithorax to select the optimal deep CNN to apply to the test sets, with the objectives of (1) minimizing the average on the initial validation set, (2) maximizing the average DSC on the initial validation set, and (3) minimizing the variance in and DSC across the three validation sets.
2.6. Statistical Analysis
Visual inspection revealed that the DSC values obtained when comparing the segmentations of the two computerized methods to the observer reference segmentations on test set 1 did not follow normal distributions. Therefore, the two-sided Wilcoxon signed-rank test was used to test the null hypothesis that the distributions of DSC values were identical for the present deep CNN-based method and the 2011 Method when compared with reference segmentations by each of the three observers on test set 1. The Bonferroni correction was applied to the significance level of all statistical tests to account for the number of comparisons; since three statistical tests were made, the significance level of individual comparisons was adjusted to . Statistical comparisons were made using MATLAB.
The Bland–Altman method was used to evaluate agreement between (1) the tumor area segmented by the 2011 Method and the average tumor area segmented by the three observers on test set 1 and (2) between the tumor area segmented by the present deep CNN-based method and the average tumor area segmented by each set of observers on the two respective test sets. Absolute differences in the segmented area of the computerized methods and average observer-segmented area were found to have a positive correlation with the average segmented tumor area of the segmentation approaches being compared, violating one of the assumptions of the Bland–Altman method. Therefore, the 95% limits of agreement were estimated using relative differences in segmented area as , where is the mean and is the standard deviation of the relative differences between the two segmentation approaches being compared (i.e., computerized and manual).34 The standard error of was estimated as and the standard error of the 95% limits of agreement was estimated as , where is the number of segmented axial sections. 95% confidence intervals (CIs) for and the 95% limits of agreement were found by adding and subtracting twice the standard error from each value in question.35
3. Results
3.1. Training
The binary cross-entropy loss and DSC values on the training and validation sets, with and without data augmentation, are shown in Fig. 2. The solid lines in Fig. 2 indicate the loss and DSC on the training and validation sets used for testing the deep CNNs, and the shaded areas indicate the range of the loss and DSC over all three pairs of training and validation sets. Table 3 lists the minimum loss achieved on the initial validation set for each hemithorax, the corresponding DSC value on the initial validation set, and ranges of and DSC across the three validation sets at the corresponding epoch, with and without data augmentation. For the left hemithorax, training epoch 19 was selected as the optimal deep CNN for application on the test sets; for the right hemithorax, epoch 12 was selected as the optimal deep CNN for application on the test sets. In both hemithoraces, the selected optimal deep CNNs were trained with data augmentation.
Fig. 2.
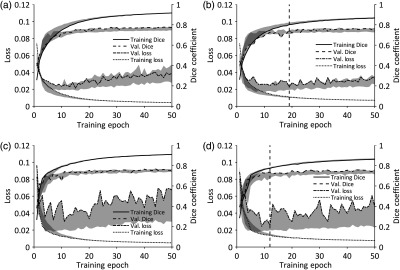
Binary cross-entropy loss and DSC on the training and validation sets during training of the left-hemithorax deep CNN [(a) without data augmentation and (b) with data augmentation] and of the right-hemithorax deep CNN [(c) without data augmentation and (d) with data augmentation]. Solid lines indicate results on the initial pairs of training/validation sets. Shaded areas indicate the range of the loss and DSC across all three pairs of training/validation sets used to assess variance in segmentation performance during training. The vertical dashed lines [at epoch 19 in (b) and epoch 12 in (d)] indicate the training epochs after which the deep CNNs trained on the initial training/validation sets were applied to the test sets.
Table 3.
Minimum binary cross-entropy loss and the corresponding DSC value achieved on the initial validation set during training of the deep CNNs of each hemithorax, and the range of and DSC at the corresponding epochs across all three validation sets used to assess variance in segmentation performance during training. Values shown for networks trained with and without data augmentation. For the right-hemithorax deep CNN trained with augmentation, the network that achieved the second-lowest value of on the initial validation set was selected for application to the test sets due to the narrower range of DSC values across the three validation sets at the corresponding epoch.
| Hemithorax | Metric | Epoch | Value (range) |
|---|---|---|---|
| Left (without augmentation) | Minimum | 15 | 0.021 (0.019 to 0.028) |
| DSC | 15 | 0.752 (0.717 to 0.752) | |
| Left (with augmentation) | Minimum | 19a | 0.023 (0.019 to 0.024) |
| DSC | 19a | 0.746 (0.704 to 0.746) | |
| Right (without augmentation) | Minimum | 11 | 0.030 (0.021 to 0.030) |
| DSC | 11 | 0.741 (0.682 to 0.742) | |
| Right (with augmentation) | Minimum | 9 | 0.024 (0.019 to 0.024) |
| DSC | 9 | 0.732 (0.650 to 0.732) | |
| Second-lowest | 12a | 0.026 (0.020 to 0.026) | |
| DSC | 12a | 0.733 (0.677 to 0.733) |
Deep CNNs selected for application to the test sets.
3.2. Test Set 1
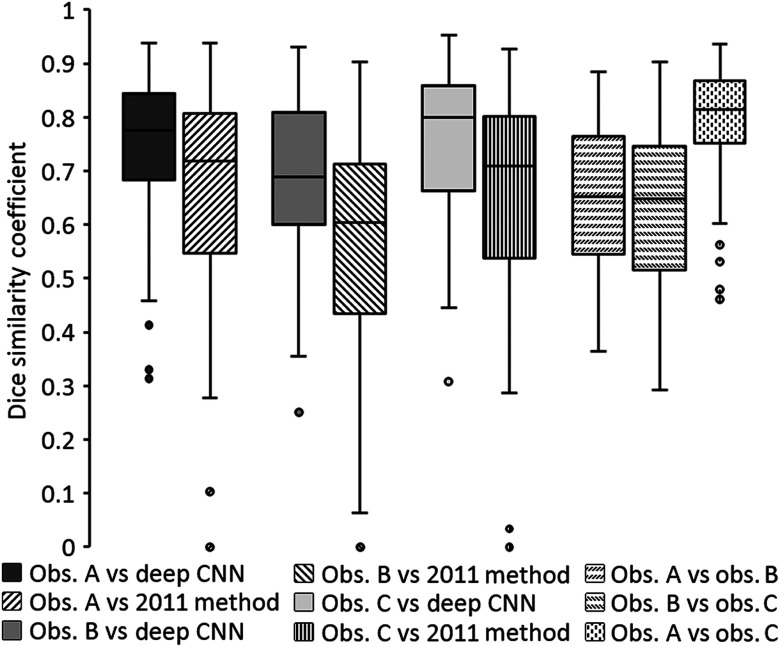
Figure 3 shows boxplots of DSC values obtained when comparing the predicted tumor segmentations of the present deep CNN method and the 2011 Method with the reference segmentations of the three observers on test set 1 and when comparing reference segmentations across observers on test set 1. The median DSC value for the deep CNN method was 0.776 (range: 0.314 to 0.938), 0.689 (range: 0.251 to 0.931), and 0.800 (range: 0.308 to 0.952) for observers A, B, and C, respectively. The median DSC value for the 2011 Method on the same CT sections was 0.720 (range: 0 to 0.938), 0.604 (range: 0 to 0.902), and 0.718 (range: 0 to 0.926) for observers A, B, and C, respectively. Differences in the distributions of DSC values between the two automated segmentation methods on test set 1 were found to be statistically significant for all observers using the two-sided Wilcoxon signed-rank test (, , and for observers A, B, and C, respectively). The median DSC value for interobserver comparisons was 0.652 (range: 0.363 to 0.885), 0.648 (range: 0.293 to 0.902), and 0.814 (range: 0.461 to 0.937) when comparing observers A and B, observers B and C, and observers A and C, respectively.
Fig. 3.
Boxplots showing DSC values obtained when comparing predicted tumor segmentations by the present deep CNN-based method and the 2011 Method with reference segmentations of all three observers on test set 1 and when comparing reference segmentations across observers on test set 1. Horizontal lines inside boxes indicate the median value of each distribution.
Figure 4(a) shows a Bland–Altman plot of the relative differences in segmented tumor area by the deep CNN method and the average tumor area segmented by observers A, B, and C on test set 1. The mean relative difference in segmented tumor area between the deep CNN method and the average observer-segmented area was (95% CI: to 8.5%) with 95% limits of agreement [, 66.1%] (95% CIs: to , 51.1% to 81.1%). Figure 4(b) shows a Bland–Altman plot of the relative differences in segmented tumor area by the 2011 Method and the average tumor area segmented by the three observers on test set 1. The mean relative difference in segmented tumor area between the 2011 Method and the average observer-segmented area was 10.3% (95% CI: to 24.1%) with 95% limits of agreement [, 115.9%] (95% CIs: to , 92.0% to 139.8%).
Fig. 4.
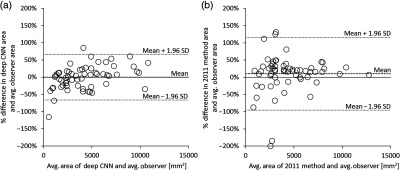
Bland–Altman plots showing (a) the relative differences between the segmented tumor area of the present deep CNN-based method and the average observer-segmented tumor area on test set 1 and (b) the relative differences between the segmented tumor area of the 2011 Method and the average observer-segmented tumor area on test set 1. Means of relative differences and 95% limits of agreement are shown as dashed lines.
3.3. Test Set 2
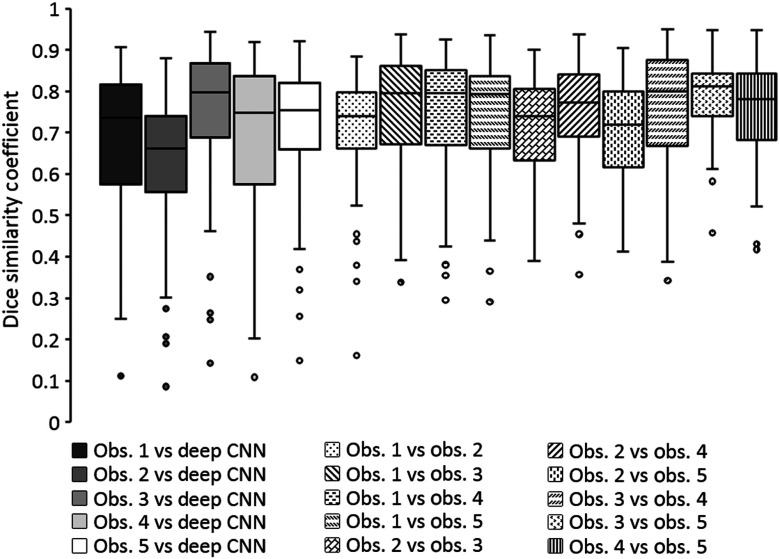
Figure 5 shows boxplots of DSC values obtained when comparing the predicted tumor segmentations of the present deep CNN method with the reference segmentations of the five observers on test set 2 and when comparing reference segmentations across observers on test set 2. The median DSC value for the deep CNN method on test set 2 was 0.735 (range: 0.111 to 0.906), 0.662 (range: 0.086 to 0.879), 0.797 (range: 0.142 to 0.944), 0.747 (range: 0.108 to 0.919), and 0.755 (range: 0.148 to 0.921) for observers 1, 2, 3, 4, and 5, respectively. The median DSC value of the interobserver comparisons of the five observers on test set 2 ranged from 0.720 (range: 0.413 to 0.905) to 0.813 (range: 0.457 to 0.948).
Fig. 5.
Boxplots showing the DSC values obtained when comparing the predicted tumor segmentations by the present deep CNN method with observer reference segmentations on test set 2 and when comparing reference segmentations across observers on test set 2. Horizontal lines inside the boxes indicate the median value of each distribution.
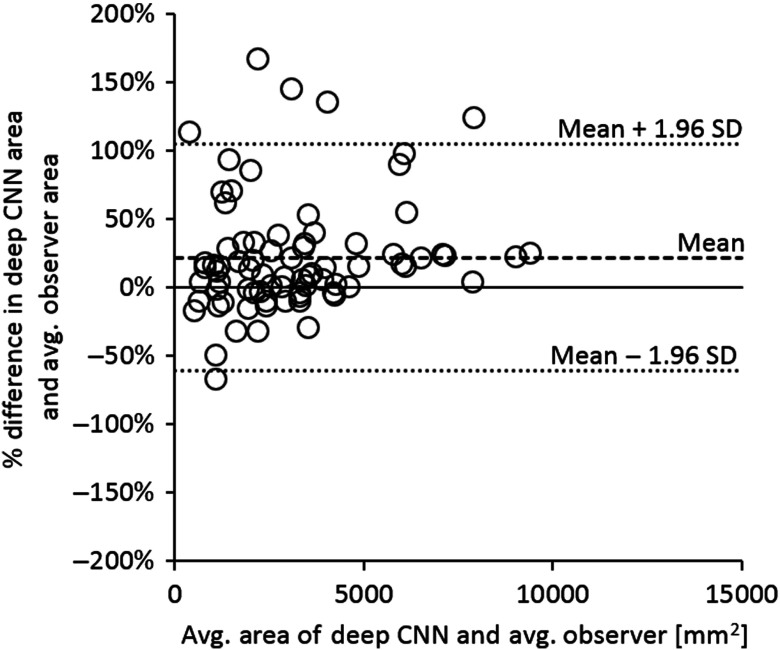
Figure 6 shows a Bland–Altman plot of the relative differences in segmented tumor area by the deep CNN method and the average tumor area segmented by all five observers on test set 2. The mean relative difference in segmented tumor area by the deep CNN method and the average observer-segmented area was 19.5% (95% CI: 9.5% to 29.4%) with 95% limits of agreement [, 101.0%] (95% CIs: to , 83.8% to 118.3%). Seven out of the 15 sections that showed a relative difference (the upper limit of the 95% CI of the mean relative difference) in segmented tumor area exhibited large pleural effusions that were classified as tumor by the deep CNN-based method and excluded from tumor segmentations by all five observers. Leaving these sections out of the calculation, the mean relative difference in deep CNN-predicted tumor area and the average tumor area segmented by the five observers on the remaining 63 sections of test set 2 was 8.7% (95% CI: 2.4% to 15.1%) with 95% limits of agreement [, 58.3%] (95% CIs: to , 47.2% to 69.3%).
Fig. 6.
Bland–Altman plot showing the relative differences between the segmented tumor area of the present deep CNN-based method and the average observer-segmented tumor area on test set 2. Mean of relative differences and 95% limits of agreement are shown as dashed lines.
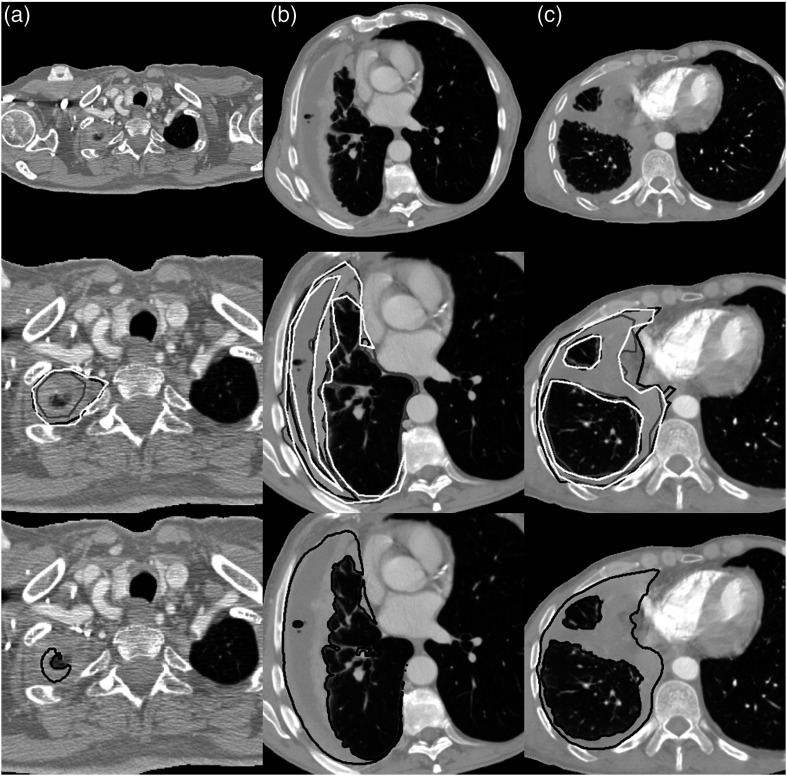
Figure 7 shows the preprocessed CT sections, observer reference segmentations, and deep CNN-predicted tumor segmentations for three example CT sections selected at random from the bottom 10th percentile, the interquartile range, and the top 10th percentile of the average DSC value when comparing deep CNN-predicted segmentations with observer reference segmentations across both test sets.
Fig. 7.
Preprocessed CT sections (top), observer reference tumor segmentations (middle; white, gray, and black outlines), and deep CNN-predicted tumor segmentations (bottom; black outlines), for three sections of the two test sets. Sections were selected at random from (a) the bottom 10th percentile (test set 1, average DSC = 0.366), (b) the interquartile range (test set 2, average DSC = 0.647), and (c) the top 10th percentile (test set 1, average DSC = 0.857) of the average DSC value when comparing deep CNN-predicted and observer reference segmentations across both test sets. In (b), only three of the five observer segmentations are shown in white, gray, and black outlines according to the lowest, highest, and median DSC value for this axial section, respectively.
4. Discussion
Scarcity of data is a common issue when applying machine learning techniques to the medical imaging domain. Studies on deep CNN-based segmentation methods have often applied extensive augmentation to overcome this problem in biomedical applications.19,36 Furthermore, data augmentation can improve both the performance and generalizability of CNNs to unseen datasets.37,38 In this study, only minimal augmentation was applied to the training set due to the inherent asymmetries of patient anatomy on chest CT scans. As shown in Fig. 2, the application of data augmentation to the training sets decreased the overall variance in validation set performance for both sides of the chest; however, Table 3 shows that similar optimal deep CNN performance was achieved with and without data augmentation. Deep CNNs trained with data augmentation were ultimately selected for application to the test sets in this study due to the improved performance and generalizability shown in previous studies on deep CNN-based segmentation.
The present deep CNN-based segmentation method of MPM tumor showed significantly greater overlap with the reference tumor segmentations of all three observers on test set 1 when compared with a previously published segmentation method (“2011 Method”). Furthermore, Bland–Altman plots comparing the segmented tumor area by the deep CNN-based method and the 2011 Method with the average observer-segmented area on test set 1 showed narrower limits of agreement for the deep CNN-based method. These results show an overall superior performance of the present deep CNN-based segmentation method when compared with the 2011 Method and indicate that, in general, deep CNN-based segmentation methods are applicable to the complex task of segmenting MPM tumor on CT scans.
The deep CNN method showed comparable overlap with the five radiologists on test set 2 as with the three observers on test set 1; however, Bland–Altman analysis of the relative differences between the deep CNN-predicted tumor area and the average observer-segmented tumor area on test set 2 showed increased bias and wider 95% limits of agreement than on test set 1, despite test set 2 including a greater number of axial sections than test set 1 (the width of the estimated 95% limits of agreement is inversely related to the number of samples). This increased bias of the deep CNN method on test set 2 could be partly due to a number of sections in test set 2 exhibiting large pleural effusions combined with the fact that tumor segmentations in the training set of this study did not uniformly exclude pleural effusion of the same laterality as visible tumor. Of the 15 axial CT sections for which the deep CNN-predicted tumor area on test set 2 exceeded 29.4% of the average observer-segmented area (the upper limit of the 95% CI of the mean relative difference), seven sections exhibited large effusions in the pleural space that were both classified as tumor by the deep CNN-based method and excluded from tumor segmentations by all five observers. The median relative difference between deep CNN-predicted tumor area and average observer-segmented area for these seven sections was 124.0% (range: 54.6% to 166.3%), and leaving these sections out of the analysis reduced the bias between the computerized tumor area and the average observer-segmented tumor area. This observation suggests that further curation of the training set, possibly combined with additional methods of pixel-wise distinction between tumor and pleural effusion, will be required in future studies to increase the agreement of deep CNN-predicted tumor area and observer-segmented tumor area.
In this study, deep CNNs were trained separately for the segmentation of MPM tumor in the left and right hemithoraces. Bilateral disease is not common among MPM patients, and preliminary investigations using deep CNNs trained on a set of scans exhibiting bilateral disease and unilateral disease in both sides of the chest indicated an increased likelihood of the erroneous classification of pleural thickening in the contralateral hemithorax.39 Given the relatively large pool of scans available for training the deep CNNs of this study, it was deemed appropriate to pursue the training of hemithorax-specific CNNs, rather than the development of a post-hoc method for filtering out pixels falsely classified as tumor in the contralateral hemithorax. While CNNs are designed to be translationally invariant, it was presumed that, given a training set of unilateral tumor segmentations, the CNNs would learn enough global context to avoid erroneously identifying pleural thickening in the contralateral hemithorax as tumor. The specificity of the deep CNNs trained in this study with respect to disease laterality was good; out of the 131 CT sections from the two test sets, only four sections (3%) from the scans of three patients (all with left-hemithorax disease) contained pixels in the contralateral hemithorax erroneously classified as tumor. In two of these sections, the erroneous inclusion was due to a large effusion in the right hemithorax (area of segmented region: and ); in one case, it was due to the deep CNN classifying 27 pixels of the outer superior surface of the liver as medial MPM tumor, and in another case, the deep CNN included a single pixel of the contralateral pleural space in the tumor segmentation.
The present deep CNN-based segmentation method was completely automated apart from user input on the laterality of disease. The trained deep CNNs can be applied to a new CT scan after minimal preprocessing has taken place: segmentation of the patient’s thorax using a simple threshold-based technique and applying the appropriate numerical conversion and linear scaling to the pixel values of the scan. Segmentation of tumor on 100 axial CT sections using the present method took on an Nvidia GeForce GTX Titan GPU (originally released in 2013) with 6 GB of memory.
5. Conclusions
In this study, a deep CNN-based method was implemented for the automated segmentation of MPM tumor on CT scans. Deep CNNs were trained separately for the segmentation of disease in the left and right hemithoraces. The present deep CNN-based method showed significantly higher overlap with observer-provided reference segmentations when compared with a previously published method on automated MPM segmentation that utilized a traditional step-wise approach. Future work will include the training of deep CNNs on larger datasets, the exploration of the application of 3-D CNNs to the segmentation task, and the investigation of approaches to distinguish more clearly between tumor pixels and nontumorous pleural thickening.
Acknowledgments
The authors would like to acknowledge Anna K. Nowak for her assistance in the collection of MPM patient scans used in the training set of this study. Partial funding for this work was provided by the National Institutes of Health under Grant Nos. S10 RR021039 and P30 CA14599. The contents of this paper are solely the responsibility of the authors and do not necessarily represent the official views of any of the supporting organizations. This work was supported, in part, by the Plooy Family and the Kazan McClain Partners’ Foundation, Inc.
Biographies
Eyjolfur Gudmundsson is a PhD student of medical physics at the University of Chicago. He received his BS degrees in physics and computer science from the University of Iceland in 2013. His thesis work with Dr. Samuel Armato at the University of Chicago is on the computer-aided diagnosis, segmentation and image analysis of malignant pleural mesothelioma. He is a student member of SPIE.
Christopher M. Straus is an associate professor of radiology and the director of Medical Student Education, The University of Chicago. He received his AB and MD degrees from the University of Chicago in 1988 and 1992, respectively. He is the author of more than 70 journal papers and two book chapters. His current research interests center on optimizing medical education, imaging mesothelioma, and public perception of radiology.
Samuel G. Armato III is an associate professor of radiology and chair of the Committee on Medical Physics at The University of Chicago. His research interests involve the development of computer-aided diagnostic methods for thoracic imaging, including automated lung nodule detection and analysis in CT scans, semiautomated mesothelioma tumor response assessment, image-based techniques for the assessment of radiotherapy-induced normal tissue complications, and the automated detection of pathologic change in temporal subtraction images.
Disclosures
S.G.A. receives royalties and licensing fees for computer-aided diagnostic technology through the University of Chicago. S.G.A. is a consultant for Aduro Biotech, Inc.
References
- 1.Henley S. J., et al. , “Mesothelioma incidence in 50 states and the District of Columbia, United States, 2003–2008,” Int. J. Occup. Environ. Health 19, 1–10 (2013). 10.1179/2049396712y.0000000016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.van Meerbeeck J. P., et al. , “Malignant pleural mesothelioma: the standard of care and challenges for future management,” Crit. Rev. Oncol. Hematol. 78(2), 92–111 (2011). 10.1016/j.critrevonc.2010.04.004 [DOI] [PubMed] [Google Scholar]
- 3.Vogelzang N. J., et al. , “Phase III study of pemetrexed in combination with cisplatin versus cisplatin alone in patients with malignant pleural,” J. Clin. Oncol. 21(14), 2636–2644 (2008). 10.1200/JCO.2003.11.136 [DOI] [PubMed] [Google Scholar]
- 4.Scherpereel A., et al. , “Guidelines of the European Respiratory Society and the European Society of Thoracic Surgeons for the management of malignant pleural mesothelioma,” Eur. Respir. J. 35(3), 479–495 (2010). 10.1183/09031936.00063109 [DOI] [PubMed] [Google Scholar]
- 5.Byrne M. J., Nowak A. K., “Modified RECIST criteria for assessment of response in malignant pleural mesothelioma,” Ann. Oncol. 15(2), 257–260 (2004). 10.1093/annonc/mdh059 [DOI] [PubMed] [Google Scholar]
- 6.Oxnard G. R., Armato S. G., III, Kindler H. L., “Modeling of mesothelioma growth demonstrates weaknesses of current response criteria,” Lung Cancer 52(2), 141–148 (2006). 10.1016/j.lungcan.2005.12.013 [DOI] [PubMed] [Google Scholar]
- 7.Pass H. I., et al. , “Preoperative tumor volume is associated with outcome in malignant pleural mesothelioma,” J. Thorac. Cardiovasc. Surg. 115(2), 310–318 (1998). 10.1016/S0022-5223(98)70274-0 [DOI] [PubMed] [Google Scholar]
- 8.Armato S. G., III, et al. , “Radiologic-pathologic correlation of mesothelioma tumor volume,” Lung Cancer 87(3), 278–282 (2015). 10.1016/j.lungcan.2014.11.019 [DOI] [PubMed] [Google Scholar]
- 9.Liu F., et al. , “Assessment of therapy responses and prediction of survival in malignant pleural mesothelioma through computer-aided volumetric measurement on computed tomography scans,” J. Thorac. Oncol. 5(6), 879–884 (2010). 10.1097/JTO.0b013e3181dd0ef1 [DOI] [PubMed] [Google Scholar]
- 10.Frauenfelder T., et al. , “Volumetry: an alternative to assess therapy response for malignant pleural mesothelioma?” Eur. Respir. J. 38(1), 162–168 (2011). 10.1183/09031936.00146110 [DOI] [PubMed] [Google Scholar]
- 11.Labby Z. E., et al. , “Disease volumes as a marker for patient response in malignant pleural mesothelioma,” Ann. Oncol. 24(4), 999–1005 (2013). 10.1093/annonc/mds535 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gill R. R., et al. , “Epithelial malignant pleural mesothelioma after extrapleural pneumonectomy: stratification of survival with CT-derived tumor volume,” Am. J. Roentgenol. 198(2), 359–363 (2012). 10.2214/AJR.11.7015 [DOI] [PubMed] [Google Scholar]
- 13.Gill R. R., et al. , “North American multicenter volumetric ct study for clinical staging of malignant pleural mesothelioma: feasibility and logistics of setting up a quantitative imaging study,” J. Thorac. Oncol. 11(8), 1335–1344 (2016). 10.1016/j.jtho.2016.04.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.LeCun Y., Bengio Y., Hinton G., “Deep learning,” Nature 521(7553), 436–444 (2015). 10.1038/nature14539 [DOI] [PubMed] [Google Scholar]
- 15.Shin H. C., et al. , “Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning,” IEEE Trans. Med. Imaging 35(5), 1285–1298 (2016). 10.1109/TMI.2016.2528162 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Krizhevsky A., Hinton G. E., Sutskever I., “ImageNet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems, Pereira F., et al., Eds, Vol. 25, pp. 1097–1105, Curran Associates, Inc. (2012). [Google Scholar]
- 17.Ronneberger O., Fischer P., Brox T., “U-Net: convolutional networks for biomedical image segmentation,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, pp. 234–241 (2015). 10.1007/978-3-319-24574-4_28 [DOI] [Google Scholar]
- 18.Kayalibay B., Jensen G., van der Smagt P., “CNN-based segmentation of medical imaging data,” arXiv:1701.03056 (2017).
- 19.Çiçek Ö., et al. , “3D U-net: learning dense volumetric segmentation from sparse annotation,” Lect. Notes Comput. Sci. 9901, 424–432 (2016). 10.1007/978-3-319-46723-8_49 [DOI] [Google Scholar]
- 20.Milletari F., Navab N., Ahmadi S.-A., “V-Net: fully convolutional neural networks for volumetric medical image segmentation,” in 2016 Fourth Int. Conf. on 3D Vision (3DV) (2016). 10.1109/3DV.2016.79 [DOI] [Google Scholar]
- 21.Kamnitsas K., et al. , “Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation,” Med. Image Anal. 36, 61–78 (2017). 10.1016/j.media.2016.10.004 [DOI] [PubMed] [Google Scholar]
- 22.Armato S. G., III, Sensakovic W. F., “Automated lung segmentation for thoracic CT: impact on computer-aided diagnosis,” Acad. Radiol. 11(9), 1011–1021 (2004). 10.1016/j.acra.2004.06.005 [DOI] [PubMed] [Google Scholar]
- 23.Mansoor A., et al. , “A generic approach to pathological lung segmentation,” IEEE Trans. Med. Imaging 33(12), 2293–2310 (2014). 10.1109/TMI.2014.2337057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Harrison A. P., et al. , “Progressive and multi-path holistically nested neural networks for pathological lung segmentation from CT images,” Lect. Notes Comput. Sci. 10435, 621–629 (2017). 10.1007/978-3-319-66179-7_71 [DOI] [Google Scholar]
- 25.Sensakovic W. F., et al. , “Computerized segmentation and measurement of malignant pleural mesothelioma,” Med. Phys. 38(1), 238–244 (2011). 10.1118/1.3525836 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ng C. S., Munden R. F., Libshitz H. I., “Malignant pleural mesothelioma: the spectrum of manifestations on CT in 70 cases,” Clin. Radiol. 54(7), 415–421 (1999). 10.1016/S0009-9260(99)90824-3 [DOI] [PubMed] [Google Scholar]
- 27.Corson N., et al. , “Characterization of mesothelioma and tissues present in contrast-enhanced thoracic CT scans,” Med. Phys. 38(2), 942–947 (2011). 10.1118/1.3537610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rusch V. W., “A proposed new international TNM staging system for malignant pleural mesothelioma,” Chest 108(4), 1122–1128 (1995). 10.1378/chest.108.4.1122 [DOI] [PubMed] [Google Scholar]
- 29.Labby Z. E., et al. , “Variability of tumor area measurements for response assessment in malignant pleural mesothelioma,” Med. Phys. 40(8), 081916 (2013). 10.1118/1.4810940 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Glorot X., Bordes A., Bengio Y., “Deep sparse rectifier neural networks,” in Proc. 14th Int. Conf. on Artificial Intelligence and Statistics (AISTATS’11), Vol. 15, pp. 315–323 (2011). [Google Scholar]
- 31.Srivastava N., et al. , “Dropout: a simple way to prevent neural networks from overfitting,” J. Mach. Learn. Res. 15, 1929–1958 (2014). [Google Scholar]
- 32.Kingma D. P., Ba J., “Adam: a method for stochastic optimization,” in Int. Conf. Learning Representations, Vol. 2015, pp. 1–15 (2014). [Google Scholar]
- 33.Abadi M., et al. , “TensorFlow: a system for large-scale machine learning,” in 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI’16), pp. 265–284 (2016). [Google Scholar]
- 34.Bland J. M., Altman D. G., “Measuring agreement in method comparison studies,” Stat. Methods Med. Res. 8(2), 135–160 (1999). 10.1177/096228029900800204 [DOI] [PubMed] [Google Scholar]
- 35.Bland J. M., Altman D. G., “Statistical methods for assessing agreement between two methods of clinical measurement,” Lancet 327, 307–310 (1986). 10.1016/S0140-6736(86)90837-8 [DOI] [PubMed] [Google Scholar]
- 36.Roth H. R., et al. , “An application of cascaded 3D fully convolutional networks for medical image segmentation,” Comput. Med. Imaging Graphics 66, 90–99 (2018). 10.1016/j.compmedimag.2018.03.001 [DOI] [PubMed] [Google Scholar]
- 37.LeCun Y., et al. , “Efficient backprop,” in Neural Networks: Tricks of the Trade, Montavon G., Orr G. B., Müller K. R., Eds., 2nd ed., pp. 9–48, Springer-Verlag, Berlin, Heidelberg: (2012). [Google Scholar]
- 38.Simard P. Y., Steinkraus D., Platt J. C., “Best practices for convolutional neural networks applied to visual document analysis,” in Proc. Seventh Int. Conf. on Document Analysis and Recognition, 2003, pp. 958–963 (2003). 10.1109/ICDAR.2003.1227801 [DOI] [Google Scholar]
- 39.Heelan R. T., et al. , “Staging of malignant pleural mesothelioma: comparison of CT and MR imaging,” AJR. Am. J. Roentgenol. 172(4), 1039–1047 (1999). 10.2214/ajr.172.4.1058714433. [DOI] [PubMed] [Google Scholar]