Improved Ribo-seq enables identification of cryptic translation events

Abstract

Ribosome profiling has predicted thousands of short open reading frames (sORFs) in eukaryotic cells, but still suffers from substantial levels of noise. PRICE (https://github.com/erhard-lab/price) is a computational method modeling the experimental noise to accurately resolve overlapping sORFs and non-canonical translation initiation. We experimentally validated translation using MHC-I peptidomics and saw that sORF-derived peptides efficiently enter the MHC-I presentation pathway and thus constitute a substantial fraction of the antigen repertoire.

Ribosome profiling (Ribo-seq) is a powerful approach to measure translational activity in a genome-wide and quantitative manner with base-pair resolution¹. It visualizes the triplet shifts of actively translating ribosomes and thereby allows the identification of codons and their corresponding ORFs translated at the time of cell lysis. This has resulted in the prediction of thousands of short open reading frames (sORFs) including upstream and upstream-overlapping ORFs (uORFs/uoORFs) revealing an important new layer of translational control in eukaryotic cells². However, accurate and reliable identification of sORFs has remained difficult for overlapping ORFs and for initiation at non-canonical (non-AUG) start codons. In addition, the vast majority of these novel cryptic gene products have remained virtually undetectable in whole cellular proteomes and thus appear to be highly unstable. Here, we present a computational approach that enables accurate identification of sORFs in Ribo-seq data. It is based on computational modeling and subsequent removal of experimental noise from Ribo-seq data, allowing for improved statistical testing for active translation. Based on the accurate identification of thousands of sORFs, we show that, albeit being dramatically underrepresented in the cellular proteome, sORF-derived peptides efficiently enter the MHC-I presentation pathway and can be quantitatively recovered by MHC-I peptidome analysis. MHC-I peptidome analysis thus represents a potent method for large-scale validation of sORF translation.

Ribosome footprints do not exhibit a singular specific size. Instead, reads are the result of two stochastic RNase cleavage events. Thus, deterministic rules (e.g. use an offset of 12) to recover the codon located in the P site of the actively translating ribosome (signal) lead to reads mapped to off-frame codons (noise). Depending on the combination of read lengths used for charting ribosome occupancy, signal is traded off for the signal to noise ratio. Moreover, untemplated nucleotide additions frequently observed in Ribo-seq experiments further increase noise levels (see Supplementary Fig. 1).

We developed Probabilistic inference of codon activities by an EM algorithm (PRICE) to model the stochastic processes involved in Ribo-seq (Fig. 1a). For each individual experiment all parameters are directly inferred from annotated, well-translated ORFs. Any codon located in the P site of a ribosome is able to produce several kinds of footprints and their proportions depend on these parameters. Our method determines the set of codons that generates the observed reads with maximum likelihood (Supplementary Fig. 2).

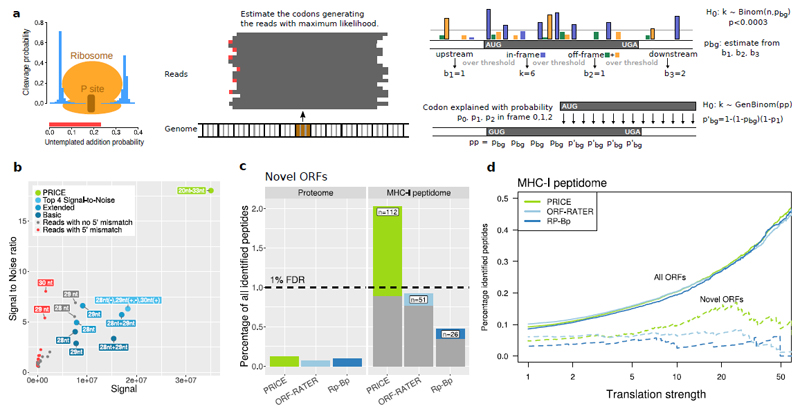
Figure 1. The PRICE approach.

(a) Schematic of the approach. Left: Bars represent parameters of the probabilistic model. Center: Translated codons are identified by solving the inverse problem of the model. Right: calling actively translated ORFs based on the generalized binomial distribution (for details see Online Methods).

(b) Approaches to map reads to codons are compared with respect to signal (total number of reads mapped in-frame) and the signal to noise ratio (noise: reads mapped out-of-frame to annotated ORFs). Colors represent deterministic mapping of read classes defined by length and 5’ mismatch state (red, grey), of combinations of read classes (blue; Basic: ignoring 5’ mismatches; Extended: considering 5’ mismatches; Top 4: combining the best read classes; see also Supplementary Fig. 4) and probabilistic mapping by PRICE (green).

(c) Total amount of peptides detected in proteome and MHC-I peptidome mass spectrometry experiments (MHC-I peptidome data set 1; see Supplementary Fig. 9a for the other experiment). The 1% peptide identification FDR is indicated. Grey bars show the peptides from ORFs also identified by ORF-RATER or Rp-Bp (for PRICE) or ORFs also identified by PRICE (for ORF-RATER and Rp-Bp).

d) Validation rates of peptides from predicted ORFs with a minimal number of reads per codon (MHC-I peptidome data set 2; see Supplementary Fig. 9b for the other experiment). Rates for all ORFs (solid lines) identified by the indicated methods and for ORFs predicted de-novo (dashed lines) are shown.

After assembling identified codons to ORF candidates, potential start codons are predicted with high accuracy using a machine-learning model (Supplementary Fig. 3). If available, this can also integrate samples treated with Lactimidomycin or Harringtonine for translation start site enrichment^3,4. In principle, experimental noise in an ORF candidate can arise due to (i) reads from overlapping ORFs, (ii) ribosome scanning or abortive translation events in the leader sequence, or (iii) due to non-ribosome-mediated mRNA protection from RNase treatment. To exclude candidate ORFs that reflect experimental noise, we use a hypothesis test based on the generalized binomial distribution that is specifically designed to also identify overlapping ORFs (Fig. 1a).

We first compared the signal and noise levels obtained by PRICE to the deterministic codon mapping approaches utilized by prior methods^5–11 (While this manuscript was under review, a further method for Ribo-seq data has been published¹²; however, it also utilizes the deterministic mapping strategy and does not address potentially overlapping ORFs). For Ribo-seq data obtained from herpes simplex virus 1 (HSV-1) infected primary human fibroblasts¹³, about 18 million of the 37 million reads mapping to CDS (49.1%) could be used for further analyses with the optimal deterministic mapping method (Supplementary Fig. 4). In contrast, applying PRICE allowed us to utilize more than 94% of the CDS mapped reads as signal and increased the signal-to-noise ratio from 6.3 to more than 18 (Fig. 1b). Similar improvements were achieved when reanalyzing various published Ribo-seq data from other labs (Supplementary Fig. 5). This included data from different organisms and experimental systems (Supplementary Table 1), which all strongly benefitted in signal-to-noise ratios and the total amount of usable reads.

We next assessed the reproducibility of different kinds of sORFs in two Ribo-seq experiments^13,14. The performance of PRICE was compared with 6 previously published Ribo-seq analysis methods^6–11. Only PRICE was able to reproducibly identify uORFs/uoORFs with the expected distribution of start codons. In addition, it was the only method able to reliably identify many uORFs/uoORFs with both canonical AUG initiation and non-canonical start codons (Supplementary Fig. 6 and 7). Of note, PRICE was >30-50 fold faster than the other method in analyzing both data sets (Supplementary Table 2), enabling Ribo-seq data analysis without special hardware.

To experimentally assess the sensitivity and specificity of our new approach, we prepared a database containing all ORFs identified by PRICE, ORF-RATER and Rp-Bp in primary human fibroblasts for validation by mass spectrometry. The number of peptides, which originated from the sORFs in our database still remained substantially underrepresented in a large published set of whole cell proteome data from primary human fibroblasts¹⁵ (Fig. 1c; Supplementary Table 3). Their detection did not exceed the false-discovery rate (FDR) of 1% used for peptide identification, which effectively renders this kind of whole proteome mass-spec data useless for the validation of sORF expression (Supplementary Fig. 8).

Peptide presentation by MHC-I is thought to mainly depend on translation rates rather than overall protein abundance¹⁶. We thus screened a published (called data set 1) and a newly obtained MHC-I peptidome data set (called data set 2) from primary human fibroblasts¹⁷ with our database. While peptides identified based on the sORFs predicted by ORF-RATER and Rp-Bp again did not significantly exceed the FDR, the sensitivity of PRICE was substantially higher (2x and 4x compared to ORF-RATER and Rp-Bp, respectively; Fig. 1c) and significantly exceeded the FDR. Of note, almost all of the validated ORFs identified by ORF-RATER and Rp-Bp were also identified by PRICE confirming its high sensitivity.

To assess the specificity of sORFs identification, we compared the percentage of validated peptides among all possible peptides from identified ORFs with their respective translation rates obtained by Ribo-seq. For large annotated ORFs, the number of validated peptides in both the whole proteome (Supplementary Fig. 8b) and the MHC-I peptidome (Fig. 1d) increased with stronger translation. In the MHC-I peptidome, validation rates for sORFs identified by PRICE (but not any of the other algorithms) accounted for up to one third of the validation rate of large proteins (Fig. 1d) in two independent experiments (Supplementary Fig. 9). Therefore, sORFs-derived peptides are efficiently presented by MHC-I in a translation rate- but not abundance-dependent manner. Of note, similar to the MHC-I-associated peptides originating from the annotated cellular proteins, sORF-derived peptides showed high predicted binding affinities¹⁸ to the HLA allotypes (Supplementary Fig. 10). Incorporation of sORF-derived peptides into MHC-I thus appears to follow the same rules as observed for large ORFs and provides compelling evidence that the bulk of these cryptic gene products do not represent artifacts of Ribo-seq experiments. Interestingly, MHC-I presentation is thought to predominantly arise from so-called ‘defective ribosomal products’ (DRiPs), which are rapidly degraded upon translation by the proteasome¹⁶. Our findings highlight striking similarities of DRiPs and sORFs suggesting that efficient targeting of sORF-derived proteins/peptides into the DRiPs pathway may contribute to their low abundance within the cellular proteome.

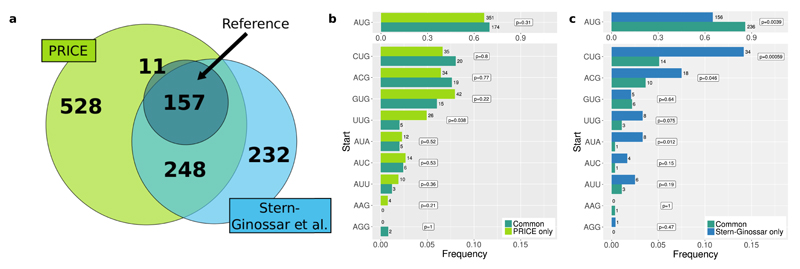
We used our validated approach to refine the annotation of the HCMV translatome¹⁴. In contrast to the original analysis of the Ribo-seq data (157 of 168 ORFs), PRICE recovered all 168 ORFs of the reference annotation. Furthermore, we confirmed more than half (248/480) of the novel ORFs identified in Ref. 14 and identified an additional 528 putative ORFs that were previously not detected (Fig. 2a). Of the 232 novel ORFs not recovered by PRICE, 141 were identified as noise, the remaining 91 did not show a clear signature of active translation (Supplementary Fig. 11a). The start codon distributions of the different sets of putative ORFs clearly show that majority of PRICE identified ORFs but not the ORFs discarded by PRICE indeed result from actively translating ribosomes (Fig. 2b-c).

Figure 2. Re-decoding human cytomegalovirus.

(a) Venn diagram comparing the indicated datasets. We merged N-terminal variants of ORFs ending at the same stop codon.

(b) Comparison of the start codon distribution of 528 novel ORFs detected only by PRICE (light green) to the distribution of the 248 confirmed ORFs (turquois) (p ≈ 0.42, Fisher's combined probability test based on indicated one-sided binomial tests). Note that an ORF may have more than one start codon.

(c) The start codon distribution of the 232 not confirmed ORFs (blue) and confirmed ORFs (turquoise) (p ≈ 3.2 × 10⁻⁵, Fisher's combined probability test based on indicated one-sided binomial tests).

It is important to note that, albeit showing a clear signature of active translation, about two-thirds of the 528 novel ORFs were expressed at low levels (Supplementary Fig. 11b). The functional role of many of these novel ORFs is therefore questionable. We also identified numerous novel large ORFs (>100aa) with low translation rates (Supplementary Fig. 11b). This is indicative of negative selection against the introduction of stop codons in the HCMV genome and strongly suggests that these indeed are, or once have been functional in the evolution of the virus.

Online Methods

Read mapping

All annotations used in this study are based on Ensembl 75. Reads were mapped using Bowtie 1.0¹⁹ to rRNA, genomic and transcriptomic sequences. rRNA reads and reads mapping to the mitochondrial genome were discarded, transcriptomic alignments preferred over genomic alignments. All alignments were mapped to genomic coordinates. Ambiguous alignments (w.r.t. genomic coordinates) were resolved using an adapted RESCUE procedure²⁰. Briefly, for each multimapping read, we assess the number of reads mapping uniquely and close to each potential mapping site. For clear-cut cases, reads are mapped to one of the potential sites (e.g. no other reads at the other potential sites), in all other cases, reads are mapped to all sites and fractional counts are used (see Supplementary Note 1).

Inference of model parameters

Reads uniquely mapping within coding sequences and not overlapping a start or stop codon were collected. We define the frame of a read as the position of the first annotated codon within the read. If a read mapped to more than one isoform in different frames, it was discarded. We counted the three frames for each read class characterized by read length and 5’ mismatch state, which are the sufficient statistics for our EM algorithm that determines the maximum likelihood parameters θ = (a, u₁, …, u_M, d₁, …, d_M) of the following model (see Supplementary Note 2 for details):

$$L\left(\theta ;R\right)={\displaystyle \prod _{r\in R}{\displaystyle \sum _{p\in F_r}\left(1-a\right)u_p{d}_{l_r-p-3}+a{u}_{p-1}{d}_{l_r-p-3}}}$$

a is the probability of an untemplated 5’ nucleotide addition, u_p and d_p are the cleavage probabilities at distance p from the P site codon. R is the set of all reads, and F_r are the potential codon positions in a read r according to the annotation.

Codon inference

Based on the inferred model parameters θ, activity values of all contained codons C are estimated for observed reads R within a chunk of the genome by maximizing the likelihood of the following model:

$$L\left(C;\theta ,R\right)={\displaystyle \prod _{r\in R}{\displaystyle \sum _{c\in C}{a}_c{p}_{r,c}}}$$

Here, a_c is the activity of codon c, and p_r,c is the probability that a ribosome at codon c has generated read r, which can be directly computed from θ (see Supplementary Note 3 for details).

Regularization

We use a greedy strategy to seek a sparse solution of codons: First, the maximum likelihood solution is identified by the EM algorithm (see Supplementary Note 3). Then, we check for each codon, starting from the weakest to the most active, whether the decrease in the log likelihood without this codon is smaller than a parameter δ, in which case the codon is removed. δ can be specified by the user or determined automatically by simulating reads from the model with a specific amount of off-frame reads and choosing δ such that the off-frame reads are still recognized as such (in this study we used 10% off-frame reads).

Start codon prediction

First, annotated ORFs were sorted according to their mean activity (geometric mean after removing zero-activity codons). Then, in bins of 1000 ORFs, a logistic regression model was trained based on the annotated start codons (positive set) and five random positions within the ORF (negative set). For each ORF, activity values from each sample were transformed using the arcsine function for variance stabilization and divided by the maximal value, providing the features for regression. To incorporate the massive difference between the start codon and the codons upstream, we used the range-score (sum of activities of the 10 codons downstream of the start codon including the start codon, divided by the sum of activities of codons +/- 10 codons around the start codon) as an additional feature for regression. To predict start codons, the probability from the logistic regression was computed for each codon in an ORF candidate and divided by the maximal probability. This was multiplied by a factor penalizing start codon candidates for which less than 60% of the total activity was downstream of the start codon (see Supplementary Fig. 12), providing the final score for start codon prediction. All codons admissible by their sequence (here, AUG and all codons with one mismatch to AUG), that exceeded a minimal score (here: 0.1), were considered as start codon candidates.

Generating ORF candidates

First, a set of transcripts from the annotation was determined that is sufficient to explain most of the active codons. In a greedy fashion, the transcript explaining most of the remaining (still unexplained) reads is added to this set and this procedure is stopped if there is no transcript having at least 5 unexplained reads. Based on the sequence, ORF candidates are generated from each transcript and filtered based on minimal criteria indicative for active translation (ending at a stop codon, not having an in-frame stop-codon, at least 5 reads, at least 25% of the codons active).

Candidate filtering

All generated ORF candidates are first filtered according to two criteria: First, the number of active codons must exceed a minimal number as inferred from annotated ORFs with similar translation strength. Specifically, a threshold for activity was computed as 10% of the geometric mean g of all codon activities (after removing zero activity codons) for all annotated ORFs. One smoothing spline was fit to the graph of g against the fraction of codons over this threshold for each annotated ORF (see Supplementary Fig. 13a-b), and one to g against the squared residuals from the first smoothing spline. For a specific ORF candidate with geometric mean g the minimal number of active codons was computed as the 5% quantile of the beta distribution with mean and variance obtained from the two splines. Second, ORFs where the total activity of the first five codons was much higher than the total activity of subsequent codons were filtered as abortive translation events. Specifically, we computed the empirical distribution of log₂ fold changes between the average activity of the first five codons and the average of subsequent codons for annotated ORFs. ORF candidates were filtered if their corresponding log₂ fold change was less than the 1% quantile of the empirical distribution.

Generalized binomial test

To test for ORF candidates being due to noise, we again computed the number of codons exceeding 10% of the geometric mean of codon activities. With no overlapping ORF the probability of a codon to be due to noise was estimated from the upstream, downstream and off-frame region and a p value was computed using the binomial distribution. Specifically, for a specific set of codons S, |S| = n, we computed the number k of codons exceeding the 10% cut-off and estimate the noise probability as $p(S)=\frac{k+1}{n+2}.$ The pseudocounts used here correspond to a beta prior distribution similar to the estimation of fold-changes in RNA-seq experiments²¹. This provides a function p(S), that maps any set of codons to a noise probability. The noise probability used for the binomial test is max {p(U₁), …, p(U_k), p(D₁), …, p(D_l), p(O)}. For an ORF candidate o of length n amino acids, the U_i contains the 3n codons from all three frames upstream of o with respect to transcript i (1 ≤ i ≤ k). D_i contains the 3n codons from all three frames downstream of o, and O contains the 2n off-frame codons of o. With overlapping ORFs, the situation is a bit more complex for both the hypothesis test and the estimate of noise probabilities. First, if an ORF q overlaps with o, then the test also has to respect that a codon exceeding the chosen cut-off in o may be due to q. Thus, the binomial probability is 1 − (1 − p_n)(1 − p_q), where p_n is the noise probability as before, and p_q is computed by a similar approach as for the filter for the minimal number of active codons. Specifically, for all annotated ORFs, a smoothing spline is fitted to the graph of the geometric means of all non-zero codons activities against the fraction of codons exceeding the current cut-off for o, and p_q is value of this spline for the geometric mean of q (see Supplementary Fig. 13c-f). If q and o overlap only partly, or there are several overlapping ORFs, the binomial probability is not the same for each of the n codons of o. Therefore, the p value is computed using the generalized binomial distribution that allows n distinct success probabilities using an efficient algorithm²². Moreover, the function p(S) does not only count codons in S exceeding or not exceeding the cut-off, but respects ORFs giving rise to active codons in S when there are overlapping ORFs. Specifically, for each s ∈ S, the probability p_s of being explained by an overlapping ORF is computed as p_s = 1 − (1 − p₀)(1 − p₁)(1 − p₂). p₀, p₁ and p₂ are the probabilities of the codon to be explained by an in-frame codon (p₀ = 1, if there is an in-frame overlapping ORF), or by an off-frame codon (estimated from smoothing splines like p_q). The expected number of unexplained codons over the cut-off in S then is $E_o={\displaystyle {\sum }_{i=0}^{\left|S\right|}f(i)\text{max}(0,k-i)}$ where k is the total number of codons exceeding the cut-off and f is the probability mass function of the generalized binomial distribution with parameters {p_s|s ∈ S}. Likewise, the expected number of codons not exceeding the cut-off is $E_b={\displaystyle {\sum }_{i=0}^{\left|S\right|}f(i)\text{max}(0,\left|S\right|-i)}.$ Thus $p(S)=\frac{E_o+1}{E_o+1+E_b+1}.$

Isoform deconvolution

Due to alternative splicing, predicted ORFs may also overlap partly in-frame, i.e. there may be codons that are shared between two or more ORFs. This gives rise to the same problem existing in RNA-seq, where many observed reads could be generated by more than one isoform. Thus, this is a well studies problem²³. PRICE uses a widely adopted EM algorithm to deconvolute the contributions of ORFs to such codons, which maximizes the following likelihood:

$$L(p)={{\displaystyle \prod _{c\in C}\left({\displaystyle \sum _{o\in O}{A}_{c,o}\frac{p_o}{l_o}}\right)}}^{{\alpha }_c}$$

C is the set of all codons, α_c is the estimated amount of reads mapped to codon c, O is the set of ORFs, A_c,o an indicator whether ORFo contains codon c, and l_o the length of ORF o in codons. The parameter that is estimated with maximum likelihood by the EM are the p_o, the probabilities of generating a ribosome footprint for ORF o.

Comparative analysis

The HSV-1 Ribo-seq data set was of better quality (according to their signal-to-noise ratio, see Fig. 2e) than the HCMV data set. Therefore, we reasoned that the ratio of the number of ORFs, which were identified in the HCMV data set (called the test data set) and reproducibly identified in the HSV-1 data set (called the reference data set), to the number of ORFs, which were only identified in the HCMV data set, is a measure for the overall reproducibility of a Ribo-seq analysis method across laboratories. An ORF was assumed reproducible, if the ORF in the HSV-1 data set showed the same stop codon, and if both ORFs were consistent with respect to introns (i.e. no intronic base pair of one ORF was present in an exon of the other ORF). This prevented the analysis to over-emphasize the prediction of the correct start codon, which is difficult for all methods not utilizing Harringtonin or Lactimidomycin data. For the inner-laboratory comparison we used the better of the two HSV-1 replicates as the reference data set and the other biological replicate as the test data set. All methods were used with default parameters and applied on the same bam files as PRICE, with the exception of Rp-Bp, which uses its own pipeline including read mapping. For Rp-Bp, we extracted all mapped reads from the respective bam files and re-appended the sequencing adapter. The Rp-Bp pipeline was then run on the corresponding fastq files. We allowed for “NTG” start codons and used the default cutoff for Bonferroni corrected p values (1%) to call ORFs. We ran ORF-RATER according to the manual, allowing for all start codons with at most one mismatch to ATG and, by default, used an 80% cutoff on the posterior probability. RibORF is not able to infer ORFs by itself, but only to score a given set of ORFs. We therefore identified all potential uORFs and uoORFs starting from start codons with at most one mismatch to ATG according to Ensembl v75, and supplied a Genpred file containing all protein coding Ensembl ORFs and the potential uORFs and uoORFs. The same is true for SPECtre, that included the computation of FLOSS and ORFScore, where we had to supply custom annotation in GTF format. For RibORF, SPECtre, FLOSS and ORFScore, score cutoffs were chosen such that the number of uORFs+uoORFs was 1000 in the test data set. We used the same cutoff for the reference data set, respectively. The offset parameters that had to be supplied to RibORF and SPECtre were taken from the study describing the HCMV data^4,14 and determined according to the optimal deterministic strategy described above for the HSV-1 data. Furthermore, except for Fig. 4a, before determining the cutoff, we removed all ORFs with an in-frame ratio (number of reads mapped to in-frame codons divided by number of reads mapped out-of-frame but within the ORF) below 50%, as previously suggested⁵.

Signal and noise

After mapping of reads to codons by any method, the signal is defined as the total number of reads mapping to in-frame codons of an annotated ORF (Ensembl 75). Noise is defined as the total number of reads mapping to annotated ORFs out-of-frame.

Statistical tests

The binomial tests for Fig. 2b-c were computed as follows: Let n_P(c) be the number of ORFs starting with codon c identified by PRICE (or Stern-Ginossar et al.) and n_b(c) the number of ORFs identified by both PRICE and Stern-Ginossar et al. Under the null hypothesis that there is no difference in codon distributions between ORFs identified by PRICE (or Stern-Ginossar et al.) only and by both, n_P(c) is binomially distributed with parameters n = n_p(c) + n_b(c) and $p=\frac{{\displaystyle {\sum }_{c^{\prime }}{n}_p(c^{\prime })}}{{\displaystyle {\sum }_{c^{\prime }}{n}_p(c^{\prime })}+n_b(c^{\prime })}.$ The p value was computed by the pbinom function of R (version 3.3.2). The combined p values were computed using Fisher’s method by computing the cumulative distribution function of the χ² distribution with 20 degrees of freedom (2 times the number of p values) for −2 ⋅ Σi log (p_i) (where the p_i are the p values of the binomial tests for all relevant codons).

Mass spectrometry

For the MHC-I peptidome data set 2, HLA class I ligands were isolated from 1ml cell pellets of mock treated or HCMV-infected HF99-7 human foreskin fibroblasts (HF99-7, HLA-A*01:01, A*03:01, B*08:01, B*51:01, C*07:01, C*01:02) by standard immunoaffinity purification using the pan-HLA class I-specific mAb W6/32 as described previously²⁴. Sample shares of 20% were analyzed in technical triplicates by LC-MS/MS. Peptides were separated by nanoflow HPLC (RSLCnano, Thermo Fisher Scientific) using a 50 μm x 25 cm Acclaim PepMap C18 column (Thermo Fisher Scientific) and a linear gradient ranging from 2.4% to 32.0% acetonitrile over the course of 90 min. Eluted peptides were analyzed in an online-coupled Orbitrap Fusion Lumos mass spectrometer (Thermo Fisher Scientific) using a data dependent “top speed” collision-induced dissociation fragmentation method. FT MS2 spectra for 2+ and 3+ precursors of 400-650 m/z were acquired at 30k resolution with AGC target values of 70,000 and maximum injection times of 150ms. Normalized collision energy was set to 35%, dynamic exclusion time was set to 7s. The published MHC-I peptidome data set was obtained from the PRIDE repository (PXD000394). The whole proteome data was the same as used in Ref. 15. All mass spectrometry data were analyzed using MaxQuant²⁵ 1.5.8.3 by using the same set of parameters as in Ref. 17 with the exception that we used a sequence database composed of the human proteome from Ensembl v75, the HCMV proteome (NC_006273) and translated ORFs identified by PRICE, Rp-Bp or ORF-RATER in any of the HSV-1 or HCMV data set. We considered only cellular ORFs and used a FDR of 1% using the target-decoy approach based on “reverted” proteins implemented in MaxQuant.