SPhyR: tumor phylogeny estimation from single-cell sequencing data under loss and error

Abstract

Motivation

Cancer is characterized by intra-tumor heterogeneity, the presence of distinct cell populations with distinct complements of somatic mutations, which include single-nucleotide variants (SNVs) and copy-number aberrations (CNAs). Single-cell sequencing technology enables one to study these cell populations at single-cell resolution. Phylogeny estimation algorithms that employ appropriate evolutionary models are key to understanding the evolutionary mechanisms behind intra-tumor heterogeneity.

Results

We introduce Single-cell Phylogeny Reconstruction (SPhyR), a method for tumor phylogeny estimation from single-cell sequencing data. In light of frequent loss of SNVs due to CNAs in cancer, SPhyR employs the k-Dollo evolutionary model, where a mutation can only be gained once but lost k times. Underlying SPhyR is a novel combinatorial characterization of solutions as constrained integer matrix completions, based on a connection to the cladistic multi-state perfect phylogeny problem. SPhyR outperforms existing methods on simulated data and on a metastatic colorectal cancer.

Availability and implementation

SPhyR is available on https://github.com/elkebir-group/SPhyR.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Cancer is a genetic disease that results from an evolutionary process, where somatic mutations accumulate in a population of cells (Nowell, 1976). These mutations arise during the lifetime of an individual and vary in genomic scale, ranging from single-nucleotide variants (SNVs) that affect a single base to copy-number aberrations (CNAs) that affect large genomic regions. Many generations of cell division, mutation and selection yield a highly heterogeneous tumor, composed of different groups of cancerous cells, where each group is characterized by a different complement of somatic mutations. This phenomenon is known as intra-tumor heterogeneity, and has important implications for both our understanding of cancer progression and for treatment outcome (Tabassum and Polyak, 2015). Knowledge on the evolutionary history of the cells of a tumor enables one to understand the mechanisms that result in intra-tumor heterogeneity. Unfortunately, DNA sequencing data alone do not describe the evolutionary history of a tumor. Rather, they only give us mutational information about a subset of tumor cells present at the time of sequencing.

Similarly to the evolution of species and languages, the evolutionary history of tumor cells can be appropriately modeled by a phylogenetic tree. We consider a character-based phylogenetic tree T, whose leaves, or taxa, correspond to cells sequenced at the present time, and whose internal nodes correspond to ancestral cells. Each node of T is labeled by the set of characters, or mutations, it contains. The root node is a non-mutated, normal cell. To reconstruct T from sequencing data, we require a generative model for the sequencing data and an evolutionary model for T.

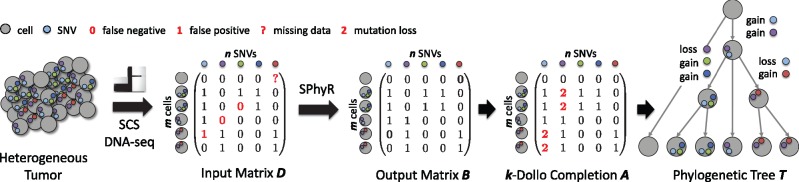
Most cancer sequencing studies use bulk DNA sequencing, where one obtains short reads from hundreds of thousands of cells that are sequenced in bulk. These mixed measurements must be deconvolved to quantify intra-tumor heterogeneity. More recently, single-cell sequencing (SCS) has been proposed as alternative to bulk sequencing in cancer (Navin, 2014). Contrary to bulk sequencing, individual tumor cells are sequenced in SCS and thus one directly observes the leaves of T. However, current SCS technology is very error-prone and suffers from elevated rates of false positives, false negatives and missing data (Fig. 1). These errors can be corrected by estimating the phylogenetic tree T, describing the evolutionary history of all mutations. This task requires an evolutionary model.

Fig. 1.

Tumor phylogeny estimation from single-cell sequencing (SCS) data. Heterogeneous tumors are composed of distinct cellular populations with distinct complements of somatic mutations, including single-nucleotide variants (SNVs) and copy-number aberrations (CNAs). During cancer progression, SNVs are frequently lost due to copy-number aberrations, but rarely introduced more than once. Here, single-cell sequencing of a tumor yields an input matrix D, whose m rows are cells and n columns are SNVs. Matrix D has incorrect and/or missing entries. We aim to simultaneously correct errors in matrix D and infer the evolutionary history of the m cells, yielding output matrix B and the corresponding phylogenetic tree T. The evolutionary model employed by our method SPhyR is the k-Dollo parsimony model, where each SNV can only be gained once but lost at most k times. SPhyR is based on a combinatorial characterization of k-Dollo phylogenetic trees T as k-Dollo completions A of a binary matrix B

Evolutionary models constrain changes of characters along the edges of T. A character can either be gained or lost on each edge of T. Multiple gains of the same character indicate parallel evolution, whereas losses indicate back mutation. A tree T whose characters do not exhibit parallel evolution or back mutation/loss is said to be homoplasy-free. The infinite sites model or perfect phylogeny model requires that T is homoplasy-free. This model has been used extensively in cancer genomics for both bulk sequencing data (Dang et al., 2017; Deshwar et al., 2015; El-Kebir et al., 2015; Malikic et al., 2015; Nik-Zainal et al., 2012; Popic et al., 2015; Yuan et al., 2015) and single cell sequencing data (Jahn et al., 2016; Ross and Markowetz, 2016). Importantly, while parallel evolution of SNVs is rare in cancer, losses of SNVs are ubiquitous due to wide-spread copy-number loss of large genomic regions (Kuipers et al., 2017). Thus, less restrictive evolutionary models are essential to accurately model the somatic mutational process of SNVs in cancer. Recently, Zafar et al. (2017) introduced a phylogeny estimation algorithm that is based on the finite sites model. In this model, a character may change state more than once, and thus parallel evolution and mutation loss may occur. The Dollo parsimony model (Dollo, 1893) is a slightly more restrictive evolutionary model: a character may only be gained once but lost multiple times. That is, the Dollo parsimony model allows back mutation/loss but does not allow for parallel evolution. This model has been applied recently in the context of tumor phylogeny estimation from bulk sequencing data (Bonizzoni et al., 2017b). As the main source of homoplasy in cancer evolution is due to loss of SNVs caused by copy-number aberrations, the Dollo parsimony model provides a good evolutionary model for the evolution of SNVs in cancer.

Here, we consider the k-Dollo parsimony model, which restricts the Dollo parsimony model to at most k losses per character. We show that the problem of inferring a k-Dollo phylogeny given an error-free binary matrix B is a variant of the cladistic multi-state perfect phylogeny problem (Fernández-Baca, 2000). We prove that solutions to this problem are constrained integer matrix completions of the input matrix B (Fig. 1), allowing us to derive an efficient integer linear programming formulation that solves practical problem instances in seconds. We introduce SPhyR (Single-cell Phylogeny Reconstruction), a coordinate-ascent based approach that infers a k-Dollo phylogeny from single-cell sequencing data with errors. On simulated data, we show that SPhyR outperforms existing methods, that are either based on the infinite sites or the finite sites evolutionary model, in terms of solution quality and run time. On real data, we show that SPhyR provides a likelier explanation of the evolutionary history of a metastatic colorectal cancer. In summary, SPhyR enables detailed evolutionary analyses of single-cell cancer sequencing data.

2 Problem statement

We consider a tumor composed of m cells that contain n SNVs. In the following, we refer to SNVs as mutations. We model the mutation state of an SNV locus as a binary character, where the 1-state denotes the presence of the mutation at the genomic locus and the 0-state its absence. We represent the cell division and mutation history of the m tumor cells by a character-based phylogenetic tree T, which is a rooted, node-labeled tree. Each node v of T is labeled by a binary vector $b_v\in {\{0,1\}}^n$, indicating the mutation state of each character. As the root node r of T is a non-mutated, normal cell, we have that $b_{r,c}=0$. for all characters $c\in \left[n\right]$, where $\left[n\right]=\{1,\dots ,n\}$. Each leaf of T corresponds to exactly one of the m cells. Here, our goal is to reconstruct a phylogenetic tree T when only given its leaves. That is, as input, we are given a binary matrix $B\in {\{0,1\}}^{m\times n}$ that defines the character states of the m leaves of T. This task requires an evolutionary model.

An edge (v, w) where $b_{v,c}=0$ and $b_{w,c}=1$ corresponds to a gain of character c—multiple gains of the same character indicate parallel evolution. On the other hand, an edge (v, w) of T where $b_{v,c}=1$ and $b_{w,c}=0$ corresponds to a loss or back mutation of character c. In the Dollo parsimony model (Dollo, 1893), a character may only be gained once but lost multiple times. Here, we consider the k-Dollo parsimony model, which restricts the Dollo parsimony model to at most k losses per character. We call a tree whose characters evolve under the k-Dollo parsimony model, a k-Dollo phylogeny, which we formally define as follows.

Definition 1 —

A k-Dollo phylogeny T is a rooted, node-labeled tree subject to the following conditions.

1. Each node v of T is labeled by a vector $b_v\in {\{0,1\}}^n$.

2. The root r of T is labeled by vector $b_r={[0,\dots ,0]}^T$.

3. For each character $c\in \left[n\right]$, there is exactly one gain edge (v, w) in T such that $b_{v,c}=0$ and $b_{w,c}=1$.

4. For each character $c\in \left[n\right]$, there are at most k loss edges (v, w) in T such that $b_{v,c}=1$ and $b_{w,c}=0$.

Let $B\in {\{0,1\}}^{m\times n}$. A tree T is a k-Dollo phylogeny for B if and only if T is a k-Dollo phylogeny with m leaves such that each row of B labels exactly one leaf of T. We call B a k-Dollo phylogeny matrix provided there exists a k-Dollo phylogeny T for B. Thus, we have the following problem.

k-Dollo Phylogeny problem (k-DP) —

Given a binary matrix $B\in {\{0,1\}}^{m\times n}$ and parameter $k\in \mathbb{N}$, determine whether there exists a k-Dollo phylogeny for B, and if so construct one.

The k-DP problem assumes error-free data. In real data, however, the error-prone whole-genome amplification step in single-cell sequencing results in an input matrix D with false positives (incorrect 1-entries), false negatives (incorrect 0-entries), and missing data (‘?’-entries). To correct these errors, we assume an evolutionary model without parallel evolution and at most k losses per character, i.e. the k-Dollo parsimony model. The task is thus to fill in the missing entries and fix incorrect entries of matrix $D\in {\{0,1,?\}}^{m\times n}$, yielding matrix $B\in {\{0,1\}}^{m\times n}$ and a k-Dollo phylogeny T for B. The false positive rate $\alpha \in [0,1]$ and the false negative rate $\beta \in [0,1]$ can be estimated from sequencing data of normal cells. Thus, the probability of observing matrix D given matrix B, false positive rate α and false negative rate β is:

$$\mathrm{Pr}\left(D\right|B,\alpha ,\beta )={\displaystyle \prod _{p=1}^m{\displaystyle \prod _{c=1}^n\mathrm{Pr}}}(d_{p,c}|b_{p,c},\alpha ,\beta ),$$ (1)

where

$$\mathrm{Pr}\left(d_{p,c}\right|b_{p,c},\alpha ,\beta )=\{\begin{array}{ll}\alpha ,\hfill & d_{p,c}=1\text{ and }{b}_{p,c}=0\hfill \\ 1-\alpha ,\hfill & d_{p,c}=1\text{ and }{b}_{p,c}=1,\hfill \\ \beta ,\hfill & d_{p,c}=0\text{ and }{b}_{p,c}=1,\hfill \\ 1-\beta ,\hfill & d_{p,c}=0\text{ and }{b}_{p,c}=0,\hfill \\ 1,\hfill & d_{p,c}=?\hfill \end{array}$$ (2)

The clonal evolution theory of cancer posits that only a small number of mutations are beneficial to the tumor and result in clonal expansions (Nowell, 1976). That is, a driver mutation that leads to a clonal expansion is often preceded by many passenger mutations that do not confer an evolutionary advantage to the tumor. As such, groups of mutations either are all present or absent in a tumor cell, and thus cluster on distinct branches of the phylogenetic tree. Moreover, cells originate from a small number of clones. Hence, we expect the output matrix B to contain multiple sets of repeated columns and repeated rows, which each correspond to a distinct branch and distinct clone, respectively. This leads to the following problem.

k-Dollo Phylogeny Flip and Cluster problem (k-DPFC) —

Given matrix $D\in {\{0,1,?\}}^{m\times n}$, error rates $\alpha ,\beta \in [0,1]$, integers $k,s,t\in \mathbb{N}$, find matrix $B\in {\{0,1\}}^{m\times n}$ and tree T such that: (i) B has at most s unique rows and at most t unique columns; (ii) $\mathrm{Pr}\left(D\right|B,\alpha ,\beta )$ is maximum and (iii) T is a k-Dollo phylogeny for B.

3 Materials and methods

3.1 Combinatorial structure and complexity

We will show that the k-DP problem is a variant of the cladistic multi-state perfect phylogeny problem with an unknown subset of incorrect 0-entries. A perfect phylogeny is defined as follows.

Definition 2 (Estabrook et al. 1975; Gusfield 1991) —

A rooted, node-labeled tree T is a perfect phylogeny provided the following conditions hold.

1. Each node v of T is labeled by a vector $a_v\in {\{0,\dots ,k+1\}}^n$.

2. The root r of T is labeled by vector $a_r={[0,\dots ,0]}^T$.

3. Nodes labeled with state i for character c form a connected subtree $T_{(c,i)}$ of T.

Each character state $(c,i)\in \left[n\right]\times [k+1]$ corresponds to the root node $v_{(c,i)}$ of the subtree $T_{(c,i)}$. For each character $c\in \left[n\right]$, character states $(c,0)$ correspond to the root node r of T. Thus, each of $v_{(1,0)},\dots ,v_{(n,0)}$ denote the root node r. We write $(c,i)⪯{}_T(d,j)$ if and only if node $v_{(c,i)}$ is on the unique path from the root of T to node $v_{(d,j)}$. Note that ${⪯}_T$ is reflexive.

Given an integer matrix $A\in {\{0,\dots ,k+1\}}^{m\times n}$, we say that a tree T is a perfect phylogeny T for A if and only if T is a perfect phylogeny with m leaves such that each row of A labels exactly one leaf of T. We call an integer matrix A a perfect phylogeny matrix provided there exists a perfect phylogeny T for A. The problem of constructing a perfect phylogeny from a given matrix A is known as the perfect phylogeny problem.

For k = 0, i.e. the two-state case, solutions to the perfect phylogeny problem are fully characterized as follows.

Theorem 1 [Perfect Phylogeny Theorem (Gusfield, 1991)] —

A binary matrix $A\in {\{0,1\}}^{m\times n}$ is a perfect phylogeny matrix if and only if no two columns of A contain the three pairs (1, 0); (0, 1) and (1, 1).

The above condition is known as the three gamete condition and can be constructively checked in linear time O(mn) (Gusfield, 1991). For any constant k, the perfect phylogeny problem is solvable in time polynomial in m and n (Agarwala and Fernández-Baca, 1994; Kannan and Warnow, 1997). However, if none of m, n or k are fixed, the perfect phylogeny decision problem is NP-complete (Bodlaender et al., 1992).

We consider a restriction of the fixed $k\ge 0$ perfect phylogeny phylogeny problem, where, in addition to matrix A, we are given a state tree S for each character. This problem is known as the cladistic perfect phylogeny problem, where for each character the given state tree imposes an ordering on the states of that character.

Definition 3 [Fernández-Baca (2000)] —

A state tree S is a rooted, node-labeled tree, whose root node is labeled by state 0, and whose other nodes are uniquely labeled by states $\{1,\dots ,k+1\}$.

We write $i\hspace{0.17em}{⪯}_S\hspace{0.17em}j$ if and only if for the two nodes v_i and v_j of S, labeled by i and j, respectively, it holds that v_i is on the unique path from the root of S to v_j. A perfect phylogeny T is consistent with state tree S for character c provided: $i\hspace{0.17em}{⪯}_S\hspace{0.17em}j$ if and only if $(c,i)\hspace{0.17em}{⪯}_T(c,j)$ for all states $i,j\in \{0,\dots ,k+1\}$. We now review a connection between the cladistic multi-state perfect phylogeny problem and the two-state perfect phylogeny problem. Given matrix $A\in {\{0,\dots ,k+1\}}^{m\times n}$ and state trees $S=\{S_1,\dots ,S_n\}$, the $m\times n(k+1)$ binary factor matrix $B\prime$ of $(A,S)$ is defined as follows (Supplementary Fig. S1).

Definition 4 [Fernández-Baca (2000)] —

Let $A\in {\{0,\dots ,k+1\}}^{m\times n}$ and let $S=\{S_1,\dots ,S_n\}$ be a set of state trees for each character. The binary factor matrix$B\prime =\left[b{\prime }_{p,e}\right]$ of $(A,S)$ has dimensions $m\times n(k+1)$, and entries

$$b{\prime }_{p,e}=\{\begin{array}{ll}0,\hfill & \text{ if }i{\cancel{\hspace{0.17em}⪯}}_{S_c}{a}_{p,c},\hfill \\ 1,\hfill & \text{ if }i\hspace{0.17em}{⪯}_{S_c}{a}_{p,c}.\hfill \end{array}$$ (3)

where $c=\lfloor e/(k+1)\rfloor +1,i=(e\mathrm{mod}(k+1\left)\right)+1$ and S_c is the state tree of character c.

Formally, the cladistic perfect phylogeny problem asks to construct a perfect phylogeny T for A whose characters are consistent with their corresponding state tree. Unlike the general problem, this problem is solvable in time O(mnk) using the binary factor matrix $B\prime$, as shown by Fernández-Baca (2000).

Theorem 2 [Fernández-Baca (2000)] —

Matrix A has a perfect phylogeny consistent with states trees $S=\{S_1,\dots ,S_n\}$ if and only if the binary factor matrix $B\prime$ of $(A,S)$ is a perfect phylogeny matrix.

We will use the above result to introduce a characterization of k-Dollo phylogenies as a subset of multi-state perfect phylogenies whose characters are consistent with the k-Dollo state tree, defined as follows (Supplementary Fig. S1).

Definition 5 —

The k-Dollo state tree$S\left[k\right]$ is a state tree with nodes $\{0,\dots ,k+1\}$ and edges $\left\{\right(0,1\left)\right\}\cup \left\{\right(1,i\left)\right|i\in \{2,\dots ,k+1\}\}$.

Intuitively, the k-Dollo state tree encodes that there is exactly one gain modeled by the edge (0, 1), and that there at most k losses modeled by edges $\left\{\right(1,i\left)\right|i\in \{2,\dots ,k+1\}\}$ that each must occur after the gain. To decide whether a binary matrix $B=\left[b_{p,i}\right]$ is a k-Dollo phylogeny matrix, we need to decide for each entry $b_{p,i}=0$ whether it is a loss or not. States $\{2,\dots ,k+1\}$ denote losses, and state 0 denotes that the mutation has not occurred. Thus, we define a k-completion A of the 0-entries of a given matrix B as follows.

Definition 6 —

Let $B\in {\{0,1\}}^{m\times n}$. Matrix $A\in {\{0,\dots ,k+1\}}^{m\times n}$ is a k-completion of B provided (1) $a_{p,c}\in \{0,\dots ,k+1\}\text{∖}\left\{1\right\}$ if and only if $b_{p,c}=0$; and (2) $a_{p,c}=1$ if and only if $b_{p,c}=1$.

We now define a restricted subset of k-completions that correspond to k-Dollo phylogenies (Fig. 1 and Supplementary Fig. S1).

Definition 7 —

Let $I^{\left(i\right)}=\{i,\dots ,k+1\}$. Matrix $A\in {\{0,\dots ,k+1\}}^{m\times n}$ is a k-Dollo completion provided there exist no two columns and three rows in A of the following form:

$$\left(\begin{array}{cc}{i}_1& 0\\ 0& j_1\\ i_1^{\prime }& j_1^{\prime }\end{array}\right)\text{ or }\left(\begin{array}{cc}{i}_1& j_1^{″}\\ 0& j_2\\ i_1^{\prime }& j_2\end{array}\right)\text{ or }\left(\begin{array}{cc}{i}_2& 0\\ i_1^{″}& j_1\\ i_2& j_1^{\prime }\end{array}\right)\text{ or }\left(\begin{array}{cc}{i}_2& j_1^{″}\\ i_1^{″}& j_2\\ i_2& j_2\end{array}\right)$$

where $i_1,i_1^{\prime },j_1,j_1^{\prime }\in I^{\left(1\right)},i_2,j_2\in I^{\left(2\right)},i_1^{″}\in I^{\left(1\right)}\text{∖}\left\{i_2\right\}$ and $j_1^{″}\in I^{\left(1\right)}\text{∖}\left\{j_2\right\}$.

Thus, the number of forbidden 3 × 2 submatrices is ${(k+1)}^4+2k^2{(k+1)}^2+k^4$. Supplementary Table S1 lists all forbidden submatrices for k = 1. Given $B\in {\{0,1\}}^{m\times n}$, we say that a matrix $A\in {\{0,\dots ,k+1\}}^{m\times n}$ is a k-Dollo completion of B if and only if A is a k-Dollo completion and A is a k-completion of B. We now prove that solutions to the k-DP problem are k-Dollo completions of input matrix B.

Theorem 3 —

Let $B\in {\{0,1\}}^{m\times n}$. The following statements are equivalent.

1. There exists a k-Dollo phylogeny T for B.

2. There exists a k-Dollo completion A of B.

3. There exists a k-completion A of B such that the binary factor matrix $B\prime$ of $(A,S[k\left]\right)$ is a perfect phylogeny matrix.

4. There exists a k-completion A of B, and perfect phylogeny T for A whose characters are consistent with $S\left[k\right]$.

Proof —

We refer to Supplementary Section S.2 for the full proof. □

In the above theorem, we established a connection between the k-Dollo phylogeny problem and the cladistic multi-state perfect phylogeny problem. This allows us to constructively determine whether a k-completion A of B is a k-Dollo completion, as stated in the following corollaries.

Corollary 1 —

Let $B\in {\{0,1\}}^{m\times n}$. We can decide in O(mnk) time if matrix $A\in {\{0,\dots ,k+1\}}^{m\times n}$ is a k-Dollo completion of B.

Corollary 2 —

Let $B\in {\{0,1\}}^{m\times n}$. Given a k-Dollo completion A of B, we can construct a k-Dollo phylogeny for B in O(mnk) time.

Note that the k = 0 case of the k-DP problem corresponds to the two-state perfect phylogeny problem. In fact, the condition for a 0-Dollo completion is precisely the three gamete condition. The k = 1 case is known as the persistent phylogeny problem. An elegant reduction to a binary matrix completion problem was introduced in (Bonizzoni et al., 2012) and formed the basis of the integer linear program (ILP) introduced by Gusfield (2015). In subsequent work, Bonizzoni et al. (2017b) extended their binary matrix completion reduction to allow for k > 1 losses. We note that the binary matrix used in these papers is precisely the binary factor matrix obtained from the multi-state matrix A and state trees $S\left[k\right]$. While a restricted variant of the k = 1 case was recently shown to be solvable in polynomial time (Bonizzoni et al., 2017a), the hardness for $k\ge 1$ remains an open question.

We now consider the k-DPFC problem. We prove that this problem is NP-hard even for k = 0.

Theorem 4 —

The k-DPFC is NP-hard even for k = 0.

Proof —

We show this by reduction from the Flip problem (Chen et al., 2002), where one is given a binary matrix $D\in {\{0,1\}}^{m\times n}$ and integer $c\in N$ and asked to decide whether there exists a matrix $B\in {\{0,1\}}^{m\times n}$ such that: (1) at most c entries in B differ from D; and (2) no two columns of B contain the three pairs (1, 0); (0, 1) and (1, 1). A matrix B is said to be conflict free if it satisfies condition (2). Let (D, c) be an instance of the Flip problem. The corresponding instance of the k-DPFC problem has the same input matrix D, has error rates $\alpha =\beta <0.5$, does not constraint the number s = m of unique rows and the number t = n of unique columns, and requires k = 0 losses for each character.

We claim that there exists a conflict-free matrix B with at most c distinct entries if and only if there exist a 0-Dollo phylogeny matrix $B\prime \in {\{0,1\}}^{m\times n}$ with likelihood

$$\mathrm{Pr}\left(D\right|B\prime ,\alpha ,\beta )\ge {\alpha }^c·{(1-\alpha )}^{mn-c}.$$ (4)

$(\Rightarrow )$ Let $B\in {\{0,1\}}^{m\times n}$ be a conflict-free matrix with at most c distinct entries. It is easy to verify that $\mathrm{Pr}\left(D\right|B,\alpha ,\beta )={\alpha }^c·{(1-\alpha )}^{mn-c}$. Moreover, by the perfect phylogeny theorem (Theorem 1), we have that B is a perfect phylogeny matrix and thus a 0-Dollo phylogeny matrix.

$(\Leftarrow )$ Let $B\prime \in {\{0,1\}}^{m\times n}$ be a 0-Dollo phylogeny matrix with likelihood $\mathrm{Pr}\left(D\right|B,\alpha ,\beta )\ge {\alpha }^c·{(1-\alpha )}^{mn-c}$. Assume for a contradiction that $B\prime$ has d > c entries that differ from matrix D. As $\alpha =\beta <0.5$, we have that

$$\mathrm{Pr}\left(D\right|B\prime ,\alpha ,\beta )={\alpha }^d·{(1-\alpha )}^{mn-d}<{\alpha }^c·{(1-\alpha )}^{mn-c},$$ (5)

which yields a contradiction. Hence, any matrix $B\prime$ with likelihood at least ${\alpha }^c·{(1-\alpha )}^{mn-c}$ must have at most c entries distinct from D. □

3.2 Cutting plane and column generation for k-DP

In this section, we introduce an integer linear program (ILP) for the k-DP problem. Let $B=\left[b_{p,c}\right]$ be an m × n binary input matrix and let $k\in \mathbb{N}$ be the maximum number of losses per character.

We model each entry $a_{p,c}$ of the m × n output matrix A by binary variables $a_{p,c,0},\dots ,a_{p,c,k+1}\in \{0,1\}$ such that $a_{p,c,i}=1$ if and only $a_{p,c}=i$. To that end, we introduce the following constraints.

$$a_{p,c,i}\in \{0,1\}\forall p\in \left[m\right],c\in \left[n\right],i\in \{0,\dots ,k+1\}$$ (6)

$${\displaystyle \sum _{i=0}^{k+1}{a}_{p,c,i}}=1\forall p\in \left[m\right],c\in \left[n\right]$$ (7)

We introduce the following constraints to ensure that A is a k-completion of B.

$$a_{p,c,1}=0\forall p\in \left[m\right],c\in \left[n\right] \text{s}.\text{t}. b_{p,c}=\text{0}$$ (8)

$$a_{p,c,1}=1\forall p\in \left[m\right],c\in \left[n\right] \text{s}.\text{t}.b_{p,c}=\text{1}$$ (9)

In addition, we introduce the following symmetry breaking constraints.

$${\displaystyle \sum _{p=1}^m{\displaystyle \sum _{c=1}^n{a}_{p,c,i}}}\ge {\displaystyle \sum _{p=1}^m{\displaystyle \sum _{c=1}^n{a}_{p,c,i-1}}}\forall i\in \{3,\dots ,k+1\}$$ (10)

Recall that $I^{\left(i\right)}=\{i,\dots ,k+1\}$. For all distinct taxa $p,q,r\in \left[m\right]$, distinct characters $c,d\in \left[n\right]$ and states $i_1,i_1^{\prime },j_1,j_1^{\prime }\in I^{\left(1\right)},i_2,j_2\in I^{\left(2\right)},i_1^{″}\in I^{\left(1\right)}\text{∖}\left\{i_2\right\}$ and $j_1^{″}\in I^{\left(1\right)}\text{∖}\left\{j_2\right\}$, the following constraints ensure that A does not contain one of the forbidden submatrices given in Definition 7.

$$a_{p,c,i_1}+a_{p,d,0}+a_{q,c,0}+a_{q,d,j_1}+a_{r,c,i_1^{\prime }}+a_{r,d,j_1^{\prime }}\le 5$$ (11)

$$a_{p,c,i_1}+a_{p,d,j_1^{″}}+a_{q,c,0}+a_{q,d,j_2}+a_{r,c,i_1^{\prime }}+a_{r,d,j_2}\le 5$$ (12)

$$a_{p,c,i_2}+a_{p,d,0}+a_{q,c,i_1^{″}}+a_{q,d,j_1}+a_{r,c,i_2}+a_{r,d,j_1^{\prime }}\le 5$$ (13)

$$a_{p,c,i_2}+a_{p,d,j_1^{″}}+a_{q,c,i_1^{″}}+a_{q,d,j_2}+a_{r,c,i_2}+a_{r,d,j_2}\le 5$$ (14)

Given k allowed losses per character, we aim to minimize the maximum number of losses across all characters. To that end, we use an objective function such that a single entry of A with state j > 2 incurs a cost that is greater than the cost incurred when all entries of A have states at most j − 1. We have the following integer linear program.

$$\begin{array}{c}\min {\displaystyle \sum _{p=1}^m{\displaystyle \sum _{c=1}^n{\displaystyle \sum _{i=2}^{k+1}{a}_{p,c,i}}}}{\left(\frac{1}{mn}\right)}^{k+1-i}\\ \text{\hspace{1em}s}.\text{t}.\left(\text{6}\right)-\left(\text{14}\right)\end{array}$$ (15)

In our ILP, the number of variables is O(mnk) and the number of constraints is $O\left(m^3{n}^2{k}^4\right)$. As such, a naive implementation of this ILP does not scale to practical problem instance sizes where typically m = 50, n = 100 and k = 1. To scale the ILP to large instances, we use column and cutting plane generation, introducing variables and constraints only as needed. More specifically, we use a slight variation of classic column generation, and include all variables $a_{p,c,i}$ (where $p\in \left[m\right],c\in \left[n\right],i\in \{0,\dots ,k+1\}$) in the model, but alter their respective domains during the procedure. First, observe that the minimum value of the objective function (15) is 0, and is only attained in the absence of loss, i.e. when $a_{p,c,i}=1$ if $b_{p,c}=i$, and $a_{p,c,i}=0$ if $b_{p,c}\ne i$. Initially, we set $a_{p,c,i}\in \left\{0\right\}$ if $b_{p,c}\ne i$ and $a_{p,c,i}\in \{0,1\}$ if $b_{p,c}=i$. In addition, we add constraints (7), (8), (9) and (10) to the model. We then solve the model. The resulting minimum-cost solution might not be a k-Dollo completion and thus violate constraints $(11-14)$. For each pair c, d of distinct characters, we identify violated constraints in $O\left(m{k}^3\right)$ time, along the same lines as described in (Chimani et al., 2010). More specifically, we consider each of the four forbidden submatrices in Definition 7 separately, and scan the m rows for the presence of one of $O\left(k^3\right)$ forbidden pairs. Let

$$\left(\begin{array}{cc}{a}_{p,c,i_1}& a_{p,d,j_1}\\ a_{q,c,i_2}& a_{q,d,j_2}\\ a_{r,c,i_3}& a_{r,d,j_3}\end{array}\right)$$ (16)

be an identified forbidden submatrix for distinct characters c, d and distinct taxa p, q, r. We introduce the associated violated constraint (which is one of $(11-14)$). In addition, we evaluate each variable $a_{p,c,i}$ of the identified forbidden submatrix. If i = 0, we extend the domain of variable $a_{p,c,2}$ such that $a_{p,c,2}\in \{0,1\}$. If $2\le i<k+1$, we set $a_{p,c,i+1}\in \{0,1\}$. In other words, when possible, we allow the ILP to resolve violations that involve a variable with a 0-state or a fixed loss state by enabling the use of (additional) loss states. Upon introducing violated constraints and extending variable domains, we restart the ILP and repeat the same procedure. We terminate if no violated constraints are identified or if the ILP solver proves the model to be infeasible. This procedure will either determine that no solution exists or it will result in a k-Dollo completion with optimal cost. To see this, observe that additional loss states can be introduced in an incremental fashion, as the objective function guarantees that setting $a_{p,c,i}=1$ for a single entry, where i > 2, results in a greater cost than any assignment of entries restricted to states $\{0,2,\dots ,i-1\}$. We refer to Supplementary Section S.3 for additional details and pseudocode of the column generation procedure and the cut separation step.

3.3 Coordinate ascent for k-DPFC

We introduce a heuristic to solve the k-DPFC problem, where we are given as input a matrix $D\in {\{0,1,?\}}^{m\times n}$, a false positive rate α, a false negative rate β and natural numbers k, s, t. We are asked to infer a maximum likelihood m × n k-Dollo phylogeny matrix B with at most s unique rows and t unique columns. Essentially, the k-DPFC problem involves three sets of constraints. That is, we wish to (i) find a clustering $\pi :\left[m\right]\to \left[s\right]$ of the m rows (taxa) of D into s clusters, (ii) find a clustering $\psi :\left[n\right]\to \left[t\right]$ of the n columns (characters) of D into t clusters and (iii) find a k-Dollo phylogeny matrix B with dimensions s × t. These constraints are connected by the objective function $\log \mathrm{Pr}(D,\pi ,\psi |B,\alpha ,\beta )$, which equals:

$${\displaystyle \sum _{p=1}^m{\displaystyle \sum _{c=1}^n\log }}\mathrm{Pr}\left(d_{p,c}\right|b_{\pi \left(p\right),\psi \left(c\right)},\alpha ,\beta ),$$ (17)

where $\mathrm{Pr}\left(d_{p,c}\right|b_{\pi \left(p\right),\psi \left(c\right)},\alpha ,\beta )$ is defined in (2). Here, we propose to optimize these three sets of constraints separately using coordinate ascent.

Algorithm 1: SPhyR$(D,\alpha ,\beta ,k,s,t)$

Input: Matrix $D\in {\{0,1,?\}}^{m\times n}$, a false positive rate $\alpha \in [0,1]$, a false negative rate $\beta \in [0,1]$ and natural numbers k, s, t

Output: k-Dollo completion $A\in {\{0,\dots ,k+1\}}^{m\times n}$ with at most s unique rows and at most t unique columns

1. $E\leftarrow D$

2. Set $e_{p,c}\leftarrow 0.5$ for each entry $d_{p,c}=?$

3. $\pi \leftarrow \text{ kMeans}(E^T,s)$

4. $\psi \leftarrow \text{ kMeans}(E,t)$

5. $L,\Delta \leftarrow \infty$

6. while$\Delta >0$do

7.  $(A,B)\leftarrow \text{ SolveAB}(D,\alpha ,\beta ,s,t,k,\pi ,\psi )$

8.  for$p\leftarrow 1 \mathbf{to} m$do

9.   $\pi \left[p\right]\leftarrow {\text{argmax}}_{h\in \left[s\right]}{\displaystyle {\sum }_{c=1}^n\log }\mathrm{Pr}\left(d_{p,c}\right|b_{h,\psi \left(c\right)},\alpha ,\beta )$

10.  for$c\leftarrow 1 \mathbf{to}n$do

11.   $\psi \left[c\right]\leftarrow {\text{argmax}}_{f\in \left[t\right]}{\displaystyle {\sum }_{p=1}^m\log }\mathrm{Pr}\left(d_{p,c}\right|b_{\pi \left(p\right),f},\alpha ,\beta )$

12.  $L\prime \leftarrow {\displaystyle {\sum }_{p=1}^m{\displaystyle {\sum }_{c=1}^n\log }}\mathrm{Pr}\left(d_{p,c}\right|b_{\pi \left(p\right),\psi \left(c\right)},\alpha ,\beta )$

13.  $\Delta \leftarrow L\prime -L$

14.  $L\leftarrow L\prime$

15. Expand A according to π and ψ

16. returnA

Computing π.

We start with the problem of finding a maximum likelihood row clustering $\pi$ given a k-Dollo phylogeny matrix B and a column clustering $\psi$ of input matrix D. For each taxon $p\in \left[m\right]$, we want to find the row $\pi \left(p\right)$ of B with maximum likelihood

$$\pi \left(p\right)=\underset{{}_{h\in \left[s\right]}}{\text{argmax}}{\displaystyle \sum _{c=1}^n\log }\mathrm{Pr}\left(d_{p,c}\right|b_{h,\psi \left(c\right)},\alpha ,\beta ).$$ (18)

Computing π given B and ψ thus takes O(mns) time.

Computing ψ.

Similarly, we can compute the maximum likelihood column clustering ψ given B and π in O(mnt) time:

$$\psi \left(c\right)=\underset{{}_{f\in \left[t\right]}}{\text{argmax}}{\displaystyle \sum _{p=1}^m\log }\mathrm{Pr}\left(d_{p,c}\right|b_{\pi \left(p\right),f},\alpha ,\beta ).$$ (19)

Computing B.

To compute the maximum likelihood k-Dollo phylogeny matrix B given row clustering π and column clustering ψ, we use the same ideas as for the k-DP problem. That is, in addition to computing B we also compute a k-Dollo completion A of B. As such, for each taxon cluster $h\in \left[s\right]$ and character cluster $f\in \left[t\right]$, we introduce binary variables $a_{h,f,0},\dots ,a_{h,f,k+1}$ and the following constraints.

$$a_{h,f,i}\in \{0,1\}\forall h\in \left[s\right],f\in \left[t\right],i\in \{0,\dots ,k+1\}$$ (20)

$${\displaystyle \sum _{i=0}^{k+1}{a}_{h,f,i}}=1\forall h\in \left[s\right],f\in \left[t\right]$$ (21)

We have the same set of symmetry breaking constraints (10) and Dollo phylogeny constraints $(11-14)$—however, note that we adjust these constraints for use with s taxon clusters and t character clusters (instead of m taxa and n characters). In contrast to the previous formulation, matrix A may change the entries of matrix D and thus we do not include constraints (8) and (9). Let $X=\left[m\right]\times \left[n\right]$. We have the following objective function and ILP.

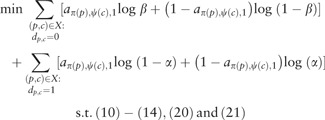This ILP has O(stk) variables and $O\left(s^3{t}^2{k}^4\right)$ constraints. Again, we use column generation to solve the ILP. To begin, we omit constraints $(11-14)$. To initialize the column generation procedure, we need to determine an initial assignment of variables $a_{h,f,i}$ that maximizes the objective function. In other words, for each taxon cluster $h\in \left[s\right]$ and character cluster $f\in \left[t\right]$, we need to determine whether $a_{h,c,1}=1$ or $a_{h,c,1}=0$ maximizes the likelihood (22). This involves a simple computation, which can be performed in O(mn) time for all pairs $(h,f)\in \left[s\right]\times \left[t\right]$. For each pair (h, f) where $a_{h,f,1}=1$ has greater likelihood than $a_{h,f,1}=0$, we set the domain of $a_{h,f,1}$ to {0, 1} and the domains of the remaining variables $a_{h,f,i}$, where $i\in \{0,2,\dots ,k+1\}$, to {0}. On the other hand, if $a_{h,f,1}=0$ has greater likelihood than $a_{h,f,1}=0$, we set the domain of $a_{h,f,1}$ to {0} and the domains of the remaining variables $a_{h,f,i}$, where $i\in \{0,2,\dots ,k+1\}$, to {0, 1}. Similarly to the column generation procedure for k-DP, we solve the model and identify for each pair f, g of character clusters whether there exists a forbidden submatrix in $O\left(s{k}^3\right)$ time. Upon finding such a forbidden submatrix, we introduce the violated constraints and extend the domains of the involved variables. More specifically, for each involved variable $a_{h,f,i}$ we extend the domain of variable $a_{h,f,1}$ to {0, 1} if $i\ne 1$; and if i = 1, we extend the domains of variables $a_{h,f,j}$ to {0, 1} where $j\in \{0,2,\dots ,k+1\}$. We subsequently restart the ILP, and repeat the same procedure. We terminate when no violated constraints are identified. See Supplementary Section S.3 for additional details and pseudocode.

SPhyR.

We initialize π and ψ using the k-Means algorithm. More specifically, we replace the? -entries of matrix D by 0.5, yielding a matrix E. To obtain π, we cluster the columns of matrix E using k-Means with k = s. Similarly, we obtain ψ by clustering the rows of matrix E using k-Means with k = t. We then compute k-Dollo phylogeny matrix B and its k-Dollo completion A given π and ψ, followed by updating π and then ψ. We repeat these steps until convergence (Algorithm 1) and allow the user to specify a number of restarts. In each restart, a different random number generator seed is used, yielding a different initial taxon and character clustering. We call the resulting algorithm Single-cell Phylogeny Reconstruction (SPhyR, pronounced ‘sapphire’). SPhyR is implemented in C++ and uses the IBM ILOG CPLEX v12.8 library. SPhyR is open source and available on https://github.com/elkebir-group/SPhyR.

4 Results

4.1 SPhyR solves practical k-DP instances in seconds

We used the ms package (Hudson, 2002) to simulate two-state perfect phylogeny trees. We set the recombination parameter to 0, and used varying number $m\in \{25,50,100\}$ of taxa and number $n\in \{25,50,100\}$ of characters. For each combination of m and n, we simulated 20 two-state perfect phylogeny matrices $B^{*}\in {\{0,1\}}^{m\times n}$. For each simulated matrix $B^{*}$, we reconstructed its unique node-labeled perfect phylogeny tree $T^{*}$, contracting internal vertices with out-degree 1. Let $b_v^{*}\in {\{0,1\}}^n$ be the states for each character at node v of T. We subsequently introduced losses in $T^{*}$ and $B^{*}$ with a loss rate λ and maximum number k of losses per character. More specifically, we performed a pre-order tree traversal: for each edge (u, v) in $T^{*}$ and character $c\in \left[n\right]$ that has been lost at most k − 1 times and where $b_{u,c}^{*}=1$, we introduced a loss for that character with probability λ. That is, we set $b_{v,c}^{*}:=0$ and $b_{w,c}^{*}:=0$ for all descendants w of v. We used varying number $k\in \{1,2,3\}$ of maximum losses per character and loss rates $\lambda \in \{0.1,0.2,0.4\}$. Thus, for each combination of m, n and k, we generated 60 k-Dollo phylogenies.

We ran SPhyR in k-DP mode using a single thread on machines with 2.6 GHz AMD Opteron 6276 CPUs and 64 GB of RAM. We used a run time limit of five hours for each instance. We show results for square input matrices in Figure 2; results for all input instances are shown in Supplementary Table S2. Our algorithm successfully solved all instances with dimensions up to 100 × 100 and at most k = 2 losses per character in only a few seconds. For k = 3 character losses and the same dimensions, SPhyR solved 75% of instances within the time limit (Fig. 2a). We find that the running time increased with increasing dimensions m × n and number k of character losses (Fig. 2b). The complexity of k-DP instances is mainly due to the (relative) number of 0-entries in the input matrix B, which increased with increasing dimensions m × n and number k of character losses (Fig. 2c). Our cutting plane and column generation procedure introduced only a tiny fraction of variables (Fig. 2d) and constraints (Fig. 2e) into the model. Remarkably, the fraction of generated variables and constraints decreased with increasing k, which is due to the incremental fashion in which our method considers character losses. Furthermore, our algorithm only required a small number of iterations (Fig. 2f). We note that instances solved in a single iteration correspond to perfect phylogeny instances.

Fig. 2.

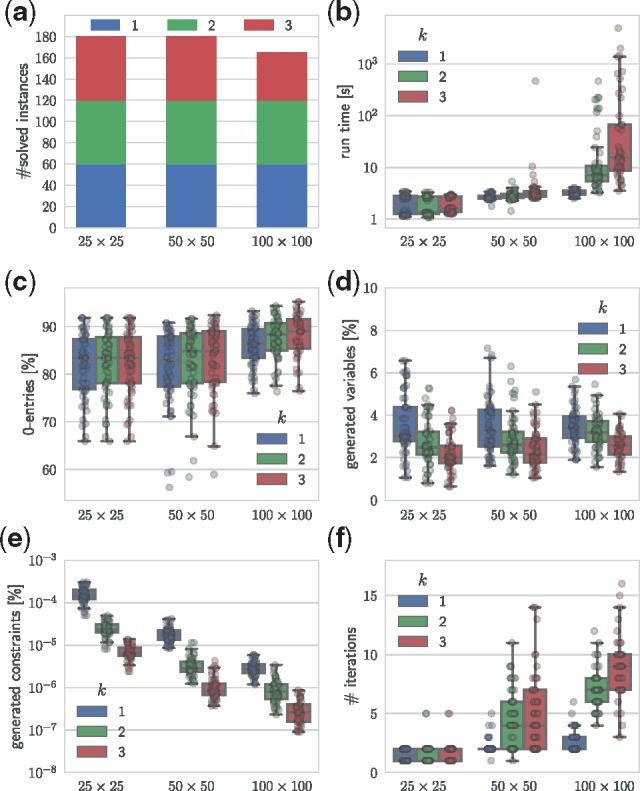
Cutting plane and column generation enables SPhyR to efficiently solve practical k-DP instances. We show results for m × n binary matrices $B=[b_{p,c}]$ where m = n. (a) The number of solved instances for varying dimensions and maximum number k of character losses. For each k and m × n, there are 60 simulated instances. SPhyR solved all k = 1 instances (blue) to optimality, but exceeded the run time limit for k = 3 instances (red) with dimensions 100 × 100. (b) The run time in seconds (logarithmic scale) increased with increasing k and m × n. (c) The fraction of entries $b_{p,c}=0$. (d) The percentage of model variables $a_{p,c,i}$ instantiated during column generation. (e) The percentage of model constraints (logarithmic scale) added during separation. (f) The number of column generation iterations. Only a single iteration is required if B is a perfect phylogeny matrix

In summary, despite the large fraction of 0-entries in practical problem instances, our algorithm quickly identifies a small fraction of variables (and constraints) that are relevant for solving the instance. As such, SPhyR is able to solve practical k-DP problem instances with varying loss rates in seconds.

4.2 SPhyR outperforms existing methods on simulated single-cell sequencing data

We now consider the problem of phylogeny estimation from an input matrix with incorrect entries. We generate such input matrices $D=\left[d_{p,c}\right]$ from the k-Dollo phylogeny matrices $B^{*}=\left[b_{p,c}\right]$ previously simulated with $m=n=50$ and k = 1 (Fig. 3a). We perturb each matrix $B^{*}$ using false positive rate ${\alpha }^{*}=0.001$ and false negative rate ${\beta }^{*}=0.2$ (Fig. 3b). That is, if $b_{p,c}^{*}=0$, we set $d_{p,c}=1$ with probability ${\alpha }^{*}=0.001$, otherwise we set $d_{p,c}=0$. If $b_{p,c}^{*}=1$, we set $d_{p,c}=0$ with probability ${\beta }^{*}=0.2$, otherwise we set $d_{p,c}=1$. Thus, we have 60 simulated instances with varying loss rate $\lambda \in \{0.1,0.2,0.4\}$.

Fig. 3.

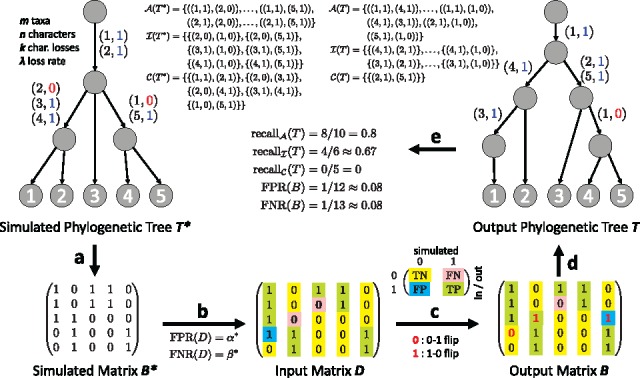
Simulation setup and comparison measures. (a) Given the number m of taxa and n of characters, we use the ms package (Hudson, 2002) to simulate a perfect phylogeny tree. Subsequently, we introduce at most k losses per character using a rate λ, yielding the simulated phylogenetic tree $T^{*}$ and matrix $B^{*}$. (b) We then perturb the entries of $B^{*}=[b_{p,c}^{*}]$ given a false positive rate $\text{FPR}(D)={\alpha }^{*}$ and false negative rate $\text{FPNR}(D)={\beta }^{*}$, yielding the input matrix $D=[d_{p,c}]$. Entry $d_{p,c}=0$ is a true negative (TN) if $b_{p,c}^{*}=0$ and a false negative (FN) if $b_{p,c}^{*}=1$. Conversely, $d_{p,c}=1$ is a false positive (FP) if $b_{p,c}^{*}=0$ and a true positive (TP) if $b_{p,c}^{*}=1$. (c) Given D, ${\alpha }^{*}$ and ${\beta }^{*}$, a phylogeny estimation method yields output matrix $B=[b_{p,c}]$. (d) In addition, such a method outputs a phylogenetic tree T whose leaves form the rows of output matrix B. (e) To compare T and $T^{*}$, we compute the recall in terms of pairs of character states that are ancestral ($\mathcal{A}$), on distinct branches (incomparable, $\mathcal{I}$), or on the same edge (clustered, $\text{C}$). A recall of 1 for all three measures implies that (the internal nodes of) T and $T^{*}$ are identical. To compare B and $B^{*}$, we compute $\text{FPR}(B)$ and $\text{FNR}(B)$—if both are 0 then $B=B^{*}$

We compared SPhyR to SCITE (Jahn et al., 2016) and SiFit (Zafar et al., 2017). While SCITE uses the infinite sites model and disallows homoplasy, SiFit uses a finite sites model allowing for parallel evolution and mutation loss. Our method SPhyR is based on the k-Dollo parsimony model, and thus disallows parallel evolution and restricts the number of losses of each character to at most k. We provided all three methods the simulated false positive rate ${\alpha }^{*}=0.001$ and false negative rate ${\beta }^{*}=0.2$. For SPhyR, we set the maximum number k of character losses to 1, the number s of taxa clusters to 10, and the number t of distinct branches to 35. We used default parameters and 100 restarts for each method. Supplementary Section S.5 provides additional details.

Given the same input matrix $D=\left[d_{p,c}\right]$, each method infers an output matrix $B=\left[b_{p,c}\right]$. We compared each output matrix B to the simulated matrix $B^{*}=\left[b_{p,c}^{*}\right]$ as follows. A false positive (FP) is a 1-entry in B that is a 0-entry in $B^{*}$. The false positive rate (FPR) is the fraction of false positives among the 1-entries of B. Conversely, a false negative (FN) is a 0-entry in B that is a 1-entry in $B^{*}$. The false negative rate (FNR) is the fraction of false negatives among the 0-entries of B. We note that, by construction, each matrix D has an expected FPR $\alpha =0.001$ and expected FNR $\beta =0.2$—thus, a straw-man algorithm that leaves the input matrix unperturbed, i.e. B = D, would achieve these rates. Moreover, note that an FPR and FNR of 0 implies that $B=B^{*}$. We find that all three methods outperformed the straw-man algorithm, significantly reducing the fraction of false positives with only a slight increase in the fraction of false negatives (Fig. 4a–c). Among the three methods, SPhyR achieved the lowest FNR while maintaining a low FPR (median FNR: 0.038; median FPR: 0.010) compared to SCITE (FNR: 0.065; FPR: 0.009) and SiFit (FNR: 0.119; FPR: 0.002). SiFit achieved the lowest FPR and the highest FNR.

Fig. 4.

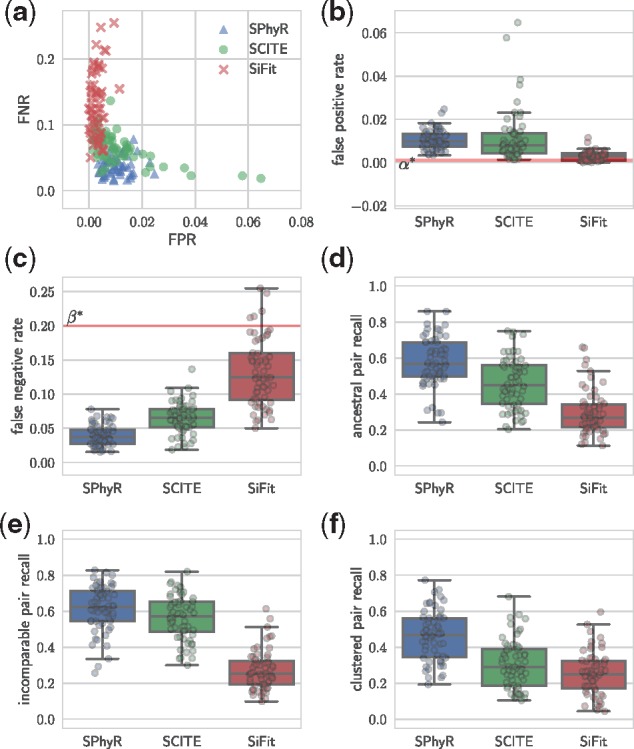
SPhyR more accurately recovers the simulated matrices $B^{*}$ and trees $T^{*}$ than SCITE and SiFit. Given the same input matrix D, each method inferred an output matrix B and phylogenetic tree T. (a–c) The tradeoff between the false negative rate (FNR) and the false positive rate (FPR) for each matrix B output by each method. (d–f) Three different measures that assess similarity between $T^{*}$ and T in terms of character states occurring on the same branch (d), on distinct branches (e) and on the same edge (f) in both $T^{*}$ and T

To explore the effect of these differences in FPR and FNR, we compared each output phylogenetic tree T to the simulated phylogenetic tree $T^{*}$. We used three different measures that consider pairs of character states (Fig. 3e). First, the ancestral pair recall is given by $\left|\mathcal{A}\right(T)\cap \mathcal{A}(T^{*}\left)\right|/\left|\mathcal{A}\right(T^{*}\left)\right|$, where the multi-set $\mathcal{A}\left(T\right)$ is composed of ordered pairs $\left(\right(c,i),(d,j\left)\right)$ of character states that are introduced on distinct edges of the same branch of T. Second, the incomparable pair recall is defined as $\left|\mathcal{I}\right(T)\cap \mathcal{I}(T^{*}\left)\right|/\left|\mathcal{I}\right(T^{*}\left)\right|$, where the multi-set $\mathcal{I}\left(T\right)$ is composed of unordered pairs $\left\{\right(c,i),(d,j\left)\right\}$ of character states that are introduced on edges from distinct branches of T. Third, the clustered pair recall is defined as $\left|\text{C}\right(T)\cap \text{C}(T^{*}\left)\right|/\left|\text{C}\right(T^{*}\left)\right|$, where the multi-set $\text{C}\left(T\right)$ is composed of unordered pairs $\left\{\right(c,i),(d,j\left)\right\}$ of character states that are introduced on the same edge of T. If all three measures equal 1 then the output tree T and the simulated tree $T^{*}$ are identical (when restricted to their internal nodes). We find that SiFit’s low FPR at the expense of the FNR significantly reduced its ability to accurately recover the simulated tree. In contrast, the more balanced FPR and FNR of SCITE and SPhyR led to more accurate output trees. Moreover, SPhyR’s evolutionary model and combinatorial coordinate-ascent algorithm, enabled our method to more accurately recover the simulated trees than SCITE and SiFit in each of the three recall measures (Fig. 4d–f), at a fraction of the run time (Supplementary Fig. S8).

In Supplementary Section S.5, we show that SPhyR is robust to varying α and β. In addition, we find that with k = 0 the output tree quality decreased, whereas the quality remained the same with k = 2, highlighting the importance of the k-Dollo parsimony model.

4.3 SPhyR reconstructs evolutionary history of a metastatic colorectal cancer with larger data likelihood

We considered metastatic colorectal cancer patient CRC1 from (Leung et al., 2017). The authors sequenced 178 cells from this patient using a cancer gene panel composed of 1000 genes. Subsequent mutation calling identified 16 single-nucleotide variants (SNVs). This yielded an 178 × 16 input matrix D with 191 missing ‘?’-entries, 614 1-entries and 2043 0-entries. Leung et al. (2017) ran SCITE on matrix D, and obtained a perfect phylogeny tree $T_{\text{SCITE}}$ and matrix $B_{\text{SCITE}}$ with $\alpha =1.52\%$ and $\beta =7.89\%$ (Supplementary Fig. S10). In a subsequent paper, Zafar et al. (2017) ran their method SiFit on the same matrix D with the same α and β, and obtained phylogenetic tree $T_{\text{SiFit}}$ and matrix $B_{\text{SiFit}}$ (Supplementary Fig. S11). We compared these two trees and two matrices to the tree and matrix inferred by SPhyR using the same α and β. In addition, we used the same number s = 10 of taxa clusters as in the simulations, and number t = 15 of character clusters. We varied the number $k\in \{0,1\}$ of losses.

Supplementary Figure S9 shows the output matrices of each method and is summarized in Table 1. We find that $B_{\text{SCITE}}$ has fewer edits from D (278) and consequently larger data likelihood (−447.66) than $B_{\text{SiFit}}$ (301 edits and likelihood −471.62). Inspection of the corresponding tree $T_{\text{SiFit}}$ of $B_{\text{SiFit}}$ reveals that 15 SNVs were introduced more than once and underwent parallel evolution (Supplementary Fig. S11), which is uncommon in the evolution of SNVs in cancer. With k = 0, i.e. no loss of mutation, SPhyR achieved similar likelihood as SCITE. By allowing each character to be lost once, i.e. k = 1, SPhyR yielded matrix $B_{\text{SPhyR}}$ with the same number of edits but a larger likelihood than $B_{\text{SCITE}}$. Supplementary Figure S12 shows the corresponding tree $T_{\text{SPhyR}}$. Unlike $T_{\text{SiFit}}$, the tree $T_{\text{SPhyR}}$ does not exhibit parallel evolution, which is by definition of the k-Dollo parsimony model. In $T_{\text{SCITE}}$, 24 cells formed a separate clade (red leaves in Supplementary Fig. S10). These cells were obtained from the liver metastasis by Leung et al. (2017). In addition to the same 24 cells (red leaves in Supplementary Fig. S12), tree $T_{\text{SPhyR}}$ assigns six additional cells to the metastatic clade (blue leaves in Supplementary Fig. S12). SPhyR inferred that these six cells have undergone loss of mutation. Five of the six cells (MD_1, MD_5, MD_6, MD_10 and MD_20) were obtained by Leung et al. (2017) from the liver metastasis, corroborating the metastatic clade in $T_{\text{SPhyR}}$. SCITE was unable to assign the original 24 metastatic cells and these five additional cells to the same clade due to the infinite sites assumption; the five additional cells appeared close to the root in $T_{\text{SCITE}}$ (blue leaves in Supplementary Fig. S10). Thus, the k-Dollo parsimony model employed by SPhyR led to more accurate reconstruction of the evolutionary history of this metastatic colorectal cancer.

Table 1.

SPhyR reconstructs a phylogenetic tree for patient CRC1 from (Leung et al., 2017) with larger data likelihood than existing methods

Method	$\log \mathrm{Pr}(D|B,\alpha ,\beta )$	$1\to 0$	$0\to 1$	$?\to 0$	$?\to 1$	# edits	# losses	# par. evo.
SCITE	−447.66	33	54	142	49	278	0	0
SiFit	−471.62	14	96	126	65	301	14	15
SPhyR (k = 0)	−450.70	19	79	138	53	289	0	0
SPhyR (k = 1)	−413.38	13	74	137	54	278	14	0

Note: The input matrix $D=[d_{p,c}]$ has m = 178 taxa (cells) and n = 16 characters (single-nucleotide variants). For each method, we show the data likelihood, the number of $1\to 0$ changes, the number of $0\to 1$ changes, the number of $?\to 0$ changes, the number of $?\to 1$ changes, the total number of changes, the number of losses, and the number of times a character is introduced more than once (parallel evolution).

5 Discussion

We introduced SPhyR, a method for tumor phylogeny estimation from single-cell sequencing data. Copy-number aberrations are ubiquitous in solid tumors and affect large genomic regions. As such, homoplasy of single-nucleotide variants in cancer is mainly due to mutation loss caused by copy number aberrations. Based on this observation, SPhyR employs the k-Dollo parsimony model, where a mutation may only be gained once but lost k times. We studied the error-free case and derived a combinatorial characterization of solutions as constrained integer matrix completions. This characterization formed the basis for our integer linear program, which we solved efficiently using column and cutting plane generation. We introduced a coordinate-ascent approach for solving the real data case with errors in the input matrix. On simulated data, we showed that SPhyR outperformed existing methods, that are either based on the infinite sites or the finite sites evolutionary model, in terms of solution quality and run time. On real data, we showed that SPhyR provided a likelier explanation of the evolutionary history of a metastatic colorectal cancer.

Our findings show that while there is a need for more realistic evolutionary models in tumor phylogeny estimation beyond the infinite sites model, evolutionary models that are too permissive, such as the finite sites model, lead to incorrect inferences. By disallowing parallel evolution but allowing for mutation loss, the k-Dollo parsimony model employed by SPhyR strikes a balance between being realistic and yet, sufficiently constrained.

There are a number of avenues for future research. From a theoretical perspective, the hardness of the k-DP problem, where $k\ge 1$, remains open. It would be interesting to investigate whether the graph sandwich approach used by Pe’er et al. (2004) for incomplete directed perfect phylogeny problem can be extended to the k-DP problem. From a practical perspective, inclusion of additional data sources and information might yield additional constrains that improve phylogeny reconstruction. For instance, for metastatic cancers the inclusion of a multi-state location character might result in evolutionary scenarios that minimize migrations, as described in (El-Kebir et al., 2018) for bulk DNA sequencing data. Moreover, inclusion of copy-number information might allow one to restrict the subset of characters that have undergone losses. Finally, one could consider joint phylogeny estimation from bulk and single-cell sequencing data of the same tumor.