Machining protein microcrystals for structure determination by electron diffraction

Significance

Electron cryomicroscopy and diffraction are increasingly powerful methods for the analysis of biological structures at near-atomic resolution. However, the very strong interaction of electrons with matter limits the thickness of specimens that can be analyzed at high resolution to ∼100 nm. We show here that a frozen, hydrated lysozyme crystal milled with a focused ion beam to a suitable thickness produces useful electron diffraction to ∼2-Å resolution. This approach provides a means to determine structures of protein crystals that would otherwise be too thick for electron crystallographic analysis. This demonstration also suggests that this technique will allow lamella of cryopreserved biological material prepared by milling to preserve the structural details, approaching atomic detail.

Abstract

We demonstrate that ion-beam milling of frozen, hydrated protein crystals to thin lamella preserves the crystal lattice to near-atomic resolution. This provides a vehicle for protein structure determination, bridging the crystal size gap between the nanometer scale of conventional electron diffraction and micron scale of synchrotron microfocus beamlines. The demonstration that atomic information can be retained suggests that milling could provide such detail on sections cut from vitrified cells.

Despite the explosive growth in cryoelectron microscopy (cryo-EM) following the “resolution revolution” (1), X-ray methods were responsible for nearly 20-fold as many macromolecular structure depositions as single-particle cryo-EM in 2017, and diffraction remains the favored method for genuine atomic resolution analysis. Crystal growth is often a bottleneck for such analyses, and it can sometimes be difficult to grow crystals of sufficient size for analysis at conventional synchrotron macromolecular crystallography (sMX) beamlines. This has led to the development of microfocus beamlines that can routinely analyze crystals down to ∼5 μm (2). However, it is unknown how often crystallographic analyses fail due to the failure to recognize smaller crystals. The next generation of synchrotron beamlines may reduce the size requirement to around 1 μm, and the potential for structure determination from submicron crystals has been demonstrated by application of X-ray free electron laser (XFEL) sources, which achieve a brightness ∼10⁸-fold greater than a typical synchrotron beamline (3). XFEL sources also sometimes mitigate, by achieving “diffraction before destruction,” the radiation damage problem that limits the collection of synchrotron X-ray data (4, 5).

Electron diffraction (ED) can provide high-resolution structure determination from 3D crystals (6–12). Electrons have potential advantages over X-rays for the analysis of very small crystals: Their interaction with matter is sufficiently strong for a measurable signal to be obtained from a typical laboratory instrument; the experiment is performed in a vacuum, thereby reducing background scatter; and the useful data obtained before radiation damage occurs are much greater (6, 13, 14). However, the strong interaction with matter is also a limitation for ED, since the beam is absorbed very strongly by a few hundred nanometers of crystal. Furthermore, it has often been held that kinematic theories of diffraction, upon which X-ray analysis rests, are useless for crystals of such thickness (15, 16). For protein crystals, due to the large size of the unit cell, many diffracted beams are stimulated simultaneously and, through conservation of energy, the amplitude of each is greatly reduced, mitigating the effects of multiple scattering. Although dynamical effects have been observed with thicker protein crystals (6), the utility of the kinematic theory for thin crystals is shown in our study below, where systematic absences, which would be polluted by multiple scattering, are maintained. Indeed, in recent years, the power of ED to analyze nanometer-sized crystals has been amply demonstrated (6, 12, 17); however, there remains a significant range of size, from a few hundred nanometers to a few microns, that is accessible only using XFEL radiation, which is both hard to access and extremely expensive.

Micromachining using a focused ion beam (FIB milling) has been established in physical science applications for many years (18), and, although far from routine, cryo-FIB milling is now increasingly applied in the life sciences, for instance, to create thin lamella milled from frozen, hydrated cells to reveal cellular architecture (19). Cryo-FIB milling has been shown to preserve the structure of frozen, hydrated biological samples better than mechanical cryosectioning, although how far the preservation of order extends has not been established (19).

Results

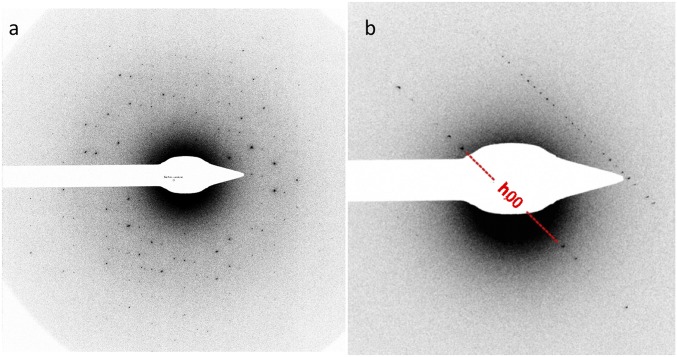
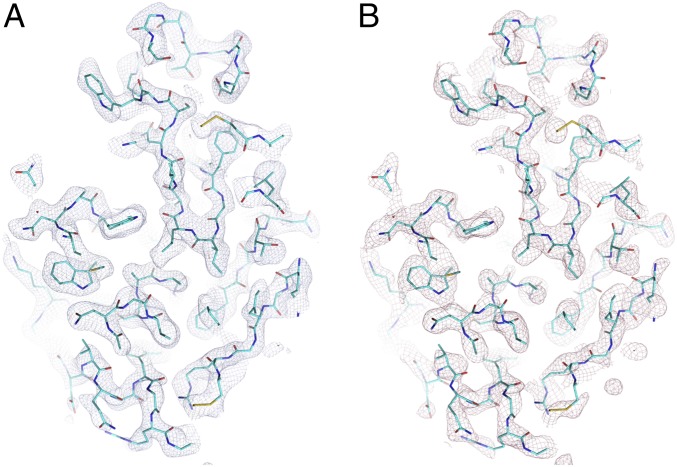
We reasoned that if cryo-FIB milling does not distort the internal structure of cut lamellae, then milled crystals would maintain their diffraction capacity and milling would provide a general vehicle to bridge the crystal size gap between sMX and ED. As a proof-of-principle experiment, we grew tetragonal microcrystals (ca. 10 × 10 × 5 μm³) of hen egg-white lysozyme. A limitation of lysozyme as a test system is that it shows significant crystal-to-crystal variation in unit cell parameters (SI Appendix, Fig. S1); however, it generally diffracts to a resolution of 2 Å or better. Crystals were grown using established methods and deposited on standard EM grids, which were then blotted and vitrified by plunging into liquid ethane (Materials and Methods). The crystals, maintained at 100 K, were coated with platinum before milling in a dual-beam instrument using a beam of gallium ions, to thicknesses of ca. 200 nm (Materials and Methods and Fig. 1A). The final stages of milling used a low-voltage ion beam, a strategy shown to minimize surface damage and strain in metallic crystals (20). Unlike some current protocols, our procedure did not involve subsequent sputtering with platinum (which is thought to allow improved dissipation of charge). A representative example of lamella used for data collection is shown in Fig. 1. Diffraction data were collected on a Thermo Fisher Scientific Talos Arctica microscope operating at 200 kV, with a beam size ∼2 μm in diameter as still snapshots with the stage tilted from −60 to +10° in steps of 0.5° between images, resulting in 134 individual diffraction patterns, at a total electron dose of ∼25 e⁻/Ų (Materials and Methods). Data were recorded on a Ceta 16M (Thermo Fisher Scientific) detector (https://www.fei.com/accessories/ceta-16m/), with measured detective quantum efficiency at 1/2 Nyquist of 0.12. No correction was made for possible saturation of the detector leading to nonlinearity of response because the distribution of pixel values shows no evidence of saturation. Typical patterns are shown in Fig. 2, and the full set is shown in Movie S1. In the early patterns, visible diffraction spots extended to a Bragg spacing of 1.9 Å, while by pattern 110, the effective resolution had declined to ∼4 Å due to severe radiation damage, as expected since we markedly exceeded the advised maximum electron dose (7, 14, 21, 22) (Movie S1). A principal axis may be seen in pattern 118, confirming that the systematic absences are well obeyed (Fig. 2B). Autoindexing procedures developed for sMX and XFEL analysis were not able to determine crystal orientation. However, using the principal axis as an anchor, the orientation matrix was fully defined using a purpose-written, graphical user interface-driven program (Materials and Methods). Since the data were monochromatic still images, and the mosaic spread of the crystal was remarkably small (∼0.01°), the data were treated as independent diffraction patterns. Further analysis of the indexed data was therefore achieved using software originally developed for XFEL images (Materials and Methods). In this initial experiment, fully automated analysis was hindered by an apparent detector tilt and by drift in the direct beam position on the detector. Details of the analysis are provided in Materials and Methods. The unit cell dimensions of the crystal were determined as a = b = 79.9, c = 38.7 Å, which is within the range expected for lysozyme crystals under cryoconditions. Clearly, the data collection method was suboptimal (essentially all reflections were partially recorded), and the detector was almost an order of magnitude less efficient than an ideal detector. Nevertheless, an RSplit of 28 (25)% and correlation coefficient (CC_1/2) of 85 (85)% between two random half datasets on all data to 2.0 Å (values to 4.5 Å are shown in parentheses) for a dataset of over 80% completeness at a resolution of 4.5 Å (falling to <30% at a resolution of 3 Å; SI Appendix, Figs. S2 and S3) was obtained from a single lamella. B-factor increases (estimated from the fall-off of the high-resolution data on successive diffraction patterns) were consistent with significant radiation damage (SI Appendix, Fig. S4). This dataset is isomorphous with previous data collected from lysozyme (CC = 74%), and rigid body refinement with no manual intervention, to avoid overfitting, against a typical lysozyme model [Protein Data Bank (PDB) ID code 5wr9] yielded Rwork = 29.1% and Rfree = 28.2%. The moderate quality of the data may be judged from the potential function maps shown in Fig. 3. Therefore, although this experiment was far from ideal (for instance, a complete dataset with little radiation damage could be collected if a more sensitive detector was used, and properly integrated measurements could be obtained from continuous recording during crystal rotation), the resulting data are not drastically worse in quality than data reported from unmilled lysozyme crystals (25.5%/27.8% Rwork/Rfree after full refinement) (6).

Fig. 1.

Images of the frozen, hydrated lysozyme crystal. Representative SEM images are shown before (A) and after (B and C) milling. (D) Transmission EM image of the milled lamella. (Scale bars: A and B, 4 μm; C, 30 μm; D, 3 μm.)

Fig. 2.

ED patterns of the frozen, hydrated lysozyme crystal. The edges of the image correspond to Bragg spacings of ∼1.8 Å. The first image collected (A) and image 118 (B), with the h,0,0 row of reflections indicated, are shown. Comparison of these reflections with those from a general h row (clearly seen running parallel to the h,0,0 row) reveals the systematic absences.

Fig. 3.

Section of the lysosome crystal density map for a traditional 2Fo-Fc synthesis (A) and a composite omit map from Phenix (B). Contours are drawn at a level of 1 σ. Note the composite omit map eliminates bias from the phases (derived from a rigid body-refined molecular replacement model), and thus represents the useful information in the measured amplitudes.

Discussion

This work is a proof of principle; better detectors, better experimental procedures, continuous rotation of the crystal, and improved data analysis methods (including consideration of dynamical scattering effects) are required to establish the full potential for the collection of diffraction data from lamellae. In addition, we have not determined the depth of any surface damage to the lamella, or the effect of beam-induced charging. We expect that, with optimization of the method, the use of multiple lamellae will enable the collection of complete, accurate, high-resolution sets of diffraction intensities, as is now routine for crystals of a few microns with microfocus sMX. Thus, the use of milled crystals will remove the size restriction on crystals for ED, bridging the size gap to synchrotron X-ray diffraction, which currently struggles with crystals less than ∼5 μm across, and potentially releasing the limited availability on XFEL beamlines for some of the structure questions. Furthermore, and perhaps more importantly, the retention of high-resolution diffraction demonstrates that cryo-FIB milling preserves atomic-level structure within the lamellae, suggesting that this method might provide a vehicle for the determination of molecular and atomic structures via electron imaging and diffraction from not only protein crystals but also cellular structures, where precision milling can isolate the region of interest in a slice thin enough to provide good signal to noise. Analysis of such lamellae, most likely via electron tomography, would provide a link from high-resolution structural biology to cell biology. Furthermore, subtomogram averaging or even in situ single-particle analysis of repeated structures might then allow the visualization at near-atomic detail within the cell.

Materials and Methods

Crystal and Grid Preparation.

A solution of 50 mg/mL lysozyme (Sigma–Aldrich) in 0.02 M sodium acetate (pH 4.6) was batch-crystallized by addition of 1 M sodium acetate (pH 3.0), 6% (wt/vol) PEG 6000, and 10% (wt/vol) NaCl in a volumetric ratio of 1:4 at 25 °C. A 4-μL aliquot of a 1:10 dilution of the batch crystallization was applied onto a glow-discharged, holey, carbon-coated copper grid (C-flat, CF-2/1-2C; Protochips) at room temperature. Grids were blotted for 3–4 s from the reverse side and plunge-frozen in liquid ethane using a manual plunger. Crystals were typically ∼10 μm in length. Frozen grids were transferred into liquid nitrogen for storage until needed.

Lamella Preparation.

Plunge-frozen grids were clipped into autogrid (Thermo Fisher Scientific) rims and loaded into the cryo-FIB (Thermo Fisher Scientific) using a Quorum cryosystem (PP3010T) with a custom-designed cryostage and shuttle (Max Planck Institute of Biochemistry and Thermo Fisher Scientific) (23, 24). The cryostage and anticontaminator were cooled for a minimum of 90 min before loading samples, using a continuous nitrogen gas flow rate of 3.6 L⋅min⁻¹ and 4 L⋅min⁻¹ at −165 °C and −175 °C, respectively. Milling was performed as previously described (23, 25). Before milling, samples were precoated with a platinum layer ∼2 μm thick using the gas injection system (GIS). This was accomplished by tilting the stage to 7°, rotating by 180° (such that the surface of the grid faced the ion column), and lowering the sample by 5 mm (12 mm as measured from the SEM column). The GIS needle was inserted and heated to 27 °C, and samples were coated for 5 s per grid. SEM imaging was performed at 5 kV and 25 pA beam current. The lamella was cut at an angle of 10° with respect to the grid, with a final thickness of ∼0.2 μm. Milling was performed in a stepwise fashion, using a 30-kV beam and beam currents of 300 pA, 100 pA, 49 pA, and 30 pA to generate lamella with a progressive thickness of ∼5 μm, ∼2 μm, ∼1 μm, and ∼0.2 μm, respectively, measured using the ion beam image. During the final milling step, lamella thickness was monitored using the SEM with a 3-kV beam at 25 pA as described previously (25). All images were recorded using an Everhart–Thornley detector to record secondary electrons or FIB-induced secondary electrons.

Data Collection.

ED data were collected from a single crystal lamella, ∼200 nm thick, over an angular range from −60 to +10° rotation around a tilt axis on the grid plane normal to the electron beam. Diffraction data were collected on an FEI Talos Arctica transmission microscope equipped with a field emission electron gun operating at an accelerating voltage of 200 kV, corresponding to a wavelength of 0.0251 Å. Images were recorded in diffraction mode as stills, separated by 0.5° tilt of the grid, on a Ceta camera with a sensor size of 4,096 × 4,096 pixels and at a physical camera length of 1.75 m, corresponding to an apparent detector distance of 2.44 m with lenses. The resolution at the edge of the detector was 1.8 Å. Individual diffraction frames were taken with exposure times of 2.5 s per diffraction pattern, with an electron dose rate of ∼0.042 e⁻⋅Ų⋅s⁻¹ (measured using a fluorescent screen) and with a 2-s wait between patterns to allow the stage to settle. The electron beam size on the lamella was ∼1.9 × 1.9 μm.

Crystal Indexing.

Software providing a graphical user interface was written to allow manual indexing of the diffraction image (Mandexing). This is a lightweight piece of software, dependent on the Qt5 framework, which implements a simple detector geometry (flat detector perpendicular to the beam center at a given distance). Portable Network Graphics files can be loaded to provide a reference diffraction image. The beam center, detector distance, and wavelength parameters can be varied. The unit cell can be set, and two chosen Miller index vectors can be brought parallel to the screen. Rotation around the beam center is controlled by the mouse, and incremental rotations can be accessed using the “WASD” keys. These keys operate on the vertical and horizontal directions, unless a particular axis perpendicular to the beam direction has been fixed. In this case, the keys operate around that fixed axis and the axis perpendicular to both that axis and the beam axes.

The parameters of the lysozyme micro-ED experiment are shown in Table 1. The sample is rotated about an axis approximately vertical on the displayed image. The 118th pattern clearly displays the axial systematic absences resulting from a 2₁ screw axis, and this was therefore defined as the a* axis (Fig. 2B). Mandexing was used to fix this axis and manually rotate the diffraction pattern around it to find an orientation that matched the remaining nonaxial spots elsewhere on the image. There were a small number of solutions that, visually, fitted equally well. From these, the correct solution was selected as that which properly predicted spots on preceding and subsequent images. Lysozyme typically crystallizes in P4₃2₁2, but the unit cell parameters can vary significantly (SI Appendix, Fig. S1). The unit cell dimension for this analysis, a = b = 79.9 Å, was chosen based on the fit to the h00 axis for the assumed wavelength and detector distance. The c-axis dimension was determined as 38.7 Å, which corresponds to an a-to-c ratio within the range observed for the majority of lysozyme datasets. Strong spots matching predicted reflections were picked out manually for each image and refined using a reciprocal lattice point size of 0.003 Å⁻¹ to minimize the distance in reciprocal space to the Ewald sphere. These orientations were used for integration.

Table 1.

Data collection and analysis

Data	Instrument/parameters	Specification/measurements
Data collection	Accelerating voltage, kV	200
	Electron source	Field emission gun
	Wavelength, Å	0.0251
	Total electron dose per crystal, e−/Å2	25
	No. of diffraction patterns per crystal	134
	No. of crystals	1
	Total reflections to 1.9 Å	8,463
Data analysis	Space group	P43212
	Unit cell dimensions, Å
	a = b	79.90
	c	38.67
	α = β = γ	90°
	Resolution, Å (highest resolution bin)	10–1.9 (2.14–1.90)
	Total unique reflections	3,510
	Reflections in working set	3,337 (307)
	Reflections in free set	173 (10)
	Multiplicity	0.82
	Completeness	38.7 (10.5)
	RSplit, %	27.9 (93.2)
	Rwork/Rfree, %	29.1/28.3 (53.2/72.9)
	Overall correlation coefficient, %	81.3 (29.2)
	Ramachandran % for outliers, favored	0, 98.4

The highest resolution shell statistics are shown in parentheses.

Data Processing.

The derived orientation matrices were used to integrate and post-refine the raw intensities using cppxfel (26). Patterns were processed using individual direct beam positions determined using custom scripts (the beam position drifted on the detector by 30 pixels perpendicular and 91 pixels parallel to the axis of rotation across the entire data collection). A residual discrepancy between predicted and observed spot positions was successfully modeled by an 8° tilt in the detector (this could be an artifact of the electron optics), after which the average deviation between observed and predicted spot positions was less than one-half of a typical spot diameter. Integration was performed as described previously (26), with a foreground integration window size of 10 × 10 pixels. The surrounding four-pixel moat was ignored, and the outer window extended to 25 × 25 pixels for background estimation. Merging and postrefinement with partiality correction were performed as described previously (26, 27) with the following beam parameters: wavelength = 0.0251 Å, mosaic spread = 0.01°, fractional energy spread of the beam = 0.00075 (modeled as a super-Gaussian), and crystal size = 0.3 μm. Individual reflections with a partiality of less than 0.2 were discarded; otherwise, their intensity was divided by the partiality to approximately recover the true intensity (Table 1).

Structure Determination.

Since the crystals were approximately isomorphous with those used for previously reported structures, the structure was determined simply by rigid body refinement of an extant structure (PDB ID code 5wr9) (Table 1) using phenix.refine with electron scattering factors and with manually added waters.

Composite omit maps were generated using Phenix with sequential 5% fractions omitted and Fc used where Fo was not recorded.

Code Availability.

Mandexing (https://www.github.com/helenginn/mandexing) and cppxfel (https://github.com/helenginn/cppxfel) are publicly available on GitHub.

Data Availability.

The partially refined model of a milled lysosome crystal has been deposited in the PDB (ID code 6H3B).