Universal quantum Hamiltonians

Significance

Quantum many-body systems exhibit a bewilderingly diverse range of behavior, which forms the central object of study in many areas of physics and beyond. Our work reveals that, in fact, the entire physics of every other quantum many-body system is replicated in certain simple, universal quantum spin-lattice models. A key application is to the field of analogue simulation of quantum systems, which has long been seen as one of the most promising near-term applications of quantum information technology. We put this field on a rigorous footing, give some rigorous justification for why it may not require error correction, and show that simple families of systems can be used as universal quantum simulators.

Abstract

Quantum many-body systems exhibit an extremely diverse range of phases and physical phenomena. However, we prove that the entire physics of any quantum many-body system can be replicated by certain simple, “universal” spin-lattice models. We first characterize precisely what it means for one quantum system to simulate the entire physics of another. We then fully classify the simulation power of all two-qubit interactions, thereby proving that certain simple models can simulate all others, and hence are universal. Our results put the practical field of analogue Hamiltonian simulation on a rigorous footing and take a step toward justifying why error correction may not be required for this application of quantum information technology.

The properties of any physical system are captured in its Hamiltonian, which describes all of the possible energy configurations of the system. Among the workhorses of theoretical many-body and condensed matter physics are spin-lattice Hamiltonians, in which the degrees of freedom are quantum spins arranged on a lattice, and the overall Hamiltonian is built up from few-body interactions between these spins. Although these are idealized, toy models of real materials, different spin-lattice Hamiltonians are able to model a wide variety of different quantum phases and many-body phenomena: phase transitions (1), frustration (2), spontaneous symmetry breaking (3), gauge symmetries (4), quantum magnetism (5), spin liquids (6), topological order (7), and more. In this paper, we prove that there exist particular, simple spin models that are universal: They can replicate to any desired accuracy the entire physics of any other quantum many-body system (including systems composed not only of spins but also bosons and fermions). This implies, in particular, that the ground state, full energy spectrum and associated excited states, all observables, correlation functions, thermal properties, time evolution, and also any local noise processes are reproduced by the universal model.

Note that this is a very different notion of “universality” from that of universality classes in condensed matter and statistical physics (8). Universality classes capture the fact that, if we repeatedly “zoom out” or course-grain the microscopic degrees of freedom of a many-body system, models that are microscopically different become increasingly similar (converge to the same limit under this “renormalization group flow”), and their macroscopic properties turn out to fall into one of a small handful of possible classes. The “universality” we are concerned with here (9) has a completely different and unrelated meaning. It is closer to the notion of universality familiar from computing. A universal computer can carry out any possible computation, including simulating completely different types of computers. Universal models are able to produce any many-body physics phenomena, including reproducing the physics of completely different many-body models.

One might expect that universal models must be very complicated for their phase diagram to encompass all possible many-body physics. In fact, some of the models we show to be universal are among the simplest possible. Nearest-neighbor Heisenberg interactions on a square lattice give rise to 2D models with the simplest possible local degrees of freedom (qubits), short-range, two-body interactions, and the largest possible local symmetry [full $SU\left(2\right)$ invariance]. Yet our results prove that, if all of the coupling strengths can be varied individually, this model is universal. Thus, it can replicate in a rigorous sense the full physics of models with higher spatial dimensions, long-range interactions, other symmetries, higher-dimensional spins, and even bosons and fermions.

In addition to the new relationships this establishes between apparently very different quantum many-body models, with implications for our fundamental understanding of quantum many-body physics, there are also potential practical applications of our results in the field of analogue quantum simulation. There is substantial interest nowadays in using one quantum many-body system to simulate the physics of another, and one of the most important applications of quantum computers is anticipated to be the simulation of quantum systems (10, 11).

Two quite different notions of Hamiltonian simulation are studied in the literature. The first concerns simulating the time dynamics of a Hamiltonian on a quantum computer using an algorithm originally proposed by Lloyd (12), and refined and improved in the decades since (13–16). This is the quantum computing equivalent of running a numerical simulation on a classical computer. However, it requires a scalable, fault-tolerant, digital quantum computer. Except for small-scale proof-of-principle demonstrations, this is beyond the reach of current technology. The second notion, called “physical” or “analogue”—in the sense of “analogous”—Hamiltonian simulation, involves directly engineering the Hamiltonian of interest and studying its properties experimentally (akin to building a model of an airfoil and studying it in a wind tunnel). This form of Hamiltonian simulation is already being performed in the laboratory using a variety of technologies, including optical lattices, ion traps, superconducting circuits, and others (10, 17, 18). Just as it is easier to study a scale model of an airfoil in a wind tunnel than an entire airplane, the advantage of artificially engineering a Hamiltonian that models a material of interest, rather than studying that material directly, is that it is typically easier to measure and manipulate the artificially engineered system. It is possible to measure the state of a single atom in an optical lattice (19–21); it is substantially harder to measure, for example, the state of a single electron spin in a 2D layer within a cuprate superconductor.

Many important theoretical questions regarding analogue quantum simulation remain open, despite its practical significance and experimental success (10, 17, 18). Which systems can simulate which others? How can we characterize the effect of errors on an analogue quantum simulator? [This was highlighted in a 2012 review article (11) as one of the key questions in this field.] On a basic level, what should the general definition of analogue quantum simulation itself be? The notions of simulation and universality we develop here enable us to answer all these questions.

This computationally inspired notion of physical universality has its origins in earlier work on “completeness” of the partition function of certain classical statistical mechanics models (22–24). Recent results by De las Cuevas and Cubitt (9) built on those ideas to establish the more stringent notion of universality for classical spin systems. Related, more practically focused notions have also been explored in recent work motivated by classical Hamiltonian engineering experiments (25). Here we consider the richer and more complex setting of quantum Hamiltonians, which requires completely different techniques.

For our explicit constructions that establish the existence of universal Hamiltonians we are able to draw on a long literature in the field of Hamiltonian complexity (26–33), studying the computational complexity of estimating ground state energies. These results per se only concern the ground state energy, and moreover only the computational complexity of estimating it. Nonetheless, the “perturbative gadget” techniques developed to prove Hamiltonian complexity results (26, 27) turn out to be highly useful in constructing the full physical simulations required for our results. By combining our precise mathematical understanding of analogue Hamiltonian simulation with these Hamiltonian complexity techniques, we are able to design “gadgets” that transform one many-body Hamiltonian into another while preserving its entire physics and local structure, as required to construct universal models.

1. Hamiltonian Simulation

We start by establishing precisely what it means for one quantum many-body system to simulate another. Any nontrivial simulation of one Hamiltonian $H$ with another $H\prime$ will involve encoding the first within the second in some way. We want this encoding $H\prime =\mathcal{E}\left(H\right)$ to “replicate all of the physics” of the original $H$. To reproduce all static, dynamic, and thermodynamic properties, the encoding $\mathcal{E}$ needs to fulfill a long list of operational requirements:

• i)$\mathcal{E}\left(H\right)$ should be a valid Hamiltonian: $\mathcal{E}\left(H\right)=\mathcal{E}{\left(H\right)}^{†}$.
• ii)$\mathcal{E}$ should reproduce the complete energy spectrum: $\text{spec}\left(\mathcal{E}\left(H\right)\right)=\text{spec}\left(H\right)$. More generally, $\mathcal{E}\left(M\right)$ should preserve the outcomes (eigenvalues) of any measurement $M$: $\text{spec}\left(\mathcal{E}\left(M\right)\right)=\text{spec}\left(M\right)$.
• iii)Individual interactions in the Hamiltonian should be encoded separately: $\mathcal{E}\left({\sum }_i{\alpha }_i{h}_i\right)={\sum }_i{\alpha }_i\mathcal{E}\left(h_i\right)$. Otherwise, encoding would require solving the full many-body Hamiltonian, obviating any need to simulate it.
• iv)There should exist a corresponding encoding of states, ${\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}$, such that measurements on states are simulated correctly: For any observable $A$, $\text{Tr}\left(\mathcal{E}\left(A\right){\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}\left(\rho \right)\right)=\text{Tr}\left(A\rho \right)$.
• v)$\mathcal{E}$ should preserve the partition function (potentially up to a physically unimportant constant rescaling): $Z_{H\prime }\left(\beta \right)=\text{Tr}\left(e^{-\beta \mathcal{E}\left(H\right)}\right)=c\text{Tr}\left(e^{-\beta H}\right)=c\hspace{0.17em}{Z}_H\left(\beta \right)$.
• vi)Time evolution according to $\mathcal{E}\left(H\right)$ should simulate time evolution according to $H$: $e^{-iH\prime t}{\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}\left(\rho \right)e^{iH\prime t}={\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}\left(e^{-iHt}\rho e^{iHt}\right)$.
• vii)Any error or noise process on the $\mathcal{E}\left(H\right)$ system should correspond to some error or noise process on the $H$ system: For any superoperator $\mathcal{N}\prime$, there should exist a superoperator $\mathcal{N}$ such that $\mathcal{N}\prime \left({\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}\left(\rho \right)\right)={\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}\left(\mathcal{N}\left(\rho \right)\right)$.

Using Jordan- and C*-algebra techniques, we prove (SI Appendix) that, remarkably, the very basic requirements i–iii already imply that all other operational requirements are satisfied too. Furthermore, any encoding map $\mathcal{E}$ that satisfies them must have a particularly simple mathematical form:

$$\mathcal{E}\left(H\right)=U\left(H^{\oplus p}\oplus {\overline{H}}^{\oplus q}\right)U^{†}$$ [1]

for some unitary $U$ and nonnegative integers $p$, $q$ such that $p+q\ge 1$. ($\overline{H}$ denotes complex conjugation of $H$.)

This characterization of Hamiltonian encodings holds if the entire simulation is to exactly replicate all of the physics of the original. However, in practice no simulation will ever be exact. What if the simulator Hamiltonian $H\prime$ only replicates the physics of the original Hamiltonian $H$ up to some approximation? As long as this approximation can be made arbitrarily accurate, $H\prime$ will be able to replicate the entire physics of $H$ to any desired precision.

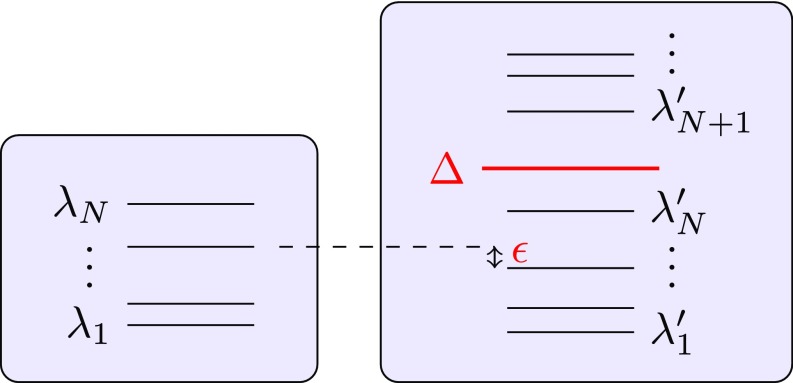
Moreover, it suffices if the physics of $H$ is replicated within some well-isolated subspace of $H\prime$, even if $H\prime$ behaves nothing like $H$ outside that subspace. An important case is when the simulation occurs within the subspace of states with energy below some cutoff $\mathrm{\Delta }$, especially if this energy cutoff can be made as large as desired (Fig. 1). Due to energy conservation, any initial state with energy less than $\mathrm{\Delta }$ will be unaffected by the high-energy sector. Indeed, as long as the cutoff is larger than the maximum eigenvalue of $H$, $H\prime$ will be able to simulate all possible states of $H$. This also holds for all of thermodynamic properties; any error in the partition function due to the high-energy sector is exponentially suppressed with increasing $\mathrm{\Delta }$. In practice, one is often interested only in low-temperature properties of a quantum many-body Hamiltonian, as these are the properties relevant to quantum phases and phase transitions. In that case, the energy cutoff does not even need to be large, merely sufficiently above the lowest excitation energy. Thus, we need to generalize our characterization to encompass approximate simulation of $H$ in the low-energy subspace of $H\prime$.

Fig. 1.

Simulating one Hamiltonian within the low-energy space of another. $H\prime$ (Right) simulates $H$ (Left) to precision $\left(\eta ,ϵ\right)$ below energy cutoff $\mathrm{\Delta }$.

Finally, for a good simulation we would also like the encoding to be local, in the sense that each subsystem of the original Hamiltonian corresponds to a distinct subset of particles in the simulator. This will enable us to map local observables on the original system to local observables on the simulator system, as well as to efficiently prepare states of the simulator.

By making all of the above mathematically precise, we show (SI Appendix) that this leads to the following rigorous notion of Hamiltonian simulation, which encompasses both exact simulation (as a special case) and, more generally, approximate simulation within a low-energy subspace (also see Fig. 1):

Definition 1 (analogue Hamiltonian simulation):

A many-body Hamiltonian $H\prime$ simulates a Hamiltonian $H$ to precision $\left(\eta ,ϵ\right)$ below an energy cutoff $\mathrm{\Delta }$ if there exists a local encoding $\mathcal{E}\left(H\right)=V\left(H\otimes P+\overline{H}\otimes Q\right)V^{†}$, where $V={\otimes }_i{V}_i$ for some isometries $V_i$ acting on 0 or 1 qudits of the original system each, and $P$ and $Q$ are locally orthogonal projectors, such that

• i)there exists an encoding $\tilde{\mathcal{E}}\left(H\right)=\tilde{V}\left(H\otimes P+\overline{H}\otimes Q\right){\tilde{V}}^{†}$ such that $\tilde{\mathcal{E}}\left(\mathbb{1}\right)=P_{\le \mathrm{\Delta }\left(H\prime \right)}$ and $\Vert \tilde{V}-V\Vert \le \eta$;
• ii)$\Vert H_{\le \mathrm{\Delta }}^{\prime }-\tilde{\mathcal{E}}\left(H\right)\Vert \le ϵ$.

Here, we write $H_{\le \mathrm{\Delta }}^{\prime }=P_{\le \mathrm{\Delta }\left(H\prime \right)}H\prime$ where $P_{\le \mathrm{\Delta }\left(H\prime \right)}$ denotes the projector onto the subspace spanned by eigenvectors of $H\prime$ with eigenvalues below $\mathrm{\Delta }$.

The first requirement (i) states that, to good approximation (i.e., within error $\eta$), the local encoding $\mathcal{E}$ approximates an encoding $\tilde{\mathcal{E}}$ onto low-energy states of $H\prime$. The second requirement (ii) says that the map $\tilde{\mathcal{E}}$ gives a good simulation of $H$ (i.e., within error $ϵ$). Note that if $\eta =ϵ=0$ and $\mathrm{\Delta }\to \infty$, the simulation is exact. Increasing the accuracy of the simulation will typically require expending more “effort,” for example by increasing the energy of the interactions.

Definition 1 requires the simulating subspace to be the low-energy sector. All our simulations achieve this. However, it is worth noting that Definition 1 can readily be generalized to other types of subspace, by replacing $P_{\le \mathrm{\Delta }\left(H\prime \right)}$ by a projector onto the subspace of interest. Physically relevant examples might include symmetric subspaces, superselection sectors, or invariant subspaces of another Hamiltonian. Constructing interesting simulations in such subspaces is an interesting direction for future research.

Our definition of Hamiltonian simulation, which follows from physical requirements, turns out to be a refinement of a definition of simulation introduced in prior work (33) in the context of Hamiltonian complexity theory. There are two important differences. We allow the encoding map $\mathcal{E}$ to be anything that satisfies the physical requirements i–iii from above, which can be more complicated than a single isometry. However, we restrict $\mathcal{E}$ to be local, since we require simulations to preserve locality. A notion of universal analogue quantum simulation was also discussed—though not formally defined—in ref. 34, along with some requirements that a quantum simulator should satisfy. Our requirements encompass these.

Our notion of Hamiltonian simulation is strong enough to imply that all our requirements i–vii are indeed satisfied: All static, dynamic, and thermodynamic properties are preserved up to any desired precision (see the next section and SI Appendix for rigorous statements).

We are usually interested in simulating entire quantum many-body models, rather than individual Hamiltonians. By “model” we mean very generally here any family of Hamiltonians (e.g., the 2D Heisenberg model consists of all Hamiltonians with nearest-neighbor Heisenberg interactions on a 2D square lattice of some given size, with uniform coupling strengths). The 2D Heisenberg model with variable couplings is another, more general model, consisting of all 2D Heisenberg Hamiltonians with any values for the individual coupling strengths.

When we say that a model $A$ can simulate another model $B$, we mean it in the following strong sense: Any Hamiltonian $H$ on $n$ qudits (i.e., $d$-dimensional spins) from model $B$ can be simulated by some Hamiltonian $H\prime$ on $m$ qudits from model $A$, and this simulation can be done to any precision $\eta ,ϵ$ with as large an energy cutoff $\mathrm{\Delta }$ as desired. The simulation is efficient if each qudit of the original system is encoded into a constant number of qudits in the simulator [i.e., each $V_i$ in Definition 1 maps to $O\left(1\right)$ qudits], $H\prime$ is efficiently computable from $H$, and the energy overhead and number of qubits of the simulation scales at most polynomially [i.e., $\Vert H\prime \Vert =\text{poly}\left(n,1/\eta ,1/ϵ,\mathrm{\Delta }\right)$ and $m=\text{poly}\left(n,1/\eta ,1/ϵ,\mathrm{\Delta }\right)$].

2. Consequences of Simulation

We arrived at a rigorous notion of Hamiltonian simulation by requiring the simulation to approximate the entire physics to arbitrary accuracy. This is clearly very strong. Just as exact simulation preserves all physical properties perfectly, approximate simulation preserves all physical properties approximately. First, all energy levels are preserved up to any desired precision $ϵ$. Second, by locality of $\mathcal{E}$, for any local observable $A$ on the original system there is a local observable $A\prime$ on the simulator and a local map ${\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}\left(\rho \right)$ such that applying $A^{\prime }$ to ${\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}\left(\rho \right)$ perfectly reproduces the effect of $A$ applied to $\rho$. This applies to all local observables, all order parameters (including topological order), and all correlation functions. Thus, all these static properties of the original Hamiltonian are reproduced by the simulation.

Third, Gibbs states of the original system correspond to Gibbs states of the simulator, and the partition function of $H$ is reproduced by $H\prime$, up to a physically irrelevant constant rescaling and an error that can be exponentially suppressed by increasing the energy cutoff $\mathrm{\Delta }$ and improving the precision $ϵ$. More precisely, if the original and simulator Hamiltonians have local dimension $d$, then (SI Appendix)

$$\frac{|{\mathcal{Z}}_{H\prime }\left(\beta \right)-\left(p+q\right){\mathcal{Z}}_H\left(\beta \right)|}{\left(p+q\right){\mathcal{Z}}_H\left(\beta \right)}\le \frac{d^{m-n}{e}^{-\beta \mathrm{\Delta }}}{\left(p+q\right)e^{-\beta \Vert H\Vert }}+\left(e^{ϵ\beta }-1\right).$$

Since it is able to reproduce the partition function to any desired precision, all of thermodynamic properties of the original Hamiltonian are reproduced by the simulation. Finally, all dynamical properties are also reproduced to any desired precision. More precisely, the error in the simulated time evolution grows only linearly in time (which is optimal without active error correction) and can be suppressed to any desired level by improving the approximation accuracy $ϵ$ and $\eta$:

$$\Vert e^{-i{H}^{\prime }t}{\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}\left(\rho \right)e^{iH\prime t}-{\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}{\left(e^{-iHt}\rho e^{iHt}\right)\Vert }_1=O\left(tϵ+\eta \right).$$ [2]

We can also derive some important consequences for simulation errors. A recurring criticism of analogue Hamiltonian simulation is that, because it does not implement any error correction, errors will accumulate over time and swamp the simulation. A common counterargument is that any real physical system is itself always subject to noise and errors. If the properties of its Hamiltonian are sensitive to noise, the behavior of the real physical system will include the effects of this, so from a physical perspective it is in fact fine to simulate this noisy system rather than an artificial, perfect, error-corrected system.

There is truth to both sides. In the absence of error correction, errors will accumulate over time, as Eq. 2 shows. It is also true that the same will happen in the original physical system, so this may not matter for simulating physical properties, but only if noise and errors in the simulation closely mimic the noise and errors experienced by the real physical system we are trying to simulate.

With our precise definition of Hamiltonian simulation in hand, we can take a first step toward a rigorous version of this argument. Most natural noise models are local: Physical errors tend to act on nearby particles, not across the entire system. The definition of Hamiltonian simulation we arrived at immediately implies that local errors in the original system correspond to local errors in the simulator. However, we can go further. We prove (SI Appendix) that, under a reasonable physical assumption, a local error in the simulator approximates arbitrarily well the encoded version of some local error on the original system. To make this precise, note that if we take the energy cutoff $\mathrm{\Delta }$ to be large enough, errors on the simulator system are unlikely to take the simulated state out of the low-energy space of $H\prime$. Assume that this happens with probability at most $\delta$, for some $\delta \le \eta$. Then for any noise operation $\mathcal{N}\prime$ acting on $\ell$ qudits of the simulator, there is always some noise operation $\mathcal{N}$ on at most $\ell$ qudits of the original system [which we can easily write down (SI Appendix)] such that, for any state $\rho$, the effect of $\mathcal{N}\prime$ on the simulator approximates (again, to any desired precision) the effect of $\mathcal{N}$ on the original system:

$${\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}\left(\mathcal{N}\left(\rho \right)\right)=\mathcal{N}\prime \left({\mathcal{E}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}\left(\rho \right)\right)+O\left(\sqrt{\eta }\right),$$

where $\mathcal{N}$ and $\mathcal{N}\prime$ are superoperators. The fact we can prove the result this way around is crucial: It shows that any local noise and errors in our simulator just reproduce the effects of local noise and errors in the original physical system. This is much stronger than merely showing that errors on the original system can be simulated.

This is as strong a result as one can hope for in a fully general, abstract description of Hamiltonian simulation. However, it still falls far short of a full justification of the lack of error correction in analogue quantum simulation. Fully justifying this would require characterizing all of the noise and error processes occurring in the particular Hamiltonian simulator implementation, then determining whether these faithfully reproduce the effects of the natural noise and error processes in the physical system it is being used to simulate. Our results provide the mathematical framework required to carry out the latter; the former is an experimental physics challenge. Even then, the validity of this argument rests on the validity of the noise characterization and model. Ultimately, determining whether or not a simulation is accurate always comes down to testing its predictions in the laboratory.

3. Universal Hamiltonians

The notion of Hamiltonian simulation we have arrived at is extremely demanding. It is not a priori clear whether any interesting simulations exist at all. In fact, not only do such simulations exist, we prove that there are even universal quantum simulators. A model is “universal” if it can simulate any Hamiltonian whatsoever, in the strong sense of simulation discussed above. Depending on the target Hamiltonian, this simulation may or may not be efficient. Typically, the simulation will be efficient for target Hamiltonians with local interactions in the same (or lower) spatial dimension. However, while universal models can also simulate Hamiltonians in higher spatial dimensions with only modest (polynomial) system-size overhead, this comes at an exponential cost in energy. More precisely, any interaction graph that is spatially sparse can be simulated efficiently by any of the universal models in 2D, whereas the complete graph can be simulated with polynomial space overhead but exponential energy overhead (see SI Appendix for details).

Remarkably, even certain simple 2D quantum spin-lattice models are universal. To show this, we in fact prove a still stronger result. We completely classify all two-qubit interactions (i.e., nontrivial interactions between two spin-1/2 particles) according to their simulation ability (SI Appendix). This classification tells us which two-qubit interactions are universal. The universal class turns out to be identical to the class of QMA-complete two-qubit interactions from quantum complexity theory (32), where QMA is the quantum analogue of the complexity class NP (35).

The classification also shows that there are two other classes of two-qubit interaction, with successively weaker simulation ability. Combining our Hamiltonian simulation results with previous work (33), we find that there is a class of two-qubit interactions that can simulate any stoquastic Hamiltonian (i.e., any Hamiltonian whose off-diagonal entries in the standard basis are nonpositive). This is the class of Hamiltonians believed not to suffer from the sign problem in numerical Monte Carlo calculations. Another class is able, by previous work (9), to simulate any classical Hamiltonian (i.e., any Hamiltonian that is diagonal in the standard basis).

The 2D Heisenberg and XY models with variable coupling strengths are important examples which we show fall into the first category and hence are universal simulators. The 2D (quantum) Ising model with transverse fields falls into the second category and so can simulate any other stoquastic Hamiltonian (33). The 2D classical Ising model with fields falls into the third category and so is an example of a universal classical Hamiltonian simulator (9).

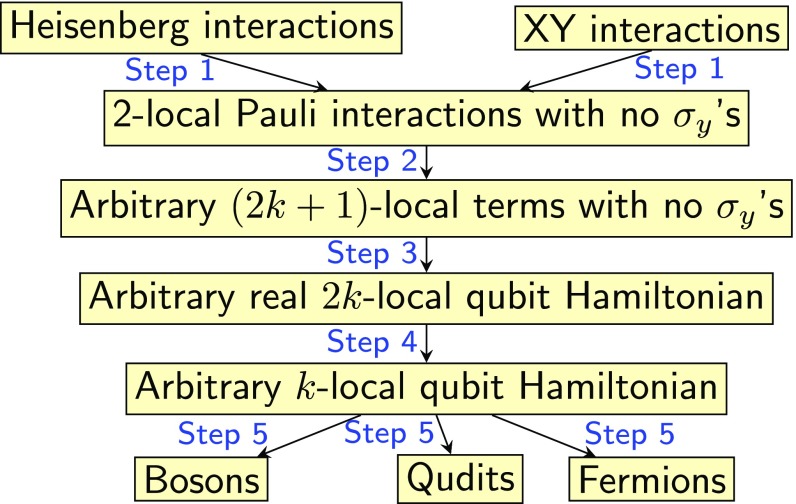
4. Universality Classification

We now summarize the proof of the universality classification result (see SI Appendix for full technical details). This involves chaining together a number of steps, the most important of which are shown in Fig. 2. In fact, most of the technical difficulty lies in proving universality of the Heisenberg and XY interactions, as these have the most restrictive symmetries of all two-qubit interactions. Once these are shown to be universal, recently developed techniques (32, 36) show that any other Hamiltonian from the universal category can simulate one of these two (this step is omitted from the illustration in Fig. 2). Hence, by universality of the Heisenberg or XY interactions, such Hamiltonians can also simulate any other Hamiltonian.

Fig. 2.

Part of the sequence of simulations used in this work. An arrow from one box to another indicates that a Hamiltonian of the first type can simulate a Hamiltonian of the second type.

Step 1.

The Heisenberg interaction $h_{\mathrm{H}\mathrm{e}\mathrm{i}\mathrm{s}}={\sigma }_x\otimes {\sigma }_x+{\sigma }_y\otimes {\sigma }_y+{\sigma }_z\otimes {\sigma }_z$ (where ${\sigma }_{x,y,z}$ are the Pauli matrices) has full local rotational symmetry. Mathematically, this is equivalent to invariance under arbitrary simultaneous local unitary rotations $U\otimes U$. The XY interaction $h_{XY}={\sigma }_x\otimes {\sigma }_x+{\sigma }_y\otimes {\sigma }_y$ is invariant under arbitrary rotations in the z-plane (i.e., $U\otimes U$ with $U=e^{i\theta {\sigma }_z}$ for any angle $\theta$). Any Hamiltonian composed of just one of these types of interaction inherits the corresponding symmetry. Thus, all its eigenspaces also necessarily have this symmetry. Yet if it is to be universal, it must simulate Hamiltonians without this symmetry.

To overcome the symmetry restriction, we develop more complicated simulations based around the use of “perturbative gadgets” [a technique originally introduced to prove QMA-completeness results in Hamiltonian complexity theory (26, 27)]. In a perturbative gadget, a heavily weighted term $C{H}_0$ (for some large constant $C$) dominates the overall Hamiltonian $H\prime =C{H}_0+H_1$ such that the low-energy part of $H\prime$ is approximately just the ground space of $H_0$. Within this low-energy subspace, an effective Hamiltonian is generated by $H_1$ and can be calculated using a precise version of perturbation theory (33), which accounts rigorously for the approximation errors resulting from neglecting the higher-order terms. The first-order term in the perturbative expansion is given by $H_1$ projected into the ground space of $H_0$, as one might expect. However, if this term vanishes, then the more complicated form of higher-order terms may be exploited to generate more interesting effective interactions.

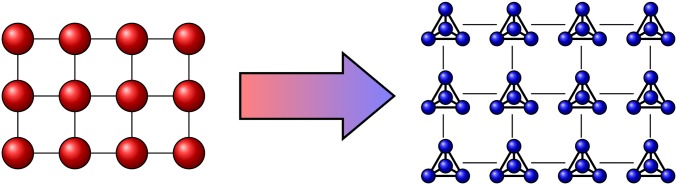
To break the symmetry of the Heisenberg and XY interactions, it is necessary for the encoded Hamiltonian to act not on the physical qubits of the system but on qubits encoded into a subspace of multiple physical qubits. To achieve this, we design a four-qubit gadget where the strong $H_0$ term, consisting of equally weighted interactions across all pairs of qubits, has a twofold degenerate ground space. This 2D space can be used to encode a qubit. This gadget is used repeatedly to encode all qubits of the systems separately, as illustrated in Fig. 3. We then add less heavily weighted interactions acting between qubits in different gadgets, to generate effective interactions between the encoded qubits. This allows us to generate any two-qubit interaction that does not involve any ${\sigma }_y$ terms.

Fig. 3.

Schematic illustrating simulation of one Hamiltonian with another. Each logical (red) qubit is encoded within four physical (blue) qubits, forced into their ground space by strong pairwise interactions. Interactions between the physical qubits implement effective interactions between the logical qubits. An error on a physical qubit only affects one logical qubit.

Steps 2 and 3.

The next steps use simpler perturbation gadgets, in which $H_0$ is used to project a system of ancilla qubits into a fixed state, such that the effective Hamiltonian that this generates couples the remaining qubits. This type of gadget is known in the Hamiltonian complexity literature as a mediator qubit gadget (27), because the ancilla qubits are seen to “mediate” an effective interaction between the other qubits in the system. Previously known gadgets of this type (27) allow many-body interactions to be simulated using two-body interactions. We combine these with a new mediator gadget (SI Appendix) to show how two-qubit Hamiltonians without ${\sigma }_y$s can simulate all real local Hamiltonians.

Step 4.

There is still a more basic obstacle to overcome. All matrix elements of $h_{\mathrm{H}\mathrm{e}\mathrm{i}\mathrm{s}}$ or $h_{XY}$ are real numbers (in the standard basis). Thus, any Hamiltonian built out of these interactions is also real (hence the lack of ${\sigma }_y$s so far). Yet, if it is to be universal it must simulate Hamiltonians with complex matrix elements.

A simple encoding overcomes this restriction, by adding an additional qubit and encoding the real and imaginary parts of $H$ separately, controlled on the state of the ancilla qubit. The Hamiltonian $H\prime =\mathrm{R}\mathrm{e}\left(H\right)\oplus \mathrm{I}\mathrm{m}\left(H\right)$ is clearly real and is easily seen to be an encoding of $H$, since $H\prime =H\otimes |{+}_y⟩+\overline{H}\otimes |{-}_y⟩$, where $|{\pm }_y⟩=\left(|0⟩\pm i|1⟩\right)/\sqrt{2}$. To make this encoding local, it can be adjusted to a simulation where there is an ancilla qubit for each qubit of the system, but these ancillas are forced by additional strong local interactions to be in $\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{n}\left\{|{+}_y{⟩}^{\otimes n},|{-}_y{⟩}^{\otimes n}\right\}$.

Step 5.

Finally, higher-dimensional spins (qudits) can be simulated by encoding each qudit into $\lceil {\log }_{2}d\rceil$ qubits in the obvious way. To simulate indistinguishable particles, one can verify that standard techniques for mapping fermions or bosons to spin systems give the required simulations (SI Appendix).

To show that Hamiltonians with arbitrary long-range interactions can be simulated with a 2D lattice model, there is a further step: embedding an arbitrary interaction pattern within a square lattice. This can be achieved by effectively drawing the long-range interactions as lines on the lattice and using further perturbative gadgets to remove crossings between lines (27). This step requires multiple rounds of perturbation theory, which can result in the final Hamiltonian containing local interaction strengths that scale exponentially in the number of particles. Thus, the final simulation, while efficient in terms of the number of particles and interactions, is not necessarily efficient in terms of energy cost for arbitrary Hamiltonians. For example, we do not know how to construct an energy-efficient simulation of a 3D lattice Hamiltonian using a 2D lattice model, nor do we necessarily expect it to be possible. However, full efficiency is recovered when the original Hamiltonian is spatially sparse (27) (a class which encompasses all 2D lattice Hamiltonians).

5. Conclusions

We close by highlighting some of the limitations of our results and possible future directions. First, while our strong notion of simulation preserves locality in the sense that a few-particle observable in the original system will correspond to a few-particle observable in the simulator, simulating, for example, a 3D system in a 2D system necessarily means that the corresponding observables in the simulation will not always be on nearby particles. Also, to simulate higher-dimensional systems in 2D, our constructions require very large coupling strengths.

From the analogue Hamiltonian engineering perspective, our results show that surprisingly simple types of interactions suffice for building a universal Hamiltonian simulator. Together with the ability to prepare simple initial states, these would even suffice to construct a universal quantum computer, or to perform universal adiabatic quantum computation (SI Appendix). (However, error correction and fault tolerance, which are essential for scalable quantum computation, would require additional active control.) The converse point of view is that, as these apparently restrictive models turn out to be universal, simulating them on a quantum computer may be more difficult than previously thought.

Furthermore, our mathematical constructions require extremely precise control over the strengths of individual local interactions across many orders of magnitude. Although some degree of control is possible in state-of-the-art experiments (10, 18), the requirements of our current universal models are beyond what is currently feasible. However, it is already possible to experimentally engineer more complex interactions than those we have shown to be universal. Now that we have shown that universal models exist, and need not be extremely complex, it may be possible to construct other universal models tailored to particular experimental setups.

From a fundamental physics perspective, an important limitation of our current results is that our universal models are not translationally invariant. Although we show there are universal models in which all interactions have an identical form, our proofs rely heavily on the fact that the strengths of these interactions can differ from site to site. Classic results showing that local symmetries together with translational invariance can restrict the possible physics (37, 38) suggest breaking translational invariance may be crucial for universality. However, much of the intuition for our proofs comes from Hamiltonian complexity, where recent results have shown that translational invariance is no obstacle to complexity (31, 39).

In light of our results, determining the precise boundary between simplicity and universality in quantum many-body physics is now an important open question for future research.