Modeling one thousand intron length distributions with fitild

Abstract

Motivation

Intron length distribution (ILD) is a specific feature of a genome that exhibits extensive species-specific variation. Whereas ILD contributes to up to 30% of the total information content for intron recognition in some species, rendering it an important component of computational gene prediction, very few studies have been conducted to quantitatively characterize ILDs of various species.

Results

We developed a set of computer programs (fitild, compild, etc.) to build statistical models of ILDs and compare them with one another. Each ILD of more than 1000 genomes was fitted with fitild to a statistical model consisting of one, two, or three components of Frechet distributions. Several measures of distances between ILDs were calculated by compild. A theoretical model was presented to better understand the origin of the observed shape of an ILD.

Availability and implementation

The C++ source codes are available at https://github.com/ogotoh/fitild.git/.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Nearly all eukaryotes and possibly all free-living eukaryotes have spliceosomal introns (‘introns’ hereinafter) in their nuclear genomes. The origin and evolutionary processes of intron gain and loss have evoked extensive debates and been studied from various perspectives (Belshaw and Bensasson, 2006; de Souza et al., 1998; Gotoh, 1998; Rodríguez-Trelles et al., 2006; Rogozin et al., 2012; Roy and Irimia, 2009; Stoltzfus et al., 1994; van der Burgt et al., 2012). In contrast, another feature of introns, intron length distribution (ILD), has attracted much less attention. Most studies on ILDs have been confined to several model organisms (Hawkins, 1988; Hong et al., 2006; Mount et al., 1992) or narrow taxonomic groups (Bondarenko and Gelfand, 2016; Kupfer et al., 2004; Zhang and Edwards, 2012). Moreover, most studies have been descriptive and lacking in quantitative details (Yan et al., 2013). This is unfortunate because ILD contributes to more than 30% of the total information contents for intron recognition in some species and is one of the most variable species-specific features used for gene prediction (Iwata and Gotoh, 2011; Lim and Burge, 2001).

Currently popular ab initio gene prediction methods (Burge and Karlin, 1997; Korf, 2004; Lomsadze et al., 2005; Salamov and Solovyev, 2000) are almost exclusively based on the generalized hidden Markov model (gHMM) (Rabiner, 1989). For the efficient calculation of gHMM or an equivalent algorithm for the thermodynamics of melting of the double-stranded DNA (Fixman and Freire, 1977; Poland, 1974), the length-dependent factor (intron probability in gene prediction and loop entropy in DNA melting) is modeled by one or more (shifted) geometric distributions. As noted by Stanke and Waack (2003), however, the (shifted) geometric distributions considerably deviate from the real distributions at both short and long ends (Fig. 1A). Although empirical distributions have sometimes been used for ab initio (Korf, 2004; Lomsadze et al., 2005; Stanke and Waack, 2003) and homology-based (van Nimwegen et al., 2006) gene prediction, a proper statistical model of ILD is desired as it would offer greater compactness and portability, less noise and easier interpolation or extrapolation to unobserved parts compared with the corresponding empirical distributions. Lim and Burge (2001) introduced a combination of two log-normal distributions to model the ILDs of five diverse organisms. Similarly, Gotoh (2008a) adopted a combination of two Frechet distributions, a class of extreme value distributions (Kotz and Nadarajah, 2000). However, very few studies (Iwata and Gotoh, 2011) have been conducted thereafter to expand and evaluate those statistical models in a wide spectrum of eukaryotic species.

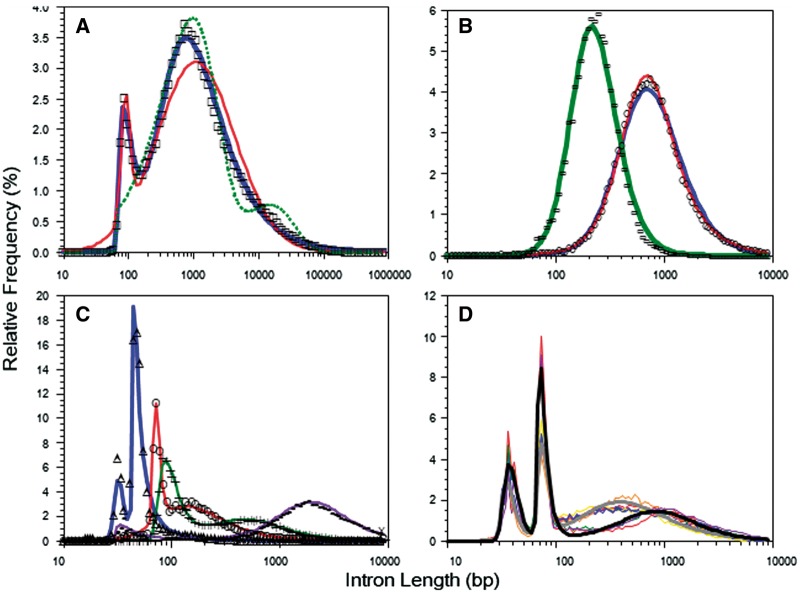
Fig. 1.

Variety of observed ILDs (symbols) and their statistical models (lines). (A) Chicken ILD. Thick line: Frechet model, thin line: log-normal model, dotted line: geometric model. (B) Single modal ILDs. Left: Chlamydomonas reinhardtii (green alga), right Ascaris suum (nematode); thin line: one-component model, thick line: two-component model. (C) Dual modal ILDs. Triangle: Dioszegia cryoxerica (fungus), circle: Emiliania huxleyi (protist), plus sign: Oryza brachyantha (plant), dot: Schistosoma haematobium (animal). (D) Triple modal ILDs of tapeworms. Black thick line: ensemble model of three Hymenolepis members, gray thick line: ensemble model of six Taeniidae plus one Mesocestoididae members. Thin lines represent individual experimental ILDs. All statistical models in B–D are Frechet models. ILDs in panels (C) and (D) are reproduced in separate panels in Supplementary Figure S2 (Color version of this figure is available at Bioinformatics online.)

Here, we report our studies of ILDs of more than 1000 eukaryotes, which have become feasible thanks to the recent upsurge of publicly available genomic and transcript sequences. By mapping transcript sequences onto their cognate genomic sequences, we collected 1022 genomes for which more than 1000 non-redundant introns were identified. By analyzing each ILD using the newly developed program fitild to fit to one or more log-normal or Frechet distributions, we arrived at the conclusion that the latter are significantly better than the former for modeling ILDs. Of the 1022 ILDs, less than 20 are best modeled by a single Frechet distribution (single component model), 490 to 670 by a composite of two Frechet distributions (two component model) and the rest, by a composite of three Frechet distributions (three component model), where the numerical ambiguity is due to the different criteria used for model selection. Although all modal types of ILDs are found in a wide range of eukaryotic taxa, definitive triple modal ILDs are confined to some flatworms and a few roundworms. The large number of ILDs obtained provides us an unprecedented opportunity to investigate not only this gross feature but also the quantitative details of ILDs, shedding light on the ‘dark side’ of intron evolution. We also developed a program called compild to compare ILDs with various measures of distance. We found that evolutionary changes in ILD are generally gradual among close species although wide variations exist within a fixed taxonomic group, such as nematodes and green algae.

The present study poses two fundamental questions. First, what are the molecular mechanisms that maintain evolutionarily stable multi-modal ILDs? Second, what forces operate to shape each ILD component that is well approximated by a Frechet distribution? To address the second question, we propose a theoretical model on the assumption that an ILD represents a steady state of a diffusion process on the intron length axis.

2 Materials and methods

2.1 Data

All genomic and transcript (cDNA, EST and EST cluster) sequences were downloaded from public databases (Supplementary Table S1). Although we preferred to use experimental data, predicted cDNA sequences were also used when experimental data were scarce. Each set of transcript sequences were mapped and aligned onto the cognate genomic sequence by Spaln (Gotoh, 2008b) with the options of –Q7 –O12 –d genome –LS –t12. Plural resources of transcript sequences for a genome, if available, were combined before mapping, or mapping results were unified at the post-process stage with sortgrcd, which was run with the options of –O15 –F2 to output non-redundant intron information under fairly stringent filtering conditions (Iwata and Gotoh, 2011). We regarded an intron as unique if the genomic co-ordinate of its either end differed from those of any other introns of the genome. If plausible, ILDs and intron/exon boundary signals of several closely related species were combined (e.g. Fig. 1D) to yield a ‘grouped species-specific’ parameter set (ssps) used by Spaln. The above processes were repeated once more with the additional option of –T ssps to Spaln. This process slightly increased the number of introns that passed the filtering conditions, but the resultant ILDs were hardly distinguishable from the first ones.

2.2 Statistical models of ILD

We examined two statistical distributions, log-normal and Frechet distributions, to model each component of an ILD that consists of c (≧ 1) components. A statistical model with log-normal distributions (log-normal model) is expressed as

$$P_{\text{LN}}\left(x\right)=\sum _{i=1,c}{a}_i\frac{1}{\sqrt{2\pi }{\sigma }_{i}x}\text{exp}\hspace{0.17em}\left(-\frac{z_{\mathrm{i\hspace{0.17em}}}^2}{2}\right),$$ (1)

where x is intron length, $z_i=(\text{log}\hspace{0.17em}x-{\lambda }_i)/{\sigma }_i$, λ_i and σ_i > 0 are specific parameters, and a_i ($0<a_i<1,\sum _{i=1,c}{a}_i=1$) is the fraction of the i-th component. Similarly, a statistical model with Frechet distributions (Frechet model) is expressed as

$$P_{\text{Fr}}\left(x\right)=\sum _{i=1,c}{a}_i\frac{{\kappa }_i}{{\theta }_i}{z_i}^{-{\kappa }_i-1}\hspace{0.17em}\text{exp}\hspace{0.17em}\left({-z}^{-{\kappa }_i}\right),$$ (2)

where μ_i, θ_i and κ_i are respectively position, scale, and shape parameters, $z_i=(x-{\mu }_i)/{\theta }_i$ > 0, and a_i is equivalent to that defined in Equation (1). For reference, we also considered composite shifted geometric distributions (geometric model) defined by:

$$P_G(x)=\sum _{i=1,c}{a}_i{q}_i{(1-q_i)}^{x-1-d_i},$$ (3)

where parameters q_i and d_i should satisfy 0 < q_i < 1 and x > d_i.

Each observed ILD was fitted to these statistical models with fitild that implements the maximum likelihood method:

$$\widehat{\Theta }=\underset{\Theta }{\mathrm{argmax}}\sum _{x}n(x)\hspace{0.17em}\text{log}\hspace{0.17em}(P(x|\Theta )),$$ (4)

where $\Theta$ represents a parameter set and n(x) denotes the observed number of introns of length x. Fitild uses four sub-routines in the GNU Scientific Library (GSL) https://www.gnu.org/software/gsl/ as optimizers: gsl_multimin_fdfminimizer_vector_bfgs2, gsl_multimin_fminimizer_nmsimplex, gsl_multimin_fdfminimizer_conjugate_fr and gsl_multimin_fdfminimizer_conjugate_pr. By default, these optimizers are examined in series, and the results are immediately returned if satisfactory convergence is obtained. Unfortunately, the success of this type of non-linear optimization of multiple variables notoriously depends on the initial values. In the early stages of this investigation, the initial values were interactively examined with the help of a visualization tool. At this stage, the optimization was performed with the Nelder–Mead simplex method (Nelder and Mead, 1965) that had a smaller chance of false convergence than the other, derivative-dependent optimization methods. After an appreciable number of successful samples were accumulated, the initial setting was copied from the existing sample that gave the best (least) AIC (Akaike, 1973) value against the experimental distribution in question. The goodness of fit was evaluated by residual root mean square error (rRMSE), AIC and BIC (Schwarz, 1978), and further manually examined with the visualization tool plotild. If the fit was unsatisfactory, interactive optimization was conducted, as described above. Note that our procedure does not guarantee that global optimization was attained at every trial, particularly for three-component models.

2.3 Comparison of ILDs

We developed compild to calculate the distance between a pair of ILDs in seven measures (Supplementary Fig. S1). Compild accepts either a set of experimental ILDs or a set of statistical models. In this study, we used only statistical models for which numerical integration was performed with gsl_integration_qagiu in GSL.

2.4 Other methods

The statistically significant difference in performance between two models was examined by bootstrapping, as follows. For a given set of introns, the same number of instances as the original set was re-sampled with replacement. The re-sampled set was fitted to each model as described in Sub-Section 2.2. The process was repeated n times (n = 1000 in this study), and the resultant paired series of rRMSE, AIC, or BIC values were subjected to the Wilcoxon signed rank test.

Hierarchical clustering by complete linkage, single linkage, UPGMA, or Ward method was performed with a custom-made program. To infer consistency between the observed clustering results and known taxonomy, we calculated the adjusted Rand index (ARI; Rand, 1971). As the reference for this test, we chose 53 disjoint eukaryotic taxonomy clusters from the NCBI Taxonomy database (Federhen, 2012). Of these clusters, 46 were realized in the 1022 genomes used in the present study. For a given combination of clustering method and distance measure, the cut-off height that separates clusters was chosen so that ARI should be maximized.

3 Results

3.1 Statistical models and model selection

We collected 1022 (411 animals, 419 fungi, 93 plants and 99 protists) genomes for which more than 1000 introns were identified. Each observed ILD was fitted to a statistical model consisting of one, two, or three components of log-normal or Frechet distributions. Figure 1A demonstrates the ILD of chicken (Gallus gallus) as a typical example. The Frechet model with two components well reproduces the observed ILD represented by open squares. The model with two log-normal distributions also achieves a fairly good fit but has non-negligible discrepancies in peak positions and the short and long tails. In contrast, the maximum likelihood model with two shifted geometric distributions fails to reproduce the overall shape of the observed ILD; the minor component is located on the opposite side of the major peak separate from the minor component in the log-normal and Frechet models as well as the observed distribution. A shifted geometric distribution is poor at representing the dense long tail of an ILD (Reese et al., 2000; Stanke and Waack, 2003). We suspect that the minor component in the geometric model favors compensating for the thin long tail of the major component rather than reproducing the observed minor peak. This situation did not change even if one more component was added into the model. From these results, we excluded geometric models from further investigations as they seem to never outperform other statistical models.

Figure 1B–D show typical ILDs with apparently one, two and three modes, respectively. Individual ILDs in Figure 1C and 1D are also shown in separate panels in Supplementary Figure S2. These figures demonstrate that the Frechet models with the corresponding number of components well reproduce the observed ILDs. To emphasize the wide distribution of each modal type among eukaryotes, the examples in Figure 1B and C were chosen from diverse kingdoms. In contrast, the peculiar triple modal ILDs (Tsai et al., 2013; Wang et al., 2016) were observed only in 17 out of 28 Platyhelminthes examined in addition to 3 Nematodes (Supplementary Table S3). Figure 1D and Supplementary Figure S2D show two ensemble models derived, respectively, from three species in genus Hymenolepis (black) and six species in family Taeniidae plus one Mesocestoididae (gray) of tapeworms.

It is noteworthy that the apparent number of modes does not necessarily equal the number of components in the best fit model, as judged by rRMSE, AIC, or BIC. For example, the ILD of Ascaris suum (nematode) is best modeled by two rather than a single Frechet distribution (Fig. 1B), as judged by any of the three criteria. However, the rRMSEs of the best fit model actually depended only weakly on the model selection criterion. As expected, the average rRMSEs decreased with an increase in the number of available introns for both log-normal and Frechet models (Table 1). Table 1 also shows that 94.0% of the Frechet models and only 78.7% of the log-normal models fit the observed ILDs at an rRMSE threshold of less than 10⁻³, if more than 1000 introns are available. In paired tests, the Frechet models markedly surpass the log-normal models as judged by any criteria at all levels of data availability (Table 1). For economy, we focused on the Frechet models in the following examinations.

Table 1.

Summary of statistical models that best fit observed ILDs

# Intronsa	# Speciesb	rRMSE < 10–3 (%)c		Fr < LN (%)d
		Fr	LN	rRMSE	AIC	BIC
>0	1082	88.8	74.3	91.5	82.8	82.3
>1000	1022	94.0	78.7	93.2	86.6	86.1
>10 000	938	98.2	82.4	93.9	86.8	86.6
>100 000	341	100.0	99.7	93.8	86.2	86.2

^aNumber of available intron samples. The cut-off sample size used in this study is shown by bold face.

^bNumber of species for which the number of available intron samples is within the range that shown in the first column.

^cPercentage of ILDs for which the rRMSE values of the best model are smaller than 10^-3. Fr, Frechet model; LN, log-normal model.

^dPercentage of ILDs for which the best Frechet model outperforms the best log-normal model with respect to the specified criterion. The numbers of components in the compared models may differ from each other.

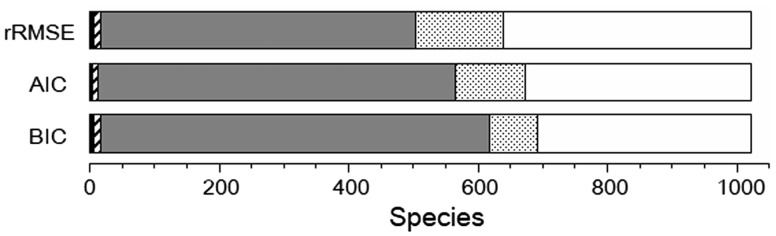
The use of AIC or BIC as the criterion for model selection is reasonable for practical purposes, e.g. gene prediction. However, the best AIC (or BIC) does not preclude the possibility that a simpler model may perform as nicely as the best model, as exemplified by the A. suum ILD in Figure 1B. To evaluate the statistical significance between the best model (Model A) and the simpler second best model (Model B), we performed bootstrap resampling coupled with Wilcoxon signed rank tests (Materials and Methods). We regarded an ILD as ‘marginal’ if the signed rank sum (W-score) of Model A is smaller than that of Model B or if the difference between the two W-scores is insignificant (P > 10⁻³). As summarized in Figure 2, the fraction of ILDs categorized into a specific component number or into their margin varies significantly with the criterion used for model selection. In general, rRMSE tends to prefer more complex models than the other criteria. This tendency is reasonable as AIC and BIC impose stronger penalties on more complex models, whereas no penalty is given to rRMSE.Figure 2 also shows that BIC tends to prefer simpler models compare with AIC. The interpretation of this tendency is not straightforward as the available sample sizes affect the preference in a subtle manner. The Frechet model parameters for the 1022 species chosen on the basis of BIC criterion are presented in Supplementary Table S2.

Fig. 2.

Fraction of ILDs that are best fit to Frechet models with one (black), two (gray), or three (white) components. Hatched and stippled boxes indicate the margin between one and two and between two and three component models, respectively. Note that the best fit model varies with the model selection criterion indicated to the left of each partition graph

3.2 ILD components

Once a multi-component statistical model is obtained for an ILD, it is easy to quantitatively characterize the individual components. Figure 3 shows an example in which 161 ILDs of tetrapods (91 mammals, 58 birds, 10 reptiles, 1 amphibian and 1 Sarcopterygii) are analyzed. All these ILDs look like dual modal, although approximately half of the mammalian ILDs are better fitted by the three-component Frechet models. To facilitate comparison among species, we used the two-component Frechet models throughout this analysis. The species in Figure 3 are arranged in the order of the median of the second (longer) component. An obvious characteristic noticed in Figure 3 is that the second components of birds are markedly shorter than those of the other tetrapods. This observation well accords with previous reports that birds have shorter intron sizes than the other tetrapods (Hughes and Hughes, 1995; Zhang and Edwards, 2012). Figure 3 further shows that the relative contribution of the first (shorter) component (indicated by large symbols) of mammals (open squares, 20.3 ± 1.9%) is significantly larger than that of the other tetrapods, including birds (open circles, 9.1 ± 1.7%) and other reptiles (filled circles, 9.4 ± 2.6%).

Fig. 3.

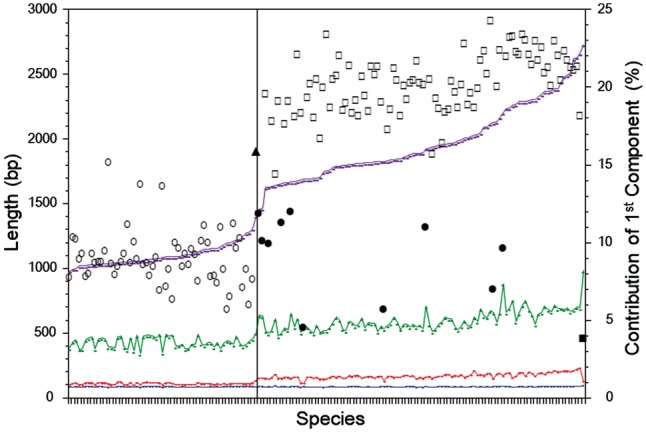
Characteristics of ILD components of tetrapods. Large symbols indicate fractional contribution of the first component: open circle: bird, filled triangle: amphibian, open square: mammal, filled circle: reptile and filled square: sarcopterygii. Small symbols with connecting lines indicate mode of the first component, median of the first component, mode of the second component and median of the second component from lower to upper. All species to the left of the solid vertical line are birds

The second noticeable feature in Figure 3 is that the mode of the first component is remarkably constant (86.1 ± 2.2 bp) for all the tetrapods examined. In fact, the constancy of the mode of the first component prevails among fishes (85.6 ± 8.5 bp), some (but not all) chordates, and even more primitive metazoans, such as sea anemone (Nematostella vectensis) and coral (Acropora digitifera) (Supplementary Fig. S4). Unlike tetrapods, however, the relative contributions of the first component vary extensively from less than 5% for spotted gar (Lepisosteus oculatus) and Australian ghostshark (Callorhinchus milii) to nearly 70% for Atlantic salmon (Salmo salar).

The third point noticeable in Figure 3 is the strong correlation (r = 0.91) between the medians of the first and second components, suggesting a common mechanism. However, this feature appears to be unique to tetrapods. The fact that the coelacanth (Latimeria chalumnae) is a clear outlier of the correlation suggests that this feature and the underlying mechanism originated relatively recently, not much earlier than 300 Mya.

Finally, as expected from the previously observed positive correlation between intron size and genome size over various species (Vinogradov, 1999), a strong positive correlation was observed between the median of the second component and the genome size (Supplementary Fig. S3A). The linear-scale and log-scale correlation coefficients for the 161 tetrapods (r = 0.92 and 0.95) were larger than those between gross median and genome size (r = 0.84 and 0.90) and those between gross geometric (log-transformed) mean and genome size (r = 0.79 and 0.86; Supplementary Fig. S3B). The reason why Vinogradov (1999) failed to recognize significant difference in intron size between mammals and birds would be partly ascribed to the use of gross geometric mean as the representative value for intron lengths of a species.

The results of similar analyses of other major taxonomic groups are presented in Supplementary Figures S4–S9 (two-component ILDs) and S10 (three-component ILDs). Numerical data are also presented in Supplementary Table S3. This topic will be revisited in the Section 4.

3.3 Comparison and clustering of ILDs

The first step toward evolutionary studies of ILDs is to measure the distance between two ILDs. As noted in Materials and Methods, we examined seven measures of distance in combination with four hierarchical clustering methods. As expected, the results were quite diverse, because the shapes and ranges of ILDs vary extensively among species (Fig. 1) and because different measures of distance and different clustering algorithms focus on different aspects of ILDs. As an indicator of consistency between the observed clustering results and known taxonomy, we calculated ARI (Materials and Methods), the larger values of which indicate greater consistency. Table 2 lists the optimized ARI values and the associated cluster numbers for the 28 combinations of distance measures and clustering algorithms. For reference, we chose a relatively coarse (roughly phylum/division) taxonomic level, although finer levels were adopted for populated phyla, such as Chordata. It should be noted that the present analysis illustrates only one cross section of the evolutionary trends of ILDs.

Table 2.

Cluster size optimized with respect to ARI

Methodsa	Complete linkage		Single linkage		UPGMA		Ward
	#cluster	ARI	#cluster	ARI	#cluster	ARI	#cluster	ARI
CS	27	0.300	311	0.467	18	0.365	32	0.374
E2	44	0.193	284	0.280	79	0.216	43	0.215
EC	44	0.193	284	0.280	80	0.237	35	0.205
JA	14	0.315	300	0.458	30	0.428	22	0.373
JS	58	0.379	244	0.459	22	0.417	25	0.415
KL	13	0.361	244	0.460	32	0.453	36	0.418
MH	16	0.318	332	0.450	31	0.432	37	0.332

^aThe abbreviations of distance measures are as follows. CS, Cosine; E2, Euclid²; EC, Euclid; JA, Jaccard; JS, Jensen-Shannon; KL, Kullback-Leibler and MH, Manhattan.

As shown in Table 2, the best ARI (underlined) was observed with the single linkage method, which prefers many (> 200) small clusters. The optimized cluster numbers using all the other methods were less than 100, among which the combination of the UPGMA method and the Kullback–Leibler distance gave the best ARI (bold). The consensus ILD for each of the 32 clusters (C1–C32) associated with this ARI is depicted in Supplementary Figure S11, and the numerical characteristics of the individual consensus ILDs are summarized in Supplementary Table S4. The relevant contingency table (Supplementary Table S5) reflects the ‘conservative and divergent’ nature of ILDs among eukaryotes. For example, all the tetrapods in our dataset belong to the ILD cluster C18 (numbering is arbitrary), which also contains seven other metazoan taxonomic groups. C14 exclusively consists of the most prominent triple modal ILDs (Fig. 1D), although the modal number was not explicitly considered in the classification procedure. Whereas fungi are dispersed among 14 of the 32 ILD clusters, 82% of fungi belong to the single ILD cluster C1, which also contains plural members in each of the other three kingdoms, e.g. fern Selaginella moellendorffii, the ILD of which is sharply different from those of the other land plants. In each kingdom, Alveolata in protists, Basidiomycota in fungi, Nematoda in animals and Chlorophyta in plants are the most heterogeneous with respect to ILD characteristics distributed in 13, 12, 11 and 5 distinct ILD clusters, respectively.

4 Discussion

4.1 ILD component as realization of conserved activity

Probably the most striking finding of this study is that each ILD of almost all eukaryotes is composed of a small number of distinguishable components. The composition of the components is evolutionarily conserved among a certain range of taxonomic groups, such as tetrapods (Fig. 3) and flowering plants (Supplementary Fig. S8). Thus, it is natural to regard each component as a realization of a certain activity conserved among species. We inclusively call such a component ‘ildent’ (ILD component), more concrete definition of which will be given later. Note that ildent is not a mere abbreviation but represents a little more general concept than ‘ILD component’ which is specific to each species. Note also that most species have more than one ildents. The conservation of an ildent does not automatically imply that the orthologous introns in different genomes should belong to the same ildent. This is apparent as the fractional contributions of each ildent significantly vary among species (Fig. 3 and Supplementary Figs S4–S10). A preliminary study on orthologous genes in the ten tapeworm genomes that exhibit definitive triple modal ILDs (cluster C14 in Supplementary Table S5) suggested that transitions between ildents occur in a quantum fashion at a low but substantial rate (unpublished data). The quantum nature of the transitions implies that introns with intermediate lengths are evolutionarily unstable. These observations appear to suggest that the existence of distinct ildents in a species is maintained by mainly the heterogeneity in splicing mechanisms, e.g. intron definition and exon definition (Berget, 1995), rather than the functional compartmentalization of introns. In other words, each ildent might be composed of a subset of introns that are processed by a (yet hypothetical) sub-class of splicing machinery conserved across species. If not ambiguous, the term ildent may also be used to refer to the ILD of the subset of introns. Supplementary Figure S12 illustrates our model of the concept of ildents.

Obviously, our hypothesis requires further verification. In this study, we have regarded individual introns as static and independent entities. To better understand the molecular mechanisms responsible for the maintenance of plural ildents, we need to consider introns in the context of orthologous genes in various phylogenetic lineages. In addition, we intend to investigate the potential relationships between ildents and various characteristics of introns, such as flanking junction and branch point signals (Gelfman et al., 2012; Iwata and Gotoh, 2011), G + C content (Zhu et al., 2009) and ordinal position within a gene (Hong et al., 2006; Zhu et al., 2009). Furthermore, a huge amount of RNA-Seq data now available might facilitate detailed analyses of the specific expression of genes that bear a particular type of ildent.

4.2 Theoretical model of an ILD component

Another important finding in this study is that each ILD component (ildent of a specific species) is well modeled by a Frechet distribution (Fig. 1, Table 1). We think this is not a coincidence but a reflection of an underlying mechanism. As a first step toward understanding this mechanism, we hypothesize that a present-day ILD, $P\left(x\right)$, represents a steady state of a diffusion process on the intron length axis. Apart from a constant factor, $h(x)=xP(x)$ represents the fraction of all intronic nucleotides that belong to introns of length x. In a time course, we assume that $h(x,t)$ follows the diffusion equation below:

$$\frac{\partial h\left(x,t\right)}{\partial t}=D\frac{{\partial }^{2}h\left(x,t\right)}{\partial x^2}+g\left(x\right)h\left(x,t\right)+c\left(x\right).$$ (5)

The first term on the right-hand side, the diffusion term, models short indels that account for a majority of length changes between orthologous introns (Hughes et al., 2008; Moriyama et al., 1998; Ogata et al., 1996), where the coefficient D is assumed to be constant. The second term represents augmentation or reduction of a nucleotide density by self-reproduction, where a positive (negative) value of the Malthusian coefficient $g\left(x\right)$ causes augmentation (reduction) of the density. Actually, several factors may contribute to $g\left(x\right)$, e.g. the long indels within an ildent, the longer indels that evoke transition between ildents and the degradation and duplication of parental genes. In the present model, these mechanical details are disregarded. The last term $c\left(x\right)$ represents the rate of de novo creation of new introns, which may be ignored to the first approximation. Then, according to the equation $h\left(x\right)=h\left(x, \infty \right)$, the steady-state formula of Equation (5) reduces to:

$$D\frac{d^{2}h\left(x\right)}{d{x}^2}+g\left(x\right)h\left(x\right)=D[\frac{d^{2}P\left(x\right)}{d{x}^2}+2\frac{dP\left(x\right)}{dx}]+xg\left(x\right)P\left(x\right)=0.$$ (6)

By putting a single term in Equation (2) into Equation (6), we obtain

$$g(x)=-D\frac{{\kappa }^{2}xG{(x)}^2+\kappa [(3\kappa +1)x+2\mu ]G(x)+(\kappa +1)(\kappa x+2\mu )}{x{(x-\mu )}^2},$$ (7)

where $G(x)=-z^{-\kappa }$ and the other notations are the same as those for Equation (2) except that the suffix i is depleted.

Figure 4 shows an example of $g\left(x\right)/D$ together with the flux defined by

$$\frac{J\left(x\right)}{D}=-\frac{\partial h\left(x\right)}{\partial x}=\left\{\kappa \left(G+1\right)+\mu \frac{\kappa G+\kappa +1}{x-\mu }\right\}P\left(x\right)$$ (8)

for a single modal ILD of Chlamydomonas reinhardtii (green alga). The deep negative values for $g\left(x\right)/D$at the left end suggest a strong repulsive force or existence of an absorbing wall that disallows introns shorter than a certain threshold. The ‘proliferative domain’ ($g\left(x\right)>0$) is confined to $x\in \left[123,\mathrm{ }306\right]$ in this example, which includes 63% of introns and 48% of intronic nucleotides. Beyond this range, the anti-proliferative pressure once strengthens again and then declines gradually. A negative (positive) value for $J\left(x\right)/D$ indicates right to left (left to right) diffusion. Overall, Figure 4 gives us an image of the population dynamics of introns, as follows. Only the introns within a restricted size range are proliferative. In a steady state, diffusion from this central domain compensates for the loss of contents due to the anti-proliferative pressure that is dominant in the peripheral domains. Elucidating this fountain-like mechanism in detail might be an interesting theme of future molecular biology and evolutionary studies on introns and the mechanisms of splicing.

Fig. 4.

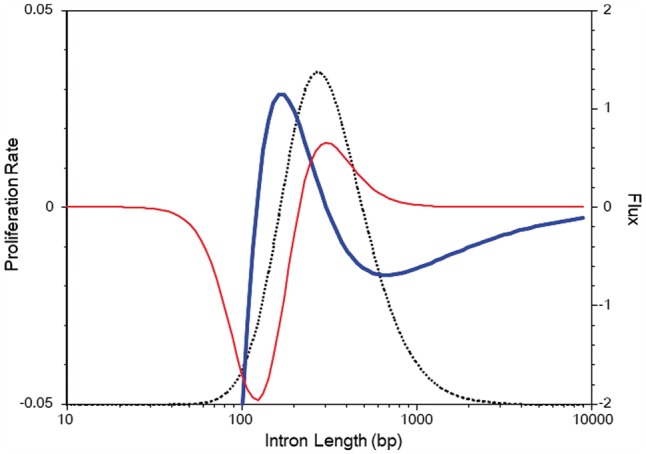
Malthusian coefficient (thick solid line) and flux (thin solid line) calculated from a diffusion equation. The stationary state quantities are derived from the Frechet model for single modal ILD of C. reinhardtii (Fig. 1B). The dotted line represents nucleotide density, h(x), included in introns of length x

4.3 Conclusion and future directions

In this report, we have presented several computational tools to quantitatively analyze ILDs. Applying these tools to more than 1000 eukaryotic genomes, we obtained two major findings. First, each ILD of almost all species are composed of a small number of distinguishable components. Compositions of these components is conserved among a certain taxonomic range, leading us to the concept of ‘ildent’ as a cross-species entity that is subject to a (yet hypothetical) sub-class of splicing activity conserved among these species. Second, each ILD component is well approximated by a Frechet distribution. The proposed theoretical model based on this observation suggests a fountain-like structure in the reproduction/diffusion profile of intronic nucleotides along the intron length axis.

However, we are only at a preliminary stage of understanding the molecular mechanisms that maintain plural ILD components and shape the fountain-like proliferative structure of each component. The evolutionary processes that have led to the present-day diversity and convergence in ILD features are also largely unknown. In addition to microscopic molecular mechanisms, ILD features might also be related to macroscopic biology of the host organism, such as metabolic activity (Vinogradov and Anatskaya, 2006) and free living, parasitic, or symbiotic (Slamovits and Keeling, 2009) life style. Incorporation of phylogenetic as well as comparative perspectives (Felsenstein, 1985; Harvey and Pagel, 1991) into ILD analyses would greatly facilitate our understanding of these phenomena. Hopefully, the present work will stimulate future studies on ILD features from both microscopic and macroscopic aspects.