Development of a Dynamic Physiologically Based Mechanistic Kidney Model to Predict Renal Clearance

Abstract

Renal clearance is usually predicted via empirical approaches including quantitative structure activity relationship and allometric scaling. Recently, mechanistic prediction approaches using in silico kidney models have been proposed. However, empirical scaling factors are typically used to adjust for either passive diffusion or active secretion, to acceptably predict renal clearances. The goal of this study was to establish a renal clearance simulation tool that allows prediction of renal clearance (filtration and pH‐dependent passive reabsorption) from in vitro permeability data. A 35‐compartment physiologically based mechanistic kidney model was developed based on human physiology. The model was verified using 46 test compounds, including neutrals, acids, bases, and zwitterions. The feasibility of incorporating active secretion and pH‐dependent bidirectional passive diffusion into the model was demonstrated using para‐aminohippuric acid (PAH), cimetidine, memantine, and salicylic acid. The developed model enables simulation of renal clearance from in vitro permeability data, with predicted renal clearance within twofold of observed for 87% of the test drugs.

Study Highlights.

What is the current knowledge on the topic?

  In silico approaches have been used to simulate renal clearance, but effects of tubular water reabsorption, dynamic tubular flow, tubular pH, and microvilli were not considered when calculating the passive reabsorption. In addition, systematic model verification using multisource permeability is lacking.

What question did this study address?

 This study addresses the impact of tubular water reabsorption, dynamic tubular flow, tubular pH, microvilli, and multisource permeability on effective drug passive diffusion and subsequent renal clearance simulation.

What does this study add to our knowledge?

 Dynamic physiologically based mechanistic kidney model was developed to capture the effect of physicochemical and physiological complexity on effective drug passive diffusion. The developed model allows prediction of renal clearance via active and passive processes from in vitro data.

How might this change drug discovery, development, and/or therapeutics?

 The study enables prediction of renal clearance together with glomerular filtration, passive diffusion, and active secretion with higher confidence. The model can also simulate drug disposition and accumulation inside renal cell upon altered transporter expression or activity and changes in kidney physiology.

Renal clearance has been estimated as the major clearance pathway for 25–31% of medications,1, 2 and contributes as a minor elimination pathway to the clearance of majority of drugs. Therefore, prediction of renal clearance during drug development is important. In addition, detailed understanding of renal clearance processes is critical to delineate the quantitative contributions of passive diffusion and active secretion in renal drug elimination. Finally, increased interest in renal toxicity and accumulation of drugs in renal tubular cells necessitates improved physiological and mechanistic modeling of drug distribution and clearance in the kidneys.

To predict renal clearance, quantitative structure activity relationship (QSAR) methods have been proposed.3, 4, 5 Although QSAR methods are useful in large scale screening and provide a qualitative prediction of high or low renal clearance, they do not allow mechanistic understanding or dynamic simulations of renal disposition. Allometric scaling from animals has also been used extensively6, 7 to predict human renal clearance. However, interspecies differences in kidney structure and physiology (e.g., glomerular filtration rate (GFR), tubular surface area, and urine pH), transporter expression and activity, and plasma protein binding remain as challenges for allometric scaling.8 Allometric scaling does not allow differentiation of clearance mechanisms or dynamic simulations of renal handling of drugs. To address the weaknesses of QSAR and allometric scaling, two static renal clearance prediction approaches have been published,9, 10 and a dynamic mechanistic kidney model has been reported and incorporated into Simcyp software.11 However, static approaches do not incorporate how water reabsorption and subsequently increased drug concentrations affect passive diffusion processes as no concentration gradient is established among blood, tubular cells, and tubular lumen. For the reported dynamic kidney model,11 comprehensive validation of the model structure, physiological parameters (e.g., tubular pH, flow, and surface area), and performance of predicting passive diffusion of drugs with known renal clearances and in vitro permeability data has not been reported. Still, several studies have used the Simcyp kidney model to simulate drug renal clearances.12, 13, 14, 15, 16, 17 Most of these studies used top‐down or middle‐out approaches and applied various scaling factors to simulate plasma concentrations or renal clearance with either fitted active secretion12, 13, 14, 15, 16 or passive diffusion clearance17 to accurately capture observed data. Although the passive diffusion clearance in these studies was based on permeability values from PAMPA, Caco‐2, and HEK cells, these values were further scaled using presumed total tubular surface area without systematic verification, or using sensitivity analyses to fit observed data. This introduces potential bias to the modeling approach. Most studies did not consider different ionization of the test compounds in blood, cells, and tubular fluid, and assumed that passive diffusion is equal for apical and basolateral sides and across different tubular segments despite known physiological differences between these sites. It is important to note that fitting active secretion values requires high confidence in the passive diffusion clearance in the kidneys as the observed renal clearance is highly dependent on both parameters. In the absence of validation of passive diffusion clearance in the kidneys, the confidence in scaled secretion clearance is low and interdependent on the error in predicted diffusion clearance. As limited in vitro‐to‐in vivo scaling data exist for renal transport clearances for the specific segments of the kidneys, the uncertainty of active transport predictions is high. Hence, there is a critical need to validate the physiological and permeability components of a kidney model using drugs that are not subject to significant active transport, to allow better mechanistic predictions of renal clearance, and to estimate the contribution of active transport to renal clearance. The aim of this study was to develop and validate a dynamic physiologically based mechanistic kidney model that allows prediction of drug renal clearance using in vitro permeability data and incorporates unbound filtration, active tubular secretion, and pH dependent bidirectional passive diffusion.

Methods

Structure of the mechanistic kidney model

The 35‐compartment mechanistic kidney model (Figure  1) was developed using Matlab and Simulink platforms.18 Detailed description of model development and the governing equations are shown in Supplementary Methods . The diameters, lengths, and tubular flow rates of different segments of the kidney were collected from literature10 and are listed in Table S1 . The physiological volume of each tubular segment was calculated as a cylinder and physiological volume of the cellular compartment of each segment was assumed to be the same as the tubular volume. The physiological surface area of each tubular segment was calculated as a cylinder except for the collecting duct, which was calculated using a published exponential method10 due to the merging of the tubules. The surface area of apical side of proximal tubule was set 30‐fold higher than the basolateral side19 to account for the effect of brush border on the apical side surface area. No other scaling factors or adjustments were made for the surface area at the other segments due to the sparsity of microvilli.20 The final volumes, surface areas, flow rates, and pH values of each kidney subsegment are listed in Table  1. The physiological fluid flow in the renal tubule was adapted from previous publication10 with further expansion (Table  1). The pH at each tubule decreased from 7.2 in the proximal segment to 6.5 in the bladder in a stepwise manner across the length of the tubule (Table  1). Glomerular filtration rate (Q _GFR), kidney blood flow (Q _kidney), and cardiac output (Q _c) were set as 7.2, 60, and 330 l/h, respectively. Central compartment volume (V _c) in the simple circulation model was set to 42 L to mimic total body water. The blood‐to‐plasma ratio was one and unbound fraction in the renal epithelial cells (f _u,cell) was the same as plasma unbound fraction (f _u,p) for each drug for all simulations. Renal intracellular pH and blood pH were set as 7.2 and 7.4, respectively.

Figure 1.

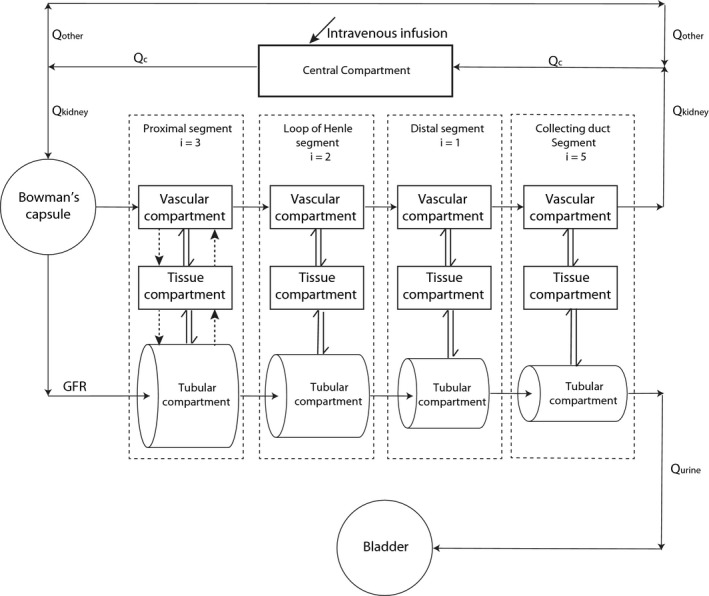
Schematic diagram of the mechanistic kidney model. Q _c, blood flow in the central compartment; Q _kidney, blood flow to the kidney; Q _other, blood flow to all other organs in the body; Q _urine, urine formation flow; GFR, glomerular filtration rate; i, the number of subsegment each segment is divided into; single solid arrow, the fluid flow; single dash arrow, active secretion or active reabsorption; double arrow, bidirectional passive diffusion.

Table 1.

Physiological parameters of the mechanistic kidney model. The tubular flow rate exiting each tubular subsegment is equal to the tubular flow rate entering the next tubular subsegment. The flow rate at the beginning of the first proximal tubule subsegment is equal to glomerular filtration rate (120 mL/min) and the exiting flow rate at the end of the last collecting duct subsegment (Collecting duct₅) is equal to normal urine formation rate (1 mL/min). The volumes, tubular surface areas, and flow rates are scaled to two kidneys with 0.9 million nephrons per kidney based on the physiological values with detailed calculation described in Table S1 and Methods section

Segment	Volume (l)	Tubular surface area (dm2)	Tubular flow rate entering each tubular subsegment (ml/min)	pH value
Proximal tubule1	0.0305	6107	120	7.2
Proximal tubule2	0.0305	6107	94	7.1
Proximal tubule3	0.0305	6107	68	7
Loop of henleD	0.0027	61	43	7
Loop of henleA	0.0027	61	24	7
Distal tubule	0.0194	156	24	6.9
Collecting duct1	0.237	6.7	11	6.8
Collecting duct2	0.237	6.7	9	6.7
Collecting duct3	0.237	6.7	7	6.6
Collecting duct4	0.237	6.7	5	6.5
Collecting duct5	0.237	6.7	3	6.5

Sensitivity analysis

To examine the impact of general structural and physiological assumptions on model performance, a sensitivity analysis of renal clearance of a hypothetical neutral drug with permeability of 10 × 10⁻⁶ cm/s and plasma unbound fraction of 0.1 was done. The sensitivity analysis was conducted according to the general guidance of physiologically based pharmacokinetic model development. The covariates tested and expected not to impact renal clearance based on pharmacokinetic principles included blood‐to‐plasma ratio (0.5–5), intracellular unbound fraction (0.1–1), volume of renal tubule (0.1–10 fold), and volume of renal cell (0.1–10 fold). The covariates tested and expected to impact renal clearance included permeability (0.01–200 × 10⁻⁶ cm/s), plasma unbound fraction (0.1–1), tubular surface area (0.1–10 fold), and GFR (15–120 mL/min).

Model verification and prediction of renal clearance for a set of test compounds

To validate the model, 46 drugs (Table  S2 ) that had renal clearance (CL_r) < 2 × f _u,p × GFR and for which adequate data of in vitro permeability, plasma unbound fraction, and in vivo renal clearance from healthy adult subjects or patients with normal creatinine renal clearance were available, were selected to test whether the developed model could accurately predict renal clearance, and to validate the passive diffusion component of the model. Of the selected drugs, six had an f _u,p × GFR value > 1.5 (Table S2 ), and are considered to be subject to active secretion based on the International Transporter Consortium recommendation.21 Nevertheless, consistent with the model acceptance criterion (twofold), these compounds were included as net secreted compounds. This inclusion likely decreases the overall model performance, but allows sufficient number of ionized compounds to be included in the analysis. For each drug, the observed renal clearance and plasma unbound fraction values were collected from literature (Table S2 ).2, 10, 22, 23, 24 Predicted pK_a values for the test drugs were collected from https://www.drugbank.ca. Caco‐2 and MDCK permeability values for the drugs of interest were collected (Table S2 ).10, 25, 26, 27, 28, 29, 30, 31, 32, 33 Drugs were categorized into four groups based on ionization at pH 7: (1) drugs with >1% ionized as negatively charged at pH 7 were classified as acids; (2) drugs with >1% ionized as positively charged at pH 7 as bases; (3) drugs with <1% ionization at pH 7 as neutrals; (4) and drugs with >1% ionized at pH 7 with both positively and negatively charged groups were classified as zwitterions. The drugs were also categorized to net secreted and net reabsorbed based on comparison of observed renal clearance with f _u,p × GFR (Table S2 ). The compound dataset included 11 neutrals, 12 weak bases, 9 weak acids, and 14 zwitterions. The compounds had a wide range of pK_as (−2.2–11.62), in vitro permeabilities (0.01–160 × 10⁻⁶ cm/s), f _u,ps (0.01–0.99), and observed renal clearances (0.5–145 mL/min) providing a robust dataset for model validation.

The methods to account for the effect of pH‐dependent drug ionization and microvilli expression in vitro and in vivo are described in Supplementary Materials . Renal clearances were simulated at distribution equilibrium. For compounds with more than one published in vitro permeability value, the renal clearance was predicted separately using each of the reported values and the mean predicted renal clearance was calculated from individual predictions.

To evaluate the quality and accuracy of the renal clearance predictions, average fold error (AFE), also called geometric mean fold error (Eq. (1)) was used to measure the extent of underprediction and overprediction. Absolute average fold error (AAFE) and root mean square error (RMSE) were calculated according to Eqs. (2) and (3) for all compound categories. In addition, a twofold acceptance criterion was applied to determine whether renal clearances were successfully simulated. A threefold criterion was reported to allow comparison with previous publications.

$$\text{AFE}={10}^{\frac{1}{n}\sum {log}_{10}\frac{\mathrm{Predicted}}{\mathrm{Observed}}}$$ (1)

$$\text{AAFE}={10}^{\frac{1}{n}\sum \mid {log}_{10}\frac{\mathrm{Predicted}}{\mathrm{Observed}}\mid }$$ (2)

$$\text{RMSE}=\sqrt{\frac{1}{n}\sum {(\text{Observed}-\text{Predicted})}^2}$$ (3)

Incorporation of active secretion to simulate renal clearance

The mechanistic kidney model also allows incorporation of active secretion and active reabsorption in the relevant subsegments of the kidney. To test the feasibility of incorporating transporter data along with in vitro permeability data to simulate renal clearance, the renal clearances of para‐aminohippuric acid (PAH), and cimetidine were simulated. PAH (f _u,p = 1, pK_a 2.7 and 4.24 (drugbank.ca), in vitro permeability 0.72 × 10⁻⁶ cm/s)34 and cimetidine (f _u,p = 0.8,13 pK_a 6.91 (drugbank.ca), in vitro permeability 1.37 × 10⁻⁶ cm/s28) are well‐known renal secretion substrates. Literature in vitro data of OAT1 mediated basolateral secretion,35 and NPT1, MRP2, and MRP4‐mediated apical secretion36, 37 of PAH were used (Table S3 ) and scaled to in vivo assuming the transporter expression/mg of protein in vitro is equal to the transporter expression/mg of the human kidney and 300 g of kidney per person. This scaling is shown as a proof‐of‐concept incorporation of active secretion into the model but is not expected to be quantitatively accurate due to the lack of transporter quantification. Total in vivo secretion clearances of 884 and 22.3 l/h were calculated for the basolateral and apical side, respectively (Table S3 ). Literature in vitro experimental data of OAT3 and OCT2 mediated basolateral secretion and MATE1/2‐K mediated apical secretion of cimetidine13 were used with scaling to 60 million proximal tubule cells/g of kidney11 and 300 g kidney/person. Total in vivo secretion clearances of 31.8 and 40.5 l/h were calculated for the basolateral and apical side, respectively (Table S4 ).

To explore the possible effect of distribution of transporter expression along the proximal tubule, the overall secretion clearance was incorporated as either uniform distribution across all three proximal tubule subsegments, or all the secretion clearance occurring only at a single tubular subsegment (first, second, or third).

Simulation of urine pH‐dependent renal clearance

Urine pH‐dependent renal clearance has been observed for many drugs due to different ionization and subsequently different effective permeabilities at different urine pHs.38 The pH‐dependent effective passive diffusion was incorporated into the model by calculating test drugs' ionization status in the specific tubule subsegment based on the hypothesized pH gradient across the tubule from glomerulus to bladder (Table  1, Supplementary Methods and Tables S5 and S6 ). To simulate changes in renal clearance upon altered urine pH, memantine (a weak base) and salicylic acid (a weak acid) renal clearances were predicted at different urine pHs.

The intrinsic permeability of memantine (f _u,p = 0.55,39 pK_a 10.7 (drugbank.ca), in vitro permeability 25–43.4 × 10⁻⁶ cm/s)40, 41 was calculated as 0.087–0.06 cm/s (average 0.073 cm/s). At acidic urine, when >99.99% of memantine is charged, observed renal clearance of memantine considerably exceeds unbound filtration clearance suggesting that memantine is a substrate for active tubular secretion. This secretion clearance was estimated via parameter optimization based on the observed renal clearance at urine pH 5 (>99.99% ionized) and average intrinsic permeability. The secretion clearance (CL_api,scr and CL_bsl,scr) was set as 10 l/h in the apical and basolateral side of each subsegment of proximal tubule. The renal clearance was then predicted for urine pH of 5.0, 7.9, and 8.1 as previously described,42 using predicted pH gradient in the kidney segments (Table S5 ). In addition, the effect of the described changes of urine flow42 on renal clearance were simulated by changing tubular flow (rate exiting the last subsegment of collecting duct) from 1 mL/min to 0.99, 1.15, 2.6, and 2.73 mL/min. The 99% confidence interval of observed renal clearances was calculated from reported median and 25% and 75% quantiles, and predictions within the 99% confidence interval were considered successful.

The intrinsic permeabilities of salicylic acid (pK_a = 2.98 (drugbank.ca)) were calculated as 0.088, 0.26, 0.32, 0.34, and 0.58 (average 0.32) cm/s based on in vitro permeabilities of 3.35, 10, 12, 13, and 22 × 10⁻⁶ cm/s.25, 28, 29, 33 The salicylic acid f _u,p used was 0.1 based on the reported relationship of salicylic acid f _u,p and plasma concentration,43 and salicylic acid plasma concentration of 150–180 mg/L in the study reporting urine pH‐dependent renal clearance.44 The observed salicylic acid renal clearance under basic urine exceeded the unbound GFR, suggesting active secretion of salicylic acid. Secretion clearance was calculated via parameter optimization based on observed renal clearance under urine pH 8 (>99.99% ionized) and the average intrinsic permeability value. An apical and basolateral secretion clearance value (CL_api,scr and CL_bsl,scr) of 36 L/h was incorporated in each proximal tubule subsegment. The renal clearance was then simulated at urine pH values 5.0, 6.0, 7.0, and 8.0 to mimic the published range of urine pH44 using the hypothesized pH gradient in the kidney (Table S6 ).

Results

Model construction and sensitivity analysis

A 35‐compartment model consisting of a simple circulation component and a mechanistic kidney model was developed based on the physiological segmentation of the human kidneys (Figure  1). Simple circulation model was used to connect renal blood flow out of the kidneys with the blood flow into the kidneys. The Bowman's capsule was the entrance site of the flow into the mechanistic kidney model, which only allowed unbound drugs to be filtered into proximal tubule. Longitudinally, the kidney was divided into four major segments: (1) the proximal tubule; (2) the loop of Henle; (3) the distal tubule; and (4) the collecting duct (Figure  1). The proximal tubule was further divided into three subsegments (S1, S2, and S3), the loop of Henle into two subsegments (descending and ascending), and collecting duct into five subsegments (connecting tubule, initial collecting duct, cortical collecting duct, medullary collecting duct, and papillary duct) based on kidney physiology. Each subsegment was divided into three sections: the tubular lumen, the cellular compartment, and the vascular section. A compartment for the bladder was created to serve as a compartment for collecting the eliminated drug. The surface areas, volumes, and flow rates in the various model compartments were assigned based on known physiology (Table  1 and Table S1 ). Glomerular filtration was incorporated into the Bowman's capsule, bidirectional passive diffusion was incorporated throughout the entire nephron, and renal metabolism and active transporter‐mediated secretion and reabsorption were included only at the proximal tubule.

To confirm the structural integrity of the model, sensitivity analysis was conducted. As expected from pharmacokinetic principles, blood‐to‐plasma ratio, intracellular unbound fraction, volume of tubular lumen, and volume of cellular compartment did not affect simulated renal clearance (Figure  2). Similarly, as expected, the plasma unbound fraction and glomerular plasma flow positively and linearly correlated with simulated renal clearance, whereas the permeability and surface area negatively and nonlinearly correlated with simulated renal clearance (Figure  2). Notably, the sensitivity analysis showed that with different tubular dimensions (length and radius) tubular surface area but not volume impacts renal clearance.

Figure 2.

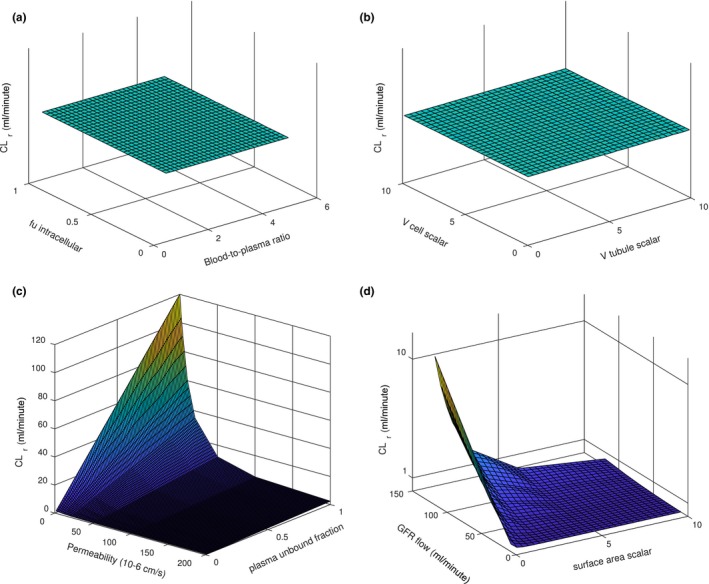
Sensitivity analysis of the developed kidney model. The sensitivity analysis was conducted using a hypothetical neutral drug with permeability of 10 × 10⁻⁶ cm/s and plasma unbound fraction of 0.1 (unless stated otherwise). Panel (a) shows the effects of unbound fraction (0.1–1) inside the renal cell and blood‐to‐plasma ratio (0.5–5) on simulated renal clearance (CL_r). Panel (b) shows the effects of tubular volume (0.1–10‐fold) and renal cell volume (0.1–10‐fold) on simulated renal clearance. Panel (c) shows the effects of in vitro permeability (0.1–200 × 10⁻⁶ cm/s) and plasma unbound fraction (0.1–1) on simulated renal clearance. Panel (d) shows the effects of glomerular filtration rate (GFR; 15–120 mL/min) and tubular surface area (0.1–10‐fold) on simulated renal clearance.

Model verification and prediction of renal clearance of test drugs

The predictive performance of the model was evaluated using 46 test drugs (Table S2 ). First, the validity of the surface area scaling from in vitro experimental systems was tested using neutral compounds (Figure  S1 ). Calculation of permeability values assuming no microvilli expression in in vitro cell systems resulted in a systematic underprediction of renal clearances (Figure S1 a), likely due to an underestimation of in vitro surface area and consequently overprediction of passive reabsorption. To account for the expression of microvilli in vitro, a surface area scaling factor was optimized using neutral compounds. Scaling factors of 1.25, 1.5, and 2 resulted in AFEs of 0.77, 0.93, and 1.25, respectively, and, therefore, a scaling factor of 1.5 was selected. Using this scaling factor, renal clearance was simulated for all 46 test drugs using all available in vitro permeability values (Figure  3 , Table S2 ) resulting in acceptable renal clearance predictions with overall AFE of 0.76, overall AAFE of 1.59, and overall RMSE of 26.9 (Table  2). At least one measured permeability value predicted renal clearance within twofold of the observed renal clearance for 40 drugs (87%) and the mean simulated renal clearance was within twofold of the observed for 37 drugs (80%; Table  2), demonstrating high predictive quality of the model. The AFEs for neutrals, bases, acids, and zwitterions ranged from 0.59 to 0.93, and the AAFEs ranged from 1.37 to 1.83 (Table  2). The RMSEs ranged from 8.27 to 38.3 (Table  2). For the majority of the drugs, the mean simulated renal clearance and at least one of the renal clearances predicted with individual in vitro permeability values were within twofold of the observed (Table  2), and only one drug had predicted renal clearance outside threefold range (Table  2). In addition, the model performance was also evaluated based on net reabsorption (CL_r < f _u,p × GFR) and net secretion (CL_r > f _u,p × GFR) and the calculated AFEs, AAFEs, and RMSEs for these two groups (Table  2) generally showed a more accurate prediction for net reabsorbed drugs than net secreted drugs.

Figure 3.

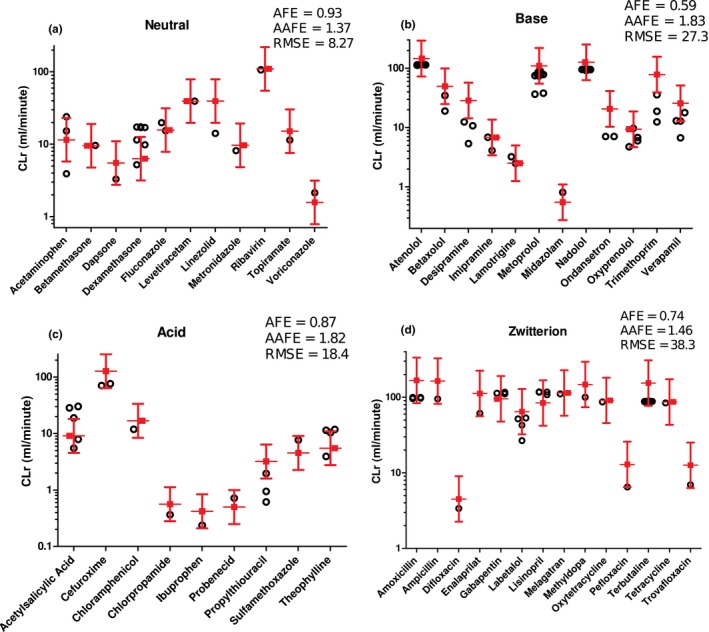
Simulation of renal clearances (CL_r) of 11 neutrals, 12 bases, 9 acids, and 14 zwitterions as verification of mechanistic kidney model. Red symbols represent the observed renal clearances of the test compounds with twofold error range. Black symbols represent the simulated renal clearances using different in vitro permeability values. The comparisons between simulated and observed renal clearances and the average fold error (AFE), absolute average fold error (AAFE) and root mean squared error (RMSE) values for neutral (a), base (b), acid (c), and zwitterion (d) are shown.

Table 2.

Summary of model performance criteria for the different drug categories. The performance parameters average fold error (AFE), absolute average fold error (AAFE), and root mean square error (RMSE) were calculated as described in Methods, and the values were obtained by comparing the predicted individual and mean values to the observed listed in Table S2

	n	AFE	AAFE	RMSE	At least one simulated CLr within twofold	Mean simulated CLr within twofold	Mean simulated CLr within threefold
Neutral	11	0.93	1.37	8.27	10 (91%)	9 (82%)	11 (100%)
Base	12	0.59	1.83	27.3	9 (75%)	8 (67%)	11 (92%)
Acid	9	0.87	1.82	18.4	8 (89%)	7 (78%)	9 (100%)
Zwitterion	14	0.74	1.46	38.3	13 (93%)	13 (93%)	14 (100%)
Net reabsorbed	32	0.87	1.51	9.67	28 (88%)	26 (81%)	32 (100%)
Net secreted	14	0.56	1.78	46.5	12 (86%)	11 (79%)	13 (93%)
Total	46	0.76	1.59	26.9	40 (87%)	37 (80%)	45 (98%)

Incorporation of active secretion to simulate renal clearance

To explore whether active secretion could be incorporated into the developed model, PAH and cimetidine were selected based on published literature to predict renal clearance that incorporates active secretion and passive diffusion. Using literature in vitro transporter data, protein binding data, and in vitro permeability data, the model successfully predicted the renal clearance of PAH and cimetidine (Table  3), demonstrating the feasibility of the model to predict complex renal clearance scenarios with both passive diffusion and secretion clearance incorporated at both apical and basolateral sides of proximal tubule in the model. Notably, when the secretion clearance was incorporated only in one subsegment, the simulated renal clearance was consistently lower than when the secretion clearance was uniformly distributed across the tubular segments. As transporter localization and quantification data are not available, these simulations are only shown to illustrate the relevance of knowledge of transporter localization within the kidney tubules.

Table 3.

Simulation of renal clearance of para‐aminohippuric acid (PAH) and cimetidine in the presence and absence of active secretion clearances. The renal clearances were simulated as described in Methods section and Supplementary Materials using collected permeability data in Caco‐2 cells, plasma unbound fraction (f _u,p), active secretion clearance at apical side of each of the three subsegments of proximal tubule CL_api,scr and active secretion clearance at basolateral side of each of the three subsegments of proximal tubule CL_bsl,scr. The tubular subsegment for secretion clearance indicates the specific subsegment in which the secretion clearance was incorporated. Secretion clearances were set as 0 in all other subsegments

f u,p	Caco‐2 permeability (10‐6 cm/s)	CLapi,scr (l/h)	CLbsl,scr (l/h)	Tubular subsegment for secretion clearance	Observed CLr (ml/min)	Simulated CLr (ml/min)	Fold difference (simulated/observed)
Para‐aminohippuric acid
1	0.72	0	0		550	93.9	0.17
		7.43	295	Each subsegment		812	1.48
		22.3	884	1st subsegment		734	1.33
		22.3	884	2nd subsegment		746	1.36
		22.3	884	3rd subsegment		770	1.40
Cimetidine
0.8	1.37	0	0		543	90.6	0.17
		10.6	13.5	Each subsegment		427	0.79
		31.8	40.5	1st subsegment		383	0.71
		31.8	40.5	2nd subsegment		387	0.71
		31.8	40.5	3rd subsegment		393	0.72

Simulation of urine pH‐dependent renal clearance

Renal clearance can be affected by changes in urine flow and urine pH. Therefore, any broadly useful kidney model must incorporate changes in ionization status and reabsorption clearance due to tubular pH and flow changes. To test the developed model, the renal clearance of memantine and salicylic acid were simulated under different urine pH conditions and with different urine flows (memantine). The effects of both urine pH and urine flow were accurately predicted by the model for memantine (Figure  4 , Table S7 ) demonstrating robust validation of ionization processes, passive diffusion, and tubular flow. Similarly, the effect of urine pH on salicylic acid renal clearance was well predicted using five different in vitro permeability values (Figure  4). The overall simulation results for both substrates were acceptable based on the calculated 99% confidence interval and visual inspection of the urine pH‐dependent renal clearance.

Figure 4.

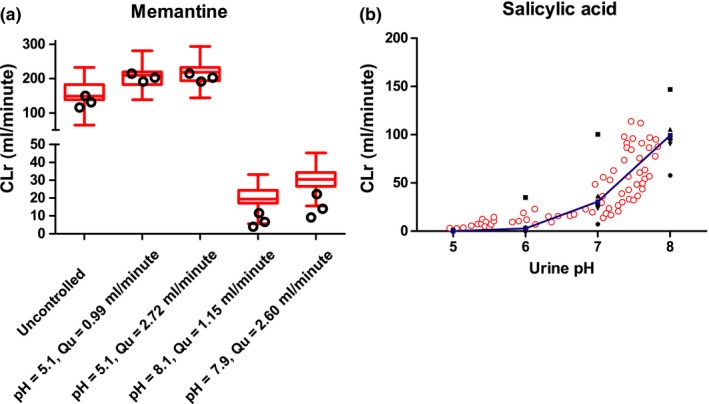
Simulation of urine pH‐dependent renal clearance (CLr) of memantine and salicylic acid. Panel (a) shows the simulation of memantine renal clearance with varying urine pH and urine flow values (open black circles) compared to the observed data of memantine renal clearance (red box and whiskers plots). The different simulated conditions were: uncontrolled urine pH and flow; urine pH of 5.1, urine flow of 0.99 mL/min; urine pH of 5.1, urine flow of 2.72 mL/min; urine pH of 8.1, urine flow of 1.15 mL/min; urine pH of 7.9, urine flow of 2.6 mL/min as described in the original report. The detailed data are listed in Table S7 . The simulations were conducted as described in the Methods section using in vitro permeability data reported in MDCK and Caco‐2 cells, and the average permeability value from the two cell lines. Panel (b) shows salicylic acid renal clearance simulated at pH 5, 6, 7, and 8 using individual permeability values from separate in vitro studies (black squares) and mean permeability values from five studies (blue squares) to explore the effect of altered ionization status of salicylic acid on renal clearance. The simulated values were compared to observed renal clearances (open red circles) of salicylic acid at different measured urine pH values. The observed data is from Macpherson 1955.44

Discussion

Since the development of the well‐stirred model of hepatic clearance, predictions of hepatic clearance from in vitro data have become commonplace and can typically predict human hepatic clearances within twofold of observed. In contrast, due to the sequential nature of renal clearance processes, and the challenges in predicting the fraction reabsorbed from the tubular lumen during the sojourn of drugs within the kidneys, at present, renal clearance cannot be effectively predicted from in vitro data prior to human dosing. In addition, considerable uncertainty exists regarding the quantitative contribution of active transport processes in drug renal clearance. The goal of this work was to develop a mechanistic and dynamic physiologically based kidney model that would consider spatiotemporal changes in drug concentrations, flows, pH, and effective permeability for renal clearance predictions, and allow true in vitro‐to‐in vivo predictions of renal clearance using plasma unbound fraction, permeability, and active transport data.

The developed method has clear advantages over QSAR, allometry, and static model approaches, although these approaches have been successfully used to predict renal clearances. For example, static models assume that passive diffusion always reaches equilibrium and urine concentration is equal to unbound plasma concentration,9, 10 an assumption readily violated with hydrophilic or low permeability drugs or when urine flow increases. Still, two static kidney models achieved 95%9 and 87%10 success rates in predicting renal clearance within threefold error using 20 and 45 test compounds, respectively. The dynamic model developed here performed equally well or better, with 45 drugs (98%) having mean simulated renal clearance within threefold of the observed and 37 drugs (80%) with mean simulated renal clearance within twofold of the observed. The developed model also provides additional power to simulate urine flow and pH‐dependent changes in renal clearance, and to incorporate active apical and basolateral transport of drugs of interest.

This is the first study that examined the effect of different in vitro permeability values from multiple data sources on the accuracy of renal clearance predictions and systematically accounted for ionization status, tubular flow, and tubular pH gradients in renal clearance mechanisms. As few experimental data in humans exist for pH gradients in the kidney tubule at various urine pH values, further refinement of the pH gradients used in this study may be necessary as data becomes available. Previous studies have relied on single source permeability values from LLC‐PK9 or Caco‐210 cells although high variability in cell culture systems is well documented,45 potentially biasing overall predictions. As the in vitro determined permeability values can vary more than an order of magnitude between studies (Table S2 ), it is expected that some predicted renal clearances will fall outside of the twofold acceptance criteria. It is also likely that active secretion processes exist for some of the test drugs with f _u,p × GFR >1.5 resulting in an underprediction of renal clearance values. This hypothesis is supported by the overall underprediction of the renal clearance values in this study and the distinct greater underprediction of renal clearances for drugs that were classified as net secreted when compared to net reabsorbed compounds (Table  2). Finally, inaccurate measurements of in vivo renal clearances and f _u,ps may introduce error into comparisons of predicted and observed data. As such, the model performance in predicting renal clearances from in vitro data and the accurate simulation of urine pH and flow dependent changes in renal clearances can be considered excellent.

The developed model can feasibly incorporate a bottom‐up prediction of renal clearance for transported drugs, as shown with the renal clearance predictions with PAH, cimetidine, memantine, and salicylic acid. Although several prior studies12, 13, 14, 15, 16, 17 have used the Simcyp kidney model to simulate drug renal clearances, to our knowledge this is the first study to predict the renal clearance of a drug with active renal transport using solely in vitro‐to‐in vivo extrapolation methods. The prior studies relied on incorporating scaling factors based on observed in vivo data to either fit active secretion clearance12, 13, 14, 15, 16 or passive diffusion clearance.17 The current study provides a model for the bottom‐up approach using plasma unbound fraction, in vitro permeability, and in vitro transporter uptake clearance to successfully simulate renal clearance. In addition, due to the incorporation of the verified passive diffusion process, an adjustment factor to account for the discrepancy of transporter expression between in vitro and in vivo can be applied with higher confidence than before. The developed model also provides a feasible approach to predict the impact of changes in urine pH and flow on renal clearance.

Funding

This work was supported in part by the National Institutes of Health grant P01 DA032507.

Conflict of Interest

The authors declared no competing interests for this work.

Author Contributions. 

W.H. and N.I. wrote the manuscript. W.H. and N.I. designed the research. W.H. performed the research. W.H. and N.I. analyzed the data.

Supporting information