Population Pharmacokinetic/Pharmacodynamic Analysis of Nociceptive Pain Models Following an Oral Pregabalin Dose Administration to Healthy Subjects

Abstract

A battery of pain models can be used in clinical trials to investigate the efficacy and to establish the concentration‐effect relationship of novel analgesics. This study quantified the pharmacokinetics (PK) of pregabalin after a single oral dose of 300 mg and the pharmacodynamics (PD) on the pain tolerance threshold (PTT) of the cold pressor, electrical stimulation, the pressure pain model, and on the pain detection threshold of a contact heat pain model. The PK were best described using a one‐compartment model with lag time, linear absorption, and linear elimination. The PTT of the cold pressor showed a negative linear decrease over time without pregabalin. A linear drug effect was identified on the PTT of the cold pressor test and an on/off effect for the electrical stimulation PTT. No PK/PD relationship could be identified on the pressure pain and heat pain test. Citation:

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

The quantification of a concentration‐effect relationship in pain is difficult, due to a highly heterogeneous patient population and variable levels of pain perception. Therefore, clinical trials should not be focused on testing only a single pain model, but use a multimodal approach. Additionally, population PK/PD modeling has been shown to increase the information obtained from clinical trials by better understanding an individual's response to analgesics.

WHAT QUESTION DID THIS STUDY ADDRESS?

Can the information obtained from a battery of pain models be used to quantify a concentration‐effect relationship of pregabalin in healthy subjects?

WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

This study quantified the PK and the PD responses to the cold pressor and electrical stimulation pain models after administration of a single dose of orally administered pregabalin.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

This study successfully quantified the concentration‐effect relationship of a known analgesic using a battery of pain models in a clinical trial with healthy subjects. This information can be used to inform future clinical trial design in the investigation of novel analgesics.

The quantification of pain is difficult, due to high interindividual and intra‐individual variability in the perception of a pain stimulus and the complexity of pain in itself (e.g., acute/chronic pain, nociceptive pain, and neuropathic pain). In analgesic drug development, the use of a single pain model, or pain questionnaire, during a clinical trial will therefore not provide a complete overview of the possible pharmacological mechanisms that may be involved in the pain reducing effects of novel analgesics.1, 2 Additionally, the perception of pain in healthy subjects may significantly differ from the target patient population, which may cause a discrepancy in the scaling of a drug effect from a phase I to a phase II clinical trial.

Therefore, to objectively measure and quantify the response of an individual to an analgesic, more than one pain model should be studied.3 The use of a multimodal battery of pain models will create a more complete overview of the analgesic effects, which has an advantage in discovering the effectiveness of drugs with an untested or novel mechanism of action in an early stage of drug development.3, 4, 5 Furthermore, the outcomes of these models can be used to establish the concentration‐effect relationship, which is important to assess analgesic effects and to inform decision making and evidence‐based dosing.6 Population non‐linear mixed effects (NLME) pharmacokinetic/pharmacodynamic (PK/PD) modeling is a commonly used tool to establish this relationship and to quantify the drug effect over time.7, 8, 9 This population PK/PD relationship can, in some cases, already be studied in a phase I clinical trial in healthy subjects by expanding the amount of data that is collected beyond the standard of safety and tolerability end points.

The results of a battery of pain models are commonly studied with a mixed model analysis of variance, in which the time interval that needs to be studied is dependent on the PK of the drug of interest.5 Previously, pregabalin was identified as a compound that showed a significant effect on multiple pain models,5 and was therefore selected as the model compound for this population PK/PD analysis. Pregabalin is a gamma‐aminobutyric acid analogue that binds to the α2‐δ auxiliary subunit of voltage‐gated calcium channels in the central nervous system.10 When pregabalin binds to this channel, the influx of Ca²⁺ is decreased, causing a reduced secretion of several neurotransmitters.11 Strong evidence suggest that the mechanism behind the acute effect is caused by the internalization of the Ca²⁺ channels after binding of pregabalin.12 Pregabalin is currently being used in the treatment of neuropathic pain in patients with diabetic neuropathy, spinal cord injury, and post herpetic neuralgia.13

The objective of this study is the quantification of the concentration‐effect relationship after the administration of a single dose of 300 mg pregabalin on cold pressor, electrical, pressure, and heat pain models using population NLME modeling in healthy subjects. The resulting population PK/PD models will act as a proof‐of‐concept for the use of a battery of pain models to quantify the concentration‐effect relationship of analgesics in healthy subjects.

Methods

Study design

The study design has been previously published in full5 and a short summary will be provided here. A two‐part four‐way crossover study was performed in healthy subjects (men and women) in which the effects of intravenous and orally administered analgesics were studied using a battery of pain tests. Ethical approval was obtained from the Medical Ethics Committee of the Leiden University Medical Center. Subjects were included either in part 1 (intravenous administration of fentanyl, phenytoin, (S)‐ketamine, and placebo) or in part 2 (oral administration of imipramine, pregabalin, ibuprofen, and placebo) of the study. The order of administration was randomized and subjects completed a total of four visits, receiving one of the drugs listed above during each visit, with a washout period of 1 week between each visit, which limited any carry‐over effect (longest t _1/2 = 22.4 hour14). A training session at the start of the study, during the initial screening visit, was included to reduce possible learning effects during the study. For the current analysis, data from only the placebo and pregabalin occasions (part 2) were included.

For PK assessments, blood samples were taken at the following time points: predose, 0.5, 1, 2, 3, 4, 5, 6, 8, and 10 hours after dosing. For PD measurements, a battery of pain models was used.15 The battery consisted of a variety of tests eliciting electrical, mechanical, and thermal (contact heat and cold pressor)‐pain and included a UVB model, the thermal grill illusion, and a paradigm for conditioned pain modulation.5, 15 For each test, an electronic visual analogue scale (eVAS) was used from which the pain detection threshold (PDT), the pain tolerance threshold (PTT), and the area under the eVAS/intensity curve were derived. The battery of pain models was performed for a total of 10 times during each visit, including two predose measurements up to 1 hour before dosing.

Population PK/PD model development was performed on the four significant pain tests after pregabalin treatment, as identified in ref. 5; the PTT of the cold pressor, electrical stimulation (single stimulus), the pressure pain test, and on the PDT of contact heat (normal skin) pain test. The actual PK sampling and PD measurement times were used for model development.

Pharmacokinetic model development

The structural PK model development explored one, two, and three‐compartment models. Both linear and non‐linear (Michaelis‐Menten) elimination kinetics were evaluated during model development. First‐order, lag time, and transit compartment absorption models were explored to describe the absorption phase. Inter‐individual variability (IIV) was implemented following a bottom‐up inclusion procedure from a ln‐normal distribution. Proportional, additive, or a combined (proportional + additive) residual error structures were explored.16

Pharmacodynamic model development

A sequential modeling approach was applied and individual post hoc Bayesian estimates of the developed PK model were added to the PD dataset. First, the existence of a learning/placebo effect over time was explored using a linear, exponential, sigmoidal maximum effect (E_max), Gompertz, and Bateman function on data from the placebo occasion only.17 Thereafter, direct and indirect effects were explored during model development to establish the drug effect of pregabalin on the pain models.7 Both linear and sigmoidal E_max concentration‐effect relationships were tested.7 The drug effect was implemented in the structural model as additive on the baseline (direct effect models) or as a proportional effect on the k _in or k _out (turnover compartment models). Between occasion variability (BOV) was estimated between the placebo and pregabalin visits within an individual. The IIV and residual error analysis were performed using the same procedure as with PK model development.

Covariate analysis

After structural PK model development, allometric scaling (centered around 70 kg) was tested on the volume of distribution (V_d; exponent = 1) and clearance (CL; exponent = 0.75). Additionally, the following covariates were explored in both the population PK and PD models: age, height, sex, body mass index (BMI), fat‐free mass (FFM), glomerular filtration rate (GFR), and serum creatinine. The FFM was calculated using the Janmahasatian equation.18 The GFR was calculated using the serum creatinine levels with the Cockcroft‐Gault equation.19 Visualizations of the post hoc Bayesian estimates vs. the covariates were generated to identify possible covariate relationships. When a correlation (r ² > 0.5) was identified, linear, exponential, and power covariate relationships were formally tested in the model.

Model evaluation

The model evaluation was done by comparing two nested models on basis of the objective function value (OFV; −2 × log likelihood), condition number, relative standard errors (RSEs), and graphical evaluation. During model comparison, a model with one additional parameter was preferred over its parent model when there was a drop of >6.64 points in OFV (P < 0.01; one degree of freedom between two nested models). The RSE of population parameters should be lower than 60%, indicating the estimation of these parameters with sufficient precision.²⁰ The degree of model overparameterization was determined by the condition number, in which a low condition number is preferred that should not exceed 1,000.

Goodness of fit (GOF) figures consisted of the individual predictions (IPREDs) and population predictions (PREDs) of the model vs. the observations and the conditional weighted residuals with interactions (CWRESI) vs. PRED and time.²⁰ GOF figures were used to assess model appropriateness, adequate model fit, and identify possible structural model misspecifications.

Visual predictive checks (VPCs) were generated using 500 samples with the “vpc” function in Perl‐speaks‐NONMEM, including both the fixed and random effects (IIV) to assess the capabilities of the model to correctly describe the population trend and IIV. The population PD model confidence interval VPCs were generated using simulations with the individual post hoc Bayesian estimates of the PK parameters. Internal validation was performed using a nonparametric bootstrap analysis of 1,000 samples.

Software

Data assembly and graphical analysis was performed in R (V3.4.0).20 Diagnostic and GOF plots were generated in R using the ggplot2 package.21 Population NLME modeling was performed using NONMEM version 7.3.22 Bootstrap and vpc analyses were performed using Perl‐speaks‐NONMEM version 4.2.0.23

Results

A total of 16 subjects were included in part 2 of the study (oral analgesics). The subject characteristics are reported in Table 1. The subject population was evenly distributed between men and women (n = 8/8).

Table 1.

Subject characteristics for the 16 subjects receiving pregabalin

Demographic	Mean (SD)	Range
Weight (kg)	68.0 (8.22)	54.25–77.50
Height (cm)	176 (8.54)	163.5–192.5
Age (years)	21.75 (1.61)	19–25
BMI (kg/m2)	21.89 (1.60)	19.4–24.9
FFMa (kg)	50.26 (9.95)	36.62–63.26
Serum creatinine (μmol/l)	82.19 (12.95)	52–99
GFRb (ml/min)	112.7 (18.18)	79–149

Mean (SD) and range (min‐max). BMI, body mass index; FFM, fat‐free mass; GFR, glomerular filtration rate.

^aCalculated using the Janmahasatian equation. ^bCalculated using the Cockcroft‐Gault formula. Mean (SD) and range (min‐max).

Pharmacokinetics

A total of 144 PK samples of pregabalin after dose administration were planned. There were four observations below the lower limit of quantification (of 20 μg/l) and four samples were missing. These eight data points were excluded from the analysis resulting in a total of 136 PK observations above the lower limit of quantification used for model building.

The PK of pregabalin was best described using a one‐compartment model with linear elimination kinetics. The addition of a peripheral compartment resulted in a nonsignificant decrease in OFV (ΔOFV = −2.1) and an increase in the condition number, a three‐compartment model was therefore not further explored. In the one‐compartment model, a structural misspecification was identified in the absorption phase. This resulted in an overestimation of the observations at 30 minutes after dosing. Inclusion of a lag time significantly improved the fit of the observations in the absorption phase, as well as the general fit of the model (ΔOFV = −27), and was thus included in the structural model. The implementation of transit compartments did not prove to be superior. Significant IIV could be identified on all population PK parameters, in order of inclusion: k _a (ΔOFV = −96), lag time (ΔOFV = −22), CL (ΔOFV = −31.7), and V_d (ΔOFV = −18.5), all estimated with acceptable precision (highest RSE = 42.3%). A proportional residual error structure was best fit for purpose.

The allometric scaling of V_d and CL gave a significant drop in OFV (ΔOFV = −22.4 points), indicating weight‐related changes in the CL and V_d for these subjects. The final PK model had a condition number of 8.14. Parameter estimates of the developed PK model of pregabalin are shown in Table 2. The bootstrap mean and confidence intervals were similar to the parameter estimates. The structural PK model is depicted in Figure 1a. The IPRED vs. observations and the CWRESI vs. time are presented in Figure 2a 2. The PRED vs. observations and CWRESI vs. time are shown in Appendix S1. The IPRED closely followed the line of unity, which indicates an accurate model fit. The central trend of the PRED vs. observations showed a clear scatter around the line of unity. The scatter at the lowest observed concentrations all originated from the absorption phase, which was corrected for in the IPRED by the IIV on the lag time parameter. The majority of the data in the CWRESI vs. PRED and the CWRESI vs. time were within the [−2,2] interval. However, a small bias in the CWRESI vs. time could be identified at the later time points, which could be due to the long half‐life of pregabalin compared to the observation period. The confidence interval VPC, showing the 95% confidence intervals around the model median and 80% prediction intervals for the developed model, is shown in Figure 3a. The confidence intervals of the pregabalin observations are in line with the developed model.

Table 2.

Pharmacokinetic model population parameter estimates of pregabalin

Parameter	Parameter estimate
	Population parameters (RSE)	Bootstrap result mean [95% CI]
k a (/hour)	6.07 [42.3%]	6.77 [2.39–15.68]
Lag time (hour)	0.495 [0.39%]	0.493 [0.47–0.50]
Vd/70 kg (L)	31.1 [3.13%]	31.1 [29.25–32.64]
CL/70 kg (L/hour)	4.5 [2.53%]	4.51 [4.30–4.75]
	IIV (CV, shrinkage)
ω2 k a	2.6 (353%, 8%)	2.44 [0.79–4.30]
ω2 lag time	7.09E‐5 (0.842%, 36%)	5.55E‐4 [1.89E‐6–2.1E‐3]
ω2 Vd/F	0.0101 (10.1%, 23%)	0.009 [0.0019–0.016]
ω2 CL/F	0.00672 (8.21%, 21%)	0.00677 [0.00031–0.014]
	Residual error (shrinkage)
σ2 proportional	0.0146 (14%)	0.0141 [0.008–0.020]

95% CI, 95% confidence interval; CL, clearance; CV, % coefficient of variation; IIV, interindividual variability; RSE, relative standard error; Vd, volume of distribution.

Figure 1.

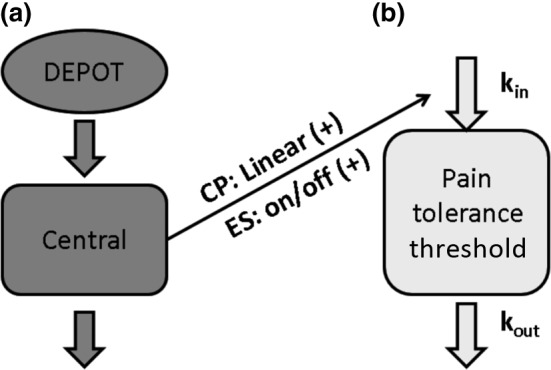
Structural pharmacokinetic (PK) model (a) of oral pregabalin. Structural pharmacodynamic (PD) model (b) with the established PK/PD relationship for both the cold pressor (CP) and the electrical stimulation (ES) models.

Figure 2.

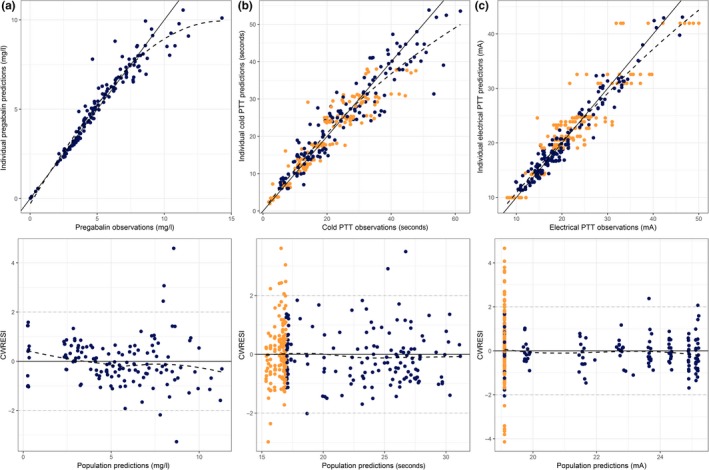
Individual model predictions vs. observations for the final pharmacokinetic model of pregabalin (a), cold pressor pain tolerance threshold (PTT) (b) and electrical stimulation pain tolerance threshold (c). Blue dots = pregabalin visit measurements, orange dots = placebo visit measurements, CWRESI = conditional weighted residuals with interaction, black solid line = line of unity, gray dashed line = [−2, 2] interval, black dashed line = loess fit.

Figure 3.

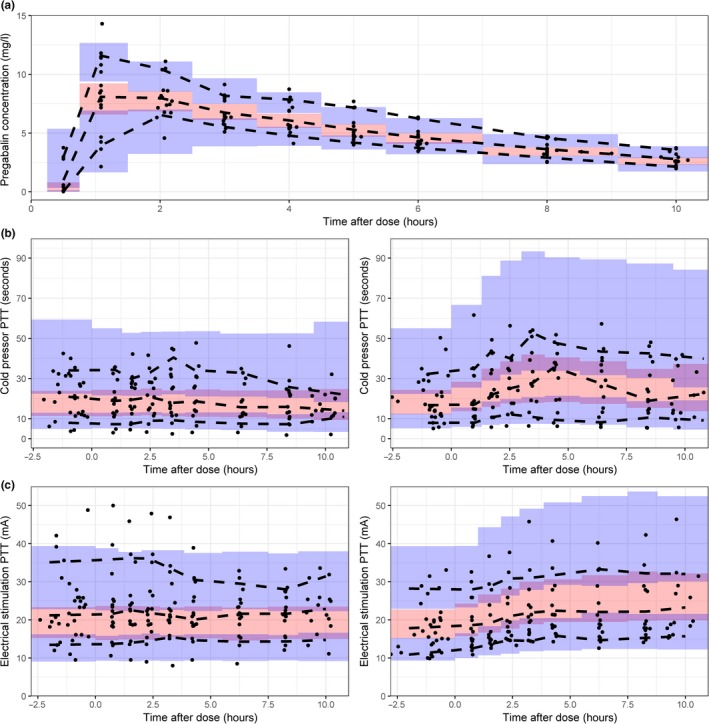
Visual predictive checks of 500 samples of the population pharmacokinetic (PK) (a), the cold pressor pain tolerance threshold (PTT) (b), and the electrical stimulation PTT (c) after administration of a single oral dose of 300 mg pregabalin. For the pharmacodynamic outcomes, the left figure indicates the placebo occasion, the right figure indicates the pregabalin treated occasion. Black dots = observations, black dashed lines = 80% confidence interval (CI) and median of the observations, red shaded area = 95% CI of the median prediction, blue shaded area = 95% CI of the 10th and 90th percentiles.

Pharmacodynamics

Cold pressor

A total of 291 (148 placebo and 143 pregabalin treated) cold pressor pain measurements were available for model development. One individual was excluded from the analysis due to a continuously maximal PTT of 120 seconds during both the placebo and pregabalin treatment visit. A linear decrease in the cold pressor PTT over time during the placebo occasion gave a significant improvement (ΔOFV = −17.17) in the model fit. BOV on the baseline was included to account for the high level of variability between the placebo and pregabalin occasion. A turnover compartment with a linear decrease over time resulted in an OFV of 1,319. Inclusion of a drug effect gave a clear improvement of the model fit. A linear relationship between the pregabalin concentrations and the k _in showed to be superior (ΔOFV = −88.8) over a direct effect model (ΔOFV = −27.3). An E_max relationship did not further improve the model fit (ΔOFV = −1.6) on this data, however, the use of additional dosing levels could better inform the full E_max curve.

Significant IIV was included on the baseline (ΔOFV = −15.8) and the k _out (ΔOFV = −7.7). A proportional residual error was best fit for purpose. The structural model is depicted in Figure 1b. The IPRED vs. observations showed a clear scatter around the line of unity and no structural model misspecification could be identified in the CWRESI vs. PRED (Figure 2b). The PRED vs. observations showed that there was a large variation in this population, which was corrected for after inclusion of IIV, no bias in the CWRESI over time was identified (Appendix S1). The model parameter estimates are listed in Table 3. The population parameters were estimated with low RSEs (<30%), with a high RSE (57.8%) on the slope over time. A coefficient of variation (CV) of 24% was estimated as BOV on the baseline, indicating that there is a clear difference in the baseline response within an individual between visits. The bootstrap mean was similar to the parameter estimates, the 95% confidence interval resembled the expected variability based on the RSE. The VPC, in Figure 3b, shows that there is a broad distribution of the variability in the confidence interval in this model, which could be due to the high level of IIV on the baseline (57.2%) and the k _out (105%), which may decrease after increasing the sample size of the study.

Table 3.

Pharmacodynamic model parameter estimates of cold pressor PTT and electrical stimulation PTT

Parameter	Cold pressor PTT		Electrical stimulation PTT
	Turnover model population parameters (RSE)	Bootstrap result mean [95% CI]	Turnover model population parameters (RSE)	Bootstrap result mean [95% CI]
Baseline	16.9 seconds (16.8%)	17.0 [12.6–22.6]	19.1 mA (7%)	19.2 [16.36–22.06]
k out	0.39/hour (21%)	0.39 [0.18–0.64]	0.494/hour (24%)	0.50 [0.28–0.77]
Slope over time	−0.07 seconds/hour (57.8%)	−0.08 [−0.16–0.04]	–	–
Slope pregabalin	0.135 1/mg/L (16.7%)	0.143 [0.09–0.20]	–	–
Effect pregabalin	–	–	0.322 (18%)	0.326 [0.215–0.450]
	IIV (CV, shrinkage)		IIV (CV, shrinkage)
ω2 BOV baseline	0.057 (24.2%, 27%)	0.060 [0.01–0.15]	0.122 (22%, 2%)	0.116 [0.070–0.172]
ω2 baseline	0.283 (57.2%, 2%)	0.267 [0.056–0.50]	–	–
ω2 k out	0.738 (105%, 19%)	0.715 [0.01–2.46]	–	–
ω2 effect	–	–	0.187 (70, 25%)	0.20 [0.02–0.60]
	Residual error (shrinkage)		Residual error (shrinkage)
σ2 proportional	0.041 (6%)	0.041 [0.032–0.050]	0.0143 (6%)	0.0144 [0.010–0.019]

CI, confidence interval; CV, % coefficient of variation; IIV, interindividual variability; PTT, pain tolerance threshold; RSE, relative standard error.

Electrical stimulation

A total of 313 (160 placebo, 153 treated) electrical stimulation pain measurements were available for model development. No effect over time in the placebo occasion was significant. Thereafter, no significant effect could be estimated when no variability in the baseline between the placebo and pregabalin treatment was included. After inclusion of BOV on the baseline, a turnover compartment with an E_max effect on the k _in gave a significant reduction in OFV compared to the steady state model (ΔOFV = −91.5). However, a low half‐maximal effective concentration (EC₅₀) was estimated (EC₅₀ < 1 μg/l), indicating that the maximal effect was already reached at the lowest pregabalin concentrations. Modeling the effect as an on/off effect resulted in a similar OFV with lower RSEs (<30%), and was, therefore, preferred. Inclusion of IIV on the effect parameter (θ _Effect) was significant (ΔOFV = −6.99), which allowed variability in drug response between individuals. A proportional residual error model was best fit for purpose. The structural model is depicted in Figure 1 1b. The IPRED vs. observations show that, despite the high variability in observations (ranging from 5–50 mA), the model was able to capture the individual response to pregabalin. The CWRESI vs. PRED shows the majority of the data between the [−2,2] interval with multiple placebo observations outside this range (Figure 2c). The PRED vs. observations shows that the inclusion of IIV in the model was needed and high variability in the population exists. No structural misspecification of the model was identified in the CWRESI vs. time (Appendix S1). Model parameters are shown in Table 3. Bootstrap means and the corresponding 95% confidence interval were similar to the final parameter estimates. The VPC for the electrical stimulation PTT is shown in Figure 3 c. A high variability in the baseline observations can be observed but the data distribution is in line with the model predictions. No strong correlations between the parameters in both the cold pressor and the electrical stimulation models were identified (Appendix S2).

Pressure pain

A total of 291 pressure pain measurements were available for model development. No significant effect over time in the placebo occasion was identified. The inclusion of a linear drug effect, driven by an effect compartment, resulted in a small but significant decrease in the OFV (ΔOFV = −12.73) after the addition of two additional parameters. A proportional residual variability of 20% was estimated and a high RSE of 84.4% on the effect compartment rate constant was identified. Furthermore, addition of IIV on the slope of the drug effect resulted in a CV of higher than 400%. These results indicate that there is high variability present within and between subjects and a small drug effect, causing difficulties in the precise estimation of the population parameter estimates. Therefore, model development was not continued.

Heat pain

At each time point, three heat pain tests were performed and the outcomes were averaged for model development. A total of 313 measurements were available for model development. A linear decrease in the heat pain PDT in the placebo occasion gave a significant, 7.5 points, decrease in the OFV (slope −0.1 °C/hour). The addition of a linear effect of pregabalin on the k _in of a turnover compartment (ΔOFV = −37.1) improved the fit of the model. However, no significant IIV was identified and parameters were estimated with high RSEs (>200%). Due to the high variability present in the data and difficulties in accurate parameter estimation, model development on the heat pain PDT was not continued. All NONMEM model codes have been added in Appendix S3.

Discussion

The developed PK model of pregabalin showed accurate model predictions for the 16 subjects in this study. The limited number of observations in the absorption phase complicated the estimation of the population parameters associated with the absorption. Consequently, the highest RSE (42.3%) and CV (353%) were on the k _a, which suggests large variability between individuals on this parameter and difficulties in the precise estimation of this parameter. Two significant concentration‐effect relationships, on the cold pressor PTT and electrical stimulation PTT, were identified in this study. Both population PD models were developed with adequate parameter precision and individual model fit. The highest pregabalin concentrations and PD response regions were underpredicted by the model, as indicated by the loess smoother in Figure 2. The use of additional dosing levels could further improve the model and the quantification of the concentration‐effect relationship over a full range of concentrations.

Our developed structural PK model corresponds with previously published models in terms of model structure and rapid absorption of pregabalin after a lag time.24, 25 The research performed by Hong et al.26 investigated different structural oral absorption models for pregabalin in which they reported that a first‐order absorption process did not suffice. However, in our developed PK model, the implementation of multiple transit compartments, which was suggested by Hong et al.,²⁷ to fit the absorption phase did not prove to be superior over a first‐order absorption with lag time. Additional sampling in the absorption phase, between 0 and 1 hour after dosing, could improve the characterization of the absorption phase of pregabalin, which would allow for a better comparison with previous analyses. The use of GFR in healthy subjects as a covariate on CL was also suggested by Hong et al.26 However, this could not be confirmed in this study, which may be explained by our inclusion of the allometric relationship of weight on CL, as there is multicollinearity between body weight and the Cockroft‐Gault derived GFR, or the low sample size used in this study. The inclusion of allometric scaling on the V_d and CL of pregabalin gave a significant drop in OFV. No other covariate relationships were identified in the developed PK/PD models. This could be due to the low level of diversity between the included subjects (young, healthy, and normal weight) in this population, which may hinder the identification of significant covariates.

In the development of analgesics, pain models supplement to the level of information from clinical trials as they provide a more objective marker for pain. A battery of pain models, as used in this study, can be used to fully explore the potential analgesic effects for different types of pain and to follow the analgesic effect over time. Intervisit variability on the baseline, which was confirmed by the significant decrease in OFV after inclusion of the BOV in both PK/PD models, showed that the baseline response to a pain model between two visits of the same individual could differ significantly. This indicates that the addition of multiple baseline values before drug administration could give a better prediction of the response at the day of testing, thereby improving the quality of the data that is collected.

Out of the four originally planned PK/PD models, we were able to quantify the concentration‐effect relationships on only two pain models. The pressure stimulation PTT and the heat PDT showed a high degree of intra‐individual and IIV and only a small drop in the OFV after inclusion of a drug effect. All four pain models were previously identified as significantly different from placebo in a mixed model analysis of variance, using the pooled data of the first 5 hours after pregabalin dosing (P value cold pressor PTT <0.0001, P value electrical stimulation PTT = 0.0121, P value pressure stimulation PTT = 0.0052, and P value heat (normal skin) PDT = 0.0049).5 The different handling of the placebo data in a mixed model analysis of variance, which increases the residual variability, and the limited improvement in outcome (e.g., 4.1% for the heat PDT) could be possible causes for the lower level of significance we identified in this population NLME analysis.

A previously performed study by Byon et al.27 studied the effects of pregabalin on self‐assessed daily pain scores and the end‐of‐treatment patient global impression of change in patients with fibromyalgia. In that study, pregabalin was able to significantly lower the pain scores compared to placebo. They estimated a dose of 174 mg/day that reached 50% of the maximal effect in reducing the pain scores and 228 mg for the global impression of change scores. They identified susceptibility to the effect of pregabalin between different age groups (<40, 40–60, and >60 years). Due to the limited range of age in our study, this covariate was not identified as a significant predictor of the effect in our study. The disadvantage of the use of these pain scores is the limited improvement (1.5 point decrease on a 10‐point scale) and the long duration of studies (>100 days), which is needed in order to assess the successful analgesic effects.27 Incorporating results from a battery of pain models in early clinical development may link the short‐term analgesic effects with long‐term drug response in patients.

The developed population PK/PD models on the PTT of the cold pressor and the electrical stimulation test gives additional insight in the quantification of the analgesic concentration‐effect of pregabalin that could not be obtained using solely a mixed model analysis of variance. In this clinical study, pregabalin was administered as a single dose. Studying the drug effect over a broad dose range would enable an improved quantification of an E_max relationship and it would allow for better extrapolation to new dosing regimens. The development of these PK/PD models would be highly preferable in the case of a first‐in‐human trial, where early‐stage identification of analgesic effects can improve the assessment of the viability of a compound, which can be used to inform the trial design of future clinical studies.

Supplementary Information

Supplementary Information accompanies this paper on the CPT: Pharmacometrics & Systems Pharmacology

website.(www.psp‐journal.com)

Funding

No funding was received for this work.

Conflict of Interest

The authors declared no competing interests for this work.

Author Contributions. 

M.J.v.E. wrote the manuscript. J.S. and G.J.G. designed the research. M.J.v.E., I.L., P.O., and J.S. performed the research. M.J.v.E., I.L., and M.L.d.K. analyzed the data.

Supporting information