Multi-Wavelength Analytical Ultracentrifugation of Human Serum Albumin complexed with Porphyrin

Abstract

The new Beckman-Coulter Optima AUC instrument, which features multi-wavelength detection that couples the hydrodynamic separation of colloidal mixtures to spectral deconvolution of interacting and non-interacting solutes present in a mixture was used to analyze the composition of human serum albumin (HSA) bound to metal-protoporphyrin. We present new methods implemented in UltraScan that permit Optima AUC derived multi-wavelength data to be spectrally decomposed in the same fashion as has been made possible for the Cölfen detector earlier. We demonstrate this approach by spectrally separating sedimentation velocity experimental data from mixtures of apo-HSA and HSA complexed to different metallo-protoporphyrins. We further demonstrate how multi-wavelength AUC can accurately recover percentages of metallo-protoporphyrin bound HSA and apo-HSA from mixtures and how multi-wavelength AUC permits the calculation of molar extinction coefficients for porphyrins bound to HSA. The presented method has broad applicability to other complex systems where mixtures of molecules with different spectral properties need to be characterized.

Introduction

Multi-wavelength analytical ultracentrifugation (MWL-AUC) is a recent technique that relies on the ultracentrifuge instrument’s ability to collect experimental data at multiple wavelengths during the same run. Collection of such data was originally developed by H. Cölfen’s group in Germany as part of the OpenAUC project [1]. For a review of the history of the Cölfen detector’s development and current state the reader is referred to Pearson et al. [2]. Analysis software for this detector was developed and validated by our group [3] and is available through the open source UltraScan software package [4, 5]. Sedanal by W. Stafford [6] also includes methods for the analysis of MWL-AUC experiments [7]. Multi-wavelength detection promises to revolutionize the field of analytical ultracentrifugation by adding a second dimension for discrimination between different solutes based on optical properties to the arsenal of solution interaction studies. AUC already excels at the hydrodynamic separation of molecules that are dissimilar in size, shape or density. A second mode of separation can be achieved through optical characterization of individual solutes with unique spectral properties. For the Cölfen designed detector, the accuracy of this capability was first demonstrated by spectrally separating contributions from proteins and DNA [3]. Later, we demonstrated how the same methodology could also be applied to the study of macromolecular interactions by identifying molar stoichiometries of interacting complexes as demonstrated for proteins and RNA [8]. These methods share their ability to attribute hydrodynamic signals to individual solutes based on their intrinsic extinction spectra when they exist in a mixture. If these components have unique chromophores that give rise to extinction spectra that are linearly independent, such components can be linearly separated from the absorbance signal, provided any interactions between them do not give rise to hypo- or hyper-chromicity upon binding. The reverse is possible as well: If intrinsic spectra are not known or available for individual components, hydrodynamic separation of individual components will give rise to their pure spectra, and their intrinsic extinction spectra can be derived [2, 9]. Additional benefits arise from the improved signal-to-noise ratio from the detection and averaging of measurements performed at multiple wavelengths. The Cölfen detector collects white light, passes it over a diffraction grating, and images the separated wavelengths on a CCD array, capturing 1024 wavelengths with approximately 0.5 nm separation. As a result, it is capable of collecting up to several hundred useful wavelength measurements in a single radial scan. The high data density generated by multi-wavelength detection improves the signal-to-noise ratio with the square-root of the number of observations, providing cleaner data and improved information content from velocity experiments [2, 3, 7]. A drawback of the current Cölfen detector is the inability to measure in the low UV range below 240 nm due to low sensitivity of the CCD detector in this range. In 2017, Beckman-Coulter released a new analytical ultracentrifuge, the Optima AUC, which employs a traditional detection method using a more UV-sensitive photomultiplier tube, capturing a single wavelength at a time. Unlike the previous model, the Beckman XLA, wavelength accuracy is on par with the Cölfen detector, and scanning speed in the new instrument is approximately 10 times faster than in the XLA, fast enough to repeatedly scan the same sample at multiple wavelengths, in effect producing multi-wavelength detection. However, in contrast to the Cölfen detector, which captures all wavelengths simultaneously, the Optima AUC captures multiple wavelengths sequentially. Since radial resolution is also about three fold higher in the Optima than in the Beckman XLA, the Optima AUC instrument still generates very high data density, approaching a similar ability to collect multi-wavelength data, albeit with higher sensitivity in the low UV range and fewer wavelengths per unit time. In our laboratory we found that the Optima AUC produces a 10 micron radial resolution and a scan speed of approximately 8 seconds/scan for speeds that are optimally synchronized with the flash rate of the Xenon flash lamp, which occurs at 14, 32, 50, and 60 krpm, and includes the time required to reset the stepping motor to its starting position. Because the data from different wavelengths are acquired sequentially in the Optima AUC, it is impossible to produce a spectral profile across multiple wavelengths from an individual radial observation at any given time, since only a single wavelength can be acquired at a given time. This poses additional challenges for the analysis of multi-wavelength data if spectral decomposition is desired for experiments of the type presented in [3, 6, 8]. In this manuscript we discuss how this problem can be circumvented by using a finite element model derived from the experimental single-wavelength data to create a time interpolation across the entire experiment which can reconstruct the missing data points for each time point and allows the wavelength decomposition to proceed.

Our test system uses mixtures of dialyzed Human Serum Albumin (apo-HSA) and HSA complexed with metallo-protoporphyrins (HSA-PPIX-metal). Several sites in HSA have been postulated to possess the ability to directly bind metal ions as well as organometallic compounds [10]. The evidence has generated considerable interest in the physiological role of HSA as a metal binding protein but also as a vehicle for synthetic biology uses of the metal binding properties (e.g., synthetic blood and solar energy conversion) [11, 12]. One of the most intriguing and potentially useful among these interaction is the ability of HSA to bind heme and other metallo-porphyrins [13]. A system such as the one investigated here presents two additional analytical challenges related to the poor solubility of many protoporphyrins in aqueous solutions. One challenge is created by the tendency of the protoporphyrin to form polydispersed aggregates which do not interact with the protein and interfere with other analytical techniques (e.g., fluorescence spectroscopy). We have shown that this challenge can be overcome by a multistep sample preparation that leaves in solution only the complexes between the monomeric porphyrins and apo-HSA [14]. A second challenge arising from the poor solubility of the porphyrins is the inability to determine their molar extinction coefficient in aqueous solutions, and to determine the fraction of complexed HSA. The direct measurement of an aqueous extinction coefficient is hindered by the formation of aggregates which alter the porphyrin’s extinction profile, and which prevents optical measurement of concentration and extinction coefficients of the monomeric porphyrin in solution. Furthermore, binding of porphyrin to the protein causes the porphyrins to substantially modify their spectral properties (peak positions and the molar extinction coefficient ε). These spectral properties, in particular ε, cannot be independently established because they require the simultaneous knowledge of the pure spectrum as well as the concentration of the bound protoporphyrin. MWL-AUC offers a potential solution to the challenge because it allows us to separate the extinction signals of apo-HSA from HSA bound to protoporphyrin, thereby allowing us to establish both missing parameters. In this work we demonstrate that MWL-AUC is able to characterize these complex mixtures in the solution phase, and to assess their purity and composition.

Methods

Binding and Purification of HSA-PPIX

HSA and dimethylsulfoxide (DMSO) were purchased from Sigma-Aldrich (St. Louis, MO). Tin as well as Zinc-protoporphyrin IX (Sn(IV)PPIX and Zn(II)PPIX), were purchased from Frontier Scientific Inc. (Logan, UT). A detailed description of the sample preparation can be found elsewhere [14]. Briefly, a small amount of solid protoporphyrin was initially dissolved in 1 ml of DMSO and allowed to equilibrate overnight to yield a highly concentrated solution of monomeric porphyrin. The concentration of this stock was then determined spectroscopically upon dilution in DMSO using the Beer-Lambert equation [14]. An aliquot (100–200 μl) of this stock solution was added to 10 ml of a solution containing ~10 μM HSA and allowed to equilibrate for an hour at room temperature. Separately, 2 ml of a stock solution of HSA (10 μl) was also prepared. All the solutions were dialyzed using a 6 kDa cut-off pore size kit (Sigma-Aldrich, St. Louis, MO) for 48 hrs. This procedure eliminates the DMSO, some of the aqueous free porphyrin and smaller aggregates as well as other possible small impurities that may be contained in the HSA samples. The dialyzed solutions were collected and centrifuged for 5 minutes at 11.5 g, using an EPPENDORF MiniSpin Plus centrifuge (Hauppauge, NY). After centrifugation the supernatant of the porphyrin/protein mixtures contains only apo-HSA and the HSA/protoporphyrin complex and the rest of the aggregates have been eliminated [14]. At this point the remaining supernatant was pooled and then separated into four 2 ml aliquots. To three of these samples were added aliquots of the dialyzed and centrifuged stock of HSA in order to yield the following solutions:

• solution 1: 100% HSA-metal-PPX complex;

• solution 2: 25% apo-HSA: 75% HSA-metal-PPX complex;

• solution 3: 50% apo-HSA: 50% HSA-metal-PPX complex;

• solution 4: 75% apo-HSA: 25% HSA-metal-PPX complex;

The assumption is that in the 100% HSA-metal-PPX complex all the available porphyrin is already bound to the protein, thus, addition of the apo-HSA only adds free protein that cannot form further complexes with the porphyrin ligand. Previous studies have shown that metal bound protoporphyrin binds to HSA in a 1:1 ratio [15, 16]. The concentration of all solutions was adjusted with 10 mM phosphate buffer to assure that the absorbance in the analyzed wavelength range stayed below 1.0 optical density units (OD) everywhere to assure all measurements fall within the dynamic range of the instrument. This resulted in concentrations of 0.7–1.0 OD at the Soret band maximum. Using the spectra of pure HSA and the difference spectrum of HSA with solution 1, we expect to accurately quantify the molar amounts of each species in the mixture by MWL-AUC, and derive a molar extinction coefficient for protoporphyrin bound to HSA. Observing the OD of the 278 nm peak (0.5 OD), HSA was combined with solution 1 to increase the OD at 278 nm up to 0.75 OD for solution 2 and 1.0 OD for solution 3, while roughly maintaining the OD of the Soret band. The concentration of the protein in each sample was determined spectroscopically using the value of the absorption of the solutions at 278 nm and assuming a molar extinction coefficient ε_278nm = 3.4 × 10⁴ M⁻¹ cm⁻¹ for HSA [14] and ε_280nm = 3.281 × 10⁴ M⁻¹ cm⁻¹ [17, 18].

UV Spectroscopy

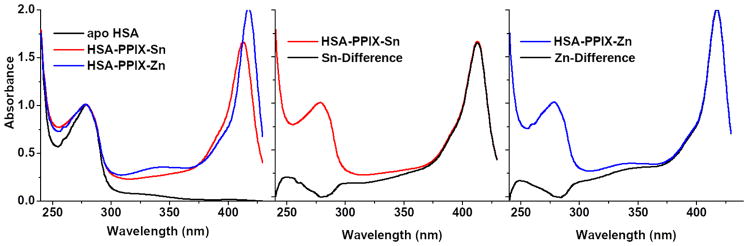
The UV/visible spectra of apo-HSA and HSA complexed with porphyrin bound to Zn and Sn were measured with a Cary-100 UV-Vis spectrophotometer (Agilent Technologies Inc., Santa Clara, CA). Spectra were measured in the 240–500 nm range which includes the Soret band of the porphyrins (> 400 nm) as well as the absorption maximum of the aromatic amino acids (~ 278 nm) from which the concentration of the protein was established. Difference spectra between apo-HSA and HSA complexed to metal-protoporphyrin with metals Sn and Zn were determined by subtracting 278 nm normalized spectra of solution 4 from solution 1. A maximum absorption of the porphyrins is found at the Soret band at 412 nm for HSA-PPIX-Sn and at 417 nm for HSA-PPIX-Zn. The maximum absorption of HSA between 240–450 nm was found to be ~278 nm (see Figure 1).

Figure 1.

Left: Overlay of normalized spectra for apo-HSA (black), HSA complexed with porphyrin (PPIX) bound to either Zn (blue) or Sn (red); center: HSA complexed to porphyrin bound to Sn (red) and difference spectrum when the HSA absorbance is subtracted (black); right: HSA complexed to porphyrin bound to Zn (blue) and difference spectrum when the HSA absorbance is subtracted(black)

AUC-MWL Data Analysis

1. Chromatic aberration correction

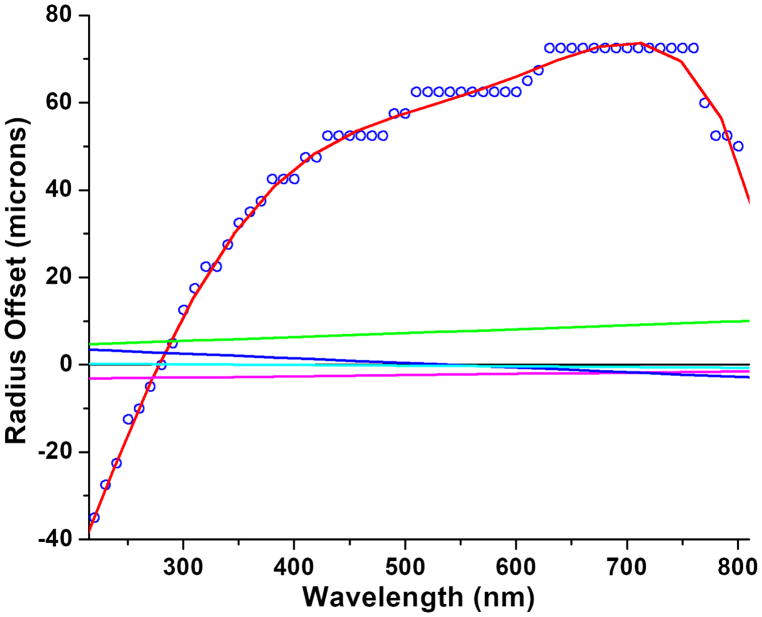
Since these experiments are collected at multiple wavelengths, we checked for chromatic aberration artifacts before analyzing any experimental data. The Optima AUC avoids lens-based refraction in the UV/visible detection optics by using mirror-based optics, but unfortunately it is not completely free of chromatic aberration in its current state. The manufacturer is aware of the problem and is searching for a solution [19]. We determined the effect of chromatic aberration on the measured radial positions by scanning the menisci of six water samples in intensity mode in the An60Ti rotor at 62 wavelengths (190–800 nm in 10 nm increments) in a single run. We repeated the same experiment using saturated NaCl solutions and 50% sucrose solutions to determine if refractive index of the solution has any effect on these measurements, but no detectable difference was observed. A radial calibration was performed at 280 nm and 3,000 rpm before scanning, and radial positions for all meniscus positions were overlayed by subtracting the observed meniscus positions at 280 nm from each dataset. The resulting overlays were found to be congruous, and were averaged and could be well approximated by a 5^th order polynomial. This polynomial then describes the average offset from the radial position measured at 280 nm for each other wavelength. Essentially identical offsets were also obtained when we independently fitted the meniscus positions of two multi-wavelength velocity experiments with 42 wavelengths spanning 240–429 nm using typical workflow procedures [20] (data not shown), increasing confidence in the systematic deviations caused by chromatic aberration. The results from our instrument are summarized in Figure 2. We found that chromatic aberration in other instruments produced a different chromatic aberration pattern, which could not always be fitted well by a 5^th degree polynomial. For those instruments we implemented a smoothing fit of the chromatic aberration data using a Gaussian kernel. In UltraScan, experimental data are directly imported from the PostgreSQL database on the Optima AUC’s Linux computer, and radial positions can now be corrected for chromatic aberration on the fly during import from the Optima AUC by reading either a 5^th degree polynomial correction function, or a correction array spanning from 190–800 nm in 1 nm increments. These corrections need to be separately established for each instrument, and correction files need to be stored on the computer used to import the experimental data.

Figure 2.

Weight-averaged meniscus offset positions from six measured menisci as a function of wavelength (blue circles), fitted with a 5th-order polynomial (red line). Green, cyan, blue and magenta lines: Variation of meniscus positions for 4 separate samples measured after chromatic aberration correction. All measured values are within the radial resolution of the Optima AUC

2. Wavelength Selection

MWL-AUC experiments collected on the Optima AUC require that individual scans for each wavelength are collected asynchronously, but in the same run. For sedimentation velocity (SV) experiments a finite time is available to collect SV data. The time required for optimal analyte characterization depends primarily on the rotor speed and the sedimentation speed of the analytes, but also on the desired signal expected from the experiment. If rotor speed is too slow, sedimentation resolution will suffer. If the rotor speed is too high, diffusion signal will suffer, and potentially not enough scans can be collected for each wavelength before the analyte is pelleted. Because individual scans require at least 8 seconds, the number of wavelengths collected with the Optima AUC will have to be smaller than with the Cölfen optics, or the sample may pellet before a sufficient number of scans have been collected. Since the number of wavelengths collected is a limiting factor, it is important to place the available wavelengths strategically so that maximum information is obtained. The choice of included wavelengths is a balancing act that should a) cover the unique chromophores from any species to be deconvoluted, b) cover regions of the spectrum where extinction is within the dynamic range of the detector, and c) provide a sufficient number of points in peak regions of the spectrum where extinction changes rapidly with wavelength so that linear interpolations between discrete wavelengths along the spectrum represent the original spectrum without missing important features of the spectrum. The number and position of wavelengths to be collected is also a function of the extinction profile and the degree of orthogonality of the spectra to be decomposed. In order for spectral data to be separable, the extinction spectra cannot be linearly dependent. A metric for separability is the angle α between the extinction spectral vectors u and v (Equ. 1). If extinction profiles are similar, inclusion of additional wavelengths, especially in regions of difference, helps to increase angle α. The closer the angle is to 90°, the more efficient will be the spectral separation. An angle close to 0° indicates linear dependence, which occurs when the spectral overlap between individual species is too great, or not enough unique wavelengths are included in the spectrum.

$$\alpha ={\text{Cos}}^{-1}\left[\frac{u·v}{\Vert u\Vert ·\Vert v\Vert }\right].$$ (1)

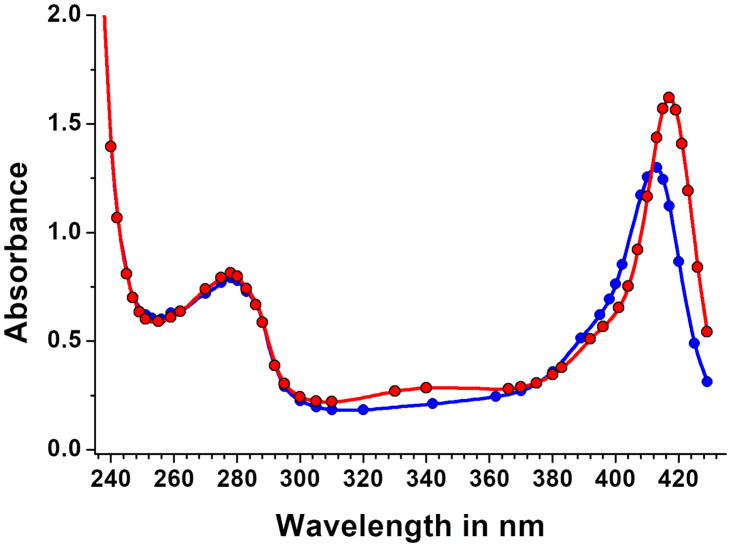
For example, two protein spectra may be linearly dependent if only a few wavelengths around 280 nm are used, but as soon as wavelengths below 240 nm are included, the ratio of aromatic amino acids contributing to a 280 nm absorbance and the protein backbone contribution may reveal differences that help make two proteins spectrally separable. In order to separate HSA complexed with metal bound porphyrin from apo-HSA, we optimally placed 42 wavelengths along the spectrum between 240–430 nm (see Figure 3). Using these values, we found angles of 82.8° between the spectra of HSA and the difference spectra of HSA complexed to Sn-protoporphyrin, and 84.0° between HSA and HSA complexed to Zn-protoporphyrin.

Figure 3.

Wavelength selection for HSA complexed to porphyrin bound to Sn (blue) and Zn (red). Selected wavelength are optimally distributed along the spectrum to capture unique chromophore information between 240–430 nm

3. Analytical Ultracentrifugation

Multi-wavelength SV experiments were carried out in 2-sector epon centerpieces (Beckman-Coulter) in an Optima AUC instrument (Beckman-Coulter) at the Center for Analytical Ultracentrifugation of Macromolecular Assemblies at the University of Texas Health Science Center at San Antonio. Experiments collected 42 wavelengths between 240–429 nm, and at 20°C, and 35 krpm in a single run. Experiments were repeated at 45 krpm and 55 krpm after thoroughly mixing the samples. Experiments at 35 krpm resulted in approximately 40 scans before all sample appeared to be pelleted. 45 krpm experiments resulted in about 30 useful scans, while 55 krpm experiments yielded only about 20 useful scans for each wavelength. For each metal, solutions 1–4 were measured in two separate experiments, since the Optima AUC does not permit data collection from a single sector, hence, two samples were measured simultaneously, one sample in each sector of the cell. Each sample contained 420 μl volume. To maximize scan numbers, only a single cell was measured in each run. All data were collected in intensity mode, and analyzed with UltraScan-III version 4.0, release 2450 [4, 5].

4. Sedimentation Velocity Analysis Workflow

Experimental MWL-AUC data were imported into UltraScan and converted to OpenAUC data format [1], while simultaneously applying the chromatic aberration correction. After conversion to pseudo-absorbance data, edit profiles defining meniscus position, and the beginning and end of the useful radial data range using the SV dataset measured at 280 nm were applied to all datasets from the other wavelengths belonging to the same channel, and analyzed by the 2-dimensional spectrum analysis (2DSA) [21] with simultaneous time-invariant noise subtraction. All 2DSA s-value ranges were fitted from 1–12 s with 64 steps and frictional ratio range 1–4 with 64 steps. Next, data from a single wavelength (typically 280 nm) were selected for a meniscus fit using 2DSA with simultaneous time- and radially-invariant noise removal. The fitted meniscus position is then applied to all datasets from each wavelength stemming from the same sector, and a final iterative 2DSA refinement with time- and radially invariant noise correction is calculated for each wavelength and dataset from the same sector. At this point, systematic noise contributions to the data have been removed [22], the meniscus position is optimized, and the intrinsic sedimentation and diffusion signal in each wavelength’s dataset are optimally described by a degenerate finite element model that produces the lowest possible root-mean square deviation (RMSD). Hence, the finite element model from the final 2DSA step can be used to generate a simulated, noise-free dataset that covers the same time and radial grid for each wavelength, in effect generating a simulated dataset that is equivalent to the experimental dataset structure obtained from the Cölfen detector. For the simulation, parameters from the same UltraScan edit profile can be used that were applied earlier to the original experimental dataset from each cell sector, but the user is also free to choose different simulation parameters. Importantly, all iterative 2DSA models are re-simulated based on the identical time grid and therefore missing datapoints required for the wavelength decomposition can now be interpolated. A new utility in UltraScan, us_mwl_species_sim, has been developed to facilitate this process (see supplemental Figure SI 1). Simulations can be performed on any desired time grid, and should use water at 20°C as a buffer since the 2DSA iterative models are already corrected to standard conditions during the original fitting session for temperature, buffer density and viscosity. If desired, rotor stretch can be reproduced by selecting the same rotor used in the actual experiment. At this point, the simulated data can be imported into the UltraScan visualization tool, us_mwlr_viewer, and displayed by individual scan surface or movie (see supplemental Figure SI 4 and video SI 2). For the next step, a second new tool has been implemented in UltraScan that allows for the decomposition of the simulated synchronous time dataset into its spectral components (us_mwl_species_fit, see SI 3). In a MWL-AUC experiment each radial observation from each scan is a complete wavelength scan of the analytes sedimenting at that position. Therefore, each radial position can be linearly decomposed into the spectral components a, b, …, n present in the mixture (see Equ. 2).

$$C_{\text{MWL}}=x_a\left[\begin{array}{c}{\epsilon }_{a1}\\ {\epsilon }_{a2}\\ \cdots \\ {\epsilon }_{aj}\end{array}\right]+x_b\left[\begin{array}{c}{\epsilon }_{b1}\\ {\epsilon }_{b2}\\ \cdots \\ {\epsilon }_{bj}\end{array}\right]+\cdots +x_n\left[\begin{array}{c}{\epsilon }_{n1}\\ {\epsilon }_{n2}\\ \cdots \\ {\epsilon }_{nj}\end{array}\right],$$ (2)

where C_MWL is a wavelength scan from the three-dimensional surface simulated above, at a radial point for a given scan, and x_a, x_b, …, x_n are the fractions of components a, b, …, n present at this point, and ε_ai and ε_bi are the extinction coefficients of components a, b, …, n (also see video SI 2). This problem is best solved using the nonnegatively constrained least squares algorithm NNLS [23] since it avoids negative fractions. This calculation is performed for each radial position in the experiment, and the collection of all fractional concentrations x_a, x_b, … generates n new 2-dimensional hydrodynamic datasets whose amplitudes represent the partial concentrations from each spectral component represented in Equ. 2 (see also references [3, 8]). This UltraScan module, us_mwl_species_fit, requires the following inputs: 1. the previously generated time-synchronous MWL-AUC dataset and 2. the intrinsic absorbance spectra for each optically unique species to be decomposed. These spectra can be scaled to molar concentration or any other concentration unit desired, and the decomposed datasets will also be written in the selected concentration scales. This approach will generate a scalar concentration for each radial position and scan time for each spectrally unique component, resulting in separate hydrodynamic experimental datasets for each spectrally unique species. In this case, we used the absorbance spectra of apo-HSA and the HSA-PPIX-metal difference spectra to separate the signals into two spectrally distinct hydrodynamic datasets. In the final step, the resulting 2-dimensional datasets from each species are analyzed as conventional SV experiments, individually or globally, using standard finite element optimization methods and other analysis approaches available in UltraScan [21, 24, 25, 26, 27, 28]. In our case, we used the parametrically constrained spectrum analysis (PCSA) with an increasing sigmoid parameterization [26], and 100 Monte Carlo iterations.

5. Extinction coefficient determination

Difference spectra between apo-HSA and HSA-PPIX-Sn or HSA-PPIX-Zn were measured to derive the exclusive contributions of the metal protoporphyrin HSA complexes (Figure 1). Using the difference spectra, the observed contribution of porphyrin to the absorbance at 280 nm is zero, providing a convenient reference point for measuring total HSA concentration. Our assumption is that noninteracting components add linearly to the composite spectrum. Since only HSA-PPIX will contribute to the Soret band, we can cleanly capture all complexed HSA using the difference spectrum. All remaining spectral signal in a mixture must therefore be originating from apo-HSA. Since there is virtually no spectral overlap in the 300+ nm region between apo-HSA and HSA-PPIX-metal, these difference spectra, when used for the decomposition of the hydrodynamic data, allow us to cleanly separate the AUC experiment into two separate hydrodynamic datasets, one for apo-HSA, and one for HSA bound to porphyrin. The SV analysis will then reveal the sedimentation coefficient and permit integration of the HSA peak (with or without porphyrin bound), which occurs at approximately 4S. This will provide the partial concentration of each species in the mixture based on their percentage of the total absorbance, integrated across all wavelengths. The percentage of apo vs. complexed HSA available for each ratio mixed can be used to relate the 280 nm absorbance to the 412 or 417 nm absorbance and calculate a molar extinction coefficient ε at 412 or 417 nm, providing for the first time an estimate for this important parameter. To calculate the molar extinction coefficient, we first determined the molar concentration of the total amount of HSA from the absorbance of the 4S species observed at 280 nm, using the molar extinction coefficient of apo-HSA. Next, we calculate a molar concentration for the fraction of complexed HSA-PPIX identified in the SV experiments. Knowing the number of mols of porphyrin bound HSA, the absolute concentration observed at 412 or 417 nm for the 4S species can then be used to estimate a molar extinction coefficient for the Soret band absorbance. Since multiple observations were made with different ratios of apo-HSA and HSA-PPIX, the average of all observations is used and a standard error for this parameter can be obtained.

Results

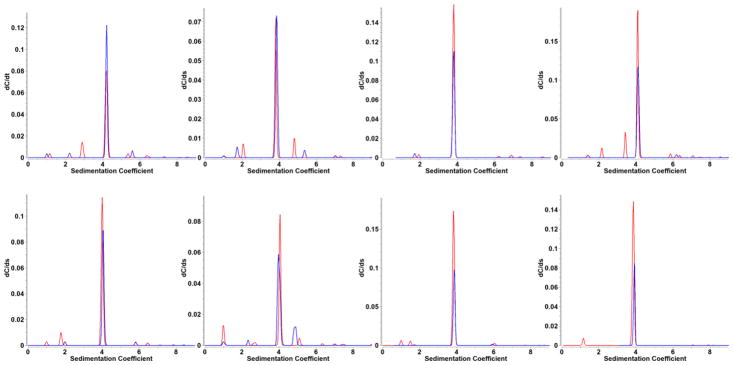
An absorbance spectrum from apo-HSA and the difference spectrum from a mixture of apo-HSA and HSA-metal-protoporphyrin complex isolated as described above were used to decompose multi-wavelength SV experiments of different ratios of the two components into hydrodynamic datasets representing pure apo-HSA and the porphyrin-bound HSA fraction. Four different ratios of mixtures containing apo-HSA and HSA-PPIX-Sn or HSA-PPIX-Zn were analyzed and the relative amount of apo-HSA compared to HSA-PPIX-metal was deduced from the integrated concentration of the 4S peak that was detected in each decomposed dataset. The SV analysis results from the PCSA-Monte Carlo analysis are shown in Figure 4, and demonstrate that there is essentially no difference in the sedimentation speed of apo-HSA and HSA-PPIX, regardless of which metal was bound. Interestingly, the analysis further shows a number of low concentration peaks with variable s-values, the majority of which originate only from the apo-HSA decomposition, suggesting the presence of a contaminant protein which does not bind protoporphyrin. It is also apparent that there is a slight run-to-run variability in the observed s-value, although both apo-HSA and HSA-PIIX always sediment with nearly the same sedimentation coefficient. This suggests the presence of a systematic instrument error, whose root cause we have not been able to determine, requiring further study.

Figure 4.

PCSA-Monte Carlo analysis of decomposed multi-wavelength SV data for four different mixtures of apo-HSA (red) and HSA-PPIX (blue) with increasing concentration of apo-HSA from left to right. Top row: HSA-PPIX-Sn, bottom row:HSA-PPIX-Zn

The extinction coefficient calculation resulted in a value of ε₄₁₀ = 1.03 ± 0.13 × 105 M⁻¹ cm⁻¹ for HSA-PPIX-Sn, and ε₄₁₇ = 1.16 ± 0.17 × 105 M⁻¹ cm⁻¹ for HSA-PPIX-Zn. This represents a 13.1% and 14.3% error for Tin and Zinc respectively.

Based on the multi-wavelength results, our analysis further shows that the preparation of solution 1 is quite efficient in complexing HSA with protoporphyrin, resulting in 96.3% HSA-PPIX-Sn and 3.7% free apo-HSA, and 86.0% HSA-PPIX-Zn and 14.0% free apo-HSA. The slight difference in composition between the two metals could indicate differences in the HSA-PPIX binding efficiencies among different metals bound to porphyrin.

Conclusion

We show that multi-wavelength SV experiments can be used to effectively quantify the presence of distinct components in a mixture that have nearly identical hydrodynamic properties, but can be spectrally separated based on their unique absorbance spectra. We further show how these data provide information that can be used to determine extinction coefficients for species that otherwise could not be obtained in a pure form. The limit of accuracy of our calculations is affected by our assumption that the extinction coefficient of HSA-PPIX at 280 nm is only negligibly affected by the addition of porphyrin, which may not be true. The new AUC analysis tools integrated into UltraScan provide a powerful new method for the analysis of multi-wavelength data acquired on the new Beckman-Coulter Optima AUC instrument. Multi-wavelength AUC experiments promise to be the method of choice whenever complex mixtures that contain components with unique absorbance spectra need to be characterized.