Structural dynamics of propeller loop: towards folding of RNA G-quadruplex

Abstract

We have carried out an extended set of standard and enhanced-sampling MD simulations (for a cumulative simulation time of 620 μs) with the aim to study folding landscapes of the rGGGUUAGGG and rGGGAGGG parallel G-hairpins (PH) with propeller loop. We identify folding and unfolding pathways of the PH, which is bridged with the unfolded state via an ensemble of cross-like structures (CS) possessing mutually tilted or perpendicular G-strands interacting via guanine-guanine H-bonding. The oligonucleotides reach the PH conformation from the unfolded state via a conformational diffusion through the folding landscape, i.e. as a series of rearrangements of the H-bond interactions starting from compacted anti-parallel hairpin-like structures. Although isolated PHs do not appear to be thermodynamically stable we suggest that CS and PH-types of structures are sufficiently populated during RNA guanine quadruplex (GQ) folding within the context of complete GQ-forming sequences. These structures may participate in compact coil-like ensembles that involve all four G-strands and already some bound ions. Such ensembles can then rearrange into the fully folded parallel GQs via conformational diffusion. We propose that the basic atomistic folding mechanism of propeller loops suggested in this work may be common for their formation in RNA and DNA GQs.

INTRODUCTION

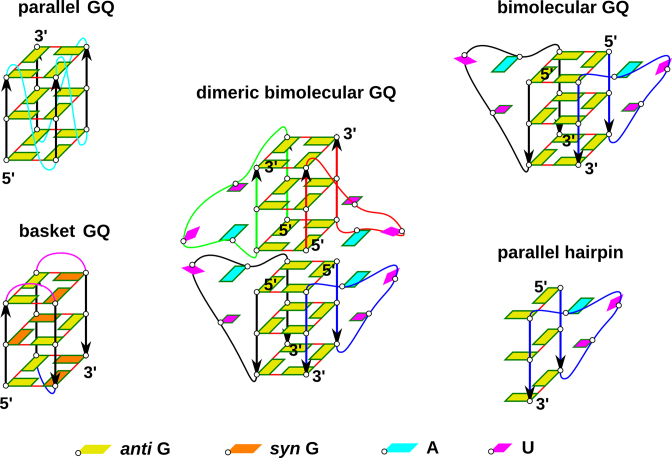
G-rich DNA and RNA sequences can form four stranded structures called G-quadruplexes (GQs) (1–24). While many different folds are known for DNA GQs, as exemplified by the exceptionally polymorphic human telomeric d(GGGTTA)_n sequence (3,5–7,11,13,15,19,24–26), the majority of RNA GQs adopt parallel-stranded topologies, including the RNA GQ formed by the telomeric repeat containing RNA (TERRA) (9,14,16,21,22,27). Parallel-stranded RNA GQs have several salient structural features: (i) anti conformation of glycosidic angle of all guanines (so called all-anti conformation); (ii) parallel orientation of all guanine strands; (iii) double reversal of chain direction present in loops—so called propeller loops (see Figure 1). Antiparallel (inverted) orientation of RNA G-quartets, but still with Gs in the anti conformation, can be achieved only in complex folds with G-strand discontinuities (28). Syn conformation of guanosines can also be compatible with RNA GQs having discontinuous strands (29).

Figure 1.

(Left) Scheme of parallel-stranded GQ and basket type GQ for comparison. Orientation of guanine strands is indicated by arrows. Propeller loops are cyan, lateral loops are pink and a diagonal loop is blue. (Middle and right) Simulated systems: stacked dimer of two bimolecular GQs containing four UUA loops (the experimental structure), a bimolecular GQ with two propeller loops and isolated PH. Different RNA chains are distinguished by different colors of their backbone. Frame around a nucleobase indicates its involvement in stacking interactions.

Contrast between the large number of known DNA GQ topologies and the (predominantly) single fold of RNA GQs indicates that DNA and RNA GQs may have very different folding landscapes. Recent research suggested that folding of DNA GQs is best described by a kinetic partitioning (KP) mechanism, known also as multiple-pathway or multiple-funnel folding process (24,30–39). KP is a consequence of a competition between two or more structurally different folds with long life times that appear as deep and well-separated free-energy basins on the folding landscape (24,40–42).

It has been argued that KP of folding landscape of DNA GQs is dominated by diverse cation-stabilized GQ folds, characterized by specific combinations of anti and syn nucleotides in their G-strands (24). The non-native GQ folds act as deep off-pathway kinetic traps. KP is the only known folding mechanism that can explain very long folding times (sometimes days or even weeks) (30–34,43–48) of many DNA GQs (24). The complexity of KP folding landscape may lead to profound dependence of the folding process on the nature of the denatured (initial) ensemble (24,49); this is an essential but often overlooked problem as one hardly knows how the unfolded state of a G-rich RNA or DNA strand in vivo looks like. However, because RNA GQs are generally unable to adopt any fold except the all-anti all-parallel one (50–52), the prime source of KP should be absent for RNA GQ-forming sequences and the basic principles of their folding should be different from DNA GQs (24). The near-inability of RNA to adopt GQs with antiparallel strands appears to be an inherent property of the GQ stem (50).

A hitherto unresolved problem, which complicates understanding of folding of both DNA and RNA parallel GQs, is formation of parallel G-hairpins (PH in the following text) containing the propeller loops (Figure 1). Experiments indicate that GQs possessing such loops are thermodynamically very stable and the shortest single nucleotide loops are likely compatible only with the propeller arrangements (53–60). However, it has been difficult to reconcile the common formation of propeller loops with molecular dynamics (MD) simulation studies (24,61–63). Obviously, the basic topology of PHs remains preserved in simulations of complete cation-stabilized GQs on μs timescale. This is, however, not surprising considering the overall structural stability of complete cation-stabilized GQs in MD simulations (24). Still, the simulations do not reproduce specific experimental conformations of DNA propeller loops (61–63). On contrary, PHs (containing TTA/UUA as well as single-nucleotide propeller loop) are exceptionally structurally unstable when simulating any type of on-pathway GQ folding intermediates, namely G-hairpins, G-triplexes as well as cation-deficient folded GQs (24,36,38,64). Loss of propeller loops typically initiates fast unfolding in denaturing no-salt simulations of GQs and in simulations of G-triplexes and isolated PHs. The propeller loops thus represent the least stable (the most brittle) regions of the simulated structures. There is no sign of even a transient formation of the PHs in enhanced sampling folding simulations of DNA G-hairpins, while antiparallel hairpins supporting diagonal and lateral loops form readily (36). The simulation instability of PHs with propeller loops is counter-intuitive considering their common occurrence in experimental GQ structures.

It has been suggested that the MD results could be affected by some propeller-loop-specific (though yet unidentified) imbalance in the simulation force field. However, it is unlikely to fully explain the MD simulation behavior (24). It thus leads to a genuine question: what is the source of stabilization of the PHs and, mainly, at which stage of the GQ folding process do the propeller loops emerge (24)? This issue is especially perplexing for the parallel GQs, which contain only propeller loops (Figure 1). In other words, how can one understand folding mechanism of parallel-stranded GQs, both DNA and RNA, when none of the on-pathway folding intermediates with propeller loops considered so far is stable? Perhaps, in case of parallel DNA GQs, they could be formed by a series of rare spontaneous transitions from other types of GQ folds while avoiding to move through a fully unfolded ensemble. However, this explanation is not straightforwardly applicable to RNA GQs since, as noted above, non-parallel GQs do not seem to be substantially populated on the RNA GQ folding landscape and the final fold must emerge directly from the unfolded ensemble.

In this work, we report a series of extended MD simulations based on RNA TERRA parallel-stranded GQs with the aim to better understand the folding of propeller loops. We have chosen a system with three stacked quartets, which is by far the most common motif found in parallel GQ structures. Conventional MD simulations are used to study structural dynamics of propeller loops in GQ structures obtained by either NMR or X-ray experiments. We study the UUA propeller loops in different contexts, namely a stacked dimer of two bimolecular GQs, isolated bimolecular GQ, and isolated PH, i.e., a single RNA chain containing half of the GQ structure (Figure 1). Standard simulations of RNA GQs complement earlier studies on propeller loops of the human telomeric DNA GQ (62,63) and characterize structural dynamics of the RNA propeller loops when being attached to a stable GQ stem. Then, we analyze the folding landscape of the rGGGUUAGGG single strand by enhanced sampling Hamiltonian replica exchange (REST2) (65) simulations initiated from folded PH as well as unfolded states. We identify mechanism of unfolding and folding of the PH and show that the PH is linked with the unfolded state via an intermediate ensemble of cross-like structures (CS), similar to those that have been suggested to occur in early stages of formation of tetramolecular parallel DNA GQs (66). A similar result is obtained also for the rGGGAGGG sequence. We suggest that although isolated PHs are not stable per se, they can form during the folding of GQs via conformational diffusion processes through antiparallel hairpin-like structures and the CS ensemble. Based on the simulation results we propose a hypothetical folding landscape for folding of RNA GQs.

MATERIALS AND METHODS

Studied TERRA structures

The simulations are based on three experimental structures of telomeric repeat-containing RNA (TERRA): 2M18 (20) (first structure of the NMR ensemble is considered), 3IBK (14), and 2KBP (27) (first structure of the NMR ensemble).

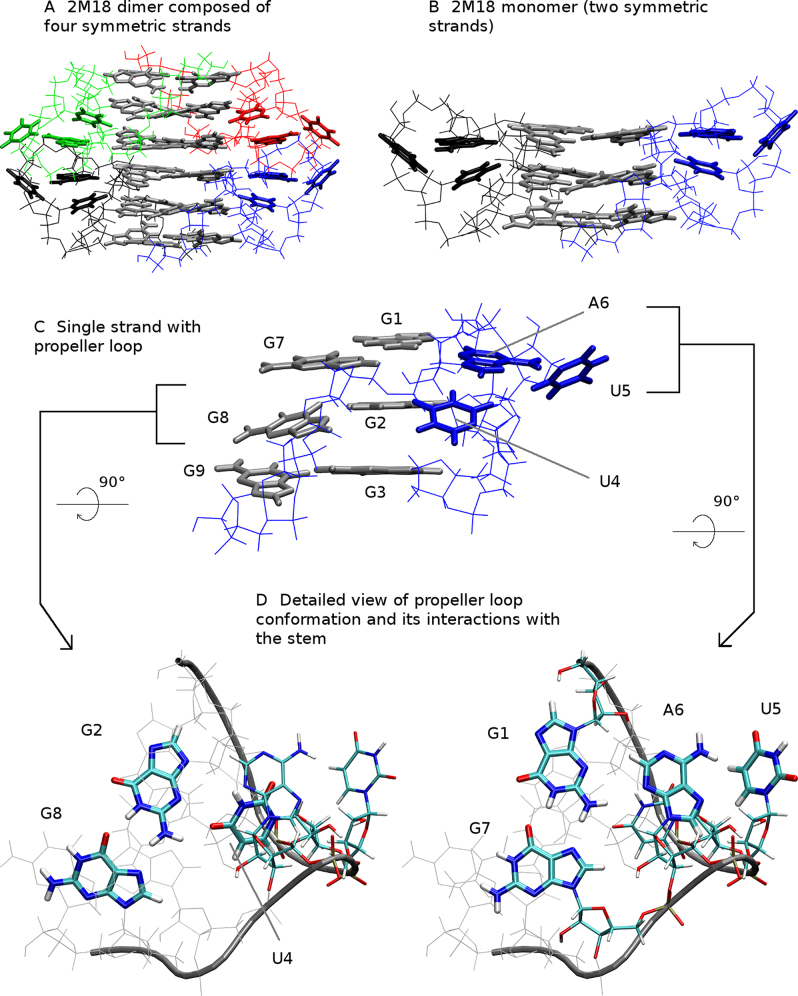
2M18 is an NMR structure of bimolecular RNA GQ with sequence [rGGGUUAGGGU]₂ (referred to as GQ monomer in this work). Two such GQs stack on each other forming a dimer composed of two complete GQs (i.e. four RNA strands), which is stabilized by head-to-head stacking of 5′ guanine quartets and adenines incident to propeller loops (Figure 2A) (12,20). The adenine stacking stabilizes specific geometry of the propeller loops that has not been observed in other TERRA structures (12,14,67). The adenines lie in the plane of the 5′ quartet and specifically interact with sugar edge of adjacent guanine. One of the uracils resides in plane of the middle quartet, stacks with the mentioned adenine and forms a hydrogen bond with G2 (Figure 2C). Described arrangement of propeller UUA loops is unambiguously supported by experimental NOEs and the whole NMR ensemble is representing the same compact fold. All four strands forming the GQ dimer are identical due to symmetry restraints (20).

Figure 2.

Solution structure of TERRA RNA GQ. (A) Dimer is composed of four symmetric rGGGUUAGGGU strands (chains)—blue, red, green and black, respectively, guanines of quartets are gray; (B) structure of bimolecular 2M18 GQ containing two propeller loops; (C) single strand of 2M18 (PH) with nucleobases of the UUA propeller loop in blue; (D) detailed view of the propeller loop conformation with numbering of nucleotides. Note that terminal (flanking) uracils were removed from all simulated structures.

3IBK (14) is a 2.2 Å resolution X-ray structure of a stacked GQ dimer composed of two crystallographically identical bimolecular GQs. Each bimolecular GQ [rUAGGGUUAGGGU]₂ contains overhanging regions at both 5′ and 3′ end of each RNA strand. The 5′UA overhangs enable dimerization of the two bimolecular GQs via formation of two UAUA quartets sandwiched between guanine quartets of neighboring GQs. Each bimolecular GQ contains two UUA propeller loops, one of which participates in crystal packing and interacts with overhanging U3′ from the adjacent crystal cell, while the other seems unaffected by the crystal packing, resulting in two different conformations of the UUA propeller loop. However, the latter propeller loop has very low electron density indicating high conformational freedom.

2KBP is an NMR structure of a bimolecular GQ [rUAGGGUUAGGGU]₂ (27). The NMR ensemble contains 10 structures. The flanking and loop bases adopt variety of positions in the ensemble. All four terminal uracils are usually stacked on the terminal quartets at their respective ends. Both flanking adenines at the 5′ end can form a trans-sugar-edge base pair with guanines in the first quartet. The bases in the loop seem flexible, they aim away from the G-stem towards bulk solvent and they neither stack nor do they form a base pair in any of the NMR models. The loop conformation does not appear to be unambiguously determined by the primary ensemble-averaged NMR data and it is possible that this loop is in reality flexible.

Simulated TERRA-based systems

We simulated diverse systems containing the UUA propeller loop. Based on the 2M18 PDB file we built: (i) dimer of two bimolecular GQs, (ii) isolated bimolecular GQ (GQ monomer) and (iii) a parallel G-hairpin (i.e. PH), as specified in Table 1.

Table 1.

List of simulations^a

	Simulated system	Abbreviation	Run length (μs)	No. of equivalent runsb	Cumulative time (μs)	No. of strands	Ions
1	2M18 dimer	2M18-D	10	3	30	4	NaCl
2	2M18 monomer	2M18-M	10	6	60	2	NaCl
3	2M18 hairpin	2M18-H	1	8	8	1	NaCl
4	3IBK monomer	3IBK-M	5–10	6	50	2	NaCl or KCl
5	3IBK hairpin A	3IBK-HA	1	18	18	1	NaCl or KCl
6	3IBK hairpin B	3IBK-HB	1	18	18	1	NaCl or KCl
7	2KBP monomer	2KBP-M	5	6	30	2	NaCl
8	3IBK REST2 hairpin A	3IBK-HA_REST	10	12	120	1	KCl
9	3IBK REST2 unfolded	3IBK-UF_REST	10	12	120	1	KCl
10	rGGGAGGG REST2 unfolded	GGGAGGG_UF_REST	10	12	120	1	KCl
11–26c	r1KF1	Set SPC/E	5	4	20	1	KCl
	r143D	Set SPC/E no-salt	1	4	4		–
	r2GKU	Set TIP3P	5	4	20		KCl
	r2MBJ	Set TIP3P no-salt	1	4	4		–

^aFor more detailed description of the simulation conditions see Supplementary Table S1.

^bFor rows 8, 9 and 10 the value represents number of replicas.

^cEach of the four listed systems was simulated in all conditions described in these four rows giving together 16 simulations with cumulative time of 48 μs.

As a starting structure for simulations of the GQ dimer we took the 2M18 (20) structure without the overhanging uracils (Figure 2A). While overhanging nucleotides could be important for structural experiments, they may complicate (and are not necessary for) GQ MD simulations, unless the simulations are specifically investigating their interactions (63,68). The NMR experiment does not provide any information on the bound monovalent ions (20). However, monovalent ions play fundamental role in formation and stabilization of GQs in experiments (69–72) as well as for structural stability of GQs in MD simulations (24,35,68,73–77). Therefore, we added monovalent ions to their expected positions in the channel of the GQ structure, including the cavity between the two stacked GQs. The resulting starting structure is abbreviated as 2M18-D.

Two of the four symmetric strands (chains) of the 2M18 system form one complete GQ and were taken as a starting structure for GQ monomer (Figure 2B; abbreviated 2M18-M). Technically, we prepared such structure from the starting structure of the dimer by removing other chains and ions, while preserving channel ions. Similarly, we took single RNA strand from the 2M18 structure as a starting structure of PH (Figure 2C; abbreviated 2M18-H).

Analogically, we prepared several structures based on the 3IBK structure. Since propeller loops of the two GQs present in the unique crystal cell do not interact with each other, we skipped simulation of the dimer. Two crystallographically different rGGGUUAGGG strands forming a GQ were taken as a starting structure of 3IBK monomer while deleting the overhanging nucleotides (this structure is abbreviated as 3IBK-M). The ions present in the X-ray structure were preserved. Further, two rGGGUUAGGG strands with distinct conformations of the propeller loop were taken as starting structures of PHs. First PH is based on residues 3–11 of chain A (3IBK-HA) while the second is based on residues 15–23 of chain B (3IBK-HB).

2KBP was treated similarly. We took the first NMR model and again removed the flanking bases and simulated the remaining GQ composed of two rGGGUUAGGG strands (abbreviated as 2KBP-M). Two ions were placed inside the GQ channel.

Finally, we prepared unfolded rGGGUUAGGG and rGGGAGGG strands as starting structures for simulations attempting to capture folding of a propeller loop. Nucleic Acid Builder package (78) of AmberTools14 (79) was employed to build initial structure as one strand of an A-form duplex.

Simulated hypothetical RNA GQs with antiparallel strands

To inspect behavior of RNA GQs with continuous antiparallel strands (i.e. with syn guanosines), we have built up such structures from known DNA GQs by in silico DNA → RNA mutation, which is a simple conversion of the sugar moieties to riboses and thymines to uracils. Starting coordinates for DNA → RNA mutants were taken from the human telomeric DNA GQs (Supplementary Figure S1). We have chosen the (2+2) antiparallel basket-type topology (PDB ID: 143D) (3), the (3+1) hybrid type-1 topology (PDB ID: 2GKU) (80) and the (2+2) antiparallel topology with one propeller loop (PDB ID: 2MBJ) (19). For a reference simulation we have taken the parallel stranded topology (PDB ID: 1KF1) (5) which is a topological equivalent of the intramolecular TERRA GQ.

Plain MD simulation protocol

Explicit-solvent MD simulations were performed using AMBER16 software package (81). The xLEaP and parmed.py modules of AMBER16 (81) were used to prepare starting topologies and coordinate files. The ff99bsc0χ_OL3 force field was utilized in all simulations (82–85). This is a default RNA force field in the recent AMBER biomolecular force-field portfolios. Starting structures were immersed in truncated octahedral box of SPC/E (86) explicit water molecules and ions were added to obtain 0.2M excess salt concentration. Three different ion models were used (Supplementary Table S1): (i) Joung and Cheatham NaCl (87); (ii) Joung and Cheatham KCl (87); (iii) AMBER adapted Aqvist Na⁺ with Smith and Dang Cl⁻ (88,89). However, no systematic effect of specific ion condition was observed in our simulations, consistently with preceding GQ benchmarks. For discussion of ions in MD simulations of GQs see Havrila et al. (68) and Rebic et al. (73). Since the ionic conditions did not have any significant influence on the GQ properties studied in this work, we do not differentiate simulations according to ionic conditions in further text and consider simulations with all sets of ion parameters as equivalent.

DNA → RNA mutants were solvated either in TIP3P (90) or SPC/E (86) water model and KCl (Joung and Cheatham parameters (87)) was added to get 0.15M excess salt concentration with exception of no-salt simulations where ions were not added. No-salt simulation is a common tool to initiate unfolding of GQs that can be used to probe parts of the folding landscape of GQs in the vicinity of the native folds, as justified elsewhere (24,35,64).

Prepared systems were minimized, heated and equilibrated in several steps before each MD run (Supplementary Table S2). The velocities of atoms were randomized in the first equilibration run to get independent starting structures for simulations with otherwise identical properties. Hydrogen mass repartitioning (91) was applied together with the SHAKE algorithm (92) to allow for the 4 fs integration time step. Simulations were performed using particle mesh Ewald method (93,94). For further details of the simulation setup see the Supplementary Information.

Replica exchange simulation protocol

The system 3IBK-HA was used as the starting structure in all replicas of REST2 (65) simulation initiated from the folded state. The other REST2 simulations started with either the rGGGUUAGGG or rGGGAGGG strand in all replicas in the unfolded state. Starting topology and coordinates were prepared using the tLEaP module of AMBER14 (79) program package. The starting structures were solvated using a rectangular box of OPC (95) water molecules with a minimum distance between box walls and solute of 10 Å. The simulations were executed with 0.15M KCl excess salt using the appropriate Joung-Cheatham ion parameters (87). Each REST2 simulation was performed with 12 replicas. The scaling factor (λ) values ranging from 1 to 0.6583 were chosen to maintain exchange rate ∼25%. The effective solute temperature thus ranged from 300 to ∼455.7 K. Exchanges were attempted every 10 ps. The lengths of all REST2 simulations were 10 μs per replica. The cumulative time of all REST2 simulations was thus 360 μs.

The REST2 simulations were done with the basic ff99bsc0χ_OL3 (82–85) RNA force field further modified to facilitate folding of the PH. We used Van der Walls modification of phosphate oxygen developed by Case et al. for phosphorylated amino acids (96). This has been accompanied by an appropriate adjustment of torsion parameters affected by the altered 1–4 Lennard–Jones interactions due to VdW modification; AMBER library file of this force-field version can be found in Supporting Information of Kuhrova et al. (97). Most importantly, the REST2 simulations were executed with additional HBfix potential function (see Kuhrova et al. (97)) to selectively increase stability of the six hydrogen bonds of the GG base pairs of the RNA PH. HBfix is a gentle structure-specific bias of the force field that does not directly promote forward folding (k_on) but increases the lifetime of the H-bonds once formed. HBfix was applied to heavy-atom distances of all native hydrogen bonds of cWH GG base pairing to increase the stability of the PH. Each native hydrogen bond was supported by 1.0 kcal/mol if the interatomic distance was shorter than 3 Å, from 3 to 4 Å the supporting energy was gradually diminishing, and there was no support if the distance was longer than 4 Å, similarly to the earlier works using the HBfix (97,98). The HBfix potential aims to compensate the suspected underestimation of the base pairing interaction caused by lack of polarization effects in AMBER force field (97,99,100).

The use of the OPC water model, modified phosphate parameters and mainly the use of HBfix in our REST2 simulations is based on prior experience with folding of the base-paired stems of RNA tetraloops; for more details see refs. (97,98,101). The aim is to shift the equilibrium populations in favor of the folded PH compared to the unmodified force field and facilitate investigation of the folding process.

Comment on the interpretation of the REST2 results

The goal of the REST2 simulations was to find plausible atomistic pathway of folding and unfolding of PHs. The REST2 procedure belongs to the class of ‘annealing’ enhanced sampling methods (101). These are very computer demanding methods that are based on the principle that a system kept at a higher (artificial) temperature can more easily cross energy (enthalpy) barriers and is thus better able to explore its conformational space than a system at low (experimental) temperature. The most widely used method of this class is parallel tempering, known also as temperature replica exchange MD (T-REMD). In T-REMD, a set of simulations (replicas) at different temperatures are performed in parallel, and exchanges among the replicas allow free-energy barriers to be crossed by coupling the cold replicas with the more ergodic hot ones, i.e. the simulated copies of the molecules travel through the replica (temperature) ladder up and down to make substantial conformational changes at the higher replicas and to model the target free-energy landscape at the lowest replica. The exchanges are performed by Metropolis algorithm that guarantees conservation of the Boltzmann canonical ensemble corresponding to the particular temperature at each replica. Thus all temperature replicas cooperate in reaching the convergence but do not statistically bias each other. In other words, a given (unbiased, reference) replica in the temperature ladder (typically one of the lowest temperature replicas) is used for a primary collection of the data while the other replicas are used to accelerate transitions between different parts of the free-energy landscape. The REST2 method is achieving the same ‘temperature effect’ as T-REMD via the scaling of the Hamiltonian, or its part.

A converged REST2 simulation would provide a converged and unbiased equilibrium population of all states at the reference replica with the unscaled (unbiased) Hamiltonian. We note, however, that the available computer resources are not sufficient to obtain a fully converged free-energy landscape for the presently studied system. However, the simulations should be robust enough to depict typical PH folding events. Besides analysis of the unbiased reference replica, to assess the convergence it is also useful to monitor developments in the other replicas in the ladder as well as to follow so-called demultiplexed replicas, i.e. continuous trajectories of the individual copies of the molecule as they travel across the replica (Hamiltonian or temperature) ladder. All these analyses are done in this study. Note also that while converged REST2 simulations would provide unbiased thermodynamics populations of different conformations they cannot easily provide kinetic information due to discontinuities introduced by the movements of the continuous trajectories through the replica ladder. So, while our REST2 simulations should correctly capture the atomistic structural pathway between the unfolded and PH states of the studied hairpins (within the limitations imposed by the simulation force field) the timescale of the folding events should not be inferred from our data.

A fundamentally different class of enhanced-sampling methods often used in studies of GQs is based on biasing populations of the simulation ensemble (based on the importance sampling principle) and is represented by techniques such as metadynamics, umbrella sampling, steered and targeted MD, etc. (101). All these methods require introduction of so-called collective variables (CVs), predefined ‘reaction-coordinate’ type of collective degrees of freedom along which some biasing potentials or forces are acting. The CV-based methods are less computer-demanding but the choice of CVs has a decisive effect on the results. It introduces prior low-dimensionality chemical information about the shape of the free-energy landscape. This can be a very serious problem when simulating processes which are intrinsically high-dimensional. Because no such prior information is used in our REST2 computations, the PH folding pathway reported in this work is not affected by any such biasing CVs. This is the reason why we decided to avoid using CV-based methods for the presently studied problem (24); for a general overview of enhanced-sampling methods applicable to nucleic acids and written for non-specialists see ref. (101).

Data analyses

We have used several metrics to monitor the simulations, namely coordinate RMSD, ϵRMSD and number of selected H-bonds. RMSD is a commonly used metrics for measurement of deviation of a given structure from a reference structure. It takes into account positions of individual atoms, and thus it is a good metrics for monitoring deviation of structures from a reference structure with precisely defined atomic coordinates. A more advanced nucleic-acids-specific structural metrics known as ϵRMSD compares mutual relative positions of whole bases and, unlike RMSD, is very sensitive to changes in base stacking and H-bonding interactions (102). On the other hand, ϵRMSD is not efficient to monitor conformational developments that are not associated with changes of structurally well-defined interactions of bases such as stacking and H-bonding. Therefore ϵRMSD is useful when base-base interactions in the reference structure and their difference from other states are of more interest than exact atomic coordinates. Number of selected H-bonds is a measure monitoring differences in base-pairing from a reference structure. It is an alternative for ϵRMSD.

In our analyses, we used RMSD to monitor conformational changes with respect to the native state or starting structure in simulations of full GQs. In addition, for clustering of 2M18-D, 2M18-M, 3IBK-M and 2KBP-M simulations and search for the native loop conformations, we monitored RMSD of the loop with trajectory fitted to the G-stem (see clustering below). Standard simulations of PHs were clustered by RMSD of the guanosines only. DNA → RNA mutants were monitored by measuring RMSD of the G-stem and of the individual G-quartets.

On the other hand, dynamics and mutual positions of the two G-strands were of main interest in standard and REST2 simulations of PHs and unfolded rGGGUUAGGG and rGGGAGGG strands. Therefore, for these systems, we used two complementary analyses, namely ϵRMSD (considering guanines only, excluding the loop nucleotides) and monitoring of the number of native GG H-bonds. ϵRMSD was calculated against the native PH structure taken from the 3IBK GQ structure and against some other selected conformations, which we identified as structures representative for possible PH (un)folding intermediates in the course of our simulations. The threshold for considering a structure to be similar to the PH was the ϵRMSD value of 0.8 Å. This value was chosen based on mutual cross-comparison of several structures (Supplementary Table S3) and analysis of the ϵRMSD fluctuations of an intact PH within the simulated 3IBK-M GQ (Supplementary Figure S2). This threshold was also adopted for comparison of a given structure to any other reference state of interest. If a given snapshot simultaneously satisfied the threshold criterion for the native state and any other state, the structure was considered as part of the native structure ensemble. We also performed analyses by counting native H-bonds. We measured how many of the six native hydrogen bonds of the native PH were present in the course of the simulations. A native H-bond was considered present if the corresponding nitrogen/oxygen to hydrogen distance was shorter than 3 Å. If all the six native H-bonds were present simultaneously, the snapshot was counted as part of the native state ensemble. If the structure was not native, but four native H-bonds were present in the middle GG base pair plus either the top or bottom GG base pair, the structure was considered partially folded. Obviously, any criteria to detect an H-bond are arbitrary and we have chosen a very generous threshold. This has been because of the large fluctuations in the monitored structural states. It should be noted that each metrics has its own advantages and disadvantages so that we have applied and combined them as optimal for particular purposes. Importantly, we have carefully analyzed all important events by visual monitoring of the trajectories.

Clustering

Conformations explored by propeller loops in standard MD simulations of full GQs were analyzed by clustering. Trajectories obtained from equivalent runs (including different ionic conditions) of a given system were clustered together and, moreover, symmetric chains were also clustered together. For example, all four loops of 2M18-D systems were clustered together over three performed simulations to give us a single output for population analyses. This approach is justified if the studied system populates similar conformations across all symmetric sites and available simulations. First, whole PHs (i.e. the sequence GGGUUAGGG) taken from all simulations of a given system were taken and best-fitted to the G-stem according to RMSD, not considering the UUA loop. Then, the conformations of the UUA nucleotides were clustered based on their own RMSD, without any further fitting. Such a procedure removes movements of the G-stem, but takes into account roto-translational movements of the loop with respect to the G-stem. The clustering was performed by the cpptraj module of Amber 16 (81,103) using the average linkage agglomerative algorithm. The sieve value was set to 200 (i.e. frames taken every 200th ns were considered in initial clustering pass). The parameter ϵ was set to 4.5 Å after testing several values between 2.1 and 5 Å.

We also performed independent clustering of the standard simulations of PHs. These were fitted to the G-stem and clustered based on RMSD of only the nucleotides G1, G2, G3, G7, G8, and G9, (i.e. excluding the loops of PHs). In this case, the parameter ϵ was set to 2.1 Å. The choice of ϵ value is always a trade-off and depends on many factors like size and dynamics of the considered system. Too low value would result in huge amount of clusters and would split some conformations into multiple clusters, while too large ϵ would merge different conformations to a single cluster. We found ϵ equal to 4.5 or 2.1 Å most convenient for our purposes, i.e. to quite unambiguously separate different conformations while keeping number of clusters as low as possible. Obviously, any clustering is necessarily affected by some degree of uncertainty due to choice of metrics, clustering method and its parameters.

RESULTS AND DISCUSSION

Propeller loops are able to sample the experimental structure in simulations of the 2M18 dimer

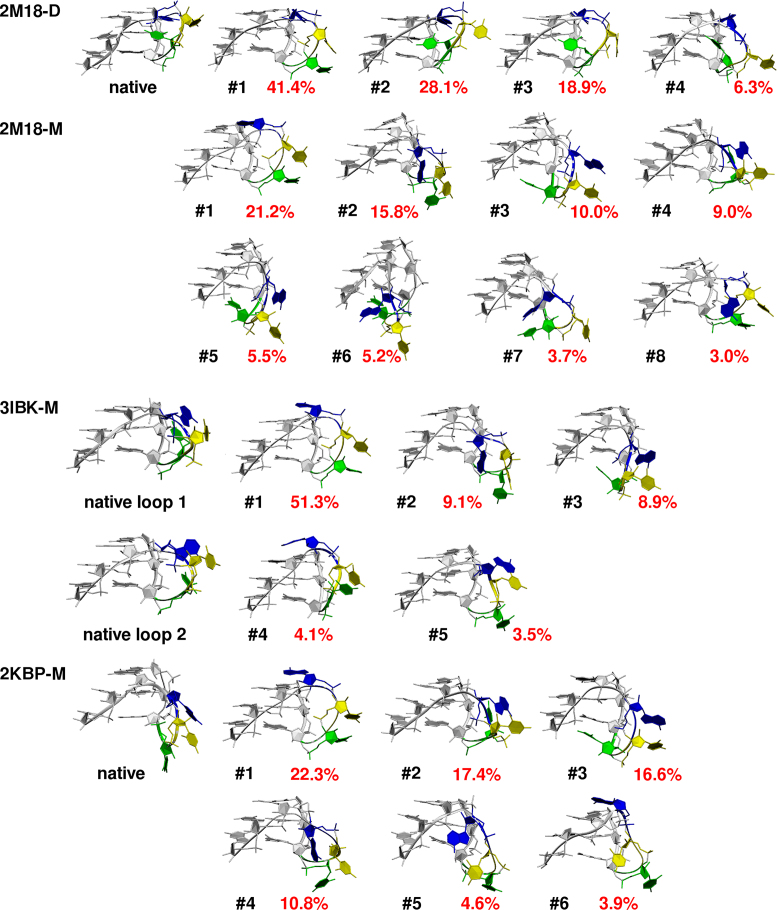
The 2M18 dimer (Figure 2A) was structurally stable in all three simulations (Table 1) and the two interacting GQs remained stacked. All guanine quartets kept their shape and thus also cores of both GQs (i.e., the G-stems) stayed stable. The propeller loops lost their initial geometry in the course of the simulations and sampled several conformations (Figures 3, 4 and Supplementary Figure S3A). We clustered the loop coordinates over all loops and all simulations of the dimer. The clustering revealed four major conformations, with populations of about 41%, 28%, 19%, and 6%, respectively. All four clusters feature A6 in the same position as the native structure, stacked with the A6 of the neighboring GQ unit. The clusters differ in position of U4 and U5. The most populated cluster has both of them pointing towards the solvent, away from the G-stem, while the remaining three have U4 in the GQ groove, pointing towards the G-stem, like in the native structure. It can be envisioned that these three clusters, with a total population of 53%, are similar to the native conformation. Essential similarity of several clusters can easily occur when one or more residues are solvent-exposed and sample a broad conformational space. Cluster #3 contains conformations most similar to the native structure (Figure 3, Supplementary Figure S4). 4.8% of conformations observed in the 2M18-D simulations have RMSD less than 2.0 Å and 10.0% less than 2.8 Å. However, we have to admit that the clusters #2, #3 and #4, which are similar to the native structure, are sampled predominantly in the first half of the simulations, while the cluster #1 is getting more and more populated as time passes (Supplementary Figure S3A). The simulations are thus not fully converged and the cluster populations would further evolve with prolongation of trajectories. It should also be taken into account that clustering procedures for GQ loops are always somewhat ambiguous (63). We have tried several different clustering attempts which, although differing in the cluster distributions, provided a similar aggregate picture of the dynamics.

Figure 3.

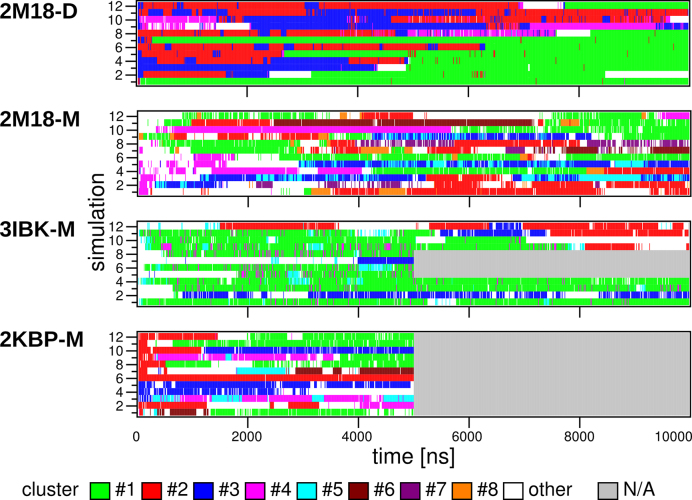
Occupation of propeller loop clusters with more than 3% population in MD simulations of 2M18-D, 2M18-M, 3IBK-M and 2KBP-M systems. The cluster numbers correspond to structures shown in Figure 4, so that clusters with the same number in different systems do not correspond to each other, though all the monomer MD simulations show similar dynamics (see the text). ‘N/A’ means not simulated. The simulations under different ionic conditions are considered equivalent. Each loop of a given system is considered a separate simulation trajectory and occupies one row (e.g. 2M18-D contains four propeller loops, and thus each 2M18-D simulation shows four propeller loop trajectories on four rows); the simulation number (y-axis) is thus only a counting guide. Average cluster populations across the simulations along time are shown in Supplementary Figure S3.

Figure 4.

Experimental structures of UUA propeller loops and centroids of clusters with more than 3% population in MD simulations of 2M18-D, 2M18-M, 3IBK-M and 2KBP-M systems. Only the loop and two adjacent G₃ stretches are shown. First uracil of the loop is green, second uracil yellow and adenine is blue. The black number shows cluster number and the red number is the cluster population. See also Figure 3 and Supplementary Figure S3 for cluster development in the course of the simulations.

In summary, the simulations of the TERRA GQ dimer reveal a rich conformational dynamics of the UUA propeller loops with geometries interconverting on the μs time scale. This is consistent with the preceding benchmark simulation study of analogous TTA DNA GQ propeller loops (63). The propeller loops have some capability to sample the structure suggested by the NMR experiment. Nevertheless, due to the genuine uncertainty of the NMR data for determination of backbone geometries of GQ loops and the expected imperfect performance of the force field (63), we did not pursue a more quantitative analysis.

Irreversible loss of experimental loop conformation was observed in 2M18 monomer simulations

All MD simulations of isolated 2M18-M GQ revealed entirely stable behavior of the G-stem, as expected (24). However, the propeller loops missing their dimer stacking partners lost the experimental conformation in the first nanoseconds of simulations and never recovered it. The subsequent rich dynamics of propeller loops is reflected by clustering analysis, which shows more diverse clusters with smaller populations in comparison to the 2M18-D system with the same clustering setup (Figures 3, 4 and Supplementary Figure S3B). Moreover, the conformations sampled by loops of the GQ monomer differ from the main clusters sampled in simulations of the GQ dimer. Only the largest cluster with a population of 21% is somewhat similar to the largest cluster from simulations of the dimer (Figure 4). The uracils are stacked in the solvent, however, unlike in simulations of the dimer, the adenine is stacked on the top of the 5′-end guanine quartet instead of the edge to edge interaction present in the GQ dimer.

Dynamic ensemble of structures is observed as the experimental conformations are lost also in 3IBK and 2KBP simulations

The simulations of the 3IBK-M GQ also revealed entirely stable behavior of the G-stem. Although the X-ray structure shows two different conformations of the UUA loop (see above), they behave identically (within the limits of the sampling) in simulations. Similarly to the 2M18-M simulations, all 3IBK-M propeller loops quickly lost their experimental structure and showed rich dynamics. Dominant structure with a population of 51% had A6 stacked on the top of the 5′-end guanine quartet with U4 and U5 oriented into bulk solvent, which resembles the dominant cluster of 2M18-M simulations (Figures 3, 4, and Supplementary Figure S3C). In fact, both propeller loops of 3IBK-M sampled geometries similar to those observed in 2M18-M simulations, albeit with different populations (Figure 4).

The GQ stem was stable also in all 2KBP-M simulations. The propeller loops show rich conformational dynamics (Figures 3, 4 and Supplementary Figure S3D). As for the previous systems, the starting loop conformation is lost in all simulations and the dominant cluster (22%) features A6 stacked on the top of the 5′-end guanine quartet and U4 and U5 pointing into bulk solvent (Figure 4). The other clusters are also similar to those found in 2M18-M and 3IBK-M simulations. It is important to note that the 2KBP NMR ensemble suggests that the loop structure is not perfectly captured by a single conformation. The experimental data for the 2KBP loop region consist of many NOEs between all three loop nucleotides and guanosine preceding the loop, however, the NOEs are mostly weak and correspond to ensemble-averaged distances of ∼7.5 Å. This may suggest that the loop structure is actually dynamic and the resulting NOEs are averaged over an ensemble of several conformations.

Overall assessment of propeller loop dynamics in simulations of complete GQs

The similarity of clusters found in simulations starting from different GQ monomer structures (Figure 4) indicates negligible influence of starting conformation on dynamics of the loops in later stages of simulations; note that 2M18-M, 3IBK-M and 2KBP-M systems have the same sequence and the overall fold. Thereby, none of the experimental loop conformations investigated in this study was stable in MD simulations and choice of the starting conformation of propeller loop did not determine its development in simulations. It implies that potential inaccuracies in starting structures should not cause any problems in MD description of the propeller loops once the simulations are extended to multiple μs. Interestingly, conformations observed in TTA propeller loops in parallel stranded human telomeric DNA GQ feature several similar clusters (cf. Figure 3 in (63)). We suggest that it is the presence of tertiary contacts between the loops and neighboring molecules that shapes up the propeller loops in experimental structures and that the loops can exist as a dynamic ensemble of structures in absence of these stabilizing interactions. Such behavior would be in agreement with higher structural stability of propeller loops in simulations of 2M18-D. This suggestion is supported also by the 3IBK X-ray structure, where the loop interacting with the neighboring molecule is nicely refined, while the second loop is not clearly differentiated in electron density map and its structure has been partly modelled (14). However, we cannot rule out force-field inaccuracy as another source of instability of the experimental conformations, especially in view of the earlier simulations of the DNA TTA propeller loops (63). Unfortunately, we lack unambiguous experimental data about the conformation of the RNA UUA propeller loop in absence of any additional interactions. Thus, we presently cannot make a more quantitative assessment of the accuracy of the propeller loop MD description. Note nevertheless that the 3IBK chain A propeller loop shows a γ-trans value of the backbone of the first uracil, which also is a characteristic feature of the most common conformation of the propeller TTA loops in human telomeric DNA GQs X-ray structures (63,104). These γ-trans conformations are eliminated (84) by the current AMBER force fields since they are tuned to suppress undesired γ-trans states in canonical helices (105); the γ-trans conformation in the propeller loop in 3IBK is no exception.

Unfolding of parallel G-hairpin with propeller loop in plain MD simulations

In order to capture the unfolding mechanism of RNA propeller loops, we have carried out a series of 44 independent 1μs long standard simulations of rGGGUUAGGG starting from folded PH structures dissected from the complete GQs (Figures 1 and 2C, see also Table 1 and Supplementary Table S1). In these simulations, the GQ core is not present, and we are only considering two adjacent parallel G₃ stretches connected by the UUA propeller loop.

The PH unfolded in very early stages of all simulations (Supplementary Figure S5). After the initial unfolding, the single strand displayed very rich dynamics, sampling a wide spectrum of structures including stacked A-form-like helical arrangements, different types of ‘non-native’ mostly antiparallel-like hairpins and many coil-like arrangements with diverse internal structures that were not further analyzed. Observed dynamics was enriched by spontaneous anti/syn fluctuations (Supplementary Figure S6). Similar broad dynamics was observed for DNA G-hairpin with equivalent sequence (36).

The basic outcome of these simulations is the exceptional instability of isolated PH, with a life-time around 1 ns. More importantly, detailed visual analysis of all performed PH simulations allowed us to depict a general mechanism of unfolding of the RNA PH which includes three consecutively sampled states: (i) there is a folded PH at the start; (ii) it transforms to an ensemble of Cross-like Structures (CS—see below) within 0–5 ns; (iii) the CS is lost. Lifetime of the CS ensemble is typically from ones to tens of ns. Its loss is a diverse/multiple-pathway process followed by the above-described large-scale and variable dynamics of the unfolded ensemble.

Spontaneous attempts to fold PH in plain MD occur via the CS ensemble

A complete refolding of PH was never observed in plain (standard) MD simulations after the initial unfolding, although several transient visits of the PH state have been observed in the initial parts of the trajectories (Supplementary Figure S5). In addition and more frequently, transient formation of CS was observed in first halves of a few of the 44 standard MD simulations, which we consider as refolding attempts (Supplementary Figure S5). All the visits of the PH state occurred from the CS ensemble.

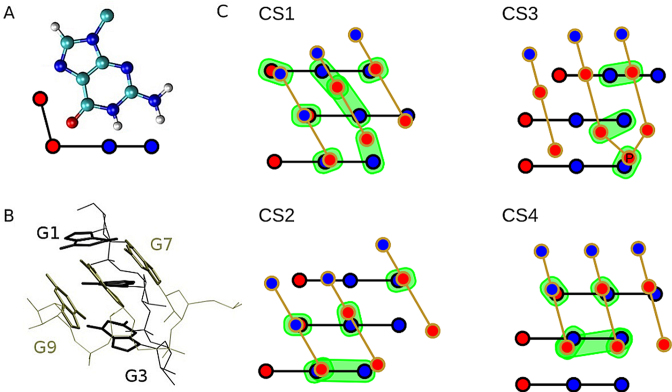
The CS ensemble can be described as an ensemble of conformations with two RNA G-strands rotated in such a way that they adopt tilted or even perpendicular position (Figure 5). Similar structures have been suggested to play a major role in early stages of formation of tetramolecular parallel-stranded DNA GQ (66). In the CS, the guanines in both G-strands remain neatly stacked while a network of H-bonds between the strands is formed. Guanines in a folded GQ always interact by cWH interaction between two adjacent in-plane guanines. However, rotation of strands in CS allows one base of the rotated strand to interact with two or three bases from the opposite strand (Figure 5). This leads to a network of hydrogen bonds, which can dynamically sample several H-bond patterns. Thus, CS forms a rather broad ensemble of similar conformations (Figure 5). Except visual identification of CSs, we detected the CS ensemble also in the course of the clustering analysis. Very low populations of CSs (due to the quick transition to the unfolded ensemble) do not allow us to provide any reliable quantitative analyses of the CS ensemble, however, we were able to pick up four different members of this ensemble (centroids of four largest clusters representing CSs; denoted CS1, CS2, CS3 and CS4; Figure 5C) for further analysis. These four CS clusters belong to some of the smaller clusters found during the overall clustering of the 44 standard unfolding simulations of the PHs (see clustering part of Methods) and they have been unambiguously identified by detailed structural inspection of all obtained centroids; they all exhibit the required interactions between the G-strands. Obviously, quantification of sampling and structures belonging to the CS ensemble is definition-dependent, i.e. the results to certain extent depend on subjective decisions, used metrics, etc. This is because of the enormous amount of data in the raw simulation trajectories, which needs to be converted into human-comprehensible information, requiring filtering and simplification of the full simulation information. Nevertheless, the essence of the PH unfolding and refolding process going through the CS ensemble should be unambiguously captured by our analyses.

Figure 5.

3D and schematic representations of selected members of the CS ensemble. (A) guanine with its hydrogen bond donor (blue) and acceptor (red) groups highlighted in a simplified scheme; (B) 3D structure of the dominant CS variant CS1; (C) schematic representation of variants CS1–CS4 of CSs; blue/red circles represent H-bond donor/acceptor groups; interacting pairs are in green background; the inclined G7–G9 strand is in front. The scheme is not a projection of 3D structure onto the plane, i.e. it is rather a sketch than an attempt to precisely describe the 3D structures. PDB files with atomic coordinates of CS1–CS4 are available as Supplementary files.

In the CS ensemble, guanines G1–G3 always employ their Watson–Crick (WC) edge while rotated guanines G7–G9 employ either WC or Hoogsteen (H) edge (in the native GQ G1–G3 use their WC edge to bind with the H edge of G7–G9). We suggest that the CS ensemble is a key basin on the folding landscape of the rGGGUUAGGG that connects the PH with the unfolded ensemble, i.e. the unfolding—folding process can be described as PH structure ↔ CS ensemble ↔ unfolded ensemble. Compared to the fully folded PH with a single well-defined conformation (except of the loop plasticity), the CS should be entropically more favorable.

It should be noted that the present simulations on isolated rGGGUUAGGG indicate that the native PH and the CS ensemble are considerably less thermodynamically stable compared to the unfolded ensemble. This can be deduced from the short lifetimes of these structures and rarity of the folding events. However, it is likely that the force field underestimates the relative stability of the fully folded PH (24,97); one reason is underestimation of the stability of the base pairs while some other imbalances are yet to be identified. On the other hand and more importantly, in the course of GQ folding, the PHs may form as part of more complex intermediates involving three or four interacting G-strands, which may increase their stability. Note that the CS ensemble provides free H-bond donors and acceptors to interact with additional G-strands, loop residues and flanking residues (Figure 5). Thus, low populations of CS and PH structures in our rGGGUUAGGG simulations do not rule out their participation on the folding processes in the context of full GQ-forming sequences, as discussed below.

The folding mechanism of PH with propeller loop revealed by REST2 simulations

In order to understand the mechanism of PH folding in greater details and to get better sampling, REST2 simulations of rGGGUUAGGG starting from fully folded (PH) and unfolded states were performed. Further, REST2 simulation of rGGGAGGG from unfolded state was carried out. The REST2 method profits from multiple independent simulations running in parallel over a range of Hamiltonians, which helps to overcome enthalpy barriers and to explore the free energy landscape more effectively than in plain MD simulations. For the REST2 simulations, we increased the stability of the native PHs using the HBfix potential energy correction introduced in ref. (63); for more details see also the Methods section and ref. (101).

A hallmark of the unbiased (reference) replica obtained by REST2 simulations of rGGGUUAGGG was sampling of compact bent antiparallel G-hairpin conformations with diverse hydrogen bond patterns between guanines. The reference replica with unbiased Hamiltonian corresponds to the unbiased 300 K ensemble of the studied system and is used to gather the data (see Methods). The bending is dominantly achieved at the two uracil nucleotides located at the loop region while guanines on both tails remain dominantly in straight stacked conformations (Supplementary Figure S7A). A similar behavior of the unfolded state was observed in folding simulations of DNA dGGGTTAGGG, where the bending towards antiparallel structures was also dominantly located at the TTA loop region (36). The bending at the loop regions is likely facilitated by weaker stacking interactions in the loop sequences compared to rather strong stacking of guanines in the G-strands. Note that in contrast to the present data (see below), our earlier dGGGTTAGGG T-REMD simulations failed to indicate any mechanism of folding towards a PH (36). This may be due to use of a less efficient simulation method, stronger competition of antiparallel DNA structures and deficiency of the force field which we, in the present work, compensated for by the used force-field adjustment supporting formation of the PH (see Methods).

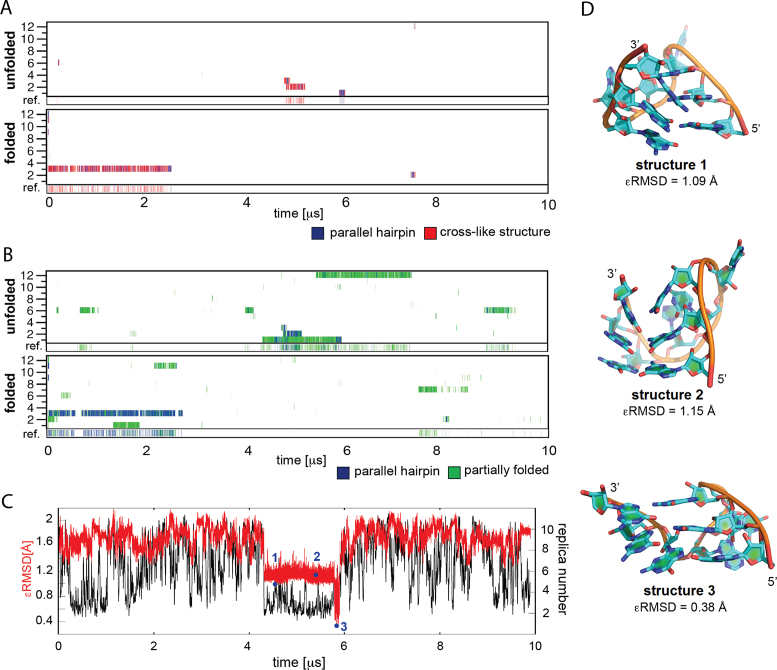
The dominant part of the REST2 ensemble with a tendency to form antiparallel bent arrangements is at first sight irrelevant for folding towards the propeller loop. However, we have detected, in the reference replica, also a minor population of cross-like structures (5.4% and 1.1% of the unbiased ensemble in REST2 starting from the folded and unfolded structure, respectively) and even a tiny population of fully folded PH (1.5% and 0.3% in REST2 starting from the folded and unfolded structure, respectively). Although these numbers bear large uncertainty as the associated statistical error is huge, the REST2 simulations do show that the CS and PH structures are accessible from the unfolded states. The CS ensemble and PH structures were unambiguously detected using the ϵRMSD metrics. We used the four CSs identified in plain MD simulations of PH and shown in Figure 5 as the reference structures for ϵRMSD comparison. We observed independent full folding events into the native PH in five continuous replicas starting from the unfolded state and in one replica starting from the folded state (excluding the replica which resided in the PH and CS state for more than 2 μs from the simulation start) (Figure 6A). However, despite the structure-based HBfix potential applied in REST2 simulations (see Methods), which stabilizes the native (folded) state by up to 6 kcal/mol, all these folding events were transient. Note that also the CS ensemble is to some extent stabilized by the HBfix potential, depending on the number of the native H-bonds that are sampled.

Figure 6.

Native and intermediate states in REST2 simulations of rGGGUUAGGG. (A) Occurrence of native PH and cross-like structures detected via ϵRMSD development with respect to the native PH structure and the four cross-like structures shown in Figure 5 (they are considered as a single CS ensemble in this figure). The twelve continuous (demultiplexed) trajectories and the reference replica (see Materials and Methods) are shown; the reference replica is at the bottom of the graph. Note that the twelve continuous replicas have equal significance and their numbering is incidental. REST2 from unfolded and folded states are at the top and bottom, respectively. (B) Occurrence of PH and partially folded structures detected based on the number of native H-bonds for the continuous trajectories and the reference replica. Note (cf. A and B) that the ϵRMSD metrics is more conservative than the native H-bond metrics. (C) ϵRMSD development (red) and position in the replica ladder (black) of the continuous trajectory (trajectory 1 in the ‘unfolded’ REST2 simulation in panels A and B containing the PH folding event occurring shortly before 6 μs; the data is averaged over 1 ns windows. The black curve showing position of the trajectory in the replica ladder looks continuous because of the averaging. (D) Structures identified at selected points during the folding event in panel C.

The overall picture is fully confirmed alternatively by monitoring the number of native H-bonds (Figure 6B); this analysis clearly shows that all the snapshots labeled as the CS state by the ϵRMSD metrics are in regions recognized as PH and its immediate vicinity according to the number of native H-bonds. In addition, other partially folded structures with four native H-bonds in two consecutive GG base pairs are visibly populated. Thus, we observed some CSs that are not detected by the ϵRMSD, e.g. CSs with one bulged-out guanosine. The H-bond analysis thus suggests that the ensemble of CSs or other nearly native structures is broader than it would seem from the ϵRMSD-based analysis, because these two metrics cover slightly different parts of the conformational space. We consider, for rGGGUUAGGG, the populations given by ϵRMSD as the lower limit (conservative estimate) of the overall CS ensemble population; it should be devoid of false-positive detections. When using the number of native H-bonds as the metrics, the reference replica of the REST2 starting from the unfolded state would contain 1.7% of PH plus additional 9.3% of partially folded structures, with a majority of the continuous trajectories contributing to these populations (Figure 6). The equivalent numbers for the REST2 started from the folded state are 5.5% and 5.0%.

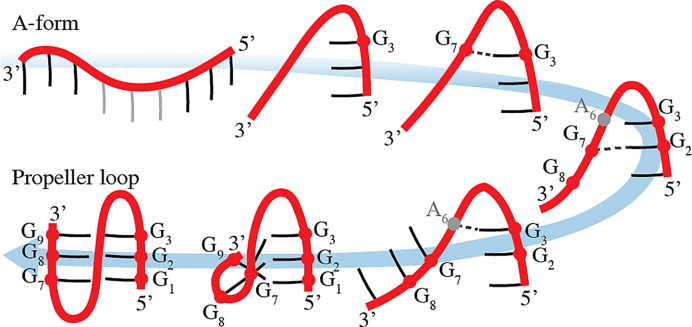
We suggest that despite the low stability (population) of the PH structure, the simulations faithfully reveal the mechanism of the folding. The detected folding events showed similar pathways. The folding starting from fully extended states was achieved by initial collapse into antiparallel hairpin-like structure (Figure 7). This brought the two G-strands into close contact. The last guanine G3 of the 5′-tail GGG strand established non-native base-phosphate interaction with the phosphate of the first guanine G7 of the opposing G-strand (Figure 7). Subsequently, the backbone around G7 guanine was shifted via strand slippage toward guanine G1, while the structures along this pathway were stabilized by various non-native base phosphate interactions between G1-G3 guanines and phosphates of the opposite G-strand. After that, the G7-G9 guanines established hydrogen bonding with G1-G3 guanines forming thus the CS, which was followed by transition into the fully folded PH structure (Figure 7).

Figure 7.

Observed folding pathway of the PH. The formation of the bent antiparallel structure was followed by establishing of the base-phosphate interaction between G3 guanine and the phosphate of G7. Subsequently, the backbone of G7 was shifted toward G1 via strand slippage, which was followed by formation of CS. Finally, the fully folded PH structure was formed. Note that all the intermediates were found in the simulations. In other words, although the antiparallel hairpin-like arrangements dominating the REST2 simulation could at first sight look like an off-pathway frustration of the folding landscape, the antiparallel ensemble contains a bridgehead for structural transformation towards the CS and finally towards the fully folded PH with the propeller loop. The process depicted is relevant not only for folding events within the context of the short rGGGUUAGGG oligonucleotide, but also in the context of the full GQ-forming sequences, where the individual G-tracts, loop residues and bound ions can synergically support step-by-step rearrangements towards the fully folded GQ via conformational diffusion.

Thus, the sequence of events starts with formation of an antiparallel arrangement of the G-strands within the unfolded ensemble, which at first sight represents an off-pathway structure (with respect to PH and the parallel-stranded GQ) on the folding landscape. However, the molecule is then capable to convert to the CS by mutual sliding of the G-strands and their reorientation, which is aided by various H-bonds. Such processes can be considered as conformational diffusion through the folding landscape via a series of step-by-step H-bond rearrangements. Conformational diffusion has been earlier hypothesized to play a role in GQ folding, mainly for movements between the dominant basins on the folding landscape (24).

The REST2 simulation of rGGGAGGG starting from the unfolded state showed a very similar picture as the rGGGUUAGGG REST2 simulations, with similar frequency of folding attempts and the total population of the PH state 1.6% with additional 0.1% of the CS state (ϵRMSD metrics, Supplementary Figure S8) in the reference replica. The small CS population is likely caused by presence of only a single nucleotide in the loop, which restricts the conformational space of the loop and in turn limits the possibility of mutual rotation of the two connected G₃ stretches, which can be seen from lower bending propensity of the loop compared to rGGGUUAGGG (Supplementary Figure S7B). It also modulates the capability of ϵRMSD to differentiate PH and CSs. Nevertheless, visual analysis confirms that the folding pathways of rGGGUUAGGG and rGGGAGGG are quite similar, with the same role of base-phosphate interactions during the conformational rearrangements. When using the number of native H-bonds as the metrics, the reference replica would contain 1% of PH plus additional 3.6% of partially folded structures.

Simulations contradict hypothetical existence of antiparallel RNA GQs

The fact that all simple RNA GQ structures observed experimentally so far form all-anti all-parallel architectures does not rule out that other types of RNA GQs are transiently populated during the folding. We have thus carried out a series of standard simulations of non-parallel RNA GQs obtained by deoxyribose to ribose conversion in several known DNA GQ topologies. Consistently with the literature (50), the simulations indicate that RNA destabilizes GQ stems containing syn nucleotides. These simulations are not robust enough to entirely exclude possibility of formation of such structures. However, they support the view that the RNA GQ folding landscape does not contain any significant free-energy basins corresponding to non-native (i.e., non-parallel) GQ topologies, and such structures are thus not populated even temporarily. Full details of these simulations are given in the Supplementary Information (pages S18-S19 and Supplementary Figures S9–S21).

CONCLUDING REMARKS

The role of parallel hairpins, cross-like structures and propeller loops in GQ folding

We have carried out an extensive set of standard and enhanced sampling MD simulations with the aim to study folding landscape of the rGGGUUAGGG and rGGGAGGG parallel hairpins (PH) with propeller loop.

Explicit solvent MD simulations have become a common tool to study GQ molecules. There are two basic attitudes how to apply MD to nucleic acids. In one, experiments are complemented by quantitative computational investigations, analyzing atomistic details of dynamic events, providing free-energy information or trying to reproduce specific primary experimental data. In this approach, a quantitative picture is most highly valued. In the second approach, quantitative data is regarded as less important outcome, as long as new experimentally testable hypotheses can be formulated, novel interpretations of experiments are provided, or even experimentally entirely not accessible phenomena, which are important to understand the behavior of the studied molecules, are revealed (101). The present work is a textbook example of the second approach. We discover a basic and hitherto unknown pathway how a parallel arrangement of two G-strands with a propeller loop emerge from the unfolded ensemble of GQ-forming sequences and suggest its potential contribution to RNA GQ folding mechanism. Although we assume that the MD simulation force field exaggerates the intrinsic instability of the isolated PH with the propeller loop (24), this should not affect the basic essence of the mechanism of the folding events as depicted in Figure 7.

Earlier simulations (see Introduction) revealed that while antiparallel DNA G-hairpins supporting lateral and diagonal loops form easily, folding of DNA PHs with propeller loops is a nontrivial problem (24). In the present study we demonstrate that isolated RNA PHs are not stable either (Supplementary Figure S5). Nevertheless, our extensive simulations ultimately identify a plausible folding and unfolding pathway of the rGGGUUAGGG PH, which is bridged with the unfolded state via an ensemble of cross-like structures (CSs; Figures 5 and 7). The sequences can reach the PH from the unfolded state via conformational diffusion through the folding landscape via a series of rearrangements of the H-bond interactions. By conformational diffusion (at the level of atomistic resolution of the folding landscape) we mean a process in which the molecule continuously travels over a large distance through the folding landscape by step-by-step structural rearrangements while not getting fully unfolded (i.e., significantly extended). The proposed role of the conformational diffusion is analogous to the role of diffusive search suggested, based on simplified lattice model simulations, to take place after the nonspecific collapse during protein folding, see Figure 3 in ref. (40); cf. e.g., also the dynamics accompanying allosteric changes described in ref. (49). Figure 7 thus suggests the first atomistic model of formation of the GQ propeller loop from the unfolded state. The rearrangements start in an ensemble of compact bent antiparallel structures and proceed through an ensemble of cross-like structures towards the PH.

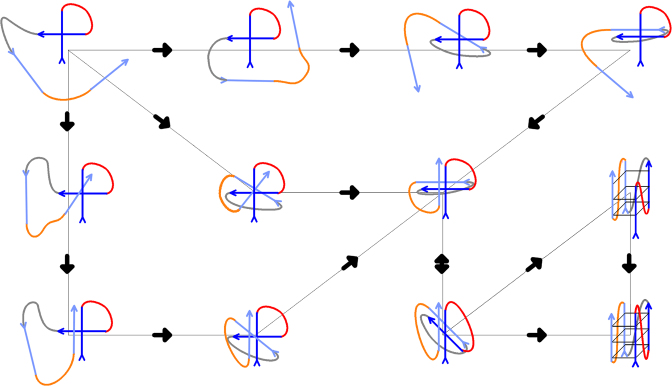
It is important to point out that with the short rGGGUUAGGG sequence, the PH does not appear to be stable per se. Its spontaneous formation is a rare event and its subsequent life time is on a nanosecond time scale. Although the simulation instability of PH may be exaggerated by the force field inaccuracies (24), it is likely that even in reality isolated PHs are not stable per se. We nevertheless suggest that the PH folding pathway documented in Figure 7 is relevant for RNA GQ folding and CS and PH-types of structures are sufficiently populated during RNA GQ folding with the complete GQ sequence. They may participate in more complex compact coil-like ensembles that involve all four G-strands and already some bound ions (Figure 8). Such ensembles can then rearrange into the fully folded parallel GQ via conformational diffusion (Figure 8), as hypothesized earlier for tetramolecular DNA GQs (66). The suggested landscape further contains parallel GQ structures with strand slippage and reduced number of G-quartets. Relative contribution of the coil-like ensembles and strand-slipped GQs to the RNA GQ folding kinetics cannot be deduced from our model.

Figure 8.

Sketch of a possible folding pathway for intramolecular three-quartet RNA GQ starting from unstructured single strand (not shown in the scheme); for more detailed view on folding pathway of PHs see Figure 7. Directionality of the chain is marked by arrows. G-strands are in blue (first and second in dark blue, third and fourth in light blue) while loops one, two and three are in red, grey and orange, respectively. The essence of the process is formation of compact coil-like structures stabilized by extensive cross-like interactions among the four G-strands. The PHs and propeller loops can form via conformational diffusion (see the text). Conformational diffusion starting from the coil-like structures may allow structuring of slipped GQs with reduced number of quartets (see refs. (66) and (35) for more information) or direct formation of the native parallel GQ. Note that the scheme is inevitably oversimplified and aims to illustrate the suggested principle of the folding rather than any exact pathway. The Figure nevertheless reflects all the knowledge that has been gathered so far by atomistic MD about properties of various types of structures that contribute to the GQ folding landscapes. The scheme shows a variant of folding that proceeds via an initial cross-like interaction between the first two strands. The Figure does not depict incorporation of the monovalent ions, however, involvement of the ions in the process is suggested to take place once extensive GQ-like GG H-bonding patterns are formed. In any case, ions should be specifically bound once first complete G-quartet forms. The scheme does not depict participation of conventional GQ-like parallel triplexes (38,109,110), as these are assumed to be more transient than the structures included in the Figure (24,38). Note that while the MD simulation method allows to suggest plausible types of structures that may be present on the folding landscape, it is not yet possible to simulate the full folding process (24). Therefore, we do not provide any estimate of the timescale of the folding (and of the relative contribution of coil-like structures and strand-slipped GQs) and its determination awaits appropriate experimental measurements. The rearrangements depicted should exist also on the free-energy (folding) landscapes of DNA GQs, which are nevertheless much more complex due to presence of deep competing basins created by alternative GQ topologies and dominating kinetic partitioning (24).

We assume that the basic mechanism of formation of PHs suggested in this work for rGGGUUAGGG can be extended also to propeller loops with other sequences, as directly demonstrated by the REST2 rGGGAGGG folding simulation. Although our study utilized, due to availability of the experimental structures, bimolecular GQs to construct some starting structures, the results should be equally valid for all types of GQs (Figure 8); especially the key REST2 simulations provide results entirely independent of the utilized experimental structures. The conformational diffusion from antiparallel hairpin-like arrangements through the CS ensemble to the PH is shown in Figure 7. Note again that in order to participate in folding of complete GQs the isolated PH does not need to be thermodynamically stable since within the context of the full GQ-folding sequence the PH, once formed, can be stabilized by some additional sequence segments. The folding of the PH itself appears as a rather rare event, but it is entirely plausible considering the overall timescale of GQ folding.

The depicted pathway should be plausible also for folding of DNA propeller loops. However, the overall folding mechanism and kinetics of DNA parallel GQs may differ due to presence of antiparallel and hybrid GQ topologies on the folding landscape. This increases the complexity and kinetic partitioning of the folding process (24). Still, those parts of the folding landscape that correspond to structuring of the propeller loops of DNA GQs could be similar to those for RNA GQs (Figure 7).

For the RNA GQ, we expect that no alternative GQ folds are sufficiently stable to substantially affect the folding process, with exception of all-parallel all-anti GQs with strand slippage and reduced number of quartets (35,66). These all-anti strand-slipped structures, however, could be part of the broader ensemble of the native GQ because the transitions between them do not require any syn/anti flips, i.e. they are unobstructed and achievable by direct vertical strand movements. They should not slow down the folding kinetics significantly, at least for GQs involving only three quartets (106). For the three-quartet GQ sequences, they could possibly act even as on-pathway intermediates rather than as competing off-pathway kinetic traps. However, the relative contribution of various coil-like structures and strand-slipped GQs to the kinetics of RNA GQ folding cannot be derived using contemporary simulation methods and would require experimental clarification. We also note that the GQ folding landscapes can be dramatically affected by the number of guanines in the G-tracts (24). As experimentally demonstrated, longer GQ stems with four to six quartets may be associated with competing kinetically-trapped slipped GQs that can survive for months (106,107), for intermediary case see also ref. (108). Nevertheless, when the native structures contain only three quartets, the slipped structures possess only two quartets and this may allow them to easily slip towards the native structure during the periods of ion-exchange with the bulk (35,66). Thus, the folding time of three-quartet RNA GQs could be very fast. On the other hand, it is likely that in case of systems with the shortest two-guanine G-tracts such as the thrombin binding aptamer (109) the CSs can be less relevant.

Additional MD simulations carried out in our study show that within the context of the fully folded RNA GQs the UUA propeller loops sample a rich dynamics with substates interconverting on the μs time scale, analogously to TTA propeller loops of DNA GQs (63). Similarly to the DNA TTA loops, the force field seems to excessively destabilize γ-trans conformations of the first U in the loops. Further, simulations of hypothetical RNA variants of antiparallel and hybrid GQs indirectly indicate that these structures are conformationally frustrated and thus likely much less stable than their DNA counterparts, consistent with the lack of any experimental observations of such structures.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

SYMBIT [CZ.02.1.01/0.0/0.0/15_003/0000477] financed by the ERDF; Ministry of Education, Youth and Sports of the Czech Republic [LO1305 to P.K., P.B., M.O.]; and Czech Science Foundation [16-13721S]. J.S. acknowledges support by Praemium Academiae. Funding for open access charge: Institute of Biophysics of the Czech Academy of Sciences.

Conflict of interest statement. None declared.