Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2018 Aug 28;4(9):1146–1154. doi: 10.1021/acscentsci.8b00330

Free Energy Landscape of the Complete Transport Cycle in a Key Bacterial Transporter

Balaji Selvam †, Shriyaa Mittal ‡, Diwakar Shukla ‡,†,#,*
PMCID: PMC6161048  PMID: 30276247

Abstract

graphic file with name oc-2018-00330z_0006.jpg

PepTSo is a proton-coupled bacterial symporter, from the major facilitator superfamily (MFS), which transports di-/tripeptide molecules. The recently obtained crystal structure of PepTSo provides an unprecedented opportunity to gain an understanding of functional insights of the substrate transport mechanism. Binding of the proton and peptide molecule induces conformational changes into occluded (OC) and outward-facing (OF) states, which we are able to characterize using molecular dynamics (MD) simulations. The structural knowledge of the OC and OF state is important to fully understand the major energy barrier associated with the transport cycle. In order to gain functional insight into the interstate dynamics, we performed extensive all atom MD simulations. The Markov state model was constructed to identify the free energy barriers between the states, and kinetic information on intermediate pathways was obtained using the transition pathway theory (TPT). TPT shows that the OF state is obtained by the movement of TM1 and TM7 at the extracellular side approximately 12–16 Å away from each other, and the inward movement of TM4 and TM10 at the intracellular halves to 3–4 Å characterizes the OC state. Helix distance distributions obtained from MD simulations were compared with experimental double electron–electron resonance spectroscopy and were found to be in excellent agreement with previous studies. We also predicted the optimal positions for placement of methane thiosulfonate spin label probes to capture the slowest protein dynamics. Our finding sheds light on the conformational cycle of this key membrane transporter and the functional relationships between the multiple intermediate states.

Short abstract

Inward facing, outward facing, and occluded conformations adopted during the transport cycle of PepTSo were characterized using molecular simulations and Markov state models.

Introduction

Understanding the exchange of biological molecules across the phospholipid bilayer is of fundamental interest to the scientific community. The transport of a large variety of molecules is essential for the pathological physiological functions of the cell. In particular, peptide transporter proteins act as carriers that facilitate the transport of small groups of amino acids across the cell membrane. These transporters belong to the peptide transporter (PTR) family which are members of the major facilitator superfamily (MFS) of secondary active membrane transporters.1 To understand the functional mechanism of MFS transporters, Kaback et al. proposed an alternate access model that involves alternate accessibility to either side of the membrane via distinct inward facing (IF), occluded (OC), and outward facing (OF) conformational states.2 Another model is the rocker-switch model where the substrate is posited to bind to the center of the transporter, causing rigid body motion of the N and C domains to alternate access between the intracellular and extracellular sides.3 The third hypothesis is the elevator-like model where the substrate binds to a single domain, locks the pore channel, slides downward, and opens up to release the substrate.4−6 Even with progress in X-ray crystallographic techniques, atomic level structural information on the distinct states and other intermediate states is still unknown. In humans, peptide transporters PepT1 and PepT2 are expressed in the intestine and kidney and are actively involved in the uptake of dietary peptide molecules.7 Hence, peptide transporters are considered as crucial targets for drug delivery and a means to improve the pharmacokinetics of drug molecules.8 Despite the known importance of peptide transporters, structural changes involved in the overall functional dynamics have not been studied comprehensively. In this work, we have chosen a bacterial peptide transporter from Shewanella oneidensis, PepTSo, to understand the conformational dynamics and mechanistic transport in this peptide transporter and by extension of the proton coupled oligopeptide transporter (POT) family.

PepTSo is a bacterial POT consisting of 12 transmembrane helices (TMs) divided into N (TM1–TM6) and C (TM7–TM12) terminal domains, each with six helices.9,10 The N and C domains are connected by two short helices (SHs) that are closely packed to the C-terminal domain. PepTSo uses an inward electrochemical potential as the driving force to transport di-/tripeptide molecules into the cell against their concentration gradient. PepTSo shares close sequence similarity and structural homology with other peptide transporters PepTSt,11−13 GkPOT,14 PepTSo2,15,16 YePEPT,17 and PepTXc.18 PepTSo and YePEPT were crystallized in the apo form (other peptide transporters were crystallized as holo structures) in the IF state. Biochemical and biophysical experiments provide insights into the functional behavior of the transporter proteins; dynamics information on the conformational transition between different structural states is missing. The repeat swap method (RSM) was used as an alternative protocol to obtain the OF conformational state of PepTSo.19 The method involves swapping the N and C domains to create a template, aligning the swaps to the template coordinate file and finally constructing the homology model to obtain the RSM model. However, the some of the limitations of this technique are that it requires careful assessment of the sequences for structural alignments of the internal repeats and cannot provide an array of intermediate states, and no information is gained regarding the dynamics of the process of peptide transport. Limited computational methods have been employed to study the functional mechanisms and conformational dynamics of transporters.20−23 These methods contributed to the investigation of substrate driven structural changes of transporters, but failed to obtain the kinetics of the crucial conformational transitions which would be critical to identify the transitions among key intermediates states that are essential to the functional mechanism. Evidently, these transporters exhibit large conformational changes, which cannot be understood using the static snapshots provided by X-ray crystallographic studies, and hence the mechanism of peptide transport is still unknown.

Molecular Dynamics (MD) simulations are an appealing methodology to determine the conformational changes and provide a mechanistic insight into PepTSo. In our study, we performed atomistic MD simulations over a duration of ∼54 μs using an adaptive sampling approach (see Methods). Further we constructed a Markov state model (MSM), a technique that has been used extensively to study conformational diversity in biological systems.24−28 Using MSMs we were able to combine a large number of shorter simulations and perform efficient analysis on the huge amount of the data. To estimate the time scales of the transitions between the intermediates in the transport cycle, trajectories were reconstructed using the kinetic Monte Carlo approach. MD simulations have unraveled the OC and OF states of PepTSo along with other intermediate states that the protein can adopt to enable transport. We compared the helix distance distributions from our MD simulation ensemble to the experimental double electron–electron resonance (DEER) spectroscopy results. To our knowledge, this is the first long time scale MD simulations based thermodynamics and kinetics study that captures key intermediate states and the functional landscape of PepTSo using unbiased computational methods.

Results

MD Simulations Reveal the Conformational Substates of PepTSo.

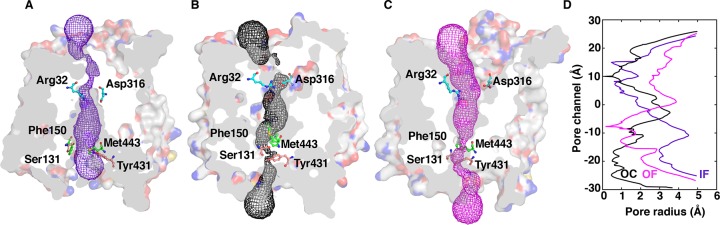
The IF state crystal structure of PepTSo (PDB: 4UVM(10)) was used as the starting conformation for simulations. The MD simulations were conducted using an adaptive sampling approach (see Methods). From our simulation data, we were successfully able to identify the functionally important intermediate states. The free energy landscape projected onto the extracellular and intracellular distances, weighted by the MSM equilibrium probability distribution, reveals the energy minima corresponding to conformations states, IF (1), partial IF–OC (2), OC (3), partial OC–OF (4), OF (5), and wide open intermediate states (6 and 7) (Figure 1). The extracellular and intracellular side distances determined between the residue pairs Arg32-CZ (TM1)–Asp316-CG (TM7) and Ser131-CO (TM4)–Tyr431-OH (TM10), respectively, show that the helices of the N and C domains are ∼7.0 and ∼10.5 Å apart in the PepTSo crystallized IF state (PDB: 4UVM). We observe that the intracellular distance between TM4 and TM10 may increase up to ∼20 Å, albeit resulting in a high energy unstable state. PepTSo adopts a partial IF-OC state as the intracellular helical distance between TM4–TM10 reduces to 5–6 Å by a movement of both helices inward toward each other. Further, this distance reduces to 3 Å, leading to the OC state. The transition from OC to OF involves two stages: first, the moving apart of TM1 and TM7 at the extracellular side to a distance of 7–8 Å by forming an intermediate partial OC–OF state, and second, extending the distance of the extracellular vestibule of TM1 and TM7 up to 12–16 Å (Figures S1 and S2). The IF, OC, and OF states can be distinguished by passing a spherical probe from one side of the protein to the other, calculated using the HOLE program.29 The probe radius through the different states is visualized in Figure 2, and the residues used to determine intracellular and extracellular distances in our study are indicated, as they constrict the IF, OC, and OF states.

Figure 1.

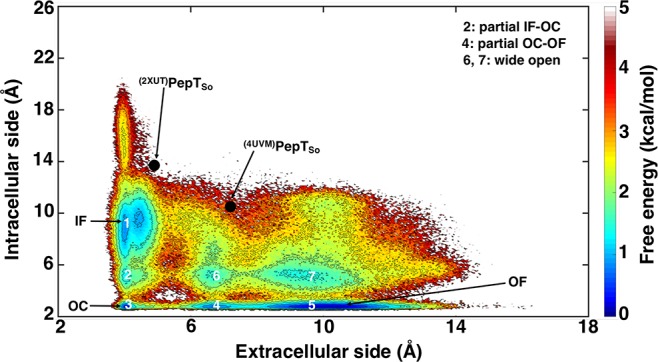
Figure 1

Open in a new tab

Conformational landscape of PepTSo. The conformational landscape is generated using the extracellular and intracellular side distances measured between atom pairs Arg32-CZ (TM1)–Asp316-CG (TM7) and Ser131-CO (TM4)–Tyr431-OH (TM10), respectively. The conformational states are depicted as IF (1), partial IF–OC (2), OC (3), partial OC–OF (4), OF (5), and wide open states (6 and 7). The black dots indicate the PepTSo crystal structures available in the Protein Data Bank.

Figure 2.

Figure 2

Open in a new tab

Distinct conformational states of PepTSo are visualized by passing a spherical probe from one side of the protein to the other through (A) the crystal structure IF state, and for the MD simulations predicted structures for (B) OC and (C) OF states, calculated using the HOLE program.29 The gating residues Arg32 (TM1)–Asp316 (TM7) and Ser131 (TM4)–Tyr431 (TM10) that act as bottlenecks for the conformational transition are indicated. (D) The pore radius along the protein for the three conformational states.

To determine the conformational exchange between these intermediate states, we performed transition pathway theory (TPT) analysis on MSM (see Methods).30 All high-ranked paths undergo a transition from the IF to OF via the OC state and other intermediate states. The free energy barrier for the transition from IF to OC via the partial IF–OC state is ∼2–2.5 kcal/mol, and for subsequent transition to OF through states partial OC–OF or a wide open state is ∼1.5–2 kcal/mol. Hence, the total free energy barrier of ∼4 kcal/mol was determined for one complete cycle from IF to OF at equilibrium.

Structural Characteristics of the OC State

The predicted OC state shows large deviations in the intracellular side of N and C domains as compared to the IF state. The intracellular halves of the helices rearrange in several positions as compared to the crystal structure—TM1 moves inward and closely packs with TM3 and TM4; TM10 and TM11 undergo inward movement and interact with TM2 and TM4, respectively; TM4 and TM5 are tilted ∼5° and ∼10°, respectively, and move inward closer to the center of the transporter. TM2 becomes more straight compared to the kinked helix in the IF crystal structure. On the extracellular half, TM7 and TM8 are rotated by ∼15° and ∼8°, respectively, and move closer to TM1; TM9 and TM10 move up to 6 and 11 Å outward and form extensive contacts with the loops joining TM7 and TM8 (Figure S3).

The OC state is stabilized by extensive intramolecular hydrogen bonds between the N and C domains. At the extracellular side, the residues Asn33 (TM1), Ser165 (TM5), Ser320 (TM7), and Gln341 (TM8) form a hydrogen bond network that acts as the lid by packing the helices close to each other (Figure S4). The closure of the pore channel is further stabilized by Arg32 (TM1)–Asp316 (TM7) salt bridge interaction on this end of the transporter. Asp316 of this ionic residue pair is known to play a major role in proton driven peptide transport.9,12,19,31 The Glu419 (TM10) interaction with Lys318 (TM7), Thr416 (TM10), and Asn344 (TM8) stabilizes the conformation of TM7 and 8. The Glu419 (TM10) is a conserved residue in the POT family, and its mutation to Gln results in loss of proton driven peptide transport.12 Another conserved motif, ExxERxxY on TM1 (Figure S5), and its interaction with Lys127 (TM4) play a crucial role in peptide transport, and its mutation abolishes the transport function.12

On the intracellular side, the Pro127 (TM4) introduces a helix kink which facilitates the inward movement of TM4 and TM5. The glycine residues (Gly418 (TM10), Gly426 (TM10), and Gly440 (TM11)) increase the structural flexibility allowing the helices to twist. Tyr431-OH (TM10) establishes a hydrogen bond contact with Ser131-CO (TM4) and stabilizes the OC state (Figure S4). Our predictions conform with the hypothesis of Stelzl et al. for the extracellular and intracellular gating residues that are critical for the conformational switch and functional mechanism of transporters.32 A comparison of the predicted OC state has been made with the multidrug transporter EmrD (PDB: 2GFP,33Figures S6 and S7) and xylose transporter XylE (PDB: 4GBY,34Figures S8 and S9), MFS family OC structures in the Protein Data Bank. The observed gating residues Thr119 (TM4)–Phe311 (TM10) in EmrD OC and Met149(TM4)–Ser396 (TM10) in XylE OC state are comparable to PepTSo.

Structural Characteristics of the OF State

The predicted OF structure reveals dramatic rearrangements at the extracellular side compared to IF (crystal structure) and OC (predicted structure) whereas only subtle changes at the intracellular side compared to OC (Figure S10). TM7 rotates ∼7° as compared to IF, and Asp316 (TM10) moves ∼12 Å away from Arg32 (TM1) forming a new contact with Asn454 (TM11), which then interacts with His61 (TM2). Our predictions are consistent with the structure proposed by Parker et al.18 His57 (His61 in PepTSo) is involved in proton driven peptide transport in PepT1.35−37 Thus, the extracellular binding partners move away from each other and increase the channel viability and hence adopt the OF state. TM7 is stabilized by an interaction between Lys318 (TM7) and Glu419 (TM10) at the extracellular part of PepTSo. The ExxERxxxY motif forms similar contacts to those seen in the OC state. The kink caused by Pro71 in TM2 results in slight bending of the helix allowing Trp76-O (TM2) to form a contact with Thr441 (TM11). The interaction of Tyr431-OH (TM10) with Ser131-CO and Gly135-O on TM4 stabilizes the intracellular half of the OF state.

Our predicted OF structure from MD simulations shows good agreement with the fucose transporter (FucP, PDB: 3O7Q), which was crystallized in the OF state,38 with an RMSD of 2.9 Å (Figures S11 and S12). The intermediate states 6 and 7 are predicted to be wide open states that may also lead to transitions to the OF state. The PepTSo OF state predicted using RSM10 was compared to the predicted OF structure and has an RMSD of 3.6 Å (Figures S13 and S14).

Switching of Gating Residues Determines Conformational Changes in PepTSo.

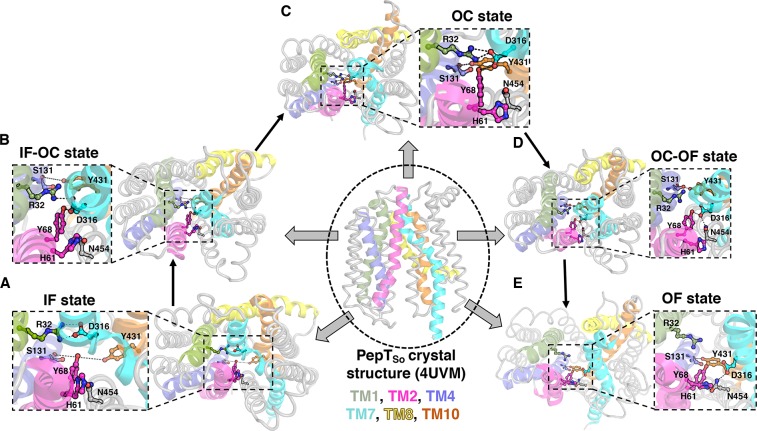
From TPT, we identified that the interaction between Arg32-CZ (TM1)–Asp316-CG (TM7) acts as the gating bottleneck on the extracellular side of the transporter. In the IF crystal structure (PDB: 4UVM), the distance between these atoms is 7.2 Å. However, our simulations reveal that these residues come closer and form a salt bridge interaction locking TM1 and TM7 to characterize an IF state (Figure 3A). Previous studies have also shown that the IF state is stabilized by the formation of this ionic lock.12 On the intracellular side, Newstead et al. observed that the hydrophobic gate between Phe150-CB (TM5) and Met443-CB (TM11) form the intracellular gate to characterize the OC state.9 We find these residues determine only the partial IF–OC state (Figure 3B, Figures S15 and S16). After PepTSo adopts the partial IF–OC state, an additional hydrogen bond between Ser131-CO (TM4) and Tyr431-OH (TM10) results in complete transition to the OC state (Figure 3C).

Figure 3.

Figure 3

Open in a new tab

PepTSo is shown in the center with TM 1, 2, 4, 7, 8, and 10 in green, magenta, blue, cyan, yellow, and orange, respectively. The short helices (SH) which join N and C domains are not shown for clarity. The remaining six helices are in gray. All state conformations are the extracellular view of the protein. (A) IF state is stabilized by ion lock at the extracellular side, and the intracellular half is wide open. (B) Inward movement of TM4 and TM10 determines the partial IF–OC state. (C) Further inward movement leads to formation of hydrogen bond interaction between Tyr431-Ser131 in the OC state. (D) Gating residues at the intracellular side weaken the extracellular interaction to form a partial OC–OF state. (E) Helices TM1 and TM7 move far away to 15 Å in the OF state.

Next, the partial OC–OF state is obtained as the distance between Arg32-CZ (TM1) and Asp316-CG (TM7) increases up to 7–8 Å. The weakening of ionic interaction between Arg32 (TM1) and Asp316 (TM7) leads Asp316 to form a new polar contact with Tyr68 (TM2). Further, it establishes a contact with Asn454 (TM11), which results in complete loss of interaction with Arg32 (Figure 3D). The extracellular halves of the N and C terminal domains start moving further away from each other (on the extracellular side) and results in loss of Tyr68 interaction with Asp316. His61 (TM2), Asn454 (TM11), and Asp316 (TM7) form a hydrogen bond triad, thus adopting the final OF state (Figure 3E). The predicted OF state reveals that the distance between the residue pairs Arg32 (TM1) and Asp316 (TM7) may increase up to 12–16 Å to recognize the substrate molecule and initiate the transport cycle.

Using a kinetic Monte Carlo reconstructed trajectory of length 25 μs from the constructed data set, the mean passage time for the transition from IF to OF, via OC was found to be ∼1 μs (Figure S17). This synthetic trajectory reveals that the rates of transitions between alternate opening of extracellular and intracellular gates shows faster dynamics as compared to previous studies where they have obtained the transition from IF to partial IF–OC and to OF in ∼0.6 μs.10,18

Comparison of Predicted OC and OF Structures with Experiments

DEER spectroscopy is a biophysical technique that allows determination of residue pair distance distributions between two cysteins that have been modified via site-directed spin labeling (SDSL). The technique has been used for widely used for the study of membrane proteins39 where multiple peaks in the distributions indicate a diverse conformational composition of the protein during the experiment. Atom-pair distances can also be obtained from the ensemble information from MD simulations and hence provide an avenue for comparison with DEER spectroscopy distance distributions.

We compared the helix distance distribution measurements obtained from our simulations with experimental data (Figures 4 and S18) by constructing augmented Markov models (AMMs)40,41 and the RotamerConvolveMD Python package32 that maps a rotamer library of the spin labels on the residues to estimate the distribution (see Methods). The overall distributions were found to be in good agreement with SDSL DEER experiments.10 For the residues pairs Ser141–Ser432, Ser141–Met438, Ile47–Val330, and Arg201–Glu364 the distance distribution ranges are larger for the simulation data than the experimental observations. This increase in distance distribution shows that the transporter may adopt a wide range of flexibility in order to transport diverse substrate molecules. Further, we compared the experimental data with distance distributions obtained from representative structures of IF, OC, and OF states individually (Figure S19) as well as other intermediate states (Figure S20) in our simulations data, to characterize the distance ranges spanned by the predicted free energy minima.

Figure 4.

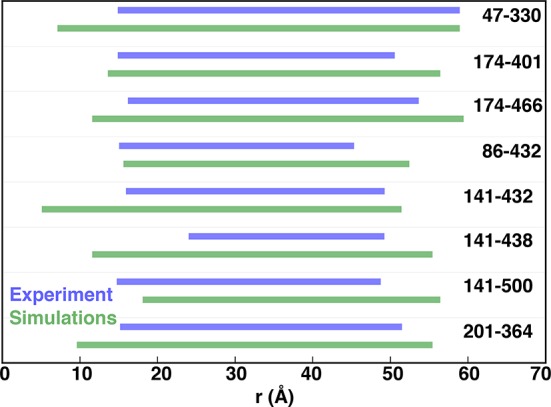
Figure 4

Open in a new tab

MD simulation predicted DEER distance distribution ranges (green) are compared to the experimental DEER distance distribution range (blue).

Crucial to this experimental technique is the choice of residue pairs to label. For a 500 residue protein, like PepTSo, one must choose a set of labeled residues pairs from ∼125 000 possibilities, which leads to combinatorial choices counting to a billion. We developed a method that could predict the smallest set of residue pairs for spin labeling that best captures the slow dynamics in a membrane protein using the large amount of MD simulation data generated and a hyper parameter optimization strategy for MSMs.42−44 To obtain an optimal set of residue pairs, we assigned an “optimal probe score” to each of the possible residue pair sets (see Methods).45 A higher score indicates slower kinetics of the MSM based on the chosen residue pair distances and hence can be considered as a better model to understand the underlying dynamics of the system. The residues pairs that are high ranked can be used for SDSL DEER spectroscopy experiments in membrane proteins.

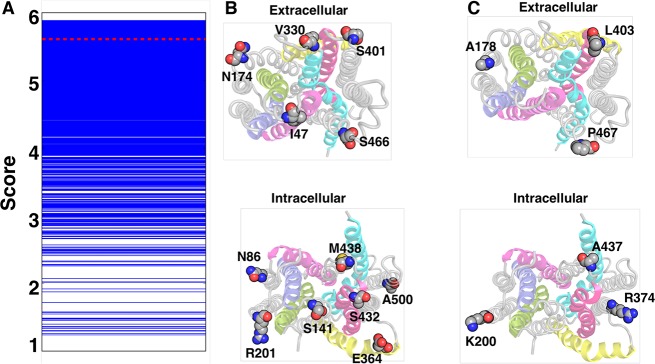
The probe scores for all constructed MSMs range from 1.24 to 5.89 (Figure 5A), and these choices vary in hugely in the number of residue–residue distances measured from 1 to 12. The residue pairs chosen for DEER experiments in PepTSo measured 8 residue pair distances with 12 probes which we used to construct an MSM yielding a lower probe score of 5.61 (red line in Figure 5A,B).10 The highest ranked choice of distances (Figure 5C) comprised of six distances, three on the extracellular side of the protein (among residues Ala178, Leu403, and Pro467) and three on the intracellular side (among residues Lys200, Ala437, and Arg374). One of the low ranked (probe score 1.24) sets with two probe positions is shown in Figure S21. It is evident that this choice would not give the necessary dynamic information on the system as, in the case of all MFS transporters, the correlated motions of helices in the N and C domain are important for functional dynamics. The distance between the residues Glu49–Tyr175 (Figure S21A) and Tyr85–Ser141 (Figure S21B) where both the potential probes are on the same domain would not provide any essential kinetic information that is not already captured in a slower MSM.

Figure 5.

Figure 5

Open in a new tab

(A) Cross-validated scores for 4300 possible DEER residue-pair sets. The red line is the score of the MSM using experimental residue distance pairs. (B) The residues used for experimental DEER10 and (C) highest ranked predicted DEER residue-pairs choices.

It is also of note that the sets where we chose to measure distances on either the extracellular side of the protein or the intracellular side are low ranked as compared to cases where we measure distances on both ends (Figure S22). Clearly from our previous observation of the switching of gating residues, understanding the complete dynamics of PepTSo requires residue pair distances on both extracellular and intracellular sides of the protein. For the residue set with the highest score, for the constructed MSM, distance distribution plots have been obtained (Figure S23) intracellular residue pair distances are shifted toward larger values for the IF state, and extracellular distributions are shifted to larger values for the OF state.

Discussion

Our results reveal the conformational changes that characterize various states of PepTSo and transitions between them. Our analysis indicates that hydrogen bonds and hydrophobic and aromatic interactions act as gating mechanisms to stabilize the key functional conformation states. The residue pair Arg32 (TM1)–Asp316 (TM7) forms the salt bridge interaction at the extracellular side and locks the PepTSo in the IF state. We show that the formation of OC state involves two steps, (i) the helices involving residues Phe150 (TM5) and Met443 (TM11) come closer to ∼5–6 Å, and (ii) the following residues from helices TM4 and TM10 form additional hydrogen bonds between Ser131-CO (TM4) and Tyr431-OH (TM10). The OF state is obtained by breakage of ionic lock between Arg32 (TM1)–Asp316 (TM7) and movement of TM1 and TM7 to 12–16 Å away from each other.

Water molecules around the lipid bilayer and the transporter protein could also play an important role in the conformational change. Figure S30 shows that water molecules have a higher preference for the phosphate group in the phosphatidylcholine (POPC) lipid head groups as compared to the nitrogen due to the hydrophobicity posed by three methyl groups around it.46 Lipid bilayers properties in our simulations, area per lipid, and membrane thickness (Figure S31) indicate that the lipid bilayer remains in the same configuration throughout the simulation time. Overall, our predicted values agree well with experimental studies,47 where the area per lipid value is 68.3 ± 1.5 Å2 and membrane thickness value is 37 Å, although a slight variation in the computed values compared to experimental observations could be due to differences in temperature and physiological conditions. Moreover, there is usually at least one water molecule between the lipid molecules that prevents them from coming close to each other (Figure S32) and hence stabilizing the lipid bilayer.

Water molecules are cotransported along with substrate molecules, and this property has been well studied for membrane transporters.48 We calculated the hydration level in three states and observed the fluctuation of number of permeating water molecules (Figure S33). A large number of water molecules were noticed for the OF state compared to OC and IF states. We also compared the water molecules in the IF state with other available crystal structures from the POT transporter family (Figure S34). The water permeation could also be associated with the transitions among the different conformational states of the protein.

The comparison of simulation DEER distance distributions exhibit good agreement with experimentally obtained DEER data. Using the Optimal Probe method,45 we also predict the best DEER SDSL positions for future experiments. We suggest six distance measurements, three on either of the sides of PepTSo which can capture the dynamics involved in the movement of the helices of this protein. In general, this method can be used to predict measurable DEER distances for any protein of interest.

PepTSo and other POT family members PepTSt, PepTSo2, PepTXc, and GkPOT have conserved sequence motifs and structural folds, suggesting that the mechanistic basis of substrate transport will be universal in this family. We posit in the OF state the binding of a proton and a peptide molecule should increase the structural plasticity of the extracellular side of the transporter and initiate structural rearrangements of helices. The movements of helices are driven through a network of hydrogen bonding interactions involving TM1, TM2, TM7, and TM11, resulting in the OC state. Tyr68 (TM2) and Asn454 (TM11) act as a key residues that drives Asp316 (TM7) to form a salt bridge with Arg32 (TM1). Biophysical studies also show that Tyr68 is critical for affinity and specificity for peptides.12 The closure of extracellular part results in formation of the OC state and the peptide molecule moves into the central cavity. The increase in strength of the salt bridge at the extracellular side results in weakening of the intracellular gating residues. Helices TM4, TM5, TM10, and TM11 increase in structural flexibility and thereby determine the functionally important conformational states to allow substrate transport. The proton and substrate translocates to the conserved ExxERxxxY motif and finally leaves the transporter into the cytoplasm of the cell.

Our study is a first large-scale simulation of a member of the POT family. It is a first extensive analysis of the diversity of the conformational states of the protein and the many rare intermediate states. However, our study is based on equilibrium simulations in the apo state of PepTSo. The varying dynamics in the presence of the proton and peptide are yet to be demonstrated and understood in great detail. Our study opens new dimensions to obtain a mechanistic understanding into the POT family of proteins and to enable design and transport of peptido-mimetic drugs.

Methods

Molecular Dynamics Simulation

The crystal structure of PepTSo was used as a starting structure for MD simulation. The three-dimensional (3D) coordinates (PDB: 4UVM(10)) were obtained from the Protein Data Bank. The tleap program in AmberTools1449 was used to build the MD system. The protein was solvated in a phospholipid bilayer (POPC) in an orthorhombic box containing TIP3P water molecules50 in a periodic box size 98 × 98 × 119 Å3. A salt (NaCl) concentration of 0.15 M was used to neutralize the MD system. All chain termini were capped with neutral acetyl and methylamide groups. The standard protonation states was used for the titratable groups, and the final MD system contained approximately 110 000 atoms. The MD system was energy minimized for 20 000 steps using the conjugate gradient method, slowly heated from 0 to 300 K and equilibrated for 40 ns. The MD simulations were performed in constant NPT conditions at 300 K and 1 atm. The temperature was controlled using a Berendsen thermostat, and the pressure was maintained using a Berendsen barostat.51 Long range electrostatic interaction was treated with the Particle Mesh Ewald method,52 and bonds involving hydrogens were constrained using the SHAKE algorithm.53 The nonbonded distance cutoff was set to 10 Å, and an integration step of 2 fs was used. All simulations were performed using the AMBER FF14SB force field.54

An adaptive sampling approach was used to select the new starting structures for the subsequent MD runs to enhance the conformational sampling of the free energy landscape. For each round, the previous sampled data were clustered using the K-means algorithm based on the extracellular and intracellular experimental DEER residue pair distances, and the least populated states were chosen to conduct the next round of simulations. The sampling bias introduced in the data set from seeding new trajectories in this manner is eliminated in the way a Markov state model (discussed below) is constructed on the data.55 Adaptive sampling is a widely used sampling methodology and has been used to predict novel conformations of the proteins, pathways of conformational change, protein folding, and even protein–protein association.25,26,28,56−58 In addition to unbiased MD simulation data obtained as above, 5 μs of accelerated MD (aMD) simulation were also performed also using the adaptive sampling protocol (Table S1). For aMD, a boost potential (4 kcal/mol) was added to the dihedrals of the protein, and a further boost potential (0.2 kcal/mol) was added to the entire MD system. The integration step chosen is 3 fs.59 The free energy landscape in shown in Figure S24. The aMD simulation data were clustered, and the starting structures were chosen for classical MD (cMD) to sample the conformational landscape efficiently (Table S2). The final cMD was performed for a total duration of ∼54 μs. Each individual MD trajectory is of ∼34 ns.

Markov State Model

Markov state models (MSM) are a powerful kinetic modeling technique that discretize the landscape explored using MD simulations into microstates and determine the transition probabilities between them. The trajectories are clustered into N microstates based on a geometric criterion. Next, a transition probability matrix, T(τ) is obtained for a lag-time, τ such that p(t + τ) = p(t)T(τ) where p(t) and p(t + τ) are vectors denoting the probability of each of the N states at times t and t + τ. We obtained the dependence of the slowest implied relaxation time-scales of the eigenvectors of T(τ) for multiple values of τ, which provides an estimate of the best Markovian lag-time to build our MSM for analysis. The MSM Builder3.4 Python package60 was used to build the MSM on the PepTSo trajectory data. The seven transmembrane helical distances and three extracellular and intracellular residue pair distances were chosen as featurization metrics to construct an MSM (Figure S25). Twenty-four nanoseconds was determined to be a Markovian lag time from the implied time-scales plot (Figure S26). The number of clusters was chosen to be 200 as it yielded the highest Generalized Matrix Rayleigh Quotient (GMRQ) score while building multiple MSMs on varying this hyper-parameter (Figure S27).44 TPT analysis was performed to obtain the top flux pathway (Figures S28 and S29).

Kinetic Monte Carlo

Kinetic Monte Carlo is a method for sampling from a kinetic model, which can be used to create trajectories of state-to-state dynamics. For any chosen initial state i, a transition to any state j from the set of all states in the MSM occurs with probability pij from the MSM’s reversible maximum-likelihood transition matrix. This is implemented as follows: (1) generate a pseudorandom number between 0 and 1, (2) take a cumulative sum of pij values over all possible j (Sn = ∑inpij), and if the pseudorandom number lies between Sn and Sn+1, (3) transition to state j = n + 1. This state, j, is added to the trajectory, and the process is repeated for the desired number of steps.

DEER Distance Distribution Analysis

To validate our predicted structures with the DEER experiments, we constructed an AMM40 for each experimental DEER distribution as constraints using pyEMMA v2.4 + 936.g26d8e55.41 The list of constraints is provided in Table S3. We extracted 50 structures from the highest weighted clusters (in the MSM or the AMM) for each of the following conformations: IF, OC, OF, partial IF-OC, partial OC-OF, and two wide-open states. Using the Python library RotamerConvolveMD,32 we calculate the distance between the methane thiosulfonate spin label (MTSSL) probe conformations, mapped onto the rotamer library, for each pair of residues on all the structures. The raw distance information is then plotted as a histogram, and the distance range spanned by the distance distribution in order to compare to the experimental information.

Optimal DEER Residue-Pair Predictions

Although the DEER experimental method serves as an effective method to understand the dynamics of the proteins, the technique is quite challenging to the study of membrane proteins and requires substantial effort ranging from obtaining a large quantity of the expressed protein to choosing an appropriate residue for site directed mutation to attach MTSSL probe. In this study, we developed a method to obtain a set of residue pairs for cysteine mutation to attach the spin label MTSSL for DEER experiments. A total of ∼4300 sets of residue pairs were obtained, which also took into account the distance constraints of DEER experiments which do not allow the placement of probes on residues that would come closer than 15 Å or farther than 60 Å in any of the ∼54 μs of our MD simulation data set. 200 clusters were obtained by clustering the MD data based on the set of distances between the residue pairs using K-means algorithm. Next, an MSM was constructed at the previously chosen Markovian lag time of 24 ns. We obtained an optimal probe score for each of the 4300 MSMs constructed. A higher score indicates slower kinetics of the MSM and can be considered as a better model to understand the underlying dynamics of the system. The set of residues pairs that led to the highest ranked MSM was chosen as the optimal residue positions to attach probes.

To predict best probe positions for future experiments, we have taken into consideration the limitations and constraints of the DEER experimental technique. Experiments can measure residues in the range of 15–60 Å.61 It cannot measure the distribution across the membrane protein by placing probes on both intracellular and extracellular side. MTSSL probes can only be placed on solvent exposed residues and not within the transmembrane region as they would collide with the helical residues and lipid molecules of the membrane.

Residue–residue distances are determined by the CA atom distances of the residues pairs through our ∼54 μs of MD simulation data. We divide the transport protein into two parts, the intracellular side and the extracellular side. On either side, the loop regions and ends of the helices are the possible residues where the probes can be attached. On the basis of the mentioned constraints, we create an N × N adjacency matrix where N is the number of residues. The matrix element Nij is 0, if probes cannot be positioned on residues i and j. The value is 1 if the probes can be positioned on residues i and j after all the checks. Further, a least effort DEER experiment would require that the number of mutations required be limited to as few as possible and hence place the least number of probes. Thus, from our adjacency matrix we determined a long list of 2000 sets, each of residues that can be simultaneously be spin labeled for DEER signal calculation. These sets are then assigned an optimal probe score. Up to this step, all our choices were with two or three residues because they were limited by residue pair sets which included only residues that are either on the intracellular half of the protein or on the extracellular half. To obtain a mixed set of probes (on both ends of the protein, but does not require any measurement across the protein), we chose the highest scored set of two residues and highest scored set of three residues. Both were on the intracellular side. We then created another list of mixed probe positions with these on the intracellular side and all possible choices from the extracellular side. We ranked these mixed sets using the same protocol.

A similar methodology as described in the previous section has been followed to predict the distance distribution for each of the optimal probe position sets obtained using the Optimal Probes algorithm. We extracted 100 structures from each of the 7 minimum free energy states observed on the free energy landscape for PepTSo. Using the Python library RotamerConvolveMD,32 we calculated the distances between the MTSSL probe conformations, mapped onto the rotamer library, for each pair of residues on all the structures. The raw distance information is then plotted as a histogram and compared to the experimental information.

Optimal Probe Score

The optimal probe score is the GMRQ (generalized matrix Rayleigh quotient) score, which is a method to assign scores to an MSM based on the hyper-parameters used for the MSM construction.42,43 The objective of the GMRQ score is to assign a score to every MSM such that the dynamics observed by the MSM maximize the sum of the first m eigenvalues of the transition probability matrix. A higher ranked MSM will capture the slow kinetics of the system as compared to an MSM with lower GMRQ. To avoid overfitting, a cross-validation methodology is followed where 50% of the data was used to train the model, and the rest of the data are used to test the model. We exploit this method to rank our featurization metric of the MSM and hence obtain the best set of distances that would lead to a high ranked MSM. We have used the mean of five cross-validated test set GMRQ scores as the optimal probe score. We then suggest these residue pairs as a metric for future experiments. A Web site for the implementation of the method is available at https://github.com/ShuklaGroup/optimalProbes/wiki.

Acknowledgments

Authors thank the Blue Waters sustained-petascale computing project, which is supported by the National Science Foundation (Awards OCI-0725070 and ACI-1238993) and the state of Illinois. D.S. acknowledges support from the New Innovator Award from the Foundation for Food and Agriculture Research. S.M. acknowledges support via the CSE Fellows Program, funded by Computational Science and Engineering at University of Illinois, Urbana-Champaign, USA.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.8b00330.

  • Additional figures and tables (PDF)

  • The Protein Data Bank format files for the occluded (OC) and outward-facing (OF) structures of PepTSo. The structures can be visualized using any standard protein visualization software (PDB1 (OC), PDB2 (OF))

Author Contributions

⊥ B.S. and S.M. contributed equally to this work. D.S. conceived this work. B.S. and S.M. performed simulations. B.S. and S.M. analyzed the data. B.S. and S.M. made figures and wrote the manuscript with inputs from D.S. S.M. wrote the optimal DEER probe python code with inputs from D.S.

The authors declare no competing financial interest.

Supplementary Material

oc8b00330_si_001.pdf (24MB, pdf)
oc8b00330_si_002.pdb (314.2KB, pdb)
oc8b00330_si_003.pdb (314.2KB, pdb)

References

  1. Pao S. S.; Paulsen I. T.; Saier M. H. Major Facilitator Superfamily. Microbiol. Mol. Biol. Rev. 1998, 62, 1–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Kaback H. R.; Dunten R.; Frillingos S.; Venkatesan P.; Kwaw I.; Zhang W.; Ermolova N. Site-Directed Alkylation and the Alternating Access Model For LacY. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 491–494. 10.1073/pnas.0609968104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Law C. J.; Maloney P. C.; Wang D. N. Ins and Outs of Major Facilitator Superfamily Antiporters. Annu. Rev. Microbiol. 2008, 62, 289. 10.1146/annurev.micro.61.080706.093329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Coincon M.; Uzdavinys P.; Nji E.; Dotson D. L.; Winkelmann I.; Abdul-Hussein S.; Cameron A. D.; Beckstein O.; Drew D. Crystal Structures Reveal the Molecular Basis of Ion Translocation in Sodium/proton Antiporters. Nat. Struct. Mol. Biol. 2016, 23, 248–255. 10.1038/nsmb.3164. [DOI] [PubMed] [Google Scholar]
  5. Ryan R. M.; Vandenberg R. J. Elevating the Alternating-Access Model. Nat. Struct. Mol. Biol. 2016, 23, 187–189. 10.1038/nsmb.3179. [DOI] [PubMed] [Google Scholar]
  6. Colas C.; Ung P. M.-U.; Schlessinger A. SLC Transporters: Structure, Function, and Drug Discovery. MedChemComm 2016, 7, 1069–1081. 10.1039/C6MD00005C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Kottra G.; Daniel H. The Proton Oligopeptide Cotransporter Family SLC15 in Physiology and Pharmacology. Pfluegers Arch. 2004, 447, 610–618. 10.1007/s00424-003-1101-4. [DOI] [PubMed] [Google Scholar]
  8. Nielsen C.; Brodin B. Di/tri-Peptide Transporters as Drug Delivery Targets: Regulation of Transport Under Physiological and Patho-Physiological Conditions. Curr. Drug Targets 2003, 4, 373–388. 10.2174/1389450033491028. [DOI] [PubMed] [Google Scholar]
  9. Newstead S.; Drew D.; Cameron A. D.; Postis V. L. G.; Xia X.; Fowler P. W.; Ingram J. C.; Carpenter E. P.; Sansom M. S. P.; McPherson M. J.; Baldwin S. A.; Iwata S. Crystal Structure of a Prokaryotic Homologue of the Mammalian Oligopeptide-Proton Symporters, PepT1 and PepT2. EMBO J. 2011, 30, 417–426. 10.1038/emboj.2010.309. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fowler P. W.; Orwick-Rydmark M.; Radestock S.; Solcan N.; Dijkman P. M.; Lyons J. A.; Kwok J.; Caffrey M.; Watts A.; Forrest L. R.; Newstead S. Gating Topology of the Proton-Coupled Oligopeptide Symporters. Structure 2015, 23, 290–301. 10.1016/j.str.2014.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Lyons J. A.; Parker J. L.; Solcan N.; Brinth A.; Li D.; Shah S. T.; Caffrey M.; Newstead S. Structural Basis for Polyspecificity in the POT Family of Proton-Coupled Oligopeptide Transporters. EMBO Rep. 2014, 15, 886–893. 10.15252/embr.201338403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Solcan N.; Kwok J.; Fowler P. W.; Cameron A. D.; Drew D.; Iwata S.; Newstead S. Alternating Access Mechanism in the POT Family of Oligopeptide Transporters. EMBO J. 2012, 31, 3411–3421. 10.1038/emboj.2012.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Molledo M. M.; Quistgaard E. M.; Flayhan A.; Pieprzyk J.; Löw C. Multispecific Substrate Recognition in a Proton-Dependent Oligopeptide Transporter. Structure 2018, 26, 467–476.e4. 10.1016/j.str.2018.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Doki S.; Kato H. E.; Solcan N.; Iwaki M.; Koyama M.; Hattori M.; Iwase N.; Tsukazaki T.; Sugita Y.; Kandori H.; Newstead S.; Ishitani R.; Nureki O. Structural Basis for Dynamic Mechanism of Proton-Coupled Symport by the Peptide Transporter POT. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 11343–11348. 10.1073/pnas.1301079110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Guettou F.; Quistgaard E. M.; Trésaugues L.; Moberg P.; Jegerschöld C.; Zhu L.; Jong A. J. O.; Nordlund P.; Löw C. Structural Insights into Substrate Recognition in Proton-Dependent Oligopeptide Transporters. EMBO Rep. 2013, 14, 804–810. 10.1038/embor.2013.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Guettou F.; Quistgaard E. M.; Raba M.; Moberg P.; Löw C.; Nordlund P. Selectivity Mechanism of a Bacterial Homolog of the Human Drug-Peptide Transporters PepT1 and PepT2. Nat. Struct. Mol. Biol. 2014, 21, 728–731. 10.1038/nsmb.2860. [DOI] [PubMed] [Google Scholar]
  17. Boggavarapu R.; Jeckelmann J.-M.; Harder D.; Ucurum Z.; Fotiadis D. Role of Electrostatic Interactions for Ligand Recognition and Specificity of Peptide Transporters. BMC Biol. 2015, 13, 1. 10.1186/s12915-015-0167-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Parker J. L.; Li C.; Brinth A.; Wang Z.; Vogeley L.; Solcan N.; Ledderboge-Vucinic G.; Swanson J. M. J.; Caffrey M.; Voth G. A.; Newstead S. Proton Movement and Coupling in the POT Family of Peptide Transporters. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 13182–13187. 10.1073/pnas.1710727114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Vergara-Jaque A.; Fenollar-Ferrer C.; Kaufmann D.; Forrest L. R.. Repeat-Swap Homology Modeling of Secondary Active Transporters: Updated Protocol and Prediction of Elevator-Type Mechanisms. Front. Pharmacol. 2015, 6. 10.3389/fphar.2015.00183 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Faham S.; Watanabe A.; Besserer G. M.; Cascio D.; Specht A.; Hirayama B. A.; Wright E. M.; Abramson J. The Crystal Structure of a Sodium Galactose Transporter Reveals Mechanistic Insights into Na+/Sugar Symport. Science 2008, 321, 810–814. 10.1126/science.1160406. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Moradi M.; Tajkhorshid E. Mechanistic Picture for Conformational Transition of a Membrane Transporter at Atomic Resolution. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 18916–18921. 10.1073/pnas.1313202110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Park M. S. Molecular Dynamics Simulations of the Human Glucose Transporter GLUT1. PLoS One 2015, 10, e0125361. 10.1371/journal.pone.0125361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Jewel Y.; Dutta P.; Liu J. Coarse-Grained Simulations of Proton-Dependent Conformational Changes in Lactose Permease. Proteins: Struct., Funct., Genet. 2016, 84, 1067–1074. 10.1002/prot.25053. [DOI] [PubMed] [Google Scholar]
  24. Shukla D.; Hernández C. X.; Weber J. K.; Pande V. S. Markov State Models Provide Insights into Dynamic Modulation of Protein Function. Acc. Chem. Res. 2015, 48, 414–422. 10.1021/ar5002999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Shukla D.; Meng Y.; Roux B.; Pande V. S.. Activation Pathway of Src Kinase Reveals Intermediate States as Targets for Drug Design. Nat. Commun. 2014, 5. 10.1038/ncomms4397 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kohlhoff K. J.; Shukla D.; Lawrenz M.; Bowman G. R.; Konerding D. E.; Belov D.; Altman R. B.; Pande V. S. Cloud-Based Simulations on Google Exacycle Reveal Ligand Modulation of GPCR Activation Pathways. Nat. Chem. 2014, 6, 15–21. 10.1038/nchem.1821. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Plattner N.; Noé F.. Protein Conformational Plasticity and Complex Ligand-Binding Kinetics Explored by Atomistic Simulations and Markov Models. Nat. Commun. 2015, 6. 10.1038/ncomms8653 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Moffett A. S.; Bender K. W.; Huber S. C.; Shukla D. Molecular Dynamics Simulations Reveal the Conformational Dynamics Of Arabidopsis Thaliana BRI1 and BAK1 Receptor-like Kinases. J. Biol. Chem. 2017, 292, 12643–12652. 10.1074/jbc.M117.792762. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Smart O. S.; Neduvelil J. G.; Wang X.; Wallace B.; Sansom M. S. HOLE: A Program for the Analysis of the Pore Dimensions of Ion Channel Structural Models. J. Mol. Graphics 1996, 14, 354–360. 10.1016/S0263-7855(97)00009-X. [DOI] [PubMed] [Google Scholar]
  30. Metzner P.; Schütte C.; Vanden-Eijnden E. Transition Path Theory for Markov Jump Processes. Multiscale Model. Simul. 2009, 7, 1192–1219. 10.1137/070699500. [DOI] [Google Scholar]
  31. Colas C.; Masuda M.; Sugio K.; Miyauchi S.; Hu Y.; Smith D. E.; Schlessinger A. Chemical Modulation of the Human Oligopeptide Transporter 1, hPepT1. Mol. Pharmaceutics 2017, 14, 4685–4693. 10.1021/acs.molpharmaceut.7b00775. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Stelzl L. S.; Fowler P. W.; Sansom M. S.; Beckstein O. Flexible Gates Generate Occluded Intermediates in the Transport Cycle Of LacY. J. Mol. Biol. 2014, 426, 735–751. 10.1016/j.jmb.2013.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Yin Y.; He X.; Szewczyk P.; Chang G. Structure of the Multidrug Transporter EmrD from Escherichia coli. Science 2006, 312, 741–744. 10.1126/science.1125629. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Sun L.; Zeng X.; Yan C.; Sun X.; Gong X.; Rao Y.; Yan N. Crystal Structure of a Bacterial Homologue of Glucose Transporters GLUT1–4. Nature 2012, 490, 361–366. 10.1038/nature11524. [DOI] [PubMed] [Google Scholar]
  35. Uchiyama T.; Kulkarni A. A.; Davies D. L.; Lee V. H. Biophysical Evidence for His57 as a Proton-Binding Site in the Mammalian Intestinal Transporter hPepT1. Pharm. Res. 2003, 20, 1911–1916. 10.1023/B:PHAM.0000008036.05892.e9. [DOI] [PubMed] [Google Scholar]
  36. Chen X. Z.; Steel A.; Hediger M. A. Functional Roles of Histidine and Tyrosine Residues in the H+-Peptide Transporter PepT1. Biochem. Biophys. Res. Commun. 2000, 272, 726–730. 10.1006/bbrc.2000.2851. [DOI] [PubMed] [Google Scholar]
  37. Terada T.; Saito H.; Mukai M.; Inui K. I. Identification of the Histidine Residues Involved in Substrate Recognition by a Rat H+/peptide Cotransporter, PEPT1. FEBS Lett. 1996, 394, 196–200. 10.1016/0014-5793(96)00952-0. [DOI] [PubMed] [Google Scholar]
  38. Dang S.; Sun L.; Huang Y.; Lu F.; Liu Y.; Gong H.; Wang J.; Yan N. Structure of a Fucose Transporter in an Outward-Open Conformation. Nature 2010, 467, 734–738. 10.1038/nature09406. [DOI] [PubMed] [Google Scholar]
  39. Mchaourab H. S.; Steed P. R.; Kazmier K. Toward the Fourth Dimension of Membrane Protein Structure: Insight into Dynamics from Spin-Labeling EPR Spectroscopy. Structure 2011, 19, 1549–1561. 10.1016/j.str.2011.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Olsson S.; Wu H.; Paul F.; Clementi C.; Noé F. Combining Experimental and Simulation Data of Molecular Processes via Augmented Markov Models. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 8265–8270. 10.1073/pnas.1704803114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Scherer M. K.; Trendelkamp-Schroer B.; Paul F.; Pérez-Hernández G.; Hoffmann M.; Plattner N.; Wehmeyer C.; Prinz J.-H.; Noé F. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 2015, 11, 5525–5542. 10.1021/acs.jctc.5b00743. [DOI] [PubMed] [Google Scholar]
  42. McGibbon R. T.; Pande V. S. Variational Cross-Validation of Slow Dynamical Modes in Molecular Kinetics. J. Chem. Phys. 2015, 142, 124105. 10.1063/1.4916292. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Noé F.; Nuske F. A Variational Approach to Modeling Slow Processes in Stochastic Dynamical Systems. Multiscale Model. Simul. 2013, 11, 635–655. 10.1137/110858616. [DOI] [Google Scholar]
  44. McGibbon R. T.; Hernández C. X.; Harrigan M. P.; Kearnes S.; Sultan M. M.; Jastrzebski S.; Husic B. E.; Pande V. S.. Osprey: Hyperparameter Optimization for Machine Learning. J. Open Source Software 2016, 1.34. 10.21105/joss.00034 [DOI] [Google Scholar]
  45. Mittal S.; Shukla D. Predicting Optimal DEER Label Positions to Study Protein Conformational Heterogeneity. J. Phys. Chem. B 2017, 121, 9761–9770. 10.1021/acs.jpcb.7b04785. [DOI] [PubMed] [Google Scholar]
  46. Hansen F. Y.; Peters G. H.; Taub H.; Miskowiec A. Diffusion of Water and Selected Atoms in DMPC Lipid Bilayer Membranes. J. Chem. Phys. 2012, 137, 204910. 10.1063/1.4767568. [DOI] [PubMed] [Google Scholar]
  47. Kučerka N.; Tristram-Nagle S.; Nagle J. F. Structure of Fully Hydrated Fluid Phase Lipid Bilayers with Monounsaturated Chains. J. Membr. Biol. 2006, 208, 193–202. 10.1007/s00232-005-7006-8. [DOI] [PubMed] [Google Scholar]
  48. Zeuthen T. Water-Transporting Proteins. J. Membr. Biol. 2010, 234, 57–73. 10.1007/s00232-009-9216-y. [DOI] [PubMed] [Google Scholar]
  49. Case D.et al. Amber 14, 2014.
  50. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  51. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684. 10.1063/1.448118. [DOI] [Google Scholar]
  52. Darden T.; York D.; Pedersen L. Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089. 10.1063/1.464397. [DOI] [Google Scholar]
  53. Kräutler V.; Van Gunsteren W. F.; Hünenberger P. H. A Fast SHAKE Algorithm to Solve Distance Constraint Equations for Small Molecules in Molecular Dynamics Simulations. J. Comput. Chem. 2001, 22, 501–508. . [DOI] [Google Scholar]
  54. Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters From ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Huang X.; Bowman G. R.; Bacallado S.; Pande V. S. Rapid Equilibrium Sampling Initiated From Nonequilibrium Data. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 19765–19769. 10.1073/pnas.0909088106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Zimmerman M. I.; Hart K. M.; Sibbald C. A.; Frederick T. E.; Jimah J. R.; Knoverek C. R.; Tolia N. H.; Bowman G. R. Prediction of New Stabilizing Mutations Based on Mechanistic Insights from Markov State Models. ACS Cent. Sci. 2017, 3, 1311–1321. 10.1021/acscentsci.7b00465. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Zhou G.; Pantelopulos G. A.; Mukherjee S.; Voelz V. A. Bridging Microscopic and Macroscopic Mechanisms of p53-MDM2 Binding with Kinetic Network Models. Biophys. J. 2017, 113, 785–793. 10.1016/j.bpj.2017.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Paul F.; Wehmeyer C.; Abualrous E. T.; Wu H.; Crabtree M. D.; Schöneberg J.; Clarke J.; Freund C.; Weikl T. R.; Noé F.. PRotein-Peptide Association Kinetics Beyond the Seconds Timescale From Atomistic Simulations. Nat. Commun. 2017, 8. 10.1038/s41467-017-01163-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Hopkins C. W.; Le Grand S. L.; Walker R. C.; Roitberg A. E. Long-Time-Step Molecular Dynamics through Hydrogen Mass Repartitioning. J. Chem. Theory Comput. 2015, 11, 1864–1874. 10.1021/ct5010406. [DOI] [PubMed] [Google Scholar]
  60. Beauchamp K. A.; Bowman G. R.; Lane T. J.; Maibaum L.; Haque I. S.; Pande V. S. MSMBuilder2: Modeling Conformational Dynamics on the Picosecond to Millisecond Scale. J. Chem. Theory Comput. 2011, 7, 3412–3419. 10.1021/ct200463m. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Jeschke G. DEER Distance Measurements on Proteins. Annu. Rev. Phys. Chem. 2012, 63, 419–446. 10.1146/annurev-physchem-032511-143716. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc8b00330_si_001.pdf (24MB, pdf)
oc8b00330_si_002.pdb (314.2KB, pdb)
oc8b00330_si_003.pdb (314.2KB, pdb)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES