The dynamical transition of hydrated proteins also occurs in nonbiological macromolecules, such as colloidal microgels.
Abstract
A low-temperature dynamical transition has been reported in several proteins. We provide the first observation of a “protein-like” dynamical transition in nonbiological aqueous environments. To this aim, we exploit the popular colloidal system of poly-N-isopropylacrylamide (PNIPAM) microgels, extending their investigation to unprecedentedly high concentrations. Owing to the heterogeneous architecture of the microgels, water crystallization is avoided in concentrated samples, allowing us to monitor atomic dynamics at low temperatures. By elastic incoherent neutron scattering and molecular dynamics simulations, we find that a dynamical transition occurs at a temperature Td ~ 250 K, independently from PNIPAM mass fraction. However, the transition is smeared out on approaching dry conditions. The quantitative agreement between experiments and simulations provides evidence that the transition occurs simultaneously for PNIPAM and water dynamics. The similarity of these results with hydrated protein powders suggests that the dynamical transition is a generic feature in complex macromolecular systems, independently from their biological function.
INTRODUCTION
Hydrated protein powders are known to undergo a so-called dynamical transition, which is related to a sudden increase in temperature of the protein atomic mean-squared displacements (MSDs). This is related to the onset of anharmonic motions, which allow the protein to explore conformational substates corresponding to the structural configurations of functional relevance (1). Thus, the transition is accompanied by the activation of the protein functionality, making it the subject of intensive research for its high relevance in the biological context. On the other hand, the dynamical transition is distinct from the protein glass transition—the latter taking place at a lower temperature and involving other types of atomic motions (2). Since its first observation in myoglobin (3), the dynamical transition has been reported for several proteins with different structures (2, 4) and in more complex biomolecules such as lipid bilayers (5) and DNA strands (6). Although it appears to be closely related to biological functionality (7), some experiments have shown that the dynamical transition also occurs in unstructured proteins (8) and even in mixtures of unbound amino acids in aqueous environment (9). Conversely, in dry biomolecules, the transition is suppressed, thus highlighting the prominent role of hydration water.
Recent studies have shown that the dynamical transition takes place simultaneously for both protein and water dynamics (10, 11), thus lifting residual doubts on the close dynamical coupling between hydration water and biomolecules (12–14). Together, this evidence suggests the hypothesis that water plays a driving role in the dynamical transition, and thus suggest that this phenomenon may be ubiquitous in the context of hydrated systems. This also opens up the possibility of investigating nonbiological systems (for example, synthetic macromolecules) to shed light on the nature of the transition and to unveil the role of water. To this aim, it is particularly important to focus on complex macromolecular environments that could, on one hand, mimic the multifaceted potential energy landscape of proteins and, on the other hand, avoid water crystallization and allow the investigation of atomic dynamics at low temperatures. These conditions can be achieved by using the peculiar characteristics of microgel particles (15). Microgels are colloids made by cross-linked polymer networks with a heterogeneous structure composed of a dense core and a loose corona.
Poly-N-isopropylacrylamide (PNIPAM) microgels have so far been extensively studied around ambient temperature as a tunable model system for elucidating phase transitions and glassy behavior (16). We now extend their investigation to a yet unexplored region of the phase diagram, encompassing PNIPAM mass fractions (wt) in the range 43 ≤ c ≤ 95 wt % and a wide range of temperatures, namely, 150 ≲ T ≲ 290 K. By combining elastic incoherent neutron scattering (EINS) experiments with all-atom molecular dynamics (MD) simulations, we probe the internal dynamics of microgels at short time and length scales. We find that our suspensions do not crystallize for PNIPAM mass fractions ≳ 43 wt % at any temperature, in good agreement with calorimetric data on PNIPAM chains (17, 18). Most crucially, we find the occurrence of a “dynamical” transition at Td ≈ 250 K, akin to that observed in proteins. The value of the transition temperature does not depend on PNIPAM mass fraction, but the transition tends to disappear when approaching dry conditions. We directly compare the measured EINS intensities and their associated MSDs with those calculated in simulations, finding quantitative agreement between the two. Moreover, simulations show a strong coupling for both PNIPAM and water dynamics, for which a discontinuity in diffusional dynamics occurs at the same temperature. These results represent, to our knowledge, the first observation of a genuine dynamical transition in a nonbiological aqueous system, providing generality for the concept of a low-temperature dynamical transition in disordered macromolecules with internal degrees of freedom.
RESULTS
EINS experiments
EINS experiments were performed on PNIPAM microgels hydrated with D2O at five polymer mass fractions between 43 and 95% (19). In thermal neutron scattering, the incoherent cross section of hydrogen atoms is more than an order of magnitude larger than both coherent and incoherent cross sections of the other atomic species in our PNIPAM suspensions. Therefore, the incoherent signal of the hydrogen atoms in the PNIPAM network dominates the mostly coherent signal of deuterated water, providing selective access to the microscopic dynamics of the polymer matrix.
EINS data were collected at the backscattering spectrometer IN13 of the Institut Laue-Langevin (ILL; Grenoble, France). IN13 has an energy resolution ΔE = 8 μeV (full width at half maximum) and covers a momentum transfer interval from 0.3 to 4.5 Å−1, thus accessing motions faster than about 150 ps taking place in a spatial region between 1 and 20 Å. In this way, we essentially probe the internal dynamics of the microgel and its behavior on the atomic scale. This is important because, although our samples are glassy on the colloidal scale (20, 21), the volume fraction occupied by the microgels is still much lower than that of the polymer glass transition (17); thus, we can safely assume that the polymeric degrees of freedom are in equilibrium. Our results confirm this assumption, as they show a progressive and smooth behavior with PNIPAM mass fraction, are reproducible with respect to sample preparation, and are fully reversible in temperature.
The measured incoherent elastic intensities I(Q,0) as a function of temperature and momentum transfer Q are shown in Fig. 1A for selected samples with PNIPAM mass fractions of 43 and 60%. Data were recorded under thermal cycles of cooling (top panels) and heating (bottom panels) in a range of temperatures between 287 and 152 K. The temperature behavior is best observed in the Q integral of I(Q,0), as shown in Fig. 1B. Upon cooling, the integrated EINS intensity progressively increases until a sharp variation occurs at a characteristic “dynamical transition” temperature Td ~ 250 K, below which the intensity increase continues with a smaller but linear slope. Such a discontinuity is more pronounced at the lowest PNIPAM concentration and gradually disappears with decreasing water content. Upon heating back, the measured data fall on top of the corresponding ones at the same T, confirming the full reversibility of the process.
Fig. 1. EINS data.
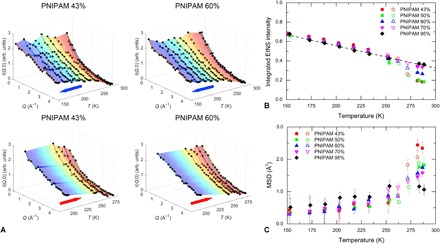
(A) Incoherent elastic intensities I(Q,0) measured on PNIPAM microgels in D2O with mass fraction concentrations of 43 and 60% as a function of temperature T. Top (bottom) panels report data recorded under cooling (heating). (B) Integral over Q of I(Q,0) as a function of T. The integrated EINS intensities are normalized to 1 for T → 0. (C) Temperature evolution of MSD as obtained using the double-well model (see the Supplementary Materials). In (B) and (C), measurements under cooling are presented with filled symbols, whereas those under heating are presented with open symbols.
At each temperature, the average atomic MSD can be calculated from the Q dependence of I(Q,0). To this end, the EINS data I(Q,0) were fitted with a double-well model, which captures the data behavior very well (see figs. S1 and S2). The resulting MSDs in Fig. 1C reflect the discontinuity observed in the Q-integrated intensity at Td ~ 250 K. Below Td, the linear temperature evolution of the MSD is typical of a harmonic solid. Conversely, the sudden slope increase above Td witnesses an enhanced mobility of the PNIPAM atoms, due to the onset of anharmonic motions and resulting in the corresponding elastic intensity drop.
It is worth noting that the observed discontinuity at Td might be attributed to an underlying crystallization process associated to the D2O. However, the measured I(Q,0) for pure D2O in the same temperature range shows defined crystalline peaks that do not appear in low-T PNIPAM suspensions (see fig. S3). This suggests that the elastic intensity drop of the PNIPAM network originates from a mechanism other than water crystallization.
MD simulations
To identify the microscopic mechanism responsible for the observed change in PNIPAM dynamics taking place at Td, we rely on all-atom MD simulations. To this aim, we designed a new microgel model (described in Materials and Methods and in the Supplementary Materials) and performed its numerical investigation at mass fractions of 40 and 60%. A snapshot of the in silico microgel is displayed in Fig. 2A. The PNIPAM network was built with a cross-linker/monomer ratio of 1:28, which, taking into account the inhomogeneous density of a PNIPAM particle, describes an inner region (for example, the core region) of the microgel. The number of water molecules per monomeric unit is smaller than the experimentally determined value of hydration molecules for PNIPAM microgels (22) for both concentrations. Thus, we can safely assume that all water molecules in the simulations are hydration water and not bulk water.
Fig. 2. MD simulation results for 40% mass fraction.
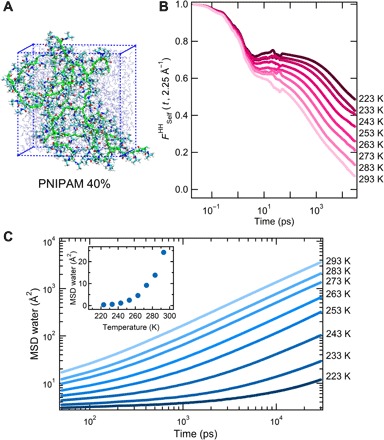
(A) Snapshot of the simulated PNIPAM microgel. Chain atoms are displayed in green to highlight the network structure. (B) SISF of PNIPAM hydrogen atoms calculated at Q = 2.25 Å−1 as a function of temperature. (C) Time evolution of the MSDs of water molecules. The inset shows the water MSD values at 150 ps as a function of T.
At each studied temperature, we monitored the dynamics of both microgel and water atoms separately. To characterize microgel dynamics, we calculated the self-intermediate scattering function (SISF) that probes the single-particle translational dynamics at a characteristic wave vector Q and time t. Figure 2B displays the SISFs calculated for the hydrogen atoms of PNIPAM 40 wt % at Q = 2.25Å− 1, that is, at the position of the first peak in the oxygen-oxygen structure factor of bulk water (23). PNIPAM internal dynamics exhibits a two-step behavior typical of glass-forming liquids: An initial fast relaxation is followed by a long-time, slow relaxation indicating structural rearrangement. At the lowest studied temperatures, the SISFs do not decay completely to zero, an indication that the system is becoming arrested on the considered time window. However, studies on longer time scales reveal that aging phenomena do not play a major role at the studied temperatures (see figs. S5 and S6). The long-time relaxation of the SISFs is well described by a stretched exponential as in standard glass formers, thus providing an estimate of the structural relaxation time τp. This is shown in Fig. 3A as a function of temperature in an Arrhenius plot. We find that τp obeys two distinct dynamical regimes, each being compatible with an Arrhenius dependence. The crossover temperature of about 250 K is strikingly similar to that found in EINS experiments. The activation energies are 28.4 ± 0.8 kJ mol−1 and 14.5 ± 0.5 kJ mol−1 for the high- and low-temperature regime, respectively.
Fig. 3. Water-PNIPAM coupling.
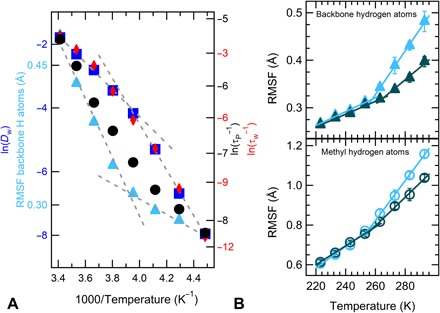
(A) Temperature dependence of water diffusion coefficient (squares); SISF relaxation times for PNIPAM hydrogen atoms (circles) and water oxygen atoms (diamonds); RMSF of backbone hydrogen atoms (triangles) calculated from MD simulations of PNIPAM 40 wt %. Dashed lines are guides to the eye. Note that data sets are represented on different scales on the y axis to improve visualization. (B) Temperature evolution of RMSF of the PNIPAM hydrogen atoms for 40 wt % (light blue) and for 60 wt % (dark green) averaged over 150 ps: methyl groups (circles) and backbone atoms (triangles).
To complement these results, we also investigated the hydration water dynamics by looking at the MSD of the oxygen atoms (see Fig. 2C). Similar to PNIPAM SISFs, we observe a slowing down of water dynamics with decreasing T. While at high T the MSD shows a diffusive behavior in the studied time interval, upon lowering the temperature the onset of an intermediate plateau is observed. This is a characteristic feature of glassy systems, indicating that atoms remain trapped in cages of nearest neighbors for a transient, before eventually diffusing away at long times. Water oxygen atoms retain a diffusive behavior at all studied T so that it is possible to estimate their self-diffusion coefficient Dw. This is also shown in the Arrhenius plot of Fig. 3A, where Dw is also found to follow two distinct regimes, each one compatible with an Arrhenius dependence, crossing again at a temperature of about 250 K. Furthermore, in the inset of Fig. 2C, the water MSD calculated at a time of 150 ps, matching the experimental time resolution, is shown as a function of T. A clear increase of the MSD is found above ~ 250 K. This strikingly matches the MSD behavior observed by EINS in our PNIPAM samples and is closely reminiscent of other experimental and simulation results on protein hydration water (10, 11, 24–26).
To make a closer connection to protein dynamics, we calculated the root mean square fluctuation (RMSF) of PNIPAM hydrogen atoms, which measures the fluctuations of the atom positions with respect to the averaged structure over a defined period of time. We monitored this quantity separately for hydrogen atoms of the methyl groups and those of the backbone. The evolution with temperature of the RMSF for both types of hydrogen atoms, averaged over the experimental resolution time, is shown in Fig. 3B. Again, a clear change is detected at a temperature of about 250 K for both types of atoms, with a stronger effect for the backbone hydrogen atoms. Such a change is observed for both studied mass fractions, suggesting that concentration does not play any role on the value of the crossover temperature, for both water and PNIPAM atoms, but it only smears out the variation, making the two regimes progressively similar to each other. These findings are in agreement with the concentration dependence of the experimental I(Q,0) (Fig. 1B). Figure 3A summarizes the MD results, showing that τp, the RMSF of PNIPAM backbone atoms, the self-diffusion constant of water, and the associated relaxation time τw all display a clear change at T ~ 250 K, a temperature strikingly similar to the one where the EINS data reveal a variation. Thus, simulations show that the dynamical properties of both PNIPAM and water are slaved to each other.
These results suggest to interpret the transition observed at Td as the analog of the protein dynamical transition for PNIPAM microgel suspensions. Several features are shared by protein and PNIPAM dynamical transition: (i) Td does not depend on the concentration, and the transition vanishes for dry conditions; (ii) the transition takes place at a temperature higher than that of the glass transition (2); (iii) the strong coupling between water and PNIPAM dynamics, as shown in Fig. 3A, is well established in hydrated proteins (10, 12–14).
It is then natural to ask whether water, through hydrogen bonding interactions with the involved macromolecule, drives the occurrence of this dynamical transition that appears ubiquitous in proteins and in PNIPAM microgels. To partially answer this question, we refer to recent simulation studies on confined water, which have provided a detailed characterization of slow dynamics in water (27). In particular, the study of hydrated lysozyme (28) has identified a new (long) time scale governing the behavior of confined water, which is characterized by two distinct Arrhenius regimes, in full analogy with the present findings for water confined in microgels. This behavior was interpreted as a strong-strong transition due to the coupling of hydration water with the fluctuations of the protein structure and found to occur in correspondence to the protein dynamical transition. The same correspondence is found in our simulations, suggesting that hydration water, through hydrogen bonding, plays a driving role in the dynamical transition. In support of this idea comes the fact that the behavior with concentration is similar for both PNIPAM microgels and hydrated proteins.
Comparison between MD simulations and EINS data
We now provide a direct comparison between experimental and numerical data. To this end, we have calculated the elastic intensity in simulations, as explained in the Supplementary Materials. The resulting I(Q,0) as a function of Q are shown in Fig. 4 for simulations (A) and experiments (B) at corresponding temperatures for the 40 wt % sample. The data are in very good qualitative agreement, also showing the presence of more pronounced peaks at comparable wave vectors. From the simulated trajectories, we can also calculate the MSD of the PNIPAM hydrogen atoms and compare them with those resulting from the fit of the experimental I(Q,0). The comparison is shown in Fig. 4C. The numerical MSDs are in striking quantitative agreement with the experimental ones, without need of any scaling factor.
Fig. 4. Quantitative comparison between experiments and simulations.
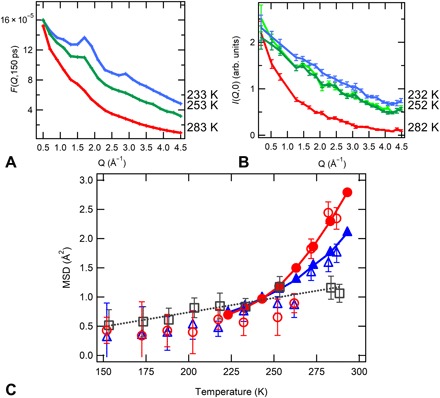
(A) Neutron spectra as a function of temperature, as calculated from the MD simulations of the PNIPAM microgel at 40%. The total intermediate scattering functions are displayed at a value of 150 ps for comparison with the experimental data. (B) EINS spectra measured on the sample with a PNIPAM concentration of 43% as a function of temperature. Data shown at 252 K compare the spectra measured under cooling (dark green) and heating (green). (C) Temperature dependence of experimental (open symbols) MSD for PNIPAM mass fractions of 43% (circles), 60% (triangles), and 95% (squares) and numerical (filled symbols) MSD, calculated at 150 ps for PNIPAM hydrogen atoms only, for PNIPAM mass fractions of 40% (circles) and 60% (squares). The dotted line is a guide to the eye, suggesting a linear behavior for the dry sample, for which the dynamical transition is suppressed.
DISCUSSION AND CONCLUSIONS
Here, we have reported evidence of the occurrence of a dynamical transition in concentrated PNIPAM microgel suspensions at low temperatures, akin to that observed in proteins. We have combined EINS measurements with atomistic MD simulations, based on a new model specifically developed to mimic the interior of a microgel network. While a detailed numerical representation of a whole microgel is currently unfeasible, our study is capable of resolving the intranetwork dynamics of PNIPAM atoms at the short time scales probed by EINS experiments. Thanks to the use of highly concentrated samples, we have extended the investigation of microgel suspensions to unprecedentedly low temperatures, avoiding water crystallization. Our findings are in agreement with calorimetric data for linear PNIPAM chains, showing that crystallization is absent for polymer mass fractions above ~ 50% (17, 18). These results open up the possibility of systematically investigating very high concentration and low-temperature microgel samples beyond current practice.
The dual colloidal/polymeric nature of microgels (29) bridges the properties of classical hard-sphere colloids and soft polymeric particles, allowing the presence of two distinct glass transitions on the colloidal and the polymeric scale, respectively. Both transitions depend on temperature, given the thermoresponsive character of PNIPAM, which is responsible for the so-called volume phase transition at TVPT ~ 305 K, from a swollen state of the microgel particles for T ≲ TVPT to a collapsed state above it. In the swollen regime, a colloidal glass transition takes place at a PNIPAM mass fraction of ~ 10 wt % (21). Although very few studies of microgels at high concentrations exist, we can expect the glass transition on the polymeric scale to be similar to that reported for PNIPAM chains, amounting to about 80 wt % at ambient temperature (17, 18). This means that, for the concentrations studied in this work, the microgel samples are macroscopically arrested in a glass-like state. A legitimate question thus concerns the reproducibility of our samples and their stability. A reliable preparation and measurement protocol allowed us to obtain homogeneous samples (see Materials and Methods), ensuring a complete reproducibility of the results and a smooth, progressive variation of the dynamical observables with microgel concentration at the investigated short time and length scales.
The study of microgels in water at low temperatures poses a numerical challenge in appropriately identifying a suitable water model that is able to realistically describe its peculiar behavior. Very accurate models, which are usually able to describe specific aspects, exist. In particular, TIP4P/ICE was devised to accurately reproduce the solid properties of water (30). We have chosen to work with this model because it reproduces water melting at ~ 270 K, much closer to reality than the ≈ 250 K predicted by the mostly adopted TIP4P/2005 (31). Thus, it should also be more realistic in describing supercooled water environments. Our results confirm this hypothesis, providing quantitative agreement with experiments in the investigated T range for the dynamical properties of PNIPAM atoms. It will be interesting to test other models under the same conditions, particularly TIP4P/2005, as well as to extend our studies at higher temperatures.
The similarity of the transition reported here for hydrated PNIPAM microgels with that commonly observed in proteins could be important to better understand the microscopic origin of such a transition. There are still controversial aspects in the literature, particularly concerning the role played by water. Two experimental studies have recently proposed an alternative picture for the dynamical transition, which would support the view that a transition may occur independently from the presence of water. Liu and coworkers (32) reported the observation of a dynamical transition also in dry deuterated proteins, mainly due to backbone heavy atoms. While the relevance of the traditional transition in hydrated proteins remains unaltered, the role of this “dry” transition is still uncertain. It might provide one of the contributions to flexibility involved in biological processes, although, in most proteins, full functionality is achieved in the hydrated state only. In addition, Mamontov and coworkers (33) investigated a simple polymeric system in nonaqueous environment, claiming to observe a dynamical transition similar to the protein one. However, in the latter study, the temperature of the transition significantly depends on the polymer concentration, differently from what was found here and for hydrated protein studies, suggesting that its microscopic nature could be different. On the other hand, the present results highlight the role of water-PNIPAM interplay in the dynamical transition, suggesting that all systems with structural complexity and water interactions similar to proteins should exhibit the same phenomenon. A natural and interesting extension of this work will be to investigate other macromolecular environments with different polymeric architectures, such as PNIPAM linear chains, to further ascertain both the occurrence and the microscopic nature of the dynamical transition.
We found that microgels are extremely efficient in confining water, because the lower limit of sample crystallization is close to 40% PNIPAM mass fraction, a value that exceeds the amount of water commonly found in other confining environments. The typical protein concentration where crystallization is avoided is about 70% in protein mass fraction (3, 10, 11, 34). Thus, our results suggest that stable samples with a majority of water can be studied down to very low temperatures, which could be of potential interest for the investigation of liquid-like water behavior in the so-called no man’s land region of the phase diagram (35–37). The efficient confinement role played by PNIPAM microgels is probably due to their intrinsic network disorder and to their inhomogeneous internal architecture. This further motivates the abovementioned investigations on PNIPAM linear chains to shed light on this aspect.
As a whole, our results strongly suggest that the dynamical transition is a generic feature of water hydrating complex macromolecular suspensions with biological and nonbiological implications. This work also puts forward colloidal PNIPAM microgels as excellent models for a deeper understanding of the functional relevance of the protein dynamical transition. In proteins, an energy landscape endowed with a large number of conformational states, each containing several tiers of substates, is considered of essential biological importance, as proteins could not function without such a reservoir of entropy (1). Likewise, the occurrence of a protein-like dynamical transition in PNIPAM-based systems might well be ascribed to a similarly rich amount of conformational substates. Future work will aim to elucidate this point and to provide generality to the present results.
MATERIALS AND METHODS
Sample preparation
Microgels were synthesized by precipitation polymerization at T = 343 K of N-isopropylacrylamide (NIPAM) in water (0.136 M) in the presence of N,N′-methylenebisacrylamide (BIS) (1.82 mM). The reaction was carried out in the presence of 7.80 mM SDS as surfactant and potassium persulfate (2.44 mM) as radical initiator. The reaction was carried out for 10 hours in nitrogen atmosphere. The obtained colloidal dispersion was purified by exhaustive dialysis against pure water, lyophilized, dispersed in D2O, lyophilized, and dispersed again in D2O to a final concentration of 10%. The obtained microgels were characterized by dynamic light scattering (Zetasizer Nano S, Malvern), and the hydrodynamic diameter was found to be 94 ± 3 nm at 293 K with a size polydispersity of 0.17 ± 0.01 nm.
EINS experiments and stability of the samples
EINS experiments were carried out on PNIPAM microgel suspensions with PNIPAM mass fractions of 43, 50, 60, 70, and 95% (dry sample). To single out the incoherent signal from PNIPAM hydrogen atoms, samples were prepared in D2O. Measurements were performed at the backscattering spectrometer IN13 of the ILL. PNIPAM samples were measured inside flat aluminum cells (3.0 cm × 4.0 cm), sealed with an In o-ring. The thickness of the cell was adjusted to achieve a transmission of about 88% for each sample. To obtain samples with the required PNIPAM concentration within the cell used at IN13, we started from the prepared microgel dispersion at 10%. We then proceeded by evaporation of the exceeding D2O in dry atmosphere using a desiccator under moderate vacuum (~ 10 mmHg). Once the final concentration was reached, cells were sealed and left to homogenize at room temperature for at least 4 days before analysis. The sample at 95% composition was prepared from film casting the PNIPAM dispersion at 10% up to dryness in a petri dish. The obtained transparent films were milled with an IKA MF 10.1. Cutting-grinding gave rise to a rough powder that was poured into an aluminum cell for neutron scattering. The weight of each sample was checked before and after the measurement without observing any appreciable variation. Moreover, after EINS measurements, the cells were opened and no changes in the sample morphology were detected, showing a homogeneous character and no compartmentalization effects. EINS data were acquired in the fixed-window elastic mode, thus collecting the intensity elastically scattered as a function of Q. Data were corrected to take into account incident flux, cell scattering, and self-shielding. The intensity of each sample was normalized with respect to a vanadium standard to account for the detector efficiency. Multiple scattering processes were neglected.
PNIPAM model and MD simulations
The model mimics, with an atomic detail, a cubic portion of PNIPAM microgel for polymer mass fractions of 40 and 60 wt %. The macromolecular network, modeled as isotropic, includes 12 atactic PNIPAM chains joined by six fourfold bisacrylamide cross-links (see fig. S4). Amide groups of PNIPAM residues are represented in the trans conformation. The three-dimensional percolation of the polymer scaffold is accounted for by the covalent connectivity between adjacent periodic images. The number average molecular weight of chains between cross-links, Mc, is 1584 g/mol, with a polydispersity index of 1.02 and an average degree of polymerization of 14. Taking into account the NIPAM/BIS feed ratio used in the synthesis and the nonuniform cross-link density of PNIPAM microgels, the model represents a region in proximity to the core-shell boundary of the particle. MD simulations of PNIPAM microgels were carried out at eight temperatures (from 293 to 223 K every 10 K). A trajectory interval of about 0.5 μs was calculated for each temperature. Additional details are given in the Supplementary Materials.
Supplementary Material
Acknowledgments
We acknowledge ILL for beam time and CINECA for computer time within the Italian SuperComputing Resource Allocation (ISCRA). Funding: L.T., M.B., E.C., and E.Z. acknowledge support from the European Research Council (ERC-CoG-2015, grant no. 681597 MIMIC). M.B., A.O., and E.Z. acknowledge support from the Italian Ministry of Education, University and Research (MIUR) through a Progetto di Rilevante Interesse Nazionale (PRIN) grant. Author contributions: A.O. and E.Z. supervised the research. E.B. and M.B. prepared the samples. M.Z., M.B., and E.Z. performed neutron scattering experiments with F.N. E.C. designed the network model. L.T., E.C., and E.Z. performed MD simulations. M.Z. and L.T. analyzed the data. M.Z., L.T., A.O., and E.Z. wrote the paper with inputs and suggestions from all authors. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/9/eaat5895/DC1
Section S1. EINS measurement and data analysis
Section S2. PNIPAM model development
Section S3. MD simulations procedure
Section S4. Reproducibility of numerical results
Section S5. Calculation of I(Q) from numerical simulations
Fig. S1. EINS data for PNIPAM 43 wt % sample.
Fig. S2. EINS data for PNIPAM 60 wt % sample.
Fig. S3. D2O contribution to EINS spectra.
Fig. S4. Schematic representation of the microgel network model.
Fig. S5. Aging effect on water dynamics.
Fig. S6. Aging effect on PNIPAM dynamics.
Fig. S7. I(Q,0) from numerical simulations.
Table S1. Thermal protocol followed during the EINS measurements.
REFERENCES AND NOTES
- 1.Fenimore P. W., Frauenfelder H., McMahon B. H., Young R. D., Bulk-solvent and hydration-shell fluctuations, similar to α- and β-fluctuations in glasses, control protein motions and functions. Proc. Natl. Acad. Sci. U.S.A. 101, 14408–14413 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Capaccioli S., Ngai K. L., Ancherbak S., Paciaroni A., Evidence of coexistence of change of caged dynamics at Tg and the dynamic transition at Td in solvated proteins. J. Phys. Chem. B 116, 1745–1757 (2012). [DOI] [PubMed] [Google Scholar]
- 3.Doster W., Cusack S., Petry W., Dynamical transition of myoglobin revealed by inelastic neutron scattering. Nature 337, 754–756 (1989). [DOI] [PubMed] [Google Scholar]
- 4.Doster W., The dynamical transition of proteins, concepts and misconceptions. Eur. Biophys. J. 37, 591–602 (2008). [DOI] [PubMed] [Google Scholar]
- 5.Peters J., Marion J., Natali F., Kats E. K., Bicout D. J., The dynamical transition of lipid multilamellar bilayers as a matter of cooperativity. J. Phys. Chem. B 121, 6860–6868 (2017). [DOI] [PubMed] [Google Scholar]
- 6.Cornicchi E., Capponi S., Marconi M., Onori G., Paciaroni A., Temperature dependence of fast fluctuations in single- and double-stranded DNA molecules: A neutron scattering investigation. Philos. Mag. 87, 509–515 (2007). [Google Scholar]
- 7.Rasmussen B. F., Stock A. M., Ringe D., Petsko G. A., Crystalline ribonuclease A loses function below the dynamical transition at 220 K. Nature 357, 423–424 (1992). [DOI] [PubMed] [Google Scholar]
- 8.He Y., Ku P. I., Knab J. R., Chen J. Y., Markelz A. G., Protein dynamical transition does not require protein structure. Phys. Rev. Lett. 101, 178103 (2008). [DOI] [PubMed] [Google Scholar]
- 9.Schirò G., Caronna C., Natali F., Koza M. M., Cupane A., The “protein dynamical transition” does not require the protein polypeptide chain. J. Phys. Chem. Lett. 2, 2275–2279 (2011). [Google Scholar]
- 10.Schirò G., Fichou Y., Gallat F. X., Wood K., Gabel F., Moulin M., Härtlein M., Heyden M., Colletier J. P., Orecchini A., Paciaroni A., Wuttke J., Tobias D. J., Weik M., Translational diffusion of hydration water correlates with functional motions in folded and intrinsically disordered proteins. Nat. Commun. 6, 6490 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wood K., Frölich A., Paciaroni A., Moulin M., Härtlein M., Zaccai G., Tobias D. J., Weik M., Coincidence of dynamical transitions in a soluble protein and its hydration water: Direct measurements by neutron scattering and MD simulations. J. Am. Chem. Soc. 130, 4586–4587 (2008). [DOI] [PubMed] [Google Scholar]
- 12.Frauenfelder H., Chen G., Berendzen J., Fenimore P. W., Jansson H., McMahon B. H., Stroe I. R., Swenson J., Young R. D., A unified model of protein dynamics. Proc. Natl. Acad. Sci. U.S.A. 106, 5129–5134 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lehnert U., Rèat V., Weik M., Zaccaï G., Pfister C., Thermal motions in bacteriorhodopsin at different hydration levels studied by neutron scattering: Correlation with kinetics and light-induced conformational changes. Biophys. J. 75, 1945–1952 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Paciaroni A., Cornicchi E., Marconi M., Orecchini A., Petrillo C., Haertlein M., Moulin M., Sacchetti F., Coupled relaxations at the protein-water interface in the picosecond time scale. J. R. Soc. Interface 6, S635–S640 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.A. Fernandez-Nieves, H. Wyss, J. Mattsson, D. A. Weitz, Microgel Suspensions: Fundamentals and Applications (John Wiley & Sons, 2011). [Google Scholar]
- 16.Yunker P., Chen K., Gratale M. D., Lohr M. A., Still T., Yodh A. G., Physics in ordered and disordered colloidal matter composed of poly (N-isopropylacrylamide) microgel particles. Rep. Prog. Phys. 77, 056601 (2014). [DOI] [PubMed] [Google Scholar]
- 17.Afroze F., Nies E., Berghmans H., Phase transitions in the system poly (N-isopropylacrylamide)/water and swelling behaviour of the corresponding networks. J. Mol. Struct. 554, 55–68 (2000). [Google Scholar]
- 18.Van Durme K., Van Assche G., Van Mele B., Kinetics of demixing and remixing in poly(N-isopropylacrylamide)/water studied by modulated temperature DSC. Macromolecules 37, 9596–9605 (2004). [Google Scholar]
- 19.E. Zaccarelli, M. Bertoldo, F. Natali, J. Ollivier, A. Orecchini, A. Paciaroni, M. Zanatta, Fast and Slow Dynamics in PNIPAM Microgels (Institut Laue-Langevin, 2015). doi: 10.5291/ILL-DATA.9-11-1736. [DOI]
- 20.Paloli D., Mohanty P. S., Crassous J. J., Zaccarelli E., Schurtenberger P., Fluid–solid transitions in soft-repulsive colloids. Soft Matter 9, 3000–3004 (2013). [Google Scholar]
- 21.Bischofberger I., Trappe V., New aspects in the phase behaviour of poly-N-isopropyl acrylamide: Systematic temperature dependent shrinking of PNiPAM assemblies well beyond the LCST. Sci. Rep. 5, 15520 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ono Y., Shikata T., Hydration and dynamic behavior of poly(N-isopropylacrylamide)s in aqueous solution: A sharp phase transition at the lower critical solution temperature. J. Am. Chem. Soc. 128, 10030–10031 (2006). [DOI] [PubMed] [Google Scholar]
- 23.Sciortino F., Gallo P., Tartaglia P., Chen S.-H., Supercooled water and the kinetic glass transition. Phys. Rev. E 54, 6331 (1996). [DOI] [PubMed] [Google Scholar]
- 24.Combet S., Zanotti J. M., Further evidence that interfacial water is the main “driving force” of protein dynamics: A neutron scattering study on perdeuterated C-phycocyanin. Phys. Chem. Chem. Phys. 14, 4927–4934 (2012). [DOI] [PubMed] [Google Scholar]
- 25.Chen S. H., Liu L., Fratini E., Baglioni P., Faraone A., Mamontov E., Observation of fragile-to-strong dynamic crossover in protein hydration water. Proc. Natl. Acad. Sci. U.S.A. 103, 9012–9016 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Doster W., Busch S., Gaspar A. M., Appavou M. S., Wuttke J., Scheer H., Dynamical transition of protein-hydration water. Phys. Rev. Lett. 104, 098101 (2010). [DOI] [PubMed] [Google Scholar]
- 27.Gallo P., Rovere M., Chen S.-H., Dynamic crossover in supercooled confined water: Understanding bulk properties through confinement. J. Phys. Chem. Lett. 1, 729–733 (2010). [Google Scholar]
- 28.Camisasca G., De Marzio M., Corradini D., Gallo P., Two structural relaxations in protein hydration water and their dynamic crossovers. J. Chem. Phys. 145, 044503 (2016). [DOI] [PubMed] [Google Scholar]
- 29.Lyon L. A., Fernandez-Nieves A., The polymer/colloid duality of microgel suspensions. Annu. Rev. Phys. Chem. 63, 25–43 (2012). [DOI] [PubMed] [Google Scholar]
- 30.Abascal J. L. F., Sanz E., García Fernández R., Vega C., A potential model for the study of ices and amorphous water: TIP4P/Ice. J. Chem. Phys. 122, 234511 (2005). [DOI] [PubMed] [Google Scholar]
- 31.Abascal J. L. F., Vega C., A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 123, 234505 (2005). [DOI] [PubMed] [Google Scholar]
- 32.Liu Z., Huang J., Tyagi M., O’Neill H., Zhang Q., Mamontov E., Jain N., Wang Y., Zhang J., Smith J. C., Hong L., Dynamical transition of collective motions in dry proteins. Phys. Rev. Lett. 119, 048101 (2017). [DOI] [PubMed] [Google Scholar]
- 33.Mamontov E., Sharma V. K., Borreguero J. M., Tyagi M., Protein-style dynamical transition in a non-biological polymer and a non-aqueous solvent. J. Phys. Chem. B 120, 3232–3239 (2016). [DOI] [PubMed] [Google Scholar]
- 34.Smith J., Kuczera K., Karplus M., Dynamics of myoglobin: Comparison of simulation results with neutron scattering spectra. Proc. Natl. Acad. Sci. U.S.A. 87, 1601–1605 (1990). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gallo P., Stanley H. E., Supercooled water reveals its secrets. Science 358, 1543–1544 (2017). [DOI] [PubMed] [Google Scholar]
- 36.Kim K. H., Späh A., Pathak H., Perakis F., Mariedahl D., Amann-Winkel K., Sellberg J. A., Lee J. H., Kim S., Park J., Nam K. H., Katayama T., Nilsson A., Maxima in the thermodynamic response and correlation functions of deeply supercooled water. Science 358, 1589–1593 (2017). [DOI] [PubMed] [Google Scholar]
- 37.Woutersen S., Ensing B., Hilbers M., Zhao Z., Angell C. A., A liquid-liquid transition in supercooled aqueous solution related to the HDA-LDA transition. Science 359, 1127–1131 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Paciaroni A., Cinelli S., Onori G., Effect of the environment on the protein dynamical transition: A neutron scattering study. Biophys. J. 83, 1157–1164 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Flory P. J., Mark J. E., Abe A., Random-coil configurations of vinyl polymer chains. The influence of stereoregularity on the average dimensions. J. Am. Chem. Soc. 88, 639–650 (1966). [Google Scholar]
- 40.S. Páll, M. J. Abraham, C. Kutzner, B. Hess, E. Lindahl, Tackling Exascale Software Challenges in Molecular Dynamics Simulations with GROMACS (Springer International Publishing, 2015), pp. 3–27. [Google Scholar]
- 41.Jorgensen W. L., Maxwell D. S., Tirado-Rives J., Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118, 11225–11236 (1996). [Google Scholar]
- 42.Siu S. W., Pluhackova K., Böckmann R. A., Optimization of the OPLS-AA force field for long hydrocarbons. J. Chem. Theory Comput. 8, 1459–1470 (2012). [DOI] [PubMed] [Google Scholar]
- 43.Goret G., Aoun B., Pellegrini E., MDANSE: An interactive analysis environment for molecular dynamics simulations. J. Chem. Inf. Model. 57, 1–5 (2017). [DOI] [PubMed] [Google Scholar]
- 44.Seeber M., Felline A., Raimondi F., Muff S., Friedman R., Rao F., Caflisch A., Fanelli F., Wordom: A user-friendly program for the analysis of molecular structures, trajectories, and free energy surfaces. J. Comput. Chem. 32, 1183–1194 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Humphrey W., Dalke A., Schulten K., VMD: Visual molecular dynamics. J. Mol. Graph. 14, 33–38 (1996). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/9/eaat5895/DC1
Section S1. EINS measurement and data analysis
Section S2. PNIPAM model development
Section S3. MD simulations procedure
Section S4. Reproducibility of numerical results
Section S5. Calculation of I(Q) from numerical simulations
Fig. S1. EINS data for PNIPAM 43 wt % sample.
Fig. S2. EINS data for PNIPAM 60 wt % sample.
Fig. S3. D2O contribution to EINS spectra.
Fig. S4. Schematic representation of the microgel network model.
Fig. S5. Aging effect on water dynamics.
Fig. S6. Aging effect on PNIPAM dynamics.
Fig. S7. I(Q,0) from numerical simulations.
Table S1. Thermal protocol followed during the EINS measurements.


